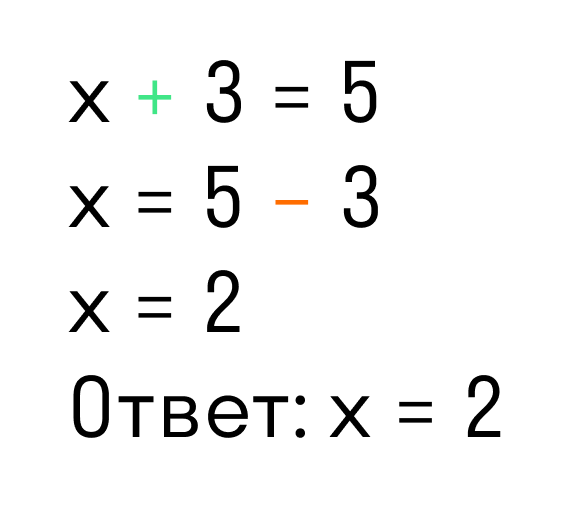Сформулируйте алгоритм решения линейного уравнения ax b 0 в случае когда а не равно 0 (3 видео)

Алгоритм решения линейного уравнения ax+b = 0 в случае, когда a≠0

ax = b, где х – переменная, a, b – любое число.

Если a ≠ 0, то Если а = 0

x = b/a ; b = 0, то b ≠ 0, то

х – любое; нет корней.

Алгоритма решения уравнений, сводящихся к линейным.

1-й шаг. Если выражения, стоящие в левой или правой части уравнения, содержат скобки, то раскрываем их по правилам.

2-й шаг. Переносим слагаемые с переменными в левую часть уравнения, а без переменных в правую.

3-й шаг. Приводим подобные слагаемые в обеих частях уравнения, приводя его к виду ax = b.

4-й шаг. Решаем получившееся линейное уравнение, равносильное исходному, в зависимости от значений коэффициентов a и b.

Содержание

Сформулируйте алгоритм решения линейного уравнения ax b 0 в случае когда а не равно 0
Как написать хороший ответ?
Алгоритм решения линейного уравнения ax b 0
Решение простых линейных уравнений
Понятие уравнения
Какие бывают виды уравнений
Как решать простые уравнения
Примеры линейных уравнений
💥 Видео

Видео:Линейное уравнение с одной переменной. 6 класс.Скачать

Сформулируйте алгоритм решения линейного уравнения ax b 0 в случае когда а не равно 0

Вопрос по алгебре:

Алгоритм решения линейного уравнения ax+b=0 в случае, когда a≠0

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
Использовать мат — это неуважительно по отношению к пользователям;
Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Алгебра.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Алгебра — раздел математики, который можно нестрого охарактеризовать как обобщение и расширение арифметики.

Видео:Алгебра 7 Линейное уравнение с одной переменнойСкачать

Алгоритм решения линейного уравнения ax b 0

‘);> //—>
Линейное уравнение ax + b = 0

Решение заключается в выполнении математической операции x = -b/a

Уравнение 10х + 5 = 0

Тогда x = -5 / 10 = -1/2 = -0.5

Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.

На этой странице представлен самый простой онлайн калькулятор решения любого линейного уравнения. С помощью этого калькулятора вы в один клик сможете быстро вычислить корень линейного уравнения.

Линейное уравнение с одной переменной.

Линейным уравнение с одной переменной х называют уравнение вида ах + b = 0. Где a и b — любые числа (коэффиценты).

Решить линейное уравнение – значит найти все значения переменной (неизвестной), при каждом из которых уравнение обращается в верное числовое равенство. Каждое такое значение переменной называют корнем уравнения.

Если а = 0 и b = 0, то есть уравнение имеет вид 0 * х + 0 = 0, то корнем уравнения является любое число (бесконечное множество корней).

Если а = 0 и b ≠ 0, то есть уравнение имеет вид 0 * х + b = 0, то ни одно число этому уравнению не удовлетворяет, уравнение не имеет корней.

Алгоритм решения линейного уравнения

ax + b = 0 в случае, когда а ≠ 0

2.Привести в левой части подобные слагаемые, в результате чего получится уравнение вида kx + m = 0, где k ≠ 0.

3.Преобразовать уравнение к виду kx = — m и записать его корень: x = -m : k.

Линейное уравнение

Если a ≠ 0, то Если а = 0

х – любое; нет корней.

Алгоритма решения уравнений, сводящихся к линейным.

1-й шаг. Если выражения, стоящие в левой или правой части уравнения, содержат скобки, то раскрываем их по правилам.

2-й шаг. Переносим слагаемые с переменными в левую часть уравнения, а без переменных в правую.

3-й шаг. Приводим подобные слагаемые в обеих частях уравнения, приводя его к виду ax = b.

4-й шаг. Решаем получившееся линейное уравнение, равносильное исходному, в зависимости от значений коэффициентов a и b.

Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Решение простых линейных уравнений

О чем эта статья:

Видео:Урок 7 ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙСкачать

Понятие уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.

Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.

Решить уравнение значит найти все возможные корни или убедиться, что их нет.

Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Видео:Неполные квадратные уравнения. Алгебра, 8 классСкачать

Какие бывают виды уравнений

Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.

Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.

Линейное уравнение выглядят так: ах + b = 0, где a и b — действительные числа. Вот, что поможет в решении:

если а ≠ 0 — уравнение имеет единственный корень: х = -b : а;

если а = 0 — уравнение корней не имеет;

если а и b равны нулю, то корнем уравнения является любое число.

Квадратное уравнение выглядит так: ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.

Числовой коэффициент — число, которое стоит при неизвестной переменной.

Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:

Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.

Видео:Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

Как решать простые уравнения

Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.

1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.

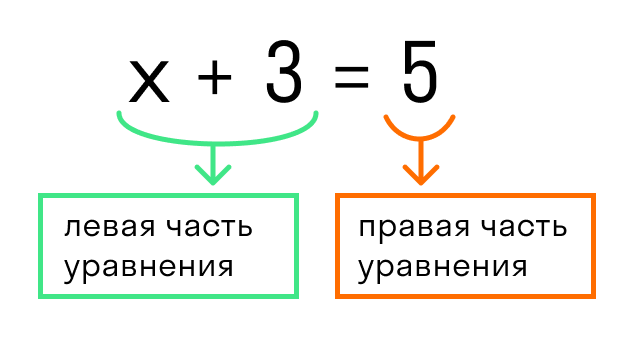
Для примера рассмотрим простейшее уравнение: x+3=5.

Начнем с того, что в каждом уравнении есть левая и правая часть.

Перенесем 3 из левой части в правую и меняем знак на противоположный.

Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.

Решим еще один пример: 6x = 5x + 10.

Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус.

Приведем подобные и завершим решение.

2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.

Применим правило при решении примера: 4x=8.

При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.

Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.

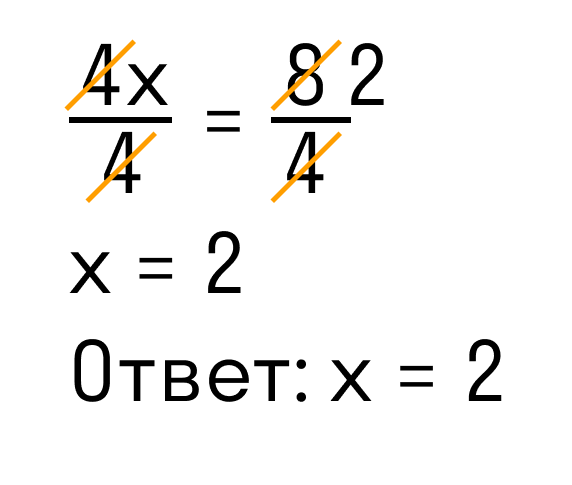
Разделим каждую часть на 4. Как это выглядит:

Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:

Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: -4x = 12

-4x = 12 | : (-4)
x = −3

Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.

Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.

Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.

Алгоритм решения простого линейного уравнения
Раскрываем скобки, если они есть. Группируем члены, которые содержат неизвестную переменную в одну часть уравнения, остальные члены — в другую. Приводим подобные члены в каждой части уравнения. Решаем уравнение, которое получилось: aх = b. Делим обе части на коэффициент при неизвестном.

Алгоритм решения простого линейного уравнения

Раскрываем скобки, если они есть.
Группируем члены, которые содержат неизвестную переменную в одну часть уравнения, остальные члены — в другую.
Приводим подобные члены в каждой части уравнения.
Решаем уравнение, которое получилось: aх = b. Делим обе части на коэффициент при неизвестном.

Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте алгоритм — храните его в телефоне, учебнике или на рабочем столе.

Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Примеры линейных уравнений

Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!

Пример 1. Как правильно решить уравнение: 6х + 1 = 19.

ЮПеренести 1 из левой части в правую со знаком минус.

Разделить обе части на множитель, стоящий перед переменной х, то есть на 6.

Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3(х − 4) + 2х − 1.

5х − 15 + 2 = 3х − 12 + 2х − 1

Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены. Не забываем при переносе из одной части уравнения в другую поменять знаки на противоположные у переносимых членов.

5х − 3х − 2х = −12 − 1 + 15 − 2

Приведем подобные члены.

Ответ: х — любое число.

Пример 3. Решить: 4х = 1/8.

Разделим обе части уравнения на множитель стоящий перед переменной х, то есть на 4.

Пример 4. Решить: 4(х + 2) = 6 − 7х.