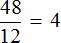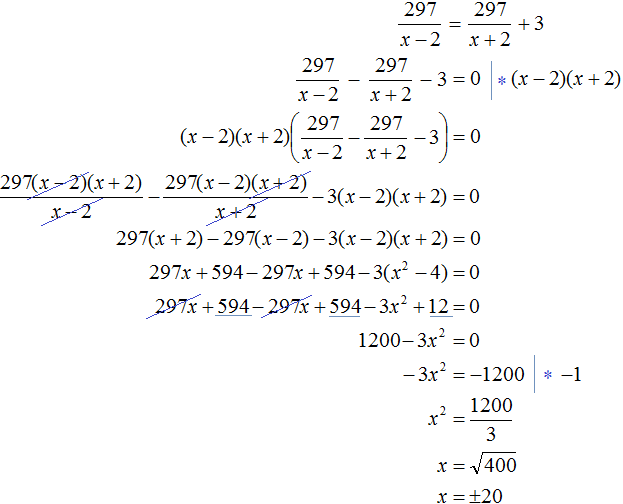Сборник задач на движение 7 класс алгебра с решением уравнением

Продолжаем изучать элементарные задачи по математике. Данный урок посвящен задачам на движение.

Видео:Задачи на движение | Математика TutorOnlineСкачать

Задача на нахождение расстояния/скорости/времени

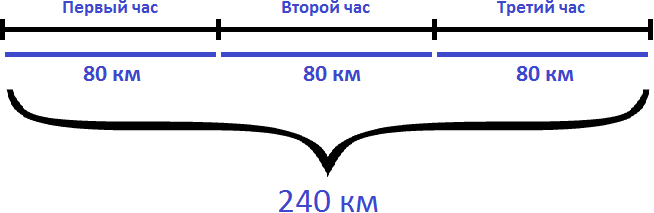
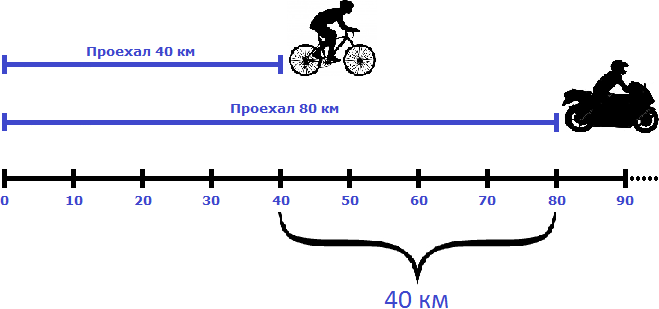
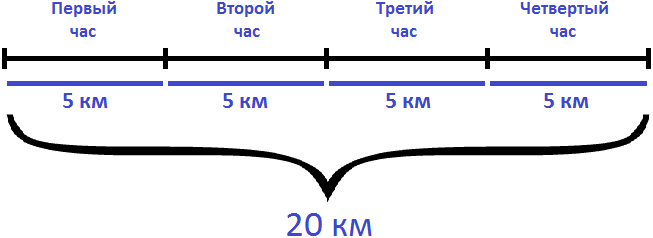
Задача 1. Автомобиль двигается со скоростью 80 км/ч. Сколько километров он проедет за 3 часа?

Решение

Если за один час автомобиль проезжает 80 километров, то за 3 часа он проедет в три раза больше. Чтобы найти расстояние, нужно скорость автомобиля (80км/ч) умножить на время движения (3ч)

Ответ: за 3 часа автомобиль проедет 240 километров.

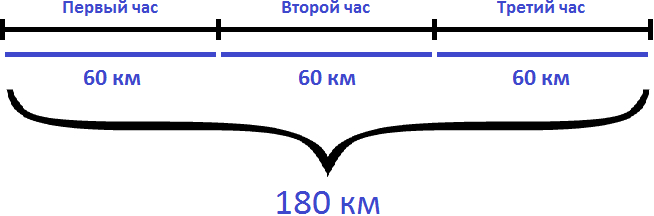
Задача 2. На автомобиле за 3 часа проехали 180 км с одной и той же скоростью. Чему равна скорость автомобиля?

Решение

Скорость — это расстояние, пройденное телом за единицу времени. Под единицей подразумевается 1 час, 1 минута или 1 секунда.

Если за 3 часа автомобиль проехал 180 километров с одной и той же скоростью, то разделив 180 км на 3 часа мы определим расстояние, которое проезжал автомобиль за один час. А это есть скорость движения. Чтобы определить скорость, нужно пройденное расстояние разделить на время движения:

Ответ: скорость автомобиля составляет 60 км/ч

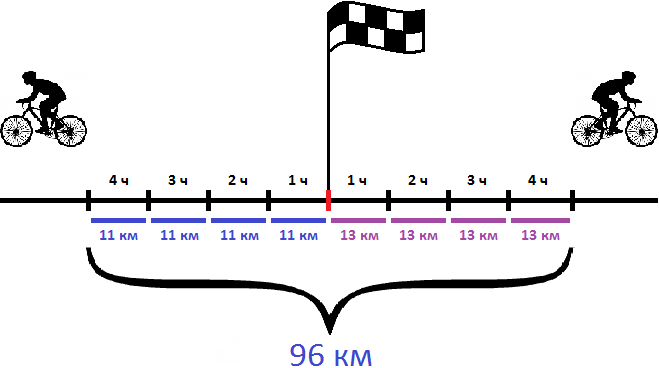
Задача 3. За 2 часа автомобиль проехал 96 км, а велосипедист за 6 часов проехал 72 км. Во сколько раз автомобиль двигался быстрее велосипедиста?

Решение

Определим скорость движения автомобиля. Для этого разделим пройденное им расстояние (96км) на время его движения (2ч)

Определим скорость движения велосипедиста. Для этого разделим пройденное им расстояние (72км) на время его движения (6ч)

Узнаем во сколько раз автомобиль двигался быстрее велосипедиста. Для этого найдем отношение 48 к 12

Ответ: автомобиль двигался быстрее велосипедиста в 4 раза.

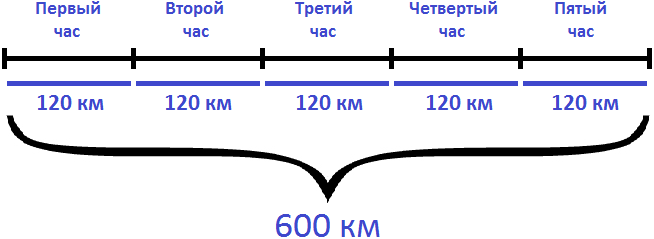
Задача 4. Вертолет преодолел расстояние в 600 км со скоростью 120 км/ч. Сколько времени он был в полете?

Решение

Если за 1 час вертолет преодолевал 120 километров, то узнав сколько таких 120 километров в 600 километрах, мы определим сколько времени он был в полете. Чтобы найти время, нужно пройденное расстояние разделить на скорость движения

600 : 120 = 5 часов

Ответ: вертолет был в пути 5 часов.

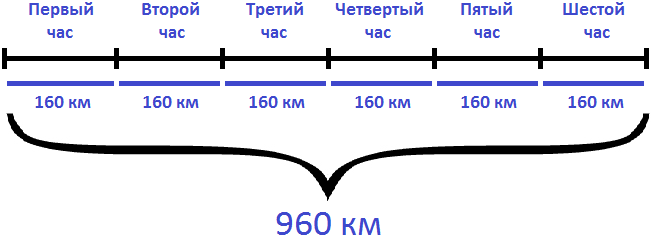
Задача 5. Вертолет летел 6 часов со скоростью 160 км/ч. Какое расстояние он преодолел за это время?

Решение

Если за 1 час вертолет преодолевал 160 км, то за 6 часов, он преодолел в шесть раз больше. Чтобы определить расстояние, нужно скорость движения умножить на время

Ответ: за 6 часов вертолет преодолел 960 км.

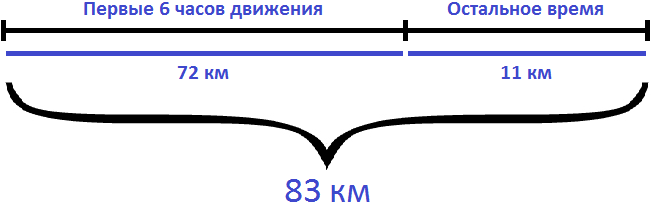
Задача 6. Расстояние от Перми до Казани, равное 723 км, автомобиль проехал за 13 часов. Первые 9 часов он ехал со скоростью 55 км/ч. Определить скорость автомобиля в оставшееся время.

Решение

Определим сколько километров автомобиль проехал за первые 9 часов. Для этого умножим скорость с которой он ехал первые девять часов (55км/ч) на 9

Определим сколько осталось проехать. Для этого вычтем из общего расстояния (723км) расстояние, пройденное за первые 9 часов движения

723 − 495 = 228 км

Эти 228 километров автомобиль проехал за оставшиеся 4 часа. Чтобы определить скорость автомобиля в оставшееся время, нужно 228 километров разделить на 4 часа:

Ответ: скорость автомобиля в оставшееся время составляла 57 км/ч

Видео:РЕШЕНИЕ ЗАДАЧ НА ДВИЖЕНИЕ С ПОМОЩЬЮ УРАВНЕНИЙ. Примеры | АЛГЕБРА 7 классСкачать

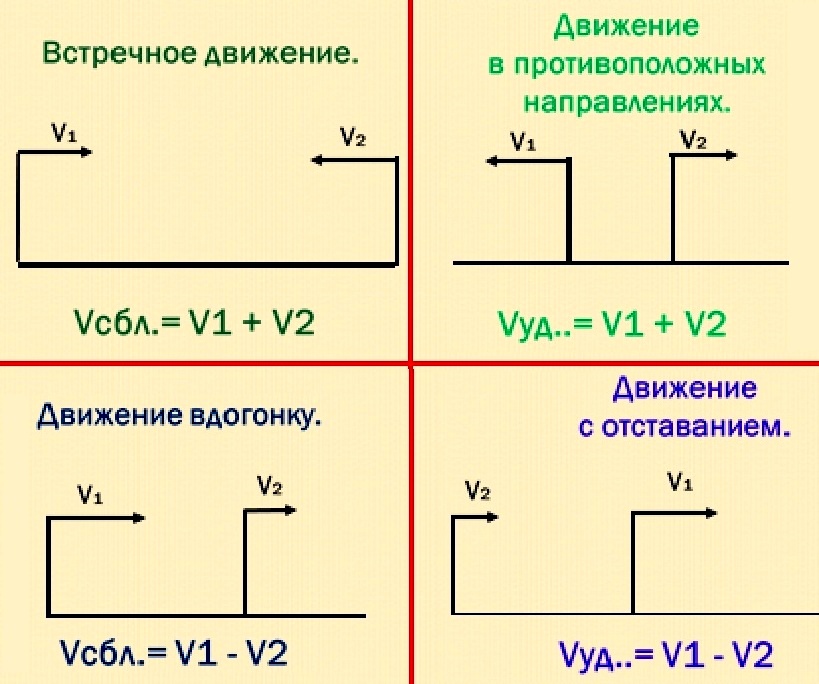
Скорость сближения

Скорость сближения — это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.

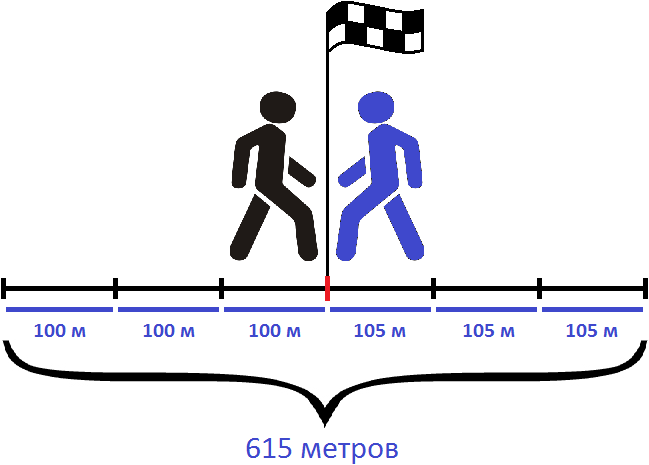
Например, если из двух пунктов навстречу друг другу отправятся два пешехода, причем скорость первого будет 100 м/м , а второго — 105 м/м , то скорость сближения будет составлять 100 + 105 , то есть 205 м/м . Это значит, что каждую минуту расстояние между пешеходами будет уменьшáться на 205 метров

Чтобы найти скорость сближения, нужно сложить скорости объектов.

Предположим, что пешеходы встретились через три минуты после начала движения. Зная, что они встретились через три минуты, мы можем узнать расстояние между двумя пунктами.

Каждую минуту пешеходы преодолевали расстояние равное двухсот пяти метрам. Через 3 минуты они встретились. Значит умножив скорость сближения на время движения, можно определить расстояние между двумя пунктами:

205 × 3 = 615 метров

Можно и по другому определить расстояние между пунктами. Для этого следует найти расстояние, которое прошел каждый пешеход до встречи.

Так, первый пешеход шел со скоростью 100 метров в минуту. Встреча состоялась через три минуты, значит за 3 минуты он прошел 100 × 3 метров

100 × 3 = 300 метров

А второй пешеход шел со скоростью 105 метров в минуту. За три минуты он прошел 105 × 3 метров

105 × 3 = 315 метров

Теперь можно сложить полученные результаты и таким образом определить расстояние между двумя пунктами:

300 м + 315 м = 615 м

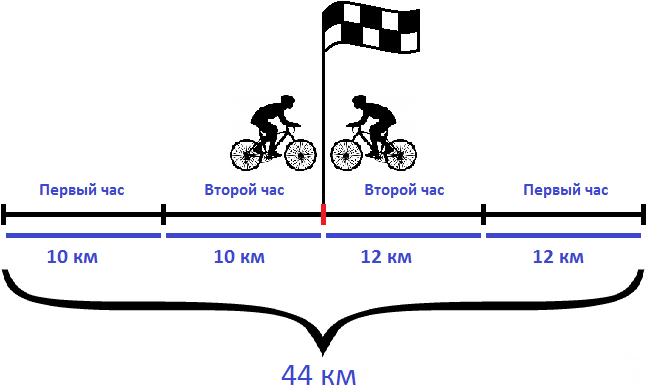
Задача 1. Из двух населенных пунктов навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 10 км/ч, а скорость второго — 12 км/ч. Через 2 часа они встретились. Определите расстояние между населенными пунктами

Решение

Найдем скорость сближения велосипедистов

10 км/ч + 12 км/ч = 22 км/ч

Определим расстояние между населенными пунктами. Для этого скорость сближения умножим на время движения

Решим эту задачу вторым способом. Для этого найдем расстояния, пройденные велосипедистами и сложим полученные результаты.

Найдем расстояние, пройденное первым велосипедистом:

Найдем расстояние, пройденное вторым велосипедистом:

Сложим полученные расстояния:

20 км + 24 км = 44 км

Ответ: расстояние между населенными пунктами составляет 44 км.

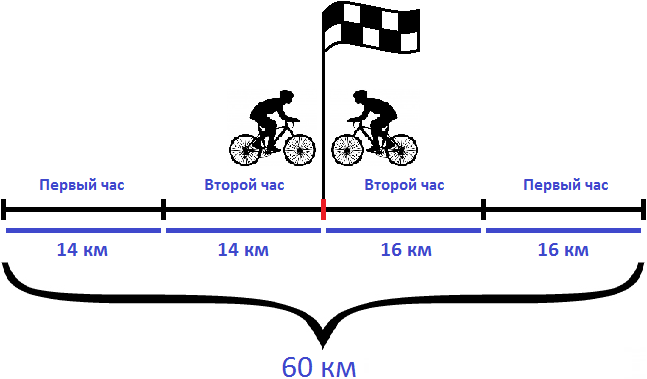
Задача 2. Из двух населенных пунктов, расстояние между которыми 60 км, навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 14 км/ч, а скорость второго — 16 км/ч. Через сколько часов они встретились?

Решение

Найдем скорость сближения велосипедистов:

14 км/ч + 16 км/ч = 30 км/ч

За один час расстояние между велосипедистами уменьшается на 30 километров. Чтобы определить через сколько часов они встретятся, нужно расстояние между населенными пунктами разделить на скорость сближения:

Значит велосипедисты встретились через два часа

Ответ: велосипедисты встретились через 2 часа.

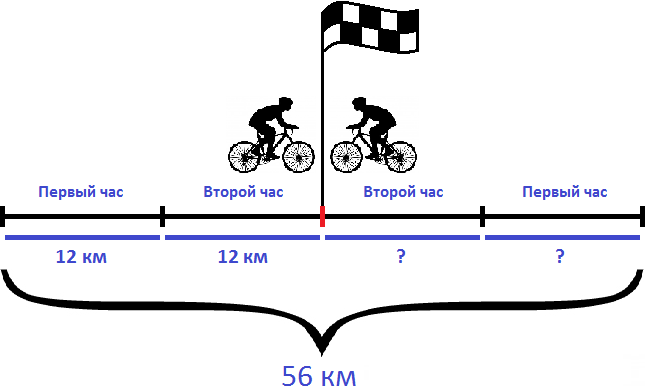
Задача 3. Из двух населенных пунктов, расстояние между которыми 56 км, навстречу друг другу выехали одновременно два велосипедиста. Через два часа они встретились. Первый велосипедист ехал со скоростью 12 км/ч. Определить скорость второго велосипедиста.

Решение

Определим расстояние пройденное первым велосипедистом. Как и второй велосипедист в пути он провел 2 часа. Умножив скорость первого велосипедиста на 2 часа, мы сможем узнать сколько километров он прошел до встречи

За два часа первый велосипедист прошел 24 км. За один час он прошел 24:2, то есть 12 км. Изобразим это графически

Вычтем из общего расстояния (56 км) расстояние, пройденное первым велосипедистом (24 км). Так мы определим сколько километров прошел второй велосипедист:

56 км − 24 км = 32 км

Второй велосипедист, как и первый провел в пути 2 часа. Если мы разделим пройденное им расстояние на 2 часа, то узнаем с какой скоростью он двигался:

Значит скорость второго велосипедиста составляет 16 км/ч.

Ответ: скорость второго велосипедиста составляет 16 км/ч.

Видео:Задачи на движение 7 классСкачать

Скорость удаления

Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.

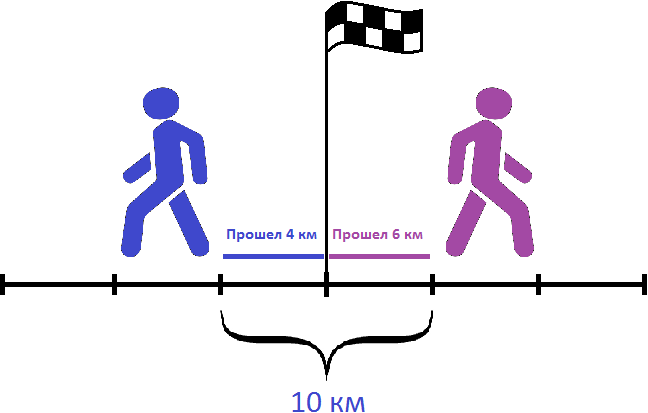
Например, если два пешехода отправятся из одного и того же пункта в противоположных направлениях, причем скорость первого будет 4 км/ч, а скорость второго 6 км/ч, то скорость удаления будет составлять 4+6, то есть 10 км/ч. Каждый час расстояние между двумя пешеходами будет увеличиться на 10 километров.

Чтобы найти скорость удаления, нужно сложить скорости объектов.

Так, за первый час расстояние между пешеходами будет составлять 10 километров. На следующем рисунке можно увидеть, как это происходит

Видно, что первый пешеход прошел свои 4 километра за первый час. Второй пешеход также прошел свои 6 километров за первый час. Итого за первый час расстояние между ними стало 4+6, то есть 10 километров.

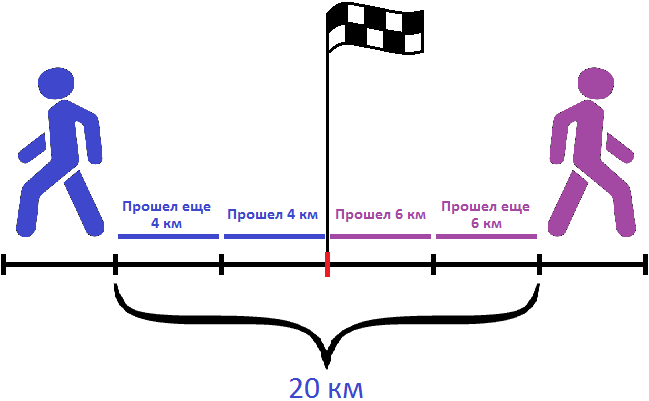
Через два часа расстояние между пешеходами будет составлять 10×2, то есть 20 километров. На следующем рисунке можно увидеть, как это происходит:

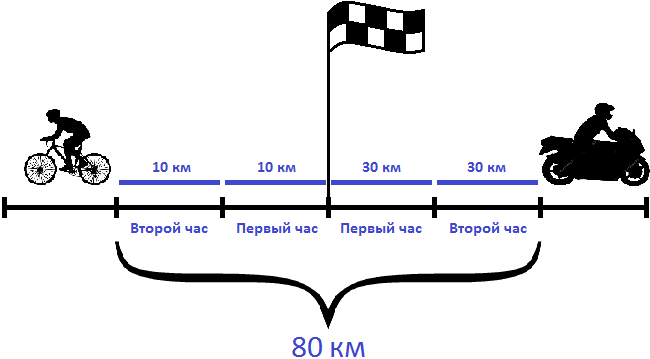
Задача 1. От одной станции отправились одновременно в противоположных направлениях товарный поезд и пассажирский экспресс. Скорость товарного поезда составляла 40 км/ч, скорость экспресса 180 км/ч. Какое расстояние будет между этими поездами через 2 часа?

Решение

Определим скорость удаления поездов. Для этого сложим их скорости:

40 + 180 = 220 км/ч

Получили скорость удаления поездов равную 220 км/ч. Данная скорость показывает, что за час расстояние между поездами будет увеличиваться на 220 километров. Чтобы узнать какое расстояние будет между поездами через два часа, нужно 220 умножить на 2

Ответ: через 2 часа расстояние будет между поездами будет 440 километров.

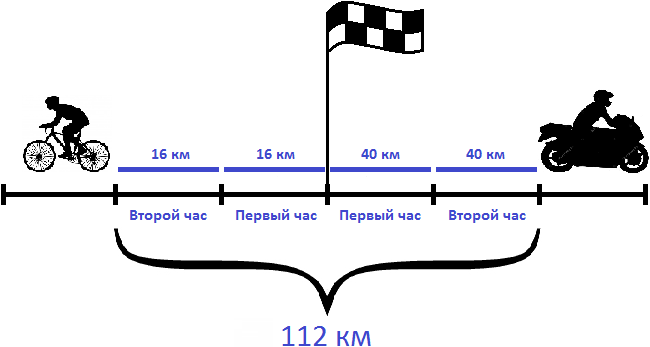
Задача 2. Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Скорость велосипедиста 16 км/ч, а скорость мотоциклиста — 40 км/ч. Какое расстояние будет между велосипедистом и мотоциклистом через 2 часа?

Решение

Определим скорость удаления велосипедиста и мотоциклиста. Для этого сложим их скорости:

16 км/ч + 40 км/ч = 56 км/ч

Определим расстояние, которое будет между велосипедистом и мотоциклистом через 2 часа. Для этого скорость удаления (56км/ч) умножим на 2 часа

Ответ: через 2 часа расстояние между велосипедистом и мотоциклистом будет 112 км.

Задача 3. Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Скорость велосипедиста 10 км/ч, а скорость мотоциклиста — 30 км/ч. Через сколько часов расстояние между ними будет 80 км?

Решение

Определим скорость удаления велосипедиста и мотоциклиста. Для этого сложим их скорости:

10 км/ч + 30 км/ч = 40 км/ч

За один час расстояние между велосипедистом и мотоциклистом увеличивается на 40 километров. Чтобы узнать через сколько часов расстояние между ними будет 80 км, нужно определить сколько раз 80 км содержит по 40 км

Ответ: через 2 часа после начала движения, между велосипедистом и мотоциклистом будет 80 километров.

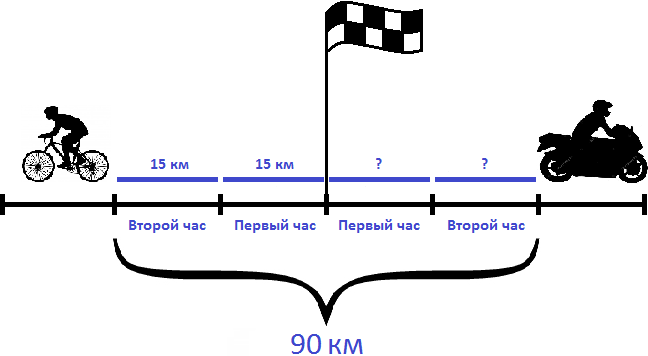
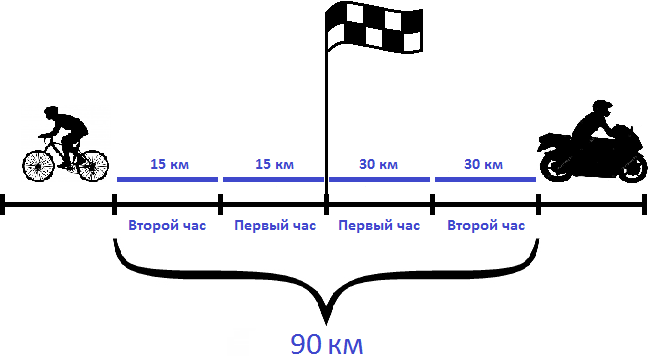
Задача 4. Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Через 2 часа расстояние между ними было 90 км. Скорость велосипедиста составляла 15 км/ч. Определить скорость мотоциклиста

Решение

Определим расстояние, пройденное велосипедистом за 2 часа. Для этого умножим его скорость (15 км/ч) на 2 часа

На рисунке видно, что велосипедист прошел по 15 километров в каждом часе. Итого за два часа он прошел 30 километров.

Вычтем из общего расстояния (90 км) расстояние, пройденное велосипедистом (30 км). Так мы определим сколько километров прошел мотоциклист:

90 км − 30 км = 60 км

Мотоциклист за два часа прошел 60 километров. Если мы разделим пройденное им расстояние на 2 часа, то узнаем с какой скоростью он двигался:

Значит скорость мотоциклиста составляла 30 км/ч.

Ответ: скорость мотоциклиста составляла 30 км/ч.

Видео:Решение задач с помощью уравнений. Алгебра 7 классСкачать

Задача на движение объектов в одном направлении

В предыдущей теме мы рассматривали задачи в которых объекты (люди, машины, лодки) двигались либо навстречу другу другу либо в противоположных направлениях. При этом мы находили различные расстояния, которые изменялись между объектами в течении определенного времени. Эти расстояния были либо скоростями сближения либо скоростями удаления.

В первом случае мы находили скорость сближения — в ситуации, когда два объекта двигались навстречу друг другу. За единицу времени расстояние между объектами уменьшалось на определенное расстояние

Во втором случае мы находили скорость удаления — в ситуации, когда два объекта двигались в противоположных направлениях. За единицу времени расстояние между объектами увеличивалось на определенное расстояние

Но объекты также могут двигаться в одном направлении, причем с различной скоростью. Например, из одного пункта одновременно могут выехать велосипедист и мотоциклист, причем скорость велосипедиста может составлять 20 километров в час, а скорость мотоциклиста — 40 километров в час

На рисунке видно, что мотоциклист впереди велосипедиста на двадцать километров. Связано это с тем, что в час он преодолевает на 20 километров больше, чем велосипедист. Поэтому каждый час расстояние между велосипедистом и мотоциклистом будет увеличиваться на двадцать километров.

В данном случае 20 км/ч являются скоростью удаления мотоциклиста от велосипедиста.

Через два часа расстояние, пройденное велосипедистом будет составлять 40 км. Мотоциклист же проедет 80 км, отдалившись от велосипедиста еще на двадцать километров — итого расстояние между ними составит 40 километров

Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.

В приведенном выше примере, скорость удаления составляет 20 км/ч. Её можно найти путем вычитания скорости велосипедиста из скорости мотоциклиста. Скорость велосипедиста составляла 20 км/ч, а скорость мотоциклиста — 40 км/ч. Скорость мотоциклиста больше, поэтому из 40 вычитаем 20

40 км/ч − 20 км/ч = 20 км/ч

Задача 1. Из города в одном и том же направлении выехали легковой автомобиль и автобус. Скорость автомобиля 120 км/ч, а скорость автобуса 80 км/ч. Какое расстояние будет между ними через 1 час? 2 часа?

Решение

Найдем скорость удаления. Для этого из большей скорости вычтем меньшую

120 км/ч − 80 км/ч = 40 км/ч

Каждый час легковой автомобиль отдаляется от автобуса на 40 километров. За один час расстояние между автомобилем и автобусом будет 40 км. За 2 часа в два раза больше:

Ответ: через один час расстояние между автомобилем и автобусом будет 40 км, через два часа — 80 км.

Рассмотрим ситуацию в которой объекты начали свое движение из разных пунктов, но в одном направлении.

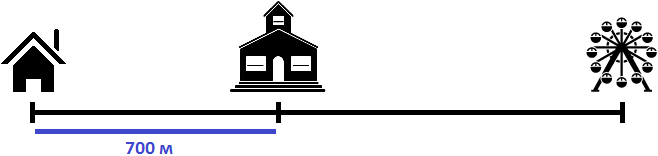
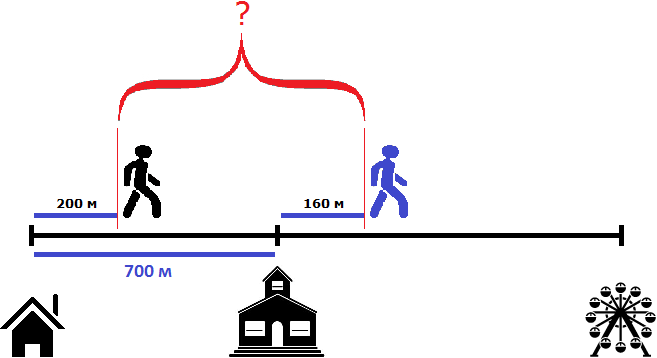
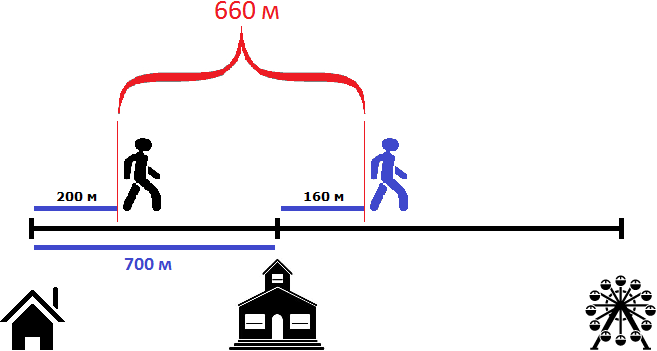
Пусть имеется дом, школа и аттракцион. От дома до школы 700 метров

Два пешехода отправились в аттракцион в одно и то же время. Причем первый пешеход отправился в аттракцион от дома со скоростью 100 метров в минуту, а второй пешеход отправился в аттракцион от школы со скоростью 80 метров в минуту. Какое расстояние будет между пешеходами через 2 минуты? Через сколько минут после начала движения первый пешеход догонит второго?

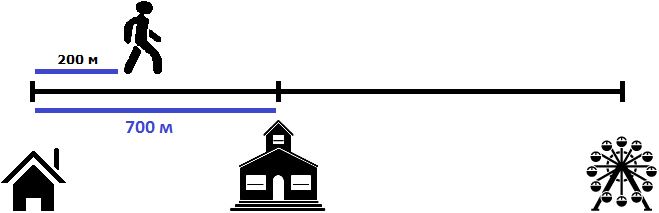
Ответим на первый вопрос задачи — какое расстояние будет между пешеходами через 2 минуты?

Определим расстояние, пройденное первым пешеходом за 2 минуты. Он двигался со скоростью 100 метров в минуту. За две минуты он пройдет в два раза больше, то есть 200 метров

100 × 2 = 200 метров

Определим расстояние, пройденное вторым пешеходом за 2 минуты. Он двигался со скоростью 80 метров в минуту. За две минуты он пройдет в два раза больше, то есть 160 метров

80 × 2 = 160 метров

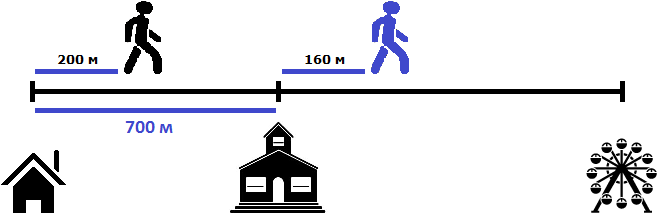
Теперь нужно найти расстояние между пешеходами

Чтобы найти расстояние между пешеходами, можно к расстоянию от дома до школы (700м) прибавить расстояние, пройденное вторым пешеходом (160м) и из полученного результата вычесть расстояние, пройденное первым пешеходом (200м)

700 м + 160 м = 860 м

860 м − 200 м = 660 м

Либо из расстояния от дома до школы (700м) вычесть расстояние, пройденное первым пешеходом (200м), и к полученному результату прибавить расстояние, пройденное вторым пешеходом (160м)

700 м − 200 м = 500 м

500 м + 160 м = 660 м

Таким образом, через две минуты расстояние между пешеходами будет составлять 660 метров

Попробуем ответить на следующий вопрос задачи: через сколько минут после начала движения первый пешеход догонит второго?

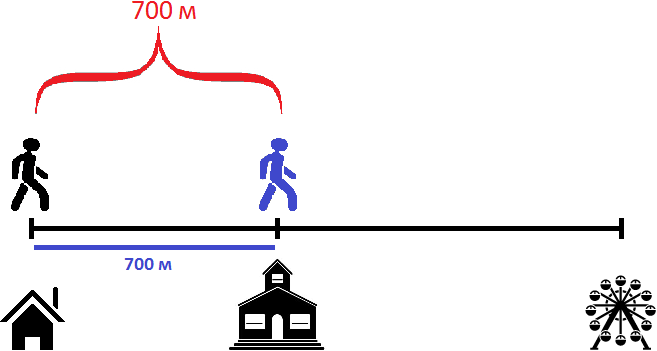
Давайте посмотрим какой была ситуация в самом начале пути — когда пешеходы еще не начали своё движение

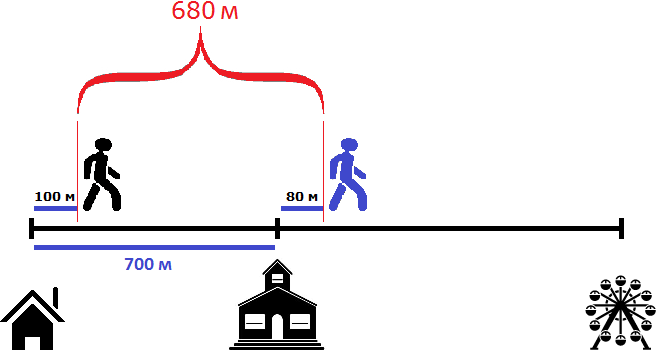
Как видно на рисунке, расстояние между пешеходами в начале пути составляло 700 метров. Но уже через минуту после начала движения расстояние между ними будет составлять 680 метров, поскольку первый пешеход двигается на 20 метров быстрее второго:

100 м × 1 = 100 м

700 м + 80 м − 100 м = 780 м − 100 м = 680 м

Через две минуты после начала движения, расстояние уменьшится еще на 20 метров и будет составлять 660 метров. Это был наш ответ на первый вопрос задачи:

100 м × 2 = 200 м

700 м + 160 м − 200м = 860 м − 200 м = 660 м

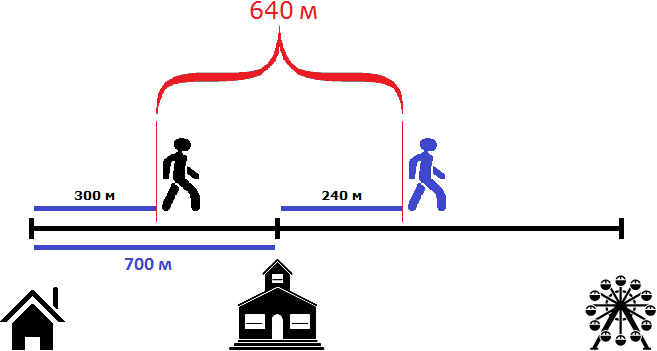
Через три минуты расстояние уменьшится еще на 20 метров и будет уже составлять 640 метров:

100 м × 3 = 300 м

700 м + 240 м − 300м = 940 м − 300 м = 640 м

Мы видим, что с каждой минутой первый пешеход будет приближáться ко второму на 20 метров, и в конце концов догонит его. Можно сказать, что скорость равная двадцати метрам в минуту является скоростью сближения пешеходов. Правила нахождения скорости сближения и удаления при движении в одном направлении идентичны.

Чтобы найти скорость сближения при движении в одном направлении, нужно из большей скорости вычесть меньшую.

А раз изначальные 700 метров с каждой минутой уменьшаются на одинаковые 20 метров, то мы можем узнать сколько раз 700 метров содержат по 20 метров, тем самым определяя через сколько минут первый пешеход догонит второго

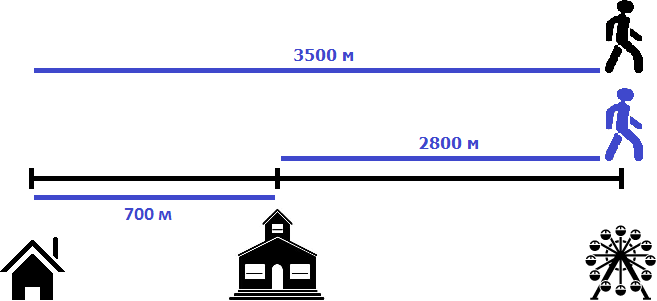
Значит через 35 минут после начала движения первый пешеход догонит второго. Для интереса узнаем сколько метров прошел к этому времени каждый пешеход. Первый двигался со скоростью 100 метров в минуту. За 35 минут он прошел в 35 раз больше

100 × 35 = 3500 м

Второй шел со скоростью 80 метров в минуту. За 35 минут он прошел в 35 раз больше

Первый прошел 3500 метров, а второй 2800 метров. Первый прошел на 700 метров больше, поскольку он шел от дома. Если вычесть эти 700 метров из 3500, то мы получим 2800 м

Рассмотрим ситуацию в которой объекты движутся в одном направлении, но один из объектов начал своё движение раньше другого.

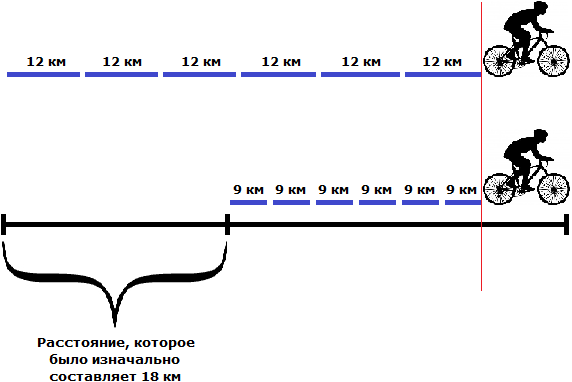
Пусть имеется дом и школа. Первый пешеход отправился в школу со скоростью 80 метров в минуту. Через 5 минут вслед за ним в школу отправился второй пешеход со скоростью 100 метров в минуту. Через сколько минут второй пешеход догонит первого?

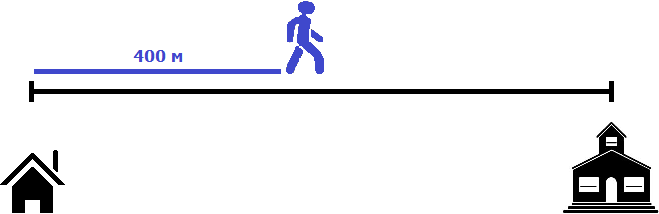
Второй пешеход начал свое движение через 5 минут. К этому времени первый пешеход уже отдалился от него на какое-то расстояние. Найдём это расстояние. Для этого умножим его скорость (80 м/м) на 5 минут

80 × 5 = 400 метров

Первый пешеход отдалился от второго на 400 метров. Поэтому в момент, когда второй пешеход начнет свое движение, между ними будут эти самые 400 метров.

Но второй пешеход двигается со скоростью 100 метров в минуту. То есть двигается на 20 метров быстрее первого пешехода, а значит с каждой минутой расстояние между ними будет уменьшáться на 20 метров. Наша задача узнать через сколько минут это произойдет.

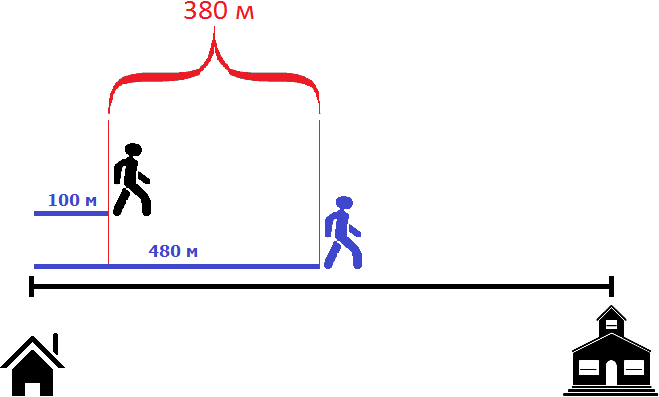
Например, уже через минуту расстояние между пешеходами будет составлять 380 метров. Первый пешеход к своим 400 метрам пройдет еще 80 метров, а второй пройдет 100 метров

Принцип здесь такой-же, как и в предыдущей задаче. Расстояние между пешеходами в момент движения второго пешехода необходимо разделить на скорость сближения пешеходов. Скорость сближения в данном случае равна двадцати метрам. Поэтому, чтобы определить через сколько минут второй пешеход догонит первого, нужно 400 метров разделить на 20

Значит через 20 минут второй пешеход догонит первого.

Задача 2. Из двух сел, расстояние между которыми 40 км, одновременно в одном направлении выехали автобус и велосипедист. Скорость велосипедиста 15 км/ч, а скорость автобуса 35 км/ч. Через сколько часов автобус догонит велосипедиста?

Решение

Найдем скорость сближения

35 км/ч − 15 км/ч = 20 км/ч

Определим через часов автобус догонит велосипедиста

Ответ: автобус догонит велосипедиста через 2 часа.

Видео:АЛГЕБРА 7 класс : Решение задач с помощью уравнений | ВидеоурокСкачать

Задача на движение по реке

Суда двигаются по реке с различной скоростью. При этом они могут двигаться, как по течению реки, так и против течения. В зависимости от того, как они двигаются (по или против течения), скорость будет меняться.

Предположим, что скорость реки составляет 3 км/ч. Если спустить лодку на реку, то река унесет лодку со скоростью 3 км/ч.

Если спустить лодку на стоячую воду, в которой отсутствует течение, то и лодка будет стоять. Скорость движения лодки в этом случае будет равна нулю.

Если лодка плывет по стоячей воде, в которой отсутствует течение, то говорят, что лодка плывет с собственной скоростью.

Например, если моторная лодка плывет по стоячей воде со скоростью 40 км/ч, то говорят что собственная скорость моторной лодки составляет 40 км/ч.

Как определить скорость судна?

Если судно плывет по течению реки, то к собственной скорости судна нужно прибавить скорость течения реки.

Например, если моторная лодка плывет со скоростью 30 км/ч по течению реки, и скорость течения реки составляет 2 км/ч, то к собственной скорости моторной лодки (30 км/ч) необходимо прибавить скорость течения реки (2 км/ч)

30 км/ч + 2 км/ч = 32 км/ч

Течение реки можно сказать помогает моторной лодке дополнительной скоростью равной двум километрам в час.

Если судно плывет против течения реки, то из собственной скорости судна нужно вычесть скорость течения реки.

Например, если моторная лодка плывет со скоростью 30 км/ч против течения реки, и скорость течения реки составляет 2 км/ч, то из собственной скорости моторной лодки (30 км/ч) необходимо вычесть скорость течения реки (2 км/ч)

30 км/ч − 2 км/ч = 28 км/ч

Течение реки в этом случае препятствует моторной лодке свободно двигаться вперед, снижая её скорость на два километра в час.

Задача 1. Скорость катера 40 км/ч, а скорость течения реки 3 км/ч. С какой скоростью катер будет двигаться по течению реки? Против течения реки?

Ответ:

Если катер будет двигаться по течения реки, то скорость его движения составит 40 + 3, то есть 43 км/ч.

Если катер будет двигаться против течения реки, то скорость его движения составит 40 − 3, то есть 37 км/ч.

Задача 2. Скорость теплохода в стоячей воде — 23 км/ч. Скорость течения реки — 3 км/ч. Какой путь пройдет теплоход за 3 часа по течению реки? Против течения?

Решение

Собственная скорость теплохода составляет 23 км/ч. Если теплоход будет двигаться по течению реки, то скорость его движения составит 23 + 3, то есть 26 км/ч. За три часа он пройдет в три раза больше

Если теплоход будет двигаться против течения реки, то скорость его движения составит 23 − 3, то есть 20 км/ч. За три часа он пройдет в три раза больше

Задача 3. Расстояние от пункта А до пункта B лодка преодолела за 3 часа 20 минут, а расстояние от пункта B до А — за 2 часа 50 минут. В каком направлении течет река: от А к В или от В к А, если известно, что скорость яхты не менялась?

Решение

Скорость яхты не менялась. Узнаем на какой путь она затратила больше времени: на путь от А до В или на путь от В до А. Тот путь, который затратил больше времени будет тем путем, течение реки которого шло против яхты

3 часа 20 минут больше, чем 2 часа 50 минут. Это значит, что течение реки снизило скорость яхты и это отразилось на времени пути. 3 часа 20 минут это время, затраченное на путь от от А до В. Значит река течет от пункта B к пункту А

Задача 4. За какое время при движении против течения реки
теплоход пройдет 204 км, если его собственная скорость
15 км/ч, а скорость течения в 5 раз меньше собственной
скорости теплохода?

Решение

Требуется найти время за которое теплоход пройдет 204 километра против течения реки. Собственная скорость теплохода составляет 15 км/ч. Двигается он против течения реки, поэтому нужно определить его скорость при таком движении.

Чтобы определить скорость против течения реки, нужно из собственной скорости теплохода (15 км/ч) вычесть скорость движения реки. В условии сказано, что скорость течения реки в 5 раз меньше собственной скорости теплохода, поэтому сначала определим скорость течения реки. Для этого уменьшим 15 км/ч в пять раз

Скорость течения реки составляет 3 км/ч. Вычтем эту скорость из скорости движения теплохода

15 км/ч − 3 км/ч = 12 км/ч

Теперь определим время за которое теплоход пройдет 204 км при скорости 12 км/ч. В час теплоход проходит 12 километров. Чтобы узнать за сколько часов он пройдет 204 километра, нужно определить сколько раз 204 километра содержит по 12 километров

Ответ: теплоход пройдет 204 километра за 17 часов

Задача 5. Двигаясь по течению реки, за 6 часов лодка
прошла 102 км. Определите собственную скорость лодки,
если скорость течения – 4 км/ч.

Решение

Узнаем с какой скоростью лодка двигалась по реке. Для этого пройденное расстояние (102км) разделим на время движения (6ч)

Определим собственную скорость лодки. Для этого из скорости по которой она двигалась по реке (17 км/ч) вычтем скорость течения реки (4 км/ч)

Задача 6. Двигаясь против течения реки, за 5 часов лодка
прошла 110 км. Определите собственную скорость лодки,
если скорость течения – 4 км/ч.

Решение

Узнаем с какой скоростью лодка двигалась по реке. Для этого пройденное расстояние (110км) разделим на время движения (5ч)

Определим собственную скорость лодки. В условии сказано, что она двигалась против течения реки. Скорость течения реки составляла 4 км/ч. Это значит, что собственная скорость лодки была уменьшена на 4. Наша задача прибавить эти 4 км/ч и узнать собственную скорость лодки

Ответ: собственная скорость лодки составляет 26 км/ч

Задача 7. За какое время при движении против течения реки лодка
пройдет 56 км, если скорость течения – 2 км/ч, а её
собственная скорость на 8 км/ч больше скорости течения?

Решение

Найдем собственную скорость лодки. В условии сказано, что она на 8 км/ч больше скорости течения. Поэтому для определения собственной скорости лодки, к скорости течения (2 км/ч) прибавим еще 8 км/ч

2 км/ч + 8 км/ч = 10 км/ч

Лодка движется против течения реки, поэтому из собственной скорости лодки (10 км/ч) вычтем скорость движения реки (2 км/ч)

10 км/ч − 2 км/ч = 8 км/ч

Узнаем за какое время лодка пройдет 56 км. Для этого расстояние (56км) разделим на скорость движения лодки:

Ответ: при движении против течения реки лодка пройдет 56 км за 7 часов

Видео:Задачи на движение двух объектовСкачать

Задачи для самостоятельного решения

Решение

За один час пешеход проходит 5 километров. Чтобы определить за какое время он пройдет 20 км, нужно узнать сколько раз 20 километров содержат по 5 км. Либо воспользоваться правилом нахождения времени: разделить пройденное расстояние на скорость движения

Решение

Определим расстояние от пункта А до пункта В. Для этого умножим скорость с которой ехал велосипедист из пункта А в пункт В (16км/ч) на время движения (5ч)

Определим сколько времени велосипедист затратил на обратный путь. Для этого расстояние (80км) разделим на скорость движения (10км/ч)

Решение

Определим путь, пройденный велосипедистом за 6 часов. Для этого из 83 км вычтем путь, который он прошел после шести часов движения (11км)

Определим с какой скоростью ехал велосипедист первые 6 часов. Для этого разделим 72 км на 6 часов

Поскольку в условии задаче сказано, что остальные 11 км велосипедист проехал с той же скоростью, что и в первые 6 часов движения, то скорость равная 12 км/ч является ответом к задаче.

Ответ: велосипедист ехал со скоростью 12 км/ч.

Решение

Найдем скорость течения реки. В условии сказано, что плот может проплыть 72 километра за 36 часов. Плот не может двигаться против течения реки. Значит скорость плота с которой он преодолевает эти 72 километра и является скоростью течения реки. Чтобы найти эту скорость, нужно 72 километра разделить на 36 часов

Найдем собственную скорость теплохода. Сначала найдем скорость его движения против течения реки. Для этого разделим 72 километра на 4 часа

Если против течения реки скорость теплохода составляет 18 км/ч, то собственная его скорость равна 18+2, то есть 20 км/ч. А по течению реки его скорость будет составлять 20+2, то есть 22 км/ч

Разделив 110 километров на скорость движения теплохода по течению реки (22 км/ч), можно узнать за сколько часов теплоход проплывет эти 110 километров

Ответ: по течению реки теплоход проплывет 110 километров за 5 часов.

Решение

Найдем скорость удаления велосипедистов

Узнаем какое расстояние будет между ними через 4 часа

Ответ: через 4 часа расстояние между велосипедистами будет 96 км.

Решение

Определим расстояние, пройденное первым теплоходом. Для этого умножим его скорость (21 км/ч) на время движения до встречи (6ч)

Определим расстояние, пройденное вторым теплоходом. Для этого умножим его скорость (24 км/ч) на время движения до встречи (6ч)

Определим расстояние между пристанями. Для этого сложим расстояния, пройденные первым и вторым теплоходами

126 км + 144 км = 270 км

Ответ: первый теплоход прошел 126 км, второй — 144 км. Расстояние между пристанями составляет 270 км.

Решение

Определим сколько километров до встречи прошел поезд, вышедший из Москвы. Для этого умножим его скорость (51 км/ч) на 16 часов

Узнаем сколько километров до встречи прошел поезд, вышедший из Уфы. Для этого из расстояния между Москвой и Уфой (1520км) вычтем расстояние, пройденное поездом, вышедшим из Москвы

1520 − 816 = 704 км

Определим скорость с которой шел поезд, вышедший из Уфы. Для этого расстояние, пройденное им до встречи, нужно разделить на 16 часов

704 : 16 = 44 км/ч

Определим расстояние, которое будет между поездами через 5 часов после их встречи. Для этого найдем скорость удаления поездов и умножим эту скорость на 5

51 км/ч + 44 км/ч = 95 км/ч

Ответ: поезд, вышедший из Уфы, шел со скоростью 44 км/ч. Через 5 часов после их встречи поездов расстояние между ними будет составлять 475 км.

Решение

Найдем скорость второго автобуса. Она на 6 км/ч больше скорости первого автобуса

48 км/ч + 6 км/ч = 54 км/ч

Найдем скорость удаления автобусов. Для этого сложим их скорости:

48 км/ч + 54 км/ч = 102 км/ч

За час расстояние между автобусами увеличивается на 102 километра. Чтобы узнать через сколько часов расстояние между ними будет 510 км, нужно узнать сколько раз 510 км содержит по 102 км/ч

Ответ: 510 км между автобусами будет через 5 часов.

Решение

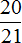
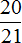
Найдем скорость ростовского поезда. Она составляет скорости московского поезда. Поэтому чтобы определить скорость ростовского поезда, нужно найти от 63 км

63 : 21 × 20 = 3 × 20 = 60 км/ч

Найдем скорость сближения поездов

63 км/ч + 60 км/ч = 123 км/ч

Определим через сколько часов поезда встретятся

1230 : 123 = 10 ч

Узнаем на каком расстоянии от Ростова встретятся поезда. Для этого достаточно найти расстояние, пройденное ростовским поездом до встречи

Ответ: поезда встретятся на расстоянии 600 км от Ростова.

Решение

Найдем скорость второй лодки. Она составляет 75% скорости первой лодки. Поэтому чтобы найти скорость второй лодки, нужно 75% от 16 км

16 × 0,75 = 12 км/ч

Найдем скорость сближения лодок

16 км/ч + 12 км/ч = 28 км/ч

С каждым часом расстояние между лодками будет уменьшáться на 28 км. Через 2 часа оно уменьшится на 28×2, то есть на 56 км. Чтобы узнать какое будет расстояние между лодками в этот момент, нужно из 75 км вычесть 56 км

75 км − 56 км = 19 км

Ответ: через 2 часа между лодками будет 19 км.

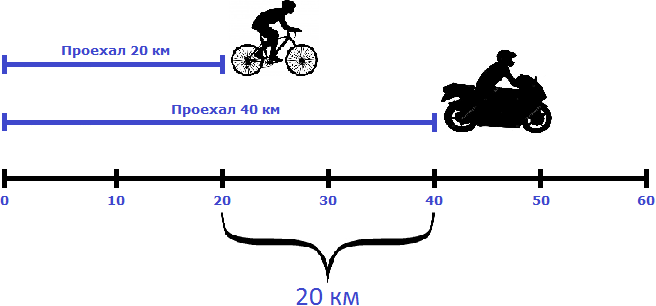
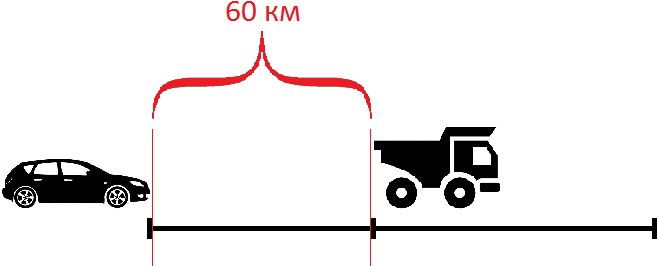
Решение

Найдем скорость сближения

62 км/ч − 47 км/ч = 15 км/ч

Если первоначально расстояние между машинами было 60 километров, то с каждым часом это расстояние будет уменьшáться на 15 км, и в конце концов легковая машина догонит грузовую. Чтобы узнать через сколько часов это произойдет, нужно определить сколько раз 60 км содержит по 15 км

Узнаем на каком расстоянии от начала движения легковая машина догнала грузовую. Для этого умножим скорость легковой машины (62 км/ч) на время её движения до встречи (4ч)

Ответ: легковая машина догонит грузовую через 4 часа. В момент встречи легковая машина будет на расстоянии 248 км от начала движения.

Решение

Найдем скорость второго мотоциклиста. Она составляет 80% скорости первого мотоциклиста. Поэтому чтобы найти скорость второго мотоциклиста, нужно найти 80% от 35 км/ч

35 × 0,80 = 28 км/ч

Первый мотоциклист двигается на 35-28 км/ч быстрее

35 км/ч − 28 км/ч = 7 км/ч

За один час первый мотоциклиста преодолевает на 7 километров больше. С каждым часом она будет приближáться ко второму мотоциклисту на эти 7 километров.

Через 5 часов первый мотоциклист пройдет 35×5, то есть 175 км, а второй мотоциклист пройдет 28×5, то есть 140 км. Определим расстояние, которое между ними. Для этого из 175 км вычтем 140 км

175 − 140 = 35 км

Ответ: через 5 часов расстояние между мотоциклистами будет 35 км.

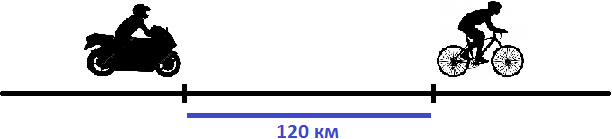
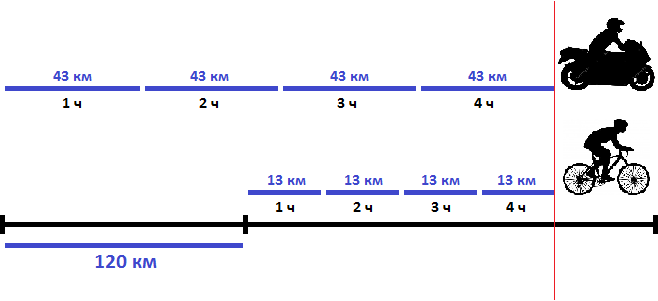
Решение

Найдем скорость сближения:

43 км/ч − 13 км/ч = 30 км/ч

Если первоначально расстояние между мотоциклистом и велосипедистом было 120 километров, то с каждым часом это расстояние будет уменьшáться на 30 км, и в конце концов мотоциклист догонит велосипедиста. Чтобы узнать через сколько часов это произойдет, нужно определить сколько раз 120 км содержит по 30 км

Значит через 4 часа мотоциклист догонит велосипедиста

На рисунке представлено движение мотоциклиста и велосипедиста. Видно, что через 4 часа после начала движения они сровнялись.

Ответ: мотоциклист догонит велосипедиста через 4 часа.

Решение

Определим скорость велосипедиста, ехавшего впереди. Для этого найдем 75% от скорости велосипедиста, ехавшего сзади:

12 × 0,75 = 9 км/ч — скорость ехавшего впереди

Узнаем сколько километров проехал каждый велосипедист до того, как второй догнал первого:

12 × 6 = 72 км — проехал ехавший сзади
9 × 6 = 54 км — проехал ехавший впереди

Узнаем какое расстояние было между велосипедистами первоначально. Для этого из расстояния, пройденного вторым велосипедистом (который догонял) вычтем расстояние, пройденное первым велосипедистом (которого догнали)

72 км − 54 км = 18 км

Ответ: между велосипедистами первоначально было 18 км.

Решение

Найдем скорость удаления автомобиля от автобуса

53 км/ч − 41 км/ч = 12 км/ч

С каждым часом автомобиль будет удаляться от автобуса на 12 километров. На рисунке показано положение машин после первого часа движения

Видно, что автомобиль впереди автобуса на 12 км.

Чтобы узнать через сколько часов автомобиль будет впереди автобуса на 48 километров, нужно определить сколько раз 48 км содержит по 12 км

Ответ: через 4 часа после выезда автомобиль будет впереди автобуса на 48 километров.

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Видео:Задачи на движение. Учимся решать задачи на движение. Способы решения задач на движение.Скачать

20 thoughts on “Задачи на движение”

Здравствуйте. Как решить такую задачу? Она вроде, и на движение, и на уравнение, но никак не мог понять как ее составить и решить.

Моторная лодка прошла против течения реки 297 км и вернулась в пункт отправления, затратив на обратный путь на 3 часа меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 2 км/ч.

Задача на составление уравнения, содержащего рациональные выражения. В данном уроке такие задачи не рассмотрены. Обычно их решают в процессе изучения рациональных выражений.

x — скорость лодки в неподвижной воде
x — 2 — скорость лодки против течения
x + 2 — скорость лодки по течению

297/x-2 — время движения против течения
297/x+2 — время движения по течению

Тогда 297/x-2 = 297/x+2 + 3

Ответ: скорость лодки в неподвижной воде 20 км/ч

Видео:РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ УРАВНЕНИЙ. §3 алгебра 7 классСкачать

Сборник текстовых задач по математике для 7 класса (открытый банк заданий ФИПИ)

Сборник текстовых задач по математике для 7 класса (открытый банк заданий ФИПИ)

Составила Коньшина Е.В.

МАОУ «Гимназия №8», г.Перми

Видео:Решение задач с помощью уравнений. Алгебра, 7 классСкачать

Оглавление

Задачи на движение по прямой (навстречу и вдогонку)3

Задачи на движение протяженных тел3

Задачи на движение по воде4

Задачи на среднюю скорость4

Задачи на проценты5

Задачи на сплавы, смеси, растворы5

Задачи на работу6

Задачи и оптимальный выбор9

Задачи на округление десятичной дроби13

Видео:Решение задач с помощью уравнений.Скачать

Задачи на движение по прямой (навстречу и вдогонку)

1. Из двух городов, расстояние между которыми равно 560 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 65 км/ч и 75 км/ч?

2. Расстояние между городами A и B равно 435 км. Из города A в город B со скоростью 60 км/ч выехал первый автомобиль, а через час после этого навстречу ему из города B выехал со скоростью 65 км/ч второй автомобиль. На каком расстоянии от города A автомобили встретятся? Ответ дайте в километрах.

3. Два пешехода отправляются из одного и того же места в одном направлении на прогулку по аллее парка. Скорость первого на 1 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 200 метрам?

4.Из городов A и B, расстояние между которыми равно 420 км, навстречу друг другу одновременно выехали два автомобиля и встретились через 4 часа на расстоянии 220 км от города B. Найдите скорость автомобиля, выехавшего из города A. Ответ дайте в км/ч.

Видео:Задача на движение по реке. Алгебра 7 классСкачать

Задачи на движение протяженных тел

5. Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо придорожного столба за 30 секунд. Найдите длину поезда в метрах.

6.Поезд, двигаясь равномерно со скоростью 54 км/ч, проезжает мимо идущего параллельно путям со скоростью 6 км/ч навстречу ему пешехода за 30 секунд. Найдите длину поезда в метрах.

7.Поезд, двигаясь равномерно со скоростью 65 км/ч, проезжает мимо идущего в том же направлении параллельно путям со скоростью 5 км/ч пешехода за 30 секунд. Найдите длину поезда в метрах.

8.Поезд, двигаясь равномерно со скоростью 90 км/ч, проезжает мимо лесополосы, длина которой равна 800 метрам, за 1 минуту. Найдите длину поезда в метрах.

Видео:Алгебра 7 класс (Урок№44 - Решение задач с помощью линейных уравнений.)Скачать

Задачи на движение по воде

9. Из двух пунктов реки, расстояние между которыми 57 км, навстречу друг другу движутся две моторные лодки, собственные скорости которых равны. Лодка, идущая по течению, до встречи шла 1 час, а лодка, идущая против течения, 2ч. Скорость течения реки 3 км/ч. Найти собственную скорость лодки.

10. По течению реки катер прошел за 7 ч столько же километров, сколько он проходит за 8 ч против течения. Собственная скорость катера 30 км/ч. Найдите скорость течения реки.

Видео:Урок по теме РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ СИСТЕМЫ УРАВНЕНИЙ 7 КЛАСССкачать

Задачи на среднюю скорость

11.Первую треть трассы автомобиль ехал со скоростью 100 км/ч, вторую треть — со скоростью 75 км/ч, а последнюю — со скоростью 60 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

12.Первые два часа автомобиль ехал со скоростью 120 км/ч, следующие два часа — со скоростью 85 км/ч, а затем три часа — со скоростью 50 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

13. Первые 100 км автомобиль ехал со скоростью 50 км/ч, следующие 240 км — со скоростью 60 км/ч, а последние 200 км — со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

14. Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 84 км/ч, а вторую половину времени — со скоростью 56 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

15. Первую половину трассы автомобиль проехал со скоростью 56 км/ч, а вторую — со скоростью 84 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

16. Первые два часа автомобиль ехал со скоростью 55 км/ч, следующий час — со скоростью 70 км/ч, а последние три часа— со скоростью 90 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

17. Треть времени, затраченного на дорогу, автомобиль ехал со скоростью 50 км/ч, вторую треть времени — со скоростью 75 км/ч, а последнюю треть — со скоростью 85 км/ч.Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

18. Первую треть трассы автомобиль ехал со скоростью60 км/ч, вторую треть — со скоростью 80 км/ч, а последнюю треть — со скоростью 120 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Видео:Как думать решая олимпиадки. Задача на движение 7 класс. #олимпиада #математика #алгебра #движениеСкачать

Задачи на проценты

19.В период распродажи магазин снижал цены дважды: в первый раз на 30%, во второй — на 20%. Сколько рублей стал стоить чайник после второго снижения цен, если до начала распродажи он стоил 1500 р.?

20.Шариковая ручка стоит 30 рублей. Какое наибольшее число таких ручек можно будет купить на 500 рублей после повышения цены на 25%?

Видео:Алгебра 7 класс с нуля | Математика | УмскулСкачать

Задачи на сплавы, смеси, растворы

21.В сосуд, содержащий 7 литров 14-процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?

22.Смешали 9 литров 20-процентного водного раствора некоторого вещества с 11 литрами 40-процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

23.Имеется два сплава. Первый содержит 5% никеля, второй — 20% никеля. Из этих двух сплавов получили третий сплав массой 150 кг, содержащий 15% никеля. На сколько килограммов масса первого сплава меньше массы второго?

24.В сосуд, содержащий 5 литров 12-процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?

25.Смешали 8 литров 10-процентного водного раствора некоторого вещества с 12 литрами 40-процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

26.Имеется два сплава. Первый содержит 10% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 175 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава меньше массы второго?

27. Сколько воды необходимо добавить к 150 мл 70-процентной уксусной эссенции, чтобы получить 6-процентный столовый уксус?

28. Скольки процентным получится раствор соляной кислоты, если к 120 мл 80%-й кислоты добавить 180 мл 20-процентного раствора кислоты?

29. Сколько литров 30-процентного раствора соли надо добавить к 6 литрам 50-процентного раствора соли, чтобы получить 45-процентный раствор?

30. Сколько миллилитров 70-процентной эссенции надодобавить к 1 литру воды, чтобы получить 7-процентный уксус?

31.Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 82 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?

32.Первый сплав содержит 10% меди, второй — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

33.Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 76 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?

34.Первый сплав содержит 5% меди, второй — 13% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 11% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

35.Имеется два сплава. Первый содержит 10% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 175 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава меньше массы второго?

Видео:РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ УРАВНЕНИЙ решение уравнений 7 МакарычевСкачать

Задачи на работу

36.Один мастер может выполнить заказ за 40 часов, а другой — за 24 часа. За сколько часов выполнят заказ оба мастера, работая вместе?

37.Две трубы наполняют бассейн за 8 часов, а одна первая труба наполняет бассейн за 12 часов. За сколько часов наполняет бассейн одна вторая труба?

38.Артем и Гриша выполняют одинаковый тест. Артем отвечает за час на 14 вопросов теста, а Гриша — на 28. Они одновременно начали отвечать на вопросы теста, и Артем закончил свой тест позже Гриши на 60 минут. Сколько вопросов содержит тест?

39.Один мастер может выполнить заказ за 24 часа, а другой — за 12 часов. За сколько часов выполнят заказ оба мастера, работая вместе?

40.Аня и Таня пропалывают грядку за 36 минут, а одна Таня — за 117 минут. За сколько минут пропалывает грядку одна Аня?

41.Для распечатки 340 страниц использовали две копировальные машины. Первая машина работала 10 мин, а вторая – 15 мин. Сколько страниц в минуту печатает каждая машина, если первая печатает в минуту на 4 стр больше, чем вторая.

42.Двое рабочих изготовили по одинаковому количеству деталей. Первый выполнил эту работу за 5 ч, а второй за 4 ч, так как изготовлял в час на 12 деталей больше первого. Сколько изготовил каждый рабочий?

43.Заказ по выпуску машин завод должен выполнить за 20 дней, но уже за 18 дней завод перевыполнил план на 6 машин, так как ежедневно выпускал на 3 машины сверх плана. Сколько машин выпустил завод?

44.Две трубы наполняют бассейн за 7 часов 55 минут, а одна первая труба наполняет бассейн за 38 часов. За сколько часов наполняет бассейн одна вторая труба?

45. Илья и Игорь выполняют одинаковый тест. Илья отвечает за час на 15 вопросов теста, а Игорь — на 20. Они одновременно начали отвечать на вопросы теста, и Илья закончилсвой тест позже Игоря на 85 минут. Сколько вопросов содержит тест?

46.Токарь должен был изготовлять в день 24 детали, чтобы выполнить задание в срок. Однако он изготавливал в день на 15 деталей больше и уже за 6 дней до срока изготовил 21 деталь сверх плана. Сколько деталей изготовил токарь?

47.Две трубы наполняют бассейн за 1 час 55 минут, а одна первая труба наполняет бассейн за 46 часов. За сколько часов наполняет бассейн одна вторая труба?

48. Коля и Слава выполняют одинаковый тест. Коля отвечает за час на 18 вопросов теста, а Слава — на 30. Они одновременно начали отвечать на вопросы теста, и Коля закончил свой тест позже Славы на 56 минут. Сколько вопросов содержит тест?

49. Придумать задачи

Заполни таблицу и реши задачу:

№ 1. Автомашина за 3,5 ч проехала на 10 км больше, чем мотоцикл за 2,5 ч. Скорость мотоцикла на 20 км/ч больше, чем скорость автомашины. Найдите скорость автомашины и скорость мотоцикла.

№ 2. Через первую трубу бассейн можно заполнить за 20 ч, а через вторую — за 30 ч. За сколько часов наполнится бассейн через обе эти трубы?

Производительность труда (w)

№ 3. Чтобы выполнить задание в срок, токарь должен был изготавливать по 24 детали в день. Однако он ежедневно перевыполнял норму на 15 деталей сверх плана и уже за 6 дней до срока изготовил 21 деталь сверх плана. Сколько деталей изготовил токарь?

Производительность труда (w)

50.Производительность труда мастера на 12 деталей в час больше чем производительность ученика. Мастер работал 2 часа, а ученик 5.Сколько деталей в час изготовил мастер если мастер изготовил в 2 раза больше деталей чем ученик?

51.Бригада рабочих должна была изготовить определённое количество деталей за 20 дней. Однако она ежедневно изготавливала на 70 деталей больше, чем планировалось первоначально. Поэтому уже за 7 дней до срока ей осталось изготовить 140 деталей. Сколько деталей должна была изготовить бригада?

52.Тракторист работал 5 дней. Сколько га он вспахал, если за день вспахивал по 12 га, 15 га, 20 га, х га?

53.Машинистка должна была печатать ежедневно по 80 страниц. Однако она печатала в день на 20 страниц больше и поэтому закончила перепечатку на 4 дня раньше срока Сколько страниц в рукописи?

Видео:Составь уравнение из текстовой задачи! Алгебра 7 класс.Скачать

Задачи и оптимальный выбор

54.Для транспортировки 45 тонн груза на 1300 км можно воспользоваться услугами одной из трех фирм-перевозчиков. Стоимость перевозки и грузоподъемность автомобилей для каждого перевозчика указана в таблице. Сколько рублей придется заплатить за самую дешевую перевозку?

Стоимость перевозки одним автомобилем
(руб. на 100 км)

Грузоподъемность автомобилей
(тонн)

55.Интернет-провайдер предлагает три тарифных плана.

Плата за трафик

550 руб. за 500 Мб трафика в месяц

2 руб. за 1 Мб сверх 500 Мб

700 руб. за 800 Мб трафика в месяц

1,5 руб. за 1 Мб сверх 800 Мб

Пользователь предполагает, что его трафик составит 600 Мб в месяц, и исходя из этого выбирает наиболее дешёвый тарифный план. Сколько рублей должен будет заплатить пользователь за месяц, если его трафик действительно будет равен 600 Мб?

56.Для изготовления книжных полок требуется заказать 48 одинаковых стёкол в одной из трёх фирм. Площадь каждого стекла 0,25 кв. м. В таблице приведены цены на стекло, а также на резку стекла и шлифовку края. Сколько рублей будет стоить самый дешёвый заказ?

Цена стекла
(руб. за 1 кв. м)

Резка и шлифовка
(руб. за одно стекло)

57.Семья из трёх человек планирует поехать из Санкт-Петербурга в Вологду. Можно ехать поездом, а можно — на своей машине. Билет на поезд на одного человека стоит 660 рублей. Автомобиль расходует 8 литров бензина на 100 километров пути, расстояние по шоссе равно 700 км, а цена бензина равна 19,5 рубля за литр. Сколько рублей придётся заплатить за наиболее дешёвую поездку на троих?

58.Для строительства гаража можно использовать один из двух типов фундамента: бетонный или фундамент из пеноблоков. Для фундамента из пеноблоков необходимо 2 кубометра пеноблоков и 4 мешка цемента. Для бетонного фундамента необходимо 2 тонны щебня и 20 мешков цемента. Кубометр пеноблоков стоит 2450 рублей, щебень стоит 620 рублей за тонну, а мешок цемента стоит 230 рублей. Сколько рублей будет стоить материал, если выбрать наиболее дешевый вариант?

59.От дома до дачи можно добраться одним их трёх видов транспорта: автобусом, электричкой или маршрутным такси. В таблице показано время, которое нужно затратить на каждый участок пути для каждого вида транспорта.

От дома до остановки
(станции)

От остановки (станции)
до дачи

Какое наименьшее время потребуется на дорогу? Ответ дайте в часах.

60.Из пункта А в пункт D ведут три дороги. Одновременно из пункта в пункт выехали грузовик, автобус и легковой автомобиль. Грузовик едет через пункт со средней скоростью 35 км/ч, автобус едет через пункт со средней скоростью 30 км/ч. По третьей дороге — без промежуточных пунктов — едет легковой автомобиль со средней скоростью 40 км/ч. На рисунке показана схема дорог и расстояние (в км) между пунктами по дорогам.
Какое транспортное средство доберётся до D позже других? В ответе укажите, сколько часов оно будет находиться в пути.

61.Для того, чтобы связать свитер, хозяйке нужно 400 граммов шерстяной пряжи синего цвета. Можно купить синюю пряжу по цене 60 рублей за 50 граммов, а можно купить неокрашенную пряжу по цене 50 рублей за 50 граммов и окрасить её. Один пакетик краски стоит 10 рублей и рассчитан на окраску 200 граммов пряжи. Какой вариант покупки дешевле? В ответ напишите, сколько рублей будет стоить эта покупка.

62.Своему постоянному клиенту компания сотовой связи решила предоставить на выбор одну из скидок. Либо скидку 25% на звонки абонентам других сотовых компаний в своём регионе, либо скидку 5% на звонки в другие регионы, либо скидку 15% на услуги мобильного интернета.
Клиент посмотрел распечатку своих звонков и выяснил, что за месяц он потратил 300 рублей на звонки абонентам других компаний в своём регионе, 200 рублей на звонки в другие регионы и 400 рублей на мобильный интернет. Клиент предполагает, что в следующем месяце затраты будут такими же, и, исходя из этого, выбирает наиболее выгодную для себя скидку. Сколько рублей составит эта скидка, если звонки и пользование Интернетом сохранятся в прежнем объёме?

63.В магазине одежды объявлена акция: если покупатель приобретает товар на сумму свыше руб., он получает сертификат на 1000 рублей, который можно обменять в том же магазине на любой товар ценой не выше 1000 руб. Если покупатель участвует в акции, он теряет право возвратить товар в магазин. Покупатель И. хочет приобрести пиджак ценой 9500 руб., рубашку ценой 800 руб. и галстук ценой 600 руб. В каком случае И. заплатит за покупку меньше всего:

1) И. купит все три товара сразу.

2) И. купит сначала пиджак и рубашку, галстук получит за сертификат.

3) И. купит сначала пиджак и галстук, получит рубашку за сертификат.

В ответ запишите, сколько рублей заплатит И. за покупку в этом случае.

64.В среднем гражданин А. в дневное время расходует 120 кВт ч электроэнергии в месяц, а в ночное время — 185 кВт ч электроэнергии. Раньше у А. в квартире был установлен однотарифный счетчик, и всю электроэнергию он оплачивал по тарифу 2,40 руб. за кВт ч. Год назад А. установил двухтарифный счётчик, при этом дневной расход электроэнергии оплачивается по тарифу 2,40 руб. за кВт ч, а ночной расход оплачивается по тарифу 0,60 руб. за кВт ч.

В течение 12 месяцев режим потребления и тарифы оплаты электроэнергии не менялись. На сколько больше заплатил бы А. за этот период, если бы не поменялся счетчик? Ответ дайте в рублях.

65.Автомобильный журнал определяет рейтинг автомобилей на основе показателей безопасности, комфорта , функциональности , качества и дизайна . Рейтинг вычисляется по формуле

В таблице даны показатели трёх моделей автомобилей.

Видео:Формула для решения задач на движение. Физика 7 класс.Скачать

Сборник задач на движение 7 класс алгебра с решением уравнением

1 мин = 60 с; 1 ч = 3600 с; 1 км = 1000 м; 1 м/с = 3,6 км/ч.

Физика 7 класс: все формулы на трех страницах

ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ

Задача № 1. Ласточка летит со скоростью 36 км/ч. Какой путь она преодолеет за 0,5 ч?

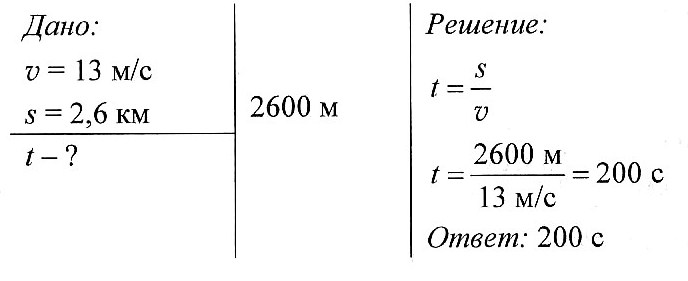
Задача № 1. Конькобежец может развивать скорость до 13 м/с. За какое время он пробежит дистанцию длиной 2,6 км?

Задача № 3. Автомобиль «Чайка» развивает скорость до 160 км/ч, а почтовый голубь — до 16 м/с. Сможет ли голубь обогнать автомобиль?

Решение. Чтобы сравнить скорости движения тел, надо перевести их в одинаковые единицы измерения. Перевод скорости из одних единиц в другие выполняют следующим образом. 160 км = 160000 м, 1 ч = 3600 с. Следовательно, за 1 с автомобиль пройдет путь 160000 : 3600 = 44 (м), значит:

Ответ: Голубь не обгонит автомобиль, так как 16 м/с

Задача № 4. Вдоль дороги навстречу друг другу летят скворец и комнатная муха. На рисунке представлены графики движения скворца (I) и мухи (II). Пользуясь графиком, определите:

1) Каковы скорости движения скворца и мухи?
2) Через сколько секунд после начала движения они встретятся?
3) Какое расстояние они пролетят до места встречи?

Решение.
1. Скорость движения скворца определим по формуле v=S/t. Выберем на графике произвольное время и определим, какое расстояние за это время пролетел скворец. Видно, что за 5 с скворец пролетел 100 м. Тогда

Аналогично найдем скорость движения мухи:

2. Точка А (точка пересечения графиков движения) соответствует моменту встречи. Скворец и муха встретятся через 4 секунды.

3. Скворец до места встречи пролетит расстояние S_I = 80 м. Муха пролетит расстояние S_II = 100 м — 80 м = 20 м.

Ответ: 1) скворец 20 м/с, муха 5 м/с, 2) через 4 с, 3) скворец 80 м, муха 20 м

Задача № 5. Определите среднюю скорость движения плота, если за 20 минут он переместился на 900 м. Скорость выразить в км/ч.

Ответ: Средняя скорость плота 2,7 км/ч.

Задача № 6. Стоящий на эскалаторе человек поднимается за 2 мин, а бегущий по эскалатору — за 40 с. За какое время этот человек поднимется по неподвижному эскалатору?

ОТВЕТ: 1 мин.

Задача № 7. Моторная лодка за 3 ч проходит расстояние от города до поселка, расположенного ниже по течению реки. Сколько времени займет обратный путь, если скорость движения лодки относительно воды в 4 раза больше скорости течения?

ОТВЕТ: 5 ч.

Задача № 8 (повышенной сложности). Рыбак плыл по реке на лодке, зацепил шляпой за мост, и она свалилась в воду. Через час рыбак спохватился, повернул обратно и подобрал шляпу на 4 км ниже моста. Какова скорость течения? Скорость лодки относительно воды оставалась неизменной по модулю.

ОТВЕТ: 2 км/ч.

Задача № 9 (олимпиадного уровня). Из городов А и Б навстречу друг другу по прямому шоссе одновременно выехали два велосипедиста. Скорость первого 10 км/ч, скорость второго 15 км/ч. Одновременно с велосипедистами из города А вылетела ласточка. Она долетает до второго велосипедиста, разворачивается, Долетает до первого велосипедиста и летает так между ними до тех пор, пока велосипедисты не встретятся. Какой путь пролетела ласточка, если скорость ее движения 50 км/ч, а расстояние между городами 100 км? Временем разворота ласточки можно пренебречь.

ОТВЕТ: 200 км.

Алгоритм решения задач на движение

При решении других задач прямолинейного равномерного движения в общем виде нужно придерживаться следующего алгоритма: 1) выбрать систему отсчёта; 2-3) определить начальные координаты и значения скоростей движения тел в этой системе отсчёта; 4) записать зависимости координат тел от времени; 5) записать в виде уравнения условие задачи; 6) объединить уравнения; 7) решить эти уравнения; 8) провести анализ полученного результата (после чего выяснить, имеет ли полученный результат физический смысл); 9) если в условии задачи даны числовые значения, необходимо подставить их в полученное выражение и получить числовой ответ.

Анализ полученного результата заключается в исследовании зависимости искомой величины от входящих в ответ величин.

Не стоит забывать и про направление движения в зависимости от типа задачи (встреча, погоня, обгон, отставание)

Конспект урока «Задачи на движение с решением».

Видео:7 класс - Алгебра - Решение задач с помощью уравненийСкачать

Конспект урока алгебры в 7 классе по теме «Решение текстовых задач на движение с помощью составления уравнений с одной переменной». Учебник «Алгебра-7» под редакцией Теляковского С.А.

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 2 500 дидактических материалов для школьного и домашнего обучения

Столичный центр образовательных технологий г. Москва

Получите квалификацию учитель математики за 2 месяца

от 3 170 руб. 1900 руб.

Количество часов 300 ч. / 600 ч.

Успеть записаться со скидкой

Форма обучения дистанционная

Видеолекции для
профессионалов

• Свидетельства для портфолио
• Вечный доступ за 120 рублей
• 311 видеолекции для каждого

Конспект урока алгебры в 7 классе

по теме «Решение текстовых задач на движение с помощью составления уравнений с одной переменной».

Учебник «Алгебра-7» под редакцией Теляковского С.А.

Тема : Решение текстовых задач на движение с помощью составления уравнений с одной переменной.

О бразовательные : формирование знаний, умений и навыков учащихся решать текстовые задачи с помощью уравнений.

Развивающие : развивать умения работать в группе, формировать учебно–познавательные навыки по работе с дополнительным материалом, развивать логическое мышление, внимание;

Воспитательные : воспитывать интерес к математике, старательность, активность, мобильность, взаимопомощь, ответственность перед товарищами.

Тип урока: усвоение знаний и умений.

Оборудование: компьютер, проектор, презентация.

Учитель приветствует учеников.

Проверка домашнего задания.

Сильные ученики отвечают на вопросы, которые возникли у более слабых учащихся в процессе выполнения домашнего задания.

Актуализация опорных знаний.

Написание «Теоретического текста».

Учитель раздает каждому учащемуся текст для проверки уровня усвоения обязательного теоретического материала. В тексте пропущены слова, которые ученики должны вставить. Проверка организована в форме «взаимопроверки» с демонстрацией правильных ответов на экране.

На предыдущем уроке мы изучали решение задач с помощью линейных уравнений . Много текстовых задач отображают некоторую жизненную ситуацию и используют нематематические понятия, такие задачи называют реальной математикой. Чтобы составить математическую модель задачи, надо сначала выбрать основную переменную , а потом составить соответствующее уравнение. Ответ необходимо проверить по содержанию задачи , а не уравнения . После того, как мы составили уравнение к задаче и чтобы его решить, уравнение необходимо привести к линейному. Для этого надо помнить такое правило-ориентир:

Избавляемся от знаменателей .;

Переносим члены с переменными в левую часть уравнения, а другие -в правую, меняя знаки на противоположные ;

Приводим подобные слагаемые;

Я считаю, что умение решать текстовые задачи необходимо для того, чтобы….

4.Мотивация учебной деятельности.

Я хочу, чтобы каждый из вас объяснил, почему считает необходимым научиться решать текстовые задачи………

Ребята! Сегодня на уроке мы должны будем с вами познакомиться с алгоритмом решения задач на движение, обращая особое внимание на табличную запись условия. Работая над новой темой, мы проследим вместе с вами, как ранее изученный материал связан с новым, как постепенно происходит расширение и углубление знаний. Одним словом, мы будем объединять отдельные факты в целостный пласт.Я буду вам помогать в процессе систематизации ваших знаний. Мы приступаем к работе.

5.Решение задач с помощью опорных схем.

Коллективное решение задачи на историческую тематику.

История сохранила нам мало фактов биографии древнего математика Диофанта. Все, что про него было известно, взято из надписи на его гробнице, составленной в виде математической задачи.

Путник! Тут прах похоронен Диофанта. И числа расскажут, о диво, как долго жизнь его длилась

Шестая часть ее прошла счастливым детством

Двенадцатая часть жизни еще прошла-

покрылась пушком его борода

Седьмую в бездетном браке провел Диофант

Прошло пятилетие: он был счастлив рождением прекрасного первенца-сына

Коему судьба только половину жизни прекрасной и светлой дала по сравнению с отцом

И в горе глубоком старик земной жизни конец принял, прожив только года 4 после того, как без сына остался.

Скажи, сколько лет жизни достигнув, принял смерть Диофант?

Решив уравнение, получаем, что х=84, имеем такие эпизоды биографии Диофанта: женился в 21 год, стал отцом в 38 лет, потерял сына в 80 лет.

Диофант Александрийский — древнегреческий математик.

До нас дошло стихотворение-задача, из которого видно, что Диофант прожил 84 года. Вот его содержание: «детство Диофанта продолжалось одну шестую часть его жизни, спустя ещё одну двенадцатую у него начала расти борода, он женился спустя ещё одну седьмую, через пять лет у него родился сын, сын прожил половину жизни отца, и отец умер через четыре года после смерти горько оплакиваемого им сына».

Своё основное произведение «Арифметика» Диофант посвятил Дионисию — вероятно, епископу Александрии. До нас дошло шесть первых книг «Арифметики» из тринадцати. Диофант ввёл буквенные обозначения для неизвестного, его квадрата, знака равенства и знака отрицательного числа.

Занимался неопределёнными уравнениями. Ввёл в алгебру буквенную символику.

Большую часть своей жизни Диофант Александрийский посвятил изучению алгебраических уравнений в целых числах. В дошедших до нас книгах «Арифметика» содержатся задачи и решения, в которых Диофант поясняет, как выбрать неизвестное, чтобы решить уравнение вида ax=b или ax =b. Способы решения полных квадратных уравнений изложены в книгах, которые не сохранились.

6.Формирование умений решать задачи на движение с помощью составления линейных уравнений с одной переменной.

Очень важно при решении любой задачи хорошо разобраться с условием и правильно его записать. Способ записи условия с помощью таблицы очень наглядный.

С задачами на движение вы встречались в начальной школе и в 5 классе. Вы знаете, что в этих задачах присутствуют три величины. Назовите мне их. Как находится расстояние? Время? Скорость?

Вы знакомы с формулами нахождения этих величин

Повторение формул: V = S : t

Интерактивная игра «Аквариум». Учитель объединяет учеников в группы по 5-6 человек и предлагает им ознакомиться с заданием. Эта группа читает задание вслух. Остальные учащиеся слушают, не вмешиваясь в процесс обсуждения. Но после дискуссии каждая группа поддерживает или выдвигает свои идеи. Наиболее удачное решение записывается на доске.

1. Катер прошел расстояние между пристанями по течению реки за 4 часа, а против течения- за 6 часов. Найдите собственную скорость катера, если течение реки 1,5 км/ч.

Пусть собственная скорость катера х км/ч. Когда катер двигался по течению реки, его скорость была (х+1,5) км/ч и за 4 часа он проплыл расстояние 4(х-1,5) км. Если катер двигался против течения река, то его скорость была (х-1,5) км/ч, и за 6 часов он проплыл расстояние 6(х-1,5) км. По условию задачи катер проплыл по течению и против течения одинаковое расстояние, поэтому

Получаем, что собственная скорость катера 7,5 км/ч.

2. По шоссе идут две машины с одной и той же скоростью. Если первая увеличит скорость на 10 км/ч, а вторая уменьшит скорость на 10 км/ч, то первая за 2ч пройдёт столько же, сколько вторая за 3ч. С какой скоростью идут автомашины?

📹 Видео

Как ПРАВИЛЬНО решать задачи по физике?Скачать