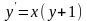Самостоятельная работа по теме дифференциальные уравнения с разделяющимися переменными

Задание для практической работы по отработки навыков решения дифференциальных уравнений первого порядка

Просмотр содержимого документа
«Практическая работа «Дифференциальные уравнения с разделяющимися переменными»»

Учебная цель: отработать навыки решения дифференциальных уравнений первого порядка.

рассмотреть задачи, приводящие к понятию дифференциального уравнения;

научиться решать простейшие дифференциальные уравнения;

научиться находить частные и общие решения;

воспитать нравственные качества; познавательные интересы к предмету;

развивать память, мышление, сообразительность, гибкость мышления;

вызывать интерес к учению с помощью показа значимости изучаемого для развития науки и техники.

Образовательные результаты, заявленные во ФГОС третьего поколения:

решать прикладные задачи в области профессиональной деятельности;

применять методы математического анализа;

значение математики в профессиональной деятельности и при освоении профессиональной образовательной программы;

основные математические методы решения прикладных задач в области профессиональной деятельности;

основные понятия и методы математического анализа, основы интегрального и дифференциального исчисления.

Задачи практической работы:

Повторить теоретический материал по теме практической работы.

Ответить на вопросы для закрепления теоретического материала.

Выполнить упражнения по вычислению дифференциального уравнения первого порядка.

Лекционная тетрадь по УД «Математика».

Тетрадь в клетку для практических работ по УД «Математика».

Ручка, цветные ручки (по желанию).

Краткие теоретические и учебно-методические материалы по теме практической работы

Формула для вычисления дифференциального уравнения с разделяющимися переменными:

,

.

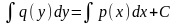
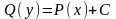
Вопросы для закрепления теоретического материала к практическому занятию

Дайте определение дифференциального уравнения 1 – го порядка.

Как мы находим частное и общее решение ДУ 1 – го порядка.

Сформулируйте определение ДУ с разделяющимися переменными.

Задания для практического занятия:

; 2) ; 3) ; 4) ;

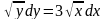
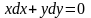
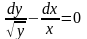
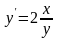
5) ; 6) ; 7) ; 8)

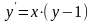
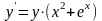
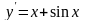
9) ; 10) ; 11) .

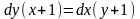
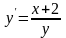
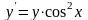
Форма контроля выполнения практических работ:

Выполненная работа представляется преподавателю в тетради для практических работ.

Задания для практического занятия:

; 2) ; 3) ; 4) ;

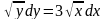
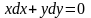
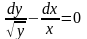
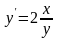
5) ; 6) ; 7) ; 8)

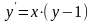
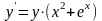
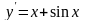
9) ; 10) ; 11) .

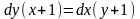
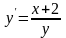
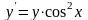
Видео:Дифференциальные уравнения с разделяющими переменными. 11 класс.Скачать

Решение дифференциальных уравнений с разделяющимися переменными. Методическая разработка.
методическая разработка на тему

Решение дифференциальных уравнений с разделяющимися переменными. Методическая разработка.

Видео:2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать

Скачать:

Видео:Дифференциальные уравнения, 2 урок, Дифференциальные уравнения с разделяющимися переменнымиСкачать

Предварительный просмотр:

Государственное автономное образовательное учреждение

среднего профессионального образования

Технологический колледж №28

Решение дифференциальных уравнений с разделяющимися переменными и применение этих понятий при решении задач прикладного характера

Соколова Л.А., Плотникова И.А. – преподаватели математики ГАОУ СПО города Москвы Технологический колледж № 28

Пособие для студентов 2-го курса «Методическая разработка

Решение дифференциальных уравнений с разделяющимися переменными и применение этих понятий при решении задач прикладного характера»

Соколова Л.А., Плотникова И.А. – М.: ГАОУ СПО ТК № 28. 2014. — 39 с.

В пособии представлены способы решения различных примеров по теме :Дифференциальные уравнения с разделяющимися переменными» и разобраны задачи , которых эти понятия используются. Пособие предназначено для студентов 2-го курса. Задания могут выполняться как во время самостоятельной работы на учебном занятии, так и как внеаудиторная самостоятельная работа.

ГАОУ СПО ТК № 28

Пособие для студентов 2-го курса «Методическая разработка

Решение дифференциальных уравнений с разделяющимися переменными и применение этих понятий при решении задач прикладного характера»

Данное пособие содержит теоретический материал по данной теме с подробным разбором примеров и задач и задания для самостоятельной работы на уроке или вне аудитории, может быть использовано при изучении данной темы для всех специальностей колледжа.

Дифференциальные уравнения первого порядка.

Основные понятия. Геометрический смысл.

Дифференциальным уравнением первого порядка называется уравнение, связывающее независимую переменную, неизвестную функцию и ее производную.

Так как производную можно представить в виде отношения дифференциалов, то уравнение может содержать не производную, а дифференциалы неизвестной функции и независимой переменной.

Итак, вид дифференциального уравнения первого порядка

В частных случаях в левую часть уравнения могут не входить х, либо у, но всегда входит у ’ .

Иногда дифференциальное уравнение первого порядка удается записать в виде

Решением дифференциального уравнения называется всякая функция, обращающая его в тождество при подстановке в него этой функции и ее производной взамен неизвестной функции и ее производной.

Рассмотренные ранее примеры показывают, что дифференциальное уравнение может иметь бесконечное множество решений, отличающие произвольной постоянной С, придавая которой разные числовые значения, получают разные решения.

Несмотря на то, что рассмотренные примеры носят частный характер, все-таки, не приводя доказательств, сделаем обобщение:

Любое дифференциальное уравнение имеет бесконечное множество решений, которые определяются формулой, содержащую одну произвольную постоянную. Записывать эту совокупность решений будем в виде

Общим решением дифференциального уравнения первого порядка называется совокупность его решений, определяемая формулой , где С – произвольная постоянная.

Придавая С произвольные числовые значения, можно получать частные решениг я

Замечание 1 .Получить решение в виде , т.е. искомая функция выражается через х и С в явном виде, не всегда возможно. Бывает, что решение получается в виде — неявное выражение у через х и С. В этом случае его – решение — называют общим интегралом .

Замечание 2 . Количество постоянных в общем решении дифференциального уравнения зависит от его порядка. Точнее: каков порядок дифференциального уравнения столько постоянных, причем различных, в общем решении этого уравнения.

Замечание 3. Процесс нахождения решений дифференциального уравнения иногда называют интегрированием дифференциального уравнения.

Выясним геометрический смысл как уравнения , так и его решений: общего и частного.

Итак, пусть дано обыкновенное дифференциальное уравнение . Как известно, — угловой коэффициент касательной к кривой, в нашем случае угловой коэффициент касательной, проведенной к , т.е. решению данного уравнения, в некоторой точке (х,у). Беря конкретные точки будем получать конкретные значения у ’ . Таким образом, в каждой взятой точке будет указано направление касательной к кривой, являющейся решением данного уравнения. Говорят, уравнение задает поле направлений в некоторой области.

Найти решение этого уравнения — значит найти кривую, касательная к которой в каждой ее точке совпадала бы с направлением поля в этой точке.

Таких кривых будет не одна, а целое семейство (построение можно начинать с любой точки области).

Пусть дано уравнение . Найдем значения у ’ , задавая х, у (х 0).

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Самостоятельная работа «Дифференциальные уравнения первого порядка с разделяющимися переменными» учебной дисциплины «Математика» для специальности: 38.02.01 Экономика и бухгалтерский учет

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 300 дидактических материалов для школьного и домашнего обучения

Самостоятельная работа №3 «Дифференциальные уравнения первого порядка с разделяющимися переменными»

1) , если ;

2) , если y

3) , если x =0.

Самостоятельная работа №3 «Дифференциальные уравнения первого порядка с разделяющимися переменными»

1) , если x ;

2) , если y

3) , если y =0.

Самостоятельная работа №3 «Дифференциальные уравнения первого порядка с разделяющимися переменными»

1) , если ;

2) , если y

3) , если y =6;

Самостоятельная работа №3 «Дифференциальные уравнения первого порядка с разделяющимися переменными»

1) , если ;

2) , если y

3) , если x =3.

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 691 человек из 75 регионов

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 861 человек из 78 регионов

Курс повышения квалификации

Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС

• Сейчас обучается 51 человек из 23 регионов

«Мотивация здорового образа жизни. Организация секций»

Свидетельство и скидка на обучение каждому участнику

• Для всех учеников 1-11 классов
  и дошкольников
• Интересные задания
  по 16 предметам

«Как закрыть гештальт: практики и упражнения»

Свидетельство и скидка на обучение каждому участнику

Видео:3. Дифференциальные уравнения с разделяющимися переменными. Часть 2.Скачать

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 841 347 материалов в базе

Ищем педагогов в команду «Инфоурок»

Другие материалы

• 07.12.2016
• 412
• 0

• 07.12.2016
• 797
• 0

• 07.12.2016
• 1906
• 0

• 07.12.2016
• 772
• 4

• 07.12.2016
• 803
• 3

• 07.12.2016
• 295
• 0

• 07.12.2016
• 397
• 1

«Учись, играя: эффективное обучение иностранным языкам дошкольников»

Свидетельство и скидка на обучение
каждому участнику

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 07.12.2016 1221
• DOCX 12.6 кбайт
• 79 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Захарова Нина Викторовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 5 лет и 4 месяца
• Подписчики: 2
• Всего просмотров: 12808
• Всего материалов: 17

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Диф. уравнения с разделяющимися переменнымиСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Госдуме предложили унифицировать школьные программы

Время чтения: 1 минута

С 1 сентября в российских школах будут исполнять гимн России

Время чтения: 1 минута

Минпросвещения рекомендует школьникам сдавать телефоны перед входом в школу

Время чтения: 1 минута

Минпросвещения проведет Всероссийский конкурс для органов опеки и попечительства

Время чтения: 1 минута

Минобрнауки отменило плановые и внеплановые проверки вузов в 2022 году

Время чтения: 1 минута

Российские школьники начнут изучать историю с первого класса

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

📺 Видео

Дифференциальные уравнения с разделяющимися переменными. Урок 1Скачать

Дифференциальные уравнения с разделенными переменными. 11 класс.Скачать

Дифференциальные уравнения с разделяющимися переменными (часть 1). Высшая математика.Скачать

Дифференциальное уравнение с разделяющимися переменнымиСкачать

Дифференциальные уравнения, сводящиеся к уравнениям с разделяющимися переменными.| poporyadku.schoolСкачать

Дифференциальные уравнения с разделяющимися переменными. Пример 1Скачать

Дифференциальные уравнения с разделяющимися переменнымиСкачать

Дифференциальные уравнения с разделяющимися переменнымиСкачать

Частное решение дифференциального уравнения с разделяющимися переменными. Урок 3Скачать

ВМ. 6.1 Дифференциальные уравнения с разделяющимися переменными. Общее и частное решения.Скачать

Дифференциальные уравнения с разделяющимися переменными Урок 2Скачать