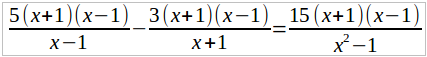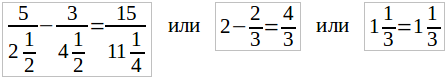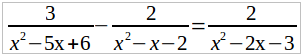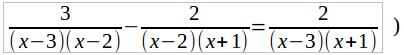Самое сложное математическое уравнение с решением

Видео:Самая сложная задача из самой сложной олимпиады [3Blue1Brown]Скачать

Математика

52. Более сложные примеры уравнений.
Пример 1 .

5/(x – 1) – 3/(x + 1) = 15/(x 2 – 1)

Общий знаменатель есть x 2 – 1, так как x 2 – 1 = (x + 1)(x – 1). Умножим обе части этого уравнения на x 2 – 1. Получим:

или, после сокращения,

5(x + 1) – 3(x – 1) = 15

5x + 5 – 3x + 3 = 15

Рассмотрим еще уравнение:

5/(x-1) – 3/(x+1) = 4(x 2 – 1)

Решая, как выше, получим:

5(x + 1) – 3(x – 1) = 4
5x + 5 – 3x – 3 = 4 или 2x = 2 и x = 1.

Посмотрим, оправдываются ли наши равенства, если заменить в каждом из рассмотренных уравнений x найденным числом.

Для первого примера получим:

Видим, что здесь нет места никаким сомнениям: мы нашли такое число для x, что требуемое равенство оправдалось.

Для второго примера получим:

5/(1-1) – 3/2 = 15/(1-1) или 5/0 – 3/2 = 15/0

Здесь возникают сомнения: мы встречаемся здесь с делением на нуль, которое невозможно. Если в будущем нам удастся придать определенный, хотя бы и косвенный, смысл этому делению, то тогда мы можем согласиться с тем, что найденное решение x – 1 удовлетворяет нашему уравнению. До этой же поры мы должны признать, что наше уравнение вовсе не имеет решения, имеющего прямой смысл.

Подобные случаи могут иметь место тогда, когда неизвестное входит как-либо в знаменатели дробей, имеющихся в уравнении, причем некоторые из этих знаменателей, при найденном решении, обращаются в нуль.

(x + 3)/(x – 1) = (2x + 3)/(2x – 2)

Можно сразу видеть, что данное уравнение имеет форму пропорции: отношение числа x + 3 к числу x – 1 равно отношению числа 2x + 3 к числу 2x – 2. Пусть кто-либо, в виду такого обстоятельства, решит применить сюда для освобождения уравнения от дробей основное свойство пропорции (произведение крайних членов равно произведению средних). Тогда он получит:

(x + 3) (2x – 2) = (2x + 3) (x – 1)

2x 2 + 6x – 2x – 6 = 2x 2 + 3x – 2x – 3.

Здесь может возбудить опасения, что мы не справимся с этим уравнением, то обстоятельство, что в уравнение входят члены с x 2 . Однако, мы можем от обеих частей уравнения вычесть по 2x 2 — от этого уравнение не нарушится; тогда члены с x 2 уничтожатся, и мы получим:

6x – 2x – 6 = 3x – 2x – 3

Перенесем неизвестные члены влево, известные вправо — получим:

Вспоминая данное уравнение

(x + 3)/(x – 1) = (2x + 3)/(2x – 2)

мы сейчас же подметим, что найденное значение для x (x = 1) обращает в нуль знаменателей каждой дроби; от такого решения мы, пока не рассмотрели вопроса о делении на нуль, должны отказаться.

Если мы подметим еще, что применение свойства пропорции усложнило дело и что можно было бы получить более простое уравнение, умножая обе части данного на общий знаменатель, а именно на 2(x – 1) — ведь 2x – 2 = 2 (x – 1), то получим:

2(x + 3) = 2x – 3 или 2x + 6 = 2x – 3 или 6 = –3,

Это обстоятельство указывает, что данное уравнение не имеет таких, имеющих прямой смысл решений, которые не обращали бы знаменателей данного уравнения в нуль.
Решим теперь уравнение:

(3x + 5)/(x – 1) = (2x + 18)/(2x – 2)

Умножим обе части уравнения 2(x – 1), т. е. на общий знаменатель, получим:

Найденное решение не обращает в нуль знаменатель и имеет прямой смысл:

или 11 = 11

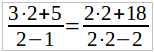
Если бы кто-либо, вместо умножения обеих частей на 2(x – 1), воспользовался бы свойством пропорции, то получил бы:

(3x + 5)(2x – 2) = (2x + 18)(x – 1) или
6x 2 + 4x – 10 = 2x 2 + 16x – 18.

Здесь уже члены с x 2 не уничтожались бы. Перенеся все неизвестные члены в левую часть, а известные в правую, получили бы

Это уравнение мы теперь решить не сумеем. В дальнейшем мы научимся решать такие уравнения и найдем для него два решения: 1) можно взять x = 2 и 2) можно взять x = 1. Легко проверить оба решения:

1) 2 2 – 3 · 2 = –2 и 2) 1 2 – 3 · 1 = –2

Если мы вспомним начальное уравнение

(3x + 5) / (x – 1) = (2x + 18) / (2x – 2),

то увидим, что теперь мы получим оба его решения: 1) x = 2 есть то решение, которое имеет прямой смысл и не обращает знаменателя в нуль, 2) x = 1 есть то решение, которое обращает знаменателя в нуль и не имеет прямого смысла.

Найдем общего знаменателя дробей, входящих в это уравнение, для чего разложим на множители каждого из знаменателей:

1) x 2 – 5x + 6 = x 2 – 3x – 2x + 6 = x(x – 3) – 2(x – 3) = (x – 3)(x – 2),

2) x 2 – x – 2 = x 2 – 2x + x – 2 = x (x – 2) + (x – 2) = (x – 2)(x + 1),

3) x 2 – 2x – 3 = x 2 – 3x + x – 3 = x (x – 3) + (x – 3) = (x – 3) (x + 1).

Общий знаменатель равен (x – 3)(x – 2)(x + 1).

Умножим обе части данного уравнения (а его мы теперь можем переписать в виде:

на общего знаменателя (x – 3) (x – 2) (x + 1). Тогда, после сокращения каждой дроби получим:

3(x + 1) – 2(x – 3) = 2(x – 2) или
3x + 3 – 2x + 6 = 2x – 4.

Это решение имеет прямой смысл: оно не обращает в нуль ни одного из знаменателей.

Если бы мы взяли уравнение:

то, поступая совершенно так же, как выше, получили бы

3(x + 1) – 2(x – 3) = x – 2

3x + 3 – 2x + 6 = x – 2

3x – 2x – x = –3 – 6 – 2,

откуда получили бы

что невозможно. Это обстоятельство показывает, что нельзя найти для последнего уравнения решения, имеющего прямой смысл.

Видео:Как выглядит самая сложная задача математики? Фрактал КоллатцаСкачать

Задачи тысячелетия. Просто о сложном

Привет, хабралюди!

Сегодня я бы хотел затронуть такую тему как «задачи тысячелетия», которые вот уже десятки, а некоторые и сотни лет волнуют лучшие умы нашей планеты.

После доказательства гипотезы (теперь уже теоремы) Пуанкаре Григорием Перельманом, основным вопросом, который заинтересовал многих, был: «А что же он собственно доказал, объясните на пальцах?» Пользуясь возможностью, попробую объяснить на пальцах и остальные задачи тысячелетия, или по крайней мере подойти в ним с другой более близкой к реальности стороны.

Равенство классов P и NP

Все мы помним из школы квадратные уравнения, которые решаются через дискриминант. Решение этой задачи относится к классу P (Polynomial time) — для нее существует быстрый (здесь и далее под словом «быстрый» подразумевается как выполняющийся за полиномиальное время) алгоритм решения, который и заучивается.

Также существуют NP-задачи (Non-deterministic Polynomial time), найденное решение которых можно быстро проверить по определенному алгоритму. Для примера проверка методом перебора компьютером. Если вернуться к решению квадратного уравнения, то мы увидим, что в данном примере существующий алгоритм решения проверяется так же легко и быстро как и решается. Из этого напрашивается логичный вывод, что данная задача относится как к одному классу так и ко второму.

Таких задач много, но основным вопросом является, все или не все задачи которые можно легко и быстро проверить можно также легко и быстро решить? Сейчас для некоторых задач не найдено быстрого алгоритма решения, и неизвестно существует ли такой вообще.

На просторах интернета также встретил такую интересную и прозрачную формулировку:

Допустим, что вы, находясь в большой компании, хотите убедиться, что там же находится ваш знакомый. Если вам скажут, что он сидит в углу, то достаточно будет доли секунды, чтобы, бросив взгляд, убедиться в истинности информации. В отсутствие этой информации вы будете вынуждены обойти всю комнату, рассматривая гостей.

В данном случае вопрос стоит все тот же, есть ли такой алгоритм действий, благодаря которому даже не имея информации о том, где находится человек, найти его так же быстро, как будто зная где он находится.

Данная проблема имеет большое значение для самых различных областей знаний, но решить ее не могут уже более 40 лет.

Гипотеза Ходжа

В реальности существуют множество как простых так и куда более сложных геометрических объектов. Очевидно, что чем сложнее объект тем более трудоемким становится его изучение. Сейчас учеными придуман и вовсю применяется подход, основная идея которого заключается в том, чтобы вместо самого изучаемого объекта использовать простые «кирпичики» с уже известными свойствами, которые склеиваются между собой и образуют его подобие, да-да, знакомый всем с детства конструктор. Зная свойства «кирпичиков», становится возможным подступиться и к свойствам самого объекта.

Гипотеза Ходжа в данном случае связана с некоторыми свойствами как «кирпичиков» так и объектов.

Гипотеза Римана

Всем нам еще со школы известны простые числа которые делятся только на себя и на единицу (2,3,5,7,11. ). С давних времен люди пытаются найти закономерность в их размещении, но удача до сих пор так никому и не улыбнулась. В результате ученые применили свои усилия к функции распределения простых чисел, которая показывает количество простых чисел меньше или равных определенного числа. Например для 4 — 2 простых числа, для 10 — уже 4 числа. Гипотеза Римана как раз устанавливает свойства данной функции распределения.

Многие утверждения о вычислительной сложности некоторых целочисленных алгоритмов, доказаны в предположении верности этой гипотезы.

Теория Янга — Миллса

Уравнения квантовой физики описывают мир элементарных частиц. Физики Янг и Миллс, обнаружив связь между геометрией и физикой элементарных частиц, написали свои уравнения, объединяющие теории электромагнитного, слабого и сильного взаимодействий. Одно время теория Янга-Миллса рассматривалась лишь как математический изыск, не имеющий отношения к реальности. Однако, позже теория начала получать экспериментальные подтверждения, но в общем виде она все еще остается не решенной.

На основе теории Янга-Миллса построена стандартная модель физики элементарных частиц в рамках которой был предсказан и не так давно обнаружен нашумевший бозон Хиггса.

Существование и гладкость решений уравнений Навье — Стокса

Течение жидкостей, воздушные потоки, турбулентность. Эти, а также множество других явлений описываются уравнениями, известными как уравнения Навье — Стокса. Для некоторых частных случаев уже найдены решения, в которых как правило части уравнений отбрасываются как не влияющие на конечный результат, но в общем виде решения этих уравнений неизвестны, и при этом даже неизвестно, как их решать.

Гипотеза Бёрча — Свиннертон-Дайера

Для уравнения x 2 + y 2 = z 2 в свое время еще Эвклид дал полное описание решений, но для более сложных уравнений поиск решений становится чрезвычайно трудным, достаточно вспомнить историю доказательства знаменитой теоремы Ферма, чтобы убедиться в этом.

Данная гипотеза связана с описанием алгебраических уравнений 3 степени — так называемых эллиптических кривых и по сути является единственным относительно простым общим способом вычисления ранга, одного из важнейших свойств эллиптических кривых.

В доказательстве теоремы Ферма эллиптические кривые заняли одно из важнейших мест. А в криптографии они образуют целый раздел имени себя, и на них основаны некоторые российские стандарты цифровой подписи.

Гипотеза Пуанкаре

Думаю если не все, то большинство точно о ней слышали. Чаще всего встречается, в том числе и на центральных СМИ, такая расшифровка как «резиновую ленту натянутую на сферу можно плавно стянуть в точку, а натянутую на бублик — нельзя». На самом деле эта формулировка справедлива для гипотезы Тёрстона, которая обобщает гипотезу Пуанкаре, и которую в действительности и доказал Перельман.

Частный случай гипотезы Пуанкаре говорит нам о том, что любое трехмерное многообразие без края (вселенная, например) подобно трехмерной сфере. А общий случай переводит это утверждение на объекты любой мерности. Стоит заметить, что бублик, точно так же как вселенная подобна сфере, подобен обычной кофейной кружке.

Заключение

В настоящее время математика ассоциируется с учеными, имеющими странный вид и говорящие о не менее странных вещах. Многие говорят о ее оторванности от реального мира. Многие люди как младшего, так и вполне сознательного возраста говорят, что математика ненужная наука, что после школы/института, она нигде не пригодилась в жизни.

Но на самом деле это не так — математика создавалась как механизм с помощью которого можно описать наш мир, и в частности многие наблюдаемые вещи. Она повсюду, в каждом доме. Как сказал В.О. Ключевский: «Не цветы виноваты, что слепой их не видит».

Наш мир далеко не так прост, как кажется, и математика в соответствии с этим тоже усложняется, совершенствуется, предоставляя все более твердую почву для более глубокого понимания существующей реальности.

Видео:Самая простая нерешённая задача — гипотеза Коллатца [Veritasium]Скачать

топ 5 самых сложных уравнений и неравенств ЕГЭ

Видео:Сложное степное уравнениеСкачать

Линейные уравнения

Линейные уравнения – уравнения типа ax=bax=b a x = b .

Например, 103x+18=4103x+18=4 1 3 x + 1 8 = 4 .

Для решения таких уравнений необходимо перенести неизвестные в одну сторону, числовые значения в другую, затем привести подобные и выразить неизвестное.

Решить уравнение 4x–8=2+3x+44x – 8 = 2 + 3x + 4 4 x – 8 = 2 + 3 x + 4

Решение

1. Перенесем неизвестные в левую часть, числа – в правую (с противоположными знаками):

4x–3x=2+4+84x – 3x = 2 + 4 + 8 4 x – 3 x = 2 + 4 + 8

1. Приведем подобные (сложим и вычтем неизвестные и числа):

x=14x = 14 x = 1 4

Ответ: x=14x = 14 x = 1 4

Противоположный знак – знак обратный исходному при переноси числа или выражения через знак =. Для знака плюс, противоположным будет знак «–» и наоборот, для частного произведение и соответственно для произведения — частное.

Выразить xx x в уравнении 18x+2x–4=10x+1618x + 2x – 4 = 10x + 16 1 8 x + 2 x – 4 = 1 x + 1 6

Решение

1. Перенесем неизвестные в левую часть, числа – в правую

18x+2x–10x=16+418x + 2x – 10x = 16 + 4 1 8 x + 2 x – 1 x = 1 6 + 4

10∗x=2010*x = 20 1 ∗ x = 2

x=20/10=2x = 20/10 = 2 x = 2 / 1 = 2

Ответ: x=2x = 2 x = 2 .

Видео:Сложные уравнения. Как решить сложное уравнение?Скачать

Примеры решения задач

Задание Решить уравнение Решение Расставим порядок действий: Отметим, что выражение, определяющее неизвестную в данном уравнении — . В данном случае последним действием является вычитание, поэтому необходимо найти неизвестное уменьшаемое: к разности надо прибавить вычитаемое: Получили простейшее уравнение с неизвестным множителем. Чтобы найти неизвестный множитель, надо произведение поделить на известный множитель: Ответ

Также некоторые сложные уравнения можно решать следующим образом, который основывается на свойствах арифметических действий.

Задание Решить уравнение Решение Упростим выражение, стоящее в левой части заданного уравнения, используя свойства вычитания: чтобы от суммы отнять число, необходимо это число вычесть из одного из слагаемых суммы и результат прибавить к другому слагаемому. То есть вначале отнимем от пяти два и результат прибавим ко второму слагаемому : Далее определяем порядок выполнения операций: Чтобы найти неизвестное слагаемое , необходимо от суммы 27 отнять известное слагаемое 3: Далее найдем решение простого уравнения, используя правило нахождения неизвестного множителя: чтобы найти неизвестный множитель, надо произведение поделить на известный множитель. Тогда или . Ответ

📽️ Видео

Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Уравнение, которое меняет взгляд на мир [Veritasium]Скачать

Математика это не ИсламСкачать

Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

8 ЛОГИЧЕСКИХ ЗАГАДОК ДЛЯ САМЫХ УМНЫХ! Насколько хорошо развит твой мозг?Скачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Считаем в уме за секунду. #математика #арифметика #счет #ментальнаяарифметика #simplemathСкачать

Как решить сложные уравненияСкачать

Сложные уравнения со скобками. Как решать уравнения в несколько действий в 5 классе.Скачать

Решение уравнений - математика 6 классСкачать

Как решать уравнения с дробью? #shortsСкачать

Решение сложных уравнений 4-5 класс.Скачать

ЖЕСТКАЯ задача на логику! Попробуй решить!Скачать

Как решать дробно-рациональные уравнения? | МатематикаСкачать

Прогульщик опоздал на 20-мин. и получил две ЗАДАЧИ... Его ответ поставил профессора в ступор...Скачать