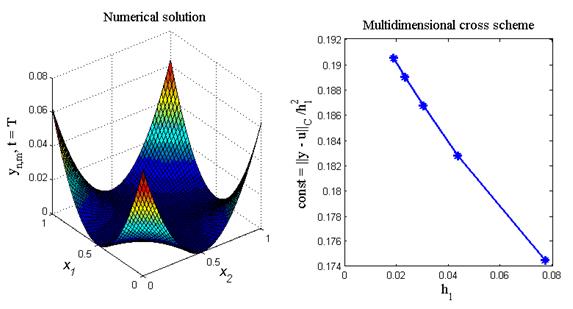
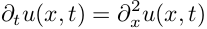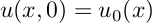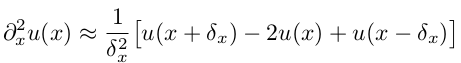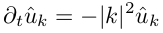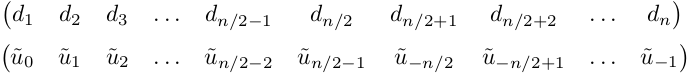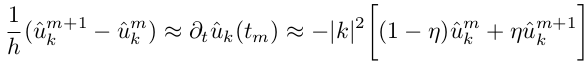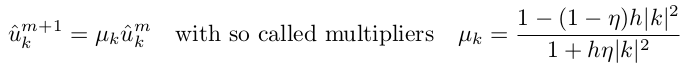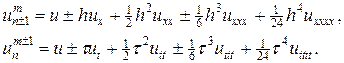Одним из наиболее распространенных в инженерной практике уравнений с частными производными второго порядка является волновое уравнение, описывающее различные виды колебаний. Поскольку колебания — процесс нестационарный, то одной из независимых переменных является время t. Кроме того, независимыми переменными в уравнении являются также пространственные координаты х, у, z. В зависимости от их количества различают одномерное, двумерное и трехмерное волновые уравнения.
Одномерное волновое уравнение – уравнение, описывающее продольные колебания стержня, сечения которого совершают плоскопараллельные колебательные движения, а также поперечные колебания тонкого стержня (струны) и другие задачи. Двумерное волновое уравнение используют для исследования колебаний тонкой пластины (мембраны). Трехмерное волновое уравнениеописывает распространение волн в пространстве (например, звуковых волн в жидкости, упругих волн в сплошной среде и т.п.).
Рассмотрим одномерное волновое уравнение, которое можно записать в виде

Для поперечных колебаний струны искомая функция U(x,t) описывает положение струны в момент t. В этом случае а2 = Т/ρ, где Т — натяжение струны, ρ — ее линейная (погонная) плотность. Колебания предполагаются малыми, т.е. амплитуда мала по сравнению с длиной струны. Кроме того, уравнение (2.63) записано для случая свободных колебаний. В случае вынужденных колебаний в правой части уравнения добавляют некоторую функцию f(x,t), характеризующую внешние воздействия, при этом сопротивление среды колебательному процессу не учитывается.
Простейшей задачей для уравнения (2.63) является задача Коши: в начальный момент времени задаются два условия (количество условий равно порядку входящей в уравнение производной по t):

Эти условия описывают начальную форму струны 

На практике чаще приходится решать не задачу Коши для бесконечной струны, а смешанную задачу для ограниченной струны некоторой длины l. В этом случае задают граничные условия на ее концах. В частности, при закрепленных концах их смещения равны нулю, и граничные условия имеют вид

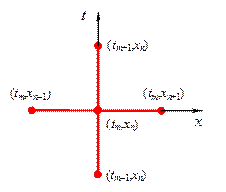
Рассмотрим некоторые разностные схемы для решения задачи (2.63)-(2.65). Простейшей является явная трехслойная схема типа крест (шаблон показан на рис. 2.21). Заменим в уравнении (2.63) вторые производные искомой функции Uпо tи х их конечно-разностными соотношениями с помощью значений сеточной функции 

Рис. 2.21. Шаблон явной схемы
Отсюда можно найти явное выражение для значения сеточной функции на ( j + 1)-ом слое:

Здесь, как обычно в трехслойных схемах, для определения неизвестных значений на (j + 1)-ом слое нужно знать решения на j-ом и (j — 1)-ом слоях. Поэтому начать счет по формулам (2.66) можно лишь для второго слоя, а решения на нулевом и первом слоях должны быть известны. Их находят с помощью начальных условий (2.64). На нулевом слое имеем

Для получения решения на первом слое воспользуемся вторым начальным условием (2.64). Производную 

Из этого соотношения можно найти значения сеточной функции на первом временном слое:

Отметим, что аппроксимация начального условия в виде (2.68) ухудшает аппроксимацию исходной дифференциальной задачи: погрешность аппроксимации становится порядка 

Вместо 

Тогда (2.70) примет вид:

Разностная схема (2.66) с учетом (2.71) обладает погрешностью аппроксимации порядка
При решении смешанной задачи с граничными условиями вида (2.65), т.е. когда на концах рассматриваемого отрезка заданы значения самой функции, второй порядок аппроксимации сохраняется. В этом случае для удобства крайние узлы сетки располагают в граничных точках (х0=0, xI = l). Однако граничные условия могут задаваться и для производной.
Например, в случае свободных продольных колебаний стержня на его незакрепленном конце задается условие

Если это условие записать в разностном виде с первым порядком аппроксимации, то погрешность аппроксимации схемы станет порядка 
Рассмотренная разностная схема (2.66) решения задачи (2.63) — (2.65) условно устойчива. Необходимое и достаточное условие устойчивости:

Следовательно, при выполнении этого условия и с учетом аппроксимации схема (2.66) сходится к исходной задаче со скоростью O(h2+τ2). Данная схема часто используется в практи-ческих расчетах. Она обеспечивает приемлемую точность получения решения U(x,t), которое имеет непрерывные производные четвертого порядка.
Рис. 2.22. Алгоритм решения волнового уравнения
Алгоритм решения задачи (2.63)-(2.65) с помощью данной явной разностной схемы приведен на рис. 2.22. Здесь представлен простейший вариант, когда все значения сеточной функции, образующие двумерный массив, по мере вычисления хранятся в памяти компьютера, а после решения задачи выводятся результаты. Можно было бы предусмотреть хранение решения лишь на трех слоях, что сэкономило бы память. Результаты в таком случае можно выводить в процессе счета (см. рис. 2.13).
Существуют и другие разностные схемы решения волнового уравнения. В частности, иногда удобнее использовать неявные схемы, чтобы избавиться от ограничений на величину шага, налагаемых условием (2.73). Эти схемы обычно абсолютно устойчивы, однако алгоритм решения задачи и программа для компьютера усложняются.
Построим простейшую неявную схему. Вторую производную по tв уравнении (2.63) аппроксимируем, как и ранее, по трехточечному шаблону с помощью значений сеточной функции на слоях j— 1, j, j + 1. Производную до х заменяем полусуммой ее аппроксимации на (j + 1)-ом и (j— 1)-ом слоях (рис. 2.23):
Рис. 2.23. Шаблон неявной схемы
Из этого соотношения можно получить систему уравнений относительно неизвестных значений сеточной функции на (j+ 1)-ом слое:

Полученная неявная схема устойчива и сходится со скоростью 
При двух или трех независимых пространственных переменных волновые уравнения принимают вид
Для них также могут быть построены разностные схемы по аналогии с одномерным волновым уравнением. Разница состоит в том, что нужно аппроксимировать производные по двум или трем пространственным переменным, что, естественно, усложняет алгоритм и требует значительно больших объемов памяти и времени счета. Подробнее двумерные задачи будут рассмотрены ниже для уравнения теплопроводности.
Видео:Численное решение волнового уравненияСкачать

Спектральный метод на примере простых задач матфизики
В этой статье описан псевдоспектральный метод численного решения уравнений матфизики, используемый в вычислительной гидродинамике, геофизике, климатологии и во многих других областях.
Одномерная задача распространения тепла по стержню
Для начала рассмотрим простую одномерную задачу распространения тепла в стержне. Уравнение, описывающее распространение тепла при некотором начальном распределении температуры по стержню:
Такое уравнение решается аналитически методом разделения переменных, например здесь, но нас интересует как это можно сделать численно. Прежде всего нужно определиться, как считать вторую пространственную производную по х. Проще всего это делается каким-нибудь разностным методом, например:
Но мы поступим иначе. Распределение температуры есть функция координаты и времени, и в каждый момент времени эта функция может быть представлена в виде суммы ряда Фурье, который в численном виде обрезается на n-ом члене:
Где u^«с крышечкой» — это коэффициенты разложения ряда Фурье. Подставим выражение для ряда в уравнение переноса тепла:
Получаем уравнение для коэффициентов Фурье, в котором отсутствует производная по координате! Теперь это обыкновенное дифференциальное уравнение, а не в частных производных, которое можно решить простым разностным методом. Уже легче, теперь остается найти коэффициенты разложения и в этом нам очень поможет быстрое преобразование Фурье (дальше FFT).
Логика здесь следующая:
1) в начальный момент времени дана функция координаты, описывающая распределение температуры по стержню;
2) разбиваем стержень на сетку из n точек;
3) находим комплексные коэффициенты Фурье с помощью алгоритма FFT, обозначим операцию как F(u);
4) умножаем полученные коэффиценты на -|k| 2 , получаем Фурье-образ второй производной. Аналогично можно получить Фурье-образ производной более высоких порядков p, достаточно умножить на (ik) p ;
5) делаем обратное преобразование Фурье F -1 (u), с помощью алгоритма IFFT, получаем значения второй производной в точках на сетке;
6) делаем шаг по времени, уже обычной разностной, явной или неявной, схемой;
7) повторяем.
Рассмотрим теперь как это работает в программе для Matlab/Octave. В качестве начального распределения температуры возьмем гладкую функцию u0=2+sin(x)+sin(2x), стержень длинной 2π разобьем на 50 точек, с шагом по времени h=0.1, граничные условия периодичные (кольцо).
Стоит отметить особенность алгоритма FFT в Matlab, связанную с тем, что полученные коэффициенты разложения на выходе d=fft(u) идут не по порядку, а смещены, первая половина на месте второй и наоборот. Cначала идут коэффициенты с номерами от 0 до n/2-1, потом с номерами от -n/2 до -1. С этим были проблемы…
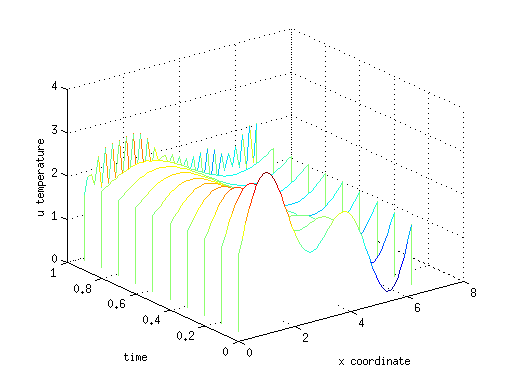
Полученное решение можно видеть на графике в виде «водопада» линий распределения температуры по х для каждого момента времени t. Видно, что решение испытывает сильные осциляции численную неустойчивость, связано это с невыполнением критерия Куранта. Избавиться от неустойчивости можно уменьшив шаг по времени, либо применяя более продвинутую неявную схему, например Кранка-Николсона.
Двумерное уравнение диффузии
Начальные условия: u0 = 1 + sin(2X) + cos(2Y), где u теперь 2d-массив u(i,j). Используем неявную схему интегрирования по времени (т.е. выразим m+1 шаг через m-й):
Можно доказать, что такая неявная схема никогда не расходится при η>0.5, будем использовать η=1. Таким образом каждое новое значение u m+1 получаем умножением u m на коэффициент μk, зависящий от временного шага и волновых чисел k, т.е. μk — это константа, которую не нужно пересчитывать на каждом шаге!
Двумерное волновое уравнение
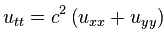
В волновом уравнении присутствует вторая производная по времени, поэтому задача сводится к системе двух обыкновенных диффуров, одна переменная — u, вторая — ut, схему по времени в коде использовал самую простую явную, поэтому точность небольшая, шаг по времени очень маленький, зато код выглядит относительно просто. Впрочем, этого хватает для демонстрации работоспособности метода.
Периодичные граничные условия:
Фиксированные граничные условия (0 на краях, отражение волн от границ):
Выводы
В статье продемонстрировано несколько примеров применения спектрального метода для простых задач матфизики. Основная суть суть спектрального метода, это замена исходных диффренциальных уравнений в частных произодных на обыкновенные диффуры для коэффициентов разложения искомых функций по некоторому базису. Базисом могут быть синусы-косинусы, комплексные экспоненты, ортогональные полиномы, если требует геометрия — цилиндрические или сферические функции. Найденные коэффициенты в каждый момент времени позволяют восстановить искомое решение, а алгоритм FFT позволяет делать это быстро.
Преимуществами метода являются:
- Хорошая точность для «хороших» функций. С увеличением количества точек сетки n ошибка метода конечных разностей падает как O(N -m )) (где m — некая постоянная, которая зависит от порядка метода и гладкости функции), а для спектрального метода точность может быть экспоненциальной O(c N ), где 0
Видео:Численное решение волнового уравнения (2)Скачать

Двухслойная акустическая схема
Лекция №13
Волновое уравнение
Гиперболическое волновое уравнение описывает колебания струны, движение сжимаемого газа, распространение электромагнитных волн и ряд других явлений.
Типичной одномерной задачей является задача описания малых колебаний натянутой струны с распределенной по длине нагрузкой f(t,x):
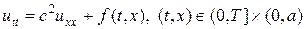
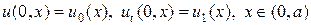
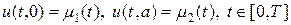
Уравнение колебания струны (1) дополняется начальными условиями (2), которые, в отличие от параболического уравнения требуют двух условий: начального смещения относительно положения равновесия u0(x) и начальную скорость движения u1(x). Кроме того, задаются краевые условия (3), которые называются краевыми условиями первого рода, они описывают смещение концов струны относительно положений равновесия. Краевые условия могут быть и иного рода.
Составим несложную, но эффективную разностную схему для численного решения задачи (1) — (3), выбирая для простоты равномерные по t и x сетки. В качестве шаблона разностной схемы возьмем, представленный на рис.1 шаблон в форме “креста”. Аппроксимируя производные в (1) конечными разностями, получим трехслойную схему следующего вида
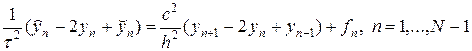
с граничными условиями
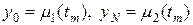
Рис.1. Разностная схема (4) в форме креста
По форме шаблона схему (4) называют схемой “крест”. Исследуем схему крест.
Процедура вычисления решения выглядит следующим образом. На нулевом слое решение известно из начального условия
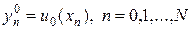
На первом слое решение можно также вычислить по начальным данным. Простейший способ получения решения на первом слое состоит в аппроксимации второго начального условия в (2) согласно представлению:
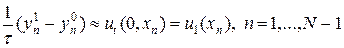
Аппроксимация (6) имеет первый порядок точности, тогда как в схеме крест разностный оператор второй производной по времени имеет второй порядок точности. Поэтому для более точной аппроксимации необходимо учесть еще один член разложения, т.е.
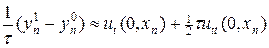
Подставляя в (6¢) utt из (1), найдем
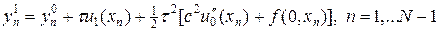
Схема крест (4) является явной, поскольку позволяет выразить решение на следующем слое 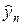
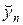
Для изучения аппроксимации схемы крест, разложим точное решение по формуле Тейлора с центром в узле (tm,xn), считая все появляющиеся в разложении производные непрерывными:
Используя данные разложения, легко можно найти невязку схемы крест:
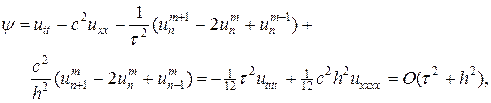
а также невязку начального условия (6):
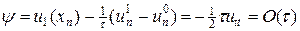
или более точного начального условия (6¢¢):
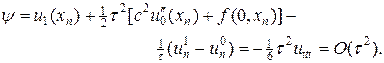
Начальные (2) и краевые условия (3) аппроксимируются точно. В итоге разностная схема (4) с начальными условиями (5), (6¢¢) имеет порядок аппроксимации 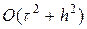
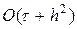
Устойчивость схемы крест исследуем методом разделения переменных, полагая
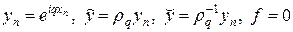
Подставляя представление (8) в (4), для множителя роста гармоник находим квадратное уравнение
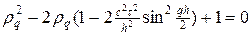
По теореме Виета произведение корней квадратного уравнения (9) равно единице, т.е. 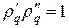
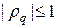
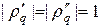
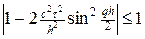
Для выполнения неравенства (10) необходимо и достаточно соблюдение условия Куранта:
ct 2 (t,x) > 0. Будем считать, что функции k(t,x), f(t,x) в (17) кусочно-непрерывны, причем разрывы неподвижны, т.е. лежат на линиях x = const. Предполагается, что на разрывах выполняется условие сопряжения [u] = [kux] = 0, т.е. решение u и поток kux являются непрерывными функциями.
Выберем по времени равномерную сетку, а по пространству специальную неравномерную сетку, у которой все точки разрыва коэффициентов являются узлами. Построим аналог наилучшей консервативной схемы (11.19) — (11.21¢), разобранной в лекции №11:
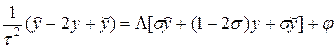
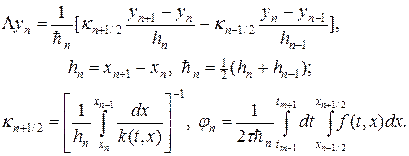
Известно[1], что при сделанных предположениях и при достаточно гладких начальных и граничных условиях схема (18), (18¢) равномерно сходится со скоростью 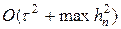
Проведем численный расчет по разностной схеме (18), (18¢) задачи (17), (2), (3) в прямоугольной области G(t,x) = [0,T]´[0,a] при условии, что
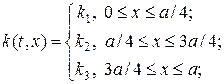
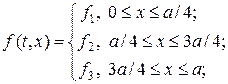
где k1, k2, k3, f1, f2, f3 — некоторые постоянные величины. С учетом положений разрывов в (19), (20) определим равномерную сетку по пространству xn = nh, n = 1,…,N, где N = 4l + 1, l = 1,2,… Определим также равномерную сетку по времени, т.е. tm = t m, 1,…,M. С учетом сделанных предположений рассмотрим следующую схему аппроксимации для интегралов в (18¢):
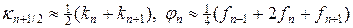
В качестве начальных и граничных условий положим
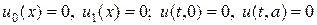
На листинге_№3 приведен код программы численного решения задачи (17), (19), (20), (22) с помощью наилучшей разностной схемы (18), (18¢), (21).
%Программа решения волнового уравнения (17), (19),
%(20) с помощью разностной схемы (18), (18′), (21)
global a k1 k2 k3 f1 f2 f3
%Определяем габариты области интегрирования по
%времени T и пространству a
%Определяем константы k1,k2,k3,f1,f2,f3
k1=1; k2=10; k3=1; f1=1; f2=10; f3=1;
%Определяем весовую константу
%Определяем число узлов по пространству и времени
%Определяем шаги по времени и пространству
%Определяем сетки по времени и пространству
%Используем начальные данные из (22) для
%определения численного решения на первом и
%втором слое по формуле (6»)
%Определяем левое и правое граничные условия,
%Применяем неявную наилучшую схему (18), (18′)
%Определяем коэффициенты прогонки
%Рисуем трехмерную поверхность решения в координатах
%Определяем функцию квадрата скорости звука k(t,x)
global a k1 k2 k3
if (x>=0)&(x 0.25*a)&(x =0.75*a)&(x =0)&(x 0.25*a)&(x =0.75*a)&(x 0), инвариант s — уравнению переноса влево. Для однородной задачи, когда F = 0, m1 = m2 =0, величины r, s переносятся по своим характеристикам без изменения, с чем и связано их наименование.
Для инвариантов можно составить разностные схемы, аналогичные разностным схемам для уравнения переноса. При этом шаблон каждой из схем должен учитывать направление характеристики данного уравнения. Рассмотрим простейшую явную разностную схему для уравнений (39):
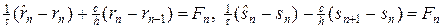
Схема (42) является схемой бегущего счета. Нетрудно показать, что при выполнении условия Куранта ct £ h схема устойчива и сходится с порядком точности 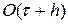
Изучим разностную схему для инвариантов на примере численного решения задачи (39) с помощью разностной схемы (42), выбирая правую часть, начальные и граничные условия согласно (35), (36). В этом случае при учете (40), (41), находим следующие выражения для правой части, начальных и граничных условий:
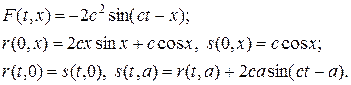
Нетрудно проверить, что аналитическим решением задачи (39), (43) являются выражения вида:
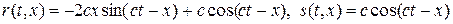
На листинге_№5 приведен код программы расчета задачи акустики в инвариантах (39) со специальной правой частью, начальными и граничными условиями (43).
%Программа решения уравнений акустики (39) в
%инвариантах с правой частью, начальными и
%граничными условиями вида (43)
%Определяем габариты области интегрирования по
%времени T и пространству a, а также определяем
%величину скорости c
%Определяем число удвоений числа узлов сетки по
%времени и пространству dmax
%Организуем цикл расчетов на различных сетках
%Определяем число узлов сетки по пространству
%определяем шаги по времени и пространству
%Определяем сетки по времени и пространству
%Определяем начальные условия (43) для
%инвариантов r и s
%Организуем цикл расчетов по времени
%Осуществляем бегущий расчет инварианта r,
%осуществляемый слева направо
%Учитываем правое граничное условие (43)
%Осуществляем бегущий расчет инварианта s,
%осуществляемый справа налево
%Учитываем левое граничное условие (43)
%Ошибку численного расчета инвариантов r и s
%оцениваем как разность численного и
%аналитического решений в норме C. Делим
%полученную ошибку на шаг по пространству h и
%находим предстепенную константу скорости
%сходимости схемы с инвариантами
%Рисуем численное решение инварианта r
%Рисуем численное решение инварианта s
%Рисуем график зависимости предстепенной
%константы от шага сетки h
%Определяем функцию правой части
%Определяем аналитический вид инварианта r
%Определяем аналитический вид инварианта s
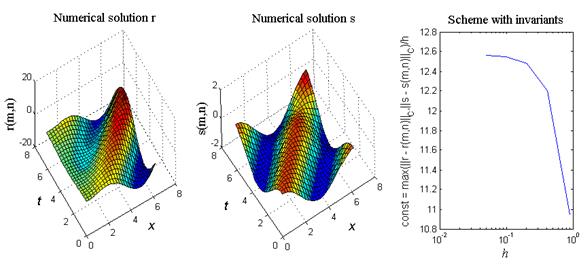
Рис.8. Решение задачи акустики (39), (43) в инвариантах
На рис.8 приведен итог работы кода программы листинга_№5. На левом рисунке приведено изображение численного решения инварианта r, на среднем рисунке — инварианта s. Правый график демонстрирует зависимость const от h в представлении для ошибки численного решения следующего вида:
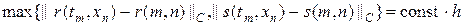
где r(t,x), s(t,x) — аналитические решения (44). Из графика видно, что по мере уменьшения шага сетки h величина const действительно выходит на некоторое постоянное значение, при этом шаг по времени выбирался порядка шага по пространству, т.е. t
h. Это подтверждает также то, что скорость сходимости разностной схемы (42) — 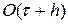
Многомерные схемы
Рассмотрим волновое уравнение в p-мерном пространстве следующего вида:
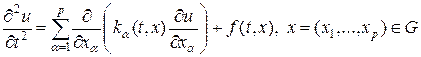
Решение задачи (45) предполагает определение начальных и краевых условий:
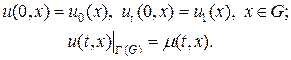
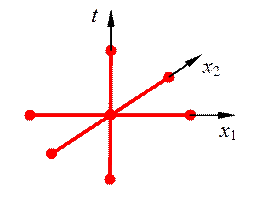
Схема “крест” строится аналогично одномерной схеме (4) на шаблоне, вид которого для случая двух измерений показан на рис.9. При произвольном числе измерений разностная схема крест может быть записана в виде:
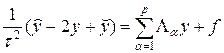
при этом в случае переменных коэффициентов ka операторы La определяются также как и для наилучшей схемы (18), (18¢).
Рис.9. Шаблон схемы крест в двумерном случае
Трехслойная схема (47) является явной. Вычисления с помощью схемы (47) одинаково просты для любого числа измерений. Легко проверить, что схема имеет порядок аппроксимации 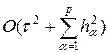
Исследуем устойчивость схемы (47) методом разделения переменных, считая коэффициенты ka постоянными. Для этого подставим в (47) многомерную гармонику, имеющую следующий вид на трех временных слоях:
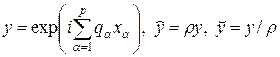
В итоге для множителя роста r получим квадратное уравнение
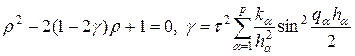
Анализ корней уравнения (48) показывает, что разностная схема (47) устойчива при условии, что
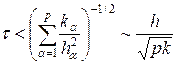
Условие устойчивости (49) является аналогом условия Куранта (11).
Изучим схему крест на примере численного решения двумерной задачи (45), (46), когда k1 = k2 = c 2 = const > 0, т.е. решим уравнение
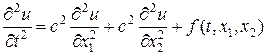
Положим вид правой части, начальные и краевые условия в прямоугольной области G(x1,x2) = [0,a]´[0,b] следующего вида:
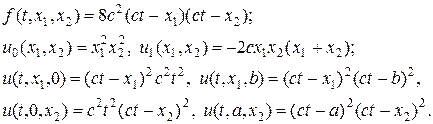
Нетрудно проверить, что задача (50), (51) в области G имеет аналитическое решение
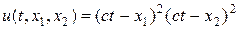
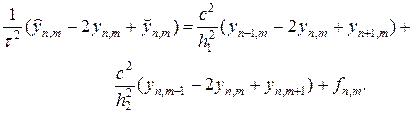
На листинге_№6 приведен код программы решения задачи (50), (51) с помощью разностной схемы (53).
%Программа решения двумерного волнового уравнения
%(50), (51) с помощью явной схемы крест (53)
%Определяем габариты области интегрирования
%(t,x1,x2)=[0,T]x[0,a]x[0,b] и скорость переноса c
%Определяем число сгущений сеток по времени и
%Определяем цикл расчетов с различными сетками
%Определяем число узлом по времени Nt и по
%пространству N и M
%Определяем шаги по времени и пространству
%Определяем сетки по времени и пространству
t=0:tau:T; x1=0:h1:a; x2=0:h2:b;
%Используем начальное условие в (51) для
%определения численного решения на первом слое
%Используем начальное условие в (51) для
%определения численного решения на втором слое
%со вторым порядком точности по времени
%Удовлетворяем граничным условиям (51) при
%Удовлетворяем граничным условиям (51) при
%Организуем основной цикл расчета по времени с
%помощью явной схемы крест (53)
%Определяем разницу между численным решением и
%аналитическим решениями в норме C, т.е. определяем
%ошибку численного решения
%Делим ошибку численного решения на квадрат шага
%сетки по пространству
%Рисуем численное решение на момент времени T
%Рисуем график зависимости предстепенной константы
%Определяем функцию правой части уравнения (50)
%Определяем аналитическое решение (52)
На рис.10 приведен итог работы кода программы листинга_№6. На левом рисунке изображено численное решение yn,m в момент времени t = T, полученное с помощью численного расчета по разностной схеме (53). На правом рисунке изображена динамика зависимости предстепенной константы cost от шага сетки h1 в оценке ошибки численного решения вида:
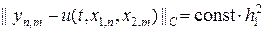
где 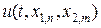
h1. Анализ правого графика показывает, что предстепенная константа немного растет. К сожалению, имеющиеся вычислительные ресурсы не позволяют за разумное время провести расчет для более подробных сеток и добиться более очевидного выхода величины const на некоторое постоянное значение при стремлении шага сетки к нулю. Это явилось бы подтверждением скорости сходимости схемы (53) — 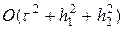
Рис.10. Численное решение двумерного волнового уравнения (50), (51) с
помощью явной схемы крест (53)
Факторизованные схемы. Ограничение на шаг по времени, возникающее в связи с условием Куранта (49), в явной схеме крест предыдущего численного примера было достаточно обременительным. Это ограничение может быть преодолено путем использования безусловно устойчивых многомерных экономичных схем, которые называются также факторизованными схемами или схемами с расщеплением. Построим такие схемы.
Для численного решения многомерного волнового уравнения (45) рассмотрим следующую разностную схему, называемую в дальнейшем исходной:
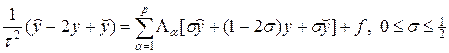
Операторы La в (54) — трехточечные и вычисляются по формуле, аналогичной (18¢). Поскольку схема (54) симметрична по пространству и времени, постольку она имеет порядок аппроксимации 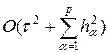
Перепишем схему (54) в виде
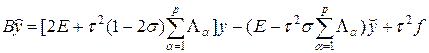
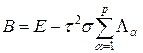
Оператор B в (56) в той же форме (11.47) уже встречался у нас при изучении локально-одномерного метода решения многомерного параболического уравнения. Обращение оператора B сводится к обращению ленточной матрицы, внешний вид которой приведен на рис.6 лекции №12. Для двумерного случая данная матрица является пятидиагональной, к которой метод прогонки не применим. Таким образом, оператор B является труднообратимым, а разностная схема (54), (55) неэкономичной.
Оператор (56) можно приближенно заменить факторизованным оператором
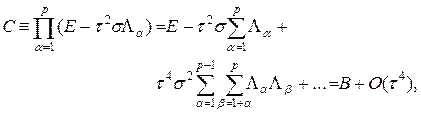
т.е. приближенно расщепить на произведение одномерных сомножителей. Заменяя в исходной схеме (55) оператор B на оператор C, получим факторизованную схему:
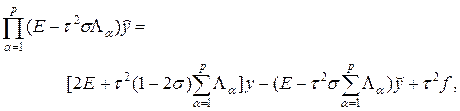
которая отличается от исходной (54). Исследуем схему (58).
Аппроксимация. Учитывая (57), раскроем произведение в левой части (58), тогда, после несложных преобразований, получим
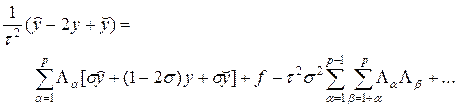
Сравнивая схемы (54) и (59) убеждаемся, что они различаются на члены порядка 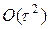
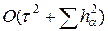
Устойчивость, как обычно, исследуем методом разделения переменных, подставляя в (58) многомерную гармонику, которая ранее уже была использована в схеме крест. Для множителя роста r можно получить квадратное уравнении
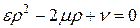
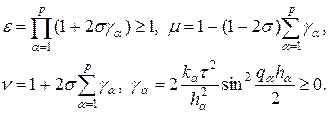
Уравнение (60) аналогично уравнению (30), поэтому оба его корня по модулю не превышают единицы, если выполняются неравенства (32):
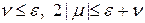
Согласно (60¢) первое из неравенств выполняется всегда. Второе неравенство заменим на более жесткое |m| £ n, которое, как нетрудно проверить, выполняется при условии, что
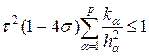
Неравенство (61) является достаточным условием устойчивости разностной схемы (58). В частности, когда s ³ ¼ неравенство (61) выполняется при любых шагах по времени и пространству, т.е. схема (58) является безусловно устойчивой.
Безусловная сходимость факторизованной схемы (58) со скоростью 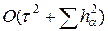
Вычисление разностного решения сводится к последовательности одномерных прогонок по всем пространственным направления xa, a = 1,…,p. В итоге, можно констатировать, что для многомерного волнового уравнения существуют экономичные разностные схемы, сходящиеся со скоростью 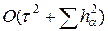
Изучим факторизованную разностную схему (58) на примере численного решения задачи (50), (51). Перепишем схему (58) для данного случая в виде системы двух уравнений, раскрывая тем самым преимущества факторизации:
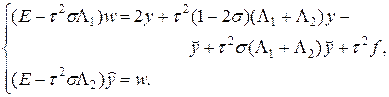
В систему (62) добавлено вспомогательное решение w. Для численного решения систему (62) необходимо преобразовать к более подробному виду:
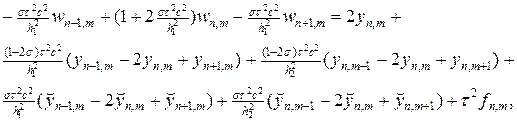
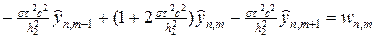
Учитывая (51), (63¢), граничные условия без потери точности для вспомогательного решения w можно представить в следующем виде:
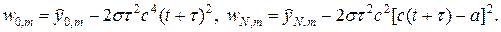
Расчет по схеме (63), (63¢) состоит из двух этапов. На первом этапе прогонками по направлению x1 решается уравнение (63) и находится w. На втором этапе прогонками по направлению x2 решается уравнение (63¢) и находится 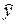
%Программа решения двумерного волнового уравнения
%(50), (51) с помощью факторизованной схемы
%Определяем габариты области интегрирования
%(t,x1,x2)=[0,T]x[0,a]x[0,b] и скорость переноса c
%Определяем число сгущений сеток по времени и
%Определяем цикл расчетов с различными сетками
%Определяем число узлом по времени Nt и по
%пространству N и M
%Определяем шаги по времени и пространству
%Определяем сетки по времени и пространству
t=0:tau:T; x1=0:h1:a; x2=0:h2:b;
%Используем начальное условие из (51) для
%определения численного решения на первом слое
%Используем начальное условие из (51) для
%определения численного решения на втором слое
%со вторым порядком точности по времени
%Удовлетворяем граничным условиям из (51) при
%Удовлетворяем граничным условиям из (51) при
%Организуем основной цикл расчета по времени с
%помощью факторизованной схемы (63), (63′)
%Решаем уравнение (63) путем осуществления
%прогонок по направлению x1
%Используем левое граничное условие из (64)
📸 Видео
Численное решение волнового уравнения HDСкачать

Метод Фурье для волнового уравненияСкачать

Решение волнового уравнения в прямоугольникеСкачать

Численное решение задачи Коши методом ЭйлераСкачать

4.3 Решение неоднородного волнового уравнения на бесконечной прямойСкачать

5. Решение волнового уравнения на отрезке методом ФурьеСкачать

10. Волновое уравнение на отрезке. Сложные задачиСкачать

Сеточные методы решения дифференциальных уравнений в частных производных.Скачать

Микропроект. Решение волнового уравнения.Скачать

3.1 Формула Даламбера, решение волнового уравнения на бесконечной прямойСкачать

Задача Коши для волнового уравнения (Часть 1)Скачать

Решение волнового уравнения в три руки под запись на камеру 8000fpsСкачать

4.1. Общее решение волнового уравненияСкачать

Уравнение колебаний струны. Метод разделения переменных. Метод ФурьеСкачать

Вывод волнового уравненияСкачать