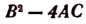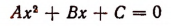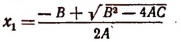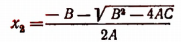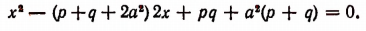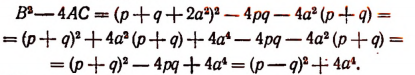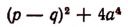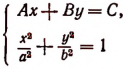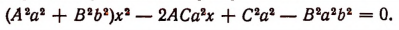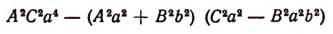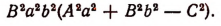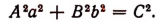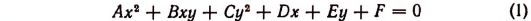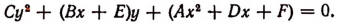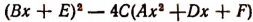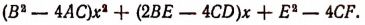- Инструменты сайта
- Основное
- Навигация
- Информация
- Действия
- Содержание
- Результант
- Результант в форме Сильвестра
- Свойства
- Результант как полиномиальная функция коэффициентов
- Субрезультанты и наибольший общий делитель
- Результант в форме Кронекера
- Результант в форме Безу
- Еще некоторые представления результанта
- Применения результанта
- Преобразование Чирнгауза
- Исключение переменных в системе полиномиальных уравнений
- Теорема Безу
- Поиск мнимого корня полинома
- Дифференциальный результант
- Задачи
- Источники
- Результант и дискриминант
- Дискриминант многочлена
- Исследование уравнений в математике с примерами решения
- Что значит исследовать уравнение
- Исследование уравнений первой степени с одним неизвестным
- Случай, когда уравнение не имеет корня
- Исследование системы двух уравнений первой степени с двумя неизвестными
- Исследование квадратного уравнения
- Исследование уравнения первой степени с одним неизвестным
- Исследование системы двух уравнений 1-й степени с двумя неизвестными
- Исследование квадратного уравнения
- Примеры решения уравнений
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Видео:Решение систем уравнений второго порядка. 8 класс.Скачать

Результант
Будем обозначать через $ mathbb A_ $ какое-либо из множеств $ mathbb Z, mathbb Q, mathbb R_ $ или $ mathbb C_ $.
Видео:9 класс, 11 урок, Методы решения систем уравненийСкачать

Результант в форме Сильвестра
Для полиномов $ f(x)=a_x^n+a_1x^+dots+a_n $ и $ g(x)=b_x^m+b_1x^+dots+b_m $ при $ a_ne 0, b_0ne 0 $ рассмотрим квадратную матрицу порядка $ m+n_ $ $$ M=left(begin a_0&a_1&a_2&ldots&ldots&a_n&0&dots &0 &0\ 0&a_0&a_1&ldots&ldots&a_&a_n&dots&0 &0\ vdots&&ddots&&&&&&ddots\ 0&0&ldots&a_0&ldots&ldots & & ldots &a_ &a_n\ 0&0&ldots&&b_0&b_1&ldots& ldots &b_&b_m\ 0&0&ldots&b_0&b_1&ldots &&ldots &b_m&0\ vdots&&&ldots&&&& &&vdots\ 0&b_0&ldots&ldots&&b_m&ldots&&ldots&0\ b_0&ldots&ldots&&b_m&0&ldots&&&0 endright) begin left.begin \ \ \ \ endright> m \ left. begin \ \ \ \ \ endright> n end $$ (элементы выше $ a_ $ и $ b_ $, и ниже $ a_ $ и $ b_ $ все равны нулю). Выражение $$ (f,g)= (-1)^<n_(n-1)/2> det M $$ называется результантом 1) (в форме Сильвестра) полиномов $ f_ $ и $ g_ $ .
Пример.
$$ (a_0x^2+a_1x+a_2, b_0x^2+b_1x+b_2)= $$ $$ =(a_0b_2-a_2b_0)^2-(a_0b_1-a_1b_0)(a_1b_2-a_2b_1) , . $$
Теорема. Если $ lambda_,dots,lambda_n $ — корни полинома $ f_(x) $, а $ mu_,dots,mu_m $ — корни полинома 2) $ g_(x) $ , то
$ (f,g)=0_ $ тогда и только тогда, когда полиномы $ f_(x) $ и $ g_(x) $ имеют общий корень.
Откуда возникает результант в форме Сильвестра см. ☞ ЗДЕСЬ
Пример. Найти все значения параметра $ <coloralpha > $, при которых полиномы
Решение. Вычисляем определитель с помощью элементарных преобразований строк: $$ (x^3+ <coloralpha >,x+1, x^2+ <coloralpha >,x+1)= (-1)^left| begin 1 & 0 & <coloralpha > & 1 & 0 \ 0 & 1 & 0 & <coloralpha > & 1 \ 0 & 0 & 1 & <coloralpha > & 1 \ 0 & 1 & <coloralpha > & 1 & 0 \ 1 & <coloralpha > & 1 & 0 & 0 end right| =- left| begin 1 & 0 & <coloralpha > & 1 & 0 \ 0 & 1 & 0 & <coloralpha > & 1 \ 0 & 0 & 1 & <coloralpha > & 1 \ 0 & 0 & <coloralpha > & 1- <coloralpha > & -1 \ 0 & <coloralpha > & 1- <coloralpha > & -1 & 0 end right|= $$ (первую строку вычли из последней, вторую — из предпоследней), разложим по элементам первого столбца: $$ =-left| begin 1 & 0 & <coloralpha > & 1 \ 0 & 1 & <coloralpha > & 1 \ 0 & <coloralpha > & 1- <coloralpha > & -1 \ <coloralpha > & 1- <coloralpha > & -1 & 0 end right|=- left| begin 1 & 0 & <coloralpha > & 1 \ 0 & 1 & <coloralpha > & 1 \ 0 & <coloralpha > & 1- <coloralpha > & -1 \ 0 & 1- <coloralpha > & -1- <coloralpha >^2 & — <coloralpha > end right|= $$ (из последней строки вычли первую, домноженную на $ <coloralpha > $), снова разложим по первому столбцу: $$ =-left| begin 1 & <coloralpha > & 1 \ <coloralpha > & 1- <coloralpha > & -1 \ 1- <coloralpha > & -1- <coloralpha >^2 & — <coloralpha > end right|= -left| begin 1 & <coloralpha > & 1 \ <coloralpha >+1 & 1 & 0 \ 1 & -1 & 0 end right|= $$ (ко второй строке прибавили первую, к третьей — первую, домноженную на $ <coloralpha > $), разложим по последнему столбцу: $$ =-left| begin <coloralpha >+1 & 1 \ 1 & -1 end right|=-(-( <coloralpha >+1)-1)= <coloralpha >+2 . $$
Ответ. $ <coloralpha >=-2_ $.
Проверка. $ x^-2,x+1equiv (x-1)(x^2+x-1), x^2-2,x+1equiv (x-1)(x+1) $.
Найти все значения параметра $ <coloralpha > $, при которых полиномы
$$ x^+ <coloralpha >,x^2-14 quad mbox x^+ <coloralpha >,x-14 $$ имеют общий корень.
В частном случае $ g_(x)equiv f^(x) $ результант превращается в дискриминант.
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Свойства
2. $$ left(f_1cdot f_2,, gright)=(f_1,,g)cdot (f_2,, g) $$ 3. $$(Af(x)+Bg(x),Cf(x)+Dg(x))=(AD-BC)^nleft(f(x),g(x)right)$$ Последнее равенство справедливо в предположении, что $$ deg f= nge m =deg g ge 1 quad u quad deg (Af(x)+Bg(x))=deg (Cf(x)+Dg(x))= n .$$ 4. Если $ f(x)=a_x^n + a_1x^ + dots + a_n $ и $ g(x)=b_x^m+b_1x^+dots+b_m $ и числа $ a_,a_n,b_0,b_m $ отличны от нуля, то $$ (f,g) = (-1)^(a_nx^n+ldots+a_0,b_mx^m+ldots+b_0) .$$
Видео:Математика | Система уравнений на желтую звездочку (feat Золотой Медалист по бегу)Скачать

Результант как полиномиальная функция коэффициентов
По построению, результант является полиномом с целыми коэффициентами относительно коэффициентов полиномов $ f_(x) $ и $ g_(x) $: $$ (a_0 x^n+ ldots + a_, b_0x^m + ldots + b_m)equiv R(a_0,dots,a_n,b_0,dots,b_m) in [a_0,dots,a_n,b_0,dots,b_m] ;$$ степень этого полинома равна $ mn_ $. Как полином от $ a_0,dots,a_ $ результант является однородным степени $ m_ $; как полином от $ b_,dots,b_m $ результант является однородным степени $ n_ $.
Теорема. Если полиномы $ f_(x) $ и $ g_(x) $ имеют единственный общий корень $ lambda_ $, то
Доказательство. Рассмотрим случай $ j=0, k=1 $. Продифференцируем по $ b_ $ определяющее результант равенство: $$ (f,g)= a_0^m prod_^n g(lambda_j) ; $$ получим: $$ frac<partial b_
>= sum_^n frac<partial b_
> cdot prod_^n g(lambda_j) = sum_^n lambda_j^ prod_^n g(lambda_j) . $$ Если полиномы $ f_(x) $ и $ g_(x) $ имеют единственный общий корень $ lambda_1 $, то последнее равенство преобразуется в $$ frac<partial b_
>=lambda_1^ prod_^n g(lambda_j) $$ и произведение $ prod $ отлично от нуля. Поскольку равенство справедливо для любых значений $ q_ $, то $$ frac<partial b_> Bigg/ frac<partial b_
>= lambda_1 , $$ а общий случай из теоремы доказывается аналогично. ♦
Видео:Симметричные системы #1Скачать

Субрезультанты и наибольший общий делитель
Рассмотрим матрицу $ M_ $ из определения результанта и удалим из нее первую и последнюю строки, а также первый и последний столбцы. Получим снова квадратную матрицу порядка $ m_+n-2 $. Определитель получившейся матрицы: $$ ^(f,g)= left|begin a_0&a_1&ldots&ldots&a_&a_n&dots&0 \ vdots&ddots&&&&&ddots\ 0&ldots&a_0&ldots&ldots & & ldots &a_ \ 0&ldots&&b_0&b_1&ldots& ldots &b_\ 0&ldots&b_0&b_1&ldots &&ldots &b_m\ vdots&&ldots&&&& &vdots\ b_0&ldots&ldots&&b_m&ldots&&0 endright| begin left.begin \ \ \ endright> m-1 \ left. begin \ \ \ \ endright> n-1 end $$ называется первым субрезультантом результанта $ (f_,g) $.
Теорема. Для того чтобы полиномы $ f_(x) $ и $ g_(x) $ имели один и только один общий корень, необходимо и достаточно, чтобы $$(f,g)=0, ^(f,g)ne 0 .$$
При выполнении условий предыдущей теоремы единственный общий корень полиномов $ f_(x) $ и $ g_(x) $ можно выразить в виде рациональной функции коэффициентов полиномов $ f_(x) $ и $ g_(x) $:
$$ lambda=-<det M_1^over ^(f,g)> . $$ Здесь матрица $ M_1^ $ получается из $ M_ $ удалением первой и последней строк, первого и предпоследнего столбцов.
Пример. При выполнении условий теоремы для полиномов
$$ f(x)=a_0x^5+a_1x^4+a_2x^3+a_3x^2+a_4x+a_5 u g(x)=b_0x^3+b_1x^2+b_2x+b_3 $$ ($ a_ ne 0, b_0 ne 0 $) их общий корень выражается формулой $$ lambda =- left| begin a_0&a_1&a_2&a_3&a_4&0\ 0&a_0&a_1&a_2&a_3&a_5\ 0&0&0&b_0&b_1&b_3\ 0&0&b_0&b_1&b_2&0\ 0&b_0&b_1&b_2&b_3&0\ b_0&b_1&b_2&b_3&0&0 endright| Bigg/ left|begin a_0&a_1&a_2&a_3&a_4&a_5\ 0&a_0&a_1&a_2&a_3&a_4\ 0&0&0&b_0&b_1&b_2\ 0&0&b_0&b_1&b_2&b_3\ 0&b_0&b_1&b_2&b_3&0\ b_0&b_1&b_2&b_3&0&0 end right| . $$ Определитель матрицы $ M_ $, получаемой из матрицы $ M_ $ вычеркиванием $ k_ $ первых и $ k_ $ последних столбцов, $ k_ $ первых и $ k_ $ последних строк, называется $ $-м субрезультантом полиномов $ f_ $ и $ g_ $ и обозначается $ ^(f,g) $. Для однообразия будем считать нулевым субрезультантом определитель матрицы $ M_ $: $$ ^(f,g)= det M =(-1)^(f,g) . $$
Пример. Для полиномов
Откуда возникают субрезультанты см. ☞ ЗДЕСЬ
Теорема. Для того чтобы полиномы $ f_(x) $ и $ g_(x) $ имели наибольший общий делитель степени $ k>0 $, необходимо и достаточно, чтобы были выполнены условия
При выполнении условий предыдущей теоремы наибольший общий делитель полиномов $ f_(x) $ и $ g_(x) $ можно представить в виде
$$ operatorname (f(x),g(x)) equiv x^k^(f,g) +x^ det M_k^ +ldots +det M_k^ . $$ Здесь $ M_k^ $ — матрица, получаемая из субрезультанта $ ^(f,g) $ заменой последнего его столбца на столбец $$ [a_, a_,dots, a_,b_,b_,dots,b_]^ $$ (полагаем $ a_=0 $ при $ K>n_ $ и $ b_=0 $ при $ L>m_ $).
Пример. Найти наибольший общий делитель полиномов
Решение. Опуская вычисления, приведем лишь окончательный результат: $$ (f,g)=0, ^(f,g)= 0, ^(f,g)= 0, ^(f,g)= left| begin 1 & -1 & 0 & 3 & -2 \ 0 & 1 & -1 & 0 & 3 \ 0 & 0 & 1 & 0 & 1 \ 0 & 1 & 0 & 1 & 1 \ 1 & 0 & 1 & 1 & 2 end right| =-7 ne 0 $$ Таким образом, $ operatorname (f(x),g(x)) $ имеет степень $ 3 $. Для его нахождения составим определитель заменой последнего столбца субрезультанта $ ^ $: $$ operatorname (f(x),g(x)) =left| begin 1 & -1 & 0 & 3 & -2,x^3+x \ 0 & 1 & -1 & 0 & 3,x^3-2,x^2+1 \ 0 & 0 & 1 & 0 & x^3+x^2+2,x+1 \ 0 & 1 & 0 & 1 & x^3+2,x^2+x \ 1 & 0 & 1 & 1 & 2,x^3+x^2 end right|=-7,x^3 +7,x^2-7,x-7 . $$
Ответ. $ x^3-x^+x+1 $.
Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Результант в форме Кронекера
Для полиномов $$ f(x)=a_0x^n+a_1x^+ldots+a_nquad u quad g(x)=b_0x^m+b_1x^+ldots+b_m $$ ($ a_ne 0 $) построим сначала формальное разложение дроби $ g_(x)/f(x) $ в ряд Лорана по отрицательным степеням $ x_ $. Для случая $ deg g ☞ ПУНКТА, заключаем, что $ operatorname(f,g) $ имеет степень, равную $ 2_ $.
Ответ. Два общих корня.
Следующий результат дает явное выражение субрезультантов через корни полинома $ f_(x) $.
Теорема. Если все корни полинома $ f_(x) $ простые, то справедливо следующее равенство:
$$ C_p=sum v(lambda_,dots,lambda_)^2 frac<g(lambda_)><f'(lambda_)>times dots times frac<g(lambda_)><f'(lambda_)> ; $$ здесь суммирование идет по всевозможным наборам индексов $$ (j_1,dots, j_p), 1le j_1 ☞ ЗДЕСЬ. ♦
Видео:Решение систем уравнений методом подстановкиСкачать

Результант в форме Безу
Рассмотрим снова полиномы из $ _[x] $: $$f(x)= a_0 x^n+ dots + a_n quad mbox quad g(x) = b_0 x^m+ dots + b_m quad (a_0 ne 0,b_0 ne 0) . $$ Найдем остатки от деления $ x^g(x) $ на $ f_(x) $: $$g_k(x)= b_x^+b_x^+dots+b_quad mbox k in , . $$ Составим матрицу из коэффициентов этих остатков: $$ B=[b_]_^ $$ и обозначим $ B_,dots,B_n $ ее главные миноры.
Теорема. Имеет место формула, связывающая миноры матрицы $ B_ $ с субрезультантами:
Доказательство проведем для случая $ n=5,, m=3_ $ и $ k=1_ $. Для элементов первых двух строк матрицы $ B_ $ имеем следующие формулы: $$ b_=0, b_=b_=b_0, b_=b_=b_1, b_=b_=b_2 , b_=b_=b_3, b_=0 ; $$ элементы остальных строк получаются по формулам, связывающим коэффициенты $ g_(x) $ с коэффициентами $ g_(x_) $: $$ b_=b_-b_a_/a_0quad npu quad j in . $$ Тогда справедливо следующее матричное равенство: $$ left( begin 1 & & & & & \ 0 & 1 & & & & \ 0 & 0 & 1 & & & \ 0 & 0 & 0 & 1 & & \ 0 & -b_/a_0 & 0 & 0 & 1 & \ -b_/a_0 & -b_/a_0 & 0 & 0 & 0 & 1 endright) cdot left(begin a_0&a_1&a_2&a_3&a_4&a_5\ &a_0&a_1&a_2&a_3&a_4\ & & &b_0&b_1&b_2\ & &b_0&b_1&b_2&b_3\ &b_0&b_1&b_2&b_3& \ b_0&b_1&b_2&b_3& & end right) =left( begin a_0 & a_1 & a_2 & a_3 & a_4 & a_5\ & a_0 & a_1 & a_2 & a_3 & a_4\ & & b_ & b_ & b_ & b_\ & & b_ & b_ & b_ & b_\ & & b_ & b_ & b_ & b_\ & & b_ & b_ & b_ & b_ endright) . $$ Переходя в этом равенстве к определителям, получим требуемое. ♦
Видео:Матричный метод решения систем уравненийСкачать

Еще некоторые представления результанта
Теорема. Пусть
$$ g(x)=b_x^m+dots+b_m in [x] $$ — произвольный полином. Вычислим полином от квадратной матрицы $ A_ $: $$ g(A)=b_A^m+dots+b_m E , .$$ Тогда $$ det g(A) = (-1)^ (f,g_) , $$ где $ (f,g_) $ — результант полиномов $ f(x) =det (A-x_ E) $ и $ g_(x) $.
Этот результат доказывается анализом собственных чисел матрицы $ A_ $.
Видео:Многочлены. 7 класс.Скачать

Применения результанта
Видео:Системы уравнений 7-11 класс. Вебинар | МатематикаСкачать

Преобразование Чирнгауза
Задача. Пусть даны два полинома из $ [x] $: $$f(x)= a_0 x^n+ dots + a_n quad mbox quad g(x) = b_0 x^m+ dots + b_m quad (a_0 ne 0,b_0 ne 0) . $$ Обозначим $ lambda_,dots,lambda_n $ (как правило, заранее неизвестные) корни $ f_(x) $. Построить полином $ F_(y) $, имеющий корни $ g(lambda_),dots,g(lambda_n) $. Нахождение этого полинома называется преобразованием Чирнгауза $ y=g_(x) $ полинома $ f_(x) $.
Теорема. Существует единственный нормализованный полином $ F_(y) $ степени $ n_ $, решающий задачу:
$$ F(y)equiv _(f(x),y-g(x))/a_0^m ; $$ здесь результант рассматривается для полиномов относительно переменной $ x_ $. Коэффициенты $ F_(y) $ рационально зависят от коэффициентов $ f_(x) $ и $ g_(x) $.
Пример. Найти преобразование Чирнгауза $ y=x^+x-1 $ полинома $ f(x)=x^-2,x+3 $.
Решение. $$ F(y)=(x^3-2,x+3, -x^2-x+(1+y))= $$ $$ =-left| begin 1 & 0 & -2 & 3 & 0 \ 0 & 1 & 0 & -2 & 3 \ 0 & 0 & -1 & -1 & 1+y \ 0 & -1 & -1 & 1+y & 0 \ -1 & -1 & 1+y & 0 & 0 endright| =y^3-y^2+6y-4 . $$ ♦
Применение преобразования Чирнгауза в задаче решения алгебраических уравнений ☞ ЗДЕСЬ
Обобщениями задачи являются следующие (и подобные им).
Задача. Для полинома $ f_(x) $ степени $ n_ $ построить полином $ F_(y) $, имеющий корнями всевозможные
a) суммы $ lambda_ + lambda_k $;
б) произведения $ lambda_ lambda_k $;
в) квадраты разностей $ (lambda_ — lambda_k)^2 $;
корней $ lambda_,dots,lambda_n $ полинома $ f(x) $ (здесь $ 1le j ☞ УСТОЙЧИВОСТЬ ПО ЛЯПУНОВУ. Следующая теорема дает один из самых распространенных критериев устойчивости.
Теорема [Льенар, Шипар] [2]. Для устойчивости полинома $ f(x)=a_x^n+a_1x^+dots+a_n $ с вещественными коэффициентами и $ a_ > 0 $ необходимо и достаточно, чтобы
а) все коэффициенты $ a_,dots, a_n $ были положительными;
б) все субрезультанты результанта $$ left(a_n+a_Y+a_Y^2+dots, a_+a_Y+a_Y^2+dots right) $$ были положительными.
Пример. Условие б) для $ n_=7 $:
То, что при соответствующих четностях $ k_ $ определители $ Delta_ $ действительно являются субрезультантами результанта из теоремы проверяется перестановкой строк.
Видео:СЛОЖИТЕ ДВА КОРНЯСкачать

Исключение переменных в системе полиномиальных уравнений
Задача. Пусть $ f_(x,y) $ и $ g_(x,y) $ — полиномы от переменных $ x_ $ и $ y_ $ с комплексными коэффициентами. Решить систему уравнений $$ f(x,y)=0, g(x,y)=0 , $$ т.е. определить все пары $ x_= alpha, y_= beta $ при $ subset mathbb C $, обращающие каждое из уравнений в верное равенство.
Представим $ f(x_,y) $ и $ g_(x,y) $ в виде сумм их форм: $$begin f(x,y)=f_n(x,y)+f_(x,y)+ldots+f_0(x,y) ,\ g(x,y)=g_m(x,y)+g_(x,y)+ldots+g_0(x,y) . end$$ Относительно коэффициентов старших форм $$ begin f_n(x,y)=a_x^n+a_x^y+dots+a_y^n ,\ g_m(x,y)=b_x^m+b_x^y+dots+b_y^m end $$ сделаем следующее
Предположение : $ a_ne 0,a_ne 0,b_ne 0,b_ne 0 . $
Пара $ x_= alpha, y= beta $ при $ subset mathbb C_ $ будет решением системы тогда и только тогда, когда полиномы $ f(alpha,y) $ и $ g(alpha,y) $ имеют общий корень $ y_=beta $, а, следовательно, на основании основного свойства результанта $$ (f(alpha,y),g(alpha,y))=0 . $$ Разложим $ f(alpha,y) $ и $ g(alpha,y) $ по убывающим степеням $ y_ $ $$begin f(alpha,y)=A_0y^n+A_1(alpha)y^+dots+A_n(alpha) ,\ g(alpha,y)=B_0y^m+B_1(alpha)y^+dots+B_m(alpha) end$$ (здесь $ A_0=a_ne0,B_0=b_ne 0 $ по предположению , $ deg A_j(alpha)le j $; $ deg B_j(alpha)le j $) и вычислим определитель Сильвестра: $$ begin mleft<begin \ \ \ \ endright. \ nleft<begin \ \ \ \ \ endright. end left|begin A_0&A_1(alpha)&dots&&A_n(alpha)&&mathbb O &\ &A_0&dots&&&A_n(alpha)& & \ &&ddots&&&dots&ddots\ &&&&A_0&A_1(alpha)&dots&A_n(alpha)\ &mathbb O &&&&B_0&dots&B_m(alpha)\ &&&&B_0&B_1(alpha)&dots&\ &&&&&dots&&\ &B_0&B_1(alpha)&dots&&B_m(alpha)&\ B_0&B_1(alpha)&dots&&B_m(alpha)&&mathbb O endright| =(alpha) . $$ Выражение $ (alpha) $ — полином по $ alpha_ $, причем, по построению, с коэффициентами из того же множества , что и коэффициенты $ f_ $ и $ g_ $. Для того, чтобы пара $ x_= alpha, y= beta $ была решением системы уравнений необходимо, чтобы значение $ alpha_ $ было корнем полинома $ (x)=0 $.
Полином $ (x) $ — результант $ f_(x,y) $ и $ g_(x,y) $, рассматриваемых как полиномы по переменной $ y_ $ $$ (x)= _y left(f(x,y),g(x,y) right) , $$ — называется элиминантой 3) системы уравнений по переменной $ x_ $. Аналогично определяется и вторая элиминанта системы $$(y) = _x(f(x,y),g(x,y)) .$$ С помощью элиминанты решение системы из двух уравнений с двумя переменными сводится к решению одного уравнения от одной переменной: $ (x)=0 $ (или $ (y)=0 $). Говорят, что другая переменная исключена. Поэтому и соответствующий раздел алгебры называется теорией исключения.
Пример. Решить систему уравнений
$$left<begin f(x,y)=4,x^2-7,xy+y^2+13,x-2,y-3=0 ,\ g(x,y)=9,x^2-14,xy+y^2+28,x-4,y-5=0 . endright. $$ Решение. Разложим полиномы системы по степеням $ y_ $ $$begin f(x,y)=y^2+(-7,x-2)y+(4,x^2+13,x-3) ,\ g(x,y)=y^2+(-14,x-4)y+(9,x^2+28,x-5) , end $$ и вычислим элиминанту: $$(x)=left|begin 1&-7x-2&4x^2+13x-3&0\ 0&1&-7x-2&4x^2+13x-3\ 0&1&-14x-4&9x^2+28x-5\ 1&-14x-4&9x^2+28x-5&0 endright|= $$ $$ =24(x^4-x^3-4,x^2+4,x) .$$ Найдем ее корни: $ alpha_1=0,alpha_2=1,alpha_3=2,alpha_4=-2 $.
Итак, найдены $ x_ $-компоненты решений системы. Как найти их $ y_ $-компоненты? Можно построить вторую элиминанту $ (y) $, отыскать ее корни, составить всевозможные пары из корней $ (x) $ и $ (y) $, подставить их в $ f_(x,y) $ и $ g_(x,y) $ и проверить на равенство нулю. Либо же найденный корень $ x_=alpha $ подставить в одно из уравнений: $ f(alpha,y)=0 $, решить его относительно $ y_ $, и каждую полученную таким образом пару подставить в $ g(x,y) $; хотя бы одна из них должна удовлетворить уравнению $ g(x,y)=0 $. В решаемом примере любой из этих подходов приведет к правильному ответу.
Ответ. $ (0,-1); (1,2) ; (2,3) ; (-2,1) $.
Известно, однако же, что, как правило, корни полинома не являются — даже не то чтобы целыми числами — но даже и выражаемыми через коэффициенты этого полинома в виде «хороших» функций (см. ☞ РЕШЕНИЕ УРАВНЕНИЙ В РАДИКАЛАХ ). Поэтому следует ожидать, что корни элиминанты могут быть найдены разве лишь приближенно. Но тогда предлагаемая в примере схема подбора соответствующей пары становится ущербной: равенство $ f(alpha,beta)=0 $ следует рассматривать как приближенное и ошибка округления может привести к неправильному заключению.
Пример. Решить систему уравнений
$$left<begin f(x,y)=3,x^2+3,xy+3,y^2-3,x-12,y+10=0 ,\ g(x,y)=x^3+y^3-x^2+xy-5,y^2-5,x+7,y-3=0 . endright. $$ Решение. Элиминанта $$ (x)=left|begin 3 & 3,x-12 & 3,x^2-3,x+10 & 0 & 0 \ 0 & 3 & 3,x-12 & 3,x^2-3,x+10 & 0 \ 0 & 0 & 3 & 3,x-12 & 3,x^2-3,x+10 \ 0 & 1 &-5 & x+7 & x^3-x^2-5,x-3 \ 1 &-5 & x+7 & x^3-x^2-5,x-3 & 0 endright| = $$ $$ =-(108,x^6-54,x^5-459,x^4+126,x^3+558,x^2+72,x+1) $$ имеет корни $$ -1.4357404546, -1.2204153656, -0.1184043714, -0.0158215507, $$ $$ 1.6451908712 pm 0.3378906924 , $$ некоторые из которых близки между собой. Заметим, что при любом корне $ x= alpha $ элиминанты $ (x) $ полиномы $ f(alpha, y) $ и $ g(alpha, y) $ должны иметь общий корень как полиномы по $ y $. Однако общий корень полиномов (в случае его единственности) может быть найден как рациональная функция от коэффициентов этих полиномов —с помощью субрезультантов. Формула $$ y=-left| begin 3 & 3,x-12 & 0 \ 0 & 3 & 3,x^2 -3,x + 10 \ 1 & -5 & x^3-x^2-5,x-3 end right| Bigg/ left| begin 3 & 3,x-12 & 3,x^2 -3,x + 10 \ 0 & 3 & 3,x-12 \ 1 & -5 & x + 7 end right|= $$ $$ =-(18,x^3-9,x^2-24,x+3)/(-9,x-3) $$ для каждого корня элиминанты задает значение $ y $ так, что получившаяся пара оказывается решением системы уравнений.
Ответ. $$ (-1.4357404546, 3.4637885415) , (-1.2204153656, 1.7326988317), (-0.1184043714, 2.9392910117), $$ $$ (-0.0158215507, 1.1818959593) , $$ $$ (1.6451908712 pm 0.3378906924 , , 0.8411628278 pm 1.5734509554 , ) . $$
Вывод. Как правило, систему полиномиальных уравнений удается привести к эквивалентному (в смысле множества решений) виду: $$ (x)=0, p_0(x)y+p_1(x)=0 . $$ Здесь $ < , p_0, p_1 > $ — полиномы по $ x_ $.
Развитие этой идеологии для случая систем уравнений многих переменных медленно производится ☞ ЗДЕСЬ.
Теорема Безу
Сколько решений имеет система уравнений $ f(x,y)=0, g(x_,y)=0 $ ? — Очевидно, что это число совпадает со степенью элиминанты.
Теорема [Безу]. Пусть выполнены условия предположения . Тогда, как правило,
Доказательство, взятое из [5], приведем для случая $ n=3_ $ и $ m=2_ $. $$begin f(x,y)=A_0y^3+A_1(x)y^2+A_2(x)y+A_3(x) ,\ g(x,y)=B_0y^2+B_1(x)y+B_2(x) , end$$ $$(x)=left|begin A_0&A_1(x)&A_2(x)&A_3(x)&\ &A_0&A_1(x)&A_2(x)&A_3(x)\ &&B_0&B_1(x)&B_2(x)\ &B_0&B_1(x)&B_2(x)&\ B_0&B_1(x)&B_2(x)&& endright| .$$ Здесь $$ A_0=a_,B_0=b_;deg A_j(x) le j; deg B_j(x) le j quad npu quad j in . $$ Старший моном $ (x_) $ образуется из старших мономов элементов определителя. Выделим их $$ begin A_0=a_;&B_0=b_ ;\ A_1(x)=a_x+ldots;&B_1(x)=b_x+ldots ;\ A_2(x)=a_x^2+ldots;&B_2(x)=b_x^2+ldots ;\ A_3(x)=a_x^3+ldots& end . $$ Следовательно, $$(x)=left|begin a_&a_x&a_x^2&a_x^3&\ &a_&a_x&a_x^2&a_x^3\ &&b_&b_x&b_x^2\ &b_&b_x&b_x^2&\ b_&b_x&b_x^2&& endright|+ldots , $$ и нам осталось извлечь степень $ x_ $ из первого определителя. Проделаем это с помощью процедуры, которую можно обобщить на случай произвольных полиномов $ f(x,y) $ и $ g(x,y) $: домножим вторую и четвертую строки на $ x_ $, третью — на $ x^ $: $$=fracleft|begin a_&a_x&a_x^2&a_x^3&\ &a_x&a_x^2&a_x^3&a_x^4\ &&b_x^2&b_x^3&b_x^4\ &b_x&b_x^2&b_x^3&\ b_&b_x&b_x^2&& endright|+ldots = $$ Из второго столбца выносим общий делитель его элементов $ x_ $, из третьего — $ x^2 $, из четвертого — $ x^3 $, из пятого — $ x^4 $: $$=frac<x^>left|begin a_&a_&a_&a_&\ &a_&a_&a_&a_\ &&b_&b_&b_\ &b_&b_&b_&\ b_&b_&b_&& endright|+ldots= $$
Доказать, что старшие коэффициенты $ (x) $ и $ (y) $ совпадают с точностью до знака.
Указание. См. свойство 4 ☞ ЗДЕСЬ.
Поиск мнимого корня полинома
Задача. Для полинома $ f_(z) $ вычислить все его корни.
Будем предполагать, что полином $ f_(z) $ степени $ n_ $ имеет вещественные коэффициенты 4) . Известно, что корни такого полинома либо вещественны, либо мнимы, причем в последнем случае они образуют комлексно-сопряженные пары $ alpha_ pm beta mathbf i $ при $ subset mathbb R^, beta ne 0 $ (см. ☞ ЗДЕСЬ ). Для поиска вещественных корней можно применять различные численные методы (Ньютона, Лагранжа и т.п.). Как решить аналогичную задачу для мнимых корней?
Представив переменную в виде $ z=x_+y mathbf i $, сведем уравнение от комплексной переменной к системе уравнений от переменных вещественных: $$ f(z)=0 iff f(x+y mathbf i)=0 iff phi(x,y)+ psi(x,y) mathbf i =0 iff left< begin phi(x,y)=0, \ psi(x,y)=0; end right. $$ здесь $ phi(x,y) = mathfrak Rmathbf e (f_(z)), psi(x,y) = mathfrak Imathbf m (f_(z)) $. Таким образом для того, чтобы найти мнимый корень полинома $ f_(z) $ нам достаточно найти вещественные решения системы алгебраических уравнений с вещественными же коэффициентами. Для решения последней задачи перспективно применить метод исключения переменной, изложенный в предыдущем пункте. Тем самым мы сведем задачу поиска корня полинома к аналогичной задаче, но только корни теперь будут вещественными; такую задачу мы умеем решать.
Теперь оформим изложенную идею аналитически. Для получения представлений полиномов $ phi_(x,y) $ и $ psi_(x,y) $ воспользуемся формулой Тейлора, разложив $ f(x_+ mathbf i y) $ по степеням $ mathbf i y_ $: $$ f(z)=f(x+ mathbf i y)=f(x)+mathbf i ,y+(mathbf i , y)^2+ dots+<f^(x)over n!>(mathbf i ,y)^n=$$ $$=left[ f(x)-y^2+<f^(x)over 4!>y^4-dotsright]+mathbf i ,yleft[ -y^2+<f^(x)over 5!>y^4-dotsright]= $$ $$ =F_1(x,Y)+mathbf i ,yF_2(x,Y) $$ при $$ Y= -y^2 , left< begin F_1(x,Y)&= & displaystyle<f(x)+Y+<f^(x)over 4!>Y^2+dots,> \ \ F_2(x,Y)&=&displaystyle<+Y+<f^(x)over 5!>Y^2+dots> end right. $$ Полиномы $ F_ $ и $ F_ $ имеют вещественные коэффициенты.
Уравнение $ f_(z) =0 $ порождает две системы уравнений $$ left< begin F_1(x,Y)=0, \ y=0, end right. quad u quad left< begin F_1(x,Y)=0, \ F_2(x,Y)=0. end right. $$ Первая из этих систем отвечает за вещественные корни полинома $ f_(z) $: все решения этой системы имеют $ y_ $-компоненту равной $ 0_ $, а $ F_1(x,0)equiv f(x) $. Вторая система состоит из уравнений четных по переменной $ y_ $: эта переменная входит в их разложение в виде квадрата $ Y=-y^2 $. Если полином $ f_(z) $ имеет корень $ lambda=alpha + mathbf i beta $ при $ subset mathbb R $ и $ beta ne 0 $, то корнем будет и $ overline=alpha — mathbf i beta $ ввиду вещественности коэффициентов $ f_(z) $ (см. ☞ ЗДЕСЬ ). Но тогда система уравнений $$ F_1(x,Y)=0, F_2(x,Y)=0 $$ должна будет иметь вещественное решение $ x= alpha, Y=-beta^2 $. Будем искать это решение исключением переменной $ Y_ $. Cоставим элиминанту системы по переменной $ x_ $: $$ mathcal X(x) = _Y(F_1,F_2) . $$
Теорема. $ deg mathcal X_=N = n(n-1)/2 $.
Действительно, по аналогии с доказательством теоремы Безу, можно установить старший член разложения $ mathcal X_ $ по степеням $ x_ $: $$ mathcal X(x)=mathcal A_0x^N+dots , quad npu mathcal A_0=(-1)^K2^Na_0^, K=leftlfloorfrac rightrfloor . $$ Здесь $ lfloor rfloor $ означает целую часть числа, $ a_ $ — старший коэффициент $ f_(z) $. ♦
Каждому значению корня полинома $ mathcal X(x) $ соответствует значение $ Y_ $ такое, что образующаяся пара становится решением системы уравнений $ F_(x,Y)=0, F_2(x,Y)=0 $. Это соответствие организуется с помощью субрезультантов, как было отмечено ☞ ЗДЕСЬ.
Нас интересуют только вещественные решения системы, более того, только те из них, что имеют $ Y_ $-компоненту отрицательной.
Пример. Найти мнимые корни полинома
Ответ. Мнимые корни полинома: $ lambda_ =1pm mathbf isqrt $, $ lambda_=-7/2pm mathbf i sqrt/2 $.
Элиминанта $ mathcal X(x) $, построенная в этом пункте, обладает рядом полезных свойств. В частности, справедлива следующая
Теорема [Раус][7,8]. Для устойчивости полинома $ f(z)in mathbb R[z] $ необходимо и достаточно чтобы
а) все коэффициенты $ f_(z) $ были одного знака;
б) все коэффициенты $ mathcal X(x) $ были одного знака.
Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Дифференциальный результант
Известная аналогия задач преобразования алгебраических уравнений и задач преобразования линейных дифференциальных и разностных уравнений позволяет перенести понятие результанта из алгебры в дифференциальные уравнения.
Пример. Найти условие, при котором два дифференциальных уравнения
Решение. Воспользуемся аналогом приема из обоснования возникновения результанта. Грубо говоря, для перенесения какого-то результата из теории полиномов на линейные дифференциальные уравнения иногда достаточно формально заменить $$ x mapsto frac , $$ т.е. операцию возведения в степень — на операцию дифференцирования. Предположим, что существует общее решение рассматриваемых уравнений: $ y=varphi(x) $; тогда эта функция должна при подстановке обращать оба уравнения в тождества: $$ begin varphi^+a_1varphi^+a_2varphi+a_3equiv 0 , \ varphi^+b_1varphi^+b_2varphi+b_3equiv 0 . end $$ Продифференцируем 5) каждое из этих тождеств по $ x_ $: $$ begin varphi^+a_1varphi^ +(a_1^ +a_2)varphi^+a_2^varphi + a_3^equiv 0 , \ varphi^+b_1varphi^ +(b_1^ +b_2)varphi^+b_2^varphi + b_3^equiv 0 ; end $$ и еще один раз: $$ begin varphi^+a_1varphi^ +(2a_1^ +a_2)varphi^+ (a_1^+2a_2^)varphi^ + a_2^varphi a_3^equiv 0 , \ varphi^+b_1varphi^ +(2b_1^ +b_2)varphi^+ (b_1^+2b_2^)varphi^ + b_2^varphi + b_3^equiv 0 . end $$ Теперь объединяем получившиеся тождества в систему, рассматриваемую относительно столбца неизвестных $$ left[varphi^(x),varphi^(x), varphi^(x),varphi^(x), varphi(x), 1 right] .$$ Эта система однородна и имеет нетривиальное решение. Следовательно ( см. ☞ ЗДЕСЬ ), определитель ее матрицы равен нулю.
Ответ. Для существования общего решения уравнений необходимо выполнение условия: $$ left| begin 1 & a_1(x) & 2a_1^(x) +a_2(x) & a_1^(x)+2a_2^(x) & a_2^(x) & a_3^(x) \ 0 & 1 & a_1(x) & a_1^(x) +a_2(x) & a_2^(x) & a_3^(x) \ 0 & 0 & 1 & a_1(x) & a_2(x) & a_3(x) \ 0 & 0 & 1 & b_1(x) & b_2(x) & b_3(x) \ 0 & 1 & b_1(x) & b_1^(x) +b_2(x) & b_2^(x) & b_3^(x) \ 1 & b_1(x) & 2b_1^(x) +b_2(x) & b_1^(x)+2b_2^(x) & b_2^(x) & b_3^(x) end right| equiv 0 . $$
Определитель, стоящий в левой части тождества, называется дифференциальным результантом.
Найти общее решение дифференциальных уравнений
Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Задачи
Видео:Исследование систем линейных уравнений на совместностьСкачать

Источники
[1]. Бохер М. Введение в высшую алгебру. М.-Л. ГТТИ, 1933
[3]. Kronecker L. Zur Theorie der Elimination einer Variabeln aus zwei algebraischen Gleichungen. Werke. Bd. 2. 1897. 113-192, Teubner, Leipzig
[4]. Гантмахер Ф.Р. Теория матриц. 4-е изд. М.Наука. 1988. с.477–478
[5]. Brill A. Vorlesungen über ebene algebraischen Kurven und algebraische Funktionen. Braunschweig. Vieweg. 1925
[6]. Калинина Е.А., Утешев А.Ю. Теория исключения. Учеб. пособие. СПб.: НИИ Химии СПбГУ, 2002. 72 с.
[7]. Утешев А.Ю., Калинина Е.А. Лекции по высшей алгебре. Часть II. Учеб. пособие. СПб. «СОЛО». 2007.
Видео:Задача 31 (общие корни двух многочленов)Скачать

Результант и дискриминант
Автор: Nastya Lass • Май 10, 2018 • Курсовая работа • 4,054 Слов (17 Страниц) • 932 Просмотры
Результант и дискриминант
Направление подготовки: педагогическое образование
Профиль: математика и физика
Дата сдачи «___» ______________ 20___г.
Дата защиты «___» ______________ 20___г.
Научный руководитель __________________ / _________________ /
1. Результант. Исключение неизвестного 4
2. Исключение неизвестного из системы двух уравнений с двумя неизвестными 13
Список использованной литературы 22
Теория многочленов — важный раздел алгебры. Одним из главных в алгебре многочленов является вопрос о существовании корней уравнения, так известно, что есть даже квадратные уравнения с действительными коэффициентами, не имеющими действительных корней. Многочлены — один из наиболее значимых классов элементарных функций. С их изучением связан целый ряд преобразований в математике: введение в рассмотрение нуля, отрицательных, а затем и комплексных чисел, появление теории групп как раздела математики и выделение классов специальных функций в анализе.
Таким образом, объект исследования: система уравнений вида f 1 ( x 1 . x n )=0, . f n ( x 1 . x n )=0.
Предмет исследования: решение системы двух уравнений произвольной степени от двух неизвестных.
Цель исследования: рассмотреть понятия результанта и дискриминанта, определить взаимосвязь данных понятий.
Цель исследования определила ее задачи:
1. Рассмотреть понятие результанта;
2. Доказать теорему о исключении одного неизвестного из системы двух многочленов с двумя неизвестными;
3. Рассмотреть понятие дискриминанта, раскрыть взаимосвязь между результантом и дискриминантом.
1. Результант. Исключение неизвестного.
В рамках данного исследования будем рассматривать многочлены над полем комплексных чисел. При этом известно, что любой многочлен вида:
где коэффициенты и переменная x – комплексные числа, имеет хотя бы один корень – это утверждение называется основной теоремой алгебры. [pic 2]
Поскольку если — корень многочлена, то многочлен делится на , то отсюда легко вывести, что любой многочлен представляется в виде: [pic 3][pic 4]
, где , , …, — корни многочлена (среди которых могут быть и совпадающие – кратные корни). В рамках данного исследования нас будет интересовать вопрос: когда у двух многочленов и ? Если это так, то у многочленов и будет общий множитель – многочлен степени 1 или выше. Тогда будут существовать многочлены и , такие что: [pic 5][pic 6][pic 7][pic 8][pic 9][pic 10][pic 11][pic 12][pic 13][pic 14]
Таким образом, рассмотрим систему уравнений
f 1 ( x 1 . x n )=0, . f n ( x 1 . x n )=0,
где f 1 . f n — полиномы по x 1 . x n .
С помощью элементарных преобразований данную систему можно привести к эквивалентной ей (т.е. имеющей тот же набор решений) системе вида:
X ( x 1 )=0, x 2 — J 2 ( x 1 )=0, . x n — J n ( x 1 )=0.
Здесь X ( x 1 ) — полином, а J 2 ( x 1 ). J n ( x 1 )- рациональные функции по x 1 . В этом случае решение первой системы сведется к решению уравнения от одной переменной; другими словами, все остальные переменные становятсяисключенными. Каждый корень полинома X ( x 1 ) задает первую компоненту (координату) решения первой системы, а остальные компоненты, которые соответствуют ему, выражаются через первую с помощью оставшихся уравнений второй системы. Еще раз выделю то обстоятельство, что все компоненты решения первой системы могут быть рационально выражены через какую-то одну, например — как во второй системе — первую.
Видео:Система уравнений Тема2 Исследование решений системных уравнений.Скачать

Дискриминант многочлена
Рассмотрим в кольце многочлен
Который можно представить в виде определителя Вандермонда
Так как определитель является кососимметричной функцией своих столбцов, то — знак перестановки . Но в таком случае — симметрический многочлен и по основной теореме его можно выразить в виде многочлена от элементарных симметрических функций
Многочлен dis от называется дискриминантом семейства . Его коэффициенты, очевидно, лежат в Z.
Мы можем представить в виде ..Действуя по правилу умножения матриц находим
где — степенные суммы. Вычислив по формулам (I) и (II) выразим . В частности , , так что
Определение. Дискриминант семейства корней многочлена f, или, что равносильно, значение дискриминанта
получающееся при подстановке вместо ,
Называется дискриминантом многочлена f и обозначается D(f). Также он называется дискриминантом алгебраического уравнения
Предложение. D(f)=0 тогда и только тогда, когда уравнение (7) имеет кратные корни (хотя бы один кратный корень кратности k>1).
Определение. Результантом Res(f, g) многочленов f и g называется однородный многочлен (однородная полиномиальная функция) от их коэффициентов (степени m относительно и степени n относительно ) вида
- 1) Res (f, g)=0 тогда и только тогда, когда или же f и g имеют общий множитель в Р[X] степени >0.
- 2) Пусть многочлены f и g полностью расщепляются на линейные множители в P[X]:
Видео:Математика это не ИсламСкачать

Исследование уравнений в математике с примерами решения
Исследовать уравнение – это значит указать, при каких значениях параметра какое именно решение имеет данное уравнение/неравенство.
Видео:СХЕМА ГОРНЕРА 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Что значит исследовать уравнение
Исследовать уравнение — значит рассмотреть все особые случаи, которые могут представиться при решении его, и уяснить значение этих случаев для той задачи, из условий которой уравнение составлено.
Видео:После этого видео, ТЫ РЕШИШЬ ЛЮБУЮ Систему Нелинейных УравненийСкачать

Исследование уравнений первой степени с одним неизвестным
Вы видели раньше, что уравнение первой степени с одним неизвестным после надлежащих преобразований (раскрытие скобок, освобождение от знаменателей, перенесение неизвестных членов в одну часть уравнения, а известных в другую и приведение подобных членов) приводится к такому простейшему виду:
ах = b,
где числа а и b могут быть положительными, отрицательными и равными нулю.
Рассмотрим, какого рода решения получает это уравнение при различных численных значениях а и b .
Положительное решение: Такое решение получается тогда, когда числа а и b оба положительны или оба отрицательны. Пусть, например, Зх = 6 или —Зх = —6. Тогда мы получим:
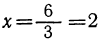
Положительное решение, удовлетворяя уравнению, вместе с тем удовлетворяет и задаче, из условий которой уравнение выведено, если только в уравнении выражены все условия задачи. Но иногда случается, что не все условия задачи выражены уравнением; тогда положительное решение может и не удовлетворять задаче. Приведём этому пример.
Задача:
Рабочий кружок, состоящий из 20 человек (взрослых и подростков), устроил сбор на покупку книг для библиотеки, причём каждый взрослый внёс по 3 руб., а каждый подросток—по 1 руб. Сколько было в этом кружке взрослых и сколько подростков, если весь сбор составил 35 руб.?
Обозначим число взрослых буквой х; тогда число подростков будет 20 — х, и сбор со взрослых окажется Зх руб., а с подростков (20 — х) руб. Следовательно, уравнение будет
3x+(20 — x)=35, откуда х =
Это положительное решение удовлетворяет уравнению, но не удовлетворяет задаче, так как по смыслу задачи искомое число должно быть целым. Различие между уравнением и задачей произошло здесь оттого, что уравнение не содержит в себе подразумеваемого в задаче требования, чтобы искомое число было целым. Предложенная задача не имеет решений.
Отрицательное решение: Такое решение получается из уравнения ax=b тогда, когда числа а и b имеют противоположные знаки. Пусть, например,
5х = — 15 или —5x=15;
тогда:
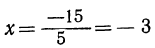
Чтобы показать, в каком смысле надо понимать отрицательное решение x=—m, обратим внимание на то, что если число —m удовлетворяет данному уравнению αx=b, то равенство —am = b должно быть тождеством; значит, тогда положительное число m удовлетворяет другому уравнению: — ax=b, которое получается из данного, если в нём заменим х на — х. Основываясь на этом замечании и получив отрицательное решение х=— m, мы можем поступить так: изменим в уравнении х на — х; от этого получим новое уравнение, которое должно иметь положительное решение х=m. Новое уравнение, конечно, не соответствует предложенной задаче; всматриваясь в него, мы легко определим, как надо изменить задачу, чтобы она имела положительное решение х=m.
Для примера приведём такую простую задачу.
Отцу 40 лет, а сыну 10 лет. Через сколько лет отец будет в 7 раз старше сына?
Обозначим искомое число буквой х.
Очевидно, что через х лет отцу будет 40+х, а сыну 10+x лет. По условию:
40+x=7 (10+x), откуда x=— 5.
Заменив в уравнении х на — х, получим новое уравнение 40 — x = 7 (10 — х), которое отвечает той же задаче, но с изменённым вопросом, а именно, вопрос должен быть такой: сколько лет назад отец был в 7 раз старше сына?
Из примеров, подобных указанному, можно усмотреть, что отрицательное решение надо понимать в смысле, противоположном тому, в каком понималось бы положительное решение; так, если положи тельное решение означает время после некоторого события, то отрицательное означает время раньше этого события; если первое означает доход, то второе — расход и т. п. Если же случается, что по смыслу задачи неизвестное число х нельзя понимать в двух противоположных смыслах, то тогда отрицательное решение означает, что задача не имеет решения.
Нулевое решение: Положим, что в уравнении ах=b число b окажется нулём, а коэффициент а будет какое-нибудь число, отличное от нуля. Пусть, например, уравнение будет 4х=0. Значит, произведение 4х должно равняться нулю. Но произведение равняется нулю только тогда, когда какой-нибудь сомножитель равен нулю; следовательно, сомножитель х должен равняться нулю. И из формулы 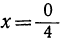
Задача:
Какое число надо прибавить к числителю и знаменателю дроби 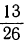
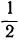
Обозначив искомое число буквой х, мы получим уравнение:
откуда:
26+2x=26+x; х=0.
Это значит, что дробь сама равна 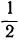
Случай, когда уравнение не имеет корня
Пусть в уравнении ax=b число а окажется нулём, а число b не равно нулю; например, 0∙x = 10. Такое равенство невозможно, так как, какое бы число мы ни взяли для х, произведение 0∙x равно нулю, а не 10.
Пусть, например, уравнение будет такое:
Решаем его, как обыкновенно (общий знаменатель 6):
Зх — 24+2x = 42+5x,
т. е.
5x = 66+5x, или 5х — 5x=66.
Какое бы число х мы ни взяли, разность 5х — 5х всегда равна нулю, а не числу 66. Значит, предложенное уравнение не имеет корня.
Если бы мы, не заметив, что коэффициент а равен нулю, разделили па него обе части уравнения ax=b, то получили бы для х такую формулу: 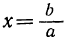
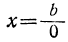
Так как деление на 0 невозможно, то из последней формулы мы пришли бы к заключению, что при α=0 уравнение ax = b не имеет корня (значит, и задача не имеет решений).
Но недостаточно ограничиться только этим одним заключением. Полезно указать ещё на одно важное обстоятельство, для уяснения которого мы предварительно должны рассмотреть, как изменяется дробь, когда знаменатель её неограниченно уменьшается, а числитель, остаётся неизменным.
Как надо понимать равенство 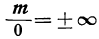
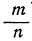
Положим, например, что знаменатель n получает такие уменьшающиеся значения:
n = 0,l; n = 0,01; n = 0,001; n = 0,0001 и т. д.
Тогда дробь будет получать такие возрастающие значения:
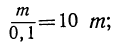
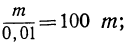
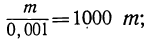
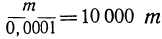
Отсюда видно, что если числитель остаётся неизменным, а знаменатель неограниченно приближается к нулю, то абсолютная величина дроби 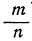
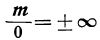
где знак ∞ выражает „бесконечность». Запись эту нельзя понимать буквально, так как деление на 0 невозможно; она только кратко означает, что абсолютная величина дроби неограниченно увеличивается (или, как иногда говорят, стремится к бесконечности), если знаменатель неограниченно приближается к нулю, а числитель остаётся неизменным, причём сама дробь остаётся или положительной, или отрицательной (смотря по тому, имеет ли знаменатель, стремящийся к нулю, одинаковый знак с числителем или противоположный).
Теперь мы можем дополнить исследования так:
При а = 0 уравнение ах = b не имеет корня, но если а не равно 0, а только приближается к 0 всё ближе и ближе, то абсолютная величина корня возрастает неограниченно.
Неопределённое решение: Если в уравнении ax=b оба числа а и b окажутся нулями, то уравнение обращается в тождество: 0∙x = 0, верное при всяком значении х. Значит, в этом случае уравнение становится неопределённым, т. е. оно допускает бесчисленное множество произвольных решений.
Если бы мы, не заметив, что α = 0, разделили обе части уравнения на а, то для х получили бы дробь 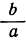
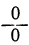
Задача:
Какое число надо прибавить к числителю и знаменателю дроби у, чтобы эта дробь сделалась равной числу m?
Обозначив искомое число буквой х, получим такое уравнение: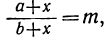
откуда:
a+x=bm+mx; х — mx=bm- a; (1-m)x = bm-a.
Если m≠l, то
Допустим, что m=1, а разность b — а есть какое-нибудь число, отличное от нуля (положительное или отрицательное). Тогда для х получим:
0∙x=b — а.
Отсюда мы можем заключить, что при m = 1 и b ≠ а не существует никакого числа х, удовлетворяющего вопросу задачи, но если m не равно 1, а только приближается к 1, то абсолютная величина числа х увеличивается неограниченно.
Если же при m=l ещё b=a, то для х получается формула:
0∙x=0,
из которой можно заключить, что всякое число х удовлетворяет вопросу задачи (и действительно: дробь 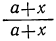
Графическое истолкование решения уравнения ax=b:
Обозначим левую часть уравнения буквой y₁ и правую часть — буквой y₂ и построим на одном и том же чертеже графики двух функций: y₁ =ax и y₂=b.
График первой функции есть прямая, проходящая через начало координат и через точку (1, а); график второй функции есть прямая, параллельная оси х-ов и отсекающая от оси у-ов отрезок ¢ ‘(на чертеже 31 мы изобразили случай, когда а>0 и b>0; предоставляем самим читателям сделать чертежи для случаев, когда 1) α>0, но 0 и 3) α 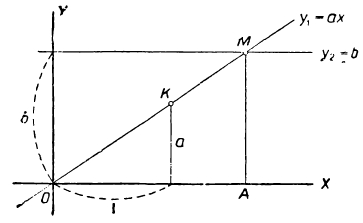
Пользуясь таким графическим изображением, мы можем наглядна
истолковать все случаи решения уравнения ax = b. Ограничимся рассмотрением двух случаев: 1) уравнение не имеет решения и 2)уравнение имеет неопределённое решение.
1) Уравнение не имеет решений (черт. 32). Уменьшая численную величину коэффициента а, мы заставляем прямую у=ах всё более и более приближаться к оси х-ов. Тогда точка M, в которой прямая у=b пересекается с прямой y=αx, всё более и более удаляется направо, проходя через положения M₁, M₂, M₃ и т. д., причём абсцисса OA точки пересечения беспредельно увеличивается, принимая значения OA₁, OA₂ , OA₃ и т. д. Значит, когда а неограниченна уменьшается, приближаясь к нулю, корень уравнения ax = b неограниченно возрастает (что можно выразить так: 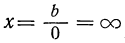
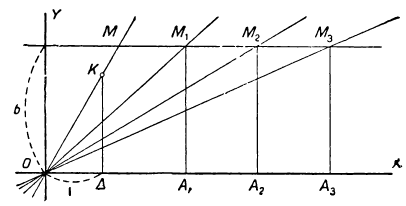
2) Неопределённое решение получается, как мы видели, при a = b=0. Чтобы истолковать этот случай графически, вообразим, что на чертеже 32 величина b уменьшается, приближаясь к нулю; тогда прямая y₂=b, оставаясь параллельной оси х-ов, будет всё более и более приближаться к этой оси и при b=0 сольётся с нею. C другой стороны, прямая y₁ = ax при а=0 обратится тоже в ось х-ов, и тогда две прямые y₂ =b и y₁=ax совпадут с осью х-ов, и, следовательно, каждую из точек этой оси можно считать за точку пересечения; значит, величина корня остаётся неопределённой.
Видео:М11 (2.31-2.40) Многочлен. Системы уравнений. Уравнения.Скачать

Исследование системы двух уравнений первой степени с двумя неизвестными
Общие формулы: Мы видели что система двух уравнений:
ax+by=с и a’x+b’y=c’
даёт следующие формулы для неизвестных:
(ab’— a’b)x=(b’c — bс’); (ab’ — a’b) y=(ac’ — а’с). (1)
Если ab’ — a’b≠0, то
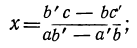
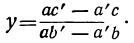
Исследование: Исследование этих формул подразделим на два случая:
1) Общий знаменатель ab’ — а’b не равен нулю.
В этом случае система имеет единственное решение. О значении этого решения для задачи, из условий которой составлена рассматриваемая система, здесь может быть сказано то же самое, что говорилось раньше при исследовании одного уравнения с одним неизвестным.
2) Общий знаменатель ab’— a’b=0. В этом случае числители в формулах (2) могут быть как отличными от нуля, так и равными нулю. Докажем, что если ни одно из чисел a, a’, b, b’ не равно нулю, то будет иметь место одно из следующих двух предположений.
а) Если один из числителей для х или для у в формулах (2) равен дулю, то и другой равен нулю.
Пусть, например, числитель для х равен нулю, для чего необходимо, чтобы:
cb’=c’b; и, кроме того, дано, что ab’=a’b.
Умножив левую часть первого из этих равенств на правую часть второго, а правую — на левую второго, получим:
cb’a’b=c’bab’, откуда cb’a’b — c,bab, =0,
и, следовательно,
bb’ (а’с — ac’)=0.
Так как числа b и b’ не равны нулю, то последнее равенство возможно только тогда, когда а’с — ac’=0, т. е. числитель для у равен нулю.
Так же, если допустим, что числитель для у в формулах (2) равен нулю (т. е. если ac’ = a’c и ab’=a’b), то получим:
ас’a’b=a’cab’ ; aa’ (c’b — cb’)=0; c’b — cb’=0.
б) Если один из числителей для х или для у в формулах (2) не равен нулю, то и числитель для другого неизвестного также не равен нулю.
Действительно, если бы для одного из неизвестных числитель был бы равен нулю, то, по доказанному, числитель для другого неизвестного также был бы равен нулю.
Если числители для обоих неизвестных в формулах (2) равны нулю, то это означает неопределённость задачи. Действительно, умножив все члены первого уравнения на b’, а члены второго на b (что можно сделать, так как, по предположению, числа b и b’ не равны 0), получим:
ab’x+bb’y=cb’ и a’bx+b’by=c’b. [А]
Но ab’ = a’b и cb’ =c’b; следовательно, оба уравнения [А] представляют собой в сущности одно уравнение с двумя неизвестными, а в этом случае, как мы знаем, неизвестные могут иметь бесчисленное множество значений.
Если числители в формулах (2) не равны нулю, a ab’ — a’b=0, то это означает несовместимость уравнений. В самом деле, если ab’ = a’b , a cb’ ≠ c’b , то левые части системы [А] имеют одинаковые численные величины, а правые — разные; значит, уравнения несовместимы, и задача не имеет решения.
Полезно заметить, что в случае, когда уравнения (1) принимают вид 0x=0, 0y=0, то это ещё не значит, что обоим неизвестным можно давать произвольные значения. Выбрав значения одного из них произвольно, мы тем самым определим другое неизвестное, найдя его из какого-нибудь одного из двух данных уравнений.
Итак, если ab’—a’b≠0, то решение системы:
ax+by=c, a’x+b’y=c’
получается по общим формулам; если же ab’ — a’b=0, но ни одно из чисел a, b, a’, b’ не обращается в нуль, то система или имеет бесчисленное множество решений, или ни одного решения. Случай, когда ab’—a’b=0 и, кроме того, какое-либо из чисел a, b, a’, b’ равно нулю, мы не рассматриваем.
Исследование квадратного уравнения
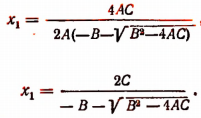
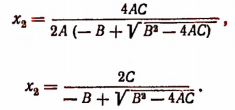
Исследование формул: Корни полного квадратного уравнения αx²+bx+c=0 выражаются, как мы знаем, формулами:
Число а мы будем считать положительным (если бы оно было отрицательное, мы могли бы переменить знаки перед всеми членами уравнения на противоположные; нулём число а быть не может, так как в противном случае уравнение перестало бы быть квадратным, оно обратилось бы в уравнение первой степени).
Мы говорили ранее, что корни квадратного уравнения будут оба вещественные или оба мнимые в зависимости от того, окажется ли дискриминант b² — 4ас величиной положительной или отрицательной.
Рассмотрим этот вопрос подробнее: 1) Если b² — 4ас > 0 , то 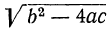
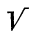
а) Оба корня — положительные числа, если 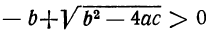
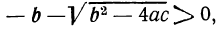
б) Оба корня — отрицательные числа, если 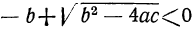
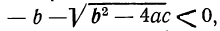
в) Один корень — положительный, а другой — отрицательный, когда b, будучи положительным или отрицательным, по абсолютной величине меньше 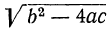
2) Если b² —4αc=0, то корни будут вещественные и равные: 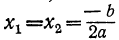
3) Если b² —4αc 
Подобно этому найдём, что точка С, отстоя от источника света В на (d— х) м, будет иметь освещённость от В в 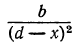
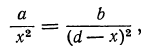
откуда:
a(d — x)²=bx², т. е. ad² — 2αdx+αx²— bx2=0,
(α — b)x² — 2adx+ad²=0.
Так как коэффициент при х делится на 2, то
Следовательно,
Исследуем эти формулы. Так как а и b — числа положительные, то мнимых решений в этой задаче не будет.
1) Если a>b, то оба корня положительны, причём, так как
Второе решение (x₂ d) ему противоречит. Чтобы принять или отвергнуть это решение, мы должны рассмотреть, какое уравнение получится, если сделаем предположение, что искомая точка находится направо от В (например, в C₁) на расстоянии х от А. Тогда по-прежнему освещённость её источником А будет 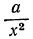
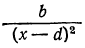
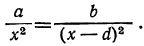
Сравнивая это уравнение с уравнением (1), находим, что они одинаковы, так как
(d-x)²=(x-d)²∙
Заметив это, мы можем утверждать, что оба положительные решения уравнения (1) удовлетворяют задаче.
2) Если a Исследование уравнений
Исследовать уравнение — значит определить, имеет ли данное уравнение решения и, если имеет, то сколько.
Кроме этого основного вопроса, в исследование уравнения может входить необходимость выяснения и других частных вопросов. Например, вопроса о числе действительных, отрицательных, рациональных и целых корней.
Решение всех этих вопросов порой представляет большие трудности и не может быть достигнуто средствами только элементарной алгебры. Эти вопросы более подробно рассматриваются в курсах высшей алгебры. Элементарная же алгебра ими занимается частично.
Исследование уравнения первой степени с одним неизвестным
Общий вид уравнения 1-й степени с одним неизвестным таков:
1. Если 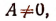
Если А и В — числа действительные, то и решение действительное.
Если А и В — мнимые, то решение может оказаться мнимым, но может оказаться и действительным.
Если А и В — действительные числа, одновременно положительные или одновременно отрицательные, то решение уравнения будет отрицательным.
Если А и В — действительные числа, из которых одно положительное, а другое отрицательное, то решение уравнения будет положительным.
Если В = 0, то единственным решением уравнения будет х = 0.
Если А=О и 
Если А = 0 и В = 0, то решением уравнения будет являться любое число. Уравнение будет иметь бесконечное множество решений.
Пусть требуется исследовать уравнение
После преобразований данное уравнение примет вид:
1. Если 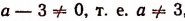
Это единственное решение окажется равным нулю лишь тогда, когда а = 5.
Если а — 3 = 0, т. е. а = 3, то уравнение примет вид:
Следовательно, при а = 3 данное уравнение не будет иметь ни одного решения.
Данное уравнение никогда не может иметь более одного решения, так как выражения (а — 3) (а — 5) не могут одновременно обратиться в нуль.
В исследование данного уравнения могут войти и другие вопросы. Например, поставим такой вопрос. «При каких значениях буквы а решение данного уравнения будет числом положительным?»
Для ответа на этот вопрос надо решить неравенство
Решив это неравенство, найдем, что корень данного уравнения будет положительным только тогда, когда
3
Исследование этого уравнения предлагается учащемуся сделать самостоятельно. Ниже приводится результат этого исследования.
- При а, равном 2, уравнение не имеет ни одного корня.
- При а, равном 3, любое число будет корнем данного уравнения.
- При всех прочих значениях а данное уравнение имеет только одни корень.
Исследование системы двух уравнений 1-й степени с двумя неизвестными
Общий вид системы двух уравнений 1-й степени о двумя неизвестными таков:
Умножим сначала обе части первого уравнения на 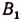
Теперь умножим обе части первого уравнения на 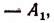
1. Если 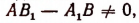
2. Если 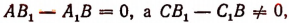
Также система не будет иметь ни одного решения, если окажется, что
3. Если 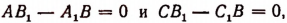
будет иметь своим решением любое число. Чтобы в этом случае находить решения системы, достаточно в одно из данных уравнений, например в уравнение
подставлять вместо буквы х любое число и после этого находить значение неизвестного у, соответствующее выбранному значению х. В этом случае данная система будет иметь бесконечное множество решений. Однако решением системы не может быть, вообще говоря, любая пара чисел, а лишь пара чисел, надлежащим образом найденная.
Если окажется 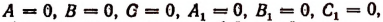
Результаты произведенного исследования системы (I) можно оформить еще и так:
1) Если 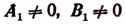
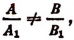
2) Если 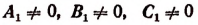
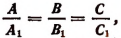
3) Если 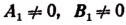
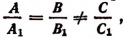
называется, как нам уже известно (см. стр. 217), определителем системы (I).
Примеры:
Следовательно, эта система имеет одно и только одно решение.
2. Определитель системы:
Следовательно, эта система не имеет ни одного решения.
3. Определитель системы:
Следовательно, эта система имеет бесконечное множество решений.
Для получения решений этой системы достаточно одной из неизвестных, например х, давать любое значение и каждый раз находить из уравнения х + у = 10 соответствующее значение неизвестного у.
Таким образом, можем получить сколько угодно решений этой системы:
Исследование квадратного уравнения
Общий вид квадратного уравнения таков:
- Если
то уравнение имеет два действительных различных корня.
- Если
то уравнение имеет два действительных одинаковых корня.
- Если
то уравнение имеет два мнимых сопряженных корня.
называется дискриминантом квадратного уравнения.
В исследование квадратного уравнения могут входить и другие вопросы. Например, исследуем характер корней уравнения
при условии, что
При
При
Таким образом, получилось следующее:
Если 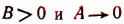
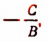
Можно убедиться, что получится такой же результат при 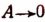
убедитесь в том, что один из корней будет близок к числу 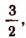
В заключение рассмотрим еще следующий пример. Может ли уравнение
иметь мнимые корни, если все числа р, q и а действительные? Преобразовав данное уравнение, получим:
Дискриминант этого уравнения
ни при каких действительных значениях р, q и а не может быть числом отрицательным. Следовательно, данное уравнение не может иметь мнимых корней.
Примеры решения уравнений
1. Найти условия, при которых система
имеет два действительных решения, два мнимых сопряженных решения и, наконец, одно решение (двукратное).
Определив у в зависимости от х из первого уравнения и подставив во второе, получим после преобразований:
Дискриминант этого квадратного уравнения
после преобразований принимает вид:
Следовательно, данная система имеет два различных действительных решения, если 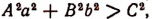
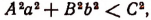
2. Вывести условие, при котором у выражается из уравнения
рационально в зависимости от х.
Преобразуем данное уравнение к форме квадратного уравнения относительно неизвестного у:
Дискриминант этого уравнения
после преобразований примет вид:
Для того чтобы у выразился в зависимости от х, рационально, необходимо и достаточно, чтобы последний трехчлен 2-й степени относительно х оказался полным квадратом, т. е. чтобы его дискриминант равнялся нулю (см. стр. 300).
является необходимым и достаточным условием того, чтобы из уравнения (1) у выражался в зависимости от х рационально.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института









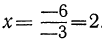
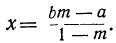
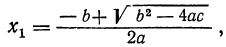
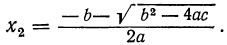
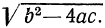
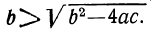
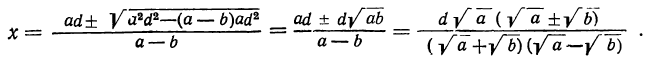
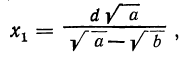
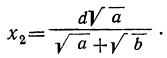
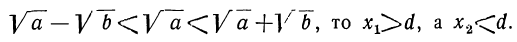
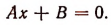

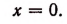
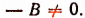
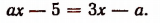
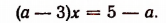
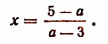
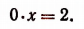
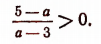

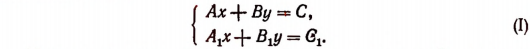
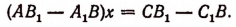
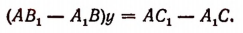
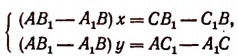
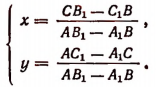
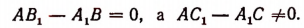
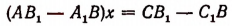
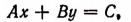
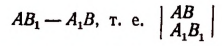
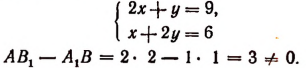
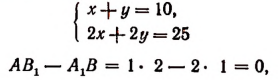
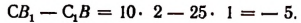
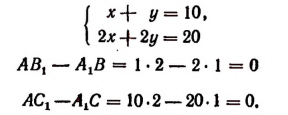
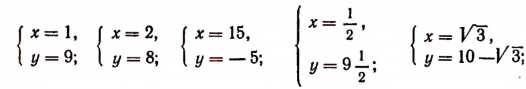
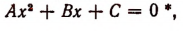
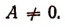
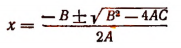
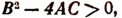 то уравнение имеет два действительных различных корня.
то уравнение имеет два действительных различных корня.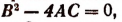 то уравнение имеет два действительных одинаковых корня.
то уравнение имеет два действительных одинаковых корня.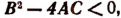 то уравнение имеет два мнимых сопряженных корня.
то уравнение имеет два мнимых сопряженных корня.