Решите уравнения с помощью единичной окружности и запишите в ответ наименьший положительный корень

Видео:Решите уравнение sin(πx/3) = 1/2 В ответе напишите наименьший положительный корень.Скачать

РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ

Простейшими тригонометрическими уравнениями называют уравнения

Чтобы рассуждения по нахождению корней этих уравнений были более наглядными, воспользуемся графиками соответствующих функций.

19.1. Уравнение cos x = a

Объяснение и обоснование

1. Корни уравненияcosx=a.

При |a| > 1 уравнение не имеет корней, поскольку |cos x| ≤ 1 для любого x (прямая y = a на рисунке из пункта 1 таблицы 1 при a > 1 или при a 1 уравнение не имеет корней, поскольку |sin x| ≤ 1 для любого x (прямая y = a на рисунке 1 при a > 1 или при a n arcsin a + 2πn, n ∈ Z (3)

2.Частые случаи решения уравнения sin x = a.

Полезно помнить специальные записи корней уравнения при a = 0, a = -1, a = 1, которые можно легко получить, используя как ориентир единичную окружность (рис 2).

Учитывая, что синус равен ординате соответствующей точки единичной окружности, получаем, что sin x = 0 тогда и только тогда, когда соответствующей точкой единичной окружности является точка C или тока D. Тогда

Аналогично sin x = 1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка A, следовательно,

Также sin x = -1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка B, таким образом,

Примеры решения задач

Замечание. Ответ к задаче 1 часто записывают в виде:

19.3. Уравнения tg x = a и ctg x = a

Объяснение и обоснование

1.Корни уравнений tg x = a и ctg x = a

Рассмотрим уравнение tg x = a. На промежутке функция y = tg x возрастает (от -∞ до +∞). Но возрастающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение tg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арктангенса равен: x₁ = arctg a и для этого корня tg x = a.

Функция y = tg x периодическая с периодом π, поэтому все остальные корни отличаются от найденного на πn (n ∈ Z). Получаем следующую формулу корней уравнения tg x = a:

При a=0 arctg 0 = 0, таким образом, уравнение tg x = 0 имеет корни x = πn (n ∈ Z).

Рассмотрим уравнение ctg x = a. На промежутке (0; π) функция y = ctg x убывает (от +∞ до -∞). Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение ctg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арккотангенса равен: x₁=arсctg a.

Функция y = ctg x периодическая с периодом π, поэтому все остальные корни отличаются от найденного на πn (n ∈ Z). Получаем следующую формулу корней уравнения ctg x = a:

таким образом, уравнение ctg x = 0 имеет корни

Примеры решения задач

Вопросы для контроля

1. Какие уравнения называют простейшими тригонометрическими?
2. Запишите формулы решения простейших тригонометрических уравнений. В каких случаях нельзя найти корни простейшего тригонометрического уравнения по этим формулам?
3. Выведите формулы решения простейших тригонометрических уравнений.
4. Обоснуйте формулы решения простейших тригонометрических уравнений для частных случаев.

Упражнения

Решите уравнение (1-11)

Найдите корни уравнения на заданном промежутке (12-13)

Видео:3,5 способа отбора корней в тригонометрии | ЕГЭ по математике | Эйджей из ВебиумаСкачать

Тригонометрические уравнения

Решение простейших тригонометрических уравнений

Градусы и радианы

Знакомство с тригонометрической окружностью

Повороты на тригонометрической окружности

Как много боли связано со словом тригонометрия. Эта тема появляется в 9 классе и уже никуда не исчезает. Тяжело приходится тем, кто чего-то не понял сразу. Попробуем это исправить, чтобы осветить ваше лицо улыбкой при слове тригонометрия или хотя бы добиться «poker face».

Начнем с того, что как длину можно выразить в метрах или милях, так и угол можно выразить в радианах или градусах .

1 радиан = 180/π ≈ 57,3 градусов

Но проще запомнить целые числа: 3,14 радиан = 180 градусов. Это все одно и то же значение числа π.

Вспомним, что если нас просят развернуться, то нам нужно повернуться на 180 градусов, а теперь можно так же сказать: Повернись на π!

О графиках синуса, косинуса и тангеса поговорим в другой статье.

А сейчас начем с декартовой (прямоугольной) системы координат.

Раньше она помогала строить графики, а теперь поможет с синусом и косинусом.

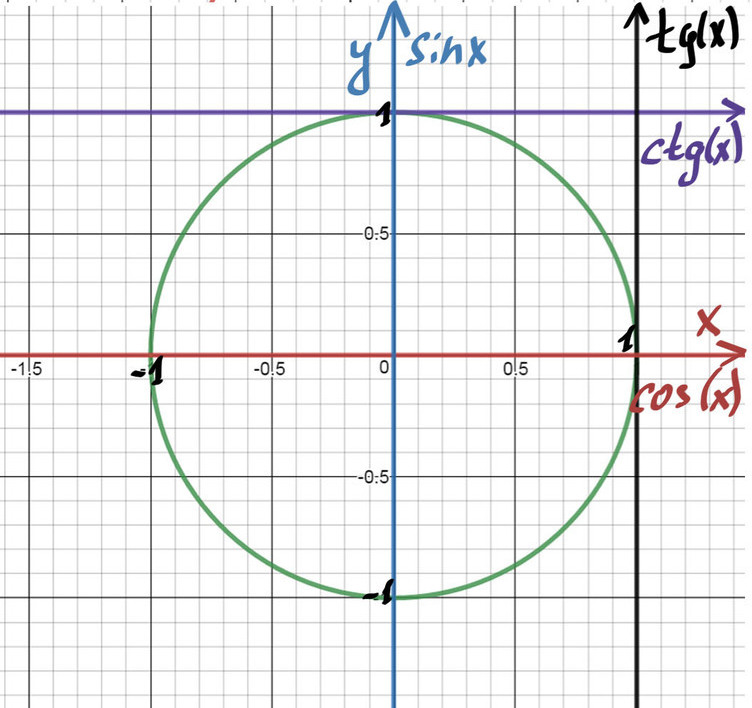
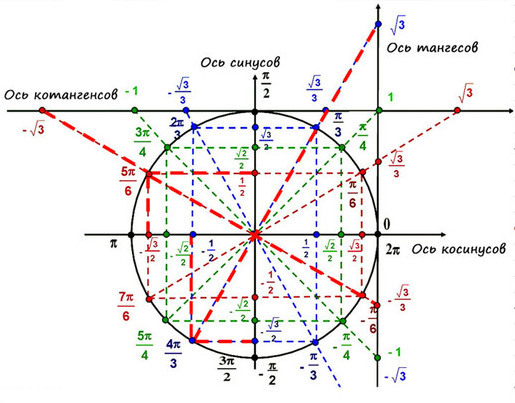
На пересечении оси Х и оси Y построим единичную (радиус равен 1) окружность:

Тогда ось косинусов будет совпадать с х, ось синусов с y. Оси тангенсов и котангенсов также показаны на рисунке.

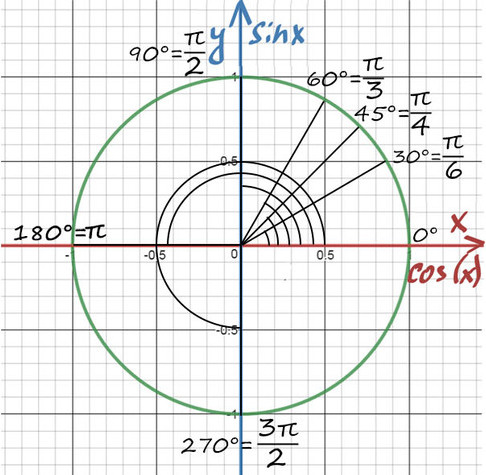
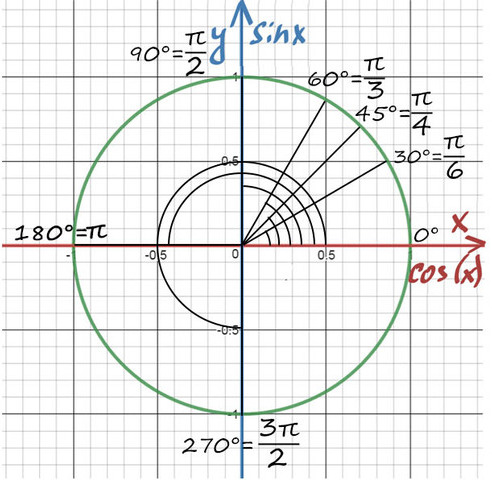
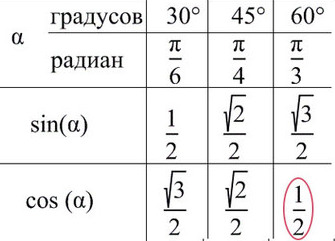
А теперь отметим основные значения градусов и радиан на окружности.

Давай договоримся с тобой, как взрослые люди: на окружности мы будем отмечать угол в радианах, то есть через Пи.

Достаточно запомнить, что π = 180° (тогда π/6 = 180/6 = 30°; π/3 = 180/3 = 60°; π/4 = 180/4 = 45°).

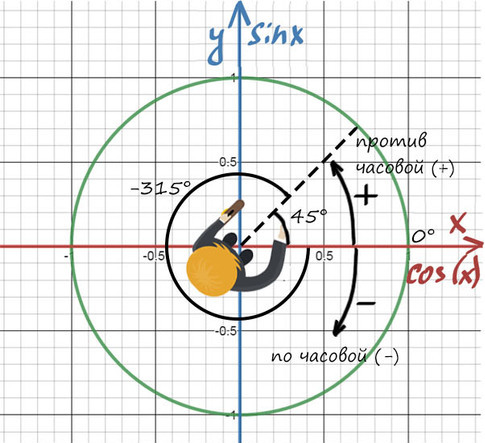
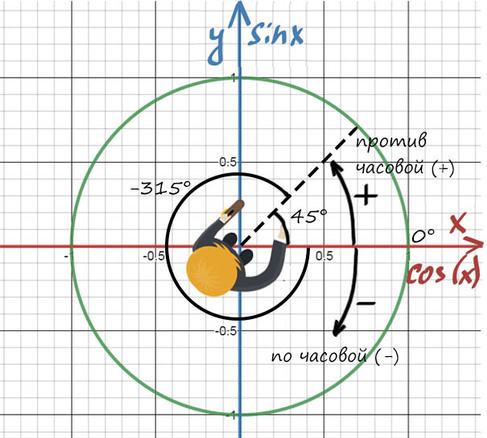
А теперь давай покрутимся на окружности! За начало отчета принято брать крайнюю правую точку окружности (где 0°):

От нее задаем дальнейший поворот. Вращаться можем как в положительную сторону (против часовой), так и в отрицательную сторону (по часовой стрелке).

Повернуться на 45° можно двумя спобами: через левое плечо на 45° в (+) сторону, либо через правое плечо на 315° в (-).

Главное — направление, куда мы будем смотреть, а не угол!

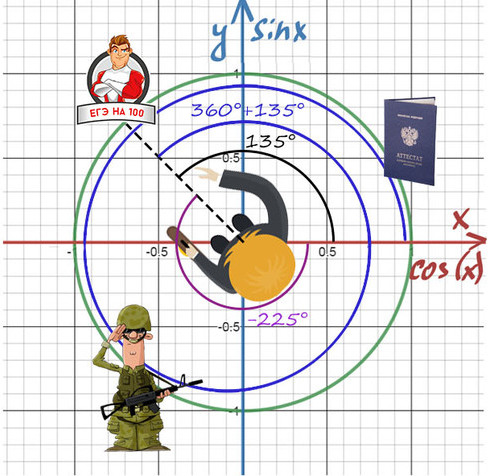
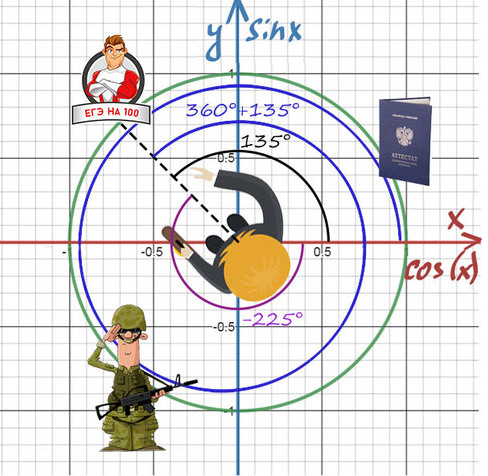
Нужно направить пунктир на 100 баллов, а сколько оборотов и в какую сторону вокруг себя мы сделаем — без разницы!

Получить 100 баллов можно поворотом на 135° или 360°+135°, или -225°, или -225°-360°.

А теперь у тебя есть два пути:

Выучить всю окружность (тригонометр). Неплохой вариант, если с памятью у тебя все отлично, и ничего не вылетит из головы в ответственный момент:

А можно запомнить несколько табличных углов и соответствующие им значения, а потом использовать их.

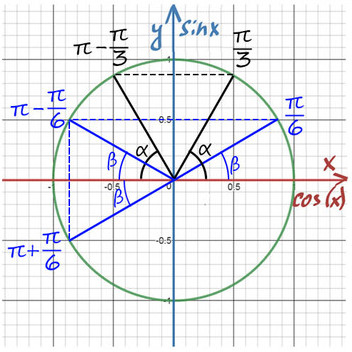
Находите равные углы (вертикальные, соответственные) на тригонометрической окружности. Попасть в любую точку можно с помощью суммы или разности двух табличных значений.

Сразу попробуем разобрать на примере:

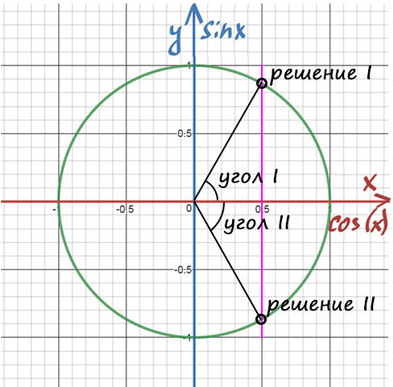
1) Помним, что ось cos(x) — это горизонтальная ось. На ней отмечаем значение ½ и проводим перпендикулярную (фиолетовую) прямую до пересечений с окружностью.

2) Получили две точки пересечения с окружностью, значение этих углов и будет решением уравнения.

Дело за малым — найти эти углы.

Лучше обойтись «малой кровью» и выучить значение синуса и косинуса для углов от 30° до 60°.

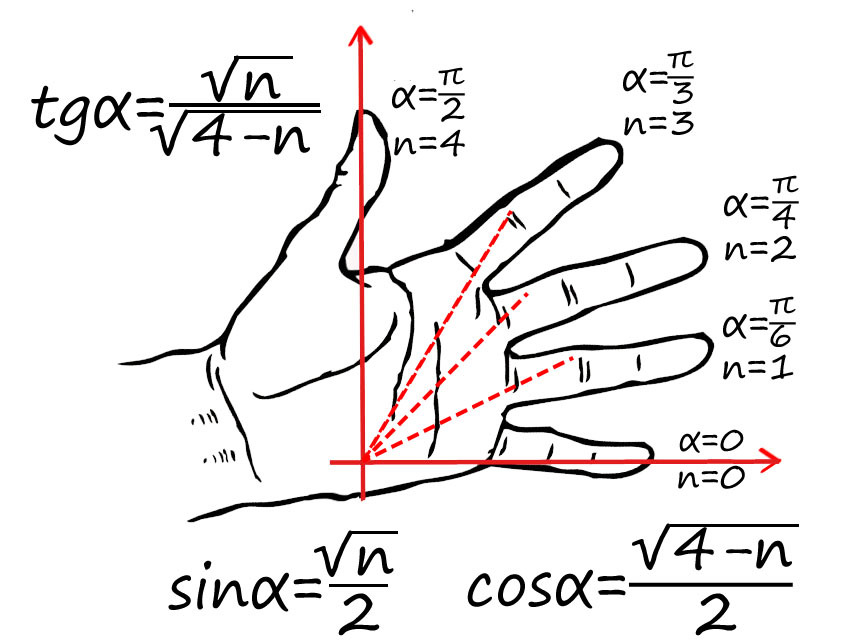
Или запомнить такой прием:

Пронумеруй пальцы от 0 до 4 от мизинца до большого. Угол задается между мизинцем и любым другим пальцем (от 0 до 90).

Например, требуется найти sin(π/2) : π/2 — это большой палец, n = 4 подставляем в формулу для синуса: sin(π/2) = √4/2 = 1 => sin(π/2) = 1.

cos(π/4) — ? π/4 соответсвует среднему пальцу (n = 2) => cos(π/4) = √2/2.

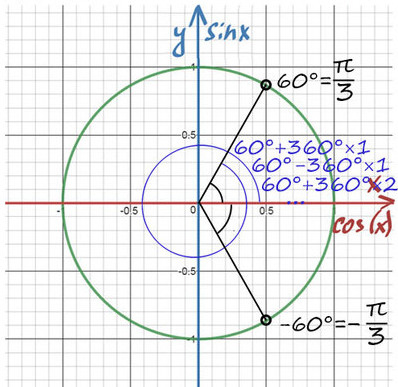
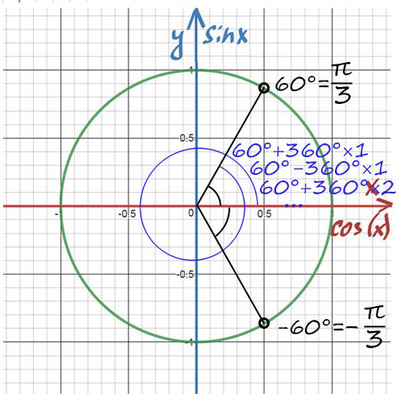
При значении cos(x) = ½ из таблицы или с помощью мнемонического правила находим x = 60° (первая точка x = +π/3 из-за того, что поворот происходил против часовой стерелки (+), угол показан черной дугой).

Вторая же точка соответствует точно такому же углу, только поворот будет по часовой стрелке (−). x = −π/3 (угол показан нижней черной дугой).

И последнее, прежде чем тебе, наконец, откроются тайные знания тригонометрии:

Когда требуется попасть в «100 баллов», мы можем в них попасть с помощью поворота на . =-225°=135°=495°=.

То же самое и здесь! Разные углы могут отражать одно и то же направление.

Абсолютно точно можно сказать, что нужно повернуться на требуемый угол, а дальше можно поворачиваться на 360° = 2π (синим цветом) сколько угодно раз и в любом направлении.

Таким образом, попасть в первое направление 60° можно: . 60°-360°, 60°, 60°+360°.

И как записать остальные углы, не записывать же бесконечное количество точек? (Хотел бы я на это посмотреть☻)

Поэтому правильно записать ответ: x = 60 + 360n, где n — целое число (n∈Ζ) (поворачиваемся на 60 градусов, а после кружимся сколько угодно раз, главное, чтобы направление осталось тем же). Аналогично x = −60 + 360n.

Но мы же договорились, что на окружности все записывают через π, поэтому cos(x) = ½ при x = π/3 + 2πn, n∈Ζ и x = −π/3 + 2πk, k∈Ζ.

Ответ: x = π/3 + 2πn, x= − π/3 + 2πk, (n, k) ∈Ζ.

Пример №2. 2sinx = √2

Первое, что следует сделать, это перенести 2-ку вправо => sinx=√2/2

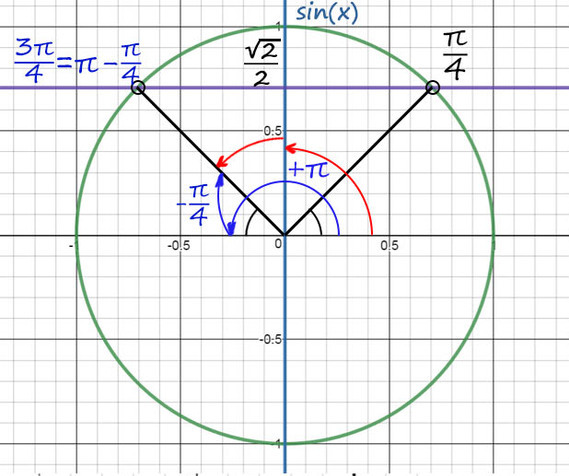
1) sin(x) совпадает с осью Y. На оси sin(x) отмечаем √2/2 и проводим ⊥ фиолетовую прямую до пересечений с окружностью.

2) Из таблицы sinx = √2/2 при х = π/4, а вторую точку будем искать с помощью поворота до π, а затем нужно вернуться обратно на π/4.

Поэтому вторая точка будет x = π − π/4 = 3π/4, в нее также можно попасть и с помощью красных стрелочек или как-то по-другому.

И еще не забудем добавить +2πn, n∈Ζ.

Ответ: 3π/4 + 2πn и π/4 + 2πk, k и n − любые целые числа.

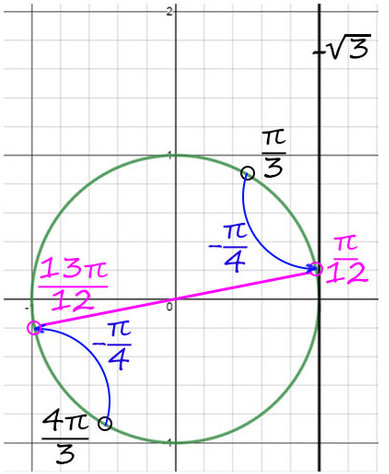
Пример №3. tg(x + π/4) = √3

Вроде все верно, тангенс равняется числу, но смущает π/4 в тангенсе. Тогда сделаем замену: y = x + π/4.

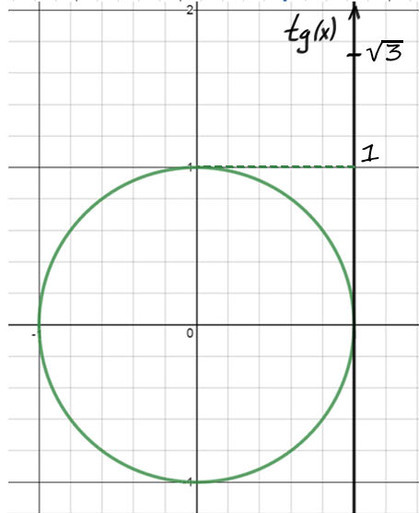
tg(y) = √3 выглядит уже не так страшно. Вспомним, где ось тангенсов.

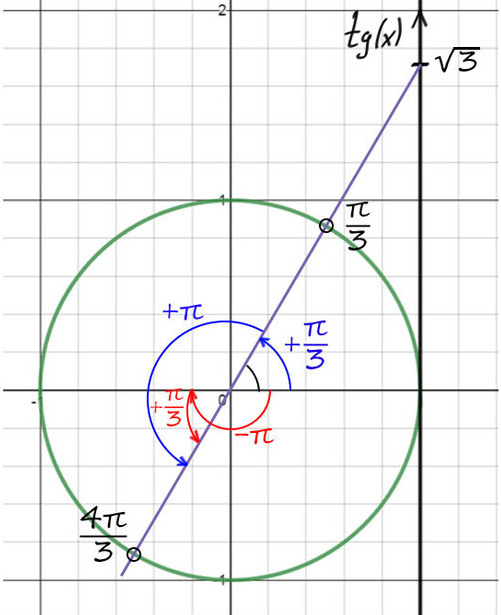
1) А теперь на оси тангенсов отметим значение √3, это выше чем 1.

2) Проведем фиолетовую прямую через значение √3 и начало координат. Опять на пересечении с окружностью получается 2 точки.

По мнемоническому правилу при тангенсе √3 первое значение — это π/3.

3) Чтобы попасть во вторую точку, можно к первой точке (π/3) прибавить π => y = π/3 + π = 4π/3.

4) Но мы нашли только y , вернемся к х. y = π/3 + 2πn и y = x + π/4, тогда x + π/4 = π/3 + 2πn => x = π/12 + 2πn, n∈Ζ.

Второй корень: y = 4π/3 + 2πk и y = x + π/4, тогда x + π/4 = 4π/3 + 2πk => x = 13π/12 + 2πk, k∈Ζ.

Теперь корни на окружности будут здесь:

Ответ: π/12 + 2πn и 13π/12 + 2πk, k и n — любые целые числа.

Конечно, эти два ответа можно объединить в один. От 0 поворот на π/12, а дальше каждый корень будет повторяться через каждый π (180°).

Ответ можно записать и так: π/12 + πn, n∈Ζ.

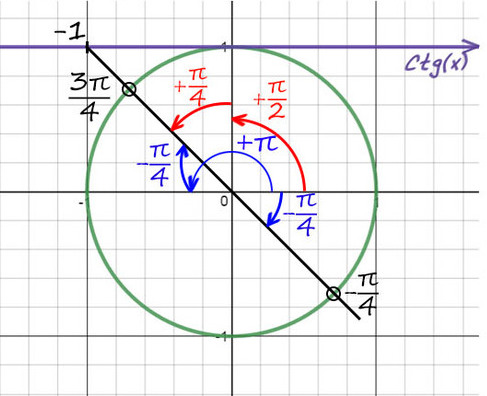
Пример №4: −10ctg(x) = 10

Перенесем (−10) в другую часть: ctg(x) = −1. Отметим значение -1 на оси котангенсов.

1) Проведем прямую через эту точку и начало координат.

2) Придется опять вспомнить, когда деление косинуса на синус даст еденицу (это получается при π/4). Но здесь −1, поэтому одна точка будет −π/4. А вторую найдем поворотом до π, а потом назад на π/4 (π − π/4).

Можно это сделать по-другому (красным цветом), но мой вам совет: всегда отсчитывайте от целых значений пи (π, 2π, 3π. ) так намного меньше шансов запутаться.

Не забываем добавить к каждой точке 2πk.

Ответ: 3π/4 + 2πn и −π/4 + 2πk, k и n — любые целые числа.

Алгоритм решения тригонометрических уравнений (на примере cos(x) = − √ 3/2) :

1. Отмечаем значение (−√3/2) на оси тригонометрической функции (косинусов, это ось Х).
2. Проводим перпендикулярную прямую оси (косинусов) до пересечений с окружностью.
3. Точки пересечения с окружностью и будут являться корнями уравнения.
4. Значение одной точки (без разницы, как в нее попадете) +2πk.

Азов достаточно, прежде чем идти дальше закрепите полученные знания.

Видео:Отбор корней по окружностиСкачать

решение тригонометрических уравнений 10 класс

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 2 500 дидактических материалов для школьного и домашнего обучения

Содержание

Ι. Решение простейших тригонометрических уравнений

ΙΙ. Общие методы решения тригонометрических уравнений

1. Метод разложения на множители

2. Метод введения новой переменной

3. Функционально-графические методы

ΙΙΙ. Решение комбинированных уравнений

ΙV. Решение тригонометрических уравнений с параметром

V. Тесты для самостоятельного решения

Ι. Решение простейших тригонометрических уравнений

Все тригонометрические уравнения сводятся к простейшим. Поэтому особое внимание следует уделять решению простейших уравнений. Начинать нужно с самых простых.

К простейшим тригонометрическим уравнениям относятся уравнения вида:

Для каждого из простейших тригонометрических уравнений определены формулы, справедливость которых обосновывается с помощью тригонометрического круга и с учетом периодичности тригонометрических функций.

sinx =0, x= πn, nєZ

sinx =–1, x= –+2πn, nєZ;

sinx =1, x=+2πn, nєZ;

x= π– arcsin а +2πn, nєZ.

В последнем случае для сокращения записи используют формулу:

x=(–1) n arcsin а + πn, nєZ.

cos x=0, x= – + π n, n є Z;

cos x=–1, x= π +2 π n, n є Z;

cos x=1, x=2 π n, n є Z;

cos x= а , | а | а +2 π n, n є Z.

Решения уравнения tg x =а и ctg x =а записываются существенно проще:

x = arctg а +π n , n є Z и, соответственно, x = arc с tg а +π n , n є Z .

Пример 1. Решить уравнение sinx = .

Решение: так как n arcsin + πn, nєZ.

Ответ: (–1) n arcsin + πn, nєZ.

Пример 2. Решить уравнение cos x =.

Решение: так как >1, значит уравнение не имеет решения.

Ответ: нет решения.

Пример 3. Решить уравнение tg x + = 0.

tg x+ = 0

tg x = –

x = arctg (– ) + π n, n є Z

x = – arctg + π n, n є Z

x = – +2 π n, n є Z;

Ответ: –+2πn, nєZ.

Пример 4. Решить уравнение 2 cos x = –.

2cos x = –

cos x = –

x= ± arccos (– )+2 π n, n є Z

x= ±( π – arccos )+2 π n, n є Z

x= ±( π – )+2 π n, n є Z

x = ± + 2 π n, n є Z

Ответ : ± + 2 π n, n є Z.

Для отработки общих формул решения простейших уравнений можно предложить для устного решения задания такого вида.

Образуют ли арифметическую прогрессию расположенные в порядке возрастания положительные корни уравнения : sinx =0; cosx = 0,5; tg x =1.

На начальном этапе, пока не отработаны навыки использования общих формул решения простейших уравнений желательно прописывать эти формулы, чтобы учащиеся быстрее их запомнили.

Далее нужно переходить к решению более сложных уравнений, которые чаще всего встречаются в вариантах ЕГЭ в разделе А.

Пример 5. Решить уравнение cos = .

Решение: cos =

Это уравнение сводится к простейшему cos t = заменой t =, которую можно не прописывать.

= ± arccos +2π n , n є Z

= ± +2π n , n є Z

х = ± + 10π n , n є Z

Ответ: ± + 10π n , n є Z .

Пример 6. Решить уравнение: sin (2 x –) = .

Решение: sin (2 x –) =

2 x –= (–1) n arcsin + π n , n є Z

2 x – = (–1) n + π n , n є Z

2 x – = ++ 2π n , n є Z

2 x – = –+ (2m + 1)π,mєZ

2 x = + 2πn, n є Z

2 x =π + 2πm, mє Z

x = + πn, n є Z

x = + πm, mє Z

Ответ: + πn, + πm, n ,mє Z .

Так же нужно обратить внимание учащихся на то, что довольно часто исходное уравнение приводится к простейшему лишь после различных тождественных преобразований и применения формул тригонометрии.

Пример 7. Решить уравнение 4 sin 3 x cos 3 x =1.

Решение : 4 sin3x cos 3x =1

2(2sin3x cos 3x) =1

sin6x =

6x = (–1) n + π n, n є Z

x = (–1) n + n, n є Z

Ответ: (–1) n + n , n є Z .

Часто предлагается решить тригонометрическое уравнение на некотором промежутке. Целесообразно начинать решать такие уравнения до вывода общих формул решения простейших тригонометрических уравнений.

Пример 8. Найдите корни уравнения 2 cosx = –1, принадлежащие промежутку [0;2π].

cosx = –

Выбор значений x , которые принадлежат указанному промежутку можно выполнить различными способами.

Наиболее рационально это делать с помощью единичной окружности.

x₁ = ; x₂ = .

Ответ: ;.

В тестах часто требуется не просто найти корни, принадлежащие данному промежутку, а вычислить их сумму или разность; определить наибольший или наименьший корень; указать количество корней.

Пример 9. Найдите сумму корней уравнения ( cos 2 x –1)(2 sin – 1) = 0, принадлежащих промежутку [–; π ).

Решение: x₁ = 0; x₂ = , x₁ + x₂ =

Ответ: .

1. Найдите сумму корней уравнения 2 sinx = –1 на указанном промежутке

2. Найдите количество корней уравнения 4 cos 2 2х = 1 на указанном промежутке

3. Найдите сумму наименьшего положительного и наименьшего отрицательного корней уравнения sinx cos + sin cos х = на указанном промежутке

Уже при решение простейших тригонометрических уравнений полезно предлагать нестандартные уравнения.

Пример 10. Решить уравнение cos x 2 = 1.

Можно дать это уравнение для самостоятельного решения.

Найдутся ученики, которые решат его в одну строчку:

х = , kЄZ.

Целесообразно продемонстрировать это решение на доске и предложить ученикам найти допущенные ошибки.

В случае затруднений, чтобы внести полную ясность, решить для начала уравнение

Его решение имеет вид х = ± при а0.

Если а sinsinx = 1.

Решение: sinsinx = 1.

sinx = +2πn, nєZ

Выражение |+2πn | > 1 при любых значениях n , nєZ.

Поэтому исходное уравнение не имеет решений.

Ответ: нет решений.

ΙΙ. Общие методы решения тригонометрических уравнений

Метод разложения на множители.

Этот метод заключается в том , что исходное уравнение сводится к уравнению вида

f ( x ) g ( x ) h ( x ) = 0, которое можно заменить совокупностью уравнений, каждое из которых сводится к простейшему.

Решив уравнения совокупности нужно взять только те решения, которые принадлежат области определения исходного уравнения, а остальные корни отбросить.

Пример 1. Решить уравнение sin 4 x = 3 cos 2х.

sin 4 x = 3 cos 2х.

2 sin 2 x cos 2х = 3 cos 2х

Получив такое уравнение, ученики достаточно часто делают ошибку, «сократив» левую и правую части уравнения на cos 2х. Некоторые из них при этом оговаривают, что cos 2х 0,но одной оговорки здесь, увы, недостаточно. Необходимо ещё рассмотреть случай, когда cos 2х = 0, и проверить, не являются ли значения х, удовлетворяющие этому равенству, корнями исходного уравнения. Разумеется, лучше всего не делить левую и правую части уравнения на cos 2х, а разложить на множители

(2 sin 2 x – 3) cos 2х = 0.

Полученное уравнение равносиьно совокупности двух уравнений

х = , nЄZ.

Первое уравнение решения не имеет, так как функция синус не может принимать значений по модулю больших единицы. К сожалению, не все ученики это понимают, а из тех, кто понимает, не всякий вспоминает вовремя.

Ответ: , nЄZ.

Пример 2. Решить уравнение sin 2 x = sin 4 x

Решение: некоторые учащиеся, встретив такое уравнение, решительно записывают

2х = 4х или 2х = 4х + 2πn, nЄZ, что приводит к потере решений исходного уравнения.

Решение исходного уравнения состоит в переходе к уравнению sin 2 x – sin 4 x = 0

и последующем применении формулы для преобразования разности тригонометрических функций в произведение

2 cos = 0

Ответ:

Пример 3. (ЕГЭ 2009г. Вариант 1, С2.).

Найдите все значения , при каждом из которых выражения

принимают равные значения.

Ответ:

Пример 4. (ЕГЭ 2009г. Вариант 2, B 7.).

Найдите наименьший корень уравнения

Решение:

Ответ:

Метод замены переменной.

В школьном курсе в основном рассматриваются уравнения, которые после введения нового неизвестного t = f ( x ),где f ( x ) – одна из основных тригонометрических функций, превращаются в квадратные либо рациональные уравнения с неизвестным t.

Пример 5. Решить уравнение cos 2 π x + 4 sin π x + 4 =0

Решение: 1 – sin 2 π x + 4 sin π x + 4 =0

– sin 2 π x + 4 sin π x + 5 =0

Заменим sin πx = t , -1

t ₂ не удовлетворяет условию -1

πx = –

х = –

Ответ: –

Решение однородных тригонометрических уравнений.

Уравнение вида а sinx + b cosx =0, где а и b –некоторые числа, называются однородными уравнениями первой степени относительно sinx и cosx .

Уравнение вида а sin 2 x + b cos 2 x + с =0, где а,b,с – некоторые числа, называются однородными уравнениями второй степени относительно sinx и cosx .

Пример 6. Решить уравнение sinx – cos х = 0.

Решение: легко убедиться, что cosx = 0 не является корнем исходного уравнения.

В самом деле, если cosx = 0, то, в силу исходного уравнения, и sinx = 0, что противоречит основному тригонометрическому тождеству. Этот факт позволяет разделить левую и правую части уравнения на cosx .

Получим уравнение tg x = 1, откуда х =

Ответ:

Пример 7. Решить уравнение sin 2 x – 3 sinx cos х + 2 cos 2 x = 0.

Решение: поскольку cosx = 0 не является корнем tg x данного уравнения,

разделим левую и правую части уравнения на cos 2 x . В результате приходим к квадратному уравнению относительно tg 2 x – 3 tg x + 2 = 0,

решив которое, получим

Ответ:

Введение вспомогательного аргумента.

Уравнение вида а cosx + b sinx = с, где а, b, с –некоторые числа, причем

называют линейными тригонометрическими уравнениями.

Для решения таких уравнений используют введение вспомогательного аргумента.

Так как а 2 + b 2 >0, то можно разделить обе части уравнения на , получим

Введём в рассмотрение угол такой, что

Угол , удовлетворяющий этим двум условиям, принято называть дополнительным (или вспомогательным) аргументом. Для любых значений а и b такой угол существует, так как

Вообще, полезно напомнить учащимся, что любые числа p и g такие, что

p 2 + g 2 = 1 можно рассматривать как косинус и синус некоторого угла.

Теперь исходное уравнение можно записывать в виде

cos cosx + sin sinx =

cos (x – ) =

Аналогично можно вводить вспомогательный угол такой, что:

Тогда исходное уравнение можно привести к виду

sin cosx + cos sinx =

sin (x + ) =

Полезно также обратить внимание учащихся, что умение преобразовывать выражения вида а cosx + b sinx может понадобиться не только при решении уравнений, но и для построения оценок, нахождения наибольших значений и т. д.

Пример 8. Решить уравнение 3 sinx – 4 cos х = 5.

Решение. 3 sinx – 4 cos х = 5

==5

, cosx = ,

cos ( x + ) = –1

x + = π + 2 πn , n Є Z

x = – + π + 2 πn , n Є Z

x = – arcsin + π + 2 πn , n Є Z

Ответ: – arcsin + π + 2 πn , n Є Z .

Пример 9. Решить уравнение 2 cos х = 1– 2 cos 2 х – sin 2 x .

Решение. Воспользуемся формулой 2 cos 2 х – 1 = cos 2 x ,

получим 2 cos х = – cos 2х – sin 2 x .

Применим к правой части процедуру введения вспомогательного аргумента.

=

2cos х = – 2( cos2 х + sin2x)

2cos х = – 2 ( с os cos2 х + sin sin2x), где

2 cos х = – 2( cos 2х – )

cos х + cos (2х – ) = 0

Последнее уравнение легко решить, преобразовав сумму косинусов в произведение:

2 cos cos

cos

Необходимо обратить внимание учащихся на то, что в тригонометрических системах и совокупностях при записи имеет смысл употреблять разные буквы, обозначающие целые числа.

Ответ: .

Универсальная тригонометрическая подстановка.

Универсальная тригонометрическая подстановка позволяет перейти от синуса и косинуса аргумента х к тангенсу половинного аргумента:

sin , cos

При таком переходе возможна потеря решений, следует помнить, что (в этих точках tg не существует). Поэтому всякий раз, когда приходится пользоваться универсальной подстановкой, значения х = π + 2πn, nЄZ необходимо проверять отдельно, подставляя в исходное уравнение.

Пример 10. Решить уравнение sinx + cos х = –1.

Решение: = –1, заменим tg , получим

2t +1 – t 2 = –1– t 2

tg

Подставим теперь в исходное уравнение значение и убедимся, что они действительно являются его решениями.

Ответ:

Уравнение вида

Уравнение вида где — многочлен, удобно решать при помощи введения новой переменной

Тогда можно получить выражение для произведения из формулы

Пример 11. Решить уравнение

Решение: введем новую переменную

Тогда

Следовательно, и исходное уравнение принимает вид

Для определения переменной получаем два уравнения

Для решения таких уравнений используют введение вспомогательного аргумента.

Ответ:

После завершения изучения рассмотренных методов, при наличии времени, рекомендуем провести урок-практикум – «Урок решения одного уравнения»

3. Функционально-графические методы

Использование свойств ограниченности функций, метод оценок.

Часто приходится иметь дело с уравнениями, имеющими вид f ( x ) = g ( x ), где f и g – некоторые функции, составленные с помощью тригонометрических выражений, такие, что можно исследовать области значений Е( f ) и Е( g ) и доказать, что эти области либо не пересекаются, либо имеют небольшое число общих точек. В таких случаях решения уравнения f ( x ) = g ( x ) следует искать среди таких x , которые удовлетворяют более простым уравнениям f ( x ) = a , g ( x ) = a , где а – такое действительное число, что

Пример 12. Решить уравнение .

Ответ: нет решения.

Пример13. Решить уравнение .

Ответ: нет решения.

Пример14. Решить уравнение .

Ответ: .

Пример15. Решить уравнение

Ответ:

Пример16. Решить уравнение

Заметим, что сумма в левой части полученного уравнения может принимать значение 2, только если одновременно, т.е. наше уравнение равносильно системе уравнений

И должно выполняться равенство Поскольку

Ответ:

Суть метода использования графиков для решения уравнения f ( x ) = g ( x ) проста: нужно построить графики функций y = f ( x ) и y = g ( x ) и найти все точки их пересечения, абсциссы которых и будут являться корнями нашего исходного уравнения.

Пример 17. Сколько корней имеет уравнение:

Решение: в данном примере для решения уравнений используются свойства графиков функций.

📺 Видео

sinπx/3=0,5 В ответе напишите наименьший положительный корень/ наибольший отрицательный кореньСкачать

🔴 Найдите корень уравнения 2+9x=4x+3 | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 7 | ШКОЛА ПИФАГОРАСкачать

Три способа отбора корней в задании 13 ЕГЭ профильСкачать

Найдите корни уравнения: cosπ(x−7)/3=1/2 В ответ запишите наибольший отрицательный корень.Скачать

Найдите наименьший положительный корень уравнения sin pi x/3=-(корень из 3)/2 (проф. ЕГЭ задача №6)Скачать

Выборка с помощью окружностиСкачать

Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

ЕГЭ-2014 Задание В-7 Урок №112 Найти наименьший положительный корень тригонометрического уравненияСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

САМЫЕ СЛОЖНЫЕ Задания #6 ЕГЭ 2024 (Тригонометрические Уравнения) | Школа ПифагораСкачать

После этого видео, ТЫ РЕШИШЬ ЛЮБУЮ Систему Нелинейных УравненийСкачать

Решаем все типы задач № 12Скачать

tg pi(2x+5)/6=корень из 3. В ответе запишите наибольший отрицательный корень (проф. ЕГЭ, задача 6)Скачать

Решите уравнение x^2+3x=54. | ОГЭ 2017 | ЗАДАНИЕ 4 | ШКОЛА ПИФАГОРАСкачать

Тригонометрические уравнения. ЕГЭ № 12 | Математика | TutorOnline tutor onlineСкачать

Решите уравнение: tg пx/4 = -1 В ответе напишите наибольший отрицательный корень.Скачать

5 задание ЕГЭ по математике профильному.САМОЕ ПОНЯТНОЕ РЕШЕНИЕ. Решите уравнение sin ПX/3=0,5Скачать