Решить систему линейных уравнений методом гаусса матлаб

Решение систем линейных уравнений

Метод обратной матрицы: для системы из n уравнений с n неизвестными , при условии что определитель матрицы не равен нулю, единственное решение можно представить в виде . Для того чтобы решить систему линейных уравнений методом обратной матрицы, необходимо выполнить следующие действия:

• сформировать матрицу коэффициентов и вектор свободных членов заданной системы;
• решить систему, представив вектор неизвестных как произведение матрицы, обратной к матрице системы, и вектора свободных членов.

Дана система уравнений:

Решаем на MATLAB :

A=[1 -2 1; 2 -5 -1; -7 0 1];

x=inv(A)*b % Решение системы x = A -1 b

Решение системы линейных уравнений при помощи метода Гаусса основывается на том, что от заданной системы, переходят к системе эквивалентной, которая решается проще, чем исходная.

Метод Гаусса состоит из двух этапов:

• Первый этап — это прямой ход, в результате которого расширенная матрица системы путем элементарных преобразований (перестановка уравнений системы, умножение уравнений на число, отличное от нуля, и сложение уравнений) приводится к ступенчатому виду.
• На втором этапе (обратный ход) ступенчатую матрицу преобразуют так, бы в первых n столбцах получилась единичная матрица. Последний, n +1 столбец этой матрицы содержит решение системы линейных уравнений.

Порядок решения задачи в MATLAB следующий:

• сформировать матрицу коэффициентов и вектор свободных членов заданной системы;
• сформировать расширенную матрицу системы, объединив и ;
• используя функцию rref, привести расширенную матрицу к ступенчатому виду;
• найти решение системы, выделив последний столбец матрицы, полученной в предыдущем пункте;
• выполнить вычисление ; если в результате получился нулевой вектор, задача решена верно.

A=[1 -2 1; 2 -5 -1; -7 0 1];

C=rref ([A b]); %Приведение расширенной матрицы к треугольному виду

x=C(1:3,4:4) %Выделение последнего столбца из матрицы

Видео:Решение системы линейных уравнений методом ГауссаСкачать

Метод Гаусса и его реализация в пакете MATLAB

Рассмотрим систему линейных алгебраических уравнений

(3.4)

при условии, что матрица A=(a_ij) невырождена.

Метод Гаусса состоит в преобразовании системы (3.4) последовательным исключением переменных к равносильной системе с треугольной матрицей

(3.5)

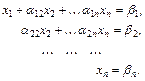
Затем из системы (3.5) последовательно находят значения всех неизвестных .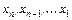

Т.о., процесс решения системы (3.4) распадается на два этапа:

1. Прямой ход — приведение системы (3.4) к треугольному виду.

2. Обратный ход — нахождение значений неизвестных переменных, в соответствие с (3.5).

Для реализации метод Гаусса в пакете MATLAB необходимо:

1. Создать файл Exchange.m, содержащий описание функции, осуществляющей перестановку строк при обнаружении в текущей строке нулевого элемента на главной диагонали.

% листинг файла Exchange.m

function z=Exchange(C,i)

k=i+1;

while C(k,i)==0

k=k+1;

End;

for j=1:size(C,1)

s=C(i,j);

C(i,j)=C(k,j);

C(k,j)=s;

End;

z=C;

2. Создание файла Simplex.m, содержащего описание функции, возвращающей расширенную матрицу системы к диагональному виду

% листинг файла Simplex.m

function z=Simplex(A,b)

N=size(A,1);% определение числа уравнений системы

C=cat(2,A,b);% создание расширенной матрицы системы

for i=1:N-1

if C(i,i)==0

C=Exchange(C,i);

End;

for j=0:N

C(i,N+1-j)=C(i,N+1-j)/C(i,i);

End;

for m=i+1:N

alpha=C(m,i);

for j=i:N+1

C(m,j)=C(m,j)-alpha*C(i,j);

End;

End;

End;

C(N,N+1)=C(N,N+1)/C(N,N);

C(N,N)=1;

z=C;

3. Создать файл Gauss.m, содержащий описание функции, возвращающей решение системы линейных уравнений методом Гаусса.

% листинг файла Gauss.m

function z=Gauss(A,b)

C=Simplex(A,b);

N=size(A,1);

v(N)=C(N,N+1);

for j=1:N-1

s=0;

for k=0:j-1

s=s+C(N-j,N-k)*v(N-k);

End;

End;

z=v’;

4. Задать матрицу системы линейных уравнений

>> A=[1,2,3,4,5;10,9,8,7,6;5,9,11,12,13;20,1,3,17,14;12,10,4,16,15]

A =

1 2 3 4 5

10 9 8 7 6

5 9 11 12 13

20 1 3 17 14

12 10 4 16 15

5. Задать вектор-столбец свободных членов

>> b=[10;20;30;40;50]

b =

10.0000

20.0000

30.0000

40.0000

50.0000

6. Решить систему уравнений, используя функцию Gauss( )

x=Gauss(A,b)

x =

0.0964

1.4324

-1.3530

1.6593

0.8921

7. Проверка правильности решения системы линейных уравнений

>> A*x

ans =

10.0000

20.0000

30.0000

40.0000

50.0000

Дата добавления: 2015-08-21 ; просмотров: 12233 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Решение СЛАУ и матрицы в Matlab

Доброго времени суток, читатели! Сегодня мы поговорим о матрицах в Matlab, об их применении в решении систем линейных алгебраических уравнений. Подробно разберем методы решения, и для этого необходимо знание нескольких базовых алгоритмов.

Также стоит отметить, что у каждого алгоритма, которым мы будем искать решение СЛАУ в Matlab, своя скорость нахождения этого решения, наличие или отсутствие условия выполнения алгоритма и т.д.

В традициях нашего сайта разберём на примере:

Решить систему линейных уравнений:

4*a + b — c = 6
a — b + c = 4
2*a — 3*b — 3*c = 4

Видео:Решение системы уравнений методом ГауссаСкачать

Метод обратной матрицы в Matlab

Начнем с достаточно распространенного метода. Его суть состоит в том, что сначала необходимо выписать коэффициенты при a, b и c (то есть те коэффициенты, которые находятся слева) в одну матрицу, а свободный член (то есть то, что справа) в другую.

В итоге у нас получится 2 матрицы:

Для реализации этого метода (и следующих методов тоже) требуется одно условие: чтобы определитель матрицы, составленной из коэффициентов левой части не был равен нулю. Проверка на определитель:

После проверки условия можем перейти к следующему шагу: нахождение обратной матрицы. В Matlab для этого используется оператор inv .
А само решение СЛАУ в Matlab находится как перемножение найденной обратной матрицы на матрицу свободных членов:

Мы получили 3 значения, которые и соответствуют нашим коэффициентам: то есть a = 2, b = -1, c = 1 . Можете проверить, подставив полученные ответы в исходную систему, и убедиться, что мы решили СЛАУ правильно.

Также следует отметить, что матрицы нужно перемножать именно, как сделали мы, то есть слева обратная матрица, справа матрица свободных членов.

Если вы не все поняли, то советую вам почитать нашу статью по основам Matlab.

Видео:2 - Решениt систем линейных алгебраических уравнений (СЛАУ) с помощью Matlab.Скачать

Метод Гаусса

Метод Гаусса в Matlab реализуется достаточно просто: для этого нам нужно всего лишь изучить один новый оператор.
() — левое деление.
При следующей записи:

Мы получим ответы на нашу исходную систему. Только заметьте, мы решили СЛАУ стандартным набором функций в Matlab, и желательно этот оператор использовать когда матрица коэффициентов квадратная, так как оператор приводит эту матрицу к треугольному виду. В других случаях могут возникнуть ошибки.

Видео:12. Решение систем линейных уравнений методом ГауссаСкачать

Метод разложения матрицы

Теперь поговорим о разложении матрицы. Нахождение решения через разложение матрицы очень эффективно. Эффективность обусловлена скоростью нахождения решения для данного вида систем и точностью полученных результатов.

Возможны следующие разложения:

• разложение Холецкого
• LU разложение
• QR разложение

Разберём решение через LU и QR разложение, так как в задачах чаще всего встречается задание на решение именно через такие разложения.

Основное отличие этих двух разложений: LU разложение применимо только для квадратных матриц, QR — возможно и для прямоугольных.

LU разложение

Решим выше предложенную задачу через LU разложение:

QR разложение

И через QR разложение соответственно:

Отметим, что апостроф ( ‘ ) после Q означает транспонирование.

Видео:Система линейных уравнений. Общее решение. Метод ГауссаСкачать

Стандартные функции Matlab

Так же Matlab предлагает функцию linsolve , с помощью которой возможно решить систему линейных алгебраических уравнений. Выглядит это так:

Как видите, ничего сложного тут нет, на то они и стандартные функции Matlab.

Видео:Решение системы уравнений методом Гаусса 4x4Скачать

Повторение

Итак, сегодня мы с вами изучили несколько методов для решения СЛАУ в Matlab, как с помощью матриц, так и с помощью стандартных функций. Давайте их повторим на другом примере:

Решить систему линейных уравнений:
6*a — b — c = 0
a — 2*b + 3*d = 0
3*a — 4*b — 4*c = -1

• Методом обратной матрицы:
• Методом Гаусса:
• LU разложение:
• QR разложение:

На этом я с вами попрощаюсь, надеюсь, вы научились применять матрицы в Matlab для решения СЛАУ.

📹 Видео

Метод Гаусса решения систем линейных уравненийСкачать

Решение системы уравнений методом Гаусса. Бесконечное множество решенийСкачать

Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Метод Гаусса и метод Жордана-Гаусса ➜ 2 метода за 7 минутСкачать

Метод Гаусса решения систем линейных уравненийСкачать

решение системы уравнений методом ГауссаСкачать

Метод Гаусса и метод Жордана-ГауссаСкачать

Линейная алгебра, Матрицы: Метод Гаусса. Высшая математикаСкачать

Исследовать систему уравнений на совместность и решить методом Гаусса и методом обратной матрицыСкачать

12. Метод Гаусса решения систем линейных уравнений. Часть 1.Скачать

Решение систем линейных уравнений, урок 4/5. Метод ГауссаСкачать

метод Гаусса СИСТЕМА ЛИНЕЙНЫХ УРАВНЕНИЙ решение СЛАУСкачать

Решение системы уравнений методом обратной матрицы - bezbotvyСкачать