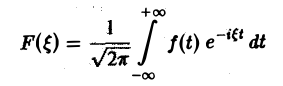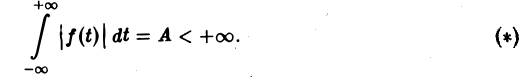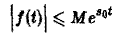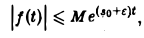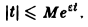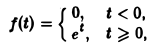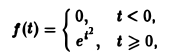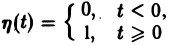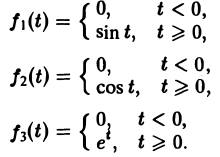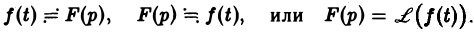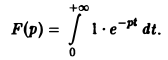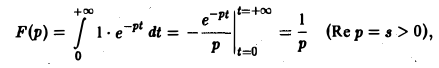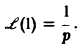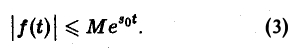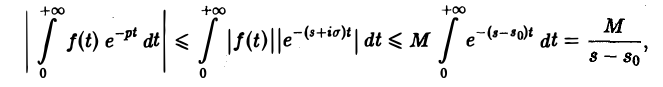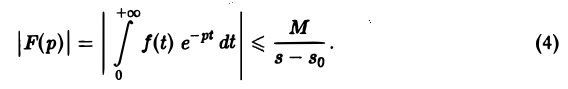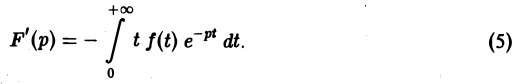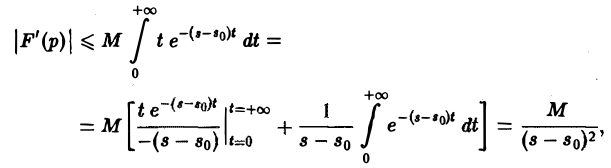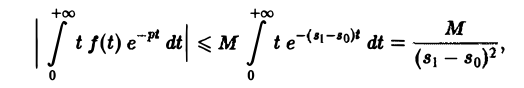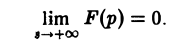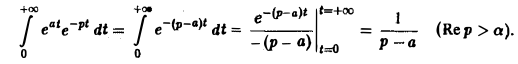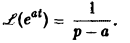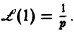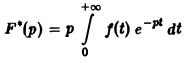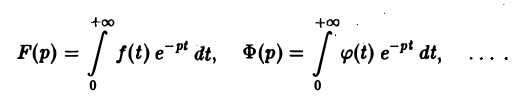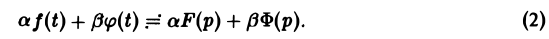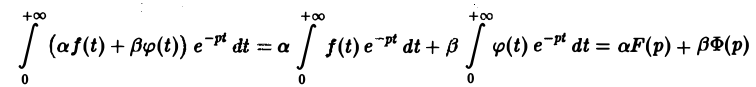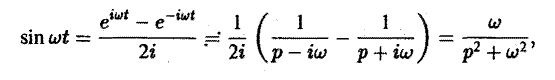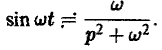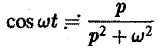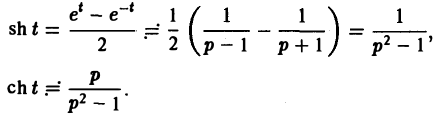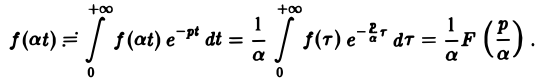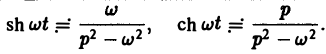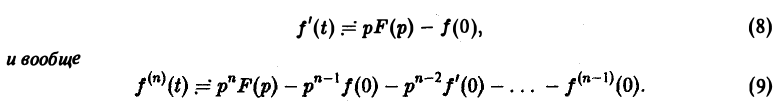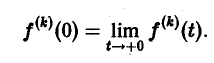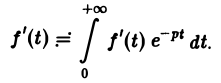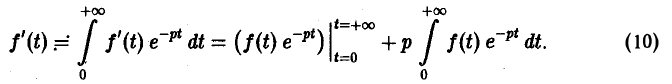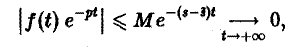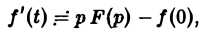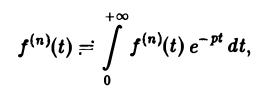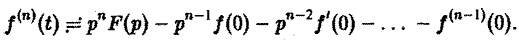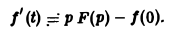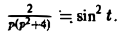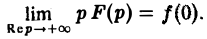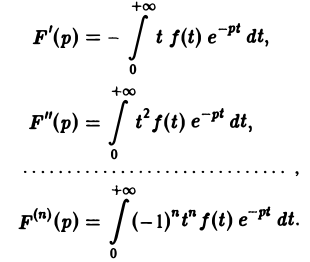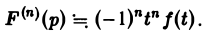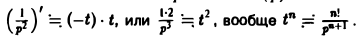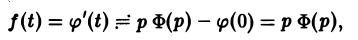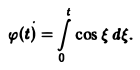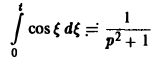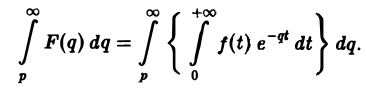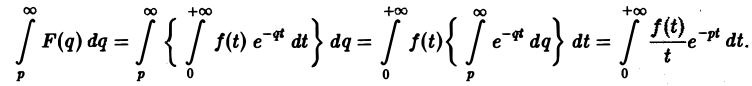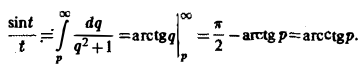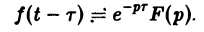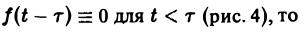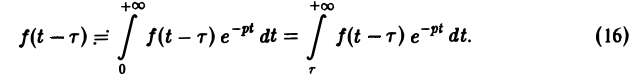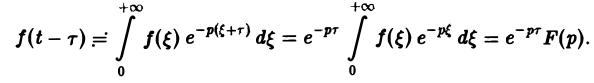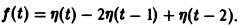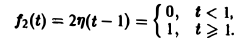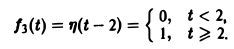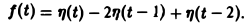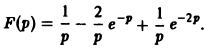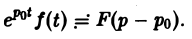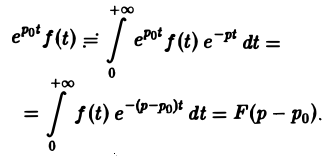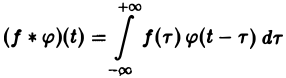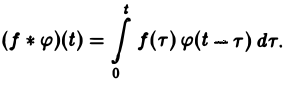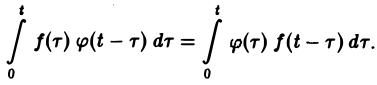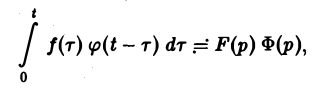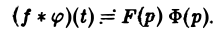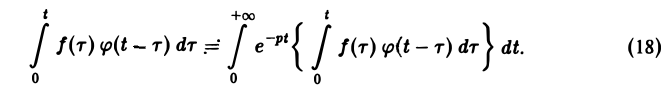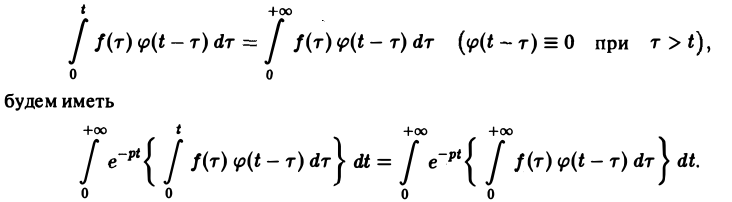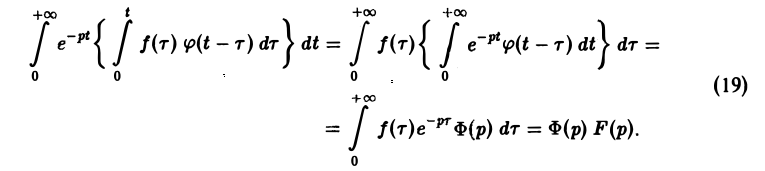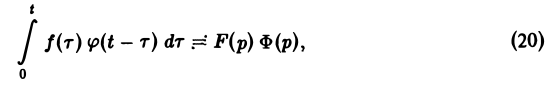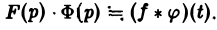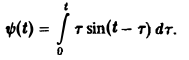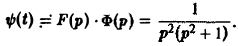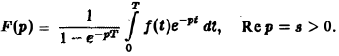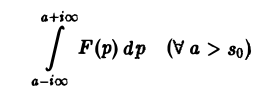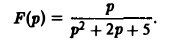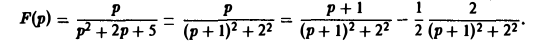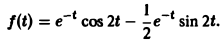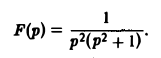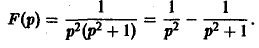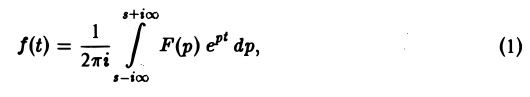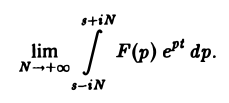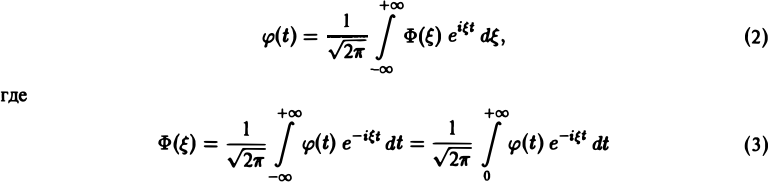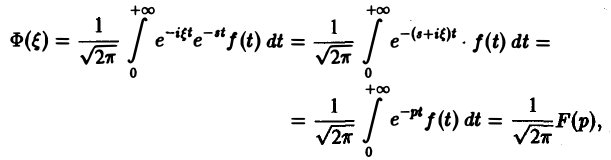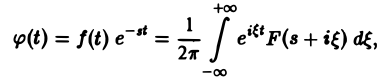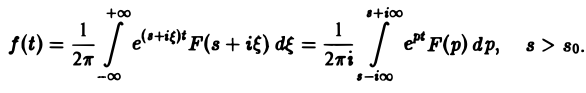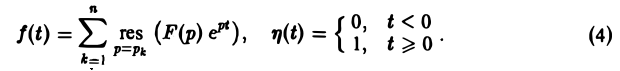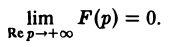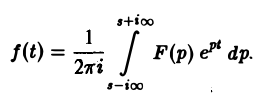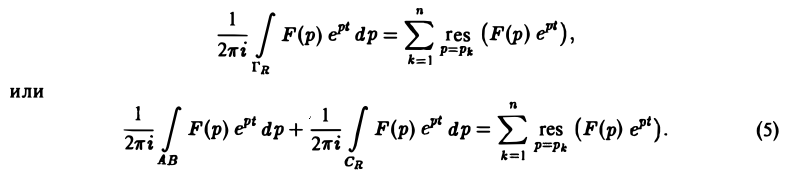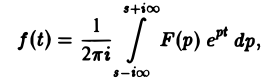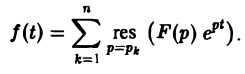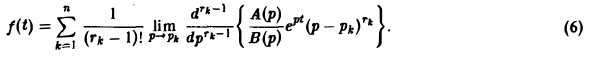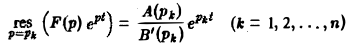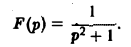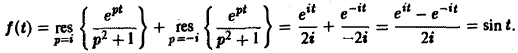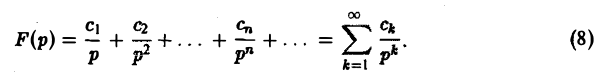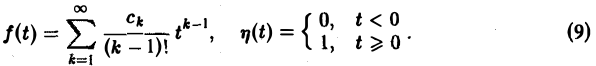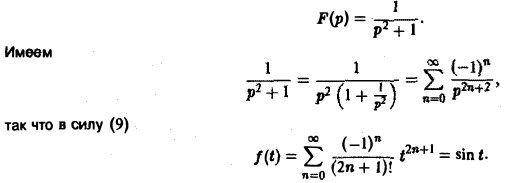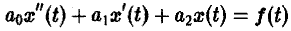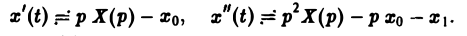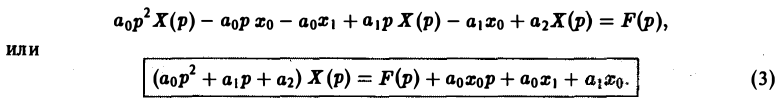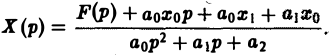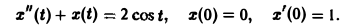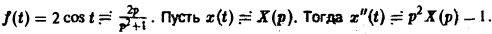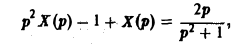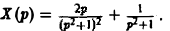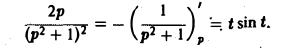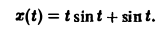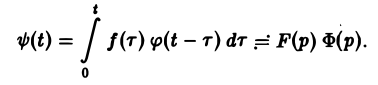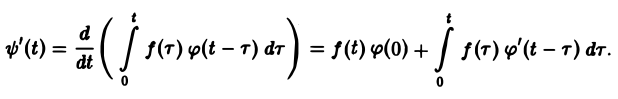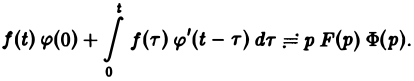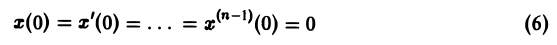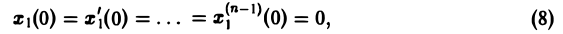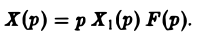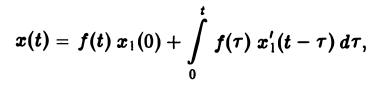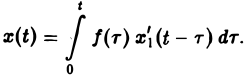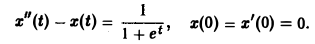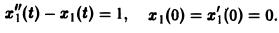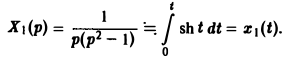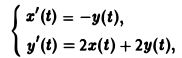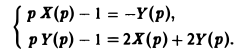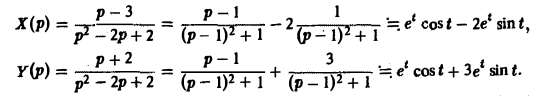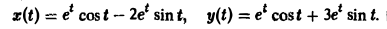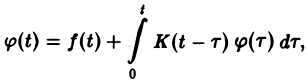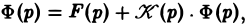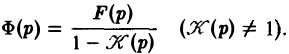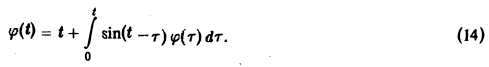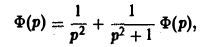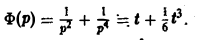Решить интегральное уравнение типа свертки

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7

.

15. Уравнение типа свертки

Это такие интегральные уравнения, ядро которых зависит от разности аргументов. Они имеют следующий вид:

Для решения уравнений типа свертки используется преобразование Фурье в следующей форме:

Введем понятие свертка функций. Она представляет из себя следующее:

Интегральный оператор Фурье будем обозначатьF(*).

Преобразование Фурье от свертки функций равно произведению отдельных преобразований Фурье от каждой функции:

Тогда после преобразования Фурье:

Отсюда можно найти :

Взяв обратное преобразование Фурье, мы получаем нашу функцию:

Пусть — это обратное преобразование Фурье от следующей функции:

Тогда решение можно найти по формуле:

16. Применение метода свертки для решения

интегральных уравнений 1-го рода

Бывают уравнения типа свертки и 1-го рода, то есть неизвестная функция есть только под знаком интеграла. Здесь также применим этот метод:

Преобразование Лапласа можно также применять как и Фурье, но нужно всегда при решении проверять область определения.

L — так будем обозначать преобразование Лапласа.

Взяв преобразование Лапласа от , получим:

Решение системы интегральных уравнений

Пусть имеем систему N интегральных уравнений следующего вида:

Применим ко всем уравнениям этой системы преобразование Лапласа:

Решив эту систему алгебраических уравнений в виде набора изображений и найдя от них оригиналы, мы найдем решение:

Это нелинейное уравнение типа свертки. Применим преобразование Лапласа к обеим частям этого уравнения:

Это квадратное уравнение, его решение:

Видео:Решить интегральное уравнение (ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ) Свёртка функций, Умножение изображенийСкачать

17. Решение интегро-дифференциальных уравнений типа свертки

Пусть дано следующее интегро-дифференциальное уравнение:

Набор начальных условий:

Используется следующее свойство преобразования Лапласа:

Применим это к нашему уравнению:

Теперь общее уравнение превращается в следующий вид:

Отсюда изображение искомой функции:

Видео:Решить интегральное уравнениеСкачать

Преобразование Меллина

Пусть есть некая функция и для нее справедливо следующее:

Для такой функции есть преобразование Меллина:

,

Преобразование Меллина устанавливает однозначную взаимосвязь между 2-мя функциями. Интеграл берется на комплексной плоскости вверх и вниз.

Гамма-функция. С помощью преобразования Меллина гамма-функция вводится следующим образом:

Преобразование Меллина во многом похоже на преобразование Лапласа:

.

Есть следующая взаимосвязь:

Видео:Уравнения математической физики. Семинар 15. Интегральные уравнения типа свертка. Ч1.Скачать

18. Применение преобразования Меллина для решения

;

;

.

Это свойство используется для решения интегрального уравнения вида:

. (*)

Преобразование Меллина используется для решения уравнений типа (*). Условие применимости этих функций состоит в том, чтобы они допускали от себя преобразование Меллина. Обозначим преобразование Меллина от через , а преобразование Меллина от — . Функции и должны иметь общую область аналитичности. Применим преобразование Меллина к обеим частям уравнения (*).

;

.

Пусть имеем интегральное уравнение вида:

;

;

;

;

;

.

Видео:Интегральные уравнения ВольтерраСкачать

19. Симметричные интегральные уравнения

Симметричными называются интегральные уравнения вида:

;

.

Если ядро комплексно — значное, то

;

;

— линейный оператор под функцией .

Если бы , то соответствующее интегральное уравнение стало бы однородным. При этом можно записать следующее: . Выяснили, что такое однородное уравнение имеет ограниченное число решений. Эти решения представляют собой набор некоторых функций . Они называются собственными функциями. Они однозначно соответствуют собственным числам.

Если мы рассматриваем симметричные ядра, то справедливы следующие свойства:

Видео:Простейшие интегральные уравненияСкачать

Примеры решений задач по операционному исчислению (преобразованию Лапласа)

Операционное (символическое) исчисление – это один из методов математического анализа, позволяющий в некоторых случаях свести исследование и решение дифференциальных, псевдодифференциальных, интегральных уравнений, к более простым алгебраическим задачам.

Изучая преобразование Лапласа, мы вводим оригинал функции $f(t)$ и ее изображение $F(p)$, находимое по формуле:

$$F(p) = int_0^infty f(t) e^dt$$

Для быстроты и удобства решения задач составлена таблица изображений и оригиналов, которая, наряду с теоремами (линейности, подобия, смещения, запаздывания), свойствами и правилами дифференцирования и интегрирования изображения/оригинала, постоянно используется в решении примеров.

В этом разделе вы найдете готовые задания разного типа: восстановление оригинала или изображения функции, нахождение свертки функций, решение ДУ, систем ДУ или интегральных уравнений с помощью преобразования Лапласа и т.д.

Видео:Интегральные уравнения с вырожденным ядромСкачать

Как найти изображение функции

Задача 1. Найти изображение данного оригинала, или оригинала, удовлетворяющего данному уравнению

Задача 2. Пользуясь определением, найти изображение функции $f(t)=3^t$.

Задача 3. Найти изображение функции: $int_0^t cos tau cdot e^dtau. $

Задача 4. Найти изображение оригинала $f(x)$ двумя способами:
1) Вычислив интеграл $F(p) = int_0^infty f(x) e^dx$;
2) Воспользовавшись таблице изображений и свойствами преобразования Лапласа.
Оригинал задается формулой (курсочно-линейная функция, см. файл).

Видео:Интегральные уравнения типа сверткиСкачать

Как найти оригинал функции

Задача 5. Найти оригинал изображения $F(p)$, где

Задача 6. Найти оригинал изображения

Задача 7. Найти оригинал для функции с помощью вычетов

Видео:Резольвента. Как легко решить интегральное уравнениеСкачать

Как решить ДУ (систему ДУ) операционным методом

Задача 8. Найти частное решение дифференциального уравнения с заданными начальными условиями операторным методом

Задача 9. Найти решение задачи Коши методами операционного исчисления

Задача 10. Методом операционного исчисления найти частное решение системы дифференциальных уравнений, удовлетворяющее заданным начальным условиям.

Задача 11. Методом операционного исчисления найти решение задачи Коши для ДУ 3-го порядка

Задача 12. Решите задачу Коши для системы дифференциальных уравнений с помощью преобразования Лапласа.

Задача 13. C помощью формулы Дюамеля найти решение уравнения

Задача 14. Решить систему ДУ с помощью преобразования Лапласа

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Как решить интегральное уравнение

Задача 15. Методом операционного исчисления найти решение интегрального уравнения

$$ y(t)=cos t +int_0^t (t-tau)^2 y(tau)d tau. $$

Задача 16. Решить интегральное уравнение

$$ int_0^t ch (tau) x(t-tau)d tau = t. $$

Видео:Методы численного анализа - Уравнения Фредгольма и ВольтерраСкачать

Как найти свертку функций

Задача 17. Найти свертку функций $f(t)=1$ и $phi(t)=sin 5t$.

Видео:Решить интегральное уравнениеСкачать

Помощь с решением заданий

Если вам нужна помощь с решением задач и контрольных по этой и другим темам математического анализа, обращайтесь в МатБюро. Стоимость подробной консультации от 100 рублей , оформление производится в Word, срок от 1 дня.

Видео:Интегральное уравнение АбеляСкачать

Преобразование Лапласа с примерами решения и образцами выполнения

Ранее мы рассмотрели интегральное преобразование Фурье

с ядром K(t, ξ) = .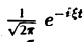

Преобразование Фурье неудобно тем, что должно быть выполнено условие абсолютной интегрируемости функции f(t) на всей оси t,

Преобразование Лапласа позволяет освободиться от этого ограничения.

Определение:

Функцией-оригиналом будем называть всякую комплекснозначную функцию f(t) действительного аргумента t, удовлетворяющую следующим условиям:

1. f(t) непрерывна на всей оси t, кроме отдельных точек, в которых f(t) имеет разрыв 1-го рода, причем на каждом конечном интервале оси t таких точек может быть лишь конечное число;
2. функция f(t) равна нулю при отрицательных значениях t, f(t) = 0 при t 0 и з такие, что для всех t

Ясно, что если неравенство (1) выполняется при некотором s = s1, то оно будет выполнятся при всяком s2 > s1.

Точная нижняя грань sо всех чисел s, so = infs, для которых выполняется неравенство (1), называется показателем роста функции f(t).

Замечание:

В общем случае неравенство

не имеет места, но справедлива оценка

где ε > 0 — любое. Так, функция f(t) = t, t ≥ 0, имеет показатель роста so =0. Для нее неравенство |t| ≤ М ∀t ≥ 0 не выполняется, но ∀ε > О, ∀t > 0 верно неравенство

Условие (1) гораздо менее ограничительное, чем условие (*).

Пример:

не удовлетворяет условию (*), но условие (1) выполнено при любом s ≥ 1 и М ≥ 1; показатель роста so = 1. Так что f(t) является функцией-оригиналом. С другой стороны, функция

не является функцией-оригиналом: она имеет бесконечный порядок роста, sо = +∞. Простейшей функцией-оригиналом является
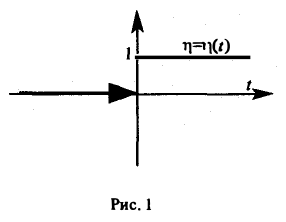
так называемая единичная функция

Если некоторая функция φ(t) удовлетворяет условиям 1 и 3 определения 1, но не удовлетворяет условию 2, то произведение f(t) = φ(t) η(t) уже является функцией-оригиналом.

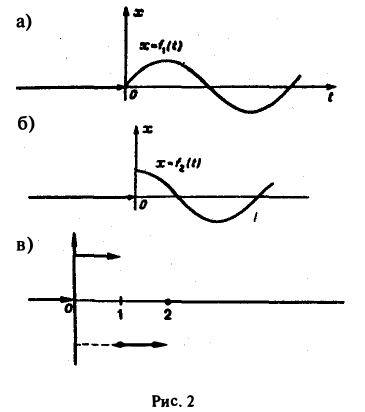
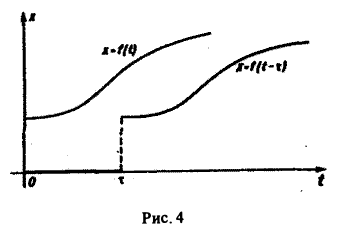
Для простоты записи мы будем, как правило, множитель η(t) опускать, условившись, что все функции, которые мы будем рассматривать, равны нулю для отрицательных t, так что если речь идет о какой-то функции f(t) например, о sin t, cos t, e t и т. д., то всегда подразумеваются следующие функции (рис. 2):

Определение:

Пусть f(t) есть функция-оригинал. Изображением функции f(t) по Лапласу называется функция F(p) комплексного переменного р = s + iσ, определяемая формулой

где интеграл берется по положительной полуоси t. Функцию F(p) называют также преобразованием Лапласа функции f(t); ядро преобразования K(t, р) = e -pt .
Тот факт, что функция f(x) имеет своим изображением F(p), будем записывать так:

Пример:

Найти изображение единичной функции η(t).

Функция 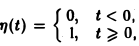является функцией-оригиналом с показателем роста s0 = 0. В силу формулы (2) изображением функции η(t) будет функция

Если р = s + iσ, то при s > 0 интеграл в правой части последнего равенства будет сходящимся, и мы получим

так что изображением функции η(t) будет функция 1/p. Как мы условились, будем писать, что η(t) = 1, и тогда полученный результат запишется так:

Теорема:

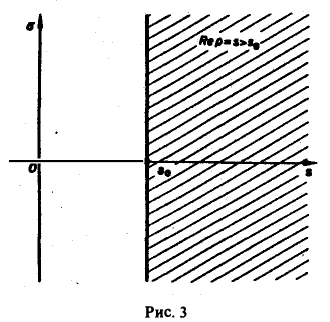
Для всякой функции-оригинала f(t) с показателем роста sо изображение F(p) определено в полуплоскости Re p = s > So и является в этой полуплоскости аналитической функцией (рис. 3).

Для доказательства существования изображения F(p) в указанной полуплоскости достаточно установить, что несобственный интеграл (2) абсолютно сходится при s > so. Используя (3), получаем

что и доказывает абсолютную сходимость интеграла (2). Одновременно мы получили оценку преобразования Лапласа F(p) в полуплоскости сходимости Re р = s > so

Дифференцируя выражение (2) формально под знаком интеграла по р, находим

Существование интеграла (5) устанавливается так же, как было установлено существование интеграла (2).

Применяя для F'(p) интегрирование по частям, получаем оценку

откуда следует абсолютная сходимость интеграла (5). (Внеинтегральное слагаемое 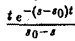— при t → + ∞ имеет предел, равный нулю). В любой полуплоскости Re р ≥ S1 > So интеграл (5) сходится равномерно относительно р, поскольку он мажорируется сходящимся интегралом

не зависящим от р. Следовательно, дифференцированиепо р законно и равенство (5) справедливо.

Поскольку производная F'(p) существует, преобразование Лапласа F(p) всюду в полуплоскости Re p = s > sо является аналитической функцией.

Из неравенства (4) вытекает

Следствие:

Если точка р стремится к бесконечности так, что Re р = s неограниченно возрастает, то

Пример:

Найдем еще изображение функции f(t) =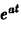, где а = а + iβ — любое комплексное число.

Показатель роста sо функции f(t) равен а.

Считая Rep = s> а, получим

При а = 0 вновь получаем формулу

Обратим внимание на то, что изображение функции 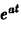является аналитической функцией аргумента р не только в полуплоскости Re p > а, но и во всех точках р, кроме точки р = а, где это изображение имеет простой полюс. В дальнейшем мы не раз встретимся с подобной ситуацией, когда изображение F(p) будет аналитической функцией во всей плоскости комплексного переменного р, за исключением изолированных особых точек. Противоречия с теоремой 1 нет. Последняя утверждает лишь, что в полуплоскости Re p > So функция F(p) не имеет особых точек: все они оказываются лежащими или левее прямой Re p = So, или на самой этой прямой.

Замечание:

В операционном исчислении иногда пользуются изображением функции f(t) по Хевисайду, определяемым равенством

и отличаюикмся от шоСражения по Лапласу множителем р.

Видео:Свертка двух функций. Найти свертку функций по определению. Теорема об умножении изображений.Скачать

Свойства преобразования Лапласа

В дальнейшем через f(t), φ(t), … будем обозначать функции-оригиналы, а через F(p), Ф(р), … — их изображения по Лапласу,

Из определения изображения следует, что если f(t) = 9 ∀t, то F(p) = 0.

Теорема единственности:

Теорема:

Справедливость утверждения вытекает из свойства линейности интеграла, определяющего изображение:

— показатели роста функций f(t) и φ(t) соответственно).

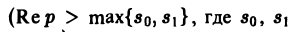
На основании этого свойства получаем

Аналогично находим, что
(4)

Теорема подобия:

Если f(t) — функция-оригинал и F(p) — ее изображение по Лапласу, то для любого постоянного а > 0

Полагая at = т, имеем

Пользуясь этой теоремой, из формул (5) и (6) получаем

Теорема:

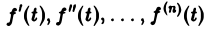
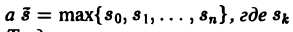
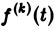
О дифференцировании оригинала. Пусть f(t) является функцией-оригиналом с изображением F(p) и пусть — также функции-оригиналы, — показатель роста функции (k = 0, 1,…, п). Тогда

Здесь под fk(0) (k = 0,1,… , п — 1) понимается правое предельное значение .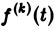

Пусть f(t) = F(p). Найдем изображение f'(t). Имеем

Интегрируя по частям, получаем

Внеинтегральное слагаемое в правой части (10) обращается в нуль при t → + ∞, т. к. при Re р = s > 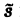имеем

подстановка t = 0 дает -f(0).

Второе слагаемое справа в (10) равно pF(p). Таким образом, соотношение (10) принимаетвид

и формула (8) доказана. В частности, если f(0) = 0, то f'(t) = pF(p). Для отыскания изображения 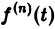запишем

откуда, интегрируя п раз по частям, получим

Пример:

Пользуясь теоремой о дифференцировании оригинала, найти изображение функции f(t) = sin 2 t.

Пусть f(t) = F(p). Тогда

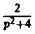
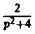
Но f(0) = О, а f'(0) = 2 sin t cos t = sin 2t = . Следовательно, = pF(p), откуда F(p) =

Теорема 5 устанавливает замечательное свойство интегрального преобразования Лапласа: оно (как и преобразование Фурье) переводит операцию дифференцирования в алгебраическую операцию умножения на р.

Формула включения. Если f(t) и f'(t) являются функциями-оригиналами, то (11)

В самом деле, f'(

Так как функция F(p) в полуплоскости Rep = s > so является аналитической, то ее можно дифференцировать по р. Имеем

Последнее как раз и означает, что

Пример:

Пользуясь теоремой 6, найти изображение функции .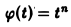

Как известно, 1 = 1/p. Здесь f(t) = 1, F(p) = 1/p. Отсюда (1/p)’= (-t) • 1, или 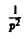= t. Вновь применяя теорему 6, найдем

Теорема:

Интегрирование оригинала. Интегрирование оригинала сводится к делению изображения на р: если f(t) = F(p), то

Нетрудно проверить, что если f(t) есть функция-оригинал, то и φ(t) будет функцией-оригиналом, причем φ(0) = 0. Пусть φ(t) = Ф(р). В силу (14)

С другой стороны, f(t) =’ F(p), откуда F(p) = рФ(р), т.е. Ф(р) =.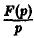

Последнее равносильно доказываемому соотношению (13).

Пример:

Найти изображение функции

В данном случае f(t) = cos t, так что F(p) = 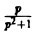. Поэтому

Теорема:

Интегрирование изображения. Если f(t) = F(p) и интеграл 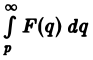сходится, то он служит изображением функции

Предполагая, что путь интегрирования (р, ∞) лежит в полуплоскости Re p ≥ а> so, мы можем изменить порядок интегрирования (t > 0):

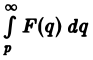
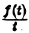
Последнее равенство означает, что является изображением функции .

Пример:

Найти изображение функции .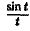

Как известно, sin t = .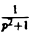

Теорема запаздывания:

Положим ξ = t- τ. Тогда dt = d ξ. При t = τ получаем ξ = 0, при t = + ∞ имеем ξ = + ∞.

Поэтому соотношение (16) принимает вид

Пример:

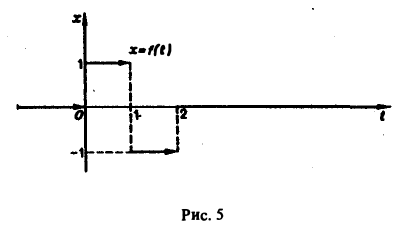
Найти изображение функции f(t), заданной графически (рис. 5).

Запишем выражение для функции f(t) в следующем виде:

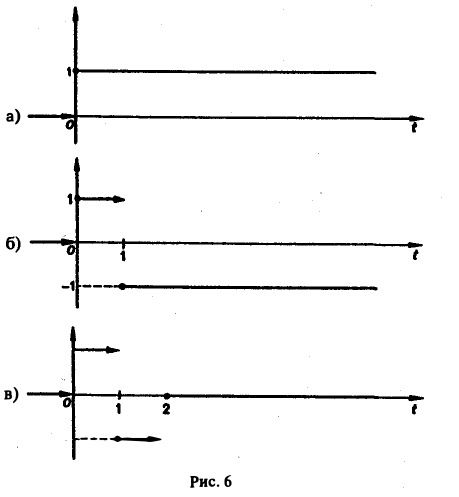
Это выражение можно получить так. Рассмотрим функцию f1(t) = η(t) для t ≥ 0 (рис. 6 а) и вычтем из нее функцию

Разность f(t) — h(t) будет равна единице для t ∈ [0,1) и -1 для t ≥ 1 (рис. 6 b). К полученной разности прибавим функцию

В результате получим функцию f(t) (рис. 6 в), так что

Отсюда, пользуясь теоремой запаздывания, найдем

Теорема смещения:

Теорема позволяет по известным изображениям функций находить изображения тех же функций, умноженных на показательную функцию 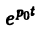, например,

Свертка функций. Теорема умножения

Пусть функции f(t) и φ(t) определены и непрерывны для всех t. Сверткой (f *φ)(t) этих функций называется новая функция от t, определяемая равенством

(если этот интеграл существует).

Для функций-оригиналов f(t) и φ(t) операция свертки всегда выполнима, причем
(17)

В самом деле, произведение функций-оригиналов f( τ ) φ(t — τ), как функция от τ, является финитной функцией, т.е. обращается в нуль вне некоторого конечного промежутка (в данном случае вне отрезка 0 ≤ τ ≤ t). Для финитных непрерывных функций операция свертки выполнима, и мы получаем формулу (17).

Нетрудно проверить, что операциясвертки коммутативна,

Теорема умножения:

Нетрудно проверить, что свертка (f * φ)(t) функций-оригиналов есть функция-оригинал с показателем роста s* = mах, где s1, s2

показатели роста функций f(t) и φ(t) соответственно. Найдем изображение свертки,

Воспользовавшись тем, что

Меняя порядок интегрирования в интеграле справа (при Re р = s > s* такая операция законна) и применяя теорему запаздывания, получим

Таким образом, из (18) и (19) находим

— умножению изображений отвечает свертывание оригиналов,

Пример:

Найти изображение функции

Функция ψ(t) есть свертка функций f(y) = t и φ(t) = sin t. В силу теоремы умножения

Задача:

Пусть функция f(t), периодическая с периодом Т, есть функция-оригинал. Показать, что ее изображение по Лапласу F[p) дается формулой

Видео:Метод определителей ФредгольмаСкачать

Отыскание оригинала по изображению

Задача ставится так: дана функция F(p), надо найти функцию f(t). изображением которой является F(p).

Сформулируем условия, достаточные для того, чтобы функция F(p) комплексного переменного р служила изображением.

Теорема:

Если аналитическая в полуплоскости Rep = s > so функция F(p)

1) стремится к нулю при |р| —» + ∞ в любой полуплоскости Re р = а > So равномерно относительно arg р;

сходится абсолютно, то F(p) является изображением некоторой функции-оригинала f<t).

Задача:

Может ли функция F(p) = 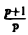служить изображением некоторой функции-оригинала? Укажем некоторые способы отыскания оригинала по изображению.

Отыскание оригинала с помощью таблиц изображений

Прежде всего стоит привести функцию F(p) к более простому, «табличному» виду. Например, в случае, когда F(p) — дробно-рациональная функция аргумента р,ее разлагают на элементарные дроби и пользуются подходящими свойствами преобразования Лапласа.

Пример:

Найти оригинал для

Запишем функцию F(p) в виде:

Пользуясь теоремой смещения и свойством линейности преобразования Лапласа, получаем

Пример:

Найти оригинал для функции

Запишем F(p) в виде

Отсюда f(t) = t — sin t.

Использование теоремы обращения и следствий из нее

Теорема обращения:

где интеграл берется вдоль любой прямой Re p = s > So и понимается в смысле главного значения, т. е. как

Формула (1) называется формулой обращения преобразования Лапласа, или формулой Меллина. В самом деле, пусть, например, f(t) — кусочно-гладкая на каждом конечном отрезке [0, а] функция-оригинал-с показателем роста so. Рассмотрим функцию φ(t) = 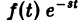, где s>so — любое.

Функция φ(t) удовлетворяет условиям применимости интегральной формулы Фурье, и, следовательно, справедлива формула обращения преобразования Фурье,

(φ(t) ≡ 0 при t

откуда получаем формулу обращения преобразования Лапласа

Как следствие из теоремы обращения получаем теорему единственности.

Теорема:

Две непрерывные функции f(t) и φ(t), имеющие одно и то же изображение F(p), тождественны.
Непосредственное вычисление интеграла обращения (1) обычно затруднительно. Отыскание оригинала по изображению упрощается при некоторых дополнительных ограничениях на F(p).

Теорема:

Пусть изображение F(p) — дробно-рациональная функция с полюсами р1, p2….pп. Тогда оригиналом для F(p) будет функция f(t) η(t), где

Пусть изображение F(p) — дробно-рациональная функция, F(p) = 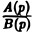, где А(р), В(р) — многочлены относительно р (взаимно простые), причем степень числителя А(р) меньше степени знаменателя В(р), т. к. для всякого изображения должно выполняться предельное соотношение

Пусть корни знаменателя В(р), являющиеся полюсами изображения F(p), суть р1, р2, …, рп, а их кратности равны r1, r2, …, rп соответственно.

Если число s, фигурирующее в формуле (1), взять большим всех Re pk (k = 1,2,…, п), то по формуле обращения, которая в этих условиях применима, получим

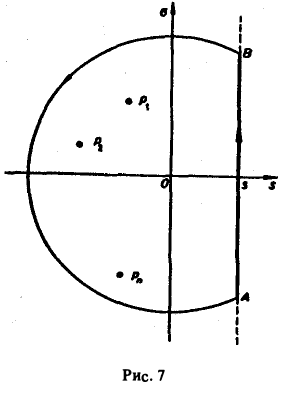
Рассмотрим замкнутый контур ГR (рис.7), состоящий из дуги CR окружности радиуса R с центром в начале координат и стягивающей ее хорды АВ (отрезка прямой Re р = s), и проходимый в положительном направлении, причем радиус R настолько велик, что все полюсы F(p) лежат внутри ГR.

По теореме Коши о вычетах при любом R, удовлетворяющем указанному условию, будем иметь

Второе слагаемое слева в равенстве (5) стремится к нулю при R → ∞. Это следует из леммы Жордана, если в ней заменить р на iz и учесть, что F(p) → 0 при Re p → + ∞. Переходя в равенстве (5) к пределу при R → ∞, мы получим слева

а справа — сумму вычетов по всем полюсам функции F(p)

Замечание:

Воспользовавшись формулой для вычисления вычетов, найдем, что

Если все полюсы p1, р2,…, рn — простые, то

и формула (6) принимает вид

Пример:

Найти оригинал для функции

Функция F(p) имеет простые полюсы р1 = i. p2 = -i. Пользуясь формулой (7), находим

Теорема:

Пусть изображение F(p) является аналитической функцией в бесконечно удаленной точке р = ∞, причем ее разложение в окрестности |р| > R бесконечно удаленной точки имеет вид

Тогда оригиналом для F(p) будет функция f(t) η<t), где

Пример:

Видео:Решение интегральных уравнений операционным методомСкачать

Приложения преобразования Лапласа (операционного исчисления)

Решение линейных дифференциальных уравнений с постоянными коэффициентами

Дано линейное дифференциальное уравнение второго порядка с постоянными коэффициентами
(1)

(ао, а1, а2 — действительные числа) и требуется найти решение уравнения (1) для t > 0, удовлетворяющее начальным условиям

Будем считать, что f(t) есть функция-оригинал. Тогда x(t) — также функция-оригинал. Пусть

f(t) = F(p), x(t) = X(p).

По теореме о дифференцировании оригинала имеем

Перейдем в уравнении (1) от оригиналов к изображениям. Имеем

Это уже не дифференциальное, а алгебраическое уравнение относительно изображения Х(р) искомой функции. Его называют операторным уравнением. Решая его, найдем операторное решение задачи (1)-(2) —

Оригинал для Х(р) будет искомым решением х(t) задачи (1)-(2).

Общий случай линейного дифференциального уравнения n-го порядка (n ≥ 1) с постоянными коэффициентами от случая п = 2 принципиально ничем не отличается.

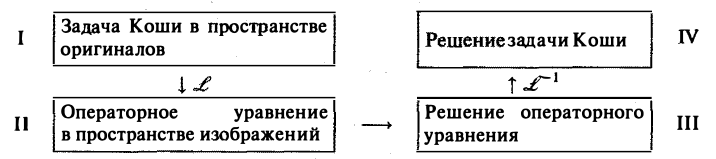
Приведем общую схему решения задачи Коши

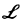
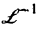
Здесь означает применение к 1 преобразование Лапласа, — применение к III обратного преобразования Лапласа.

Пример:

Решить задачу Коши

По теореме о дифференцировании изображения

Формула Дюамеля

В приложениях операционного исчисления к решению дифференциальных уравнений часто пользуются следствием из теоремы умножения, известным под названием формулы Дюамеля.

Пусть f(t) и φt) — функции-оригиналы, причем функция f(t) непрерывна на [0, + ∞), a φ(t) — непрерывно дифференцируема на [0,+ ∞). Тогда если f(t) = F(p), φ<t) = Ф(р),то по теореме умножения получаем, что

Нетрудно проверить, что функция ψ(t) непрерывно дифференцируема на [0, + ∞), причем

Отсюда, в силу правила дифференцирования оригиналов, учитывая, что ψ(0) = 0, получаем формулу Дюамеля
(4)

Покажем применение этой формулы.

Пусть требуется решить линейное дифференциальное уравнение n-го порядка (n ≥ 1) с постоянными коэффициентами

при нулевых начальных условиях

(последнее ограничение несущественно: задачу с ненулевыми начальными условиями можно свести к задаче с нулевыми условиями заменой искомой функции).

Если известно решение x(t) дифференциального уравнения с той же левой частью и правой частью, равной единице,

L[x(t)] = l (7)

при нулевых начальных условиях

то формула Дюамеля (4) позволяет сразу получить решение исходной задачи (5)-(6).

В самом деле, операторные уравнения, отвечающие задачам (5)-(6) и (7)-(8), имеют соответственно вид

где F(p) — изображение функции f(t). Из (9) и (10) легко находи

Отсюда по формуле Дюамеля

или, поскольку x1(0) = 0, (11)

Пример:

Решить задачу Коши

Рассмотрим вспомогательную задачу

Применяя операционный метод, находим

По формуле (11) получаем решение x(t) исходной задачи:

Интегрирование систем линейных дифференциальных уравнений с постоянными коэффициентами

Интегрирование систем осуществляется так же, как и решение одного линейного дифференциального уравнения — путем перехода от системы дифференциальных уравнений к системе операторных уравнений. Решая последнюю как систему линейных алгебраических уравнений относительно изображений искомых функций, получаем операторное решение системы. Оригинал для негобудетрешением исходной системы дифференциальных уравнений.

Пример:

Найти решение линейной системы

удовлетворяющее начальным условиям х(0) = у(0) = I.

Пусть х(

Решая последнюю относительно Х(р) и У(р), получаем

Решение исходной задачи Коши

Решение интегральных уравнений

Напомним, что интегральным уравнением называют уравнение, в котором неизвестная функция входит под знак интеграла. Мы рассмотрим лишь уравнение вида (12)

называемое линейным интегральным уравнением Вольтерра второго рода с ядром K(t — т), зависящим от разности аргументов (уравнение типа свертки). Здесь φ(t) — искомая функция, f(t) и K(t) — заданные функции.

Пусть f(t) и K(t) есть функции-оригиналы, f(t) =’ F(p), K(t) =’ K(p).

Применяя к обеим частям (12) преобразование Лапласа и, пользуясь теоремой умножения, получим
(13)

где Ф(р) = φ(t). Из (13)

Оригинал для Ф(р) будет решением интегрального уравнения (12).

Пример:

Решить интегральное уравнение

Применяя преобразование Лапласа к обеим частям (14), получим

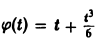
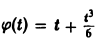
Функция является решением уравнения (14) (подстановка в уравнение (14) обращает последнее в тождество по t).

Замечание:

Преобразование Лапласа может быть использовано также при решении некоторых задач для уравнений математической физики.

Видео:Сведение дифференциального уравнения к интегральномуСкачать

Таблица преобразования Лапласа

Видео:Уравнения Фредгольма - 1Скачать

Дополнение к преобразованию Лапласа

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

🎦 Видео

Метод итерированных ядерСкачать