Реши задачу с помощью уравнения из одного поселка вышли одновременно

Видео:Решение задач с помощью уравнений. Видеоурок 29. Математика 6 классСкачать

Учебник Моро 4 класс 2 часть. Страница 33

Продолжаем учиться решать, составлять, сравнивать задачи, выполнять вычисления.

Упражнения

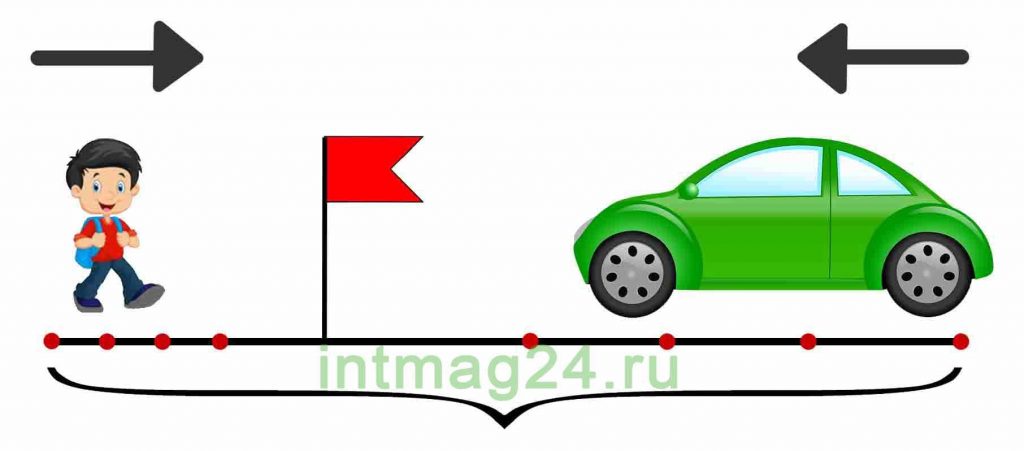
125. 1) Из посёлка вышли одновременно в противоположных направлениях два пешехода. Скорость одного пешехода 5 км/ч, скорость другого 4 км/ч. На каком расстоянии друг от друга будут пешеходы через 3 ч?

1) 5 + 4 = 9 (км/ч) — совместная скорость (скорость удаления) пешеходов.

2) 9 • 3 = 27 (км) — будет расстояние между пешеходами через 3 часа.

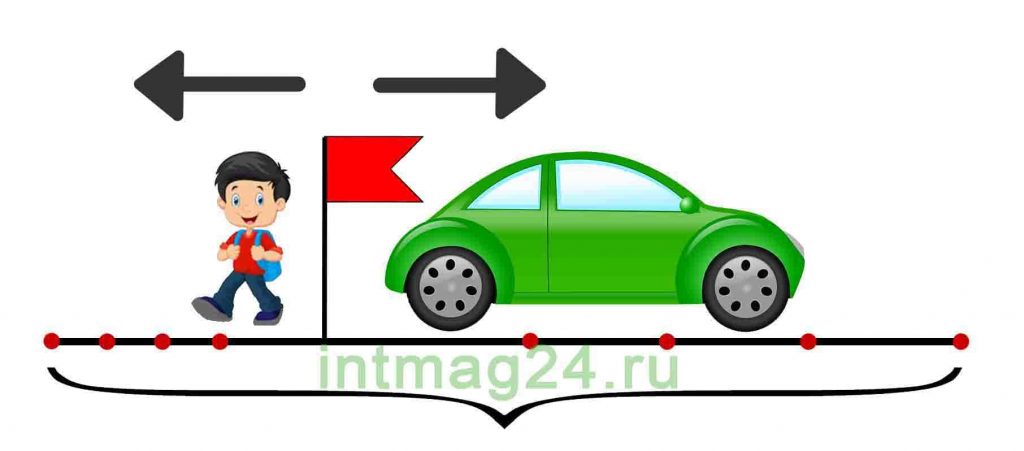
2) Из посёлка вышли одновременно в противоположных направлениях два пешехода. Скорость одного пешехода 5 км/ч, скорость другого 4 км/ч. Через сколько часов расстояние между ними будет 27 км?

1) 5 + 4 = 9 (км/ч) — совместная скорость (скорость удаления) пешеходов.

2) 27 : 9 = 3 (часа) — двигались пешеходы, чтобы между ними стало 27 км.

Ответ: через 3 ч.

3) Из посёлка вышли одновременно в противоположных направлениях два пешехода. Через 3 ч расстояние между ними было 27 км. Первый пешеход шёл со скоростью 5 км/ч. С какой скоростью шёл второй пешеход?

1) 5 • 3 = 15 (км) — прошёл первый пешеход за 3 часа.

2) 27 — 15 = 12 (км) — прошёл второй пешеход за 3 часа.

3) 12 : 3 = 4 (км/ч) — скорость второго пешехода.

126. Составь и реши 3 похожие задачи.

1) От вокзала отошли одновременно в противоположных направлениях грузовой и пассажирский поезд. Скорость пассажирского поезда 70 км/ч, а грузового — 50 км/ч. На каком расстоянии они будут друг от друга через 2 часа?

1) 70 + 50 = 120 (км/ч) — совместная скорость (скорость удаления) поездов.

2) 120 • 2 = 240 (км) — будет расстояние между поездами через 2 часа.

2) От вокзала отошли одновременна в противоположных направлениях грузовой и пассажирский поезд. Скорость пассажирского поезда 70 км/ч, скорость грузового поезда 50 км/ч. Через сколько часов расстояние между ними будет 240 км?

1) 70 + 50 = 120 (км/ч) — совместная скорость (скорость удаления) поездов.

2) 240 : 120 = 2 (часа) — поезда удалятся на 240 км друг от друга.

Ответ: через 2 часа.

3) От вокзала отошли одновременно в противоположных направлениях грузовой и пассажирский поезд. Через 2 часа расстояние между ними было 240 км. Скорость пассажирского поезда 70 км/ч. Какова скорость грузового поезда?

1) 70 • 2 = 140 (км) — прошёл пассажирский поезд за 2 часа.

2) 240 — 140 = 100 (км) — прошёл грузовой поезд за 2 часа.

3) 100 : 2 = 50 (км/ч) — скорость грузового поезда.

127. В киоске продавали тетради: школьные по цене а р. за тетрадь, общие по цене с р. за тетрадь. Сколько стоят вместе 5 школьных тетрадей и 5 общих? Запиши выражения, которые показывают, как можно решить эту задачу двумя способами.

1 способ: 5 • а + 5 • с — рублей стоят 5 школьных и к общих тетради вместе.

2 способ: (а + с) • 5 — рублей стоят 5 школьных и к общих тетради вместе.

Видео:Решение задач с помощью уравнений.Скачать

РЕШИТЕ С ПОМОЩЬЮ УРАВНЕНИЯ : из одногопосёлка однновременно в противоположных направлениях вышли два пешехода через 1, 3 ч расстояние между ними было 10, 4 км?

Математика | 5 — 9 классы

РЕШИТЕ С ПОМОЩЬЮ УРАВНЕНИЯ : из одногопосёлка однновременно в противоположных направлениях вышли два пешехода через 1, 3 ч расстояние между ними было 10, 4 км.

Скорость одного пешехода составляет 7 / 9 скорости другого .

Найдите скорость каждого пешехода .

Пусть скорость одного пешехода будет — х км / ч, тогда скорость другого 7 / 9х, общая скорость 10, 4 / 1, 3 получаем следующее уравнениех + 7 / 9х = 104 / 13 ⇒16 / 9 x = 104 / 13 ⇒ x = (104 * 9) / (13 * 16) ⇒ x = 4, 5 км / ч, тогда скорость другого 7 / 9 * 4, 5 = 3, 5 км / ч.

Видео:Решение задач с помощью уравнений. Алгебра 7 классСкачать

Два пешехода вышли одновременно из одного места в противоположных направлениях?

Два пешехода вышли одновременно из одного места в противоположных направлениях.

Через 0, 8 ч расстояние между ними стало равным 6, 8 км.

Скорость одного пешехода была в 1, 5 раза больше скорости другого.

Найдите скорость каждого пешехода.

Видео:Решение задач с помощью уравнений. Алгебра, 7 классСкачать

Два пешехода вышли одновременно из одного места в противоположных направлениях?

Два пешехода вышли одновременно из одного места в противоположных направлениях.

Через 0, 8 часа расстояние между ними стало равным 6, 8 км.

Скорость одного пешехода была в 1, 5 раза больше скорости другого.

Найдите скорость каждого пешехода.

Видео:Задачи на движение двух объектовСкачать

Решите задачу уравнением ?

Решите задачу уравнением !

Два пешехода вышли одновременно из одного места в противоположных направлениях.

Через 0, 8 ч расстояние между ними стало равным 6, 8 км.

Скорость одного пешехода была в 1, 5 раза больше скорости другого.

Найдите скорость каждого пешехода.

Видео:Задача на движение в одном направленииСкачать

Два пешехода вышли одновременно из одного места в противоположных направлениях?

Два пешехода вышли одновременно из одного места в противоположных направлениях.

8ч расстояние между ними стало равным 6.

8км. Скорость одного пешехода была в 1.

5 раза больше скорости другого.

Найдите скорость каждого пешехода.

Видео:АЛГЕБРА 7 класс : Решение задач с помощью уравнений | ВидеоурокСкачать

Два пешехода вышли одновременно из одного места в противоположных направлениях ?

Два пешехода вышли одновременно из одного места в противоположных направлениях .

Через 0, 8 чеса расстояние между ними стало равным 6, 8 км.

Скорость одного пешехода была в 1, 5 раза больше скорости другого .

Найдите скорость каждого пешехода.

Видео:Задачи на движение. Учимся решать задачи на движение. Способы решения задач на движение.Скачать

Два пешехода вышли одновременно из одного и того же места в противоположные направления ?

Два пешехода вышли одновременно из одного и того же места в противоположные направления .

Через 0, 8 ч расстояние между ними стало равным 6, 8 км .

Скорость одного пешехода была в 1, 5 раза больше скорости другого .

Найдите скорость каждого пешехода.

Видео:Задачи по математике на Движение. Как объяснить ребенку задачи на движение?Скачать

Два пешехода вышли одновременно из одного места в противоположных направлениях, Через 0, 8 часов расстояние между ними стало равным 6?

Два пешехода вышли одновременно из одного места в противоположных направлениях, Через 0, 8 часов расстояние между ними стало равным 6.

Скорость одного пешехода была в 1.

5 раза больше скорости другого.

Найдите скорость каждого пешеходы,.

Видео:Математика 4 класс (Урок№45 - Задачи на движение в противоположных направлениях.)Скачать

Два пешехода вышли одновременно из одного места в противоположных направлениях?

Два пешехода вышли одновременно из одного места в противоположных направлениях.

Через 0, 8 часа расстояние между ними стало равным 6, 8 км.

Скорость одного пешехода была в 1, 5 раза больше скорости другого.

Найдите скорость каждого пешехода.

Видео:Задачи на движение | Математика TutorOnlineСкачать

Два пешехода вышли одновременно из одного места в противоположных направлениях?

Два пешехода вышли одновременно из одного места в противоположных направлениях.

8 ч расстояние между ними стало равным 6.

8км. Скорость одного пешехода была в 1.

5 раза больше скорости другого.

Найдите скорость каждого пешехода.

Видео:Решение задач с помощью уравненийСкачать

Из одного посёлка одновременно в противоположных направлениях вышли два пешехода?

Из одного посёлка одновременно в противоположных направлениях вышли два пешехода.

Через 1, 3 часа расстояние между ними было 10, 4 км.

Скорость одного пешехода составляет 7 / 9 скорости другово.

Найдите скорость каждого пешехода.

На этой странице сайта, в категории Математика размещен ответ на вопрос РЕШИТЕ С ПОМОЩЬЮ УРАВНЕНИЯ : из одногопосёлка однновременно в противоположных направлениях вышли два пешехода через 1, 3 ч расстояние между ними было 10, 4 км?. По уровню сложности вопрос рассчитан на учащихся 5 — 9 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.

1)3км 6м•7 = 21км 42м 3км 6м = 3006м 3006•7 = 21042м = 21км 42м 2)4м 5см•8 = 32м 40см (32м 4дм) 4м 5см = 405см 405•8 = 3240см = 32м 40см (32м 4дм) 3)76кг 5г•5 = 380кг 25г 76кг 5г = 76005г 76005•5 = 380025г = 380кг 25г 4)7т 82кг•6 = 42т 429кг (42т 4ц ..

14. Один корень 18. Два + и — 16. Тоже два такие же.

1523 + 249 = 1772 1788 — 1772 = 16 проверка : 1788 — 1523 = 265.

Найдите переменную, исходя из данных на рисунке. A, b, c , e.

1) 420 — 180 = 240( км ) уже пройдено 2)240 — 180 = 60(км) разница в пройденном пути ответ : на 60 км больше проехал, чем осталось пройти.

900000 — 800 — х = 100000 899200 — х = 100000 х = 899200 — 100000 х = 799200.

Видео:Урок 14 Решение задач с помощью уравнений (5 класс)Скачать

ГДЗ, Моро М.И, математика, 4 класс Часть 2, Задание № 125Из посёлка вышли одновременно в противоположных направлениях

1) Из посёлка вышли одновременно в противополож-
ных направлениях два пешехода. Скорость одного пе-
шехода 5 км/ч, скорость другого 4 км/ч. На каком
расстоянии друг от друга будут пешеходы через 3 ч?
2) Из посёлка вышли одновременно в противополож-
ных направлениях два пешехода. Скорость одного пе-
шехода 5 км/ч, скорость другого 4 км/ч. Через
сколько часов расстояние между ними будет 27 км?

3) Из посёлка вышли одновременно в противополож-
ных направлениях два пешехода. Через 3 ч расстоя-
ние между ними было 27 км. Первый пешеход шёл
со скоростью 5 км/ч. С какой скоростью шёл вто-
рой пешеход?

Видео:Математика 4 класс (Урок№39 - Задачи на встречное движение.)Скачать

Задачи на движение

Задачи на движение (скорость, время и расстояние) являются одной из основных типов задач по математике, которые должен уметь решать каждый школьник. В данной статье рассмотрены все типы задач на движение:
— простые задачи на скорость, время и расстояние;
— задачи на встречное и противоположное движение;
— задачи на движение в одном направлении (на сближение и удаление);
— решение задач на движение по реке.

Видео:Решение задач с помощью уравненийСкачать

Скорость, время и расстояние: определения, обозначения, формулы

скорость = расстояние: время — формула нахождения скорости;

время = расстояние: скорость — формула нахождения времени;

расстояние = скорость · время — формула нахождения расстояния.

Скорость – это расстояние, пройденное за единицу времени: за 1 секунду, за 1 минуту, за 1 час и так далее.
Пример обозначения: 7 км/ч (читается: семь километров в час).
Если весь путь проходится с одинаковой скоростью, то такое движение называется равномерным.

На сайте представлены калькуляторы онлайн, с помощью которых можно перевести скорость, время и расстояние в другие единицы измерения:

Примеры простых задач.

Задача 1.

Автомобиль проехал 180 км за 2 часа. Чему равна скорость автомобиля?
Решение: 180:2=90 (км/ч.)
Ответ: Скорость автомобиля равна 90 км/ч.

Задача 2.

Автобус проехал путь в 240 км со скоростью 80 км/ч. Сколько времени ехал автобус?
Решение: 240:80=3 (ч.)
Ответ: Автобус проехал 3 часа.

Задача 3.

Грузовик ехал 5 часов со скоростью 70 км/ч. Какое расстояние проехал грузовик за это время?
Решение: 70 · 3 = 350 (км)
Ответ: Грузовик за 5 часов проехал 350 км.

Видео:Задачи на движение по воде | Математика | TutorOnlineСкачать

Задачи на встречное движение

В таких задачах два объекта движутся навстречу друг другу.
Задачи на встречное движение можно решать двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость сближения объектов (как сумму их скоростей), общие время и расстояние. Скорость сближения — это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.

Задача 4.

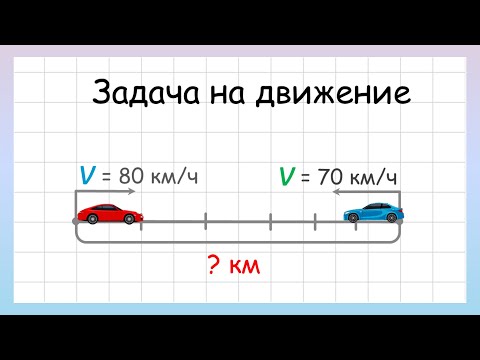
Из двух пунктов навстречу друг другу одновременно выехали два поезда и встретились через 3 часа. Первый поезд ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. На каком расстоянии друг от друга находятся пункты?
Решение:
Первый способ. Найти расстояние, которое проехал каждый автобус, и сложить полученные данные:
80*3=240 (км) – проехал 1й автобус, 70*3=210 (км) – проехал 2й поезд,
240+210=450 (км) – проехали два поезда.
Второй способ. Найти скорость сближения поездов, то есть на сколько сокращалось расстояние между ними каждый час; а затем найти расстояние:
80+70=150 (км/ч), 150*3=450 (км).
Ответ: города находятся на расстоянии 450 км.

Задача 5.

Из двух городов навстречу друг другу одновременно выехали два автобуса. Первый автобус ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. Какое расстояние будет между ними через 2 часа, если расстояние между городами 450 км?
Решение:
Первый способ. Определить, сколько километров проехал каждый автобус и найти расстояние, которое осталось проехать:
80*2=160 (км)-проехал 1й автобус, 70*2=140 (км)-проехал 2й автобус,
160+140=300 (км)-проехали два автобуса, 450-300=150 (км)-осталось проехать.
Второй способ. Найти скорость сближения автобусов и умножить ее на время в пути.
80*70=150 (км/ч) – скорость сближения; 150*2=300 (км) – проехали два автобуса; 450-300=150 (км) – осталось проехать.
Ответ: Через 2часа расстояние между автобусами будет 150 км.

Видео:Решение задач с помощью уравнений. 5 классСкачать

Задачи на движение в противоположных направлениях

В таких задачах два объекта движутся в противоположных направлениях, отдаляясь друг от друга. В таком типе задачи используется скорость удаления. Задачи на движение в противоположных направлениях также можно решить двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость удаления объектов (как сумму их скоростей), общие время и расстояние. Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.

Задача 6.

Два автомобиля выехали одновременно из одного и того же пункта в противоположных направлениях. Скорость первого автомобиля 100 км/ч, скорость второго – 70 км/ч. Какое расстояние будет между автомобилями через 4 часа?
Решение:
Первый способ. Определить расстояние, которое проехал каждый автомобиль и найти сумму полученных результатов:
1) 100 · 4 = 400 (км) – проехал первый автомобиль
2) 70 · 4 = 280 (км) – проехал второй автомобиль
400 + 280 = 680 (км)
Второй способ. Найти скорость удаления, то есть значение увеличения расстояния между автомобилями за каждый час, а затем скорость удаления умножить на время в пути.
100 + 70= 170 км/ч – это скорость удаления автомобилей.
170 · 4 = 680 (км)
Ответ: Через 4 часа между автомобилями будет 680 км.

Задача 7.

Из двух населённых пунктов, расстояние между которыми 40 км, вышли в противоположных направлениях два туриста. Первый турист шёл со скоростью 4 км/ч, а второй — 5 км/ч. Какое расстояние между туристами будет через 5 часов?
Решение:
Первый способ. Определить сколько километров прошёл каждый из туристов за 5 часов, сложить полученные результаты, а затем к полученному расстоянию прибавить расстояние между населенными пунктами.
1) 4 · 5 = 20 (км) – прошёл первый турист;
2) 5 · 5 = 25 (км) – прошёл второй турист;
3) 20 + 25 = 45 (км);
4) 45 + 40 = 85 (км).
Второй способ. Найти скорость удаления пешеходов, затем найти пройденное расстояние, к полученному результату прибавить расстоянием между населёнными пунктами.
4 + 5 = 9 (км/ч);
9 · 5 = 45 (км);
45 + 40 = 85 (км);
Ответ: Через 5 часов расстояние между пешеходами будет 85 км.

Видео:Задача на встречное движение. Как решить задачу на движение?Скачать

Задачи на движение в одном направлении

В таких задачах два объекта движутся в одном направлении с разной скоростью, при этом они сближаются друг с другом или отдаляются друг от друга. Соответственно находится скорость сближения или скорость удаления объектов.

Формула нахождения скорости сближения или удаления двух объектов, которые движутся в одном направлении: из большей скорости вычесть меньшую.

Задача 8.

Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?,
Решение:
Задачу можно решить с помощью уравнения.
В этом случае скорость первого автомобиля 40 км/час, время в пути на 4 часа больше, чем время второго автомобиля (или t+4). Скорость второго автомобиля 60 км/час, время в пути – t. Расстояние оба автомобиля проехали одинаковое. Поэтому можно составить уравнение: 40*(t+4)=60*t. Отсюда получаем t=8 (часов) – время в пути второго автомобиля, за которое он догонит первый.
Решение задачи без использования уравнения.
Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалиться от города на: 40 · 4 = 160 (км).
Второй автомобиль движется быстрее первого, значит, каждый час расстояние между автомобилями будет сокращаться на разность их скоростей: 60 — 40 = 20 (км/ч) – это скорость сближения.
Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся: 160 : 20 = 8 (ч)
Ответ: Второй автомобиль догонит первый через 8 часов.

Задача 9.

Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?
Решение: Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов: 5 — 4 = 1 (км/ч).
Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого: 5 : 1 = 5 (ч)
Ответ: Через 5 часов второй пешеход догонит первого.

Задача 10.

Два автомобиля выехали одновременно из одного и того же пункта в одном направлении. Скорость первого автомобиля 80 км/ч, а скорость второго – 40 км/ч.
1) Чему равна скорость удаления между автомобилями?
2) Какое расстояние будет между автомобилями через 3 часа?
3) Через сколько часов расстояние между ними будет 200 км?
Решение:
1) 80 — 40 = 40 (км/ч) — скорость удаления автомобилей друг от друга.
2) 40 · 3 = 120 (км) – расстояние между ними через 3 часа./
3) 200 : 40 = 5 (ч) – время, через которое расстояние между автомобилями станет 200 км.
Ответ:
1) Скорость удаления между автомобилями равна 40 км/ч.
2) Через 3 часа между автомобилями будет 120 км.
3) Через 5 часов между автомобилями будет расстояние в 200 км.

Видео:РЕШЕНИЕ ЗАДАЧ НА ДВИЖЕНИЕ С ПОМОЩЬЮ УРАВНЕНИЙ. Примеры | АЛГЕБРА 7 классСкачать

Задачи на движение по реке

Рассмотрим задачи, в которых речь идёт о движении объекта по реке. Скорость любого объекта в стоячей воде называют собственной скоростью этого объекта.

Чтобы узнать скорость объекта, который движется по течению реки, надо к собственной скорости объекта прибавить скорость течения реки. Чтобы узнать скорость объекта, который движется против течения реки, надо из собственной скорости объекта вычесть скорость течения реки.

Задача 11.

Лодка движется по реке. За сколько часов она преодолеет расстояние 120 км, если ее собственная скорость 27 км/ч, а скорость течения реки 3 км/ч?
Решение:
1) лодка движется по течению реки.
27 + 3 = 30 (км/ч) – скорость лодки по течению реки.
120 : 30 = 4 (ч) – проплывет путь.
2) лодка движется против течения реки.
27 — 3 = 24 (км/ч) — скорость лодки против течения реки
120 : 24 = 5 (ч) – проплывет путь.
Ответ:
1) При движении по течению реки лодка потратит 4 часа на путь.
2) При движении против течения реки лодка потратит 5 часов на путь.

Видео:Математика 5 класс (Урок№35 - Задачи на движение.)Скачать

Итак, для решения задач на движение:

1. Основная формула:S=ν*t;
2. Нужно сделать чертеж, который поможет определить тип задачи.
3. Все цифры нужно привести в единые единицы измерения: длина и время

Заключение.

Решая много задач по данной теме, ученик обязательно научится быстро ориентироваться в понятиях «скорость», «время» и «расстояние» и быстро решать задачи всех типов. Получить карточки с задачами разных видов можно по ссылке.