Про уравнения - легко » Статьи

Решение задачи дирихле для уравнения лапласа методом конформных отображений

Обновлено
Конформные отображения

Содержание:

Решение задачи дирихле для уравнения лапласа методом конформных отображений

Решение задачи дирихле для уравнения лапласа методом конформных отображений

Решение задачи дирихле для уравнения лапласа методом конформных отображений

Решение задачи дирихле для уравнения лапласа методом конформных отображений

Решение задачи дирихле для уравнения лапласа методом конформных отображений

Решение задачи дирихле для уравнения лапласа методом конформных отображений

Решение задачи дирихле для уравнения лапласа методом конформных отображений

Решение задачи дирихле для уравнения лапласа методом конформных отображений

Решение задачи дирихле для уравнения лапласа методом конформных отображений

Решение задачи дирихле для уравнения лапласа методом конформных отображений

Решение задачи дирихле для уравнения лапласа методом конформных отображений

Решение задачи дирихле для уравнения лапласа методом конформных отображений

Решение задачи дирихле для уравнения лапласа методом конформных отображений

Решение задачи дирихле для уравнения лапласа методом конформных отображений

Решение задачи дирихле для уравнения лапласа методом конформных отображений

Решение задачи дирихле для уравнения лапласа методом конформных отображений

Решение задачи дирихле для уравнения лапласа методом конформных отображений

Решение задачи дирихле для уравнения лапласа методом конформных отображений

Решение задачи дирихле для уравнения лапласа методом конформных отображений

Решение задачи дирихле для уравнения лапласа методом конформных отображений

Решение задачи дирихле для уравнения лапласа методом конформных отображений

Решение задачи дирихле для уравнения лапласа методом конформных отображений

Решение задачи дирихле для уравнения лапласа методом конформных отображений

По этой ссылке вы найдёте полный курс лекций по математике:

Содержание
  1. Преобразования
  2. Преобразования плоскости
  3. Пример с решением:
  4. Пример с решением:
  5. Решение задачи дирихле для уравнения лапласа методом конформных отображений
  6. Дистанционное занятие на тему «Регулярные ветви многозначных функций (часть 1)»
  7. Содержание
  8. Дистанционное занятие на тему «Регулярные ветви многозначных функций (часть 2)»
  9. Дистанционное занятие на тему «Регулярные ветви многозначных функций (часть 3)»
  10. Дистанционное занятие на тему «Принцип аргумента. Теорема Руше»
  11. Содержание
  12. Дистанционное занятие на тему «Принцип максимума модуля голоморфной функции»
  13. Дистанционное занятие на тему «Конформные отображения (часть 1)»
  14. Содержание
  15. Дистанционное занятие на тему «Конформные отображения (часть 2)»
  16. Содержание
  17. Дистанционное занятие на тему «Конформные отображения (часть 3)»
  18. Содержание
  19. Дистанционное занятие на тему «Применение методов ТФКП при решении задачи Дирихле для уравнения Лапласа на плоскости»
  20. Содержание
  21. Дистанционное занятие на тему «Метод стационарной фазы»
  22. 🔥 Видео

Преобразования

Преобразования, наделенные таким свойством, позволяют успешно решать задачи аэро- и гидродинамики, теории упругости, теории полей различной природы и многие другие. Мы ограничимся преобразованиями плоских областей. Непрерывное отображение го = /(г) плоской области в область на плоскости называется конформным в точке , если в этой точке оно обладает свойствами постоянства растяжения и сохранения углов.

Открытые области и называются конформно эквивапентными,если существует взаимнооднозначное отображение одной из этих областей на другую, конформное в каждой точке. Теорема Римана. Любые две плоские открытые односвязные области, границы которых состоят более чем из одной точки, конформно эквивалентны. Основной проблемой при решении конкретных задач является построение по заданным плоским областям явного взаимно однозначного конформного отображения одной из них на другую.

Один изспособоврешенияэтой проблемы в плоском случае — привлечение аппарата теории функций комплексного переменного. Какужеотмечалось выше, однолистная аналитическаяфункция с отличной от нуля производной осуществляет конформное отображение своей области задания на ее образ. При построении конформных отображений весьма полезно следующее правило. Принцип соответствия границ.

Видео:Задача Дирихле для круга. Уравнение ЛапласаСкачать

Задача Дирихле для круга. Уравнение Лапласа

Пусть в односвязной области Я) комплексной плоскости z, ограниченной контуром 7, задана однозначная аналитическая функция w = f(z), непрерывная в замыкании 9) и отражающая контур 7 на некоторый контур 7′ комплексной п/юскости w. Если при этом сохраняется направления обхода контура, то функция w — f(z) осуществляет конформное отображение области комплексной плоскости z на область З1 комплексной плоскости w, ограниченную контуром 7′ (рис. 1).

Возможно вам будут полезны данные страницы:

Цель настоящего параграфа состоит в том, чтобы, используя найденные ранее области однолистности основных элементарных фуннций комплексного переменного, научиться строить конформные отображения открытых одно-связных плосжх областей, часто встречающихся в приложениях, надвестан- КОНФОРМНЫЕ ОТОБРАЖЕНИЯ дартныс области — верхнюю полуплоскость и единичный круг (рис. 2). Для более эффективного использо- Рис.2 вания приводимой ниже таблицы полезны некоторые простейшие преобразования комплексной плоскости.

Преобразования плоскости

Преобразования плоскости, осуществляющие: 1. параллельный перенос (сдвиг на заданное комплексное число а) (рис. 3), Рис.3 2. поворот (на заданный угол 3. растяжение (fc > 1) ил и сжатие (рис. 5). Тем самым, преобразование вида 0 любой круг можно сделать единичным кругом с центром в нуле (рис. 6), любую полуплоскость можосделать верхней полуплоскостью, любой отрезок прямой можно преобразовать в отрезок [0, 1) вещественной оси (рис. 7), любой луч — в положительный луч вещественной оси (рис. 8). б) Рис. 6 растяжение (им) О перенос в) поворот перенос рас гяжение Рис. 7 перенос поворот Рис.8 в) б) В) 4.

Преобразование плоскости z,

переводящее три различные точки z, zi, z3 в три различныеточт плоскости (рис.9). Рассмотрим пример, показывающий, как пользоваться приведенной ниже табли- цей.

Пример с решением:

Отобразить круг с разрезом по радиусу (рис. 10) взаимно однозначно и конформно на единичный круг с центром в нуле. 4 А. Применяя простейшие преобразования плоскости, приведем заданную область к области, имеющейся в таблице. 1. Переместим центр заданного круга в нулевую точку (см. рис. 11): .

Имеем: круг с разрезом 2. Повернем полученный круг по часовой стрелке на угол (см. рис. 12) . Имеем: круг с разрезом arg 3. Сожмем круг в три раза (см. рис. 13) Имеем: круг с разрезом Таким образом, исходная область приводится к имеющейся в таблице при помощи следующего преобразования Б. 1. Указанная область — круг с разрезом — приведена в таблице под № 30. Функция Жуковского КОНФОРМНЫЕ ОТОБРАЖЕНИЯ преобразует эту область в плоскость с разрезом по отрезку [-1, 5] вещественной оси (рис. 14). 2. Указанная область приведена в таблице под № 22.

Применяя дробно-линейное преобразование преобразуем эту область в плоасость с разрезом по лучу [0, +оо) вещественной оси (рис. 15).

3. Указанная область приведена в таблице под № 6. Извлекая квадратный корень преобразуем эту область в верхнюю полуплоскость Im z6 > 0 (рис. 16). 4. Указанная область приведона в таблице под Ng 11. Применяя дробно- линейное преобразование преобразуем эту область в единичный круге центром в нуле Последовательно выражая z* через z^-i, получим взаимно однозначное и конформное преобразование заданного на комплексной плоскости г круга с разрезом по радиусу на единичный круг комплексной плоек ости tr. р- Конформное отображение заданными областями определяется неоднозначно.

Пример с решением:

Отобразить полукруг (рис.18) взаимно однозначно и конформно на верхнюю полуплоскость Im w > 0. . Дробно-линейное отображение преобразует заданный полукруг в прямой угол 2. Указанная область приведена в таблице под Ne 4 (п = 2). Возводя в квадрат Б. Заданная область приведена в таблице за No 9. Искомое преобразование имеет вид чю- Оба отображения w -заданный полукруг в верхнюю полуплоскость переводит взаимно однозначно и конформно Организация таблицы и правила пользования ею.

Видео:Методы математической физики. Задача Дирихле для уравнения Лапласа в круге. 19.05.21 Фролова Е.В.Скачать

Методы математической физики. Задача Дирихле для уравнения Лапласа в круге. 19.05.21 Фролова Е.В.

Как будет показано в конце параграфа, такая стандартизация удобна для практического использования. Часто приводится только преобразование, сводящее заданную область к ранее рассмотренной. В этом случае дается ссылка на преобразование, переводящее полученную область в стандартную (единичный круг с центром в нуле или верхнюю полуплоскость). Основные элементарные функции.

Таблица Плоскость с разрезом по действительному лучу [О, Плоскость с разрезами Плоскость с разрезом по действительному лучу [0, +ю[ Плоскость с разрезом по отрезку 10, 1] Плоскость с разрезом по действительному лучу (0, +«>( Плоскость с разрезами по действительным лучам J -оо, 0] и (I, +оо[ Плоскость с разрезом по действительному лучу [0, +«>( Плоскость с разрезом по отрезку lu. zi] Плоскость с разрезом по отрезку (О, 1J № 21 1лоскость с разрезами ю лучам, лежащим ia прямой, проходящей через ачало координат по действительным лучам ]-«ю, 0] и (1.

Плоскость с разрезом по действительному лучу (0, +во( Плоскость с разрезом по дуге окружности Ixl — 1, lm z > О Плоскость с разрезом по дуге окруж ности III — I, Re z > О Плоскость с разрезом по действительн ому лучу (0, Плоскость с разрезом no дуге окруж ности Плоскость с разрезом по действительному лучу [С, + со [ № 25 Полуплоскость с разрезами Полуплоскость l с разрезом по отрезку [0, />

Плоскость с разрезом по действительному лучу [ — I, Полуплоскость с разрезом по отрезку Полуплоскость Im г > О с разрезами по отрезку [0, oi) и мнимому лучу №28 Полуплоскость с разрезом по ду| е окружности по действительным лучам |- по действительным лучам 1 — оо, -Л2] с разрезом по мнимому лучу Круг с разрезами Круг 1 с разрезом по отрезку (1/2, 1J №30 Плоскость с разрезом по отрезку <-1, 5/4] Круг Izl с разрезами по отрезкам (-1. -1/2] и (1/2, 1] № 31

Плоскость с разрезами по отрезиам I -5/4, 5/4] Круг Ijl симметричными разрезами по мнимой оси Круг lie с симметричными разрезами по действительной оси Внешность круга с разрезами Внешность единичного круга I с разрезом по отрезку [1, 2J №33 Внешность единичного круга с разрезом по отрезкам 1-2, -1] и 11, 2) №34 Плоскость с разрезом по отрезку [ -1, 5/4] Плоскость с разрезом по отрезку I — 5/4, 3/4] w = e’^z Внешность единичного круга Izl > 1 с разрезами по отрезкам, являющимися продолжениями его диаметра Внешность единичного круга Iwl > 1 с разрезами по отрезкам, лежащим на действительной оси Полуируг с разрезами -г2

Nfc 36 Круг Iwl с разрезом по отрезку [ -1/4, 1] Полукруг , с разрезом по отрезку (0, i/2) Полукруг , с разрезом по отрезку [//2, /) Круг с разрезами по отрезкам № 37 Полукруг с разрезами по отрезкам [0. al) и [Ы. /). где N? 38 Круг с разрезами по отрезкам 1-1. — угол с разрезами Угол с разрезом по действительному лучу Ах» г — т/4 с началом в точке 1 + / Полуплоскость Im W > 0 с разрезом по мнимому лучу с началом в точке 12/, +/•©( Nf39 Плоскость с разрезами по действительным лучам Угол с разрезом по действительному лучу Arg z — т/л с началом в точке Полоса с разрезами w — с*

Полуплоскость Im с разрезом по дуге окружности иг » с Полоса 0 т с разрезом по мнимому отрезку ( Полуплоскость Im с разрезом по дуге окружности w — е Полоса 0 разрезом по мнимому отрезку fW/2, TiJ N? Полоса Полуплоскость Im w > О с разрезами по мнимым с разрезами по дуге отрезкам [0, al и [Ы, «1, окружности w « t*, КОНФОРМНЫЕ ОТОБРАЖЕНИЯ М43 Полоса Плоскость с разрезом по действительному лучу (0. +«( №44 Полоса с разрезом Полуплоскость Im по действительному с разрезом по мнимому лучу I отрезку [О, /I

Видео:Попов И.Ю. Функция Грина задачи Дирихле для уравнения ЛапласаСкачать

Попов И.Ю. Функция Грина задачи Дирихле для уравнения Лапласа

Полоса 0 Полоса с разрезом по действительному лучу I №46 Полоса Полоса 0 с разрезом по действительному лучу R №47 Область 1 Полоса 01 Область с удаленным кругом Re Полоса Полуплоскость Im z > О с удаленным круговым сегментом Угол №50 -Ш Полуплоскость Im с удаленным круговым сегментом Полуплоскость Im w > 0 № 51 Полуполоса Полуплоскость Im w > Полуплоскость Im Полуполоса с удаленными полукругами № 53

Полуполоса Полуполоса N? 54 Угол Полуплоскость Im w > 0 с удаленным сектором единичного круга Ne 55 Угол Im z с удаленным полукругом Полуполоса 0 Внешность параболы Полуплоскость Im w Внутренность параболы Полуплоскость Im № 58 Внешность гиперболы Полуплоскость Im w Внутренность правой ветви гиперболы Полуплоскость Iro W > О Внешность эллипса Внешность круга М > I

Присылайте задания в любое время дня и ночи в ➔ Решение задачи дирихле для уравнения лапласа методом конформных отображений

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Решение задачи дирихле для уравнения лапласа методом конформных отображений

Решение задачи дирихле для уравнения лапласа методом конформных отображений

На этой странице нашего сайта размещены учебно-методические пособия по теории функций комплексного переменного (ТФКП), которые использовались при проведении дистанционных занятий со студентами МФТИ в 2020 — 2021 годах.

Каждое из учебно-методических пособий содержит теоретические сведения и примеры решения типовых задач по изучаемому разделу теории функций комплексного переменного (ТФКП). Практически все разобранные в учебно-методических пособиях задачи ранее предлагались для решения студентам МФТИ в заданиях для самостоятельной работы, на семестровых контрольных работах и на устных экзаменах по теории функций комплексного переменного (ТФКП). В справочной форме приводится необходимая для решения задач теория.

Видео:Задача Дирихле и НейманаСкачать

Задача Дирихле и Неймана

Мы надеемся, что эти учебные материалы будут полезными не только студентам МФТИ, осваивающим курс теории функций комплексного переменного (ТФКП), но и студентам других ВУЗов.

Дистанционное занятие на тему «Регулярные ветви многозначных функций (часть 1)»

На дистанционном занятии рассматриваются методы решения задач, в которых используются регулярные ветви многозначных функций Ln f(z) и 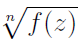Решение задачи дирихле для уравнения лапласа методом конформных отображений, где f(z) — голоморфная функция. В качестве примеров приводятся решения задач на разложение регулярных ветвей в ряды Тейлора и Лорана и вычисление интегралов от регулярных ветвей многозначных функций с помощью вычетов.

Содержание

  1. Регулярные ветви многозначной функции Ln f(z) .
  2. Регулярные ветви многозначной функции Решение задачи дирихле для уравнения лапласа методом конформных отображений.
  3. Примеры решения задач на разложения регулярных ветвей многозначных функций в ряды Тейлора и Лорана
  4. Примеры решения задач на вычисление интегралов от регулярных ветвей с помощью вычетов.
Решение задачи дирихле для уравнения лапласа методом конформных отображенийУчебно-методическое пособие на тему «Регулярные ветви многозначных функций (часть 1)»

Дистанционное занятие на тему «Регулярные ветви многозначных функций (часть 2)»

Это дистанционное занятие является продолжением дистанционного занятия «Регулярные ветви многозначных функций (часть 1)». На этом занятии рассматриваются методы вычисления интегралов от действительных функций по бесконечному интервалу действительной оси с использованием регулярных ветвей многозначных функций и теории вычетов.

Решение задачи дирихле для уравнения лапласа методом конформных отображенийУчебно-методическое пособие на тему «Регулярные ветви многозначных функций (часть 2)»

Дистанционное занятие на тему «Регулярные ветви многозначных функций (часть 3)»

Это дистанционное занятие является продолжением дистанционных занятий «Регулярные ветви многозначных функций (часть 1)» и «Регулярные ветви многозначных функций (часть 2)&raquo. На этом занятии рассматриваются методы вычисления интегралов от действительных функций по конечному интервалу действительной оси с использованием регулярных ветвей многозначных функций и теории вычетов.

Решение задачи дирихле для уравнения лапласа методом конформных отображенийУчебно-методическое пособие на тему «Регулярные ветви многозначных функций (часть 3)»

Дистанционное занятие на тему «Принцип аргумента. Теорема Руше»

На дистанционном занятии рассматриваются методы решения задач, использующие теорему Руше.

Содержание

  1. Принцип аргумента.
  2. Теорема Руше.
  3. Основная терема алгебры.
  4. Примеры решения задач.
Решение задачи дирихле для уравнения лапласа методом конформных отображенийУчебно-методическое пособие на тему «Принцип аргумента. Теорема Руше»

Дистанционное занятие на тему «Принцип максимума модуля голоморфной функции»

На дистанционном занятии рассматриваются применения принципа максимума модуля голоморфной функции к решению задач.

Решение задачи дирихле для уравнения лапласа методом конформных отображенийУчебно-методическое пособие на тему «Принцип максимума модуля голоморфной функции»

Дистанционное занятие на тему «Конформные отображения (часть 1)»

На дистанционном занятии рассматриваются методы решения задач, в которых требуется построить конформное отображение заданной области расширенной комплексной плоскости на другую заданную область. Изучаются свойства конформных отображений и, в частности, свойства дробно-линейных отображений.

Содержание

  1. Определение конформного отображения области расширенной комплексной плоскости на область расширенной комплексной плоскости..
  2. Свойства конформных отображений.
  3. Дробно-линейные отображения и их свойства.
  4. Примеры решения задач.
Решение задачи дирихле для уравнения лапласа методом конформных отображенийУчебно-методическое пособие на тему «Конформные отображения (часть1)»

Дистанционное занятие на тему «Конформные отображения (часть 2)»

Это дистанционное занятие является продолжением дистанционного занятия «Конформные отображения (часть 1)». На этом занятии изучаются свойства функции Жуковского, функции, обратной к функции Жуковского и комплексной экспоненты.

Содержание

  1. Функция Жуковского и ее свойства.
  2. Функция, обратная к функции Жуковского.
  3. Комплексная экспонента и ее свойства.
  4. Примеры решения задач.
Решение задачи дирихле для уравнения лапласа методом конформных отображенийУчебно-методическое пособие на тему «Конформные отображения (часть 2)»

Дистанционное занятие на тему «Конформные отображения (часть 3)»

Видео:7.1 Решение уравнения Лапласа в прямоугольникеСкачать

7.1 Решение уравнения Лапласа в прямоугольнике

Это дистанционное занятие является продолжением дистанционных занятий «Конформные отображения (часть 1)» и «Конформные отображения (часть 2)». На этом занятии изучаются применения принципа симметрии и теоремы Римана.

Содержание

  1. Принцип симметрии.
  2. Теорема Римана.
  3. Примеры решения задач.
Решение задачи дирихле для уравнения лапласа методом конформных отображенийУчебно-методическое пособие на тему «Конформные отображения (часть 3)»

Дистанционное занятие на тему «Применение методов ТФКП при решении задачи Дирихле для уравнения Лапласа на плоскости»

Это дистанционное занятие посвящено применению функций комплексного переменного при решении задачи Дирихле для уравнения Лапласа на плоскости.

Содержание

  1. Гармонические функции комплексного переменного.
  2. Инвариантность уравнения Лапласа относительно конформных отображений.
  3. Постановка задачи Дирихле для уравнения Лапласа на плоскости.
  4. Формула Пуассона для решения задачи Дирихле в круге.
  5. Примеры решения задач.
Решение задачи дирихле для уравнения лапласа методом конформных отображенийУчебно-методическое пособие на тему «Применение методов ТФКП при решении задачи Дирихле для уравнения Лапласа на плоскости»

Дистанционное занятие на тему «Метод стационарной фазы»

Это дистанционное занятие посвящено исследованию асимптотического поведения функций специального вида с помощью метода стационарной фазы.

🔥 Видео

Уравнение Лапласа. Задача Дирихле для уравнения Лапласа внутри и вне кругаСкачать

Уравнение Лапласа. Задача Дирихле для уравнения Лапласа внутри и вне круга

Радкевич Е.В. - Уравнения математической физики - 6.Задача Неймана для уравнения ЛапласаСкачать

Радкевич Е.В. - Уравнения математической физики - 6.Задача Неймана для уравнения Лапласа

Уравнения математической физики 15+16 Задача Дирихле для уравнения Лапласа - Пуассона в кругеСкачать

Уравнения математической физики 15+16 Задача Дирихле для уравнения Лапласа - Пуассона в круге

Задача Дирихле для шараСкачать

Задача Дирихле для шара

6.2 Решение задач для уравнения Лапласа в круге, вне круга и в кольцеСкачать

6.2 Решение задач для уравнения Лапласа в круге, вне круга и в кольце

Задача Дирихле для уравнения Лапласа в кольце и сектореСкачать

Задача Дирихле для уравнения Лапласа в кольце и секторе

Задача Неймана для уравнения Лапласа. Третья краевая задача для уравнения ЛапласаСкачать

Задача Неймана для уравнения Лапласа. Третья краевая задача для уравнения Лапласа

Метод Лапласа решения ДУСкачать

Метод Лапласа решения ДУ

6.1 Уравнение Лапласа в полярных координатах. Принцип решения и постановка задачСкачать

6.1 Уравнение Лапласа в полярных координатах. Принцип решения и постановка задач

Белошапка В. К. - Теория функции комплексного переменного I - Задача Дирихле для уравнения ЛапласаСкачать

Белошапка В. К. - Теория функции комплексного переменного I - Задача Дирихле для уравнения Лапласа

Решение уравнения Лапласа в шареСкачать

Решение уравнения Лапласа в шаре

Колыбасова В.В. - Методы математической физики. Семинары - 7.Внешняя краевая задача для ур.Лапласа 2Скачать

Колыбасова В.В. - Методы математической физики. Семинары - 7.Внешняя краевая задача для ур.Лапласа 2

6-2. Метод сетокСкачать

6-2. Метод сеток
Поделиться или сохранить к себе: