Решение задач с помощью рациональных уравнений 8 класс самостоятельная работа

Просмотр содержимого документа
«Самостоятельная работа . Решение дробных рациональных уравнений. Решение задач с помощью рациональных уравнений.»

Самостоятельная работа 8 класс

Решение дробных рациональных уравнений.

Решение задач с помощью рациональных уравнений

№ 1 Решите уравнение: .

№2 Теплоход, собственная скорость которого 18км/ч прошёл 50 км по течению реки и 8 км против течения, затратив на весь путь 3ч.Какова скорость течения реки?

№3 Два куска латуни имеют массу 30 кг. Первый кусок содержит 5 кг чистой меди, а второй кусок – 4 кг. Сколько процентов меди содержит первый кусок латуни, если второй содержит на 15% больше первого?

№ 1 Решите уравнение:

.

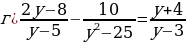
№2 Катер прошёл 40 км по течению реки и 6км против течения, затратив на весь путь 3ч. Какова собственная скорость катера, если скорость течения реки 2 км/ч?

№3 Одна бригада выполняла задание в течение 3,5 дня. Сменившая ее бригада закончила работу за 6 дней. Сколько дней выполняла бы задание каждая из бригад, если известно, что вторая бригада выполняла бы задание на 5 дней больше первой?

Видео:Решение задач с помощью рациональных уравнений. Алгебра, 8 классСкачать

Самостоятельная работа по теме: «Решение задач составлением дробного рационального уравнения»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 300 дидактических материалов для школьного и домашнего обучения

1. Лодка за одно и то же время может проплыть 36 км по течению реки или 20 км – против течения. Найдите скорость лодки по течению реки, если скорость течения составляет 2 км/ч.

2. Велосипедист проехал 24 км, а мотоциклист – 10 км. Скорость мотоциклиста на 18 км/ч больше скорости велосипедиста. Найдите скорости обоих, если известно, что велосипедист был в пути на 1 час больше, чем мотоциклист.

3. Грузчики планировали за некоторое время разгрузить 160 ящиков. Однако они справились с работой на три часа раньше срока, так как разгружали в час на 12 ящиков больше, чем планировали раньше. Сколько ящиков в час они разгружали на самом деле?

1. Моторная лодка за одно и то же время может проплыть 36 км против течения реки или 48 км – по течению. Найдите скорость лодки против течения реки, если скорость течения составляет 2 км/ч.

2. Пешеход прошел 15 км, а велосипедист проехал 27 км. Скорость велосипедиста на 12 км/ч больше скорости пешехода. Найдите скорости обоих, если известно, что велосипедист был в пути на 1 час меньше, чем пешеход.

3. Машинистка должна была напечатать за определенное время 200 страниц. Печатая в день на 5 страниц больше, чем планировала, она завершила работу на два дня раньше срока. Сколько страниц в день печатала на самом деле машинистка?

1. За одно и то же время велосипедист проехал 4 км, а мотоциклист – 10 км. Скорость мотоциклиста на 18 км/ч больше скорости велосипедиста. Найдите скорость мотоциклиста.

2. Скорость течения реки на 5 км/ч меньше собственной скорости моторной лодки. Найдите обе эти скорости, если 18 км по течению лодка проплывает на 1 час быстрее, чем 15 км против течения реки.

3. Два трактора израсходовали 168 литров горючего, причем первый израсходовал в час на 1 литр меньше, чем второй, а работал на два часа больше. Сколько горючего в час расходовал каждый трактор, если они израсходовали горючего поровну?

1. За одно и то же время пешеход прошел 5 км, а велосипедист проехал 15 км. Скорость велосипедиста на 12 км/ч больше скорости пешехода. С какой скоростью двигался велосипедист?

2. Собственная скорость моторной лодки на 12 км/ч больше скорости течения реки. Найдите обе эти скорости, если 36 км против течению лодка проплывает на 1 час медленнее, чем 32 км по течению реки.

3. Два ателье сшили 252 костюма. Первое ателье изготавливало в день на два костюма больше, чем второе, и затратило на всю работу на четыре дня меньше. Сколько костюмов в день изготавливало в день каждое ателье, если они сшили одинаковое количество костюмов?

1. Весельная лодка за одно и то же время может проплыть 18 км по морю или 10 км – против течения реки. Найдите скорость лодки по течению реки, если скорость течения составляет 2 км/ч.

2. Велосипедист проехал 30 км, а пешеход прошел 25 км. Скорость пешехода на 10 км/ч меньше скорости велосипедиста. Найдите скорости обоих, если известно, что пешеход был в пути на 3 часа дольше, чем велосипедист.

3. Грузчики планировали за некоторое время разгрузить 200 ящиков. Однако они справились с работой на час раньше срока, так как разгружали в час на 10 ящиков больше, чем планировали раньше. Сколько ящиков в час они разгружали на самом деле?

1. Моторная лодка за одно и то же время может проплыть 18 км по морю или 20 км – по течению реки. Найдите скорость лодки против течения реки, если скорость течения составляет 2 км/ч.

2. Спортсмен-бегун пробежал дистанцию в 16 км на час быстрее, чем велосипедист проехал 24 км. Найдите скорости обоих, если известно, что скорость бегуна на 16 км/ч меньше скорости велосипедиста.

3. Машинистка должна была напечатать за определенное время 160 страниц. Печатая в день на 4 страницы больше, чем планировала, она завершила работу на два дня раньше срока. Сколько страниц в день печатала на самом деле машинистка?

1. За одно и то же время пешеход прошел 6 км, а велосипедист проехал 18 км. Скорость пешехода на 10 км/ч меньше скорости велосипедиста. Найдите скорость велосипедиста.

2. Скорость течения реки на 2,5 км/ч меньше собственной скорости весельной лодки. Найдите обе эти скорости, если 27 км по морю лодка проплывает на 2 часа медленнее, чем 26 км по течению реки.

3. Два трактора израсходовали 144 литра горючего, причем первый израсходовал в час на 1 литр меньше, чем второй, а работал на час больше. Сколько горючего в час расходовал каждый трактор, если они израсходовали горючего поровну?

1. За одно и то же время бегун пробежал 1 км, а велосипедист проехал 3 км. Скорость бегуна на 16 км/ч меньше скорости велосипедиста. С какой скоростью двигался велосипедист?

2. Скорость моторной лодки на 16 км/ч больше скорости течения реки. Найдите обе эти скорости, если 27 км по морю лодка проплывает на час быстрее, чем 40 км против течения реки.

3. Два ателье сшили 180 костюмов. Первое ателье изготавливало в день на один костюм больше, чем второе, и затратило на всю работу на три дня меньше. Сколько костюмов в день изготавливало в день каждое ателье, если они сшили одинаковое количество костюмов?

СР по решению задач составлением дробного рационального уравнения

Видео:Алгебра 8 класс (Урок№32 - Решение задач с помощью рациональных уравнений.)Скачать

урок алгебры в 8 классе по теме «Решение задач с помощью дробных рациональных уравнений»
методическая разработка по алгебре (8 класс) по теме

урок — путешествие по городам Белгородской области (с презентацией)

Видео:Решение задач с помощью рациональных уравнений. Видеоурок 20. Алгебра 8 классСкачать

Скачать:

Видео:Алгебра 8. Урок 12 - Задачи на составление дробно-рациональных уравнений (Часть 1)Скачать

Предварительный просмотр:

Закрепить умения учащихся решать дробные рациональные уравнения, вырабатывать умения составлять уравнения по условию задач, создать условия для освоения учащимися методов и приемов исследовательской деятельности;

Способствовать развитию мышления, умений анализировать, сопоставлять, работать по алгоритму, устанавливать цепочки логических рассуждений;

Способствовать развитию коммуникативных способностей личности учеников;

Содействовать формированию навыков самостоятельной работы, навыков работы на компьютере;

Способствовать расширению кругозора учащихся, формированию чувства гордости за родной край.

Сегодня у нас необычный урок. У нас присутствуют гости, и на уроке мы немного попутешествуем.

Эпиграфом к уроку будут слова Д. Пойа: «Умения решать задачи – практическое искусство, подобное плаванию или катанию на лыжах, или игре на фортепиано: научиться этому можно, лишь подражая избранным образцам и постоянно тренируясь». Поэтому на уроке мы будем подражать избранным образцам и решать задачи с помощью уравнений.

1. Проверка домашнего задания.

Дома вы должны были, решив задания, из мозаики составить герб города, определить чей это герб и найти яркие факты про этот город или район Белгородской области.

( учащиеся должны были решить дома 4 задания, из ответов которых надо составить герб какого – либо города Белгородской области и подготовить небольшое сообщение о нем; один ученик отмечает этот город красным флажком с гербом, другой в это время делает небольшое сообщение)

2. При каких значениях x значение функции равно 5.

3. Катер, развивающий в стоячей воде скорость 20 км/ч, прошел 36 км против течения и 22 км по течению, затратив на весь путь 3 ч. Найти скорость течения реки.

Основан в 1647 году во время создания Белгородской черты как город – крепость Царев – Алексеев. Через 8 лет получил название, которое носит и поныне. Сейчас в городе есть техникум механизации сельского хозяйства(1935), завод железобетонных изделий, мебельная фабрика, кирпичный завод и другие объекты социального значения.

2. При каких значениях x значение функции равно -3.

3. Моторная лодка, скорость которой в стоячей воде 15 км/ч, прошла по течению реки 35 км, а против течения 25 км. На путь по течению реки она затратила столько же времени, сколько на путь против течения. Какова скорость течения реки?

В 17 веке на месте города была слобода, которая названа по имени первого владельца – князя Алексея Михайловича Черкасского. Здесь впервые было получено масло из семян подсолнечника. Сейчас здесь действуют эфирный, молочноконсервный комбинаты, завод химического машиностроения, сахарный и другие. Есть профессиональное училище, педагогический и сельскохозяйственный колледжи.

2. При каких значениях x значение функции равно 0

3. Турист проплыл на лодке против течения реки 6 км и по озеру 15 км, затратив на путь по озеру на 1 ч больше, чем на путь по реке. Зная, что скорость течения реки равна 2 км/ч, найти скорость лодки при движении по озеру.

Центр крупного района, расположен в живописной долине при впадении рек Кореня и Корчи в Нежеголь, приток Северского Донца. В 1928 году Шебекино стал районным центром, а в 1938 году – был преобразован в город. С июня 1942 года город был оккупирован фашистами. Освобожден 1943 года 9 февраля. В послевоенные годы в Шебекино развивается химическая промышленность. Здесь также работают машиностроительный, авторемонтный, кожевенный заводы, комбинаты стеновых и строительных материалов.

2. При каких значениях x значение функции равно 2.

3. Числитель несократимой дроби на 5 меньше ее знаменателя. Если числитель этой дроби кменьшить на 2, а знаменатель увеличить на 16, то дробь уменьшится на . Найти эту дробь.

Районный центр. Возник в 1637 году как крепость Белгородской черты. Короча славится садами. В городе – крупнейший завод по переработке фруктов. Работают также кирпичный завод, маслозавод, пищекомбинат. В Короче существует сельскохозяйственный техникум, преобразованный в 1965 году в совхоз – техникум, готовящий полеводов и плодоовощоведов.

Вы уже немало знаете об истории Белгородской области. Эта история очень древняя.

История Белгородского края берет свои истоки в глубокой древности. Первые следы пребывания древних людей на Белгородчине относятся к межледниковому периоду. Позднее эту территорию населяли скифские племена.

В 8 веке на территории Белгородчины разместились ирано – язычные аланские племена, пришедшие сюда из Предкавказья. В 9 веке в землях восточных славян возникло Древнерусское государство, столицей которого был Киев. Белгородчина – это пограничная лесостепная полоса. Жителям ее приходилось отражать набеги степняков – кочевников.

Одно из произведений древнерусской литературы повествует о походе Новгород – северского князя против половцев в 1185 году.

Определить название этого произведения нам помогут ответы следующего теста:

1. Восстановите формулу а 2 — в 2 =:

А. а 2 + 2ав + в 2 ; Б. а 2 — 2ав + в 2 ; В. (а – в)(а + в); Г. (а – в ) 2 .

2. Какое из квадратных уравнений является приведенным:

А. х 2 – 11х + 30 = 0; Б. 8х 2 — 7х = 0; В. х + 4 = 12; Г. х(4х + 9) = 0.

3. Выбрать формулу для вычисления дискриминанта квадратного уравнения:

А. в – 4ас; Б. в 2 + 4ас; В. в 2 – ас; Г. в 2 — 4ас;

4. Квадратное уравнение х 2 – 9х + 20 = 0 имеет корни:

А. 5 и 4; Б. -5 и 4; В. -5 и -4; Г. 5 и -4.

5. Какое из выражений не имеет смысла при х = 1 и х = 5?

6. Даны выражения: 1) 2) 3) Какие из них не имеют смысл при х = 1?

А. 1 и 2; Б. 1 и 3; В. только 1; Г. 1, 2 и 3.

События, описанные там непосредственно связаны с историей Белгородского края. Именно на нашей земле произошла встреча русских князей, после чего объединенное войско направилось к местам кочевий половцев, желая застигнуть их врасплох.

Эта встреча произошла на реке Оскол у Холок.

В «Слове» описана и природа Белгородской земли. Кроме того, по мнению белгородских историков, солнечное затмение, описанное в «Слове», дружины князя Игоря встретили на Белгородчине в районе Тавровой горы.

Свидетелем еще многих событий была белгородская земля. Но лишь во времена царствования Екатерины Первой (1725 – 1721) была образована Белгородская губерния. Это 1727 год. В те времена Белгородская губерния объединяла многие города, которые сейчас образуют другие области.

1. Сообщение темы и цели урока.

За прошедшие времена Белгородская губерния, область претерпевала многие территориальные изменения. На сегодняшнее время в состав Белгородской области входят 21 район и 10 городов. Сегодня на уроке мы совершим небольшое путешествие по городам и районам Белгородской области.

Темой урока будет: «Решение задач с помощью дробных рациональных уравнений».

Какие цели вы ставите перед собой на этом уроке?

(закрепить решение дробных рациональных уравнений, продолжать учиться составлять уравнения по условию задачи, получить новые сведения о Белгородской области)

Я согласна с вашими целями. Но мне бы хотелось посмотреть как вы умеете рассуждать, обосновывать свое решение, работать по алгоритму.

— какое уравнение называется дробным рациональным?

— что значит решить уравнение?

— по какому алгоритму решаются дробные рациональные уравнения?

— почему знаменатель не должен равняться 0?

У – На прошлой неделе вы получили карточки с числами. Ваша задача была найти в истории Белгородского края факты, связанные с этими числами и подготовить небольшую презентацию. Решая задачи и уравнения, мы проверим, как вы справились дома с этим заданием.

(ученики решают задачи: 1 – условие и составляет уравнение, 2 – решает это уравнение)

Перед вами карточки с задачами…

1. Для перевозки 44 тонн груза необходимо некоторое количество машин. Поскольку на каждую машину грузили на 2 тонны меньше, чем планировали, то дополнительно понадобилось 11 машин. Сколько машин планировалось использовать вначале?

Каким образом вы связали число «11» с Белгородской областью?

Группа учеников, у которых была карточка с числом «11», герб города укрепляют на карте Белгородской области в положенном месте; в это время показывая слайды рассказывают более подробно про этот город ( в рассказе должно упоминаться число «11»)

В 11 км восточнее поселка Ровеньки расположен природный парк «Ровеньский» площадью 1338 га. Организован в 1998 году. Характеризуется разнообраными биогеоценозами. Является охраняемой природной территорией Белгородской области. Здесь произрастают редкие виды растений, отмечены редкие виды насекомых, встречаются птицы, нуждающиеся в охране.

1. Во время прогулочного рейса теплоход прошел по течению реки 104 км, затем, развернувшись обратно, — 96 км. На весь путь теплоход затратил 4 часа. Найти собственную скорость теплохода, если скорость течения реки 2 км/ч.

Каким образом вы связали число «50» с Белгородской областью?

Группа учеников, у которых была карточка с числом «50», герб города укрепляют на карте Белгородской области в положенном месте; в это время показывая слайды рассказывают более подробно про этот город ( в рассказе должно упоминаться число «50»)

В 2004 году исполнилось 50 лет со дня строительства Лебединского рудника, расположенного в Губкинском районе, где было открыто Лебединское железорудное месторождение Курской магнитной аномалии. Свое название город Губкин получил по имени геолога, создателя нефтяной геологии, исследователя железорудных месторождений Курской магнитной аномалии.

Как вы считаете, мы хорошо работаем?

А для чего нужны глаза?

А для чего нужны уши?

А для чего нужна голова?

Откиньтесь на спинку стула. Посмотрите в потолок. Поднимите руки вверх, и пусть вся ваша усталость и лень уйдет…

1. Самостоятельная работа. Тест.

Работаем хорошо, но чтобы получить полное удовлетворение от своей проделанной работы, надо проверить, как мы научились ее делать. Для этого вам предлагаю решить небольшой тест.

( ученики работают индивидуально)

(выполняют задания, по истечении определенного времени обмениваются работами и проверяют ответы с ключом теста, который находится на экране)

Выставляют оценку друг другу в оценочный лист.

1. Какие из уравнений являются дробными рациональными?

А. 2х + 5 = 3(8 — х); Б. В. Г.

2. Даны выражения: 1) 2) 3) . Какие из них не имеют смысл при у = 2?

А. 1 и 2; Б. 1 и 3; В. только 1; Г. 1, 2 и 3.

3. Уравнение имеет корни:

А. 13; Б. -2 и 4; В. 13, -2 и 4; Г. нет решений.

4. Расстояние по реке между двумя деревнями равно 2 км. На путь туда и обратно моторная лодка затратила 22 мин. Чему равна собственная скорость лодки, если скорость течения реки равна 1 км/ч?

Пусть х км/ч – собственная скорость лодки. Какое из уравнений соответствует условию задачи?

А. 2(х + 1) + 2(х – 1) = 22; Б. В.

5. Уравнение имеет корни:

А. 2,5 и -5; Б. 2,5; В. -5 и 5; Г. 5, -5 и 2,5.

1. Какие из уравнений являются дробными рациональными?

А. 8х + 24 = 3(8 – х 2 ); Б. В. Г.

2. Даны выражения: 1) 2) 3) Какие из них не имеют смысл при х = 0?

А. только 1; Б. только 2; В. 2 и 3; Г. 1, 2 и 3.

3. Уравнение имеет корни:

А. 1 и 3; Б. -1, -3 и 11; В. 11; Г. нет решений.

4. Моторная лодка курсирует между двумя пристанями, расстояние между которыми по реке равно 4 км. На путь по течению у нее уходит на 3 мин меньше, чем на путь против течения. Чему равна скорость течения реки, если известно, что скорость лодки в стоячей воде равна 18 км/ч?

Пусть х км/ч – скорость течения реки. Какое из уравнений соответствует условию задачи?

🎬 Видео

решение задач с помощью рациональных уравнений 8 класс алгебра № 619Скачать

Дробно-рациональные уравнения. 8 класс.Скачать

Алгебра 8 класс (Урок№29 - Решение задач с помощью квадратных уравнений.)Скачать

8 класс, 28 урок, Рациональные уравнения как математические модели реальных ситуацийСкачать

Как решать дробно-рациональные уравнения? | МатематикаСкачать

Решение дробных рациональных уравнений. Алгебра, 8 классСкачать

Рациональные уравнения как математические модели реальных ситуаций - алгебра 8 классСкачать

Алгебра 8. Урок 14 - Задачи на составление дробно-рациональных уравнений (Часть 3)Скачать

Решение задач с помощью квадратных уравнений. Алгебра, 8 классСкачать

Алгебра 8. Урок 13 - Задачи на составление дробно-рациональных уравнений (Часть 2)Скачать

Решение задач с помощью рациональных уравненийСкачать

8 класс Решение задач с помощью рациональных уравнений.Скачать

Решение задач с помощью рациональных уравнений (урок 1))Скачать

Алгебра 8 класс 23 неделя Решение задач с помощью рациональных уравненийСкачать

Алгебра 8 класс. Тема: "Решение задач с помощью рациональных уравнений"Скачать

Как Решать Задачи по Химии // Задачи с Уравнением Химической Реакции // Подготовка к ЕГЭ по ХимииСкачать