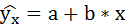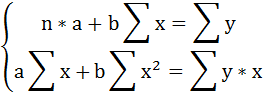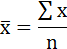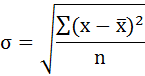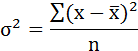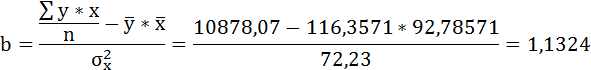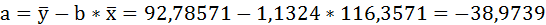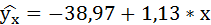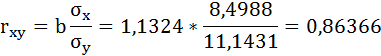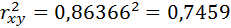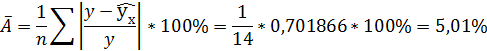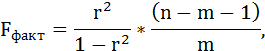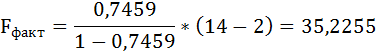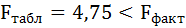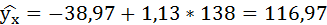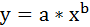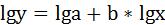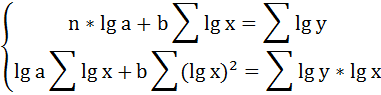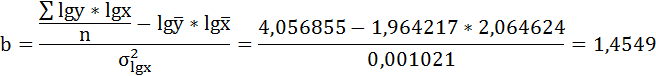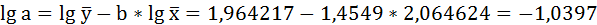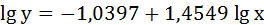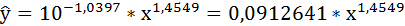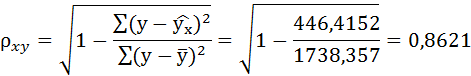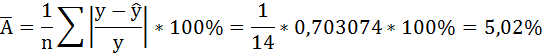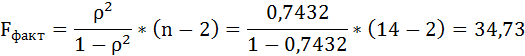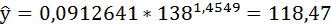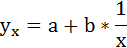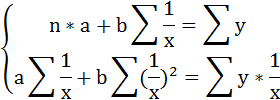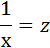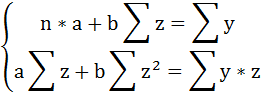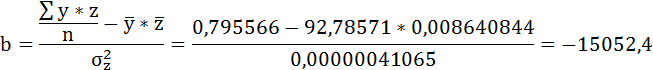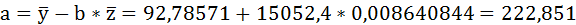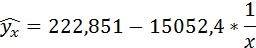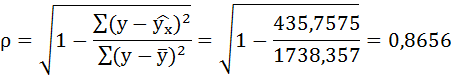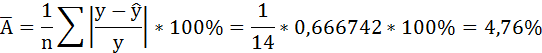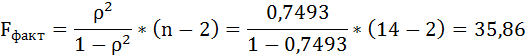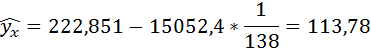Решение задач по уравнению линейной регрессии (5 видео)

Решения задач: линейная регрессия и коэффициент корреляции

Парная линейная регрессия — это зависимость между одной переменной и средним значением другой переменной. Чаще всего модель записывается как $y=ax+b+e$, где $x$ — факторная переменная, $y$ — результативная (зависимая), $e$ — случайная компонента (остаток, отклонение).

В учебных задачах по математической статистике обычно используется следующий алгоритм для нахождения уравнения регрессии.

Выбор модели (уравнения). Часто модель задана заранее (найти линейную регрессию) или для подбора используют графический метод: строят диаграмму рассеяния и анализируют ее форму.
Вычисление коэффициентов (параметров) уравнения регрессии. Часто для этого используют метод наименьших квадратов.
Проверка значимости коэффициента корреляции и параметров модели (также для них можно построить доверительные интервалы), оценка качества модели по критерию Фишера.
Анализ остатков, вычисление стандартной ошибки регрессии, прогноз по модели (опционально).

Ниже вы найдете решения для парной регрессии (по рядам данных или корреляционной таблице, с разными дополнительными заданиями) и пару задач на определение и исследование коэффициента корреляции.

Содержание

Примеры решений онлайн: линейная регрессия
Простая выборка
Корреляционная таблица
Коэффициент корреляции
Уравнение регрессии
Задача №1 Построение уравнения регрессии
Требуется:
Решение:
🎦 Видео

Видео:Решение задачи регрессии | Глубокое обучение на PythonСкачать

Примеры решений онлайн: линейная регрессия

Простая выборка

Пример 1. Имеются данные средней выработки на одного рабочего Y (тыс. руб.) и товарооборота X (тыс. руб.) в 20 магазинах за квартал. На основе указанных данных требуется:
1) определить зависимость (коэффициент корреляции) средней выработки на одного рабочего от товарооборота,
2) составить уравнение прямой регрессии этой зависимости.

Пример 2. С целью анализа взаимного влияния зарплаты и текучести рабочей силы на пяти однотипных фирмах с одинаковым числом работников проведены измерения уровня месячной зарплаты Х и числа уволившихся за год рабочих Y:
X 100 150 200 250 300
Y 60 35 20 20 15
Найти линейную регрессию Y на X, выборочный коэффициент корреляции.

Пример 3. Найти выборочные числовые характеристики и выборочное уравнение линейной регрессии $y_x=ax+b$. Построить прямую регрессии и изобразить на плоскости точки $(x,y)$ из таблицы. Вычислить остаточную дисперсию. Проверить адекватность линейной регрессионной модели по коэффициенту детерминации.

Пример 4. Вычислить коэффициенты уравнения регрессии. Определить выборочный коэффициент корреляции между плотностью древесины маньчжурского ясеня и его прочностью.
Решая задачу необходимо построить поле корреляции, по виду поля определить вид зависимости, написать общий вид уравнения регрессии Y на Х, определить коэффициенты уравнения регрессии и вычислить коэффициенты корреляции между двумя заданными величинами.

Пример 5. Компанию по прокату автомобилей интересует зависимость между пробегом автомобилей X и стоимостью ежемесячного технического обслуживания Y. Для выяснения характера этой связи было отобрано 15 автомобилей. Постройте график исходных данных и определите по нему характер зависимости. Рассчитайте выборочный коэффициент линейной корреляции Пирсона, проверьте его значимость при 0,05. Постройте уравнение регрессии и дайте интерпретацию полученных результатов.

Корреляционная таблица

Пример 6. Найти выборочное уравнение прямой регрессии Y на X по заданной корреляционной таблице

Пример 7. В таблице 2 приведены данные зависимости потребления Y (усл. ед.) от дохода X (усл. ед.) для некоторых домашних хозяйств.
1. В предположении, что между X и Y существует линейная зависимость, найдите точечные оценки коэффициентов линейной регрессии.
2. Найдите стандартное отклонение $s$ и коэффициент детерминации $R^2$.
3. В предположении нормальности случайной составляющей регрессионной модели проверьте гипотезу об отсутствии линейной зависимости между Y и X.
4. Каково ожидаемое потребление домашнего хозяйства с доходом $x_n=7$ усл. ед.? Найдите доверительный интервал для прогноза.
Дайте интерпретацию полученных результатов. Уровень значимости во всех случаях считать равным 0,05.

Пример 8. Распределение 100 новых видов тарифов на сотовую связь всех известных мобильных систем X (ден. ед.) и выручка от них Y (ден.ед.) приводится в таблице:
Необходимо:
1) Вычислить групповые средние и построить эмпирические линии регрессии;
2) Предполагая, что между переменными X и Y существует линейная корреляционная зависимость:
А) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию полученных уравнений;
Б) вычислить коэффициент корреляции, на уровне значимости 0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными X и Y;
В) используя соответствующее уравнение регрессии, оценить среднюю выручку от мобильных систем с 20 новыми видами тарифов.

Коэффициент корреляции

Пример 9. На основании 18 наблюдений установлено, что на 64% вес X кондитерских изделий зависит от их объема Y. Можно ли на уровне значимости 0,05 утверждать, что между X и Y существует зависимость?

Пример 10. Исследование 27 семей по среднедушевому доходу (Х) и сбережениям (Y) дало результаты: $overline=82$ у.е., $S_x=31$ у.е., $overline=39$ у.е., $S_y=29$ у.е., $overline =3709$ (у.е.)2. При $alpha=0,05$ проверить наличие линейной связи между Х и Y. Определить размер сбережений семей, имеющих среднедушевой доход $Х=130$ у.е.

Видео:Линейная регрессияСкачать

Уравнение регрессии

Вместе с этим калькулятором также используют следующие:
Уравнение множественной регрессии

В сервисе для нахождения параметров регрессии используется МНК. Система нормальных уравнений для линейной регрессии: 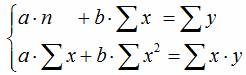. Также можно получить ответ, используя матричный метод. см. также Статистические функции в Excel

Уравнение парной регрессии относится к уравнению регрессии первого порядка. Если эконометрическая модель содержит только одну объясняющую переменную, то она имеет название парной регрессии. Уравнение регрессии второго порядка и уравнение регрессии третьего порядка относятся к нелинейным уравнениям регрессии.

Пример . Осуществите выбор зависимой (объясняемой) и объясняющей переменной для построения парной регрессионной модели. Дайте графическое изображение регрессионной зависимости. Определите теоретическое уравнение парной регрессии. Оцените адекватность построенной модели (интерпретируйте R-квадрат, показатели t-статистики, F-статистики).
Решение будем проводить на основе процесса эконометрического моделирования.
1-й этап (постановочный) – определение конечных целей моделирования, набора участвующих в модели факторов и показателей, их роли.
Спецификация модели — определение цели исследования и выбор экономических переменных модели.
Ситуационная (практическая) задача. По 10 предприятиям региона изучается зависимость выработки продукции на одного работника y (тыс. руб.) от удельного веса рабочих высокой квалификации в общей численности рабочих x (в %).
2-й этап (априорный) – предмодельный анализ экономической сущности изучаемого явления, формирование и формализация априорной информации и исходных допущений, в частности относящейся к природе и генезису исходных статистических данных и случайных остаточных составляющих в виде ряда гипотез.
Уже на этом этапе можно говорить о явной зависимости уровня квалификации рабочего и его выработкой, ведь чем опытней работник, тем выше его производительность. Но как эту зависимость оценить?
Парная регрессия представляет собой регрессию между двумя переменными – y и x , т. е. модель вида:

Видео:Эконометрика Линейная регрессия и корреляцияСкачать

Задача №1 Построение уравнения регрессии

Имеются следующие данные разных стран об индексе розничных цен на продукты питания (х) и об индексе промышленного производства (у).

Индекс розничных цен на продукты питания (х)	Индекс промышленного производства (у)
1	100	70
2	105	79
3	108	85
4	113	84
5	118	85
6	118	85
7	110	96
8	115	99
9	119	100
10	118	98
11	120	99
12	124	102
13	129	105
14	132	112

Требуется:

1. Для характеристики зависимости у от х рассчитать параметры следующих функций:

В) равносторонней гиперболы.

2. Для каждой модели рассчитать показатели: тесноты связи и среднюю ошибку аппроксимации.

3. Оценить статистическую значимость параметров регрессии и корреляции.

4. Выполнить прогноз значения индекса промышленного производства у при прогнозном значении индекса розничных цен на продукты питания х=138.

Решение:

1. Для расчёта параметров линейной регрессии

Решаем систему нормальных уравнений относительно a и b:

Построим таблицу расчётных данных, как показано в таблице 1.

Таблица 1 Расчетные данные для оценки линейной регрессии

№ п/п	х	у	ху	x 2	y 2
1	100	70	7000	10000	4900	74,26340	0,060906
2	105	79	8295	11025	6241	79,92527	0,011712
3	108	85	9180	11664	7225	83,32238	0,019737
4	113	84	9492	12769	7056	88,98425	0,059336
5	118	85	10030	13924	7225	94,64611	0,113484
6	118	85	10030	13924	7225	94,64611	0,113484
7	110	96	10560	12100	9216	85,58713	0,108467
8	115	99	11385	13225	9801	91,24900	0,078293
9	119	100	11900	14161	10000	95,77849	0,042215
10	118	98	11564	13924	9604	94,64611	0,034223
11	120	99	11880	14400	9801	96,91086	0,021102
12	124	102	12648	15376	10404	101,4404	0,005487
13	129	105	13545	16641	11025	107,1022	0,020021
14	132	112	14784	17424	12544	110,4993	0,013399
Итого:	1629	1299	152293	190557	122267	1299,001	0,701866
Среднее значение:	116,3571	92,78571	10878,07	13611,21	8733,357	х	х
	8,4988	11,1431	х	х	х	х	х
	72,23	124,17	х	х	х	х	х

Среднее значение определим по формуле:

Cреднее квадратическое отклонение рассчитаем по формуле:

и занесём полученный результат в таблицу 1.

Возведя в квадрат полученное значение получим дисперсию:

Параметры уравнения можно определить также и по формулам:

Таким образом, уравнение регрессии:

Следовательно, с увеличением индекса розничных цен на продукты питания на 1, индекс промышленного производства увеличивается в среднем на 1,13.

Рассчитаем линейный коэффициент парной корреляции:

Связь прямая, достаточно тесная.

Определим коэффициент детерминации:

Вариация результата на 74,59% объясняется вариацией фактора х.

Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчётные) значения .

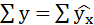
следовательно, параметры уравнения определены правильно.

Рассчитаем среднюю ошибку аппроксимации – среднее отклонение расчётных значений от фактических:

В среднем расчётные значения отклоняются от фактических на 5,01%.

Оценку качества уравнения регрессии проведём с помощью F-теста.

F-тест состоит в проверке гипотезы Н₀ о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического F_факт и критического (табличного) F_табл значений F-критерия Фишера.

F_факт определяется по формуле:

где n – число единиц совокупности;

m – число параметров при переменных х.

Таким образом, Н₀ – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.

Полученные оценки уравнения регрессии позволяют использовать его для прогноза.

Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:

2. Степенная регрессия имеет вид:

Для определения параметров производят логарифмирование степенной функции:

Для определения параметров логарифмической функции строят систему нормальных уравнений по способу наименьших квадратов:

Построим таблицу расчётных данных, как показано в таблице 2.

Таблица 2 Расчетные данные для оценки степенной регрессии

№п/п	х	у	lg x	lg y	lg x*lg y	(lg x) 2	(lg y) 2
1	100	70	2,000000	1,845098	3,690196	4,000000	3,404387
2	105	79	2,021189	1,897627	3,835464	4,085206	3,600989
3	108	85	2,033424	1,929419	3,923326	4,134812	3,722657
4	113	84	2,053078	1,924279	3,950696	4,215131	3,702851
5	118	85	2,071882	1,929419	3,997528	4,292695	3,722657
6	118	85	2,071882	1,929419	3,997528	4,292695	3,722657
7	110	96	2,041393	1,982271	4,046594	4,167284	3,929399
8	115	99	2,060698	1,995635	4,112401	4,246476	3,982560
9	119	100	2,075547	2,000000	4,151094	4,307895	4,000000
10	118	98	2,071882	1,991226	4,125585	4,292695	3,964981
11	120	99	2,079181	1,995635	4,149287	4,322995	3,982560
12	124	102	2,093422	2,008600	4,204847	4,382414	4,034475
13	129	105	2,110590	2,021189	4,265901	4,454589	4,085206
14	132	112	2,120574	2,049218	4,345518	4,496834	4,199295
Итого	1629	1299	28,90474	27,49904	56,79597	59,69172	54,05467
Среднее значение	116,3571	92,78571	2,064624	1,964217	4,056855	4,263694	3,861048
	8,4988	11,1431	0,031945	0,053853	х	х	х
	72,23	124,17	0,001021	0,0029	х	х	х

Продолжение таблицы 2 Расчетные данные для оценки степенной регрессии

№п/п	х	у
1	100	70	74,16448	17,34292	0,059493	519,1886
2	105	79	79,62057	0,385112	0,007855	190,0458
3	108	85	82,95180	4,195133	0,024096	60,61728
4	113	84	88,59768	21,13866	0,054734	77,1887
5	118	85	94,35840	87,57961	0,110099	60,61728
6	118	85	94,35840	87,57961	0,110099	60,61728
7	110	96	85,19619	116,7223	0,11254	10,33166
8	115	99	90,88834	65,79901	0,081936	38,6174
9	119	100	95,52408	20,03384	0,044759	52,04598
10	118	98	94,35840	13,26127	0,037159	27,18882
11	120	99	96,69423	5,316563	0,023291	38,6174
12	124	102	101,4191	0,337467	0,005695	84,90314
13	129	105	107,4232	5,872099	0,023078	149,1889
14	132	112	111,0772	0,85163	0,00824	369,1889
Итого	1629	1299	1296,632	446,4152	0,703074	1738,357
Среднее значение	116,3571	92,78571	х	х	х	х
	8,4988	11,1431	х	х	х	х
	72,23	124,17	х	х	х	х

Решая систему нормальных уравнений, определяем параметры логарифмической функции.

Получим линейное уравнение:

Выполнив его потенцирование, получим:

Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата 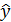. По ним рассчитаем показатели: тесноты связи – индекс корреляции и среднюю ошибку аппроксимации.

Связь достаточно тесная.

В среднем расчётные значения отклоняются от фактических на 5,02%.

Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:

3. Уравнение равносторонней гиперболы

Для определения параметров этого уравнения используется система нормальных уравнений:

Произведем замену переменных

и получим следующую систему нормальных уравнений:

Решая систему нормальных уравнений, определяем параметры гиперболы.

Составим таблицу расчётных данных, как показано в таблице 3.

Таблица 3 Расчетные данные для оценки гиперболической зависимости

№п/п	х	у	z	yz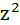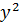
1	100	70	0,010000000	0,700000	0,0001000	4900
2	105	79	0,009523810	0,752381	0,0000907	6241
3	108	85	0,009259259	0,787037	0,0000857	7225
4	113	84	0,008849558	0,743363	0,0000783	7056
5	118	85	0,008474576	0,720339	0,0000718	7225
6	118	85	0,008474576	0,720339	0,0000718	7225
7	110	96	0,009090909	0,872727	0,0000826	9216
8	115	99	0,008695652	0,860870	0,0000756	9801
9	119	100	0,008403361	0,840336	0,0000706	10000
10	118	98	0,008474576	0,830508	0,0000718	9604
11	120	99	0,008333333	0,825000	0,0000694	9801
12	124	102	0,008064516	0,822581	0,0000650	10404
13	129	105	0,007751938	0,813953	0,0000601	11025
14	132	112	0,007575758	0,848485	0,0000574	12544
Итого:	1629	1299	0,120971823	11,13792	0,0010510	122267
Среднее значение:	116,3571	92,78571	0,008640844	0,795566	0,0000751	8733,357
	8,4988	11,1431	0,000640820	х	х	х
	72,23	124,17	0,000000411	х	х	х

Продолжение таблицы 3 Расчетные данные для оценки гиперболической зависимости

№п/п	х	у
1	100	70	72,3262	0,033231	5,411206	519,1886
2	105	79	79,49405	0,006254	0,244083	190,0458
3	108	85	83,47619	0,017927	2,322012	60,61728
4	113	84	89,64321	0,067181	31,84585	77,1887
5	118	85	95,28761	0,121031	105,8349	60,61728
6	118	85	95,28761	0,121031	105,8349	60,61728
7	110	96	86,01027	0,10406	99,79465	10,33166
8	115	99	91,95987	0,071112	49,56344	38,6174
9	119	100	96,35957	0,036404	13,25272	52,04598
10	118	98	95,28761	0,027677	7,357059	27,18882
11	120	99	97,41367	0,016024	2,516453	38,6174
12	124	102	101,46	0,005294	0,291565	84,90314
13	129	105	106,1651	0,011096	1,357478	149,1889
14	132	112	108,8171	0,028419	10,1311	369,1889
Итого:	1629	1299	1298,988	0,666742	435,7575	1738,357
Среднее значение:	116,3571	92,78571	х	х	х	х
	8,4988	11,1431	х	х	х	х
	72,23	124,17	х	х	х	х

Значения параметров регрессии a и b составили:

Связь достаточно тесная.

В среднем расчётные значения отклоняются от фактических на 4,76%.

По уравнению равносторонней гиперболы получена наибольшая оценка тесноты связи по сравнению с линейной и степенной регрессиями. Средняя ошибка аппроксимации остаётся на допустимом уровне.