Рассмотрены приемы решения обыкновенных дифференциальных уравнений (ОДУ) с помощью модуля scipy.integrate языка Python
- Краткое описание модуля scipy.integrate
- Решение одного ОДУ
- Решение системы ОДУ
- Руководство по SciPy: что это, и как ее использовать
- Что такое SciPy?
- NumPy vs SciPy
- Пакеты в SciPy
- Базовые функции
- Взаимодействие с NumPy
- Специальные функции
- Экспоненциальные и тригонометрические функции
- Интегральные функции
- Двойные интегральные функции
- Функции оптимизации
- Функция Розенброка
- Nelder-Mead
- Функции интерполяции
- Одномерная интерполяция
- Многомерная интерполяция
- Функции преобразования Фурье
- Функции обработки сигналов
- Линейная алгебра
- Нахождение обратной матрицы
- Нахождение определителей
- Разреженные собственные значения
- Разреженные структуры данных и алгоритмы
- Триангуляции Делоне
- Функции многомерной обработки изображений
- Как решить пару нелинейных уравнений с помощью Python?
- 7 ответов
Видео:Решение n го нелинейных алгебраических уравнений в PythonСкачать

Краткое описание модуля scipy.integrate
Модуль scipy.integrate имеет две функции ode() и odeint(), которые предназначены для решения систем обыкновенных дифференциальных уравнений (ОДУ) первого порядка с начальными условиями в одной точке (т.е. задача Коши).
Функция ode() более универсальная, а функция odeint() (ODE integrator) имеет более простой интерфейс и хорошо решает большинство задач.
Функция odeint() имеет три обязательных аргумента и много опций. Она имеет следующий формат
Видео:Решение 1 го нелинейного алгебраического уравнения в PythonСкачать

Решение одного ОДУ
Допустим надо решить диф. уравнение 1-го порядка
Получилось что-то такое:
Видео:Основы SciPy | Научные И Математические Вычисления На PythonСкачать

Решение системы ОДУ
Пусть теперь мы хотим решить (автономную) систему диф. уравнений 1-го порядка
Выходной массив w состоит из двух столбцов — y1(t) и y2(t).
Также без труда можно построить фазовые траектории:
Видео:34 Задача: Найти корни квадратного уравнения при помощи PythonСкачать

Руководство по SciPy: что это, и как ее использовать
Математика — это масса понятий, которые являются одновременно важными и сложными. Для работы с ними в Python есть библиотека SciPy. В этом материале вы познакомитесь с ее функциями на примерах.
Видео:FreeDy010 Решение Системы нелинейных уравнений scipy sympyСкачать

Что такое SciPy?
SciPy — это библиотека Python с открытым исходным кодом, предназначенная для решения научных и математических проблем. Она построена на базе NumPy и позволяет управлять данными, а также визуализировать их с помощью разных высокоуровневых команд. Если вы импортируете SciPy, то NumPy отдельно импортировать не нужно.
Видео:01.02. Модель SIR. Численное решение системы дифференциальных уравнений с помощью SciPyСкачать

NumPy vs SciPy
И NumPy, и SciPy являются библиотеками Python, которые используются для математического и числового анализов. NumPy содержит данные массивов и операции, такие как сортировка, индексация, а SciPy состоит из числового кода. И хотя в NumPy есть функции для работы с линейной алгеброй, преобразованиями Фурье и т. д., в SciPy они представлены в полном виде вместе с массой других. А для полноценного научного анализа в Python нужно устанавливать и NumPy, и SciPy, поскольку последняя построена на базе NumPy.
Видео:#5. Математические функции и работа с модулем math | Python для начинающихСкачать

Пакеты в SciPy
В SciPy есть набор пакетов для разных научных вычислений:
| Название | Описание |
|---|---|
| cluster | Алгоритмы кластерного анализа |
| constants | Физические и математические константы |
| fftpack | Быстрое преобразование Фурье |
| integrate | Решения интегральных и обычных дифференциальных уравнений |
| interpolate | Интерполяция и сглаживание сплайнов |
| io | Ввод и вывод |
| linalg | Линейная алгебра |
| ndimage | N-размерная обработка изображений |
| odr | Метод ортогональных расстояний |
| optimize | Оптимизация и численное решение уравнений |
| signal | Обработка сигналов |
| sparse | Разреженные матрицы |
| spatial | Разреженные структуры данных и алгоритмы |
| special | Специальные функции |
| stats | Статистические распределения и функции |
Подробное описание можно найти в официальной документации.
Эти пакеты нужно импортировать для использования библиотеки. Например:
Прежде чем рассматривать каждую функцию в подробностях, разберемся с теми из них, которые являются одинаковыми в NumPy и SciPy.
Видео:Использование библиотеки SymPy для работы с системами уравнений в PythonСкачать

Базовые функции
Взаимодействие с NumPy
SciPy построена на базе NumPy, поэтому можно использовать функции последней для работы с массивами. Чтобы узнать о них подробнее, используйте функции help() , info() или source() .
help():
Функция help() подойдет для получения информации о любой функции. Ее можно использовать двумя способами:
Вот пример для обоих:
При исполнении этого кода, первая help() вернет информацию о подмодуле cluster . А вторая — попросит пользователя ввести название модуля, ключевого слова и др., о чем требуется предоставить дополнительную информацию. Для выхода достаточно ввести quit и нажать Enter.
info():
Эта функция возвращает информацию о конкретных функциях, модулях и так далее.
source():
Исходный код можно получить только для тех объектов, которые были написаны на Python. Функция не вернет ничего важного, если методы или объекты были написаны, например, на C. Синтаксис простой:
Видео:Решения системы линейных уравнений на Python (Sympy).Скачать

Специальные функции
SciPy предоставляет набор специальных функций, используемых в математической физике: эллиптические настраиваемые функции, гамма, бета и так далее. Для их поиска нужно использовать функцию help() .
Экспоненциальные и тригонометрические функции
Набор специальных функций SciPy включает такие, с помощью которых можно искать экспоненты и решать тригонометрические задачи.
Есть и масса других функций из SciPy, с которым стоит познакомиться.
Видео:Как решить линейное и квадратное уравнение в Python?Скачать

Интегральные функции
Есть и функции для решения интегралов. В их числе как обычные дифференциальные интеграторы, так и методы трапеций.
В SciPy представлена функция quad , которая занимается вычислением интеграла функции с одной переменной. Границы могут быть ±∞ (± inf ) для обозначения бесконечных пределов. Синтаксис этой функции следующий:
А здесь она внедрена в пределах a и b (могут быть бесконечностями).
В этом примере функция a находится в пределах 0 и 1. После выполнения вывод будет такой:
Двойные интегральные функции
SciPy включает также и dblquad , которая используется для вычисления двойных интегралов. Двойной интеграл, как известно, состоит из двух реальных переменных. Функция dblquad() принимает функцию, которую нужно интегрировать, в качестве параметра, а также 4 переменных: две границы и функции dy и dx .
В SciPy есть другие функции для вычисления тройных интегралов, n интегралов, интегралов Ромберга и других. О них можно узнать подробнее с помощью help .
Функции оптимизации
В scipy.optimize есть часто используемые алгоритмы оптимизации:
Функция Розенброка
Функция Розенброка ( rosen ) — это тестовая проблема для оптимизационных алгоритмов, основанных на градиентах. В SciPy она определена следующим образом:
Nelder-Mead
Это числовой метод, который часто используется для поиска минимума/максимума функции в многомерном пространстве. В следующем примере метод использован вместе с алгоритмом Нелдера — Мида.
Видео:Решение простых задач на python | Решить квадратное уравнениеСкачать

Функции интерполяции
В сфере числового анализа интерполяция — это построение новых точек данных на основе известных. Библиотека SciPy включает подпакет scipy.interpolate, состоящий из сплайновых функций и классов, одно- и многомерных интерполяционных классов и так далее.
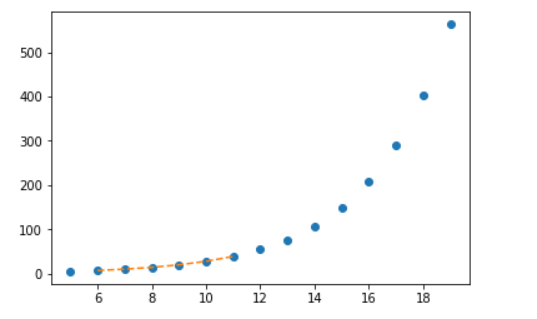
Одномерная интерполяция
Одномерная интерполяция — это область построения кривой, которая бы полностью соответствовала набору двумерных точек данных. В SciPy есть функция interp1d , которая используется для создания одномерной интерполяции.
Вывод:
Многомерная интерполяция
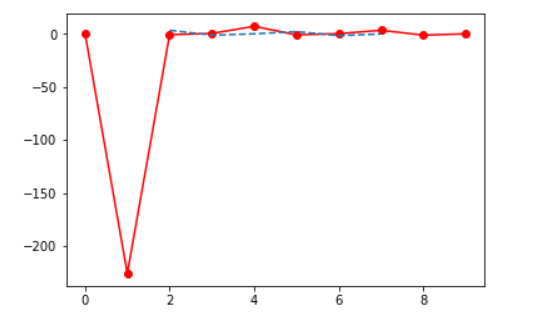
Многомерная интерполяция (пространственная интерполяция) — это тип интерполяции функций, который состоит из более чем одной переменной. Следующий пример демонстрирует работу функции interp2a .
При интерполяции на двумерную сетку функция использует массивы x, y и z для приближения функции f: «z = f(x, y)» и возвращает функцию, у которой вызываемый метод использует сплайновую интерполяцию для поиска значения новых точек.
Вывод:
Видео:Графический калькулятор квадратных уравнений на python (питон) tkinterСкачать

Функции преобразования Фурье
Анализ Фурье — это метод, который помогает представлять функцию в виде суммы периодических компонентов и восстанавливать сигнал из них. Функции fft используются для получения дискретной трансформации Фурье реальной или комплексной последовательности.
Похожим образом можно найти обратное значение с помощью функции ifft .
Видео:Python - численное решение дифференциального уравнения 1го порядка и вывод графикаСкачать

Функции обработки сигналов
Обработка сигналов — это область анализа, модификации и синтеза сигналов: звуков, изображений и т. д. SciPy предоставляет некоторые функции, с помощью которых можно проектировать, фильтровать и интерполировать одномерные и двумерные данные.
Фильтрация:
Фильтруя сигнал, можно удалить нежелаемые составляющие. Для выполнения упорядоченной фильтрации используется функция order_filter . Она выполняет операцию на массиве. Синтаксис следующий:
a — N-мерный массив с входящими данными
domain — массив масок с тем же количеством размерностей, что и у массива a
rank — неотрицательное число, которое выбирает элементы из отсортированного списка (0, 1…)
Сигналы
Подпакет scipy.signal также состоит из функций, с помощью которых можно генерировать сигналы. Одна из таких — chirp . Она является генератором частотно-модулированного сигнала, а ее синтаксис следующий:
Вывод:
Видео:Solve Differential Equations in Python by Using odeint() SciPy FunctionСкачать

Линейная алгебра
Линейная алгебра работает с линейными уравнениями и их представлениями с помощью векторных пространств и матриц. SciPy построена на базе библиотек ATLAS LAPACK и BLAS и является очень быстрой в сфере решения проблем, связанных с линейной алгеброй. В дополнение к функциям из numpy.linalg scipy.linalg также предоставляет набор продвинутых функций. Если numpy.linalg не используется вместе с ATLAS LAPACK и BLAS, то scipy.linalg работает намного быстрее.
Нахождение обратной матрицы
С математической точки зрения обратная матрица A — это матрица B, где AB = I, а I — это единичная матрица, состоящая из единиц по диагонали. Это можно обозначить как B=A-1. В SciPy такого можно добиться с помощью метода linalg.inv .
Нахождение определителей
Значение, полученное арифметическим путем из коэффициентов матрицы является определителем квадратной матрицы. В SciPy это делается с помощью функции det с таким синтаксисом:
det(a, overwrite_a=False, check_finite=True)
a — (M, M) — это квадратная матрица
overwrite_a(bool, optional) — разрешает перезаписывать данные
check_finite(bool, optional) — для проверки состоит ли матрица только из конечных чисел
Видео:Решение ОДУ в PythonСкачать

Разреженные собственные значения
Разреженные собственные значения — это набор скаляров, связанных с линейными уравнениями. ARPACK предоставляет способ быстрого нахождения этих значений (собственных векторов). Вся функциональность скрыта в двух интерфейсах: scipy.sparse.linalg.eigs и scipy.sparse.linalg.eigsh .
Интерфейс eigs позволяет находить собственные значения реальных или комплексных несимметричных квадратных матриц, а eigsh содержит интерфейсы реальных симметричных или комплексных Эрмитовых матриц.
Функция eigh решает обобщенную проблему собственного значения для комплексной Эрмитовой или реально симметричной матрицы
Видео:Решение системы ОДУ в PythonСкачать

Разреженные структуры данных и алгоритмы
Разреженные данные состоят из объектов, которые в свою очередь состоят из линий, точек, поверхностей и так далее. Пакет scipy.spatial из SciPy может вычислять диаграммы Вороного, триангуляцию и другое с помощью библиотеки Qhull. Он также включает реализации KDTree для точечных запросов ближайших соседей.
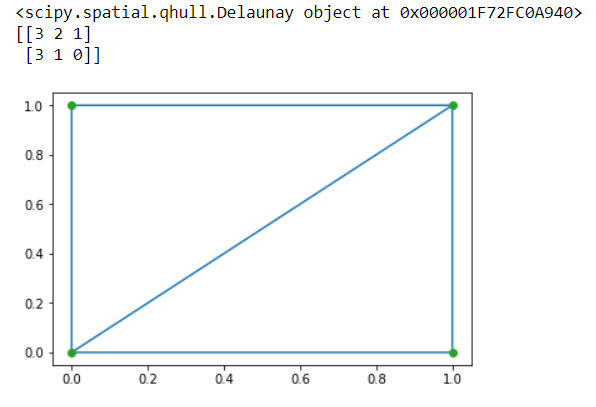
Триангуляции Делоне
С математической точки зрения триангуляции Делоне для набора дискретных точек на плоской поверхности — это триангуляция, где ни одна точка из представленных не расположена внутри описанной окружности любого треугольника.
Вывод:
Видео:Урок 3. Изучаем Python. Запись математических выражений. Библиотека MathСкачать

Функции многомерной обработки изображений
Обработка изображений — это выполнение операций над изображением по получению информации или улучшенной копии этого изображения из оригинала. Пакет scipy.ndimage состоит из нескольких функций обработки и анализа изображений, которые нужны для работы с массивами с произвольной размерностью.
Свертка и корреляция
В SciPy есть несколько функций для свертки и корреляции изображений.
- Функция correlate1d используется для вычисления одномерной корреляции по заданной оси
- Функция correlate предлагает многомерную корреляцию для любого массива с определенным ядром
- Функция convolve1d используется для вычисления одномерной свертки вдоль заданной оси
- Функция convolve предлагает многомерную свертку для любого массива с определенным ядром
Файловый ввод/вывод
Пакет scipy.io предоставляет несколько функций, которые помогают управлять файлами в разных форматах, включая MATLAB, файлы IDL, Matrix Market и другие.
Для использования его нужно сначала импортировать:
Видео:[ОТКРЫТЫЙ КУРС] Python для финансистов - Scipy.Optimize. Численные методы оптимизации - Урок 6Скачать
![[ОТКРЫТЫЙ КУРС] Python для финансистов - Scipy.Optimize. Численные методы оптимизации - Урок 6](https://i.ytimg.com/vi/QPv8t66PyYU/0.jpg)
Как решить пару нелинейных уравнений с помощью Python?
каков (лучший) способ решить a пара нелинейных уравнений с использованием Python. (Numpy, Scipy или Sympy)
фрагмент кода, который решает вышеуказанную пару, будет отличным
Видео:Python для самых маленьких. Линейные уравнения. Решение задачСкачать

7 ответов
для численного решения, вы можете использовать fsolve:
Если вы предпочитаете sympy вы можете использовать nsolve.
первый аргумент-это список уравнений, второй-список переменных, а третий-начальная догадка.
попробуйте этот, я уверяю вас, что он будет работать отлично.
к вашему сведению. как упоминалось выше, вы также можете использовать «приближение Бройдена», заменив «fsolve» на «broyden1». Это работает. Я сделал это.
Я точно не знаю, как работает приближение Бройдена, но это заняло 0.02 s.
и я рекомендую вам не использовать функции Sympy
вы можете использовать пакет openopt и его метод NLP. Он имеет много алгоритмов динамического программирования для решения нелинейных алгебраических уравнений, состоящих из:
goldenSection, scipy_fminbound, scipy_bfgs, scipy_cg, scipy_ncg, amsg2p, scipy_lbfgsb, scipy_tnc, bobyqa, ralg, ipopt, scipy_slsqp, scipy_cobyla, lincher, algencan, который вы можете выбрать.
Некоторые из последних алгоритмов могут решить ограниченную задачу нелинейного программирования. Итак, вы можете представить свою систему уравнения для openopt.НЛП () С такой функцией:
lambda x: x[0] + x[1]**2 — 4, np.exp(x[0]) + x[0]*x[1]
Я получил метод Бройдена для работы для связанных нелинейных уравнений (обычно с полиномами и экспонентами) в IDL, но я не пробовал его в Python:
scipy.оптимизировать.broyden1
найти корни функции, используя первый аппроксимация Якобиана Бройдена по.
этот метод также известен как»хороший метод Бройдена».