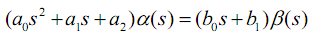Физические законы в дифференциальных уравнениях (8 видео)

Физические законы в дифференциальных уравнениях

Дифференциальные уравнения в физике. Общие понятия

Многие задачи физики приводят к необходимости решения дифференциальных уравнений. Это обусловлено тем, что практически все физические законы, описывающие физические процессы являются дифференциальными уравнениями, относительно некоторых функций, характеризующих эти процессы. Данные физические законы представляют собой теоретическое обобщение многочисленных экспериментов и описывают эволюцию искомых величин в общем случае, как в пространстве, так и во времени. В частности, второй закон Ньютона, является не чем иным, как дифференциальным уравнением второго порядка:

(1)

и основной задачей динамики является определение закона движения материальной точки по заданным силам , действующим на эту точку, что в математическом отношении означает решение уравнения (1) и определение координат материальной точки как функций времени: .

С учётом сказанного, учитывая важность дифференциальных уравнений для изучения как общей, так и теоретической физики, рассмотрим основные понятия и приёмы интегрирования некоторых видов дифференциальных уравнений, наиболее часто встречающихся в физических приложениях, сопровождая изложение материала конкретными примерами.

Дифференциальным уравнением называется уравнение, которое кроме независимых переменных и неизвестных функций этих переменных, содержит ещё и производные неизвестных функций.

Если функции, входящие в дифференциальное уравнение зависят от одной независимой переменной, то уравнение называется обыкновенным дифференциальным уравнением.

Если же в уравнение входят частные производные неизвестных функций по нескольким независимым переменным, то уравнение называют дифференциальным уравнением с частными производными.

Наивысший порядок производных неизвестной функции, входящих в дифференциальное уравнение называется порядком дифференциального уравнения.

Мы будем рассматривать лишь обыкновенные дифференциальные уравнения. При этом, поскольку при описании динамики физических процессов, все величины, характеризующие эти процессы, зависят от времени, то при изложении материала, независимое переменное обозначим через t .

Содержание

Физические законы в дифференциальных уравнениях
Классическая механика: о диффурах «на пальцах»
Введение
Физический смысл
Динамика в картинках
На правах PS
🎥 Видео

Видео:Откуда появляются дифференциальные уравнения и как их решатьСкачать

Физические законы в дифференциальных уравнениях

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО БЮДЖЕТНОГО

ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ ВЫСШЕГО

«БАШКИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

Кафедра математического анализа

Физические задачи, приводящие к дифференциальным уравнениям

Выполнила: студентка 2 курса

Научный руководитель: к.ф.-м.н.,

доцент Сабитова Ю.К.

1. Электрические цепи

2. Распространение тепла

3. Построение ортогонального семейства кривых

4. Уравнение химической кинетики

5. Реактивное движение

6. Из пушки на Луну

7. Форма равновесия жидкости во вращающемся сосуде

8. Фокусирующее зеркало

10. Уравнение струны

В настоящее время складываются основы новой методологии научных исследований — математического моделирования.

Сущность этого исследования состоит в замене исходного объекта математической моделью, и решения поставленной задачи с помощью современных вычислительных средств.

Моделирование — это метод исследования каких-либо процессов, явлений, который предполагает создание искусственных или естественных систем, имитирующих существенные свойства оригинала.

Математическое моделирование в настоящий момент является одной из главных составляющих научно-технического прогресса. Без применения этой методологии не реализуется ни один крупномасштабный технологический, социальный, экологический проект.

В частности, в качестве математических моделей реальных процессов могут быть использованы дифференциальные уравнения. Довольно часто при изучении многих процессов, протекающих в природе, бывает довольно сложно установить зависимость между функциями, характеризующими те или иные величины. Но зато в некоторых случаях возможно установить связь между теми же функциями и их производными. Это приводит к уравнениям, содержащим неизвестные функции под знаком производной, то есть к дифференциальным уравнениям (с их помощью процесс может быть описан проще и полнее). Отрасль математического анализа, изучающая дифференциальные уравнения, является одной из самых важных по своим положениям.

Эффективность использования дифференциальных уравнений в качестве математических моделей обеспечивается историческими истоками самих дифференциальных уравнений и современными взглядами на многие законы природы с позиции дифференциальных уравнений, приложениями дифференциальных уравнений в современной науке и технике, развитием методов интегрирования и общей теории дифференциальных уравнений, высоким уровнем вычислительной математики и техники.

В различных областях человеческой деятельности возникает большое число задач, решение которых сводиться к дифференциальным уравнениям. Например, происходит какой-либо физический, химический или биологический процесс. Зачастую закономерности данного явления можно описать при помощи дифференциальных уравнений.

Тема курсовой работы обуславливает преимущественное рассмотрение физических процессов. Например, закон изменения температуры, давления или массы с течением времени. Если имеется достаточно полная информация о течении данного процесса, то строят его математическую модель. Во многих случаях такой моделью является дифференциальное уравнение, находят все его решения и выделяют то решение, для которого выполняются дополнительные (начальные или граничные) условия.

Надо отметить, что разные по содержанию задачи приводятся к одинаковым или исходным дифференциальным уравнениям.

Цель курсовой работы: изучение физических задач, приводящих к дифференциальным уравнениям.

Рассмотреть физические задачи, приводящие к дифференциальным уравнениям;

Анализ практичности решения физических задач, приводящих к дифференциальным уравнениям.

1. Электрические цепи

Электрические цепи описываются двумя величинами: током I и падением напряжения ?U . При этом для различных элементов цепи соотношения между током и напряжением различны:

конденсатор, — его емкость,

Сумма падений напряжения на всех участках цепи равна ЭДС этой цепи (тому напряжению, которое подается в цепь извне). Получаем уравнение:

Величины L,R,C нам, как правило, известны — это характеристики эле-
ментов цепи, E(t) — заданная функция. Остается две величины: I и Q.
Но, поэтому уравнения электрического тока в цепи обычно записывают относительно неизвестной функции — заряда на обкладках конденсатора:

Все знают, что более холодное тело (или часть тела) нагревается от более горячего. Каков закон этого процесса? Чтобы выяснить это, необходимо понять, что и как описывает тепловые процессы.

Во-первых, это температура. Температура может измеряться по разным шкалам, но нас интересует не абсолютная величина температуры, а ее изменение (со временем или при переходе от одной точки тела к другой). Температуру обычно обозначают буквой T.

Во-вторых, изменение температуры связано с изменением энергии тела, причем зависимость эта линейная. Для того чтобы различать температуру и энергию, для последней введено специальное название количество теплоты (обозначается обычно Q). Таким образом, Коэффициент С называют теплоемкостью. Он зависит как от материала, из которого сделано тело, так и от его размеров (чтобы нагреть большое тело надо больше тепла). Простые соображения показывают, что для однородного материала С = M/с, где М — масса, с — удельная (на единицу массы) теплоемкость.

Если мы мысленно разобьем тело на две или несколько частей, то количество теплоты, необходимое для нагревания всего тела на 1 градус, равно сумме количеств теплоты, необходимых для нагревания его частей. Количество теплоты оказывается аддитивной функцией множества (при складывании частей в одной целое соответствующие количества теплоты складываются). Однородность означает, что одинаковые (по форме) куски нагреваются одинаково, в какой бы части тела они не находились. Другими словами, эта функция множества инвариантна относительно сдвигов и поворотов. И, наконец, множества с нулевой массой не могут поглощать тепла — это свойство типа непрерывности (если говорить точно, оно называется абсолютной непрерывностью функции множества относительно другой функции — в данном случае массы). Всякая абсолютно непрерывная функция множества, инвариантная относительно сдвигов, пропорциональна в одномерном случае — длине, в двумерном — площади, а в трехмерном — объему множества (или, что то же самое, его массе).

В случае неоднородного тела зависимость Q от Т более сложная и выражается через интеграл

где — количество теплоты, поглощенное объемом V, р(х), с(х) и Т(х)- распределение, соответственно, плотности, удельной теплоемкости и изменения температуры внутри объема.

Далее опишем процесс теплопередачи.

Для этого представим себе обыкновенный кирпич, одна стенка которою имеет температуру Т1, а противоположная — температуру Т2. Если поддерживать температуры стенок постоянными, то, в конце концов, внутри кирпича температура распределится по убыванию от одной стенки к другой.

Практический опыт, с одной стороны, и соображения подобия, с другой, показывают, что это убывание линейно:

В формуле (2) L — расстояние между стенками кирпича, l — «текущая» координата (l = 0 соответствует первой стенке с температурой Т1 , l=L — второй с температурой Т2). Что при этом происходите количеством теплоты? Тепло передается от более горячей стенки к менее горячей, однако для каждого внутреннего «среза» кирпича количество теплоты, приходящей с одной стороны, и количество теплоты, уходящей в другую, совпадают, поскольку процесс установившийся. Это количество теплоты называют тепловым потоком через соответствующий срез и обозначают той же буквой Q, что и количество теплоты.

Рис.1. Тепло передается от более горячей стенке к менее горячей

Тепловой поток зависит от:

разницы температур на стенках кирпича (чем она больше, тем интенсивней идет теплообмен);

расстояния между стенками (чем они ближе друг к другу,
тем интенсивней теплообмен); на самом деле он не зависит ни от того, ни от другого. Чтобы убедиться в этом, совершим следующий мысленный эксперимент. Пусть нас интересует, например, срез, находящийся в левой части кирпича. Распилим кирпич пополам (напомним, в середине кирпич имеет температуру ) и выбросим правую половину, а на сделанном распиле просто будем поддерживать ту же температуру. Что изменится

Рис.2. Распилим кирпич пополам

с точки зрения нашего среза? Да ничего. Тепловой поток, проходящий через него, будет в точности таким же, как и в нераспиленном кирпиче. Дальше мы можем повторить процедуру, отпилив еще один кусок кирпича, и так продолжать дальше и дальше. В итоге получаем, что на самом деле тепловой поток зависит не от разности температур, и не от расстояния между стенками, а от той самой константы, которая фигурировала у нас в формуле (2), и, которая как раз и выражается, в случае однородного тела, через отношение разности температур и расстояния, а в случае неоднородного тела — через производную по направлению нормали к нашему срезу;

г)тепловой поток пропорционален площади среза. Если
мы возьмем кирпич вдвое шире (или просто сложим два кирпича), то
тепловой поток удвоится. Здесь опять срабатывает теория аддитивных
функций множества; д)тепловой поток пропорционален времени, в течение которого он про-
ходил: за 2 часа через тот же срез пройдет вдвое больше тепла, чем за
1 час. Получаем формулу: (3)

Рис.3. Возьмем кирпич вдвое шире

или, если сделать бесконечно малым,

Знак плюс или минус выбирается в зависимости направления нормали к срезу (она ведь может быть направлена как в ту, так и в другую сторону), k — коэффициент, зависящий только от материала, называемый коэффициентом теплопроводности.

Мы не зря так долго говорили о таком банальном объекте, как кирпич. Для неоднородной среды все те же рассуждения повторяются в точности, только с той разницей, что «кирпич» является бесконечно малым (и при этом неоднородностью внутри него можно пренебречь). Формула (4) описывает тепловой поток, протекающий через любую бесконечно малую площадку S любой поверхности в любом теле. Если же мы выделили в произвольном теле некоторый объем V и хотим вычислить тепловой поток, выходящий из этого тела, нам надо проинтегрировать формулу (4) по поверхности S,

Обыкновенные дифференциальные уравнения возникают из формулы (5) при наличии в процессе распространения тепла какой-то симметрии. Тогда за счет подходящего выбора системы поверхностей «расслаивающей» тело на пласты с одинаковой температурой, удается описать процесс обыкновенным дифференциальным уравнением.

Возьмем тот же кирпич: в нем зависит только от одной координаты (например, ). Тогда, выбирая в качестве поверхностей

плоскости , получаем, интеграл просто равен этой производной, умноженной на площадь поперечного сечения кирпича с коэффициентом k, и для установившегося процесса теплоотдачи, получаем уравнение

Если наш процесс имеет сферическую симметрию (т.е. температура зависит только от расстояния r от некоторой точки, то, выбирая в качестве

системы поверхностей сферы, получим , интеграл равен

этой производной, умноженной на площадь сферы с коэффициентом k, и мы получаем другое уравнение:

Аналогично в случае цилиндрической симметрии (температура одинакова на цилиндрических поверхностях) получаем еще одно уравнение:

(здесь r — расстояние до общей оси цилиндров, l — длина образующей цилиндров).

Наконец, мы можем из того же уравнения (5) получить и общее уравнение теплопередачи, пригодное для любого тела. Подставив в него связь между изменением количества теплоты и изменением температуры (1) и воспользуемся известной формулой преобразования интеграла по поверхности от нормальной производной функции в интеграл по объему от оператора Лапласа, примененного к этой функции :

Отсюда, пользуясь тем, что справа и слева стоит интеграл по одному и тому же объему, и тем, что это равенство выполнено для любого объема, получаем равенство подынтегральных функций

известное как уравнение теплопроводности.

3. Построение ортогонального семейства кривых

В некоторых задачах физики и механики бывает необходимо по данному семейству кривых построить семейство ортогональных к ним кривых (ортогональность двух кривых в точке их пересечения понимается, естественно, как ортогональность касательных к ним).

Рис.4. Ортогональные семейства кривых

Пусть нам задано семейство, описываемое уравнением с параметром

Для построения ортогонального семейства нам необходимо вычислить касательные к кривым исходного семейства. Пусть у(х) одна из кривых. Тогда Дифференцируя, получаем

Таким образом, угловой коэффициент касательной к кривой семейства, проходящей через точку (х, y), может быть вычислен без знания самой кривой. Но тогда угловой коэффициент касательной к кривой из ортогонального семейства мы тоже можем вычислить (условие ортогональности прямых):

Это и есть уравнение ортогонального семейства. Например, для семейства окружностей получаем уравнение ортогонального семейства кривых: . Решения этого уравнения — семейство прямых у = Сх, действительно ортогональных к окружностям.

. Уравнение химической кинетики

Скорость реакции пропорциональна количеству каждого из реагирующих веществ. Опишем математически химическую реакцию. Пусть имеются два вещества А и Б, и из них в результате реакции образуется вещество X. Количества веществ А, В и X в момент времени t обозначим, соответственно, через и.Тогда

где k — коэффициент пропорциональности. Оказывается, величины а(t) и b(t) можно выразить через x(t): ведь в любой химической реакции количества веществ А и В, необходимых для образования единицы вещества X, строго фиксированы и определяются формулой реакции! Пусть на единицу вещества Х необходимо вещества A и вещества В. Тогда , (здесь , — начальные количества реагирующих веществ), и мы получаем уравнение

Аналогично в случае трех реагирующих веществ и одною на выходе получается уравнение

Уравнения (10) и (11) и называют обычно уравнениями химической кинетики.

Одним из фундаментальных законов физики является закон сохранения импульса: при распаде тела на части сумма импульсов каждой из частей равна импульсу тела до распада. И хоть этот закон обычно представляется связанным с одноактным действием (одно тело единожды распалось), его оказывается разумным использовать и в более сложных процессах, когда от тела последовательно отпадают части, как идеализация этого процесса (когда части очень мелкие и их очень много и интервал между их отпадениями

Рис.5. Закон реактивного движения

очень мал) — когда из тела непрерывно вытекает (вылетает, высыпается) какая-то масса. Именно в такой форме и записывается закон реактивного движения:

или (если, как обычно, обозначать через )

Здесь и соответственно масса и скорость ракеты в момент времени t, V — скорость истечения горючего из ракеты (точнее, это — V: обычно систему координат направляют вдоль движения ракеты, тогда горючее вытекает с отрицательной скоростью, и именно ее обозначают — V, где V — положительное число, равное абсолютной величине мой скорости). Разность — это масса вытекшего горючего, а — V — его скорость в неподвижной системе координат (напомним, что — V — это скорость движения вытекающего горючего относительно ракеты). На самом деле равенство в (12)-(13) не является вполне точным, так как процесс истечения горючего и изменения скорости происходит не «толчком», а непрерывно. Однако если промежуток времени уменьшать, то равенство перейдет в точное равенство отношению дифференциалов

(если предварительно его разделить на ). После несложных преобразований получаем закон реактивного движения

или, через производные,

который иногда записывают в форме:

. Из пушки на Луну

Еще один известный «космический» сюжет: тело (в классической интерпретации — барона Мюнхгаузена) «выстреливается» с Земли в направлении Луны и долетает до нее в свободном полете. Опишем закон полета. Пусть полет происходит по прямой, соединяющей центры Луны и Земли (расстояние между центрами обозначим R), расстояние до летящего тела от центра Земли в момент времени t будет описываться функцией (таким образом, в начальный момент времени , в конечный ). Если масса тела m, то сила притяжения Земли равна

, cила притяжения Луны , и второй закон Ньютона дает нам уравнение полета на Луну:

Рис.6. Полет от Земли до Луны

. Форма равновесия жидкости во вращающемся сосуде

цепь тепло реактивное равновесие жидкость

Пусть у нас есть цилиндрический сосуд, вращающийся вокруг своей оси с угловой скоростью . Поверхность жидкости при этом не остается плоской, а принимает форму поверхности вращения некоторой кривой. Выведем уравнение этой кривой. Для этого воспользуемся тем фактом, что частица, движущаяся по окружности радиуса r с угловой скоростью , должна иметь ускорение, равное направленное к центру окружности. Рассмотрим сечение сосуда плоскостью, проходящей через ось вращения. Пусть независимая переменная описывает расстояние от точки до оси вращения, а — форма поверхности. Изобразим ускорение. Откуда оно взялось? Конечно же, как результат (сумма) различных воздействий. Прежде всего, это — сила тяжести (она дает ускорение , направленное вертикально вниз) и сила упругой реакции самой жидкости (она дает ускорение, направленное по нормали к поверхности). Величина силы реакции и придаваемое ею ускорение нам неизвестны, но, поскольку частицы на поверхности жидкости двигаются в горизонтальной плоскости по окружностям, естественно предполагать, что реакция жидкости «компенсирует» вертикальную тяжесть, и при этом ее горизонтальная

Рис.7. Форма жидкости во вращающемся сосуде

Рис.8. Вид сверху: частица, движущаяся по окружности, должна иметь ускорение, направленное к центру

Рис.8. Вид сбоку (сечение)

составляющая и придает частицам ускорение . Изобразим силы на чертеже:

Чтобы записать соответствующие уравнения, обозначим через В абсолютную величину ускорения, придаваемого частице реакцией жидкости, расположим ось x горизонтально и направим ее вправо, ось у вертикально и направим ее вверх, угол, образуемый касательной к точке кривой у(r) с

Рис.9. Изобразим наши ускорения на чертеже

положительным направлением оси r, обозначим через. Тогда угол между направлением реакции жидкости и положительным направлением оси r равен, вертикальная проекция ускорения реакции жидкости равна, а горизонтальная . Получаем:

откуда, исключая В, получаем

Остается вспомнить, что — это производная и получить уравнение поверхности вращающейся жидкости

8. Фокусирующее зеркало

Пусть у нас есть отражающая поверхность (в плоской интерпретации отражающая кривая), позволяющая отразить параллельный пучок лучей в пучок, сходящийся в одну точку. Постараемся описать эту кривую. Для этого нам понадобится закон отражения лучей, который, для случая плоскости, мы прекрасно знаем (угол падения равен углу отражения), но который, в случае кривой поверхности, мы не сможем сформулировать. Для неплоского случая закон не намного сложнее плоского: луч, падающий в точку х поверхности, отражается от нее так же, как и от плоскости, касающейся в этой точке нашей поверхности.

Запишем задачу в математической форме. Для этого в качестве начала координат удобно взять как раз ту точку, в которую будут собираться лучи, за положительное направление движения лучей и эту ось обозначим через х, другую ось обозначим через у, а функцию, описывающую форму зеркала, — через у(х). Нарисуем траекторию луча, отразившегося в точке нашей кривой, и касательную, проходящую через эту точку. Поскольку до отражения луч шел

Рис.10. Фокусирующее зеркало

горизонтально, угол падения луча совпадает с углом, образованным касательной,

Вычислим угол отражения. Для этого заметим, что в треугольнике МОА (точка А — это точка пересечения касательной с осью абсцисс) угол МО — его внешний угол и он равен сумме двух внутренних, одни из которых — это угол отражения, а другой — угловой коэффициент касательной, то есть опять же. Поскольку угол МО — это угол поворота вектора (х,у(х)), его тангенс равен отношению, откуда получаем

В принципе можно было бы выразить из уравнений (16) и (17) углы и (или их тангенсы) и воспользоваться законом отражения , воспользовавшись тем, что равен , а он, в свою очередь, в силу (16) равен у'(х), подставим их в (17) с раскрытым тангенсом суммы. В результате получается уравнение

являющееся уравнением фокусирующего зеркала. Решение этого уравнения не гипербола, а парабола (а — параметр).

Получаем параболоид вращения (образуемый вращением этой параболы).

Задачу эту относят к классическим задачам математики. Она возникла еще в Древней Греции. Состоит она в том, чтобы определить длину цепи, подвешенной за концы (в античной формулировке эта цепь перегораживала вход в город). Мы несколько расширим задачу и постараемся определить форму цепи (при этом длина ее будет вычисляться по классическим формулам из анализа).

Рис.11. Висящая цепь

Пусть наша цепь описывается функцией у(х), заданной на некотором отрезке [а,b]. Напишем условия для этой функции, при выполнении которых цепь будет находиться в равновесии. Для этого определим действующие на нее силы. Прежде всего — это сила тяжести. На любой участок цепи [х, х+х] она действует с силой, равной

здесь — линейная плотность цени (т.е. масса на единицу длины) в точке — дифференциал дуги кривой. Интеграл, по существу, есть соответствующего участка цепи. Эта сила направлена вниз.

Кроме силы тяжести, на наш участок действуют еще какие-то силы (т.к. цепь находится в равновесии). Это — силы упругой реакции цепи, или силы натяжения. Убедиться в их существовании нетрудно. Представьте себе, что вы «оторвали» этот участок цепи и, растягивая его за концы, стараетесь придать ему ту же форму, которую он имел, находясь внутри цепи. Не надо никого убеждать в том, что этого можно добиться лишь, прикладывая к концам участка силы (причем значительные). Это и есть те самые (имеется в виду величина и направление, а не происхождение) силы, которые действуют внутри висящей цепи. Эти силы всегда направлены по касательной к точке, в которой они приложены. Обозначим величину силы натяжения, приложенной в точке х, через T(х). Теперь мы можем изобразить все на чертеже и записать условия равновесия. Если обозначить

Рис.12. Изобразим все силы на чертеже

через угол, образованный касательной в точке х с положительным направлением оси абсцисс, то горизонтальная составляющая силы натяжения в точке будет равна , а в точке х — соответственно (обратите внимание на знак минус: в точке х сила натяжения действует не вправо, а влево). Поскольку наш участок цепи находится в равновесии, их сумма равна нулю, откуда

где А — константа (параметр задачи). Она может быть определена, например, по величине натяжения в концах цепи: .

Вертикальные составляющие сил натяжения, действующие на наш участок в точках и х, соответственно, равны и — . Сумма этих сил, вместе с силой тяжести, также равна нулю.

Получаем, с учетом (19), следующее уравнение:

или, учитывая, что ,

Разделив на и устремив его к нулю, получим уравнение висящей цепи:

Задача состоит в том, чтобы описать форму струны, натянутой горизонтально за концы и находящейся под воздействием внешней нагрузки.

Эта задача практически идентична предыдущей, роль внешней нагрузки в которой играет тяжесть. Фактически, правая часть (20) — это «сила», действующая на точку х. Мы слово «сила» употребляем в кавычках потому, что это на самом деле не сила, а ее плотность распределения. «Настоящая» сила (та, которая измеряется, например, в ньютонах) на самом деле действует лишь на конечные, имеющие ненулевую длину участки цепи. Если же мы попытаемся найти силу, действующую на точку, то она окажется равной нулю. Воздействие же на одну точку описывается в терминах и равно

. Если через F(x) обозначить силу, действующую на участок струны левее х, то.

В случае висящей цепи . Теперь уже понятен общий вид уравнения деформаций струны:

Мы уже говорили, что это — уравнение равновесия, которое можно

переписать в виде

при этом второе слагаемое — это действие внешних сил, а первое определяется силами упругости. Струна находится в равновесии, значит, их сумма равна нулю. А если сумма не будет равна нулю? Тогда на нашу струну будет действовать сила, и эта сила, по второму закону Ньютона, будет вызывать ускорение. Если обозначить его буквой а, то мы получим уравнение движения:

Чтобы получить уравнение в окончательном виде, нам остается заметить, что, поскольку струна двигается, ее форма меняется с течением времени и описывается функцией не одной, а двух переменных. При фиксированном t — это форма струны (мгновенный снимок), при фиксированном х — закон движения точки с координатой x. То, что раньше было у», теперь станет второй производной функции по пространственной переменной x, а ускорение оказывается просто второй производной по временной переменной t. Добавим еще, что внешнее воздействие может теперь и меняться со временем, т.е. описываться функцией , и мы получили уравнение колебаний струны

Дифференциальные уравнения являются теоретической основой многих моделей, используемых в науке и технике. Такие процессы отражаются в физике, химии, биологии и многих других областях науки. Многие задачи физики приводят к необходимости решения дифференциальных уравнений. Это обусловлено тем, что практически все физические законы, описывающие физические процессы являются дифференциальными уравнениями, относительно некоторых функций, характеризующих эти процессы. Данные физические законы представляют собой теоретическое обобщение многочисленных экспериментов и описывают эволюцию искомых величин в общем случае, как в пространстве, так и во времени. Решение ДУ представляется важной задачей для многих сфер деятельности человека, а также играет важную роль в познании окружающего мира.

Во многих случаях составление дифференциального уравнения основывается на так называемой «линейности процесса в малом», т.е. на дифференцируемости функций, выражающих зависимость величин. Как правило, можно считать, что все существующие в том или ином процессе величины в течение малого промежутка времени изменяются постоянной скоростью. Это позволяет применить известные из физики законы, описывающие равномерно протекающие явления, для составления соотношения между значениями , т.е. величинами, участвующими в процессе, и их приращениями.

Получающееся равенство имеет лишь приближенный характер, поскольку величины меняются даже за короткий промежуток времен неравномерно. Но если разделить обе части получившегося равенства на , то получиться точное равенство. Оно содержит время t, меняющиеся с течением времени физические величины и их производные, т.е. является дифференциальным уравнением, описывающим данное явление. Таким образом, при составлении дифференциального уравнения мы делаем как бы «мгновенный снимок» процесса в данный момент времени.

В курсовой работе рассмотрены различные физические задачи, приводящие к дифференциальным уравнениям. Описаны процессы протекания данных физических явлений и составлены соответствующие дифференциальные уравнения. В основе решения физических задач с помощью дифференциальных уравнений лежит общая идея — линеаризации — замены функций на малых промежутках изменения аргумента линейными функциями.

Аксененко Е.М. Применение дифференциальных уравнений к решению задач: практикум / Е.М. Аксененко, Г.М. Чуванова. — Южно-Сахалинск, изд-во СахГУ, 2013. — 52с.

Боровских А.В., Перов А.И. Лекции по обыкновенным дифференциальным уравнениям. — Москва — Ижевск: НИЦ «Регулярная и хаотическая динамика», Институт компьютерных исследований, 2004, 540 стр.

Сабитов К.Б. Функциональные, дифференциальные и интегральные уравнения. — М.:Высш. шк., 2005,671с.

Вагапов В.З. Обыкновенные дифференциальные уравнения: учеб.пособие для студ.вузов — Стерлитамак: изд-во СГПА, 2008. 191 с.

Арнольд В.И. Обыкновенные дифференциальные уравнения — Ижевск: Ижевская республиканская типография. 2000. — 386с.

Егоров А.И. Обыкновенные дифференциальные уравнения с приложениями. — 2-е изд., испр. — М.: ФИЗМАТЛИТ, 2005. — 384 с. — ISBN 5-9221-0553-1.

Теги: Физические задачи, приводящие к дифференциальным уравнениям Курсовая работа (теория) Математика

Видео:Решение физических задач с помощью дифференциальных уравненийСкачать

Классическая механика: о диффурах «на пальцах»

Введение

В этой статье я продолжаю тему цифровой обработки сигналов. В ней я постараюсь простым языком рассказать о концепции игровой механики (физики) с использованием подхода на основе дифференциальных уравнений. В будущем я собираюсь оценить действительно ли реализация такого подхода приведет к резкому увеличению вычислительной нагрузки. В рамках этой статьи не получится — слишком большой объем. В этой я собираюсь описать назначение коэффициентов, входящих в математическую модель динамического объекта, описать их физический смысл, т.е. их влияние на поведение динамического объекта.
Начнем пожалуй…

Физический смысл

В своей статье про Фильтр Калмана я описал что такое уравнения вида «вход-выход», передаточная функция и операторная форма записи дифференциальных уравнений (см. раздел «Основные понятия» в [2]). Примером части математической модели динамического объекта в операторной форме записи может служить следующее уравнение:
(1)
Это распространенная упрощенная модель динамических систем. Опережая напишу, что модель тела в движке «Farseer» использует урезанный аналог представленной выше модели (динамического звена второго порядка). Ниже представлено описание принятых в ней обозначений.

а0, а1, а2 — коэффициенты инерции, демпфирования и жесткости, соответственно.
b0, b1 — коэффициенты входного воздействия.
s — оператор Лапласса (d/dt).
α(s), β(s) — выходная и входная переменные, как функции оператора Лапласса.

Представленное уравнение описывает динамическую систему типа «один вход — один выход» (SISO). Ее можно использовать для описания динамики объекта по одной из его степеней свободы. Как Вам, возможно, известно, у свободного тела есть шесть степеней свободы — три поступательные (линейное движение вдоль трех осей системы координат (СК) ) и три вращательные (повороты вокруг осей СК). Таким образом, полная модель физического тела будет описываться шестью такими уравнениями (или четырьмя для 2D случая). Вы сразу можете сказать, что уже это свидетельствует о слишком высокой сложности такого подхода. Но на самом деле в Farseer, к примеру, класс тела (Body) содержит и линейные координаты тела (по сути это пара α(s) по OX и OY), и линейные скорости (пара s*α(s) по OX и OY) и параметры ориентации и угловой скорости. Эти параметры обсчитываются раздельно для каждой из осей, т.е. количество уравнений такое же — два уравнения по оси OX (линейное и угловое движение) и два для оси OY. Разница лишь в форме уравнений.
Алгоритм в движке Farseer — приближенный и упрощенный, но позволяет работать с варьируемыми квантами времени. В функцию обсчета параметров движения (Island.Solve(ref TimeStep step, ref Vector2 gravity)) передается время, прошедшее после последнего обсчета параметров. Это позволяет при недостаточной производительности компьютера держать скорость течения игрового времени примерно постоянным в ущерб плавности и реалистичности движения игровых объектов.
При построении дискретной модели на основе диференциальных уравнений мы четко завязываемся на фиксированный квант времени. Уравнения интегрируются для изначально заданной частоты дискретезации, и если с момента последнего обсчета по какой-то причине прошло времени больше, чем заданный квант (в англоязычной литературе его называют «time sample»), то мы либо должны произвести обсчет несколько раз, либо получим замедление движения объекта. Последнее я как раз и наблюдал в игре «Command Cortex» на слабой машине. Движения акторов были плавными но медленными (акторы, управляемые человеком, получают преимущество). Таким образом, нельзя говорить об исключительном преимуществе одного из этих подходов.
Теперь о том, за что отвечают коэффициенты представленного выше уравнения. Это уравнение описывает движение физического тела относительно положения равновесия при α(s) = 0. Это еще одна из причин кажущегося неудобства применения такой модели в игровой механике. При отсутствии приложенных внешних сил данная модель рано или поздно возвратит (при условии устойчивости модели) тело в положение равновесия. Представьте игровой мир, наполненный шариками, которые все время стремятся в начало координат (например, в левый верхний угол экрана). К такому поведению приводит наличие коэффициента жесткости (см. а2 выше). Представьте, что тело соединено с началом координат пружиной. Пока на тело действуют силы, пружина растянута, но стоит убрать внешнее воздействие и тело устремится к нулю. Тела в движке Farseer таким поведением не обладают. Если мы зададим коэффициент a2 равным нулю, то и в данном случае тела не будут стремиться к началу координат (см. выше я писал, что модели в Farseer по сути урезанные варианты этой модели). Ну и зачем этот коэффициент тогда нужен, спросите Вы. Если раскрыть скобки в левой части уравнения (1) и вместо слагаемого
a2*α(s)
напишем
a2*(α(s) — α0)
то через α0 мы получим возможность задать положение, к которому игровой объект будет стремиться. Величина коэффициента а2 отвечает за то, насколько быстро тело переместится в заданное положение равновесия (чем больше значение, тем выше жесткость пружины). Как такое реализовывается в Farseer я пока не выяснил, но думаю придется создать дополнительный источник воздействия.
Теперь коэффициент a1. Это коэффициент демпфирования. Чем больше значение этого коэффициента, тем быстрее гасится скорость (линейная или угловая). Аналогия из жизни — вязкие жидкости, такие как масло, мед, эпоксидная смола. Эти жидкости очень вязкие (имеют большое значение коэффициента демпфирования). Чем выше скорость движения тела в них, тем выше сопротивление этому движения. Если медленно двигать в них ложку, например, то преодолеть сопротивление большого труда не составит, а вот если ударить с размаху, то удар будет жестким.
Величина коэффициента а0 характеризует инерцию объекта. При описании линейного движения в качестве коэффициента а0 используется масса. Чем выше его значение, тем медленнее тело набирает скорость при приложении к нему внешних сил.
Теперь о коэффициентах в правой части уравнения (1). Тут нужно заметить, что данная модель расширенная на случай, когда входное воздействие определяется не только самим значением внешней силы, но и ее изменением. Для описания динамики игровых объектов это, возможно, будет излишним. Однако в промышленных системах управление встречаются и такие модели. Каков же их физический смысл? Коэффициент b1 это по сути коэффициент передачи внешней силы вовнутрь объекта. Обычно он равен еденице, т.е. сила передается как есть.
Коэффициент b0 интересен. Он играет роль форсирующего коэффициента. Представьте очень инерционный объект, к которому прикладывают силу, плавно нарастающую со временем. Если скорость нарастания и конечная величина силы будут малы, то объект очень медленно набирать скорость. Но если силу сделать большой, то после достижения внешней силой заданного значения объект не остановится в каком-то положении, а будет колебаться под действием инерции. Форсирование — это воздействие, пропорциональное скорости нарастания внешней силы. Если мы выберем его большим, то даже при малой скорости нарастания внешней силы наш объект будет достаточно быстро набирать скорость, а когда внешняя сила достигнет заданного значения, форсирование отключится. Вот такой вот хитрый этот «b0».

Динамика в картинках

Чтобы наглядно показать влияние коэффициентов дифф. уравнения на поведение динамического объекта решил построить графики переходного процесса при ступенчатом (step response) и импульсном (impulse response) входных воздействиях. Всего представлено 6 групп графиков (по одной группе для каждого коэффициента). Графики построены в пакете Octave (v. 3.4) с установленным пакетом «Signal Processing».
Итак, в качестве исходной возьмем модель вида:
=========================================
>>> w = tf([1 1],[1 1 1])

Transfer function «w» from input «u1» to output…

y1: (s + 1)/(s^2 + s + 1)

Continuous-time model.
=========================================

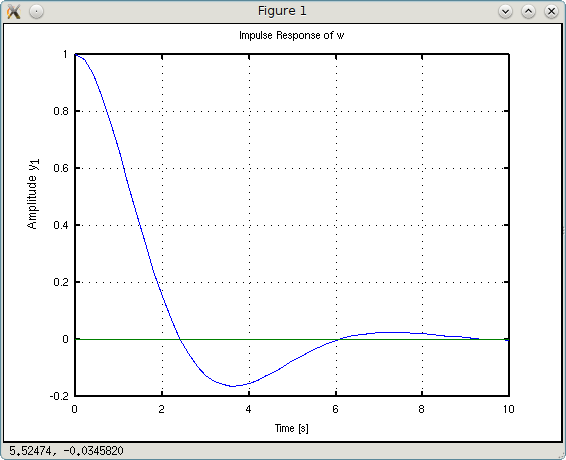
Код «w = tf([1 1],[1 1 1])» в символьном виде имеет вид:
>>> w = tf([b0 b1],[a0 a1 a2])
На скриншотах внизу-справа — примерное время стабилизации (коридором стабильности считаем ± 5% от заданной величины).

Попробуем поиграться с коэффициентом жесткости a2.
>>> w1 = 0.1*tf([1 1],[1 1 0.1])
y1: (s + 1)/(s^2 + s + 0.1)

>>> w2 = 10*tf([1 1],[1 1 10])
y1: (s + 1)/(s^2 + s + 10)
Примечание: пришлось подшаманить с коэффициентами усиления, чтобы результирующий коэффициент усиления был равен единице.

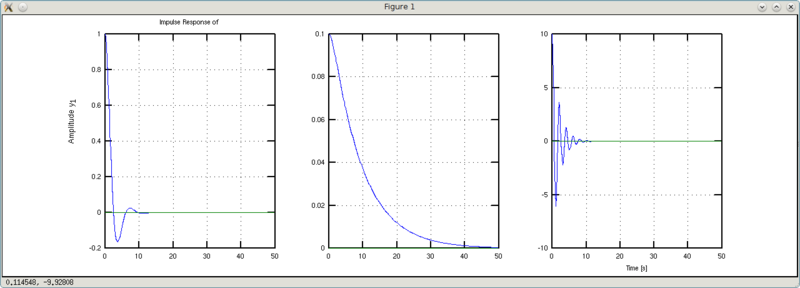
Что видно на графиках? Слева-направо представлены графики для w, w1 и w2, соответственно. Графики w1 более плавные и медленнее достигают установившегося значения. Графики w2 имеют более колебательный характер, но быстрее достигают установившегося значения. Вывод: жестче пружина — больше колебаний, но короче переходный процесс.

Попробуем поиграться с демпфированием (а1).
>>> w1 = tf([1 1],[1 0.25 1])
y1: (s + 1)/(s^2 + 0.25s + 1)

>>> w2 = tf([1 1],[1 2 1])
y1: (s + 1)/(s^2 + 2s + 1)

Сразу вывод: больше вязкость — быстрее затухают колебания.

Попробуем поиграться с инерцией (а0).
>>> w1 = tf([1 1],[0.1 1 1])
y1: (s + 1)/(0.1s^2 + s + 1)

>>> w2 = tf([1 1],[2 1 1])
y1: (s + 1)/(2s^2 + s + 1)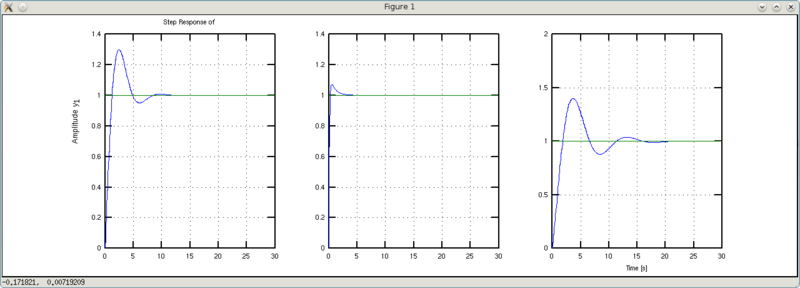

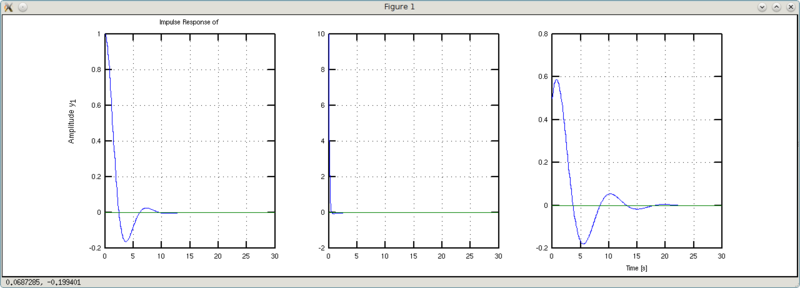
Вывод: меньше масса чугуняки — меньше болтанки и короче переходный процесс.

Перейдем к правой части и поиграемся с b1.
>>> w1 = 10*tf([1 0.1],[1 1 1])
y1: (10 s + 1)/(s^2 + s + 1)

>>> w2 = 0.25*tf([1 4],[1 1 1])
y1: (0.25 s + 1)/(s^2 + s + 1)

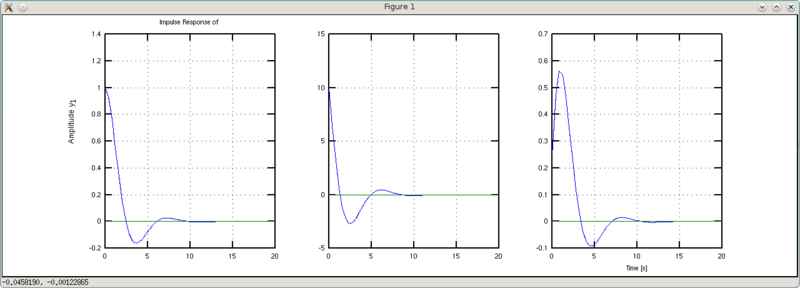
Вроде бы разница еле заметна, если смотреть на графики Step Response. Но на графиках Impulse Response хорошо виден эффект этого коэффициента. Если он равен единице, то график импульсного переходного процесса начинается с единицы (на самом деле он выходит из нуля, но не суть важно — второе значение в графике еденица). График w1 «начинается» со значения 10 (обратная величина от 0.1), а график w2 — начинается со значения 0.25 (обратное к 4). Таким образом, коэффициент b1 можно «обозвать» коэффициентом эффективности управления (входного воздействия).

И напоследок вкусненькое — игры с коэффициентом b0. Это хитрый коэффициент, потому и сравнение будет не таким как было выше. Чтобы показать его эффект придется варьровать несколько коэффициентов.
>>> w1 = tf([6 1],[1 1 1])
y1: (6 s + 1)/(s^2 + s + 1)

>>> w2 = tf([6 1],[1 3 1])
y1: (6 s + 1)/(s^2 + 3 s + 1)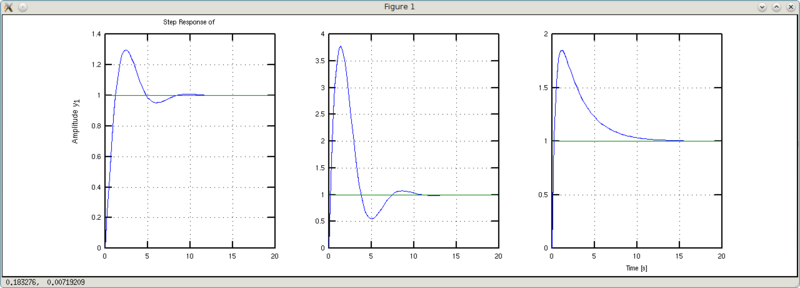

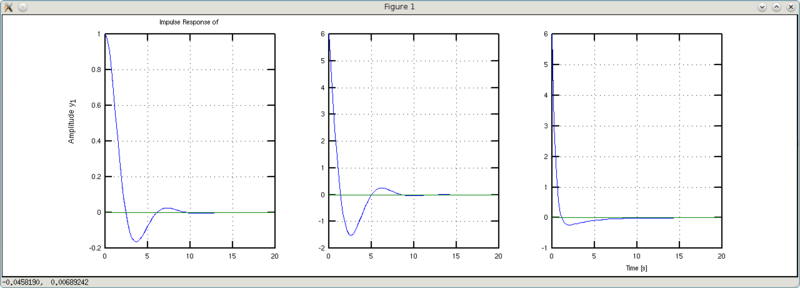
Чем отличаются друг от друга w1 и w2? У w2 в три раза больше коэффициент демпфирования. В результате получаем интересные выводы. Графики w1 и w2 раньше пересекают уровень установившегося значения чем дефолтный график. Однако график w1 сохраняет форму дефолтного с его колебательностью, а график w2 за счет увеличенного демпфирования более сглаженный. Таким образом, играясь с форсированием и демпфированием мы можем заставить даже чугунный утюг порхать по рингу как бабочка без колебаний туда-сюда.

На правах PS

В данной статье я рассматривал лишь положительные значения коэффициентов. Их положительность — необходимое условие устойчивости мат. модели. Однако можно попробовать поиграться и с отрицательными значениями. Неустойчивой системой также можно управлять. Вспомните о самолетах пятого поколения (например, наш Беркут). Обратная стреловидность крыла — это неустойчивый планер, но зато высокая маневренность. Автоматика способна скорректировать эту неустойчивость и при этом, когда нужно, закладывать крутые виражи.
Если получится, состряпаю игрушку, с которой можно будет наглядно увидеть все эти эффекты.