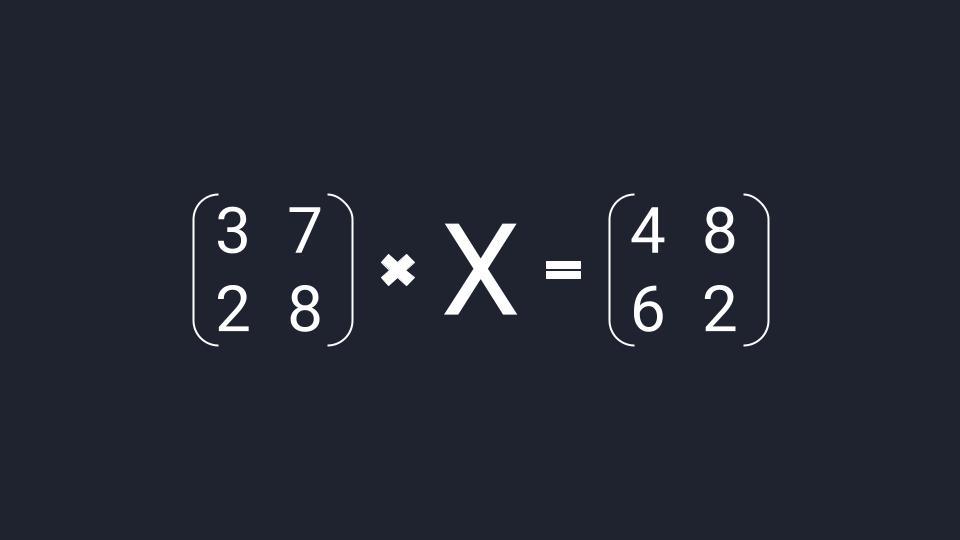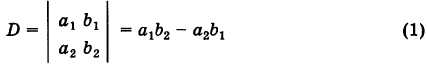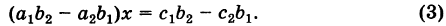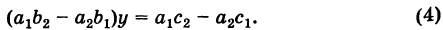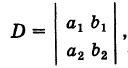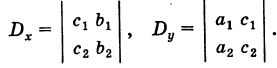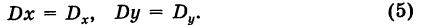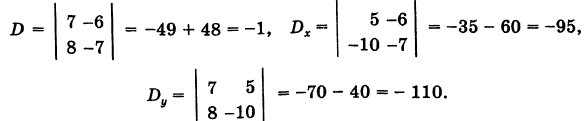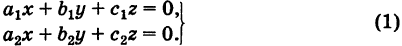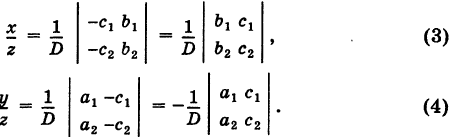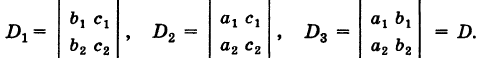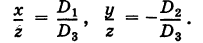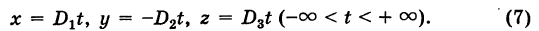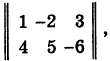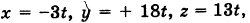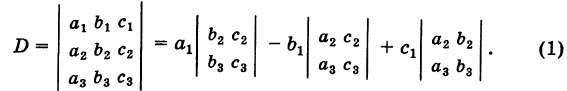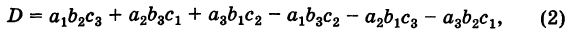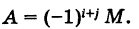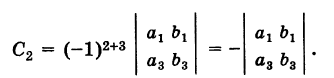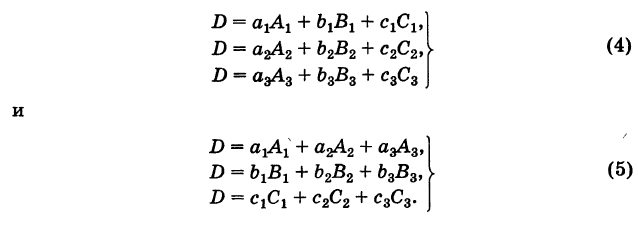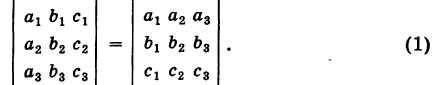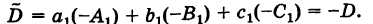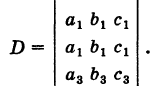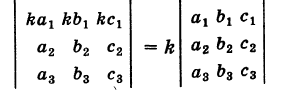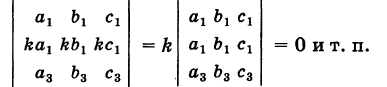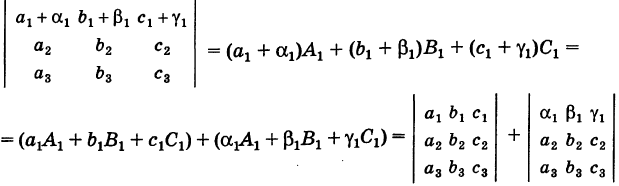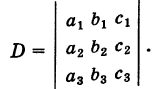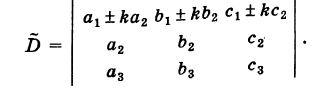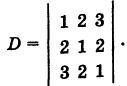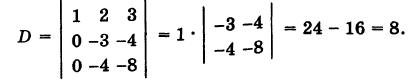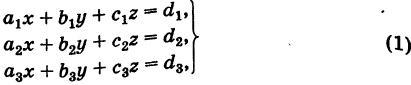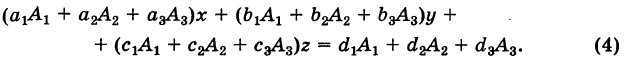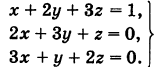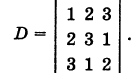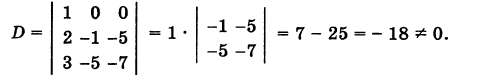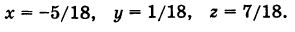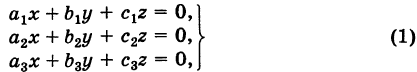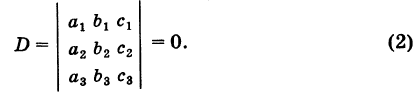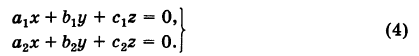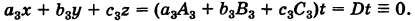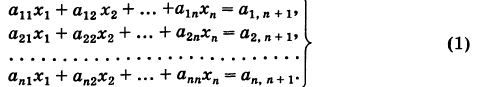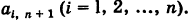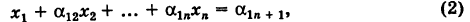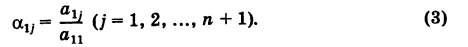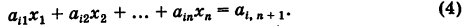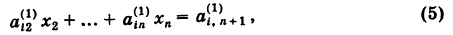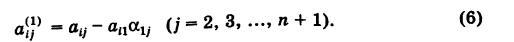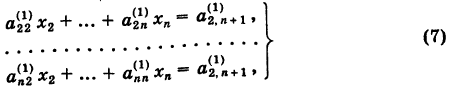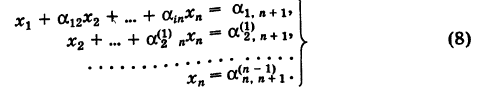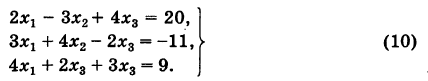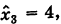Финальная глава саги.
Линейная алгебра и, в частности, матрицы — это основа математики нейросетей. Когда говорят «машинное обучение», на самом деле говорят «перемножение матриц», «решение матричных уравнений» и «поиск коэффициентов в матричных уравнениях».
Понятно, что между простой матрицей в линейной алгебре и нейросетью, которая генерирует котов, много слоёв усложнений, дополнительной логики, обучения и т. д. Но здесь мы говорим именно о фундаменте. Цель — чтобы стало понятно, из чего оно сделано.
Краткое содержание прошлых частей:
- Линейная алгебра изучает векторы, матрицы и другие понятия, которые относятся к упорядоченным наборам данных. Линейной алгебре интересно, как можно трансформировать эти упорядоченные данные, складывать и умножать, всячески обсчитывать и находить в них закономерности.
- Вектор — это набор упорядоченных данных в одном измерении. Можно упрощённо сказать, что это последовательность чисел.
- Матрица — это тоже набор упорядоченных данных, только уже не в одном измерении, а в двух (или даже больше).
- Матрицу можно представить как упорядоченную сумку с данными. И с этой сумкой как с единым целым можно совершать какие-то действия. Например, делить, умножать, менять знаки.
- Матрицы можно складывать и умножать на другие матрицы. Это как взять две сумки с данными и получить третью сумку, тоже с данными, только теперь какими-то новыми.
- Матрицы перемножаются по довольно замороченному алгоритму. Арифметика простая, а порядок перемножения довольно запутанный.
И вот наконец мы здесь: если мы можем перемножать матрицы, то мы можем и решить матричное уравнение.
❌ Никакого практического применения следующего материала в народном хозяйстве вы не увидите. Это чистая алгебра в несколько упрощённом виде. Отсюда до практики далёкий путь, поэтому, если нужно что-то практическое, — посмотрите, как мы генерим Чехова на цепях Маркова.
- Что такое матричное уравнение
- Шаг 1. Упрощаем уравнение
- Шаг 2. Вводим единичную матрицу
- Шаг 3. Находим обратную матрицу
- Шаг 4. Вычисляем неизвестную матрицу
- Шаг 5. Проверяем уравнение
- Ну и что
- Решение матричных уравнений: теория и примеры
- Решение матричных уравнений: как это делается
- Решение матричных уравнений: примеры
- Определители второго и третьего порядков и их свойства с примерами решения
- Определители второго порядка
- Система двух однородных уравнений с тремя неизвестными
- Определители третьего порядка
- Основные свойства определителей
- Система трех линейных уравнений
- Однородная система трех линейных уравнений
- Система линейных уравнений с многими неизвестными. Метод Гаусса
- 🔍 Видео
Видео:Решите уравнение ➜ Определитель третьего порядка равен нулюСкачать

Что такое матричное уравнение
Матричное уравнение — это когда мы умножаем известную матрицу на матрицу Х и получаем новую матрицу. Наша задача — найти неизвестную матрицу Х.
Видео:Вычислить определитель 3 порядка. Правило треугольникаСкачать

Шаг 1. Упрощаем уравнение
Вместо известных числовых матриц вводим в уравнение буквы: первую матрицу обозначаем буквой A, вторую — буквой B. Неизвестную матрицу X оставляем. Это упрощение поможет составить формулу и выразить X через известную матрицу.
Видео:Определитель матрицы 3 порядка. Как легко найти? Метод треугольников и Саррюса. Просто и наглядноСкачать

Шаг 2. Вводим единичную матрицу
В линейной алгебре есть два вспомогательных понятия: обратная матрица и единичная матрица. Единичная матрица состоит из нулей, а по диагонали у неё единицы. Обратная матрица — это такая, которая при умножении на исходную даёт единичную матрицу.
Можно представить, что есть число 100 — это «сто в первой степени», 100 1
И есть число 0,01 — это «сто в минус первой степени», 100 -1
При перемножении этих двух чисел получится единица:
100 1 × 100 -1 = 100 × 0,01 = 1.
Вот такое, только в мире матриц.
Зная свойства единичных и обратных матриц, делаем алгебраическое колдунство. Умножаем обе известные матрицы на обратную матрицу А -1 . Неизвестную матрицу Х оставляем без изменений и переписываем уравнение:
А -1 × А × Х = А -1 × В
Добавляем единичную матрицу и упрощаем запись:
А -1 × А = E — единичная матрица
E × Х = А -1 × В — единичная матрица, умноженная на исходную матрицу, даёт исходную матрицу. Единичную матрицу убираем
Х = А -1 × В — новая запись уравнения
После введения единичной матрицы мы нашли способ выражения неизвестной матрицы X через известные матрицы A и B.
💡 Смотрите, что произошло: раньше нам нужно было найти неизвестную матрицу. А теперь мы точно знаем, как её найти: нужно рассчитать обратную матрицу A -1 и умножить её на известную матрицу B. И то и другое — замороченные процедуры, но с точки зрения арифметики — просто.
Видео:Обратная матрицаСкачать

Шаг 3. Находим обратную матрицу
Вспоминаем формулу и порядок расчёта обратной матрицы:
- Делим единицу на определитель матрицы A.
- Считаем транспонированную матрицу алгебраических дополнений.
- Перемножаем значения и получаем нужную матрицу.
Собираем формулу и получаем обратную матрицу. Для удобства умышленно оставляем перед матрицей дробное число, чтобы было проще считать.

Видео:Решение системы трех уравнений по формулам КрамераСкачать

Шаг 4. Вычисляем неизвестную матрицу
Нам остаётся посчитать матрицу X: умножаем обратную матрицу А -1 на матрицу B. Дробь держим за скобками и вносим в матрицу только при условии, что элементы новой матрицы будут кратны десяти — их можно умножить на дробь и получить целое число. Если кратных элементов не будет — дробь оставим за скобками.

Видео:5 способов вычисления определителя ★ Какой способ лучше?Скачать

Шаг 5. Проверяем уравнение
Мы решили матричное уравнение и получили красивый ответ с целыми числами. Выглядит правильно, но в случае с матрицами этого недостаточно. Чтобы проверить ответ, нам нужно вернуться к условию и умножить исходную матрицу A на матрицу X. В результате должна появиться матрица B. Если расчёты совпадут — мы всё сделали правильно. Если будут отличия — придётся решать заново.
👉 Часто начинающие математики пренебрегают финальной проверкой и считают её лишней тратой времени. Сегодня мы разобрали простое уравнение с двумя квадратными матрицами с четырьмя элементами в каждой. Когда элементов будет больше, в них легко запутаться и допустить ошибку.

Видео:6. Вычисление определителя 2 и 3 порядка.Скачать

Ну и что
Алгоритм решения матричных уравнений несложный, если знать отдельные его компоненты. Дальше на основе этих компонентов математики переходят в более сложные пространства: работают с многомерными матрицами, решают более сложные уравнения, постепенно выходят на всё более и более абстрактные уровни. И дальше, в конце пути, появляется датасет из миллионов котиков. Этот датасет раскладывается на пиксели, каждый пиксель оцифровывается, цифры подставляются в матрицы, и уже огромный алгоритм в автоматическом режиме генерирует изображение нейрокотика:
Видео:Решение матричных уравненийСкачать

Решение матричных уравнений: теория и примеры
Видео:Урок 1. Матрицы, определитель матрицы и ранг матрицы | Высшая математика | TutorOnlineСкачать

Решение матричных уравнений: как это делается
Матричные уравнения имеют прямую аналогию с простыми алгебраическими уравнениями, в которых присутствует операция умножения. Например,
где x — неизвестное.
А, поскольку мы уже умеем находить произведение матриц, то можем приступать к рассмотрению аналогичных уравнений с матрицами, в которых буквы — это матрицы.
Итак, матричным уравнением называется уравнение вида
где A и B — известные матрицы, X — неизвестная матрица, которую требуется найти.
Как решить матричное уравнение в первом случае? Для того, чтобы решить матричное уравнение вида A ⋅ X = B , обе его части следует умножить на обратную к A матрицу 

По определению обратной матрицы, произведение обратной матрицы на данную исходную матрицу равно единичной матрице: 

Так как E — единичная матрица, то E ⋅ X = X . В результате получим, что неизвестная матрица X равна произведению матрицы, обратной к матрице A , слева, на матрицу B :

Как решить матричное уравнение во втором случае? Если дано уравнение
то есть такое, в котором в произведении неизвестной матрицы X и известной матрицы A матрица A находится справа, то нужно действовать аналогично, но меняя направление умножения на матрицу, обратную матрице A , и умножать матрицу B на неё справа:



Как видим, очень важно, с какой стороны умножать на обратную матрицу, так как 
Как решить матричное уравнение в третьем случае? Встречаются случаи, когда в левой части уравнения неизвестная матрица X находится в середине произведения трёх матриц. Тогда известную матрицу из правой части уравнения следует умножить слева на матрицу, обратную той, которая в упомянутом выше произведении трёх матриц была слева, и справа на матрицу, обратную той матрице, которая располагалась справа. Таким образом, решением матричного уравнения

Видео:Решение системы уравнений методом ГауссаСкачать

Решение матричных уравнений: примеры
Пример 1. Решить матричное уравнение

Решение. Данное уравнение имеет вид A ⋅ X = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде 
Сначала найдём определитель матрицы A :

Найдём алгебраические дополнения матрицы A :

Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

Теперь у нас есть всё, чтобы найти матрицу, обратную матрице A :

Наконец, находим неизвестную матрицу:
Пример 2. Решить матричное уравнение

Пример 3. Решить матричное уравнение

Решение. Данное уравнение имеет вид X ⋅ A = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде 
Сначала найдём определитель матрицы A :

Найдём алгебраические дополнения матрицы A :

Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

Находим матрицу, обратную матрице A :

Находим неизвестную матрицу:
До сих пор мы решали уравнения с матрицами второго порядка, а теперь настала очередь матриц третьего порядка.
Пример 4. Решить матричное уравнение

Решение. Это уравнение первого вида: A ⋅ X = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде 
Сначала найдём определитель матрицы A :

Найдём алгебраические дополнения матрицы A :
Составим матрицу алгебраических дополнений:
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

Находим матрицу, обратную матрице A , и делаем это легко, так как определитель матрицы A равен единице:

Находим неизвестную матрицу:
Пример 5. Решить матричное уравнение

Решение. Данное уравнение имеет вид X ⋅ A = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде 
Сначала найдём определитель матрицы A :

Найдём алгебраические дополнения матрицы A :
Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

Находим матрицу, обратную матрице A :

Находим неизвестную матрицу:
Пример 6. Решить матричное уравнение

Решение. Данное уравнение имеет вид A ⋅ X ⋅ B = C , то есть неизвестная матрица X находится в середине произведения трёх матриц. Поэтому решение следует искать в виде 
Сначала найдём определитель матрицы A :

Найдём алгебраические дополнения матрицы A :

Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

Находим матрицу, обратную матрице A :

Найдём матрицу, обратную матрице B .
Сначала найдём определитель матрицы B :

Найдём алгебраические дополнения матрицы B :
Составим матрицу алгебраических дополнений матрицы B :

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей B :

Находим матрицу, обратную матрице B :

Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Определители второго и третьего порядков и их свойства с примерами решения
Содержание:
Определители второго порядка:
Под определителем (детерминантом) второго порядка понимается выражение
Числа
Формула (1) дает правило «развертывания» определителя второго порядка, а именно: определитель второго порядка равен разности произведений его элементов первой и второй диагоналей.
Видео:Как найти определитель матрицы 2х2, 3х3 и 4х4Скачать

Определители второго порядка
С помощью определителей второго порядка удобно решать линейные системы двух уравнений с двумя неизвестными:
Такую линейную систему, в которой свободные члены находятся в правых частях, для определенности мы будем называть стандартной.
Под решением системы (2) понимается всякая пара чисел (х, у), обращающая эту систему в тождество. Если существует только одна такая пара, то решение называется единственным. Аналогично вводится понятие решения для системы, содержащей п неизвестных 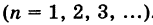
Для нахождения решений системы (2) применим метод исключения. Умножая первое уравнение системы (2) на 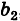
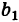
Аналогично, умножая первое уравнение системы (2) на а2 второе — на 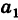
Введем определитель системы
а также дополнительные определители
Заметим, что дополнительные определители Dx и Dy получаются из определителя системы D путем замены коэффициентов при указанном неизвестном на соответствующие свободные члены.
Уравнения (3) и (4) принимают вид
Если 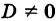
Замечание. Если определитель D = 0, то система (2) или не имеет решений (т. е. несовместна), или имеет бесконечно много решений (т. е. система неопределенная).
Пример:
Решение:
Имеем
Отсюда на основании формул Крамера (6) получаем
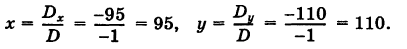
Видео:Решение системы уравнений методом Крамера.Скачать

Система двух однородных уравнений с тремя неизвестными
Рассмотрим однородную систему
Эта система всегда совместна, так как, очевидно, имеет нулевое решение х = 0, у = 0, z = 0. Однако интересно найти не н у л е в ы е решения (х, у, z) системы (1). Пусть, например, 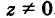
Тогда систему (1) можно переписать в виде
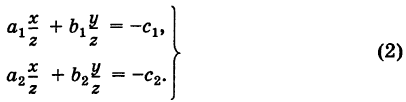
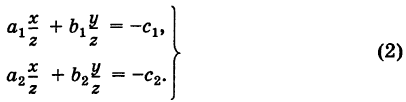
Введем в рассмотрение матрицу коэффициентов системы (1)
Определители второго порядка 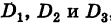
Используя эти обозначения, уравнения (3) и (4) можно переписать в следующем виде:
Равенства (6), очевидно, справедливы также и для нулевого решения.
Таким образом, имеем следующее правило: неизвестные однородной системы (1) пропорциональны соответствующим минорам ее матрицы коэффициентов, взятым с надлежащими знаками.
Обозначая через t коэффициент пропорциональности для отношений (6), получим полную систему решений системы (1):
При выводе формул (7) мы предполагали, что 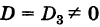
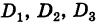
Замечание. Если все миноры 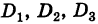
Пример:
Решение:
Составляя матрицу коэффициентов
находим ее миноры: 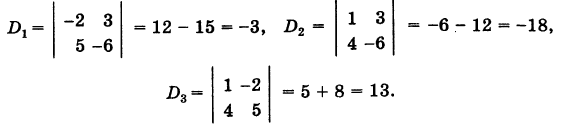
где
Простейшее ненулевое решение системы (1), получающееся при t — 1, есть х = -3, у = 18, z = 13.
Видео:Решение системы уравнений методом обратной матрицы.Скачать

Определители третьего порядка
Числа 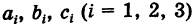
Раскрывая определители второго порядка (миноры) в формуле (1) и собирая члены с одинаковыми знаками, получаем, что определитель третьего порядка представляет собой знакопеременную сумму шести слагаемых:
из которых три берутся со знаком плюс, а три — со знаком минус.
Пример:
Решение:
Используя формулу (1), имеем 
Определение: Под минором элемента определителя третьего порядка понимается определитель младшего (второго) порядка, получающийся из данного определителя в результате вычеркивания строки и столбца, содержащих данный элемент.
Например, для определителя (3) минором его элемента 2, стоящего во второй строке и в первом столбце, является определитель 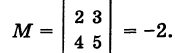
Определение: Алгебраическим дополнением (минором со знаком) элемента определителя третьего порядка называется минор этого элемента, взятый со знаком плюс, если элемент занимает четное место у и со знаком минус, если его место нечетное.
Таким образом, если М есть минор элемента определителя, a i и j — соответственно номер строки и номер столбца, на пересечении которых находится данный элемент, то его алгебраическое дополнение есть
Например, для элемента с2 определителя (1), находящегося во второй строке и в третьем столбце, его алгебраическое дополнение есть
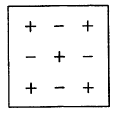
Соответствующие знаки, приписываемые при этом минорам элементов определителя, можно задать таблицей
В дальнейшем алгебраические дополнения элементов определителя с буквенными элементами условимся обозначать соответствующими прописными (большими) буквами.
Теорема Разложения: Определитель третьего порядка равен сумме парных произведений элементов какого-либо ряда его на их алгебраические дополнения (под рядом понимается строка или столбец).
Таким образом, для определителя (1) справедливы шесть разложений:
Легко проверить, что формулы (4) и (5) дают одно и то же выражение (2), принятое за определение.
Замечание. С помощью формул типа (4) или (5), по индукции, можно ввести определители высших порядков.
Видео:Определитель третьего порядкаСкачать

Основные свойства определителей
При формулировках мы не будем указывать порядок определителя, так как эти свойства справедливы для определителей любого порядка.
I. (Равноправность строк и столбцов.) Определитель не меняет своего значения при замене всех его строк соответствующими столбцами, т. е.
Действительно, разлагая первый определитель по элементам первой строки, а второй — по элементам первого столбца, в силу теоремы разложения мы получим один и тот же результат.
II. При перестановке двух параллельных рядов определителя его модуль сохраняет прежнее значение, а знак меняется на обратный.
Пусть, например, в определителе 
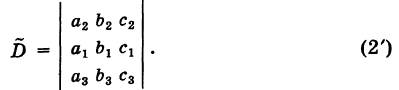
Аналогичное положение получается и в других случаях.
Следствие 1. Определитель, у которого два параллельных ряда одинаковы, равен нулю.
В самом деле, пусть, например,
Переставляя первую и вторую строки определителя, в силу теоремы получим определитель -D. Но очевидно, эта операция не изменяет определитель D, поэтому -D = D и, следовательно, D = 0.
Следствие 2. Сумма парных произведений элементов какого-либо ряда определителя на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю, т. е. для определителя (2) имеем 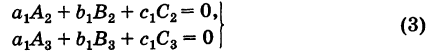
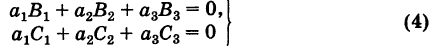
Левые части всех соотношений (3) и (4) представляют собой разложения соответствующих определителей третьего порядка, содержащих два одинаковых параллельных ряда и, следовательно, равны нулю. Например, 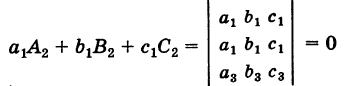
III. Общий множитель элементов какого-либо ряда определителя можно выносить за знак определителя, т. е.
Это свойство непосредственно вытекает из разложения определителя по элементам соответствующего ряда.
Следствие 1. Если все элементы какого-либо ряда определителя равны нулю, то определитель равен нулю.
Следствие 2. Если элементы какого-либо ряда определителя пропорциональны соответствующим элементам параллельного ряда его, то определитель равен нулю.
Например, имеем
IV. Если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.
Следствие. Величина определителя не изменится, если /с элементам какого-либо ряда его прибавить (или отнять) числа, пропорциональные соответствующим элементам параллельного ряда с одним и тем же коэффициентом пропорциональности (так называемые «элементарные преобразования определителя»).
Рассмотрим, например, определители
Используя свойства IV и III, будем иметь 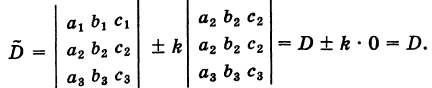
Пример:
Вычислить симметричный определитель
Решение:
Вычитая из второй строки удвоенную первую строку, а из третьей строки утроенную первую строку, получим
Система трех линейных уравнений
Рассмотрим стандартную линейную систему трех уравнений
свободные члены которых находятся в правых частях. Под решением системы понимается всякая тройка чисел (х, у, г), удовлетворяющая этой системе. Введем определитель системы
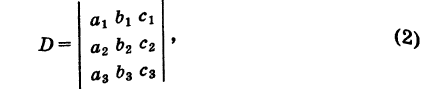
Последовательно умножая уравнения системы (1) на алгебраические дополнения 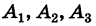
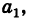
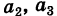
Отсюда, применяя теорему разложения и следствие 2 к свойству II, будем иметь 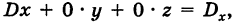

Если определитель системы 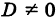
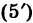
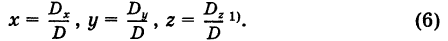
Замечание. Если определитель системы D = 0, то система (1) или несовместна, или имеет бесконечно много решений.
Пример:
Решение:
Вычитая из второго столбца удвоенный первый столбец, а из третьего столбца утроенный первый столбец, получим
Для дополнительных определителей находим следующие значения: 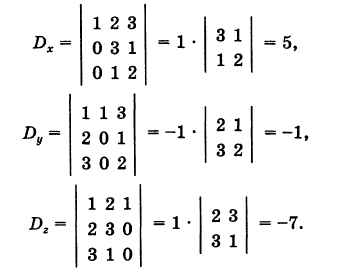
Однородная система трех линейных уравнений
Рассмотрим линейную систему
свободные члены которой равны нулю. Такая линейная система называется однородной.
Однородная линейная система (1), очевидно, допускает нулевое решение х = 0, у = 0, z = 0 и, следовательно, всегда совместна.
Интересно выяснить случаи, когда однородная система имеет ненулевые решения.
Теорема: Линейная однородная система трех линейных уравнений с тремя неизвестными имеет ненулевые решения тогда и только тогда, когда ее определитель равен нулю, т. е.
Доказательство: Пусть система (1) имеет ненулевое решение 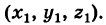
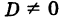
Пусть D = 0. Тогда линейная система (1) либо несовместна, либо имеет бесконечно много решений. Но наша система совместна, так как имеется нулевое решение. Следовательно, система (1) допускает бесконечно много решений, в том числе и ненулевые.
Замечание. Укажем способ нахождения ненулевых решений однородной системы (1) в типичном случае.
Пусть определитель системы D = 0, но не все его миноры второго порядка равны нулю.
Мы будем предполагать, что
(этого всегда можно добиться с помощью перестановки уравнений и изменения нумерации неизвестных).
Рассмотрим подсистему, состоящую из двух первых уравнений системы (1):
В силу решения этой системы имеют вид
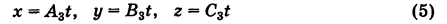
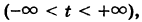
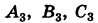
Следовательно, формулы (5), где t произвольно, дают все решения полной системы (1).
Геометрически уравнения системы (1) представляют собой уравнения трех плоскостей в пространстве Oxyz. Если определитель 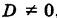
Система линейных уравнений с многими неизвестными. Метод Гаусса
Рассмотрим систему 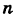
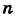
Здесь для коэффициентов системы введена двойная индексация, а именно: у коэффициента 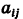
Наиболее простой метод решения системы (1) — это метод исключения. Мы изложим его в форме схемы Гаусса (обычно называемой методом Гаусса).
Пусть для определенности 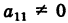
Рассмотрим i-e уравнение системы (1):
Для исключения xx из этого уравнения умножим приведенное уравнение (2) на ап и полученное уравнение вычтем из уравнения (4). Тогда будем иметь
Таким образом, получаем укороченную систему
коэффициенты которой определяются по формулам (6).
Если ее ведущий коэффициент 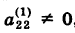
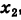
Для определения неизвестных 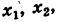
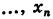
Отсюда последовательно находим неизвестные (обратный ход) 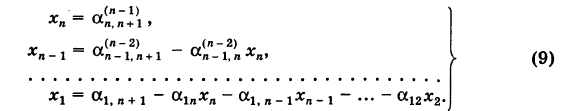
Если очередной ведущий коэффициент окажется равным нулю, то уравнения системы следует переставить надлежащим образом. Возможно, конечно, что система (1) несовместна. Тогда, естественно, метод Гаусса не допускает реализации.
Пример:
Методом Гаусса решить систему
Решение:
Составляем таблицу коэффициентов системы (10), рассматривая свободные члены ее как коэффициенты при 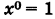
Последний столбец 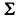
Считая отмеченный коэффициент 2 ведущим и деля на этот коэффициент все элементы первой строки таблицы (включая и входящий в столбец 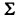
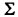
Далее, используя формулу (6), подсчитываем коэффициенты укороченной системы, не содержащей неизвестного xv Для наглядности будем называть строку, содержащую коэффициенты приведенного уравнения, приведенной, а столбец, содержащий ведущий элемент раздела, — ведущим. Тогда на основании формулы (6) справедливо правило: преобразованные коэффициенты схемы Гаусса, равны ее прежним коэффициентам минус произведение «проекций» их на соответствующие приведенную строку и ведущий столбец таблицы. Пользуясь этим, заполняем раздел II таблицы, включая контрольный столбец. Для удобства вычислении в качестве ведущего коэффициента раздела П берем элемент 8 (см. табл.).
Аналогично производится заполнение раздела III таблицы. Этим заканчивается прямой ход схемы Гаусса.
Неизвестные 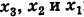
(обратный ход). Результаты обратного хода помещены в разделе IV таблицы.
Заметим, что если в качестве свободных членов взять элементы столбца 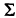
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Метод Гаусса — определение и вычисление
- Прямая линия на плоскости и в пространстве
- Плоскость в трехмерном пространстве
- Функция одной переменной
- Ряды в математике
- Дифференциальные уравнения с примерами
- Обратная матрица — определение и нахождение
- Ранг матрицы — определение и вычисление
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
🔍 Видео
Матричный метод решения систем уравненийСкачать

§28 Матричные уравненияСкачать

Решение системы уравнений методом обратной матрицы - bezbotvyСкачать

Как вычислить определитель матрицы четвертого порядка | Высшая математикаСкачать