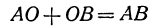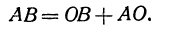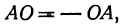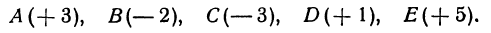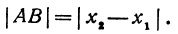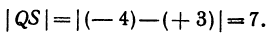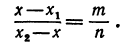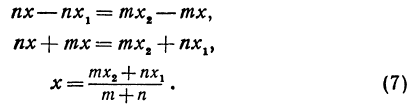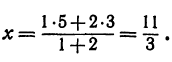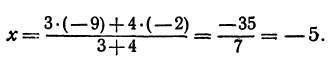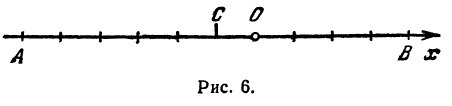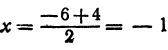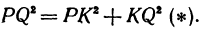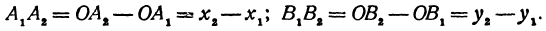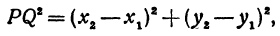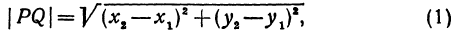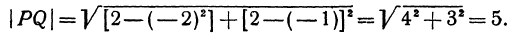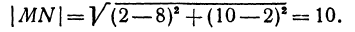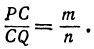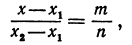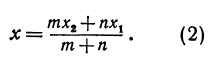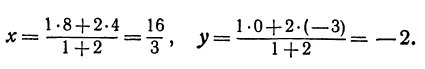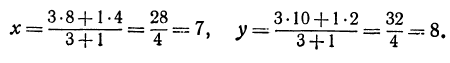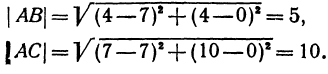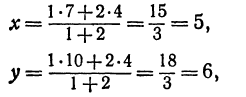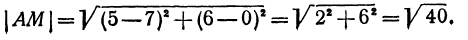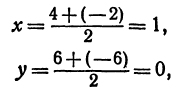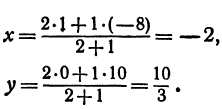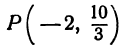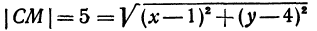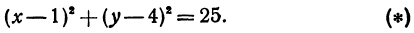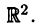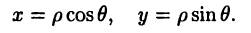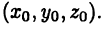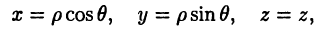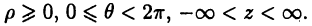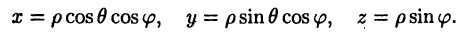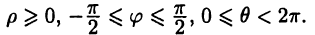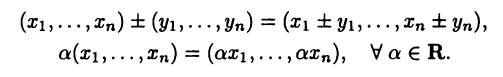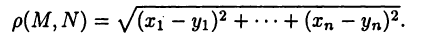- Понятие декартовой системы координат
- Сферы применения
- Прямоугольная декартова система координат на плоскости
- Прямоугольная декартова система координат в пространстве
- Задачи о точках в декартовой системе координат
- Решить задачи на декартову систему координат самостоятельно, а затем посмотреть решения
- Продолжаем решать задачи вместе
- Декартовы координаты точек плоскости. Уравнение окружности
- Числовая ось
- Прямоугольная декартова система координат на плоскости
- Формула для расстояния между двумя точками координатной плоскости
- Уравнение окружности на координатной плоскости
- Система координат в математике с примерами решения и образцами выполнения
- Координаты на прямой
- Координаты на плоскости
- Числовая ось
- Декартова система координат
- Полярная система координат
- Системы координат в пространстве
- Пространство
Видео:Лекция 22. Декартова система координат на плоскости и полярная система координатСкачать

Понятие декартовой системы координат
Если вы находитесь в некоторой нулевой точке и размышляете над тем, сколько единиц расстояния нужно пройти строго вперёд, а затем — строго вправо, чтобы оказаться в некоторой другой точке, то вы уже пользуетесь прямоугольной декартовой системой координат на плоскости. А если точка находится выше плоскости, на которой вы стоите, и к вашим расчётам добавляется подъём к точке по лестнице строго вверх также на определённое число единиц расстояния, то вы уже пользуетесь прямоугольной декартовой системой координат в пространстве.
Упорядоченная система двух или трёх пересекающихся перпендикулярных друг другу осей с общим началом отсчёта (началом координат) и общей единицей длины называется прямоугольной декартовой системой координат .
С именем французского математика Рене Декарта (1596-1662) связывают прежде всего такую систему координат, в которой на всех осях отсчитывается общая единица длины и оси являются прямыми. Помимо прямоугольной существует общая декартова система координат (аффинная система координат). Она может включать и не обязательно перпендикулярные оси. Если же оси перпендикулярны, то система координат является прямоугольной.
Прямоугольная декартова система координат на плоскости имеет две оси, а прямоугольная декартова система координат в пространстве — три оси. Каждая точка на плоскости или в пространстве определяется упорядоченным набором координат — чисел в соответствии единице длины системы координат.
Заметим, что, как следует из определения, существует декартова система координат и на прямой, то есть в одном измерении. Введение декартовых координат на прямой представляет собой один из способов, с помощью которого любой точке прямой ставится в соответствие вполне определённое вещественное число, то есть координата.
Метод координат, возникший в работах Рене Декарта, ознаменовал собой революционную перестройку всей математики. Появилась возможность истолковывать алгебраические уравнения (или неравенства) в виде геометрических образов (графиков) и, наоборот, искать решение геометрических задач с помощью аналитических формул, систем уравнений. Так, неравенство z геометрически означает полупространство, лежащее ниже плоскости, параллельной координатной плоскости xOy и находящейся выше этой плоскости на 3 единицы.
С помощью декартовой системы координат принадлежность точки заданной кривой соответствует тому, что числа x и y удовлетворяют некоторому уравнению. Так, координаты точки окружности с центром в заданной точке (a; b) удовлетворяют уравнению (x — a)² + (y — b)² = R² .
Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Сферы применения
Декартова система координат является основой рассмотрения плоских и пространственных объектов во многих разделах математики, и применяется, в частности (все ссылки — работающие):
Видео:Построение кривой в полярной системе координатСкачать

Прямоугольная декартова система координат на плоскости
Две перпендикулярные оси на плоскости с общим началом и одинаковой масштабной единицей образуют декартову прямоугольную систему координат на плоскости. Одна из этих осей называется осью Ox , или осью абсцисс, другую — осью Oy , или осью ординат. Эти оси называются также координатными осями. Обозначим через M x и M y соответственно проекции произвольной точки М на оси Ox и Oy . Как получить проекции? Проведём через точку М прямую, перпендикулярную оси Ox . Эта прямая пересекает ось Ox в точке M x . Проведём через точку М прямую, перпендикулярную оси Oy . Эта прямая пересекает ось Oy в точке M y . Это показано на рисунке ниже.
Декартовыми прямоугольными координатами x и y точки М будем называть соответственно величины направленных отрезков OM x и OM y . Величины этих направленных отрезков рассчитываются соответственно как x = x 0 — 0 и y = y 0 — 0 . Декартовы координаты x и y точки М называются соответственно её абсциссой и ординатой. Тот факт, что точка М имеет координаты x и y , обозначается так: M(x, y) .
Координатные оси разбивают плоскость на четыре квадранта, нумерация которых показана на рисунке ниже. На нём же указана расстановка знаков координат точек в зависимости от их расположения в том или ином квадранте.
Помимо декартовых прямоугольных координат на плоскости часто рассматривается также полярная система координат. О способе перехода от одной системы координат к другой — в уроке полярная система координат.
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Прямоугольная декартова система координат в пространстве
Декартовы координаты в пространстве вводятся в полной аналогии с декартовыми координатами на плоскости.
Три взаимно перпендикулярные оси в пространстве (координатные оси) с общим началом O и одинаковой масштабной единицей образуют декартову прямоугольную систему координат в пространстве.
Одну из указанных осей называют осью Ox , или осью абсцисс, другую — осью Oy , или осью ординат, третью — осью Oz , или осью аппликат. Пусть M x , M y M z — проекции произвольной точки М пространства на оси Ox , Oy и Oz соответственно.
Проведём через точку М плоскость, перпендикулярную оси Ox . Эта плоскость пересекает ось Ox в точке M x . Проведём через точку М плоскость, перпендикулярную оси Oy . Эта плоскость пересекает ось Oy в точке M y . Проведём через точку М плоскость, перпендикулярную оси Oz . Эта плоскость пересекает ось Oz в точке M z .
Декартовыми прямоугольными координатами x , y и z точки М будем называть соответственно величины направленных отрезков OM x , OM y и OM z . Величины этих направленных отрезков рассчитываются соответственно как x = x 0 — 0 , y = y 0 — 0 и z = z 0 — 0 .
Декартовы координаты x , y и z точки М называются соответственно её абсциссой, ординатой и аппликатой.
Попарно взятые координатные оси располагаются в координатных плоскостях xOy , yOz и zOx .
Видео:9 класс, 7 урок, Уравнение прямойСкачать

Задачи о точках в декартовой системе координат
Пример 1. В декартовой системе координат на плоскости даны точки
Найти координаты проекций этих точек на ось абсцисс.
Решение. Как следует из теоретической части этого урока, проекция точки на ось абсцисс расположена на самой оси абсцисс, то есть оси Ox , а следовательно имеет абсциссу, равную абсциссе самой точки, и ординату (координату на оси Oy , которую ось абсцисс пересекает в точке 0), равную нулю. Итак получаем следующие координаты данных точек на ось абсцисс:
Пример 2. В декартовой системе координат на плоскости даны точки
Найти координаты проекций этих точек на ось ординат.
Решение. Как следует из теоретической части этого урока, проекция точки на ось ординат расположена на самой оси ординат, то есть оси Oy , а следовательно имеет ординату, равную ординате самой точки, и абсциссу (координату на оси Ox , которую ось ординат пересекает в точке 0), равную нулю. Итак получаем следующие координаты данных точек на ось ординат:
Пример 3. В декартовой системе координат на плоскости даны точки
Найти координаты точек, симметричных этим точкам относительно оси Ox .
Решение. Поворачиваем на 180 градусов вокруг оси Ox направленный отрезок, идущий от оси Ox до данной точки. На рисунке, где обозначены квадранты плоскости, видим, что точка, симметричная данной относительно оси Ox , будет иметь такую же абсциссу, что и данная точка, и ординату, равную по абсолютной величине ординате данной точки, и противоположную ей по знаку. Итак получаем следующие координаты точек, симметричных этим точкам относительно оси Ox :
Видео:9 класс. Геометрия. Декартовы координаты. Уравнение окружности. Уравнение прямой. Урок #6Скачать

Решить задачи на декартову систему координат самостоятельно, а затем посмотреть решения
Пример 4. Определить, в каких квадрантах (четвертях, рисунок с квадрантами — в конце параграфа «Прямоугольная декартова система координат на плоскости») может быть расположена точка M(x; y) , если
Пример 5. В декартовой системе координат на плоскости даны точки
Найти координаты точек, симметричных этим точкам относительно оси Oy .
Видео:11. Прямая в пространстве и ее уравненияСкачать

Продолжаем решать задачи вместе
Пример 6. В декартовой системе координат на плоскости даны точки
Найти координаты точек, симметричных этим точкам относительно оси Oy .
Решение. Поворачиваем на 180 градусов вокруг оси Oy направленный отрезок, идущий от оси Oy до данной точки. На рисунке, где обозначены квадранты плоскости, видим, что точка, симметричная данной относительно оси Oy , будет иметь такую же ординату, что и данная точка, и абсциссу, равную по абсолютной величине абсциссе данной точки, и противоположную ей по знаку. Итак получаем следующие координаты точек, симметричных этим точкам относительно оси Oy :
Пример 7. В декартовой системе координат на плоскости даны точки
Найти координаты точек, симметричных этим точкам относительно начала координат.
Решение. Поворачиваем на 180 градусов вокруг начала координат направленный отрезок, идущий от начала координат к данной точке. На рисунке, где обозначены квадранты плоскости, видим, что точка, симметричная данной относительно начала координат, будет иметь абсциссу и ординату, равные по абсолютной величине абсциссе и ординате данной точки, но противоположные им по знаку. Итак получаем следующие координаты точек, симметричных этим точкам относительно начала координат:
Пример 8. В декартовой системе координат в пространстве даны точки
Найти координаты проекций этих точек:
1) на плоскость Oxy ;
2) на плоскость Oxz ;
3) на плоскость Oyz ;
4) на ось абсцисс;
5) на ось ординат;
6) на ось апликат.
1) Проекция точки на плоскость Oxy расположена на самой этой плоскости, а следовательно имеет абсциссу и ординату, равные абсциссе и ординате данной точки, и апликату, равную нулю. Итак получаем следующие координаты проекций данных точек на Oxy :
2) Проекция точки на плоскость Oxz расположена на самой этой плоскости, а следовательно имеет абсциссу и апликату, равные абсциссе и апликате данной точки, и ординату, равную нулю. Итак получаем следующие координаты проекций данных точек на Oxz :
3) Проекция точки на плоскость Oyz расположена на самой этой плоскости, а следовательно имеет ординату и апликату, равные ординате и апликате данной точки, и абсциссу, равную нулю. Итак получаем следующие координаты проекций данных точек на Oyz :
4) Как следует из теоретической части этого урока, проекция точки на ось абсцисс расположена на самой оси абсцисс, то есть оси Ox , а следовательно имеет абсциссу, равную абсциссе самой точки, а ордината и апликата проекции равны нулю (поскольку оси ординат и апликат пересекают ось абсцисс в точке 0). Получаем следующие координаты проекций данных точек на ось абсцисс:
5) Проекция точки на ось ординат расположена на самой оси ординат, то есть оси Oy , а следовательно имеет ординату, равную ординате самой точки, а абсцисса и апликата проекции равны нулю (поскольку оси абсцисс и апликат пересекают ось ординат в точке 0). Получаем следующие координаты проекций данных точек на ось ординат:
6) Проекция точки на ось апликат расположена на самой оси апликат, то есть оси Oz , а следовательно имеет апликату, равную апликате самой точки, а абсцисса и ордината проекции равны нулю (поскольку оси абсцисс и ординат пересекают ось апликат в точке 0). Получаем следующие координаты проекций данных точек на ось апликат:
Пример 9. В декартовой системе координат в пространстве даны точки
Найти координаты точек, симметричных этим точкам относительно:
7) начала координат.
1) «Продвигаем» точку по другую сторону оси Oxy на то же расстояние. По рисунку, отображающему координатное пространство, видим, что точка, симметричная данной относительно оси Oxy , будет иметь абсциссу и ординату, равные абсциссе и ординате данной точки, и апликату, равную по величине апликате данной точки, но противоположную ей по знаку. Итак, получаем следующие координаты точек, симметричных данным относительно плоскости Oxy :
2) «Продвигаем» точку по другую сторону оси Oxz на то же расстояние. По рисунку, отображающему координатное пространство, видим, что точка, симметричная данной относительно оси Oxz , будет иметь абсциссу и апликату, равные абсциссе и апликате данной точки, и ординату, равную по величине ординате данной точки, но противоположную ей по знаку. Итак, получаем следующие координаты точек, симметричных данным относительно плоскости Oxz :
3) «Продвигаем» точку по другую сторону оси Oyz на то же расстояние. По рисунку, отображающему координатное пространство, видим, что точка, симметричная данной относительно оси Oyz , будет иметь ординату и апликату, равные ординате и апликате данной точки, и абсциссу, равную по величине абсциссе данной точки, но противоположную ей по знаку. Итак, получаем следующие координаты точек, симметричных данным относительно плоскости Oyz :
По аналогии с симметричными точками на плоскости и точками пространства, симметричными данным относительно плоскостей, замечаем, что в случае симметрии относительно некоторой оси декартовой системы координат в пространстве, координата на оси, относительно которой задана симметрия, сохранит свой знак, а координаты на двух других осях будут теми же по абсолютной величине, что и координаты данной точки, но противоположными по знаку.
4) Свой знак сохранит абсцисса, а ордината и апликата поменяют знаки. Итак, получаем следующие координаты точек, симметричных данным относительно оси абсцисс:
5) Свой знак сохранит ордината, а абсцисса и апликата поменяют знаки. Итак, получаем следующие координаты точек, симметричных данным относительно оси ординат:
6) Свой знак сохранит апликата, а абсцисса и ордината поменяют знаки. Итак, получаем следующие координаты точек, симметричных данным относительно оси апликат:
7) По аналогии с симметрии в случае с точками на плоскости, в случае симметрии относительно начала координат все координаты точки, симметричной данной, будут равными по абсолютной величине координатам данной точки, но противоположными им по знаку. Итак, получаем следующие координаты точек, симметричных данным относительно начала координат:
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Декартовы координаты точек плоскости. Уравнение окружности
 Числовая ось Числовая ось |
 Прямоугольная декартова система координат на плоскости Прямоугольная декартова система координат на плоскости |
 Формула для расстояния между двумя точками координатной плоскости Формула для расстояния между двумя точками координатной плоскости |
 Уравнение окружности на координатной плоскости Уравнение окружности на координатной плоскости |
Видео:9 класс, 6 урок, Уравнение окружностиСкачать

Числовая ось
Определение 1 . Числовой осью ( числовой прямой, координатной прямой ) Ox называют прямую линию, на которой точка O выбрана началом отсчёта (началом координат) (рис.1), направление
указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины.
Определение 2 . Отрезок, длина которого принята за единицу длины, называют масштабом .
Каждая точка числовой оси имеет координату , являющуюся вещественным числом. Координата точки O равна нулю. Координата произвольной точки A , лежащей на луче Ox , равна длине отрезка OA . Координата произвольной точки A числовой оси, не лежащей на луче Ox , отрицательна, а по абсолютной величине равна длине отрезка OA .
Видео:Уравнения прямой в декартовой системе координат.Скачать

Прямоугольная декартова система координат на плоскости
Определение 3 . Прямоугольной декартовой системой координат Oxy на плоскости называют две взаимно перпендикулярных числовых оси Ox и Oy с одинаковыми масштабами и общим началом отсчёта в точке O , причём таких, что поворот от луча Ox на угол 90° до луча Oy осуществляется в направлении против хода часовой стрелки (рис.2).
Замечание . Прямоугольную декартову систему координат Oxy , изображённую на рисунке 2, называют правой системой координат , в отличие от левых систем координат , в которых поворот луча Ox на угол 90° до луча Oy осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат, не оговаривая этого особо.
Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат Oxy , то каждая точка плоскости приобретёт две координаты – абсциссу и ординату, которые вычисляются следующим образом. Пусть A – произвольная точка плоскости. Опустим из точки A перпендикуляры AA1 и AA2 на прямые Ox и Oy соответственно (рис.3).
Определение 4 . Абсциссой точки A называют координату точки A1 на числовой оси Ox , ординатой точки A называют координату точки A2 на числовой оси Oy .
Обозначение . Координаты (абсциссу и ординату) точки A в прямоугольной декартовой системе координат Oxy (рис.4) принято обозначать A (x ; y) или A = (x ; y).
Замечание . Точка O , называемая началом координат , имеет координаты O (0 ; 0) .
Определение 5 . В прямоугольной декартовой системе координат Oxy числовую ось Ox называют осью абсцисс , а числовую ось Oy называют осью ординат (рис. 5).
Определение 6 . Каждая прямоугольная декартова система координат делит плоскость на 4 четверти ( квадранта ), нумерация которых показана на рисунке 5.
Определение 7 . Плоскость, на которой задана прямоугольная декартова система координат, называют координатной плоскостью .
Замечание . Ось абсцисс задаётся на координатной плоскости уравнением y = 0 , ось ординат задаётся на координатной плоскости уравнением x = 0.
Видео:Видеоурок "Преобразование координат"Скачать

Формула для расстояния между двумя точками координатной плоскости
Утверждение 1 . Расстояние между двумя точками координатной плоскости
вычисляется по формуле
Доказательство . Рассмотрим рисунок 6.
| | A1A2| 2 = = ( x2 – x1) 2 + ( y2 – y1) 2 . | (1) |
что и требовалось доказать.
Видео:Полярная система координатСкачать

Уравнение окружности на координатной плоскости
Поскольку расстояние от любой точки окружности до центра равно радиусу, то, в соответствии с формулой (1), получаем:
Уравнение (2) и есть искомое уравнение окружности радиуса R с центром в точке A0 (x0 ; y0) .
Следствие . Уравнение окружности радиуса R с центром в начале координат имеет вид
Видео:Координаты на плоскости и в пространстве. Вебинар | МатематикаСкачать

Система координат в математике с примерами решения и образцами выполнения
Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение и перемещение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки. В математике координаты — совокупность чисел, сопоставленных точкам многообразия в некоторой карте определённого атласа.
Видео:Видеоурок "Полярная система координат"Скачать

Координаты на прямой
Если на прямой задано направление, то такую прямую называют направленной, а выбранное направление — положительным. Например, на горизонтальной прямой можно отметить направление вправо, тогда будем говорить, что направленная прямая имеет положительное направление вправо. Можно с таким же правом считать положительным и направление влево. Направление прямой будем указывать стрелкой (рис. 1).
Выберем на направленной прямой точку, которую назовем началом отсчета или началом координат, и будем обозначать ее буквой О.
Кроме того, выберем отрезок, длину которого будем считать единицей длины. Этот отрезок назовем единицей масштаба.
Определение:
Прямая линия, на которой указаны: начало отсчета, единица масштаба и направление отсчета, называется осью координат.
Рассмотрим отрезок, расположенный на оси координат. Если одну из точек, ограничивающих отрезок, назовем началом отрезка, а другую—его концом, то отрезок будем называть направленным отрезком. Направленный отрезок обозначают двумя буквами, например: АВ, СМ, КР, причем на первом месте ставят букву, обозначающую начало, на втором—букву, обозначающую конец. Таким образом, запись АВ показывает, что начало отрезка есть точка А, а конец — точка В. Направление отрезка считается от начала к концу.
Если направление отрезка совпадает с направлением оси, то отрезок называют положительно направленным; если же его направление противоположно направлению оси, то — отрицательно направленным. Таким образом, отрезки АВ и ВА имеют противоположные направления. Это записывают так:
Отметим, что положительный отрезок может находиться в любом месте координатной оси, только его направление должно совпадать с направлением оси.
Сложение направленных отрезков производится по следующему правилу:
Для того чтобы сложить два направленных отрезка, нужно к концу первого приложить начало второго; тогда отрезок, имеющий началом начало первого отрезка и концом конец второго, называют суммой двух направленных отрезков.
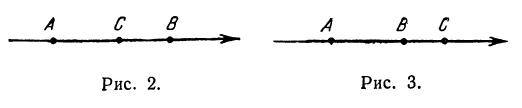
Из этого определения вытекает, что сумма отрезков АВ и ВС равна отрезку АС при любом расположении точек А, В, С, т. е. всегда:
Координатным отрезком точки А называется направленный отрезок, имеющий начало в точке О (т. е. в начале координат), а концом — рассматриваемую точку А.
Всякий направленный отрезок, лежащий на оси, можно выразить через координатные отрезки его начала и конца. В самом деле, рассмотрим направленный отрезок АВ. На основании равенства (2) можно написать
(здесь вместо точки В поставлена точка О, а вместо точки С точка В) или
Отрезок ОВ есть координатный отрезок (его начало есть точка О), но отрезок АО не является координатным, поскольку его начало не является началом координат. Но в силу равенства (1)
поэтому можно написать
Получен следующий результат:
Направленный отрезок равен разности координатного отрезка его конца и координатного отрезка его начала.
Это верно для любого отрезка, лежащего на координатной оси.
Теперь дадим одно из самых важных определений: Координатой точки на координатной оси называется число, равное по абсолютной величине длине координатного отрезка этой точки и по знаку совпадающее со знаком координатного отрезка.
Точку А, имеющую координатной число х, будем обозначать А (х).
Указанные на рис. 4 точки имеют следующие координаты:
Будем также писать
Если даны точки А(х1) и В(х2), то на основании формул (3) и (4) получим
т. е. направленный отрезок равен разности координат его конца и начала.
Отсюда сразу получаем, что длина отрезка равна абсолютной величине разности координат его конца и начала.
Длину отрезка будем обозначать, пользуясь знаком | |, т. е. знаком абсолютной величины. Таким образом, длина отрезка АВ будет записываться так:
Пример:
Если даны точки А (+4), В (+8), то отрезок АВ = (+8) — (+4), а его длина |АВ|= |+ 4 | = 4.
Если даны точки М (+5) и Р (+3), то отрезок МР = (+3)—(+5) = —2, а его длина |МР| = | —2| = 2. Даны две точки: Q (+ 3) и S (—4). Длина отрезка
Даны две точки R (— 6) и Т (—2); отрезок RТ = ( — 2) — (—6) = +4, а его длина | RТ | = 4.
Пример:
Начало отрезка АВ находится в точке А (—950), а конец—в точке В ( —1200); найти его направление и длину.
Отрезок АВ = ( — 1200)—( — 950) = —250. Так как он
получился отрицательным, то его направление противоположно направлению оси. Его длина равна | АВ | = | —250 | = 250.
Задача:
На координатной оси даны две точки: A (x1) и В (x2) Найти точку С, лежащую между ними и делящую отрезок АВ в отношении т : п.
Чтобы найти точку, надо найти ее координату. По условию задачи должно быть
Обозначая координату искомой точки С через х и выражая отрезки через координаты, т. е. применяя формулу (5), получим, что АС = х—х1, СВ = х2 — х. Подставляя эти выражения в равенство (6), будем иметь
Решая последнее уравнение относительно х, найдем:
Это и есть координата искомой точки.
Пример:
Найти точку С, делящую отрезок АВ в отношении 1:2, если даны начало отрезка А (+ 3) и конец В ( + 5) (рис. 5).
Здесь т = 1, п = 2, х1=-3, х2 = 5. Применяя формулу (7), получим
Пример:
Найти точку М, делящую расстояние между точками Р ( — 2) и Q (—9) в отношении 3:4 (рис. 5). Здесь т = 3, п = 4, х1 = —2, х2 = —9. По формуле (7) находим
Если т = n т. е. точка С делит отрезок АВ пополам, тогда формула (7) перепишется так:
Таким образом, координата точки, делящей отрезок пополам, равна средней арифметической координат его начала и конца.
Пример:
Найдем середину отрезка, заключенного между точками А (—6) и B (4) (рис. 6).
Применяя формулу (8), получим, что
Видео:Решение задач на параллельный перенос в декартовой системе координат. Геометрия 8 классСкачать

Координаты на плоскости
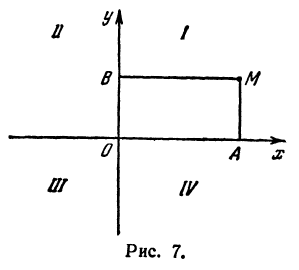
Возьмем на плоскости две взаимно перпендикулярные прямые, пересекающиеся в точке О. На каждой из этих прямых зададим направление, указав его стрелкой (рис. 7).
Установим масштаб, общий для обеих прямых, а за начало отсчета выберем точку О.
Определение:
Координатными осями на плоскости называются две взаимно перпендикулярные прямые, на которых установлены: 1) на-правления, 2) масштаб и 3) общая точка отсчета.
Назовем одну из осей осью Ох или осью абсцисс, другую — осью Оу или осью ординат. Точку их пересечения назовем началом координат.
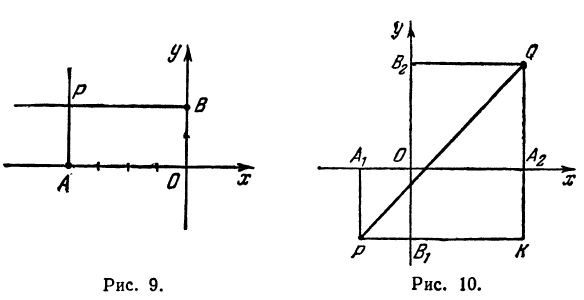
Возьмем произвольную точку M, лежащую на плоскости, и опустим из нее перпендикуляры на оси координат, т. е. найдем ее проекции на оси. Обозначим проекцию на ось Ох через А, а проекцию на ось Оу через В. Обозначим координату точки А (по оси Ох) через х, а координату точки В (по оси Оу) через у. Введем определение:
Определение:
Абсциссой точки называется координата ее проекции на ось Ох. Ординатой точки называется координата ее проекции на ось Оу.
Абсциссу точки обычно обозначают буквой х, ординату— буквой у. Точку М, имеющую абсциссу х и ординату у, обозначают следующим образом: пишут скобку и в ней на первом месте ставят абсциссу, на втором ординату и разделяют эти два числа запятой или точкой с запятой. Таким образом, запись точки выглядит так: М(х, у).
Координатные оси разделяют плоскость на четыре части, которые называют четвертями.
Первой четвертью называется та часть плоскости, в которой абсцисса и ордината положительны.
Второй четвертью — та часть, в которой абсцисса отрицательна, а ордината положительна.
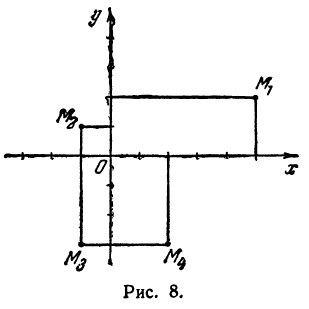
Третьей четвертью — та часть, в которой абсцисса и ордината отрицательны, и, наконец, четвертой, — та часть, в которой абсцисса положительна, а ордината отрицательна (рис. 7), На рис. 8 указаны точки M1 (5, 2), М2 ( — 1, 1), М3 (-1, -3), М4 (2, -3). Заметим, что абсцисса х = ОА по абсолютной величине равна расстоянию точки от оси ординат, так как ОА = ВМ (см. рис. 7), а ордината — расстоянию точки М от оси абсцисс, так как ОВ = АМ.
Пример:
Найти точку Р( — 4, 2) (рис. 9), Возьмем на оси Ох точку А с координатой —4, ее координатный отрезок ОА = —4. На оси Оу возьмем точку В с координатным отрезком ОВ= 2. Восставим перпендикуляры к осям из точек А и В, точка их пересечения и даст искомую точку Р.
Задача:
Найти расстояние между точками Р (х1, у1) и Q( х1, у1 ). Иначе говоря, нужно найти длину отрезка РQ(рис. 10).
Обозначим проекцию точки Р на ось Ох через А1, а ее проекцию на ось Оу — через В1. Проекцию точки Q на ось Ох обозначим через А2 и через В2— ее проекцию на ось Oy. Тогда ОА1 = х1, ОВ1 = y1, ОА2 = х2, ОВ2 = у2. Из точки Р проведем прямую, параллельную оси Ох, до пересечения с прямой A2Q в точке К. Рассмотрим треугольник PKQ. По теореме Пифагора имеем
Но РК = А1А2, KQ = B1B2, как противоположные стороны прямоугольников; кроме того, на основании формулы (3 из § 1) направленные отрезки А1А2 и В1В2 будут равны
Подставляя полученные выражения в (*), получим
т. е. расстояние между двумя точками равно корню квадратному из суммы квадратов разностей координат.
Примечание:
Расстояние между двумя точками, так же как длина отрезка, всегда положительно, поэтому в формуле (1) перед квадратным корнем берут только знак плюс.
Пример:
Найти расстояние между точками Р (— 2, — 1) и Q (2, 2). Применяя формулу (1), получим
Пример:
Найти длину отрезка MN, если даны М (8, 2) и N(2, 10). Применяя формулу (1), получим
Задача:
Найти точку С, делящую отрезок PQ в отношении т : п, если известны координаты точек Р (х1, у1) и Q (х2, у2). По условию задачи надо найти такую точку С, чтобы было выполнено равенство
Решение:
Обозначим, как и выше, проекции точки Р на оси через А1 и В1, а проекции точки Q—через А2 и В2; тогда ОА1 = х1 , OB1 = y1, ОА2 =х2, ОВ2=у2 (рис. 11). Кроме того, обозначим координаты искомой точки С через х и у, а ее проекции на оси — через А и В, т. е. ОА = х, ОВ = у.
Так как прямые А1Р, АС и А2Q параллельны между собой, то на основании теоремы о пропорциональных отрезках можно записать, что
Но А1А = ОА — ОА1 = х—х1, АА2 = ОА2 — ОА = х2—х; поэтому, подставляя в равенство (*), будем иметь уравнение
решая которое найдем абсциссу точки С:
Рассуждая аналогично о проекциях на ось Оу, т. е. о точках В1, В и В2, получим ординату точки С, делящей отрезок в отношении т : п,
Итак, искомая точка С имеет координаты, определяемые равенствами (2) и (3).
Пример:
Найти точку, делящую в отношении 1:2 отрезок PQ, где Р (4, —3) и Q (8, 0). Здесь х1 = 4, у1 = — 3, х2 = 8, у2 = 0, т = 1, п = 2. Применяя формулы (2) и (3), получим:
Пример:
Найти точку, делящую расстояние между точками А (4, 2) и B (8, 10) в отношении 3 : 1. Здесь х1=-4, у1 = 2, х2 = 8, у2= 10, т = 3, п = 1. По формулам (2) и (3) находим:
Следствие (из формул (2) и (3)). Если точка С делит отрезок РQ пополам, то т = n, поэтому
т. е. абсцисса середины отрезка равна средней арифметической абсцисс его начала и конца; ордината середины отрезка равна средней арифметической ординат его начала и конца.
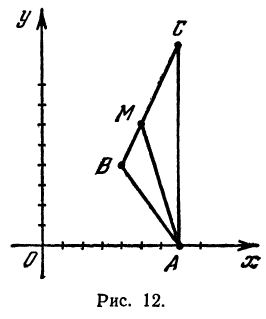
Задача:
Даны три вершины треугольника: А (7, 0), В (4, 4) и С (7, 10). Найти длину биссектрисы угла A (рис. 12).
Найдем длины сторон АВ и АС. Для этого применим формулу (1):
Обозначим точку пересечения биссектрисы угла А с противоположной стороной ВС через М, а ее координаты—через х и у. Помня, что биссектриса внутреннего угла треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам, можно утверждать, что точка М делит отрезок ВС в отношении 5 : 10 = 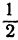
Теперь вычисляем длину биссектрисы между точками А(7, 0) и М(5, 6):
Задача:
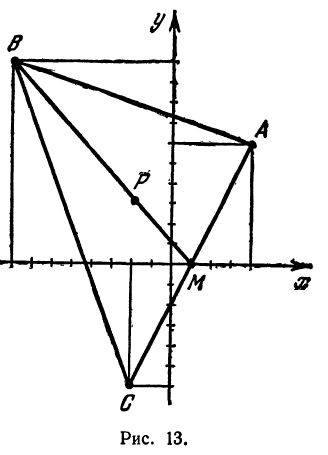
Найти точку пересечения медиан треугольника, вершинами которого являются точки А(4, 6), В(—8, 10), С( —2, —6) (рис. 13).
Точка пересечения медиан делит каждую из медиан в отношении 2:1, считая от вершины треугольника. Обозначим через М середину стороны АС; по формулам (4) и (5) можно найти ее координаты:
т. е. М(19 0). Точка Р пересечения медиан делит отрезок ВМ в отношении 2:1, поэтому ее координаты найдутся по формулам (2)
Итак, искомая точка
Задача:
Записать условие того, что точка М (х, у) находится на расстоянии По формуле (1) имеем
или, возводя обе части равенства в квадрат, получим
Это равенство есть уравнение с двумя неизвестными х и у. Этому уравнению удовлетворяют координаты любой точки, лежащей на расстоянии 5 от точки С. Иначе говоря, ему удовлетворяют координаты любой точки, принадлежащей геометрическому месту точек, расстояние которых от точки С равно 5. Это геометрическое место есть окружность.
Следовательно, можно сказать, что уравнение (*) есть уравнение окружности с центром в точке С и радиуса 5.
В следующих главах будут рассмотрены уравнения с двумя неизвестными х и у и те линии (геометрические места), точки которых имеют координаты, удовлетворяющие этим уравнениям.
Видео:A.6.6 Переход между декартовой и другими системами координатСкачать

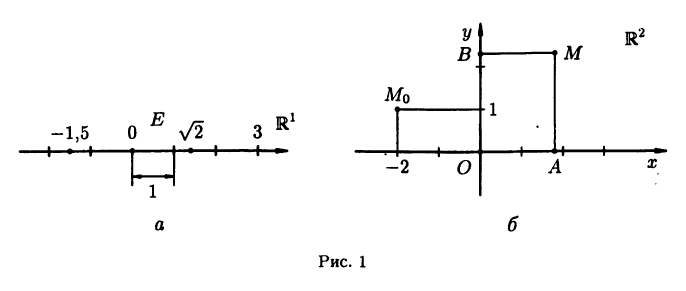
Числовая ось
Числовой осью называют направленную прямую, на которой указывается начальная точка О и задается некоторый «эталон» длины Е. Каждой точке 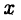
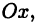
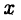
длине со знаком минус — в противном случае (см. рис. 1 а). Числовую ось будем обозначать 
Указанное соответствие между точками числовой оси 
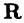
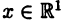
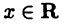
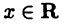
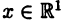
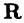

Видео:ДЕКАРТОВЫ КООРДИНАТЫ. Контрольная № 3 Геометрия 9 класс.Скачать

Декартова система координат
Декартовой (прямоугольной) системой координат на плоскости называют две взаимно перпендикулярные числовые оси 
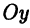

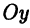
Пусть М — произвольная точка координатной плоскости. Опустим из нее перпендикуляры МА и МВ на оси 
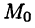
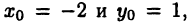
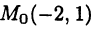
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

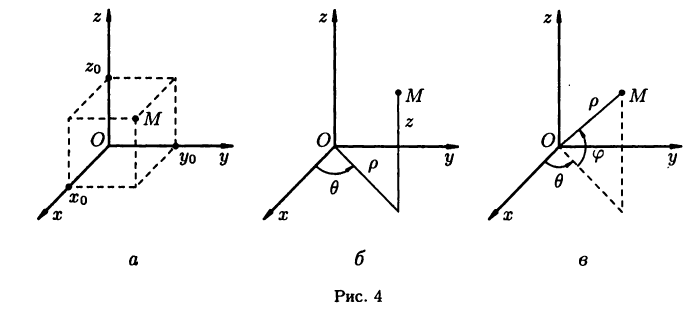
Полярная система координат
В плоскости зададим луч 
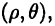
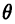

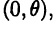
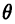
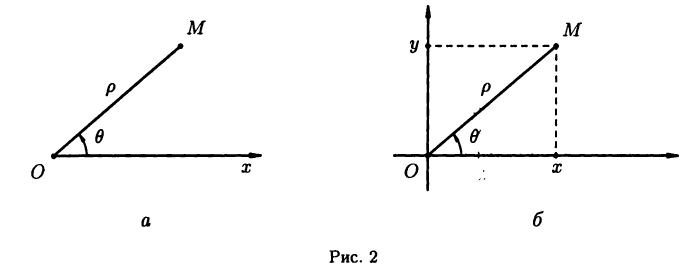
Полярные и декартовы координаты, заданные на одной плоскости (см. рис. 2 6), связаны очевидными равенствами:
Полярные координаты удобны для задания многих кривых. Например, уравнение р=2 описывает окружность, изображенную на рис. За. Уравнение 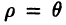
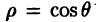
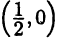
Видео:Графический способ решения систем уравнений. Алгебра, 9 классСкачать

Системы координат в пространстве
Декартова система координат в пространстве определяется тремя взаимно перпендикулярными осями 
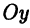
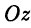
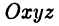
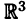
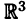
Аналогами полярной системы координат в пространстве служат цилиндрическая и сферическая системы координат.
Цилиндрическая система координат (рис. 4 б) представляет собой объединение полярной системы координат в плоскости 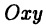
где
Сферическая система координат (рис. 4 в) связана с декартовой системой равенствами
где
Видео:Алгебра 8 класс (Урок№6 - Решение уравнений графическим способом.)Скачать

Пространство
Пространство
На плоскости и в пространстве положение точки в декартовых координатах полностью определяется соответственно, парой и тройкой чисел вида [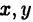
Упорядоченную систему из 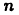

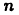
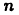
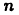
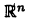
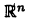
Понятие пространства 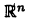
Наконец, обобщая известную из аналитической геометрии формулу, определяют расстояние между двумя точками 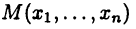
Прямую, плоскость и пространство можно рассматривать как пространства 

Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института