Решение уравнений сравнений первой степени (3 видео)

Онлайн НОД и НОК, разложение на множители, сравнения по модулю

С помощью данного онлайн-калькулятора можно вычислить НОД и НОК нескольких чисел, разложить число на простые множители, решить линейные и нелинейные сравнения, системы сравнений.

Наибольший общий делитель (НОД, англ. GCD) нескольких целых чисел есть наибольшее из натуральных чисел, которое делит каждое из данных чисел.

Наименьшее общее кратное (НОК, англ. LCM) нескольких целых чисел есть наименьшее из натуральных чисел, которое делится на каждое из данных чисел.

Запишите свои числа через запятую и/или пробел и нажмите кнопку.

Видео:✓ Сравнение по модулю. Арифметика остатков | Ботай со мной #034 | Борис ТрушинСкачать

Сравнения первой степени.

Любое сравнение первой степени можно привести к виду ax ≡ b (mod m). Рассмотрим случай, когда (a, m)=1. Согласно утверждению 2 пункта 3 §3, когда x пробегает полную систему вычетов по модулю m, ax тоже пробегает полную систему вычетов по по модулю m. Следовательно, при одном и только одном значении x из полной системы вычетов, ax будет сравнимо с b, т.е. при (a, m)=1 сравнение имеет ровно 1 решение.

Нахождение решения: Так как (a, m) = 1, то по теореме обратимости 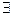a -1 , и тогда исходному сравнению равносильно x ≡ a -1 ∙b (mod m).

Пусть теперь (a,m)=d>1. Для того, чтобы сравнение имело решение, необходимо, чтобы db, иначе сравнение невозможно (свойство сравнений №14).

Если же a=a₁d, b=b₁d, m=m₁d , то исходному сравнению равносильно a₁x≡b₁(mod m₁), причем (a₁,m₁)=1 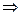сравнение имеет 1 решение по mod m₁: x≡x₁(mod m₁), или d решений по модулю m:

Решить сравнение 6x = 5 (mod 35).

Вычислим НОД(6, 35), пользуясь алгоритмом Евклида:

5 = 5∙1+0 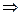НОД(6, 35)=1.

Вычислим обратный элемент к 6 по модулю 35, пользуясь расширенным алгоритмом Евклида:

1 = 6–5=6–(35–6∙5)=6–35+6∙5= 6∙6–35

Домножим правую и левую части исходного сравнения на 6:

6 -1 ∙6x≡6 -1 ∙5(mod 35)

Ответ: x ≡ 30 (mod 35)

Решить сравнение 18x = 6 (mod 24).

Вычислим НОД(18, 24), пользуясь алгоритмом Евклида:

18 = 2∙6+0 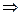НОД(18, 24)=6.

Правая и левая части сравнения, а также модуль, делятся на 6. Разделим исходное сравнение на 6 и получим равносильное сравнение:

Вычислим НОД(3, 4), пользуясь алгоритмом Евклида:

3 = 3∙1 + 0 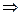НОД(3, 4)=1.

Вычислим обратный элемент к 3 по модулю 4, пользуясь расширенным алгоритмом Евклида:

1=4–3 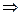3 -1 = –1(mod 4).

Домножим правую и левую части сравнения (*) на –1:

3 -1 ∙3x=–1∙1 (mod 4) 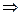x≡ –1 (mod 4).

Или, переводя решение в систему наименьших неотрицательных вычетов, x≡ 3 (mod 4).

Видео:Теория чисел. 6. Методы решения сравнений 1 й степениСкачать

Линейные сравнения с одним неизвестным (стр. 1 )

Решение уравнений сравнений первой степени

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5

§ 4. Линейные сравнения с одним неизвестным.

1. Общие определения.

Определение 1. Сравнением с одним неизвестным по модулю называется сравнение вида , (1)

левая часть которого – многочлен с целыми коэффициентами. Если не делится на число , то число называется степенью сравнения; если , то старший член сравнения (1) удовлетворяет условию и поэтому в (1) его можно отбросить.

Определение 2. Решением сравнения всякое целое число , которое удовлетворяет сравнению, то есть такое, что .

Легко понять, что в этом случае вместе с числом сравнению удовлетворяют и все числа класса . Поэтому класс вычетов по модулю , числа которого удовлетворяют сравнению , считается за одно решение этого сравнения. При таком соглашении сравнение (1) будет иметь столько решений, сколько вычетов ПСВ ему удовлетворяют. Поскольку ПСВ по модулю состоит из вычетов, то сравнение (1) может иметь только конечное количество решений или не может иметь их совсем.

Сравнения решают путем построения более простых сравнений, равносильных заданным.

Определение 3. Два сравнения называются равносильными, если множества их решений совпадают.

Чтобы построить сравнения, равносильные заданному сравнению, над заданным сравнением проводят операции, которые основываются на свойствах сравнимости, рассмотренных раньше. К операциям, которые не меняют множества решений, принадлежат такие:

а) прибавление к обеим частям сравнения произвольного многочлена с целыми коэффициентами,

б) прибавление к одной из частей сравнения многочлена с коэффициентами, кратными модулю ,

в) умножение обеих частей сравнения на число, взаимно простое с модулем,

г) умножение обеих частей сравнения и модуля на одно и тоже положительное целое число.

2. Сравнение первой степени.

Сравнения первой степени имеют вид (2). Перенеся свободный член в правую часть сравнения, и меняя обозначения коэффициентов, получим

. (3)

При решении таких сравнений рассматривают два случая: и .

Теорема 1. Если , то сравнение (3) имеет единственное решение.

Доказательство. Сравнение может иметь не более решений, в соответствии с количеством чисел в ПСВ. Если пробегает ПСВ, то и линейная форма также пробегает ПСВ. При этом один раз линейная форма примет то значение, которое сравнимо с нулем, та как нуль есть один из вычетов ПСВ.

Теорема 2. Если и число не делится на , то сравнение не имеет решений.

Доказательство проводится методом от противного, с использованием свойств делимости.

Теорема 3. Если и , то сравнение (3) имеет решений.

Доказательство. Пусть . Тогда сокращая (3) на , получим сравнение (4), которое равносильное сравнению (3). Поскольку , то последнее сравнение по теореме 1 имеет единственное решение — , то есть . Рассмотрим последовательность классов

(5)

Нетрудно убедиться, что эти классы являются решениями сравнения (3), для этого достаточно подставить их в сравнение, причем они различны (это доказывается методом от противного и с использованием свойств сравнимости) и других решений нет.

Замечание. Неопределенное уравнение первой степени сводится к решению сравнения или .

Способы решения сравнения первой степени.

Рассмотрим некоторые наиболее распространенные способы решения сравнений первой степени.

I способ. Подстановка в сравнение чисел ПСВ. Этот способ применяется при небольших модулях. При больших модулях подстановку вычетов ПСВ проводят только на заключительном этапе построения равносильных сравнений.

II способ. Приведение сравнения первой степени к равносильному сравнению с коэффициентом при , равному единице. Этот способ основывается на проведение ряда равносильных преобразований заданного сравнения с помощью операций, рассмотренных нами выше.

III способ. Способ Эйлера. Пусть задано сравнение , (6)

где . Сравнение имеет единственное решение. По теореме Эйлера , верным будет и сравнение и сравнивая его с (6), видим, что (7).

IV способ. Решение сравнения при помощи цепных дробей.. Пусть задано сравнение , (6) где . Разложим в цепную дробь. Если и являются последними подходящими дробями, то по свойству подходящих дробей имеем, . Учитывая, что первое слагаемое кратно модулю, получим дальше . Умножая левую и правую часть сравнения на , получим . Следовательно, решением сравнения будет . (8)