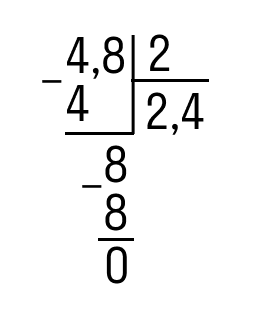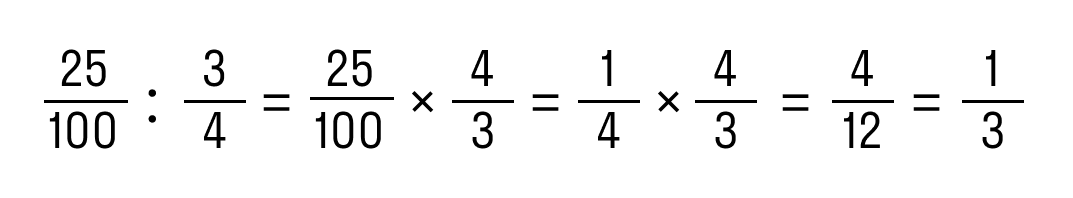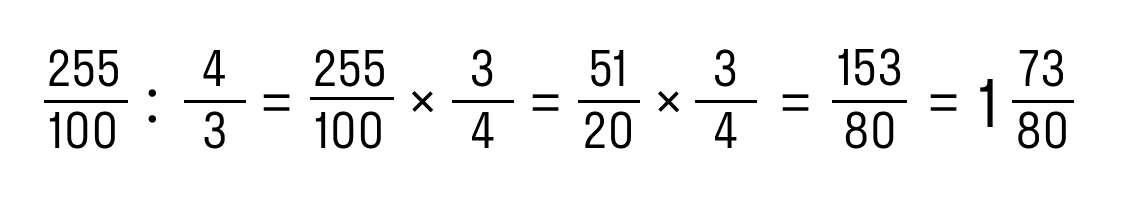О чем эта статья:
5 класс, 6 класс
- Понятие десятичной дроби
- Свойства десятичных дробей
- Как записать десятичную дробь
- Как читать десятичную дробь
- Преобразование десятичных дробей
- Как перевести десятичную дробь в проценты
- Преобразование десятичных дробей
- Как перевести десятичную дробь в обыкновенную
- Действия с десятичными дробями
- Как разделить десятичную дробь на натуральное число
- Как разделить десятичную дробь на обыкновенную
- Как умножить десятичную дробь на обыкновенную
- Как решать десятичные дроби 5 класс объяснение примеры
- Понятие десятичной дроби 5 класс
- Правила сравнения десятичных дробей
- Правила округления десятичных дробей
- Сложение вычитание десятичных дробей примеры
- Умножение и деление десятичных дробей 5 класс
- урок по математике 5 кл — Действия с десятичными дробями, решение уравнений план-конспект урока по алгебре (5 класс) по теме
- Скачать:
- Предварительный просмотр:
- Подписи к слайдам:
- Предварительный просмотр:
- По теме: методические разработки, презентации и конспекты
- 📸 Видео
Видео:Уравнения с десятичными дробями в 5 классе (на умножение и деление).Скачать

Понятие десятичной дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
- обыкновенный вид — ½ или a/b,
- десятичный вид — 0,5.
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Видео:Как решать уравнения с десятичными дробями - математика 5 классСкачать

Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
- 0,600 = 0,6
- 21,10200000 = 21,102
| Основные свойства |
|---|
|
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
- Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
- Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде.
- Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.
Обучение на курсах по математике — отличный способ закрепить полученные знания на практике и подтянуть сложные темы.
Видео:Уравнения с десятичными дробями. Математика 5 классСкачать

Как записать десятичную дробь
Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.
Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.
- Знаменатель равен 10 — это один ноль.
- Отсчитываем справа налево в числителе дробной части один знак и ставим запятую.
- В полученной десятичной дроби цифра 1 — целая часть, цифра 6 — дробная часть.
Пример 2. Перевести 37/1000 в десятичную дробь.
- Знаменатель равен 1000 — это три нуля.
- Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
- Так как в числителе только две цифры, то на пустующие места пишем нули.
- В полученной десятичной дроби цифра 0 — целая часть, 037 — дробная часть.
Ответ: 37/1000 = 0,037.
Видео:Сложные уравнения со скобками. Как решать уравнения в несколько действий в 5 классе.Скачать

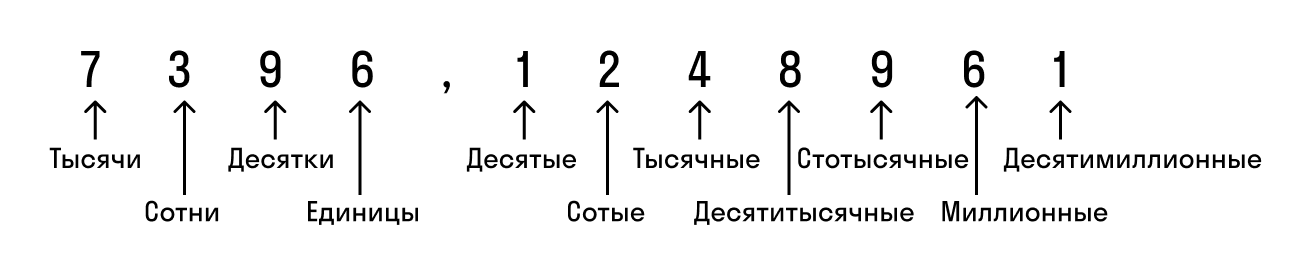
Как читать десятичную дробь
Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:
| Сколько цифр после запятой? | Читается, как |
|---|---|
| одна цифра — десятых; | 1,3 — одна целая, три десятых; |
| две цифры — сотых | 2,22 — две целых, двадцать две сотых; |
| три цифры — тысячных; | 23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных; |
| четыре цифры — десятитысячных; | 0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных; |
| и т.д. |
Сохраняй наглядную картинку, чтобы быстрее запомнить.
Видео:КАК РЕШИТЬ УРАВНЕНИЕ С ДЕСЯТИЧНЫМИ ДРОБЯМИ? Примеры | МАТЕМАТИКА 5 классСкачать

Преобразование десятичных дробей
Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!
Как перевести десятичную дробь в проценты
Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.
Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.
А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:
0,15 = 0,15 · 100% = 15%.
Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.
2/5 = 0,4
0,4 · 100% = 40%
8/25 = 0,32
0,32 · 100% = 32%
Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого. Наглядная табличка — наш друг-помощник:
Преобразование десятичных дробей
Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.
Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).
Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся!
Пример 1. Перевести 5,4 в смешанное число.
- Читаем вслух: пять целых четыре десятых. «Четыре десятых» подсказывают, что в числителе будет 4, а в знаменателе — 10. В смешанном виде эта дробь выглядит так: 5 4/10.
- А теперь сократим числитель и знаменатель на два (потому что можно) и получим: 5 2/5.
Пример 2. Перевести 4,005 в смешанное число.
- Читаем вслух: четыре целых пять тысячных. Значит 5 — идет в числитель, а 1000 — в знаменатель. В смешанном виде получается так: 4 5/1000. После сокращения: 4 1/200.
Ответ: 4,005 = 4 1/200.
Пример 3. Перевести 5,60 в смешанное число.
- Читаем вслух: пять целых шестьдесят сотых. Отправляем 60 в числитель, а 100 — в знаменатель. В смешанном виде дробь такая: 5 60/100.
- Сократим дробную часть на 10 и получим 5 6/10. Или можно вспомнить про свойство десятичной дроби и просто отбросить нули в числителе и знаменателе.
Ответ: 5,60 = 5 6/10.
Как перевести десятичную дробь в обыкновенную
Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:
- Перепишем исходную дробь в новый вид: в числитель поставим исходную десятичную дробь, а в знаменатель — единицу. Например:
- 0,35 = 0,35/1
- 2,34 = 2,34/1
- Умножим числитель и знаменатель на 10 столько раз, чтобы в числителе исчезла запятая. При этом после каждого умножения запятая в числителе сдвигается вправо на один знак, а у знаменателя соответственно добавляются нули. На примере легче:
- 0,35 = 0,35/1 = 3,5/10 = 35/100
- 2,34 = 2,34/1 = 23,4/10 = 234/100
- А теперь сокращаем — то есть делим числитель и знаменатель на кратные им числа:
- 0,35 = 35/100, делим числитель и знаменатель на пять, получаем 6/20, еще раз делим на 2, получаем итоговый ответ 3/10.
- 2,34 = 234/100 = 117/50 = 2 17/50.
Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!
Видео:Уравнение. 5 класс.Скачать

Действия с десятичными дробями
С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.
Как разделить десятичную дробь на натуральное число
- Разделить целую часть десятичной дроби на это число.
- Поставить запятую в частном и продолжить вычисление, как при обычном делении.
Пример 1. Разделить 4,8 на 2.
- Записать деление уголком.
- Разделить целую часть на два. Записать полученный результат в частное и поставить запятую.
- Умножить частное на делитель, записать, посмотреть на остаток от деления. Но мы еще не закончили, поэтому остаток «ноль» не записываем. Сносим 8 и делим её на 2.
- Делим еще раз. Записываем полученную 4 в частном и умножаем её на делитель:
Ответ: 4,8 : 2 = 2,4.
Пример 2. Разделить 183,06 на 45.
- Записать деление уголком.
- Разделить целую часть 183 на 45. Записать результат, поставить запятую в частном.
- Записать результат разницы 183 и 180. Снести 0. Записать 0 в частное, чтобы снести 6.
- Записать результат разницы 306 и 270. 36 не делится на 45, поэтому добавляем ноль и производим разницу.
Ответ: 183,06 : 45 = 4,068.
Как разделить десятичную дробь на обыкновенную
Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.
Пример 1. Разделить 0,25 на 3/4.
- Записать 0,25 в виде обыкновенной дроби: 0,25 = 25/100.
- Разделить дробь по правилам:
Ответ: 0,25 : 3/4 = 1/3.
Пример 2. Разделить 2,55 на 1 1/3.
- Записать 2,55 в виде обыкновенной дроби: 2,55 = 255/1000.
- Записать 1 1/3 в виде обыкновенной дроби: 1 1/3 = 4/3.
- Разделить дробь по правилам:
Ответ: 2,55 : 1 1/3 = 1 73/80.
Как умножить десятичную дробь на обыкновенную
Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.
Пример 1. Умножить 2/5 на 0,8.
- Записать 0,8 в виде обыкновенной дроби: 0,8 = 8/10.
- Умножаем по правилам: 2/5 ∗ 8/10 = 2/5 ∗ 4/5 = 8/25 = 0,32.
Ответ: 2/5 ∗ 0,8 = 0,32.
Пример 2. Умножить 0,28 на 6 1/4.
- Записать 6 1/4 в виде десятичной дроби: 6 1/4 = 6,25.
- Умножаем по правилам: 0,28 ∗ 6,25 = 0,8.
Ответ: 0,28 ∗ 6 1/4 = 0,8.
Видео:Уравнения с дробями. Как решать уравнения с дробями в 5 классе.Скачать

Как решать десятичные дроби 5 класс объяснение примеры
Для многих учеников десятичные дроби, как и действия с ними, вполне понятны. Но, есть и такие, которым трудно разобраться в данной теме. Чтобы помочь справиться с этой проблемой, учителям и родителям следует объяснить материал пятиклассникам в простой и доступной форме.
Видео:Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Понятие десятичной дроби 5 класс
Дроби, в написании которых, используют разделительную запятую, называют десятичными. Их особенность, знаменатель, являющийся степенью числа 10, т.е., это всегда единица с нулями. При чем, сначала пишут целую часть числа, затем — запятую, а после нее пишут дробную часть. Знаменатель нельзя увидеть в обычной форме записи, так как он «спрятан» за знаками после запятой.
Обычно, такие дроби пишут без знаменателя. При этом, отделяется запятой целая часть, а следом за запятой должно стоять такое количество цифр, сколько нулей в обычной дроби.
Деление и умножение на 10; 100; 0,1; 0,01 и т.д. только сдвигает запятую, но не меняет цифры.
Видео:Уравнение с десятичными дробямиСкачать

Правила сравнения десятичных дробей
Прежде всего, необходимо понимать, что дробь 0,2 и дробь 0,20 друг другу равны. Нули, стоящие в конце десятичной дроби, величины ее не меняют и располагаться будут на координатном луче в одной точке. При сравнивании десятичных дробей, прежде всего сравниваются целые части, они расположены от запятой слева.
Например: 8,57 > 3,87, так как 8 > 3.
В случае, если равны целые части, сравнивают дробные.
На луче координат меньшие десятичные дроби находятся левее, так же, как натуральные числа:
0,2 Округление натуральных чисел 5 класс
Практически каждый день мы используем округление. Например, если от школы до дома расстояние — 602 метра, мы говорим, округляя значение, что это расстояние — 600 метров. Т.е., число 602 мы приблизили к числу 600, что воспринимается легче. Еще один пример — батон хлеба весит 397 грамм, округлив можно сказать, что батон весит 400 грамм.
Округление — это замена числа более приближенным и легким для восприятия.
В результате, при округлении, мы получаем «приближенное» число. Обозначается округление знаком ≈, который читается — приближенно равно (приблизительно).
Пример: 604≈600; 597≈600. Читается — шестьсот четыре приближенно равно шестистам и пятьсот девяносто семь приближенно равно шестистам.
Посмотрим еще примеры:
В примере мы видим округление до тысяч. Обратите внимание, что округление происходит в одном случае в большую сторону, а в другом в меньшую. Все числа после округления заменены на нули.
Видео:Уравнение с дробями видео урок ( Математика 5 класс )Скачать

Правила округления десятичных дробей
Видео:Уравнения с десятичными дробями в 5 классе (на сложение и вычитание).Скачать

Сложение вычитание десятичных дробей примеры
Чтобы найти разность или сумму 2-х чисел, следует выполнить такие действия:
- Запишите в столбик числа, чтобы совпадали соответствующие разряды. Десятичные точки являются главным ориентиром. Не смотря на то, что они отдельным разрядом не являются, они должны находится на одной вертикали.
- Складывайте или вычитайте столбиком полученные дроби, подобно сложению и вычитанию обычных чисел. Между разрядами ставится десятичная точка.
Больше никаких действий предпринимать не надо. Как мы видим, складываются десятичные дроби, так же, как и обычные.
Главное в этих математических действиях — сопоставить правильно разряды слагаемых таким образом, чтобы десятичные точки были расположены друг под другом, на одной вертикале.
Необходимо придерживаться следующих правил:
- Уравнивать после запятой количество знаков нулями.
- Ставить запятые друг под другом.
- При сложении или вычитании не обращать внимание на запятую.
- Ставить запятую под запятыми
- Запятую следует ставить под запятыми, вычитаемых или складываемых дробей.
Видео:Уравнение. Практическая часть - решение задачи. 2 часть. 5 класс.Скачать

Умножение и деление десятичных дробей 5 класс
Следует сказать, что эта тема для учеников 5-го класса совсем не сложная. Но, между тем, ученики часто допускают ошибки в правильной постановке запятой. Разберем подробнее, чтобы не допускались подобные ошибки.
При умножении, следуйте простому алгоритму:
- Посчитайте у обоих множителей после запятой количество знаков. Обратите внимание на количество цифр после запятой. Посчитайте сначала значение для одного множителя, затем для другого, после этого сложите.Таким образом, вы получите число «x» — общее количество знаков у 2-х множителей после запятой.
- Далее убираются запятые и перемножаются числа, как целые.
- С конца числа ставится запятая, отсчитав «x» количества знаков.
Рассмотрим небольшой пример:
0,13*0,3 — после запятой количество знаков равно 3-м. Убираем запятые и выполняем умножение
запятую вернем обратно — 0,13*0,3=0,039
Обратите внимание — мы поставили 0, так как не хватило знака для правильной постановки запятой, перед числом. При этом, не пишут нули во множественном количестве, хотя их и можно поставить.
Теперь рассмотрим деление дробей по следующему алгоритму:
- Выберите из 2-х чисел то, которое имеет после запятой больше знаков. Это будет число «m».
- Передвиньте запятую в делителе и делимом вправо, у каждого из них не должно остаться дробных частей.
- Выполняйте деление. Получившийся результат будет ответом, больше запятых не нужно добавлять.
Если, у одного из чисел, не хватает части дробей, чтобы переместить запятую, добавьте нули. Например, если в числе 0,14 передвинуть на три знака, получится число — 140.
0,14:0,2 — число знаков наибольшее: 2, значит, запятую передвигаем и выполняем деление
Таким образом, на основе приведенных примеров, можно объяснить пятиклассникам простые математические действия с десятичными дробями.
Видео:Все действия с десятичными дробями (Сложение, вычитание, деление и умножение)Скачать

урок по математике 5 кл — Действия с десятичными дробями, решение уравнений
план-конспект урока по алгебре (5 класс) по теме
Подробное описание хода урока для 5 класса по теме «Действия с десятичными дробями. Решение уравнений». Прилагаемая презентация выводится на доску / экран в качестве наглядного пособия для учеников.
Видео:Сложение и вычитание десятичных дробей. 5 класс.Скачать

Скачать:
| Вложение | Размер |
|---|---|
| презентация к уроку-сказке | 2.54 МБ |
| урок-сказка 5 кл | 338.74 КБ |
Предварительный просмотр:
Видео:Уравнения с дробями 5 класс (задания, примеры) - как решать?Скачать

Подписи к слайдам:
В некотором царстве, в некотором государстве
И было у него три сестры МАРЬЯ ОЛЬГА АННА
Отдал Иван-царевич сестер своих замуж за царей медного царства серебряного царства золотого царства
и отправился в путь дорогу Целый год жил без сестер, и сделалась ему скучно. Решил он проведать сестриц
По дороге повстречал Елену Прекрасную
Они полюбили друг друга, но злой Кощей Бессмертный похитил Елену
Иван –царевич взял верных воинов и поехал выручать свою любимую
Вышли они к реке, а там огромный камень закрыл дорогу на мост (y — 0,371)+ 5,44= 27,7 (0,127 + m) – 9,8= 3,2 (x + 0,379) – 1,97=1,83 Если их правильно решить, то камень повернется и освободит дорогу
Долго ехали они по лесу, пока дорога не привела их к избушке Бабы-Яги
Она долго враждовала с Кощеем и согласилась помочь Ивану-царевичу, но только в том случае, если его воины решат шесть уравнений 2,4 – 3 x = 0,21 (2) 2,5 x + 0,8 x = 99 (2) 5 x – 7,35 = 0,3 (3) 0,65 + 2 x = 5,9 (1) 7,2 y – 0,3 y = 27,6 (3) 5,8 y – 2,7 y = 62 (1)
Прощаясь с Иваном-царевичем, Баба Яга рассказала ему о силе уравнения. Коль нужно тебе какой запор отпереть или закрыть накрепко, произнеси вслух корни уравнения. Мигом исполнится.
Черный ворон подслушал этот разговор и рассказал обо всем Кощею.
Кощей подстерег Ивана –царевича и его воинов, схватил их и бросил в глубокое подземелье. Замкнул на шесть замков. m : 0,12 * 0,2 = 7,2 (3) (0,7 + x ) * 5 = 0,8 * 5 + 0,6 * 5 (3) (0,3 + x ) * 4 = 0,3 * 3 + 0,7 * 3 (2) y: 0,2 + 0,35 = 3,6 (2) ( x – 0,5) * 5 =0,4 * 2 – 0,3 * 2 (1) 3,5 😡 – 2 = 1,5 (1)
Иван-царевич произнес «волшебные слова», назвал корни всех уравнений. Двери подземелья открылись. Стали воины перед воротами Кощеева дворца y + 0,0015 : 0,001 = 1,5
Ворота открылись Елена Прекрасная была освобождена и в тот же день сыграли свадьбу
После этого Иван-царевич вместе с Еленой прекрасной проведали его сестриц, приехали домой и стали жить –поживать и добра наживать Конец сказки
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Видео:Уравнения с дробями ( Математика - 5 класс )Скачать

По теме: методические разработки, презентации и конспекты
Урок-путешествие по теме «Действия с десятичными дробями»
Урок разработан в форме путешествия на математическом поезде. Содержание материала соответствует учебнику «Математика5» Н.Я.Виленкина.
Обобщающий урок по теме «Арифметические действия с десятичными дробями»
Повторение арифметических действий в ходе расчета стоимости ремонта в квартире.
Контрольная работа №1, самостоятельные работы «Совместные действия обыкновенных и десятичных дробей», «Решение уравнений ( совместные действия)» в 6классе по математике
Данный материал оформлен в виде раздаточных карточек для распечатки. Материал работ взят из сборника «Самостоятельные и контрольные работы по математике для 6 класса » Е.С.С.
Урок по математике. Тема: «Действия с десятичными дробями». 5 класс.
Урок — закрепления в форме сказки для учащихся 5 класса по теме «Действия с десятичными дробями». Учебник: Математика 5 класс. Н.Я.Виленкин.
Конспект урока по математике в 5 классе «Десятичные дроби и действия над ними»
Цели урока: 1. Обобщение и систематизация знаний учащихся о десятичных дробях и действиях над ними.
Разработка урока по математике в 5 классе «Десятичные дроби. Действия с десятичными дробями»
Цели урока. Образовательные:Систематизация знаний по темам: «Десятичные дроби», «Сложение, вычитание, умножение, деление, округление и сравнение десятичных дробей».
Урок-игра по математике: «Все действия с десятичными дробями»
Шалькевич Анастасия Александровна Урок-игра по математике по теме:«Все действия с дес.
📸 Видео
ДЕЛЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ 😉 #егэ #егэ #математика #профильныйегэ #shorts #образованиеСкачать

Уравнение. Практическая часть - решение задачи. 1 часть. 5 класс.Скачать

Как решать Уравнения с дробями ( Математика 5 класс )Скачать

Обыкновенные дроби и действия над ними. Практическая часть. 5 класс.Скачать