Решение уравнений по закону кирхгофа калькулятор (3 видео)

Первый и второй законы Кирхгофа для электрических цепей

Понятия узла, ветви и контура электрической цепи.
Решения систем линейных уравнений, составленных на основе правил Кирхгофа.
Преобразование электрической цепи треугольник-звезда с онлайн калькулятором.

Законы Кирхгофа, они же правила Кирхгофа (ибо фундаментальными законами не являются) – это ряд условий (в количестве двух штук) для составления системы линейных уравнений, описывающих соотношения между токами и напряжениями в разветвлённых электрических цепях.
Законы Кирхгофа довольно универсальны. Они справедливы для линейных и нелинейных цепей, постоянного и переменного токов и в совокупности с законом Ома позволяют определить параметры электрических цепей любой сложности.

Для формулирования своих правил Кирхгоф ввёл несколько понятий, таких как: узел, ветвь и контур, значение которых поясним на простом примере (Рис.1).

Узлом называется точка соединения трёх и более ветвей (на принципиальных схемах обычно обозначается жирной точкой).
На Рис.1, приведённом в качестве примера электрической цепи – это точки А, В, С.

Ветвью называют участок электрической цепи с одним и тем же значением тока.
На Рис.1 – это 5 ветвей с токами I1. I5.

Контуром называется замкнутый путь, по которому протекает электрический ток, проходя через несколько участков цепи, включающих в себя узлы и ветви. На Рис.1 контуры изображены круглыми стрелками.

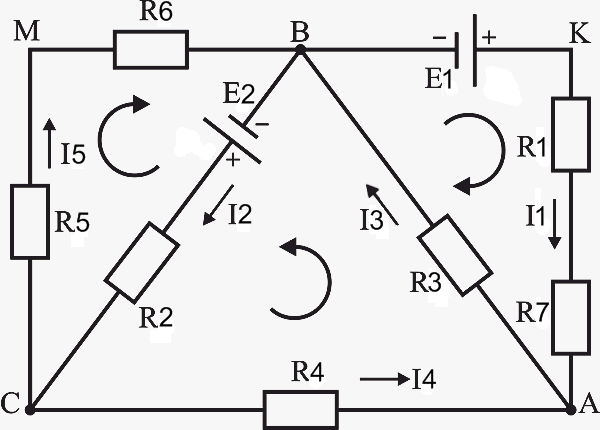Решение уравнений по закону кирхгофа калькулятор

Рис.1 Пример схемы электрической цепи

Теперь, определившись с терминами, можно переходить к формулированию законов Кирхгофа.

Первый закон или правило Кирхгофа вытекает из закона сохранения заряда и провозглашает, что алгебраическая сумма токов, сходящихся в каждом узле любой цепи, равна нулю.
Иными словами, сколько тока втекает в узел, столько из него и вытекает. При этом направленный к узлу ток принято считать положительным, а направленный от узла – отрицательным.
Если следовать примеру, приведённому на Рис.1, то для узла А: I1+I4-I3=0 .

Переходим ко второму закону Кирхгофа, который вытекает из третьего уравнения Максвелла и формулируется следующим образом:
Алгебраическая сумма ЭДС в замкнутом контуре равна алгебраической (т. е. с учётом знака) сумме падений напряжений на всех элементах этого контура. Если в контуре нет источников ЭДС (генераторов напряжения), то суммарное падение напряжений равно нулю.
Направление обхода ветвей контура выбирается произвольно. Падение напряжения считают положительным, если направление тока ветви совпадает с ранее выбранным направлением обхода, в противном случае – отрицательным.
Припадаем к рисунку Рис.1, выбираем один из трёх контуров и констатируем:
U_R2 + U_R4 + U_R3 = Е2 .

Законы законами, да и правила – вещь не самая бесполезная в радиолюбительском хозяйстве, только как воспользоваться всей этой полученной информацией на практике? Давайте с этим разберёмся и рассмотрим схему более приближённую к реальной жизни, чем та, которую мы приводили ранее в качестве примера, а конкретно – схему несбалансированного резистивного моста (Рис.2).

Для расчёта токов, протекающих в цепях, для начала воспользуемся первым правилом Кирхгофа:
I_общ = I1 + I4 = I2 + I5 ;
I1 = I2 + I3 . .

Согласно второму правилу и закону Ома:
I1*R1 + I2*R2 = E ;
I4*R4 + I5*R5 = E ;
I1*R1 + I3*R3 + I5*R5 = E .

Ну и хватит: пять уравнений, пять неизвестных – вполне достаточно, для того чтобы получить искомые значения всех токов.

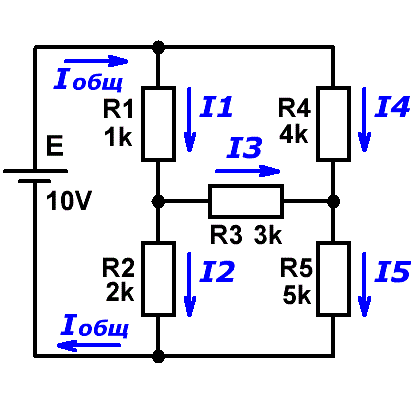Рис.2 Пример применения правил
Кирхгофа

Правда возникает резонный вопрос – КАК? Отвечу – матричным методом решения систем линейных алгебраических уравнений с ненулевым определителем. Согласен – геморрой! А поскольку мы ребята ленивые, но местами сообразительные, то и не станем искать сложных путей, а воспользуемся широко известным в узких кругах методом эквивалентного преобразования пассивных цепей – треугольник-звезда. Как это выглядит?

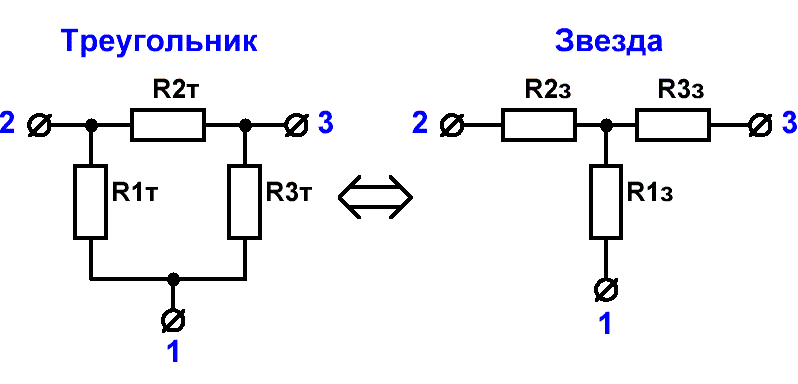Рис.3 Преобразование треугольник-звезда

Сопроводим рисунок простыми онлайн калькуляторами.

Калькулятор рсчёта элементов эквивалентного преобразования треугольник ⇒ звезда

Калькулятор рсчёта элементов эквивалентного преобразования звезда ⇒ треугольник

Вот теперь в схеме несбалансированного резистивного моста (Рис.2) можно выделить треугольник, состоящий из резисторов R2, R3 и R5, и заменить его на звезду (R1з. R3з, Рис.4 б).

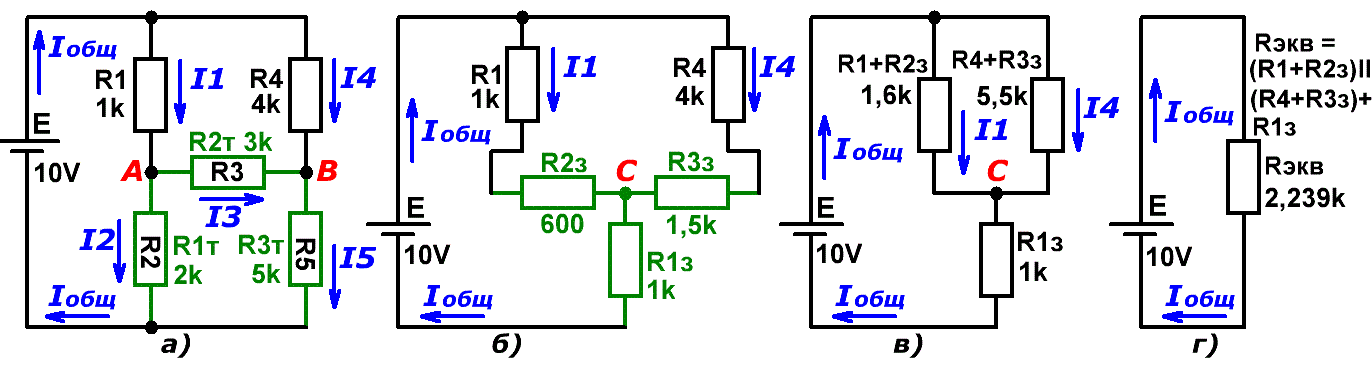
Рис.4 Эквивалентное преобразование треугольник-звезда

Нужно нам это для того, чтобы, используя правила параллельного и последовательного соединения резисторов, свести всю нашу многозвенную цепь к одному элементу (Rэкв, Рис.4 г), после чего посредством простейшей манипуляции на калькуляторе или деревянных счётах вычислить величину: Iобщ = Е/Rэкв = 10В/2.239кОм = 4.47мА .
Теперь, перемещаясь к Рис.4 в) и воспользовавшись первым правилом Кирхгофа, констатируем:
I_R1з = I1 + I4 = Iобщ = 4.47мА .
Далее напрочь забываем о Густаве Робертовиче Кирхгофе вместе с его правилами и юзаем исключительно закон Ома в самом что ни на есть его чистом виде:
U_C = I_R1з * R1з = Iобщ * R1з = 4.47мА * 1кОм = 4.47В (Рис.4 в).
I1 * (R1 + R2з) = E — U_C (Рис.4 б),
отсюда:
I1 = (10В — 4.47В) / (1кОм + 600Ом) = 3.46мА .
Точно так же:
I4 = (E — U_C) / (R4 + R3з) = (10В — 4.47В) / (4кОм + 1.5кОм) = 1.01мА .
И последний финишный рывок мы совершим, вернувшись к первоначальной схеме (Рис.4 а):
U_А = Е — R1 * I1 = 10 В — 1кОм * 3.46мА = 6.54В .
U_В = Е — R4 * I4 = 10 В — 4кОм * 1.01мА = 5.96В .
I3 = (U_А — U_В) / R3 = (6.54В — 5.96В) / 3кОм = 0.19мА .
I2 = U_А / R2 = 6.54В / 2кОм = 3.27мА .
I5 = U_В / R5 = 5.96В / 5кОм = 1.19мА .

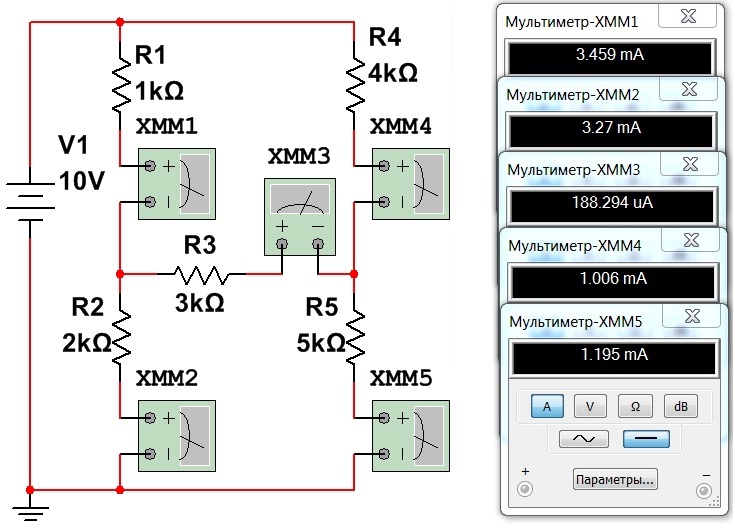
Всё, расчёт окончен! Ну а поскольку мы ребята не только сообразительные, но и пытливые умом и трезвым взглядом на вещи, то нам будет не влом проверить полученные результаты на симуляторе:

Вот теперь – точно всё! Отныне мы не только освоили оба правила Кирхгофа, но и основательно освежили в памяти основной закон электротехники – закон Ома.

Содержание

Решение уравнений по закону кирхгофа калькулятор
Инструкция — пример
Литература
Расчёт электрических цепей онлайн
Методы расчёта
Расчёт по закону Ома
Расчёт по законам Кирхгофа
Рекомендуемые записи
📽️ Видео

Видео:решение задачи составлением уравнений по правилам киргофа. Законы киргофа кратко на практикеСкачать

Решение уравнений по закону кирхгофа калькулятор

Решение: x1 = ; x2 = ; x3 = ; x4 = ; x5 = ; x6 = .

Практическая инженерия связана с расчетом энергопреобразующих цепей. Вне зависимости от природы энергонесущей материи, подобные задачи решаются одинаково, поскольку любые цепи подчинятся постулатам о сохранении материи и энергетического потенциала. Предложенный инструмент может быть использован для расчета линейных цепей, не содержащих пассивных элементов способных накапливать энергию, с постоянными источниками движущей силы.

Инструкция — пример

Дано:

Найти все токи в схеме

Решение:

1. В представленной схеме три электрических узла. Следовательно, по I закону Кирхгофа надо записать два уравнения (3-1). Ветвей же в схеме пять (пять неизвестных). Поэтому по II закону Кирхгофа надо записать три уравнения

2. Произвольно назначим направления токов в ветвях и направления обхода контуров (на рисунке они уже указаны).

3. Запишем уравнения по I и II законам Кирхгофа:

4. Перепишем уравнения так, чтоб было ясно что и как подставлять в форму, которая приведена выше:

Ответ:

Примечание: В результате решения, все токи получились со знаком «+». Это означает, что выбранные произвольно их направления совпали с действительными.

Литература

Клиначёв Н. В., Клиначёва Н. В. Открытое математическое ядро K2.SimKernel: Руководство пользователя. — Offline версия 1.3.0.1, . 1.4.0.4. — Челябинск, 2005. — файлов 67, ил.
Клиначёв Н. В. Библиотека SimLib4Visio — инструмент программирования математических ядер моделирующих программ. — v1.4. — Челябинск, 2004. — файлов 36, ил.
Клиначёв Н. В. Электротехника: Лабораторные работы для дистанционного образования. — Offline версия 1.9. — Челябинск, 2005. — файлов 51, ил.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Видео:Решение задачи. Расчет электрической цепи по законам КирхгофаСкачать

Расчёт электрических цепей онлайн

На сайте появилась программа для расчёта установившихся режимов электрических цепей по законам ТОЭ. На настоящий момент реализованы методы расчёта по законам Ома, по законам Кирхгофа, по методу узловых потенциалов, методу контурных токов, методу эквивалентного генератора. Также программа позволяет рассчитать эквивалентное сопротивление цепи относительно источника питания. Программа позволяет нарисовать схему, задать параметры её элементов и рассчитать схему. В результате формируется текстовое описание порядка расчёта, рассчитывается баланс мощностей и строятся векторные диаграммы.

Рисование схемы производится путём перетаскивания элементов методом drag-and-drop из боковой панели и последующим соединением выбранных элементов.

В боковой панели доступны следующие элементы с задаваемыми параметрами:

резистор :
- номер элемента;
- сопротивление, Ом;
конденсатор :
- номер элемента;
- сопротивление, Ом;
катушка индуктивности :
- номер элемента;
- сопротивление, Ом;
источник ЭДС :
- номер элемента;
- амплитудное значение, В;
- начальная фаза, °;
источник тока :
- номер элемента;
- амплитудное значение, В;
- начальная фаза, °.

Инструкция по применению программы приведена здесь.

Методы расчёта

После завершения рисования схемы при нажатии кнопки «Расчёт» запускается расчёт электрической цепи. Программа анализирует исходную схему и при выявлении каких-либо ошибок сообщает об этом. При успешном анализе схемы запускается расчёт по методам ТОЭ.

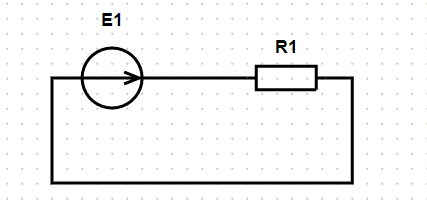
Расчёт по закону Ома

Расчёт по закону Ома осуществляется для одноконтурных схем. Используемая методика расчёта приведена здесь.

Пример схемы и расчёт:

Исходные данные и схема:

E1:
- Номер элемента: 1
- Амплитудное значение: 100 В
- Начальная фаза: 0
R1:
- Номер элемента: 1
- Сопротивление, Ом: 1

После нажатия кнопки «Расчёт» формируется решение:

В исходной схеме только один контур. Рассчитаем её по закону Ома.

Согласно закону Ома, ток в замкнутой цепи равен отношению ЭДС цепи к сопротивлению. Составим уравнение, приняв за положительное направление тока $ underline $ направление источника ЭДС $ underline_ $:

$$ R_cdot underline = underline_ $$

Подставим в полученную систему уравнений значения сопротивлений и источников и получим:

Отсюда искомый ток в цепи равен

$$ underline = 100space textrm$$

Расчёт по законам Кирхгофа

Для многоконтурных схем расчёт осуществляется по законам Кирхгофа. Используемая методика расчёта приведена здесь.

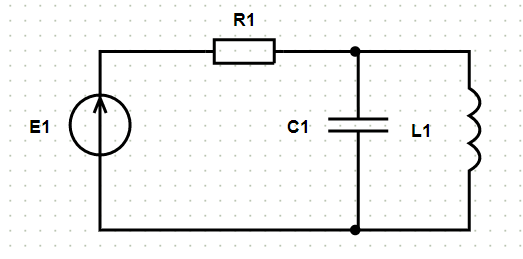
Пример схемы и расчёт:

Исходные данные и схема:

E1:
Номер элемента: 1
Амплитудное значение: 100 В
Начальная фаза: 0
R1:
Номер элемента: 1
Сопротивление, Ом: 1
L1:
Номер элемента: 1
Сопротивление, Ом: 1
C1:
Номер элемента: 1
Сопротивление, Ом: 1

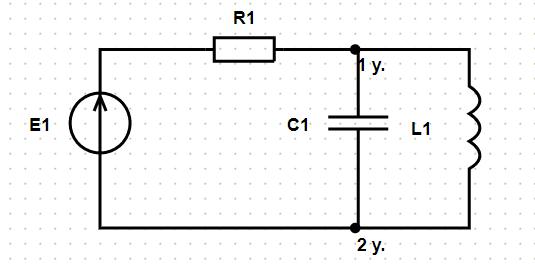
После нажатия кнопки «Расчёт» на исходной схеме появляется нумерация узлов и формируется решение:

Рассчитаем схему по законам Кирхгофа.

В данной схеме: узлов − 2 , ветвей − 3, независимых контуров − 2.

Произвольно зададим направления токов в ветвях и направления обхода контуров.

Принятые направления токов:
Ток $ underline_ $ направлен от узла ‘2 у.’ к узлу ‘1 у.’ через элементы $ underline_ $, $ R_ $.
Ток $ underline_ $ направлен от узла ‘1 у.’ к узлу ‘2 у.’ через элементы $ L_ $.
Ток $ underline_ $ направлен от узла ‘1 у.’ к узлу ‘2 у.’ через элементы $ C_ $.

Принятые направления обхода контуров:
Контур №1 обходится через элементы $ underline_ $, $ R_ $, $ L_ $ в указанном порядке.
Контур №2 обходится через элементы $ L_ $, $ C_ $ в указанном порядке.

Составим уравнения по первому закону Кирхгофа. При составлении уравнений «втекающие» в узел токи будем брать со знаком «+», а «вытекающие» − со знаком «−».

Количество уравнений, составляемых по первому закону Кирхгофа, равно $ N_textrm − 1 $, где $ N_textrm $ − число узлов. Для данной схемы количество уравнений по первому закону Кирхгофа равно 2 − 1 = 1.

Составим уравнение для узла №1:

$$ underline_ − underline_ − underline_ = 0 $$

Составим уравнения по второму закону Кирхгофа. При составлении уравнений положительные значения для токов и ЭДС выбираются в том случае, если они совпадают с направлением обхода контура.

Количество уравнений, составляемых по второму закону Кирхгофа, равно $ N_textrm − N_textrm + 1 $, где $ N_textrm $ — число ветвей. Для данной схемы количество уравнений по второму закону Кирхгофа равно 3 − 2 + 1 = 2.

Составим уравнение для контура №1:

$$ R_cdot underline_ + jX_cdot underline_=underline_ $$

Составим уравнение для контура №2:

$$ jX_cdot underline_ − (−jX_)cdot underline_=0 $$

Объединим полученные уравнения в одну систему, при этом перенесём известные величины в правую сторону, оставив в левой стороне только составляющие с искомыми токами. Система уравнений по законам Кирхгофа для исходной цепи выглядит следующим образом:

$$ beginunderline_ − underline_ − underline_ = 0 \ R_cdot underline_+jX_cdot underline_ = underline_ \ jX_cdot underline_−(−jX_)cdot underline_ = 0 \ end $$

Подставим в полученную систему уравнений значения сопротивлений и источников и получим:

$$ beginunderline_ − underline_ − underline_=0 \ underline_+ j cdot underline_=100 \ j cdot underline_+ j cdot underline_=0 \ end $$

Решим систему уравнений и получим искомые токи: