Вычитание рациональных чисел – это обратное действие сложению рациональных чисел. Пользуясь простым алгоритмом действий, вы легко разберетесь в уроке математике: “Вычитание рациональных чисел”.
- Урок: понятие вычитания рациональных чисел.
- Вычитание рациональных чисел с одинаковым знаменателем.
- Вычитание рациональных чисел с разными знаменателями.
- Сложение и вычитание рациональных чисел
- Рациональные числа и действия над ними с примерами решения
- Рациональные числа и действия над ними
- Положительные и отрицательные числа. Число 0
- Координатная прямая. Рациональные числа
- Модуль числа
- Сравнение чисел
- Сложение отрицательных рациональных чисел
- Сложение двух чисел е разными знаками
- Вычитание рациональных чисел
- Раскрытие скобок
- Рациональные числа и действия над ними
- Умножение рациональных чисел
- Переместительное и сочетательное свойства умножения. Коэффициент
- Распределительное свойство умножения. Приведение подобных слагаемых
- Деление рациональных чисел
- Решение уравнений
- Решение задач с помощью уравнений
- Параллельные и перпендикулярные прямые
- Координатная плоскость
- Примеры графиков зависимостей между величинами
- Рациональные числа и действия над ними
- Положительные и отрицательные числа. Число нуль
- Координатная прямая
- Модуль числа
- Свойства модуля числа
- Целые числа. Рациональные числа
- Сравнение рациональных чисел
- Правила сравнения рациональных чисел
- Сложение рациональных чисел
- Правило сложения чисел с разными знаками
- Правило сложения чисел с одинаковыми знаками
- Вычитание рациональных чисел
- Правило замены вычитания сложением
- Умножение рациональных чисел
- Правило умножения чисел с разными знаками
- Правило умножения двух отрицательных чисел
- Деление рациональных чисел
- Правило деления чисел с разными знаками
- Правило деления двух отрицательных чисел
- Рациональные числа
- Положительные и отрицательные числа
- Пример №58
- Координатная прямая
- Пример №59
- Целые и дробные числа
- Пример №60
- Пример №61
- Модуль числа
- Пример №62
- Пример №63
- Сравнение рациональных чисел
- Пример №64
- 🎦 Видео
Видео:Сложение и вычитание рациональных и отрицательных рациональных чисел. Практическая часть. 6 класс.Скачать
Урок: понятие вычитания рациональных чисел.
Вспомним, что такое сумма рациональных чисел. Рассмотрим формулу суммы рациональных чисел.
a+b=c
где a и b – слагаемые, c – сумма.
Если нам не известно одно из слагаемых мы его будем искать по такой формуле:
c-a=b или с-b=a
Чтобы найти неизвестное слагаемое надо от суммы отнять известное слагаемое. Отсюда мы получаем вычитание рациональных чисел.
Пример:
Рассмотрим смысл вычитания рациональных числе.
(beginfrac+frac=frac=frac\\ end)
Если нам одно из слагаемых не известно, то мы воспользуемся вычитанием.
Видео:Вычитание рациональных чисел . Решение уравнений . 6 класс .Скачать

Вычитание рациональных чисел с одинаковым знаменателем.
Чтобы выполнить вычитание рациональных чисел, применяем следующее правило:
Так как у дробей одинаковый знаменатель, переписываем знаменатель в итоговую дробь и выполняем вычитание числителей по правилам вычитания целых чисел.
Пример:
Выполните вычитание рациональных чисел с одинаковыми знаменателями (frac-frac).
Решение:
У дробей знаменатели одинаковые, поэтому считаем числители.
Видео:Сложение и вычитание рациональных чисел. 6 класс.Скачать

Вычитание рациональных чисел с разными знаменателями.
Правила вычитания рациональных чисел с разными знаменателями:
- Найти общий знаменатель дробей.
- После того как нашли общий знаменатель, вычислить числители.
- Если возможно, то сократить итоговую дробь.
Пример:
Выполните вычитание рациональных чисел с разными знаменателями: а) (frac-frac) б) (-frac-(-frac)) в) (-frac-frac)
Решение:
а) Нужно найти общий знаменатель дробей (frac) и (frac), она равен 36. Первую дробь (frac) умножаем на дополнительный множитель 2, а вторую дробь (frac) на 3 .
б) Сначала находим общий знаменатель, он равен 14, а потом вычисляем числитель. Числитель считаем по правилам вычитания целых отрицательных чисел.
в) Находим общий знаменатель, он равен 30. Потом считаем числитель по правилу вычитания целых чисел.
Видео:Вычитание рациональных чисел . 6 классСкачать

Сложение и вычитание рациональных чисел
В данном уроке рассматривается сложение и вычитание рациональных чисел. Тема относится к категории сложных. Здесь необходимо использовать весь арсенал полученных ранее знаний.
Правила сложения и вычитания целых чисел справедливы и для рациональных чисел. Напомним, что рациональными называют числа, которые могут быть представлены в виде дроби , где a – это числитель дроби, b – знаменатель дроби. При этом, b не должно быть нулём.
В данном уроке дроби и смешанные числа мы всё чаще будем называть одним общим словосочетанием — рациональные числа.
Пример 1. Найти значение выражения:
Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что плюс который дан в выражении, является знаком операции и не относится к дроби . У этой дроби свой знак плюса, который невидим по причине того, что его не записывают. Но мы запишем его для наглядности:
Это сложение рациональных чисел с разными знаками. Чтобы сложить рациональные числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить знак того рационального числа, модуль которого больше. А чтобы понять какой модуль больше, а какой меньше, нужно суметь сравнить модули этих дробей до их вычисления:
Модуль рационального числа больше, чем модуль рационального числа . Поэтому мы из вычли 

Некоторые примитивные действия, такие как заключение чисел в скобки и проставление модулей, можно пропустить. Данный пример вполне можно записать покороче:
Пример 2. Найти значение выражения:
Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что минус, стоящий между рациональными числами 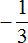
Заменим вычитание сложением. Напомним, что для этого нужно к уменьшаемому прибавить число, противоположное вычитаемому:
Получили сложение отрицательных рациональных чисел. Чтобы сложить отрицательные рациональные числа, нужно сложить их модули и перед полученным ответом поставить минус:
Запишем решение данного примера покороче:
Примечание. Заключать в скобки каждое рациональное число вовсе необязательно. Делается это для удобства, чтобы хорошо видеть какие знаки имеют рациональные числа.
Пример 3. Найти значение выражения:
В этом выражении у дробей разные знаменатели. Чтобы облегчить себе задачу, приведём эти дроби к общему знаменателю. Не будем подробно останавливаться на том как это сделать. Если испытываете с этим затруднения, обязательно повторите урок действия с дробями.
После приведения дробей к общему знаменателю выражение примет следующий вид:
Заключим каждое рациональное число в скобки вместе своими знаками:
Это сложение рациональных чисел с разными знаками. Вычитаем из большего модуля меньший модуль, и перед полученным ответом ставим знак того рационального числа, модуль которого больше:
Запишем решение данного примера покороче:
Пример 4. Найти значение выражения
Заключим каждое рациональное число в скобки вместе со своими знаками:
Вычислим данное выражение в следующем порядке: слóжим рациональные числа 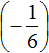
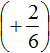
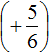
Первое действие:
Второе действие:
Таким образом, значение выражения равно
Пример 5. Найти значение выражения:
Представим целое число −1 в виде дроби 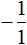

Приведём данные дроби к общему знаменателю. После их приведения к общему знаменателю, они примут следующий вид:
Заключим каждое рациональное число в скобки вместе со своими знаками:
Получили сложение рациональных чисел с разными знаками. Вычитаем из большего модуля меньший модуль, и перед полученным ответом ставим знак того рационального числа, модуль которого больше:
Есть и второй способ решения. Он заключается в том, чтобы сложить отдельно целые части.
Итак, вернёмся к изначальному выражению:
Заключим каждое число в скобки. Для этого смешанное число 
Вычислим целые части:
В главном выражении вместо (−1) + (+2) запишем полученную единицу:
Полученное выражение 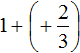
Запишем решение этим способом покороче:
Пример 6. Найти значение выражения
Переведём смешанное число 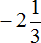
Заключим каждое рациональное число в скобки вместе со своими знаками:
Заменим вычитание сложением:
Получили сложение отрицательных рациональных чисел. Слóжим модули этих чисел и перед полученным ответом поставим минус:
Запишем решение данного примера покороче:
Пример 7. Найти значение выражение
Представим целое число −5 в виде дроби 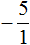

Приведём данные дроби к общему знаменателю. После их приведения к общему знаменателю, они примут следующий вид:
Заключим каждое рациональное число в скобки вместе со своими знаками:
Заменим вычитание сложением:
Получили сложение отрицательных рациональных чисел. Слóжим модули этих чисел и перед полученным ответом поставим минус:
Таким образом, значение выражения 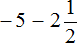
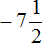
Решим данный пример вторым способом. Вернемся к изначальному выражению:
Запишем смешанное число 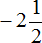
Заключим каждое рациональное число в скобки вместе своими знаками:
Заменим вычитание сложением там, где это можно:
Вычислим целые части:
В главном выражении вместо 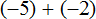
Выражение 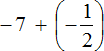
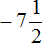

Запишем это решение покороче:
Пример 8. Найти значение выражения
Переведём смешанные числа в неправильные дроби:
Заключим каждое рациональное число в скобки вместе своими знаками:
Заменим вычитание сложением:
Получили сложение отрицательных рациональных чисел. Слóжим модули этих чисел и перед полученным ответом поставим минус:
Таким образом, значение выражения равно
Данный пример можно решить и вторым способом. Он заключается в том, чтобы сложить целые и дробные части по отдельности. Вернёмся к изначальному выражению:
Заключим каждое рациональное число в скобки вместе со своими знаками:
Заменим вычитание сложением:
Получили сложение отрицательных рациональных чисел. Слóжим модули этих чисел и перед полученным ответом поставим минус. Но в этот раз слóжим по отдельности целые части (−1 и −2), и дробные 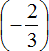
Запишем это решение покороче:
Пример 9. Найти выражения выражения
Переведём смешанные числа в неправильные дроби:
Заключим рациональное число 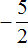
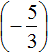
Приведём данные дроби в общему знаменателю. После их приведения к общему знаменателю, они примут следующий вид:
Получили сложение отрицательных рациональных чисел. Слóжим модули этих чисел и перед полученным ответом поставим минус:
Таким образом, значение выражения 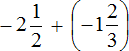
Теперь попробуем решить этот же пример вторым способом, а именно сложением целых и дробных частей по отдельности.
В этот раз, в целях получения короткого решения, попробуем пропустить некоторые действия, такие как: запись смешанного числа в развёрнутом виде и замена вычитания сложением:
Обратите внимание, что дробные части были приведены к общему знаменателю.
Пример 10. Найти значение выражения
Заменим вычитание сложением:
В получившемся выражении нет отрицательных чисел, которые являются основной причиной допущения ошибок. А поскольку нет отрицательных чисел, мы можем убрать плюс перед вычитаемым, а также убрать скобки:
Получилось простейшее выражение, которое вычисляется легко. Вычислим его любым удобным для нас способом:
Пример 11. Найти значение выражения
Это сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль, и перед полученными ответом поставим знак того рационального числа, модуль которого больше:
Пример 12. Найти значение выражения
Выражение состоит из нескольких рациональных чисел. Согласно порядку действий, в первую очередь необходимо выполнить действия в скобках.
Сначала вычислим выражение 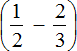
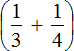
Первое действие:
Второе действие:
Третье действие:
Ответ: значение выражения 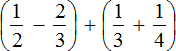
Пример 13. Найти значение выражения
Переведём смешанные числа в неправильные дроби:
Заключим рациональное число 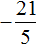
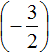
Приведём данные дроби в общему знаменателю. После их приведения к общему знаменателю, они примут следующий вид:
Заменим вычитание сложением:
Получили сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль, и перед полученными ответом поставим знак того рационального числа, модуль которого больше:
Таким образом, значение выражения 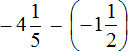
Рассмотрим сложение и вычитание десятичных дробей, которые тоже относятся к рациональным числам и которые могут быть как положительными, так и отрицательными.
Пример 14. Найти значение выражения −3,2 + 4,3
Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что плюс который дан в выражении, является знаком операции и не относится к десятичной дроби 4,3. У этой десятичной дроби свой знак плюса, который невидим по причине того, что его не записывают. Но мы его запишем для наглядности:
Это сложение рациональных чисел с разными знаками. Чтобы сложить рациональные числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить знак того рационального числа, модуль которого больше. А чтобы понять какой модуль больше, а какой меньше, нужно суметь сравнить модули этих десятичных дробей до их вычисления:
Модуль числа 4,3 больше, чем модуль числа −3,2 поэтому мы из 4,3 вычли 3,2. Получили ответ 1,1. Ответ положителен, поскольку перед ответом должен стоять знак того рационального числа, модуль которого больше. А модуль числа 4,3 больше, чем модуль числа −3,2
Таким образом, значение выражения −3,2 + (+4,3) равно 1,1
Этот пример можно записать покороче:
Пример 15. Найти значение выражения 3,5 + (−8,3)
Это сложение рациональных чисел с разными знаками. Как и в прошлом примере из большего модуля вычитаем меньший и перед ответом ставим знак того рационального числа, модуль которого больше:
3,5 + (−8,3) = −(|−8,3| − |3,5|) = −(8,3 − 3,5) = −(4,8) = −4,8
Таким образом, значение выражения 3,5 + (−8,3) равно −4,8
Этот пример можно записать покороче:
Пример 16. Найти значение выражения −7,2 + (−3,11)
Это сложение отрицательных рациональных чисел. Чтобы сложить отрицательные рациональные числа, нужно сложить их модули и перед полученным ответом поставить минус.
Запись с модулями можно пропустить, чтобы не загромождать выражение:
−7,2 + (−3,11) = −7,20 + (−3,11) = −(7,20 + 3,11) = −(10,31) = −10,31
Таким образом, значение выражения −7,2 + (−3,11) равно −10,31
Этот пример можно записать покороче:
Пример 17. Найти значение выражения −0,48 + (−2,7)
Это сложение отрицательных рациональных чисел. Слóжим их модули и перед полученным ответом поставим минус. Запись с модулями можно пропустить, чтобы не загромождать выражение:
−0,48 + (−2,7) = (−0,48) + (−2,70) = −(0,48 + 2,70) = −(3,18) = −3,18
Пример 18. Найти значение выражения −4,9 − 5,9
Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что минус который располагается между рациональными числами −4,9 и 5,9 является знаком операции и не относится к числу 5,9. У этого рационального числа свой знак плюса, который невидим по причине того, что он не записывается. Но мы запишем его для наглядности:
Заменим вычитание сложением:
Получили сложение отрицательных рациональных чисел. Слóжим их модули и перед полученным ответом поставим минус:
(−4,9) + (−5,9) = −(4,9 + 5,9) = −(10,8) = −10,8
Таким образом, значение выражения −4,9 − 5,9 равно −10,8
Запишем решение этого примера покороче:
Пример 19. Найти значение выражения 7 − 9,3
Заключим в скобки каждое число вместе со своими знаками
Заменим вычитание сложением
Получили сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль, и перед ответом поставим знак того числа, модуль которого больше:
(+7) + (−9,3) = −(9,3 − 7) = −(2,3) = −2,3
Таким образом, значение выражения 7 − 9,3 равно −2,3
Запишем решение этого примера покороче:
Пример 20. Найти значение выражения −0,25 − (−1,2)
Заменим вычитание сложением:
Получили сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль, и перед ответом поставим знак того числа, модуль которого больше:
−0,25 + (+1,2) = 1,2 − 0,25 = 0,95
Запишем решение этого примера покороче:
Пример 21. Найти значение выражения −3,5 + (4,1 − 7,1)
Выполним действия в скобках, затем слóжим полученный ответ с числом −3,5
Первое действие:
4,1 − 7,1 = (+4,1) − (+7,1) = (+4,1) + (−7,1) = −(7,1 − 4,1) = −(3,0) = −3,0
Второе действие:
−3,5 + (−3,0) = −(3,5 + 3,0) = −(6,5) = −6,5
Ответ: значение выражения −3,5 + (4,1 − 7,1) равно −6,5.
Пример 22. Найти значение выражения (3,5 − 2,9) − (3,7 − 9,1)
Выполним действия в скобках. Затем из числа, которое получилось в результате выполнения первых скобок, вычтем число, которое получилось в результате выполнения вторых скобок:
Первое действие:
3,5 − 2,9 = (+3,5) − (+2,9) = (+3,5) + (−2,9) = 3,5 − 2,9 = 0,6
Второе действие:
3,7 − 9,1 = (+3,7) − (+9,1) = (+3,7) + (−9,1) = −(9,1 − 3,7) = −(5,4) = −5,4
Третье действие
0,6 − (−5,4) = (+0,6) + (+5,4) = 0,6 + 5,4 = 6,0 = 6
Ответ: значение выражения (3,5 − 2,9) − (3,7 − 9,1) равно 6.
Пример 23. Найти значение выражения −3,8 + 17,15 − 6,2 − 6,15
Заключим в скобки каждое рациональное число вместе со своими знаками
Заменим вычитание сложением там, где это можно:
Выражение состоит из нескольких слагаемых. Согласно сочетательному закону сложения, если выражение состоит из нескольких слагаемых, то сумма не будет зависеть от порядка действий. Это значит, что слагаемые можно складывать в любом порядке.
Не будем изобретать велосипед, а слóжим все слагаемые слева направо в порядке их следования:
Первое действие:
(−3,8) + (+17,15) = 17,15 − 3,80 = 13,35
Второе действие:
13,35 + (−6,2) = 13,35 − 6,20 = 7,15
Третье действие:
7,15 + (−6,15) = 7,15 − 6,15 = 1,00 = 1
Ответ: значение выражения −3,8 + 17,15 − 6,2 − 6,15 равно 1.
Пример 24. Найти значение выражения
Переведём десятичную дробь −1,8 в смешанное число. Остальное перепишем без изменения:
Далее вычисляем данное выражение, применяя ранее изученные правила:
Пример 25. Найти значение выражения
Заменим вычитание сложением. Попутно переведём десятичную дробь (−4,4) в неправильную дробь
В получившемся выражении нет отрицательных чисел. А поскольку нет отрицательных чисел, мы можем убрать плюс перед вторым числом, и убрать скобки. Тогда получим простое выражение на сложение, которое решается легко
Пример 26. Найти значение выражения
Переведём смешанное число 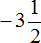
Получили сложение отрицательных рациональных чисел. Слóжим их модули и перед полученным ответом поставим минус:
Пример 27. Найти значение выражения
Переведём обе дроби в неправильные дроби. Чтобы перевести десятичную дробь 2,05 в неправильную дробь, можно перевести ее сначала в смешанное число, а затем в неправильную дробь:
После перевода обеих дробей в неправильные дроби, получим следующее выражение:
Получили сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль и перед полученным ответом поставим знак того числа, модуль которого больше:
Пример 28. Найти значение выражения
Заменим вычитание сложением. Далее переведём десятичную дробь в обыкновенную дробь. Затем вычислим получившееся выражение, применяя ранее изученные правила:
Пример 29. Найти значение выражения
Переведём десятичные дроби −0,25 и −1,25 в обыкновенные дроби, остальное перепишем без изменения. Получим следующее выражение:
Можно сначала заменить вычитание сложением там, где это можно и сложить рациональные числа одно за другим.
Есть и второй вариант: сначала сложить рациональные числа 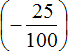
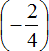
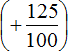
Первое действие:
Второе действие:
Ответ: значение выражения 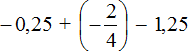
Пример 30. Найти значение выражения
Переведём десятичные дроби в обыкновенные. Остальное перепишем без изменения:
Получили сумму из нескольких слагаемых. Если сумма состоит из нескольких слагаемых, то выражение можно вычислять в любом порядке. Это следует из сочетательного закона сложения.
Поэтому мы можем организовать наиболее удобный для нас вариант. В первую очередь можно сложить первое и последнее слагаемое, а именно рациональные числа 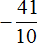
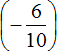
Первое действие:
Полученное число можно сложить со вторым слагаемым, а именно с рациональным числом 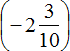
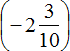
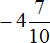
Второе действие:
Ну и слóжим полученное число −7 с последним слагаемым, а именно с рациональным числом 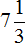
Третье действие:
Ответ: значение выражения 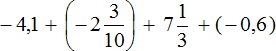
Видео:Вычитание рациональных чисел, 6 классСкачать

Рациональные числа и действия над ними с примерами решения
Содержание:
Понятие числа, как величины какого-либо объекта, является одним из основных математических понятий.
Первые представления о числе возникли из счета предметов. Результатом счет являются числа 1,2,3 и т.д. Первоначально рассматривались лишь целые и положительные числа, которые теперь называют натуральными числами.
Впоследствии возникло понятие о дробях. Источник его есть измерение непрерывных величин (длины, веса и др.). Это понятие укрепилось только в 16 веке после изобретения десятичных дробей и логарифмов.
Значительно позже начали появляться и входить в обиход отрицательные числа. Лишь в 16 веке Декарт, разрабатывая аналитическую геометрию, дал геометрическое истолкование отрицательных чисел как направленных отрезков, которое с тех пор и стало общепринятым.
Целые числа (т.е. натуральные числа 1,2,3, .. отрицательные числа -1 ,-2,-3, и т.д. и нуль) и дроби называются рациональными числами.
Всякое рациональное число можно записать в виде
Иррациональные числа. Ещё ранее, Пифагором была открыта несоизмеримость отрезков, например, стороны и диагонали квадрата, т.е. невозможность выражения этого отношения никакими рациональными числами или их комбинациями, что привело к понятию иррациональных чисел. Иррациональные, т.е. «не имеющие отношения» (латинский термин иррациональный есть перевод греческого слова «алогос»).
Геометрически, иррациональное число выражает длину отрезка, несоизмеримого с единицей масштаба. Иррациональное число не может точно равняться рациональному. Но для всякого иррационального числа можно найти рациональное (в частности, десятичные) числа, приближенно равные ему (с избытком или с недостатком). При этом погрешность можно сделать сколь угодно малой.
Например, для числа
Видео:Сложение и вычитание рациональных чисел. Математика 6 класс.Скачать

Рациональные числа и действия над ними
Положительные и отрицательные числа. Число 0
Рассмотрим несколько примеров.
Пример:
Лагерь туристов находится у дороги, проходящей с запада на востоком. (рис. 25). Туристы вышли из лагеря и пошли по дороге со скоростью 5 км/ч.
Где будут находиться туристы через час?
Решение:
Чтобы определить местонахождение туристов через час после их выхода из лагеря, необходимо знать, идут они от лагеря на запад или на восток.
Если туристы идут на восток, то через час они будут в пункте А. О пункте А можно сказать, что он находится на расстоянии 5 км восточнее пункта О.

Итак, положение туристов относительно лагеря можно задать числом и направлением: 5 км восточнее пункта О; 5 км западнее пункта О.
Пример:
Вечером хозяйка оставила возле колодца ведро с водой. На следующее утро температура воздуха была 4°С. Что в ведре: вода или лед?
Решение:
Чтобы ответить на поставленный вопрос, нужно знать, показывает термометр 4° тепла или 4° мороза. Если термометр показывает 4° тепла, то в ведре вода. О такой температуре еще говорят: 4°С выше нуля, или плюс 4°С, пишут: +4°С. Если термометр показывает 4° мороза, то в ведре лед. О такой температуре еще говорят: 4°С ниже нуля, или минус 4°С, пишут: -4°С.
Итак, температуру можно задавать числом со знаком «+» или «-»: + 4°С; — 4°С.
Температура может быть равна и +15°С, +7,6°С, -12°С, -1,5°С и т. п. Числа со знаком «+» находятся на шкале термометра (рис. 26) выше нуля, а числа со знаком «-» — ниже нуля.
Числа со знаком «+» называют положительными.
Например: 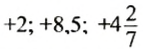
Числа со знаком «-» называют отрицательными.
Например:- 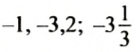
Число 0 отделяет положительные числа от отрицательных. Оно не является ни отрицательным, ни положительным.
При записи положительных чисел знак «+», как правило, опускают и, например, вместо +4 пишут 4. При этом понимают, что +4 = 4, то есть +4 и 4 — это разные обозначения одного и того же числа.
Отрицательными числами обозначают не только температуру. Ими, например, можно задавать положение любого места земной поверхности относительно уровня моря (см. рис. 27).
Пример:
В тетради в клетку начертили горизонтальную прямую и отметили на ней точку О. Точка А лежит на 3 клетки левее точки О. Точку А сместили на 5 клеток вправо и получили точку В. Каково положение точки В относительно точки О?
Решение:
Точка В лежит на 2 клетки правее точки О.
Интересные рассказы
Об отрицательных числах
Первыми столкнулись с потребностью в отрицательных числах географы, моряки, картографы, так как им необходимо было характеризовать положение городов, расположенных на север или юг от главною города и на запад или восток от него. Главными точками отсчета были избраны экватор и Гринвичский меридиан. Позже у археологов и историков появилась потребность характеризовать шкалу времени.
Геологам нужно было характеризовать неровности земного рельефа, а именно — высоту гор, глубину впадин морей и океанов, принимая за точку отсчета уровень моря (рис. 31).
Физикам, инженерам, астрономам, врачам нужно было измерять температуру. В XVIII в. шведским ученым Цельсием (1701-1744) была предложена измерительная шкала, в которой за точку отсчета (ноль) была принята температура плавления льда, а температура кипения воды — за 100 о С.
Отрицательные числа люди придумали намного позже, чем натуральные числа и обыкновенные дроби. К идее отрицательного числа первыми пришли китайцы во II в. до н. э. Необходимость введения новых для того времени чисел обусловливалась проблемами самой математики — отрицательные числа нужны были для решения уравнений. Потом индусы дали толкование положительных и отрицательных чисел в виде «имущества» и «долга».
В Европе отрицательные числа стали использовать с XII в., однако относились к ним с недоверием, называя их «фиктивными», «абсурдными», «ложными» и г. п. «Настоящими» числами считали лишь положительные числа. 11 только в XVII в., когда выдающийся французский математик Пене Декарт (1596 — 1650) предложил изображать отрицательные и положительные числа точками координатой прямой, отрицательные числа были полностью признаны и стали полноправным атрибутом математики.
Координатная прямая. Рациональные числа
Начертим горизонтальную прямую и отметим на ней некоторую точку О — начало отсчета (рис. 32). В соответствие точке О поставим число 0. Выберем единичный отрезок. На проведенной прямой можно отметить числа (точки, соответствующие этим числам). Положительные числа принято отмечать правее точки О, а отрицательные — левее. Чтобы отметить, например, число 2, нужно от точки О отложить два единичных отрезка вправо. Чтобы обозначить число -2. нужно от точки О отложить два единичных отрезка влево.
Направление вправо от начала отсчета называют положительным, а влево — отрицательным. Положительное направление показывает стрелка (см. рис. 33).
Прямую с выбранными на ней началом отсчета, единичным отрезком и указанным положительным направлением называют координатной прямой.
Число, указывающее положение точки на координатной прямой, называют координатой этой точки. Точка А (рис. 34) имеет координату 2,5, точка В — координату 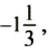
Точки А и В с координатами 3 и -3 (рис. 35) одинаково удалены от точки О и лежат с разных сторон от нее. Чтобы попасть из точки О в эти точки, нужно пройти одинаковые расстояния, но в противоположных направлениях Числа 3 и -3 называют противоположными числами: число 3 является противоположным числу -3, а число -3 — противоположным числу 3. Числа 1,5 и -1,5 также являются противоположными.
Два числа, отличающиеся друг от друга только знаком, называют противоположными числами.
Число, противоположное числу а, обозначают -а. Если а = 4,2, то -а = -4,2; если а = -1,5, то -а = 1,5.
Число 0 противоположно самому себе: если а = 0, то -а = 0.
Натуральные числа, противоположные им числа и число О называют целыми числами.
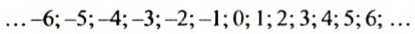
Положительные числа (цепые и дробные), отрицательные числа (целые и
дробные) и число 0 называют рациональными числами.
Например, 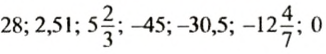
Пример:
Найти число, противоположное числу -5, и записать соответствующее равенство.
Пример:
Найти значение 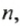
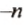
Число 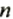
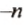
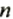
Пример:
Точка В имеет координату -3 (рис. 36). Эту точку переместили на 5 единиц вправо и получили точку С. Какова координата точки С?
Точка С имеет координату 2:
Модуль числа
Пусть из пункта О в противоположных направлениях выехали два автомобиля и через некоторое время первый был в точке А(-20). а второй — в точке В(15) (рис. 40).
Какой из автомобилей проехал большее расстояние?
Чтобы ответить на этот вопрос, нужно сравнить расстояния OA и ОВ. Поскольку OA = 20, ОВ = 15 и 20 > 15, то большее расстояние проехал первый автомобиль.
Итак, чтобы ответить на вопрос, мы сравнивали не числа -20 и 15, а числа «без знаков» 20 и 15, или еще говорят: сравнивали модули чисел -20 и 15.
Модулем положительною числа и нуля называют само число.
Для обозначения модуля числа используют две вертикальные черты, то есть пишут |15| = 15 (читают: модуль пятнадцати равен пятнадцать).
Для положительных чисел 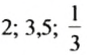
Модулем отрицательного числа называют противоположное ему положительное число.
Для отрицательных чисел 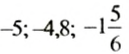
Итак, модулем любого числа является положительное число или число 0. С геометрической точки зрения модуль числа равен расстоянию на координатной прямой от начала отсчета до точки, изображающей это число (рис. 41).
Модуль числа 3 равен 3, и расстояние от начала отсчета до точки, соответствующей этому числу, равно 3. Модуль числа -4 равен 4, и расстояние от начала отсчета до точки, соответствующей этому числу, равно 4.
не существует числа, для которого выполнялось бы равенство 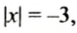
Противоположные числа имеют равные модули. Например, для противоположных чисел -2 и 2 имеем:
Пример:
Решить уравнение:
Решение:
Пример:
Найти отрицательные целые числа, для которых
Решение:
Такими числами являются:
Модули остальных отрицательных целых чисел (-3; -4; -5; -6; -7; . ) больше 3 или равны 3.
Пример:
На координатной прямой отметить точки, координаты которых удовлетворяют условию 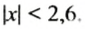
Решение:
Условию 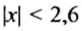
Отрицательными целыми числами, удовлетворяющими условию 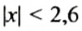
Сравнение чисел
Вы уже умеете сравнивать положительные числа. Например, 5 > 4; 1,5 5, то |-8| > |-5|. Итак,
- из двух отрицательных чисел меньшим является то, модуль которого больше;
- большим является го, модуль которого меньше.
Если о числе 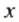
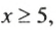
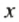
Запись 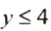
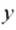
Например, натуральными числами, удовлетворяющими условию 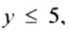
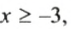
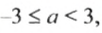
Прочитайте
1. Записать в виде неравенства утверждение:
а) 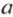
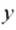
в) 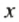
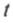
д) число 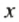
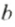
а)
б)
в) неотрицательное число — что нуль или положительное число, то есть число, равное нулю или больше нуля:
г) неположительное число — это нуль или отрицательное число, то есть число, равное нулю или меньше нуля:
д) если число 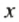
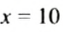
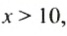
е)
Сложение отрицательных рациональных чисел
К рациональным числам относятся положительные числа (целые и дробные), отрицательные числа (целые и дробные) и число нуль. Мы уже выучили действия сложения, вычитания, умножения и деления над положительными рациональными числами и нулем. А теперь научимся выполнять их над рациональными числами в случаях, когда оба числа отрицательные или одно положительное, а другое отрицательное (числа с разными знаками). Рассмотрим пример.
Пусть в марте фермер взял в банке кредит 5 тыс. руб., а в апреле— еще 3 тыс. руб. Тогда за март и апрель вместе фермер взял 5 + 3 = 8 (тыс. руб.) кредита. Так как кредиты являются долгами фермера перед банком, обозначим их отрицательными числами: -5 тыс. руб.; -3 тыс. руб.; -8 тыс. руб. Тогда сумму кредитов в тысячах гривен за 2 месяца можно записать так:
Какой знак имеет сумма двух отрицательных чисел?
Найдите модули слагаемых и модуль суммы. Какая между ними существует зависимость?
Как видим, суммой чисел -5 и -3 является отрицательное число; модуль суммы равен сумме модулей слагаемых: 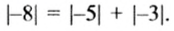
Итак, суммой двух отрицательных чисел является отрицательное число, модуль которого равен сумме модулей слагаемых. Чтобы сложить два отрицательных числа, нужно сложить их модули и поставить перед полученным числом знак «-».
В сумме отрицательных слагаемых первое слагаемое пишут, как правило, без скобок. Например:
Для сложения отрицательных чисел выполняются переместительное и сочетательное свойства.
Например,
Пример:
Решение:
Для тех, кто хочет знать больше
Договоримся уменьшение величины выражать отрицательным числом, а увеличение — положительным. Если температура уменьшилась на 2°С, то можно скатать, что она изменилась на -2°С. Если же температура увеличилась на 2°С, то можно сказать, что она изменилась на 2°С. Если в течение первой половины дня температура воздуха уменьшилась на 3°С, а в течение второй она уменьшилась на 4°С, то в течение дня температура уменьшилась на 3° + 4° = 7°. При помощи отрицательных чисел изменение величины температуры в течение дня можно записать так:
Сложение двух чисел е разными знаками
Пусть в августе фермер взял в банке беспроцентный кредит 5 тыс. руб., а в начале следующего месяца вернул его, то есть вернул банку 5 тыс. руб. Тогда расчет фермера с банком в тысячах гривен можно записать так:
Числа 5 и -5 — противоположные, их сумма равна нулю
Сумма двух противоположных чисел ровна нулю.
Если в августе фермер взял кредит 7 тыс. руб., а в начале следующего месяца вернул банку 4 тыс. руб., то его долг перед банком составляет 3 тыс. руб. Расчет фермера с банком можно записать так:
Если бы в августе фермер взял кредит 5 тыс. руб., а в начале следующего месяца положил в банк 6 тыс. руб., то фермер не только покрыл бы долг перед банком, но и оставил бы на своем счету 1 тыс. руб. Расчет фермера с банком можно записать так:
Вернемся к равенству
Найдите модули слагаемых и модуль суммы. Какова зависимость между модулями слагаемых и модулем суммы? С каким из слагаемых сумма имеет одинаковый знак?
В равенстве -1 + (+4) = -3 модули слагаемых равны 7 и 4, модуль суммы равен 3, то есть модуль суммы равен разности большего и меньшего модулей. Знак разности совпадает со знаком слагаемого, модуль которою больше. Поэтому нахождение суммы чисел -7 и +4 можно записать так:
Вернемся к равенству
Объясните, как в данном случае находят модуль суммы и так суммы.
В равенстве 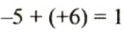
Итак, чтобы сложить два числа с разными знаками, нужно из большего модуля вычесть меньший и поставить перед полученным числом знак того слагаемого, модуль которого больше.
Производя вычисления, сначала, как правило, определяют и записывают знак суммы, а потом находят разность модулей. Например:
В сумме слагаемых с разными знаками первое положительное слагаемое пишут, как правило, без знака.
Проиллюстрируем сложение чисел при помощи координатной прямой
Для сложения чисел с разными знаками выполняются переместительное и сочетательное свойства. Например,
Для любого рационального числа 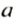
При помощи свойств сложения можно упростить нахождение суммы нескольких слагаемых, выполняя действия в удобной последовательности. В частности, если нужно сложи ть несколько чисел, среди которых есть положительные и отрицательные, то можно сложить отдельно положительные числа и отдельно отрицательные, а потом сумму положительных чисел сложить с суммой отрицательных.
Пример:
Вычислить
Решение:
Вычитание рациональных чисел
Вычитание отрицательных чисел и чисел с разными знаками имеет тот же смысл, что и вычитание положительных чисел. Напомним, что при помощи вычитания находят неизвестное слагаемое по известной сумме и одному из слагаемых.
Так как
Такой же результат получим, если число -15 сложим с числом, противоположным числу — 8, то есть числом +8. Поэтому разность -15 — (-8) можно заменить суммой 15 + (+8). в которой уменьшаемое складывается с числом, противоположным вычитаемому:
Итак, чтобы из одного числа вычесть другое, достаточно уменьшаемое сложить с числом, противоположным вычитаемому.
Это правило вычитания можно записать так:
где 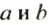
Так как вычитание можно заменить сложением с противоположным числом, то любое выражение, содержащее действия сложения и вычитания, можно записать в виде суммы.
Например, выражение -10 — (+7) является разностью чисел -10 и +7, его можно -записать в виде суммы чисел -10 и -7, так как 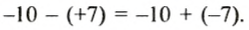
Договоримся далее положительные числа записывать без знака «+», то есть сумму -10 + (+7) будем записывать так: -10 + 7, а разность 14 — (+18) так: 14-18.
Пусть на координатной прямой заданы две точки А(-2) и В(5) (рис. 49) и нужно найти длину отрезка АВ.
Чтобы найти длину отрезка АВ (или расстояние А В), нужно знать, сколько единичных отрезков содержит этот отрезок. Как видно по рисунку, длина отрезка АВ равна 7 единичным отрезкам. Через координаты концов отрезка АВ его длина выражается так:
Итак, чтобы найти длину отрезка на координатной прямой, координаты его правого конца вычесть координату левого конца.
Для тех, кто хочет знать больше
Если бы при нахождении длины отрезка АВ (рис. 49) из координаты левою конца вычли координату правого, то получили бы число -2-5=7. Длина отрезка А В является положительной величиной, и в этом случае она равна модулю найденного числа:
Итак, длина отрезка АВ равна модулю разности координат его левого и правого концов. Эта длина также равна модулю разности координат правого и левого концов:
Длина отрезка равна модулю разности координат его концов.
Длину отрезка АВ с концами 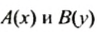
Пример:
Вычислить:
Решение:
Запишем выражение в виде суммы и сгруппируем числа:
Пример:
Упростить выражение:
Решение:
Запишем выражение в виде суммы и сгруппируем слагаемые:
Пример:
Решить уравнение:
Решение:
а) Сначала упростим выражение в левой части уравнения:
Получили уравнение 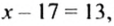
6) Если модуль числа равен 2, то этим числом является 2 или -2, поэтому 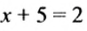
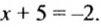
Итак,
Раскрытие скобок
Вы уже знаете, что на основании сочетательного свойства сложения выражение 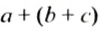
Эту операцию называют раскрытием скобок.
Так как 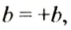
Мы раскрыли скобки, перед которыми стоит знак «+» При этом опустили скобки, знак «+», стоящий перед ними, и записали все слагаемые, которые были в скобках, со своими знаками.
Итак, чтобы раскрыть скобки, перед которыми стоит знак «+», нужно опустить скобки и знак «+», стоящий перед ними, и записать все слагаемые, которые были в скобках, со своими знаками.
Из этого правила следуют такие равенства:
Из правила вычитания рациональных чисел следует, что
При выполнении этого действия мы раскрыли скобки, перед которыми стоит знак «-». При этом опустили скобки и знак «-», стоящий перед ними, и записали слагаемое, которое было в скобках, с противоположным знаком. Так будем раскрывать скобки, перед которыми стоит знак «-» и тогда, когда слагаемых будет несколько:
Итак, чтобы раскрыть скобки, перед которыми стоит знак «-», нужно опустить скобки и знак «-», стоящий перед ними, и записать все слагаемые, которые были в скобках, с противоположными знаками.
Воспользовавшись этим правилом, получим:
Пример:
Упростить выражение:
Решение:
Пример:
Взять два последних слагаемых в скобки, поставив перед скобками знак «+», в выражении:
Решение:
После первого слагаемого поставили знак «+», раскрыли скобки, два последних слагаемых переписали с теми же знаками и закрыли скобки.
(Перед первым слагаемым в скобках знак «+» можно не ставить.)
Пример:
Взять два последних слагаемых в скобки, поставив перед скобками знак «-», в выражении:
Решение:
После первого слагаемого поставили знак «-», раскрыли скобки, знак «-» в слагаемом -4,2 заменили на «+», но не написали, так как в скобках это слагаемое первое; в слагаемом +3,7 знак «+» заменили на «-».
Памятка: 1. 
2. -7 и 7 — противоположные числа (отличаются знаком).
3. |6| = 6 — модулем положительного числа является само число;
|0| = 0 — модуль нуля равен нулю;
|-10| = 10 — модулем отрицательного числа является противоположное ему положительное число.
4. 6 > 0 — положительное число больше нуля;
-7 |-12|. 5. 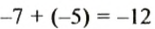
6. 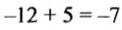
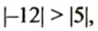
7. 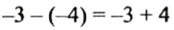
8. 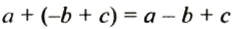
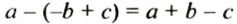
Видео:Вычитание рациональных чисел. Математика 6 классСкачать

Рациональные числа и действия над ними
Умножение рациональных чисел
Пусть в феврале, марте и апреле фермер брал в банке кредиты по 5 тыс. руб. ежемесячно. Тогда за эти три месяца он взял кредит на сумму 5 • 3= 15(тыс. руб.). Так как кредиты являются долгами фермера перед банком, мы обозначали их отрицательными числами: -5 тыс. руб.;-15 тыс. руб. Тогда весь кредит фермера в банке за 3 месяца в тысячах гривен можно записать так:
Какие знаки имеют множители? Какой знак имеет произведение? Какова зависимость между модулями множителей и модулем произведения?
Числа -5 и 3 имеют противоположные знаки, их произведением является число отрицательное, а модуль произведения (числа -15) равен произведению модулей множителей (чисел -5 и 3):
Произведением двух чисел с разными знаками является число отрицательное; модуль произведения равен произведению модулей множителей.
Итак, чтобы найти произведение двух чисел с разными знаками, достаточно перемножать их модули и поставить перед полученным числом знак «-».
Видим: если поменять знак одного множителя (вместо множителя 5 взять множитель -5), то знак произведения тоже меняется, а модуль произведения остается тем же (|15| = |-15|). Следовательно, если изменить знак множителя, то знак произведения изменится, а его модуль останется таким же.
Используем найденную зависимость для нахождения произведения отрицательных чисел -5 и -3.
Так как 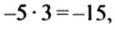
Какие знаки имеют множители? Какой знак имеет произведение?
Числа -5 и -3 отрицательные, их произведение — положительное число; модуль произведения 15 равен произведению модулей чисел -5 и -3.
Произведением двух отрицательных чисел является число положительное; модуль произведения равен произведению модулей множителей.
Итак, чтобы найти произведение двух отрицательных чисел, достаточно перемножить модули этих чисел.
Если число 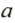
Пример:
Выполнить умножение:
Решение:
Переместительное и сочетательное свойства умножения. Коэффициент
Для умножения рациональных чисел справедливы переместительное и сочетательное свойства.
Переместительное свойство: для любых рациональных чисел 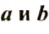
Для положительных чисел что свойство было установлено раньше. Проверим на примерах, что оно выполняется и тогда, когда один или оба множителя являются отрицательными числами:
Сочетательное свойство: для любых рациональных чисел 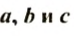
Проверим это равенство, взяв
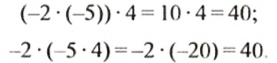
Для любого рациональною числа 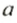
Рассмотрим выражение 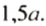
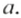
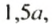
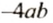
Так как 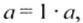
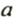
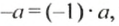
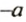
Используя переместительное и сочетательное свойства умножения, упростим выражение
Пример:
Найти коэффициент произведения:
Решение:
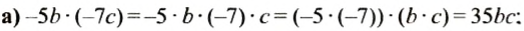
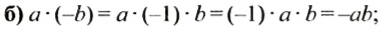
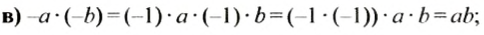
Распределительное свойство умножения. Приведение подобных слагаемых
Для рациональных чисел справедливо распределительное свойство умножения относительно сложения.
Для любых рациональных чисел a, b и с справедливо равенство:
Проверим это равенство, взяв, например,
Итак,
Замену выражения 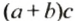
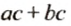
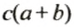
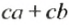
Замену выражения 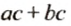
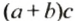
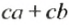
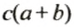
В выражении 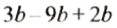
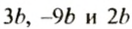
Записав выражение 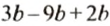
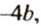
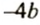
Чтобы привести подобные слагаемые, нужно сложить их коэффициенты и результат умножить на общую буквенную часть.
В выражении может быть несколько групп подобных слагаемых. При упрощения таких выражений нужно сначала выделить группы подобных слагаемых, а потом в каждой группе привести подобные. Например:
Пример:
Раскрыть скобки и привести подобные слагаемые:
Пример:
Решение:
Пример:
В выражении 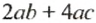
Решение:
Деление рациональных чисел
Деление двух отрицательных чисел и двух чисел с разными знаками и мест тот же смысл, что и деление положительных чисел: по данному произведению и одному из множителей при помощи деления находят другой множитель. Так как 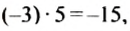
Какой знак имеет делимое; делитель? Какой знак имеет частное? Какова зависимость между модулем частного и модулями делимого и делителя?
В равенстве 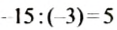
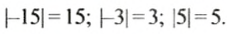
Частным двух отрицательных чисел является число положительное. Чтобы найти модуль частного, нужно модуль делимого разделить на модуль делителя.
Итак, чтобы найти частное двух отрицательных чисел, достаточно разделить модули этих чисел.
Так как
Какой знак имеет делимое; делитель? Какой знак имеет частное? Как найти модуль частного?
В равенстве 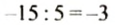
Частным двух чисел с разными знаками является число отрицательное. Чтобы найти модуль частного, нужно модуль делимого разделить на модуль делителя.
Особые случаи деления:
где 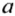
Пример:
Вычислить:
Решение:
Решение уравнений
На рисунке 50 изображены весы, находящиеся в равновесии. На одной чаше весов лежат арбуз и гиря массой 1 кг, а на другой чаше — гири общей массой 6 кг.
Пусть масса арбуза равна 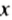
Снимем с обеих чаш гири массой 1 кг. Весы останутся в равновесии. Поэтому получим уравнение:
Как можно получить второе уравнение из первого?
Второе уравнение можно получить из первою, если перенести слагаемое 1 из левой част уравнения в правую, изменив знак слагаемою на противоположный.
На рисунке 51 вы видите весы, находящиеся в равновесии. На одной чаше лежат 4 батона, а на второй — 2 батона и гиря массой I кг.
Пусть масса одного батона 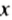
Снимем с обеих чаш по 2 батона, весы останутся в равновесии, поэтому получим уравнение:
Как можно получить второе уравнение из первого?
Второе уравнение можно получить из первою, если из правой части перенести в левую слагаемое 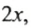
решая уравнение, слагаемые можно переносить из одной части уравнения в другую, изменяя при этом их знаки на противоположные.
Пусть нужно решить уравнение
Перенесем слагаемое 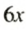
Упростим левую и правую части уравнения:
Найдем неизвестный множитель:
Левая часть:
Правая часть:
Обе части уравнения имеют равные значения при 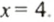
Пример:
Решить уравнение
Решение:
Решение задач с помощью уравнений
Пример:
В двух бидонах 36 л молока, причем в первом бидоне молока в 1,4 раза больше, чем во втором. Сколько молока в каждом бидоне?
Решение:
Пусть во втором бидоне 



Решим это уравнение:
Итак, во втором бидоне 15 л молока, а в первом — 1,4 • 15 = 21 (л).
Проверка. В обоих бидонах молока 15 + 21 =36 (л), что соответствует условию задачи.
Пример:
На трех полках 129 книг, причем на второй полке на 15 книг больше, чем на первой, а на третьей — на 12 книг меньше, чем на первой. Сколько книг на каждой полке?
Решение:
Пусть на первой полке 

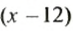



Решим это уравнение:
На первой полке 42 книги, на второй — 42+15=57 (книг), на третьей — 42-12=30 (книг).
Проверка. На трех полках 42 + 57 + 30= 129 (книг), что соответствует условию задачи.
Ответ. 42, 57 и 30 книг.
Для тех, кто хочет знать больше
Пример:
В поселке три школы. Количество учеников первой школы составляет 30% количества всех учеников поселка. Во второй школе учеников в 1,5 раза больше, чем в первой. Сколько учеников в трех школах вместе, если в третьей школе — 550 учеников?
Решение:
Пусть в трех школах вместе учится 





Получили уравнение:
Решим это уравнение:
Итак, в трех школах поселка учится 2200 учеников.
Ответ. 2200 учеников.
Пример:
Из города А в город В выехал грузовой автомобиль. Через 30 мин навстречу ему из города В выехал легковой автомобиль, скорость которого на 15 км/ч больше, чем грузового. Когда легковой автомобиль приехал в город А, грузовому оставалось проехать до города В еще 3 км. Найти расстояние между городами, если на путь от В до А легковой автомобиль затратил 2,2 ч.
Решение:
Пусть скорость легкового автомобиля 

За 2,2 ч легковой автомобиль проехал 2,2 



Получили уравнение:
Решим это уравнение:
Следовательно, скорость легкового автомобиля 75 км/ч. Умножив лу скорость на время движения легкового автомобиля получим расстояние между городами:
Параллельные и перпендикулярные прямые
Вы уже знаете, что представление о плоскости дает поверхность стола, оконного стекла, водоема в безветренную погоду (если представить, что они неограниченно продлены во все стороны).
Пусть на столе лежит тонкая спица, а другая в него воткнута. Будем рассматривать поверхность стола как плоскость, а спицы — как прямые 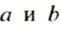
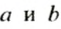
Рассмотрим другой случай. Пусть обе спицы лежат на столе (рис. 52б). В этом случае говорят, что прямые 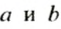
Впредь будем рассматривать прямые, лежащие в одной плоскости. Пусть имеем две прямые АВ и CD (рис. 53). Они пересекаются, хотя на рисунке не изображена точка их пересечения. Эту точку можно найти, продлив изображение прямой CD.
Прямые 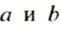
Две прямые называют параллельными, если они не пересекаются и лежат в одной плоскости.
Представление о параллельных прямых дают рельсы железной дороги на прямом участке, след от санок при прямолинейном движении, противоположные края доски и т. п.

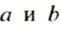
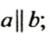
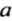
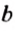
Возьмем линейку и угольник. Приложим угольник к линейке одной стороной прямого угла и проведем прямую 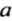
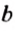
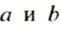
Построим прямую, параллельную данной прямой 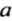
- Приложим к прямой а угольник одной из сторон прямого угла.
- К другой стороне прямого угла приложим линейку.
- Будем передвигать угольник вдоль линейки до тех пор, пока сторона прямого угла не пройдет через точку А. Эта сторона прямого угла принадлежит прямой
, параллельной прямой
и проходящей через точку А.
Через каждую точку плоскости, не принадлежащую данной прямой, можно провести только одну прямую, параллельную данной.
На рисунке 56 изображены прямые 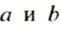
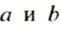
Если при пересечении прямых AD и ВС (рис. 57) в точке О лучи OA и ОВ образуют прямой угол, то прямые AD и ВС называют перпендикулярными.
Две прямые называют перпендикулярными, если они пересекаются под прямым углом.
Итак, прямые ВС и AD на рисунке 57 перпендикулярны. Перпендикуляр-носгь прямых обозначают значком 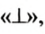
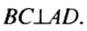
Так как угол DOA является развернутым (рис. 57), а развернутый угол равен 180°, то
Аналогично можно установить, что 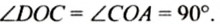
Построить перпендикулярные прямые можно при помощи угольника и линейки. Выполнение построения показано на рисунке 58. 
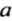
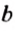
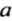
Если точка О принадлежит прямой 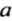
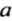
Координатная плоскость
Положение точки на координатой прямой определяется числом — координатой этой точки. Положение точки на плоскости можно задать двумя числами.
Места для зрителей в зале кинотеатра можно задавать парой чисел: первое число указывает на номер ряда, а второе — на номер кресла в этом ряду (рис. 69). Причем места (3; 7) и (7; 3) — разные: первое является креслом в третьем ряду под номером 7, а второе — креслом в седьмом ряду под номером 3.
Проведем две перпендикулярные координатные прямые, пересекающиеся в начале их отсчета — точке О — и имеющие равные единичные отрезки (рис. 70). Эти прямые называют осями координат, точку О — началом координат. Горизонтальную координатную прямую называют осью aбсцисс и обозначают буквой 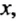
Ось абсцисс и ось ординат образуют прямоугольную систему координат. Плоскость, на которой задана прямоугольная система координат, называют координатной плоскостью.
Пусть А —точка координатной плоскости (рис. 71). Проведем через нее прямую 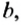
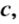
Положение точки А на координатной плоскости определяется парой чисел (-3; 2), которые называют координатами этой точки. Координаты точки записывают в скобках: А(-3; 2), читают: точка А с координатами -3 и 2. Первую координату точки А (число -3) называют абсциссой этой точки, а вторую координату (число 2) — ординатой. Точка К (рис. 71), наоборот, имеет абсциссу 2 и ординату -3, поэтому К(2; -3) (на первом месте всегда записывают абсциссу точки, а на втором — ее ординату).
Если точка лежит на оси абсцисс, то ее ордината равна нулю; если точка лежит на оси ординат, то ее абсцисса равна нулю. Точки М и N (рис. 71) имеют координаты: М(4; 0), N(Q -2).
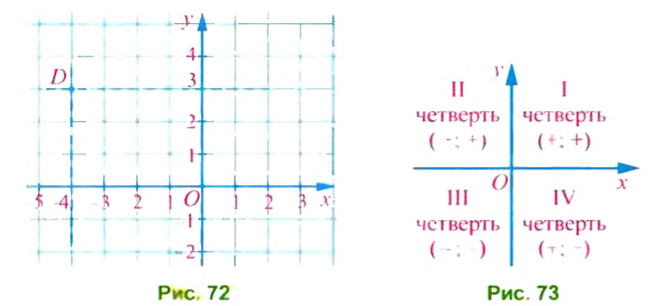
Чтобы построить, например, точку D(-4; 3), можно провести перпендикулярную прямую до оси 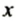
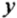
Оси координат разбивают плоскость на 4 части, которые называют координатными четвертями. Нумерация четвертей и знаки координат точек в каждой четверти показаны на рисунке 73.
Интересные рассказы
Из истории системы координат
Координаты были нужны астрономам и географам для определения положения светил на небе и различных мест на Земле, для составления звездных и географических карт.
Прямоугольная система координат в виде квадратной сетки (палетки) была известна еще в Древнем Египте, ею пользовались и художники эпохи Возрождения.
Идея использования координат в математике принадлежит уже упоминавшемуся французскому математику Рене Декарту. В честь Декарта прямоугольную систему координат называют еще прямоугольной декартовой системой координат.
Термин абсцисса происходит от латинского слова abscissus, что означает «отрезанный», «отделенный», а буквально переводится как «отрезок» (на оси 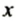
Слово ордината происходит от латинского слова ardinatus — упорядоченный.
Эти термины в их современном понимании ввел в конце XVII в. немецкий учений Г. Лейбниц (1646 — 1716). Чтобы подчеркнуть равноправность понятий «абсцисса» и «ордината», Г. Лейбниц применил термин координата, которое происходит от латинских слов со — с, вместе, и ardinatus — упорядоченный. Этот термин означает «взятые в определенной последовательности числа, определяющие положение точки на плоскости».
Примеры графиков зависимостей между величинами
Метеорологи измеряли температуру воздуха в течение первой половины суток и результаты записали в таблицу:
Потом они решили нанести результаты измерений на координатную плоскость, отложив на оси абсцисс значения времени 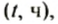
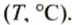
Если точки, построенные таким образом на координатной плоскости, соединить плавной линией, то получим фигуру, которую называют графиком зависимости температуры воздуха от времени (рис. 78).
Рассмотрим другие примеры.
Пример:
Туристу нужно пройти 12 км. Он подсчитал время движения в зависимости от скорости, с которой будет идти, и получил такую таблицу:
Решение:
Построим на координатной плоскости точки по этой таблице, отложив на оси абсцисс значения скорости 
Соединив плавной линией построенные точки, получим график зависимости времени от скорости при постоянном расстоянии (12 км) (рис. 79).
Эту зависимость времени 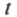
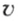
Пример:
Известно, что в бассейн каждую секунду вливается 0,5 м 3 воды Нужно найти, сколько воды будет в бассейне через 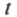
Решение:
Зависимость объема воды 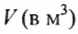
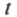
Возьмем определенные значения 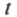
По данным таблицы построим на координатной плоскости точки, отложив на оси абсцисс значения времени 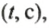
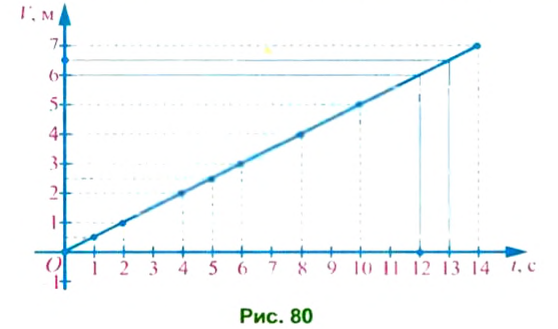
Пример:
Пользуясь графиком зависимости объема воды в бассейне oт времени его наполнения (рис. 80), найти: а) объем при 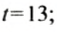
Решение:
а) На оси абсцисс, на которой отложили время 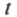
б) На оси ординат, на которой откладывали объем 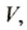
Памятка:
— умножили модули множителей
— знаки множителей разные, произведение — число отрицательное.
— разделили модуль делимого на модуль делителя
— знаки делимого и делителя разные, частное — число отрицательное.
— коэффициент.
— подобные слагаемые
— привели подобные слагаемые, сложили коэффициенты, умножили на общую буквенную часть.
— слагаемые можно переносить из одной части уравнения в другую, меняя при этом их знаки на противоположные
— параллельные прямые.
— перпендикулярные прямые.
Видео:Математика 6 класс. Вычитание рациональных чисел.Скачать

Рациональные числа и действия над ними
Положительные и отрицательные числа. Число нуль
Рассмотрите рисунок 78. Вы видите эскиз улицы, на которой расположена школа. Саша сказал, что он вышел из школы и прошёл мимо трёх домов вдоль этой улицы.
Пример:
Можно ли определить, где оказался Саша? Нет. Точно ответить мы не сможем, поскольку не знаем, в каком направлении от школы двигался Саша. Если Саша пошёл от школы налево, то оказался возле бассейна, а если направо — то возле библиотеки.
Итак, чтобы определить новое местонахождение на прямолинейном участке дороги, нужно указывать не только расстояние, но и направление движения от некоторой начальной точки.
Рассмотрим ещё один пример. Определяя температуру воздуха с помощью термометра, мы фиксируем не только значение, на кагором остановился столбик термометра, но и обращаем внимание на то, где именно находится это значение на шкале термометра: ниже нуля или выше нуля (рис. 79). Например, если температура поднялась на 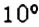
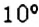
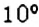
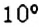
Обозначают: 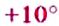
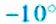
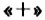
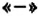
Проведём прямую и отметим на ней точку 
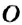
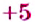
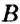
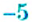
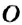
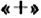
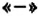
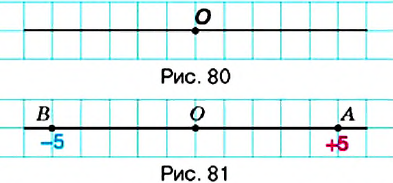
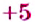

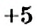
Числа со знаком 
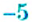
Определение:
Любое натуральное число является положительным.
Пример:
Положительным или отрицательным является число 0? Ни тем, ни другим. Число 0 отделяет положительные числа от отрицательных.
Неотрицательные числа — это положительные числа вместе с числом 0, а неположительные числа — это отрицательные числа вместе с числом 0.
Для математических вычислений в древности использовали палочки. Палочками красного цвета изображали положительные числа, чёрного — отрицательные. В Индии отрицательные числа толковали как долг, а положительные — как имущество. Многие математики называли отрицательные числа ложными числами, поскольку не могли понять существования чисел, меньших чем «ничто» (нуль). Лишь начиная с XVIII в., отрицательные числа стали использовать наравне с положительными числами.
Координатная прямая
В пятом классе положительные числа и число 0 вы отмечали на координатном луче (рис, 88). Продлим координатный луч 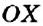
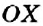
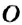
Определение:
Прямая, на которой отмечено начало отсчёта, единичный отрезок и направление, называется координатной прямой.
Стрелкой на координатной прямой указывают положительное направление. На луче 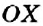
Посмотрите на рисунок 91. Вы видите, что точке 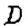
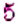
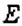
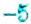
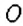

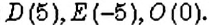
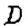
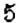
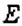
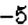
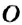
Пример:
Что показывает координата точки на координатной прямой с началом отсчета 
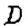
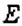
Обратите внимание:
каждой точке на координатной прямой соответствует единственная координата.
Пример:
На координатной прямой отметьте точки: 1) 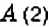
Решение:
1. Координата 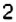
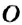
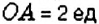
2. Координата 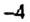
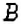
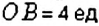
Парад планет — астрономическое явление, когда несколько планет Солнечной системы оказывается по одну сторону от Солнца и почти на одном луче (рис. 93). Иногда говорят: «Планеты выстроились в одну линию». Во время большого парада планет в одну линию выстраиваются 6 планет — Венера. Земля, Марс. Юпитер, Сатурн. Уран Если считать планету точкой на координатной прямой, а нашу планету Земля — началом отсчёта, то какие знаки будут иметь координаты других планет во время большого парада планет? Подумайте самостоятельно.
Модуль числа
Отметим на координатной прямой точки 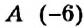
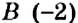
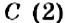
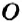
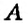
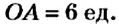
Сравнивая расстояния от точек 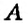
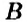
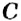
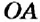
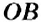
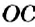
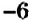
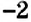
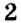
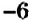
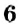
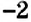
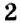
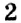

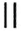
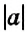
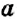
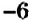
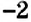
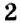
Обратите внимание:
модуль числа показывает, на каком расстоянии от начала отсчёта находится данное число на координатной прямой.
В этом заключается геометрический смысл модуля числа. Значит, модуль числа не может быть отрицательным числом, а фраза «модуль числа равен -24» не имеет смысла.
Пример:
Чему равен модуль числа 0? Нулю:
Точки 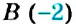
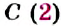
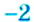

Определение: Два числа, имеющие равные модули, но противоположные знаки, называются противоположными числами. Число 0 противоположно самому себе.
Пример:
Как записать число, противоположное данному числу? Для этого достаточно изменить знак данного числа на противоположный. Например, для числа 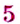
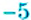
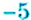
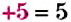
Пример:
Чему равен модуль: 1) положительного числа; 2) отрицательного числа?
Решение:
1. Пусть 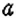
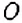
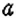
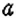
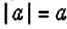
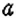
2. Пусть 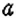
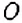
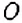
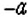
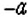
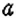
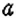
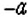
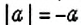
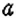
Свойства модуля числа
Свойства модуля числа
- Модуль положительного числа равен самому числу.
- Модуль отрицательного числа равен противоположному числу.
- Модуль числа 0 равен нулю.

Пример:
Найдите расстояние между точками: 1) 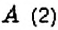
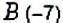
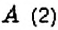
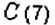
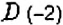
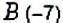
Решение:
1. На координатной прямой отметим точки 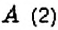
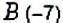
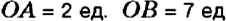
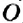
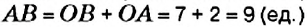
2. На координатной прямой отметим точки 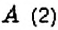
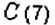
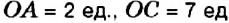
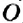
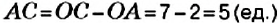
3. На координатной прямой отметим точки 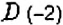
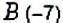
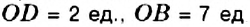
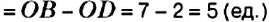
Обратите внимание:
чтобы найти расстояние между двумя точками по их координатам, нужно:
- — прибавить модули координат, если координаты имеют разные знаки;
- — из большего модуля координаты вычесть меньший модуль координаты, если координаты имеют одинаковые знаки.
Слово «модуль» — латинского происхождения: modulus — мера. До недавнего времени вместо «модуль числа» говорили абсолютная величина. Так раньше называли «числа без знаков», противопоставляя им так называемые «относительные числа» — числа со знаками. Сейчас термины «относительные числа» и «абсолютная величина числа» считают устаревшими и их не используют.
Целые числа. Рациональные числа
В 5 классе вы изучали натуральные числа. Это числа, используемые для счёта: 1; 2; 3; 4; . Все натуральные числа образуют множество натуральных чисел. Его обозначают буквой 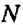
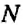

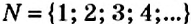
Кроме множества натуральных чисел, существуют и другие числовые множества.
Натуральные числа, противоположные им числа и число ноль образуют множество целых чисел. Его обозначают буквой 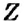

Каким бы ни было натуральное число, оно является элементом множества целых чисел. Однако не каждое целое число является элементом множества натуральных чисел. Действительно, любое отрицательное число, противоположное натуральному числу, является элементом множества целых чисел. Но такое число не является натуральным. Соотношение между целыми и натуральными числами показано на рисунке 114.
Пример:
Можно ли считать, что положительные целые числа являются натуральными числами? Да.
Кроме целых чисел, вы знаете ещё и дробные числа. Некоторые из дробей обозначают целые числа, а некоторые — нет. Например, дробь 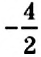
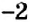
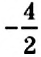
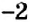
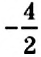
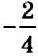
Обратите внимание:
не все числа, записанные в виде дроби, являются дробными.
Целые числа и дробные числа образуют множество рациональных чисел. Его обозначают буквой 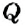
Пример:
Среди чисел 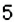
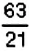
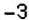
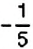
1) натуральные числа; 2) целые числа; 3) рациональные числа.
Решение:
1. Натуральными являются числа 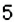
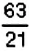
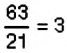
2. Целыми являются числа 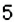
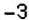
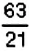
3. Рациональными являются числа 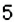
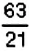
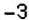
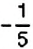
Обратите внимание:
- — каждое натуральное число является и целым числом, и рациональным числом;
- — каждое целое число является рациональным числом;
- — не каждое рациональное число является целым числом;
- — не каждое рациональное число является натуральным числом.
Пример:
На координатной прямой отметьте такую точку между точками 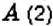
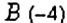
Решение:
Построим координатную прямую и отметим на ней точки 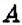
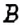
1. Между точками 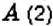
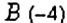
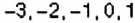
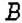
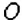
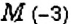
2. Вообще, между точками 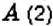
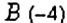
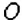
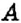
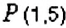
Обратите внимание:
между двумя числами на координатной прямой лежит бесконечно много рациональных чисел.
Понятие «множество» — одно из первичных понятий математики Множество можно создавать не только из чисел, но и любых других объектов. Например, конфеты в коробке тоже образуют множество и каждая конфета — его элемент. Для обозначения множеств обычно используют большие латинские буквы 
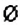
Сравнение рациональных чисел
Со сравнением рациональных чисел вы встречаетесь едва ли не ежедневно. Например, зимой, когда на улице мороз 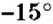

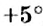
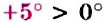
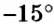
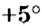

Сравним числа 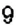
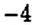
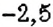
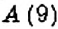
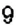
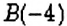
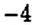
Определение:
- Сравнить два рациональных числа —значит установить, какое из них больше, а какое —меньше.
- Из двух рациональных чисел большим является то число, для которого соответствующая точка на координатной прямой расположена правее.
Результат сравнения рациональных чисел записывают с помощью числовых неравенств. Например,
Пример:
Какие целые числа больше-5 и меньше 6,8?
Решение:
Отметим точки 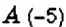
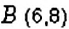
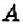
Какую закономерность заметим, сравнивая с числом -5 отрицательные числа-4, -3, -2, -1? Числа от -5 до -1 увеличиваются, но их модуль уменьшается. Для положительных чисел 1, 2, 3, 4, 5, 6 закономерность иная — и числа увеличиваются, и их модули увеличиваются. Но число 0 всегда больше любого отрицательного числа и меньше любого положительного числа.
Вообще, для сравнения чисел необязательно строить координатную прямую.
Правила сравнения рациональных чисел
Правила сравнения рациональных чисел
- Отрицательное число всегда меньше положительного числа.
- Число 0 меньше положительного числа, но больше отрицательного числа.
- Из двух положительных чисел больше то число, модуль которого больше.
- Из двух отрицательных чисел больше то число, модуль которого меньше.
- Если число
положительное, то записывают:
.
- Если число
отрицательное, то записывают:
.
- Если число
неположительное, то записывают:
.
- Если число
неотрицательное, то записывают:
.
Пример:
Верно ли, что любое рациональное число всегда больше противоположного ему числа? Нет. Например, для числа-5 противоположным является число 5, но 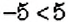
Обратите внимание:
чтобы опровергнуть некоторое утверждение, достаточно одного примера.
Древнейшей математической деятельностью был счёт. Число 0 не использовали. Индейцы племени Майя первыми применяли специальный символ для обозначения нуля. но он имел не то толкование, к которому мы привыкли. Ноль у Майя означал начало. Цифра ноль, которой мы сейчас пользуемся, пришла к нам из Индии. Ноль записывали кружочком. Индийские учёные произвели революцию в математике, определив ноль не как отсутствие числа, а как число. Первая запись с использованием нуля датируется 876 годом.
Сложение рациональных чисел
Каждое рациональное число характеризует его модуль и знак. Поэтому для сложения двух рациональных чисел важно выяснить, каким будет модуль и знак суммы в зависимости от модулей и знаков слагаемых. Для положительных чисел эта связь очевидна, поскольку сумма двух положительных чисел является числом положительным.
Пример:
Как к отрицательному числу прибавить положительное число? Поразмышляем, опираясь на координатную прямую.
Пусть нужно сложить числа 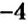
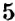
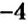
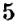

Пусть нужно сложить числа 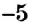
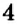
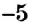
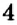
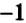
Получается, что при сложении чисел 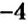
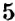
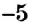
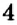
Пример:
Изменится ли сумма чисел с разными знаками, если их складывать в другом порядке — к положительному числу прибавлять отрицательное? Нет, сумма не изменится. Используя координатную прямую, попробуем поразмышлять по-другому.
Пусть к числу 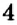
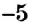
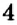
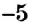
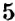
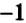
Сравним этот результат и результат, полученный в предыдущем примере. Видим, что:
Правило сложения чисел с разными знаками
Чтобы найти сумму двух чисел с разными знаками, нужно:
- найти модули слагаемых;
- из большего модуля вычесть меньший модуль;
- перед полученным числом поставить знак того из слагаемых, модуль которого больше.
Пример:
Как сложить два отрицательных числа? Будем рассуждать аналогично последнему примеру.
Пусть к числу 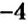
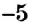
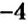
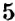
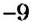
Правило сложения чисел с одинаковыми знаками
Чтобы найти сумму двух чисел с одинаковыми знаками, нужно:
- найти модули слагаемых;
- сложить модули слагаемых;
- перед полученным числом поставить знак слагаемых.
Пример:
В чём особенность сложения противоположных чисел? Поразмышляем. Посмотрите на рисунки 126 и 127. Вы видите, как складывали противоположные числа 
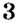
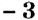
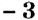
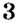
Обратите внимание:
сумма двух противоположных чисел равна 0: 
Пример:
Вычислите: 1) 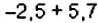
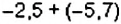
Решение:
1)
2)
Обратите внимание:
изменение числа зависит от того, какое число к нему прибавляют:
- — если прибавляют положительное число, то данное число увеличивается;
- — если прибавляют отрицательное число, то данное число уменьшается.
Пример:
Справедливы ли переместительный и сочетательный законы сложения для рациональных чисел? Да. Для любых рациональных чисел 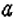
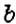
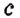
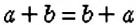
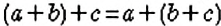
Пример:
Найдите сумму 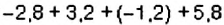
Решение:
Задачу можно решить двумя способами.
Способ 1. Сгруппируем слагаемые с одинаковыми вычислим сумму:
Способ 2. Сгруппируем слагаемые с разными знаками и вычислим сумму:
Если одно из слагаемых равно 0, то сумма равна другому слагаемому:
Индийский математик Брахмагупта (VII в.) использовал следующие правила для сложения положительных и отрицательных чисел.
Вычитание рациональных чисел
Вы уже умеете вычитать положительные числа и можете найти разность, когда уменьшаемое больше вычитаемого или равно ему.
Пример:
Можно ли из меньшего числа вычесть большее? Да, если выполняем действия с рациональными числами. Поразмышляем, опираясь на координатную прямую.
Пусть нужно найти разность чисел 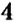
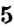
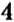
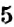
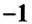
Обратите внимание:
при вычитании рациональных чисел уменьшаемое может быть меньше вычитаемого.
Пример:
Можно ли находить разность рациональных чисел без помощи координатной прямой? Да. Для этого нужно знать правила вычитания рациональных чисел.
В предыдущем параграфе вы узнали, как выполнять сложение чисел с разными знаками. Действие вычитания числа 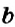
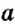
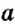
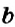
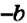
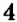
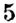
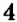
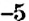
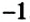
Правило замены вычитания сложением
Чтобы из одного числа вычесть другое, можно к уменьшаемому прибавить число, противоположное вычитаемому:
Пример:
Вычислите: 1) 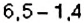
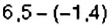
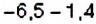
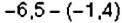
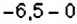
Решение:
Пример:
Верно ли, что вследствие вычитания рациональных чисел уменьшаемое всегда уменьшается? Нет. В задаче 1 в примерах 1 и 3 уменьшаемое уменьшилось, поскольку вычитаемое — положительное число. В примерах 2 и 4, наоборот, уменьшаемое увеличилось, поскольку вычитаемое — отрицательное число. А в примере 5 уменьшаемое не изменилось, поскольку вычитаемое равно 0.
Обратите внимание:
1) в результате вычитания рациональных чисел уменьшаемое:
- — уменьшается, если вычитаемое является положительным;
- — увеличивается, если вычитаемое является отрицательным;
- — не изменяется, если вычитаемое равно 0;
2) о вычитании рационального числа 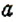
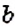
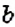
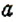
Пример:
Как найти разность нескольких чисел? Рассмотрим пример.
Пример:
Вычислите разность 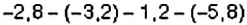
Решение:
Заменим действие вычитания действием сложения:
В полученной сумме можно сгруппировать слагаемые одним из двух способов так, как показано в задаче 2 параграфа 26. Используем первый из них. Тогда получим:
Следовательно,
Натуральные числа, а также положительные дробные числа возникли в древности при решении практических задач. Потребность ввести целые числа была обусловлена развитием математики, в частности, необходимостью решать уравнения. Поскольку вычитать натуральные числа было возможно лишь при условии, что уменьшаемое больше вычитаемого, то множество натуральных чисел требовало расширения. Целые числа и являются расширением множества натуральных чисел. В множестве целых чисел всегда можно выполнить вычитание. Теорию отрицательного числа наиболее содержательно разработал немецкий математик М. Штифель (1487—1567). Свою теорию он изложил в книге «Полная арифметика», которая увидела свет в 1544 г.
Умножение рациональных чисел
Вы знаете, что сложение нескольких равных положительных чисел можно заменить действием умножения. Например, 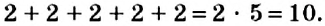
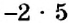
Полученное число 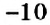
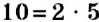
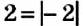
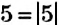
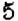
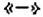
Пример:
Как умножить числа 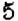
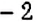
Пусть число 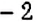
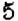
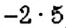
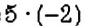
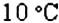
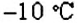
Получили, что 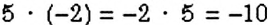
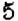
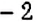
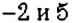
Правило умножения чисел с разными знаками
Произведение двух чисел с разными знаками — число отрицательное.
Чтобы умножить два числа с разными знаками, нужно умножить их модули и перед полученным произведением поставить знак 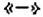
Пример:
Как умножить два отрицательных числа? Рассмотрим задачу.
Пример:
Температура воздуха каждый час изменялась на 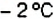
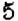
Решение:
Если число 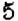
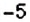
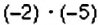
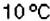
Получим, что произведение двух отрицательных чисел — число положительное. Например:
Правило умножения двух отрицательных чисел
Произведение двух отрицательных чисел — число положительное.
Чтобы умножить два отрицательных числа, достаточно умножить их модули.
Вообще, знак произведения двух рациональных чисел определяется знаками множителей.
Пример:
Можно ли по знаку произведения двух чисел определить, одинаковые или разные знаки у множителей? Да. Например, число равно произведению чисел с одинаковыми знаками: 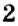
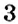
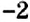
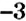
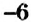
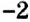
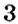
Свойства умножения на 0 рациональных чисел аналогичны таким же свойствам умножения положительных чисел. Если один из множителей равен нулю, то произведение равно нулю:
В дальнейшем будем рассматривать рациональные числа, отличные от нуля, а случаи, связанные с числом 0, будем анализировать отдельно.
Обратите внимание:
- — если произведение
положительно, то числа
и
имеют одинаковые знаки, и наоборот;
- — если произведение
отрицательно, то числа
и
имеют разные знаки, и наоборот;
- — если произведение
равно нулю, то хотя бы одно из чисел,
или
, равно нулю, и наоборот.
Если один из множителей равен 1, то произведение равно другому множителю:
Умножение числа на 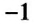
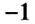
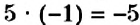
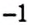
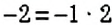
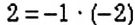
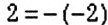
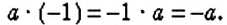
Пример:
Найдите произведение: 1) 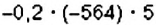
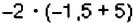
Решение:
1. Переставим множители и сгруппируем их так, чтобы вычисления упростились: 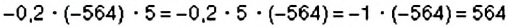
2. Применим распределительный закон умножения, а также правила умножения отрицательных чисел и чисел с разными знаками:
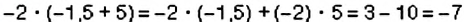
Пример:
Можно ли, не вычисляя произведения нескольких рациональных чисел, определить знак этого произведения? Да. При этом нужно учесть, что положительные множители не влияют на знак произведения.
Пример:
Положительным или отрицательным является произведение: 1) 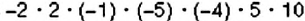
2) 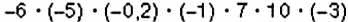
Решение:
1. В данном произведении — четыре отрицательных множителя: -2, -1, -5, -4. Произведение первой пары этих чисел положительно, второй пары — тоже, поэтому произведение всех четырёх чисел — положительно. Следовательно:
2 В данном произведении 5 отрицательных множителей, поэтому:
Обратите внимание:
- — произведение чётного количества отрицательных множителей — положительно;
- — произведение нечётного количества отрицательных множителей — отрицательно.
Индийские математики сформулировали правила умножения, деления, сложения, вычитания рациональных чисел. В таблице 14 вы видите, какими суждениями они пользовались при умножении рациональных чисел.
Деление рациональных чисел
Вы знаете, что для положительных чисел действие деления можно свести к действию умножения на число, обратное делителю. Пусть нужно разделить число 20 на число 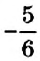
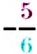
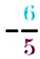
Тогда, по правилу умножения чисел с разными знаками, получим: 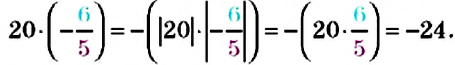
Видим, что частное чисел 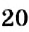
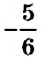
Аналогично, частное чисел 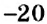
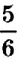
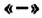
Правило деления чисел с разными знаками
Частное двух чисел с разными знаками — число отрицательное.
Чтобы найти частное чисел с разными знаками, нужно разделить модуль делимого на модуль делителя и перед полученным частным поставить знак 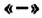
Пример:
Как разделить одно отрицательное число на другое? Рассуждая аналогично предыдущему случаю, для чисел 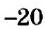
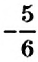
Правило деления двух отрицательных чисел
Частное двух отрицательных чисел — число положительное.
Чтобы найти частное двух отрицательных чисел, достаточно разделить модуль делимого на модуль делителя.
Вообще, знак частного рациональных чисел определяется знаками делимого и делителя. Например:
Если число 0 разделить на любое рациональное число, отличное от нуля, то в частном получим 0:
Действие деления на 0 не имеет смысла и для рациональных чисел. Поэтому:
на 0 делить нельзя!
Обратите внимание:
- — в частном
число
не может быть равным нулю;
- — если частное
положительно, то числа
и
имеют одинаковые знаки, и наоборот;
- — если частное
отрицательно, то числа
и
имеют разные знаки, и наоборот;
- — если частное
равно нулю, то
равно нулю, и наоборот.
Поскольку 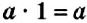
Если число, отличное от нуля, разделить на 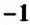
Частное двух противоположных чисел, отличных от нуля, равно 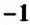
Название рациональных чисел происходит от латинского «ratio» — «отношение», поскольку эти числа с момента своего появления представляют с помощью отношения целого числа к натуральном у числу.
Если разделить рациональное число на рациональное число, отличное от нуля, то частное всегда будет рациональным числом. А если разделить целое число на целое число, отличное от нулю, то в частном не всегда получим целое число. Например, частное чисел 2 и 3 не является целым числом. Интересно, что исторически проблема деления чисел была решена значительно раньше, чем проблема, связанная с их вычитанием.
Видео:Как решать дробно-рациональные уравнения? | МатематикаСкачать

Рациональные числа
Этот раздел содержит очень важный и нужный материал. Натуральные и дробные числа, с которыми вы имели дело до сих пор, были известны людям более 4 тысячелетий назад. А отрицательные числа вошли в математику намного позже — несколько веков назад. Основное содержание этого раздела такое.
- Положительные и отрицательные числа.
- Действия с положительными и отрицательными числами.
- Преобразование простейших выражений.
- Перпендикулярные и параллельные прямые.
- Координатная плоскость и графики.
Весь этот материал является фундаментом математики, физики и других наук, которые вы будете изучать в последующих классах.
Положительные и отрицательные числа
Существуют числа, значения которых меньше 0. Их называют отрицательными числами. Например, отрицательными числами обозначают значение температуры.
Температура, при которой начинает замерзать вода — 0 градусов по Цельсию (°С). А бывает еще холодней. Тогда столбик ртути в термометре опускается ниже отметки О °С. Если столбик ртути размещен так, как на рисунке 86, то говорят, что термометр показывает «4 градуса мороза», или «4 градуса ниже нуля», или «минус 4 градуса». Пишут: -4 °С. Иногда передают такие сведения о погоде: «В Ялте сегодня 5 градусов, в Одессе — 0 градусов, в Харькове — минус 2 градуса, в Киеве -минус 3 градуса». Эти значения температуры можно записать так: 5, 0, -2, -3 градуса. Числа 5 и 0 вам уже известны. А числа -2 и -3 — примеры отрицательных чисел.
Отрицательные числа записывают со знаком минус «-».
Приводим еще примеры отрицательных чисел:
Те числа, что рассматривались раньше (кроме 0), теперь будем называть положительными числами. Иногда положительные числа пишут со знаком плюс «+». Число 0 — ни положительное, ни отрицательное.
Все положительные числа вместе с нулем называют неотрицательными .
Отрицательными и положительными числами обозначают не только значения температуры, но и расположение местности над уровнем моря (рис. 87), изменение количества денег в кассе (задача 857), они используются также во многих других случаях.
Обратите внимание на правильное произношение положительных и отрицательных чисел. Например,
равно десяти;
равно минус четырнадцати;
больше двух целых пяти десятых;
меньше минус семи.
Названия знаков чисел («+» и «-») не склоняются. Например, минус три, минус трех, минус трем и т. п.
Выполнение заданий:
Пример №58
Просклоняйте словосочетание «положительная разность», «минус семь».
Решение:
И. положительная разность минус семь
Р. положительной разности минус семи
Д. положительной разности минус семь
В. положительную разность минус семь
Т. положительной разностью минус семью
П. положительной разности минус семи
Координатная прямая
Посмотрите на линейку с делениями. Ее штрихи (черточки) делят линейку на равные деления. Большие штрихи обозначают числа О, 1,2, 3, . . Расстояние между каждыми двумя соседними большими штрихами равно 1 см. Малым штрихам также соответствуют числа, но дробные (рис. 90). Все нанесенные на линейку штрихи образуют шкалу. Шкала линейки содержит штрихи, которым соответствуют только неотрицательные числа. А на шкале термометра есть штрихи, которым соответствуют и отрицательные числа (см. рис. 88).
Для математики наиболее пригодна прямолинейная тикала с равными делениями, бесконечная в обе стороны.
Вы уже знаете, что такое координатный луч (вспомните!). На координатный луч чем-то похожа и координатная прямая. Представим себе прямую (бесконечную). Обозначим на ней какую-либо точку О — это начало отсчета. Справа от нее на равных расстояниях друг от друга обозначим точки и поставим им в соответствие числа: 1, 2, 3, 4, . . На таких же расстояниях друг от друга обозначим на прямой точки слева от точки О и поставим им в соответствие числа: -1, -2, -3, -4. (рис. 91). Такую прямую называют координатной прямой.
Направление вправо от начала отсчета называют положительным, на координатной прямой его обозначают стрелкой.
Каждому числу на координатной прямой соответствует определенная единственная точка. Например, на координатной прямой, изображенной на рисунке 92, числу 2 соответствует точка 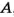
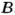
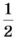
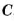
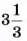
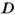
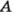
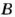
Координата точки О — число 0. Это — начало координат. Отрезок, концы которого имеют координаты 0 и 1, принимают за единичный отрезок (рис. 93).
Расстояние между точкой О(0) и точкой 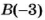
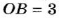
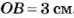
За единичный отрезок можно взять и любой другой, в частности, длиной 1 дм, 5 мм. Например, на рисунке 93 длина единичного отрезка равна 1,7 см.
Своеобразной координатной прямой является лента времени, на которой изображают годы и столетия (рис. 94). Христиане за начало отсчета времени берут день рождения Иисуса Христа (Рождество Христово). Время после этого дня называют новой эрой, а до него — до новой эры. Вместо до новой эры сокращенно пишут до н. э. или до P. X.
В Западной Европе такой отсчет времени введен с XVI в., а у нас (бывшей Российской империи) — только в 1700 г. До этого восточные славяне счет годам вели «от сотворения мира». Считали, что мир был создан 5508 лет до н. э.
Выполнение заданий:
Пример №59
Длина единичного отрезка координатной прямой равна 2 см.
а) Чему равно расстояние между точками 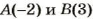
б) Найдите координату точки 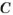
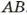
Решение:
а) Начертим координатную прямую и обозначим на ней точки 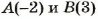
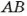
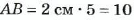
б) Точка 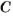
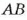
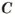
Целые и дробные числа
Числа 3 и -3 отличаются только знаками. Точки с такими координатами расположены по разные стороны от точки О и на одинаковых расстояниях от нее. Такие числа называются противоположными: число 3 противоположно числу -3, а -3 противоположно числу 3. Противоположными являются также числа:
Для каждого числа существует только одно противоположное ему число (рис. 100). Число 0 противоположно самому себе.
Противоположными натуральным числам 1, 2, 3, 4, 5, 6, . являются числа -1,-2,-3,-4, -5, -6, . .
Натуральные числа, противоположные им и число 0 вместе называют целыми числами.
Существуют три вида целых чисел: целые положительные (натуральные), целые отрицательные (-1,-2, -3, -4. ) и 0. Кроме них, есть и дробные положительные и отрицательные числа. Например,
Целые и дробные числа вместе называют рациональными числами (рис. 101).
Соотношения между упомянутыми видами чисел можно изобразить такой схемой.
Примечание. Числа 
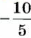
Все целые числа образуют множество целых чисел. На координатной прямой целым числам соответствуют точки, которые расположены равномерно и бесконечно далеко вправо и влево от начала координат.
Множество рациональных чисел — это совокупность целых и дробных чисел. Каждому рациональному числу на координатной прямой соответствует единственная точка. Точки с рациональными координатами расположены на координатной прямой очень плотно, между любыми двумя из них находится бесконечно много других точек с рациональными координатами. И все же на координатной прямой точек, координаты которых — не рациональные числа, еще больше. Об этом вы узнаете в 8-м классе.
Выполнение заданий:
Пример №60
Противоположные ли числа 0,2 и 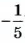
Решение:
0,2 и 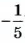
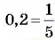
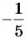
Пример №61
Точки 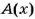
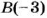
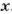
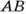
Решение:
Поскольку числа 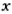
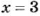
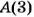
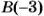
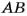
Модуль числа
Расстояние от начала координат до точки с координатой а называется модулем числа 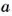
Какими бы небыли противоположные числа, их модули равны. Например, модуль каждою из чисел -12 и 12 равен 12, модуль каждого из чисел 0,9 и -0,9 равен 0,9.
Модулем неотрицательного числа является само число, модулем отрицательного числа является противоположное ему число.
Модуль числа 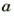
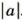
Модуль любого числа число неотрицательное.
Понятие модуля в математике используют очень часто. В частности решают уравнения и неравенства с модулями.
Уравнение 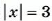
Неравенству 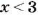
Слово модуль латинского происхождения: «modulus» — мера. Это слово в разных значениях используют не только в математике, но и в технике, архитектуре, во многих других науках и отраслях производства. От этот слова происходят также слова мода, модель.
Еще совсем недавно вместо «модуль числа» говорили абсолютная величина числа. Так раньше называли «числа без знаков», противопоставляя им относительные числа -числа со знаками. Теперь термины «относительные числа» и «абсолютная величина числа» устарели.
Выполнение заданий:
Пример №62
Вычислите значение 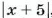
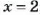
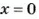
Решение:
а) Если 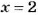
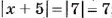
б) если 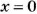
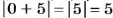
Пример №63
Найдите два решения уравнения 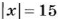
Решение:
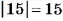
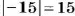
Сравнение рациональных чисел
Сравнить два числа — это значит установить, какое из них больше, какое меньше, или показать, что они равны.
Сравнивать положительные числа вы уже умеете. Например, 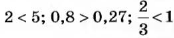
Из двух положительных чисел меньше то, которому на координатной прямой соответствует точка, расположенная левее. Например, точка 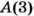
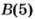
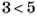
Из двух рациональных чисел меньшим считается то, которому на координатной прямой соответствует точка, расположенная левее.
Например, точка 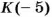
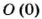
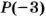
Поэтому каждое отрицательное число меньше 0 и любого положительного числа.
Например,
Точка 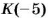
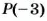
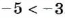
Из двух отрицательных чисел меньше то, модуль, которого больше.
Если одно число меньше другого, то второе число больше первого. Если 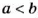
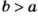
Поскольку каждое отрицательное число меньше 0, а каждое положительное число больше 0, то:
- запись
означает, что число
— положительное;
- запись
означает, что число
— отрицательное.
Знак «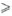
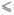
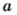
Выполнение заданий:
Пример №64
Между какими соседними целыми числами на координатной прямой находится число 2,4? Запишите это при помощи знака «
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
🎦 Видео
Решение уравнений, 6 классСкачать

МЕРЗЛЯК-6. ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ. ПАРАГРАФ-36Скачать

Дробно-рациональные уравнения. 8 класс.Скачать

Решение уравнений с отрицательными числами.Скачать

Умножение рациональных чисел. 6 класс.Скачать

ДРОБНО-РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ ЧАСТЬ I #shorts #егэ #огэ #математика #профильныйегэСкачать

ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ. Примеры | МАТЕМАТИКА 6 классСкачать

Виленкин. 6 класс за 100 минут. Математика: теория чисел, дроби, уравненияСкачать

Вычитание рациональных чисел с помощью координатной прямой. 6 класс.Скачать

Сложение и вычитание рациональных чисел 6-класс • +как решать задания!)Скачать

как ЛЕГКО сложить отрицательные числа , ПРИМЕРЫСкачать
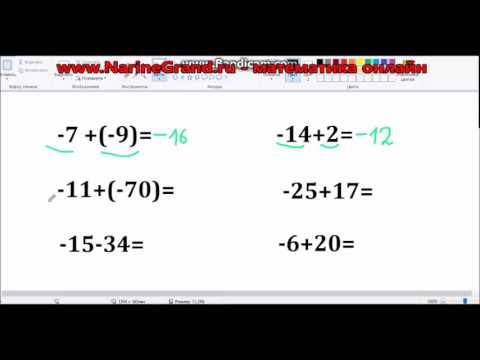
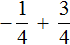
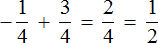
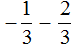
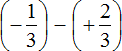
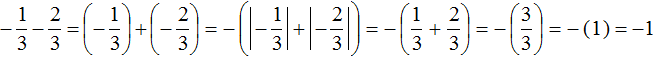
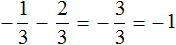
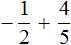
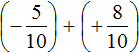
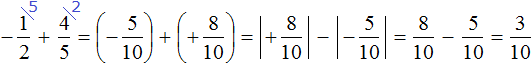
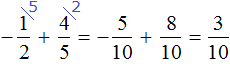
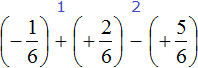
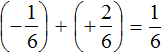
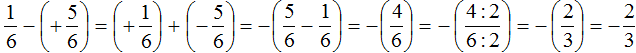
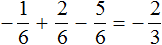
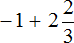
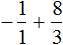
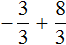
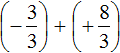
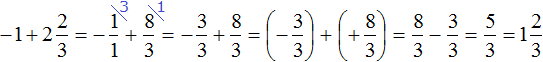
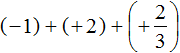
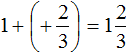
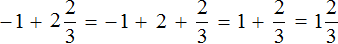
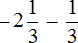
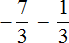
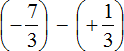
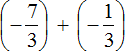
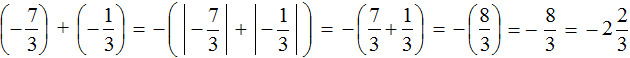
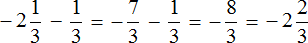
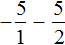
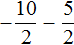
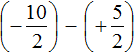
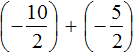
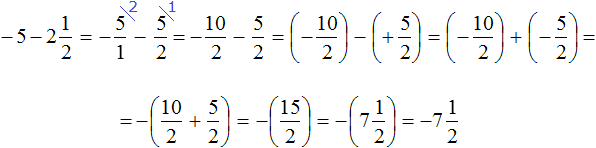
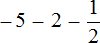
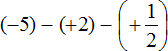
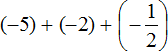
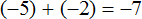
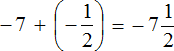
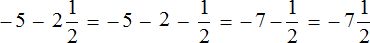
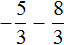
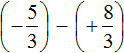
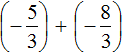
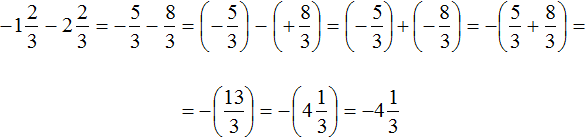
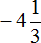
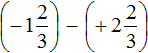
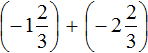
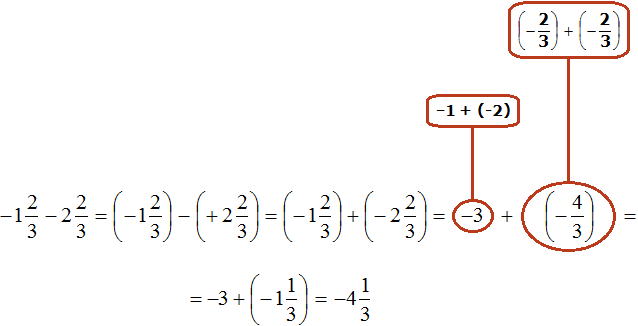
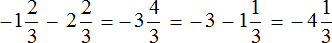
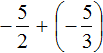
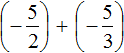
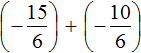
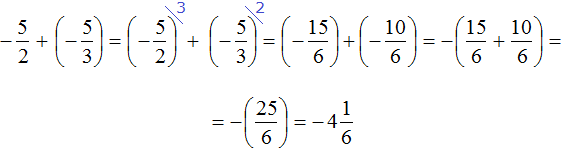
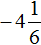
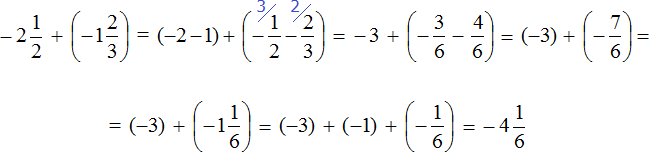
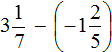
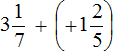
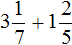
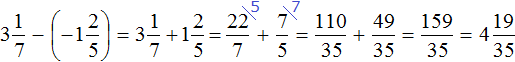
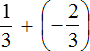
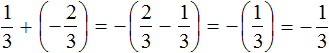
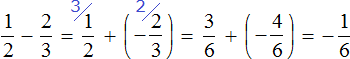
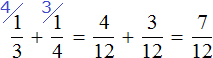
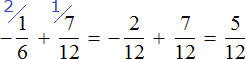
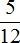
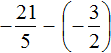
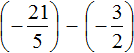
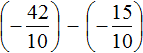
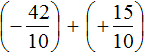
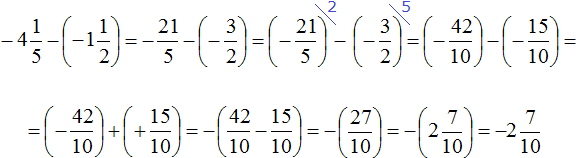
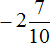
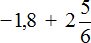
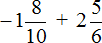
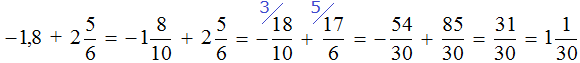
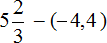
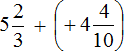
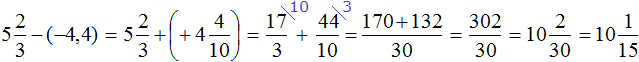
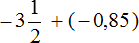
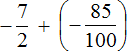
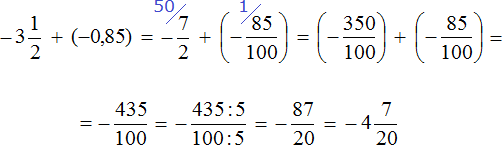
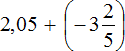
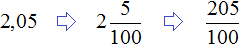
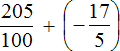
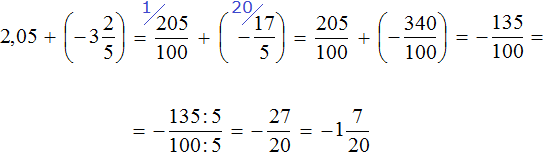
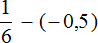
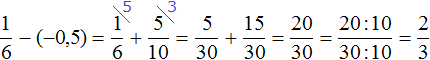
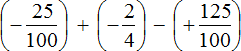
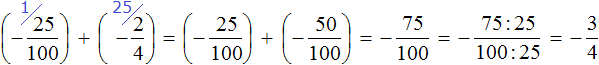
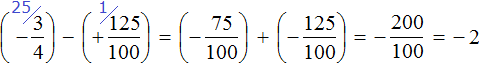
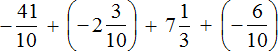
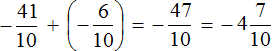
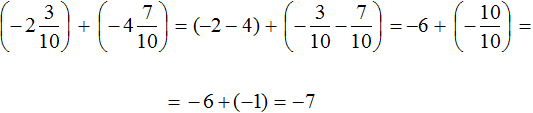
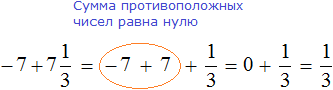

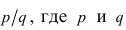
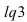
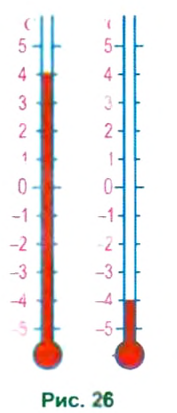
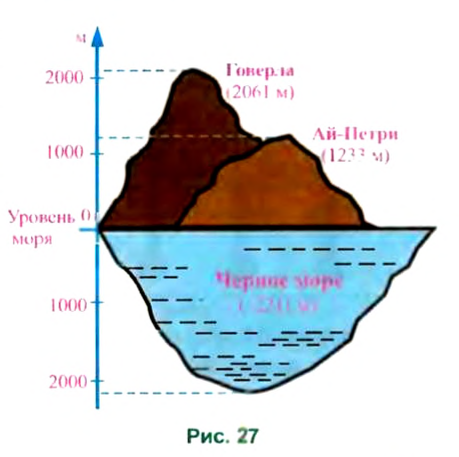
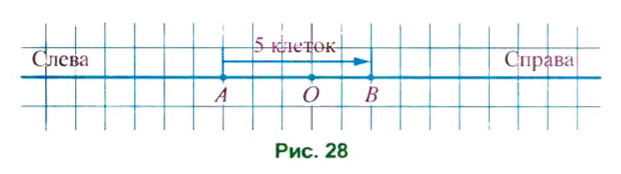
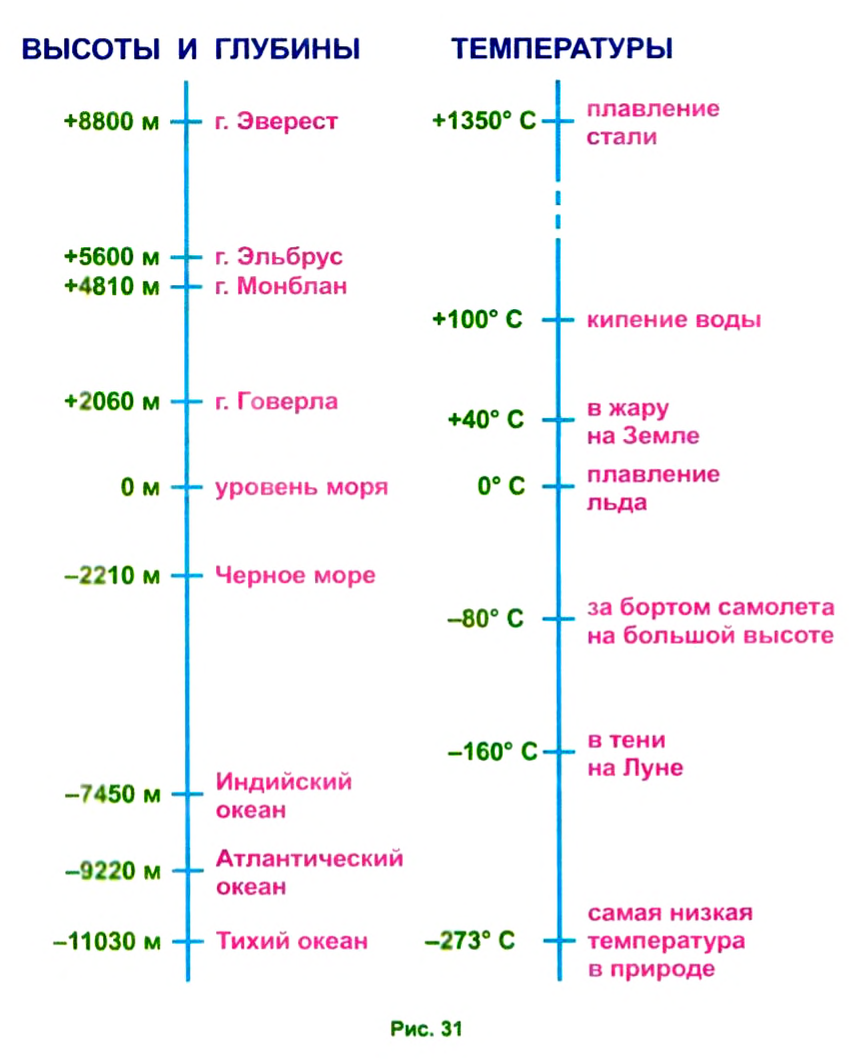
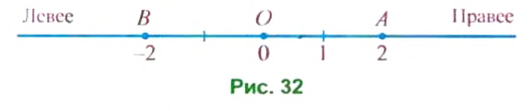

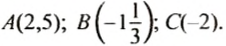


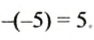
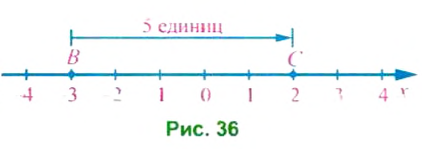
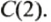
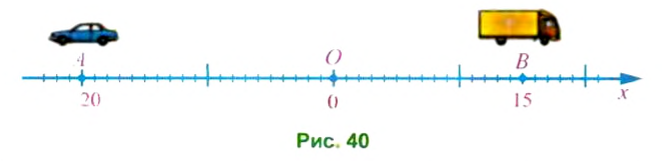
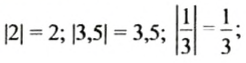
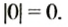
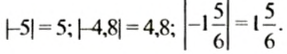
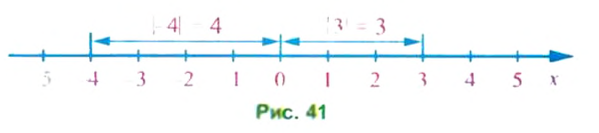
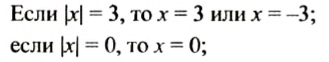
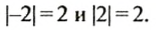
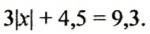
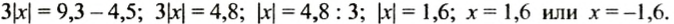
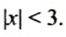
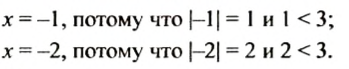

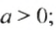
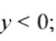
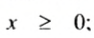
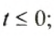
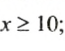
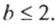
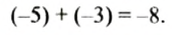
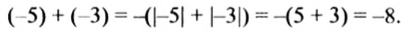

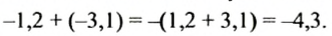
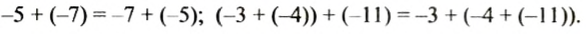

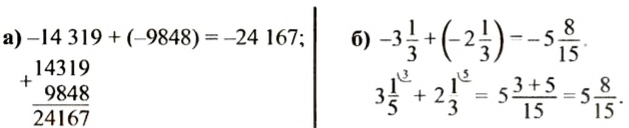
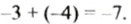
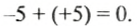
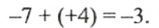
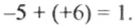
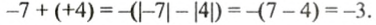

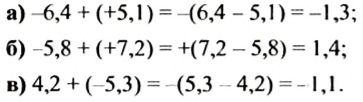
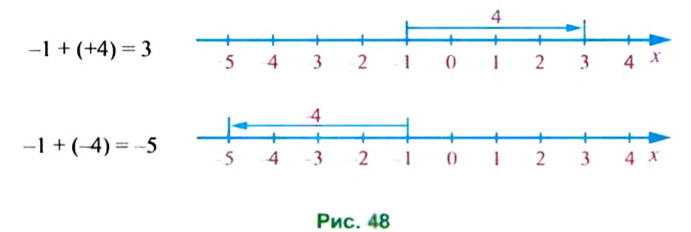
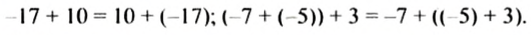
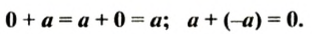
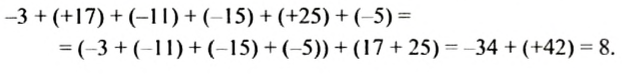
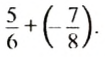
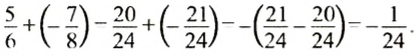
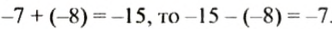
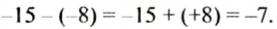
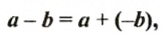
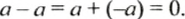
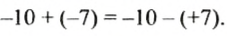

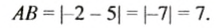
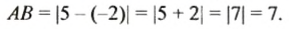
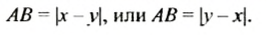
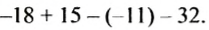
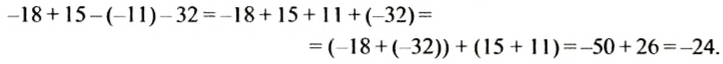
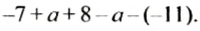
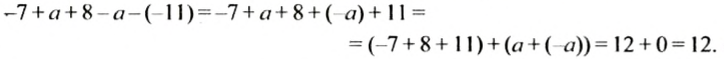
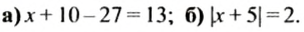
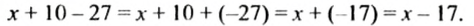
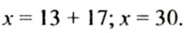

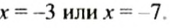
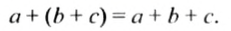
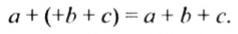
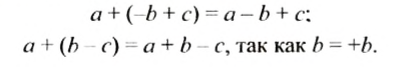
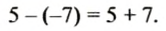
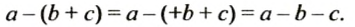
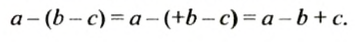
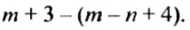
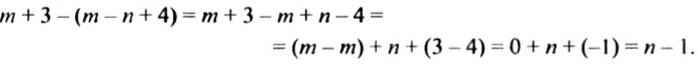
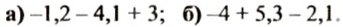
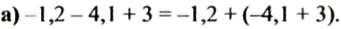
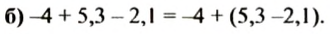
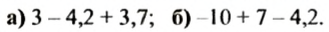
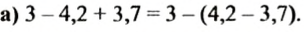
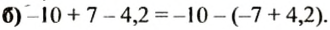
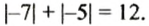
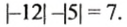
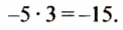
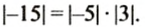
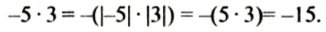
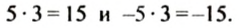
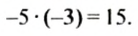
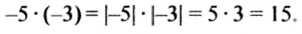
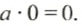
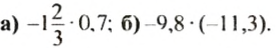
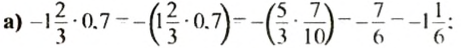
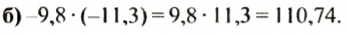
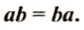
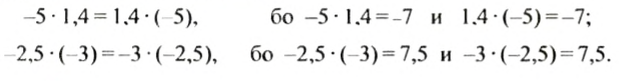
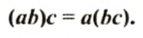
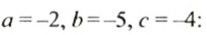
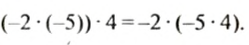
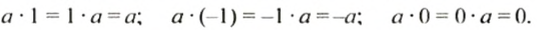
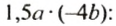
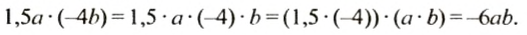
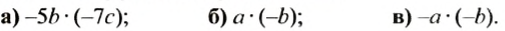
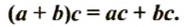
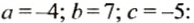
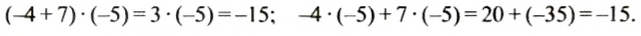
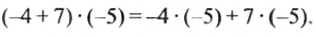
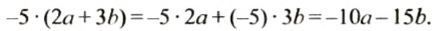
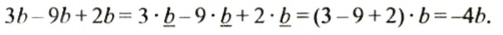
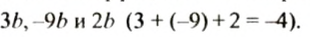
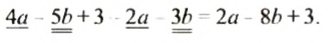
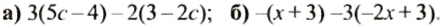
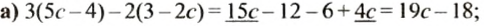
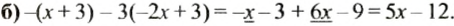

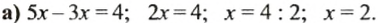
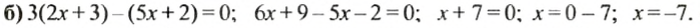
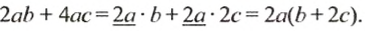
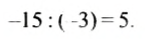
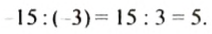
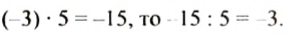
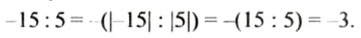
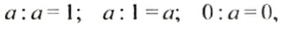
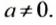

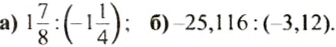
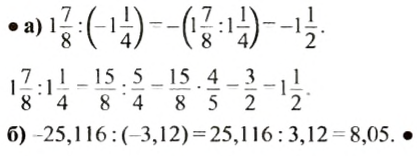

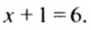
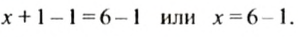
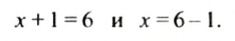
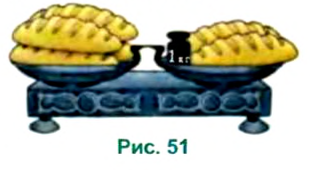
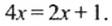
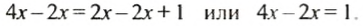
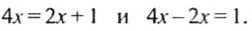
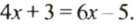
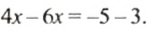
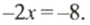
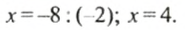
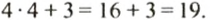
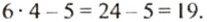
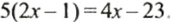
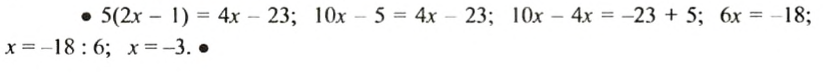
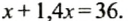
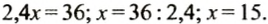
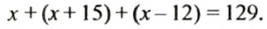
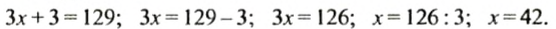
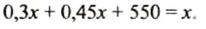
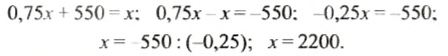
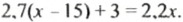
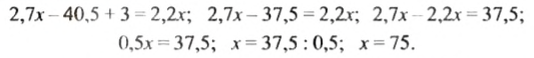
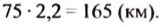
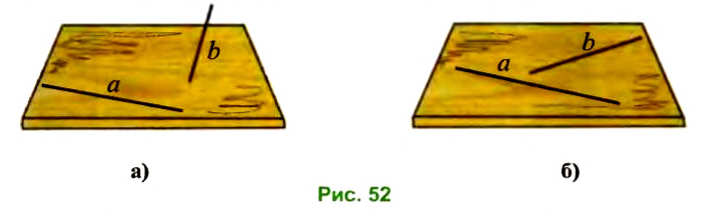

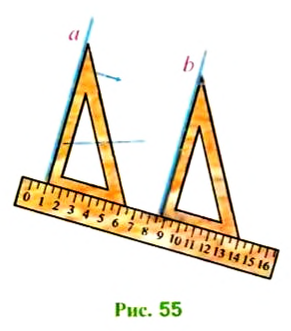
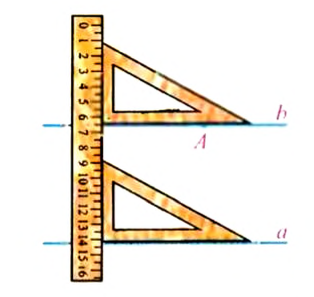
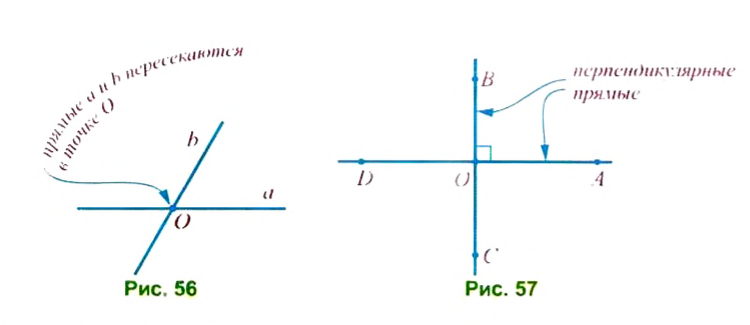
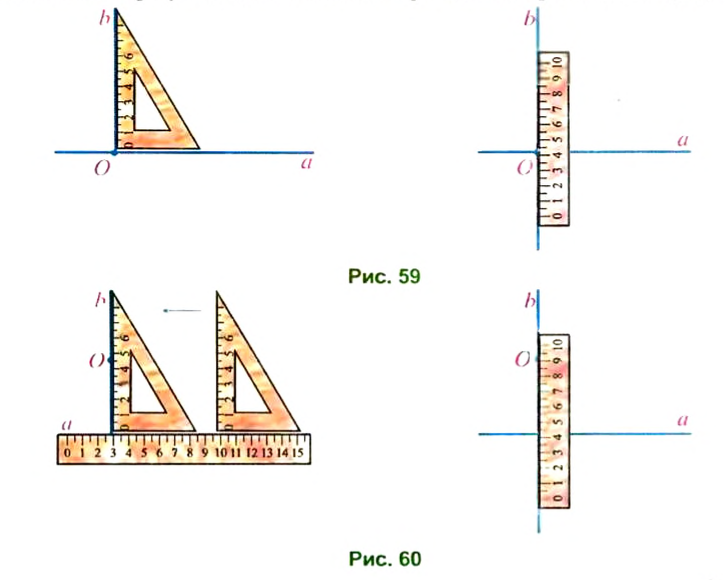

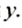
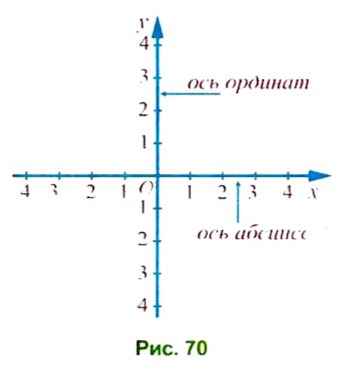
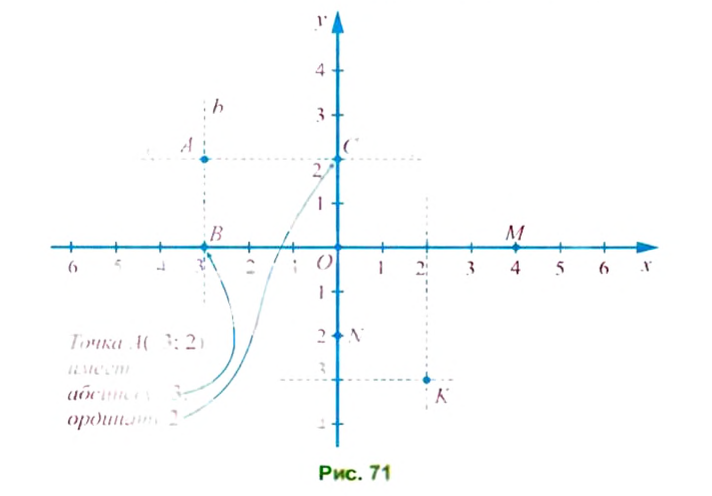

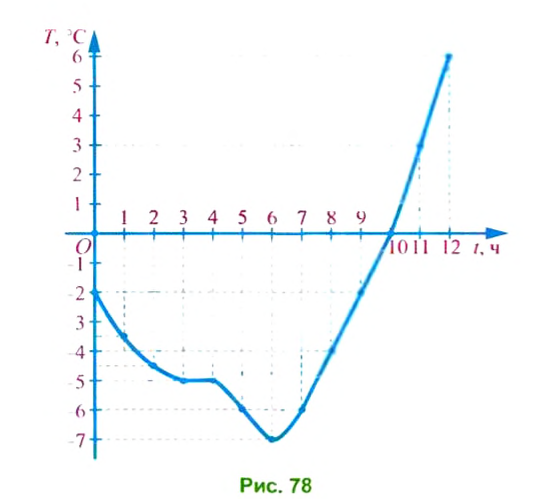
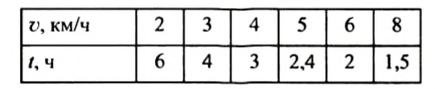
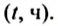
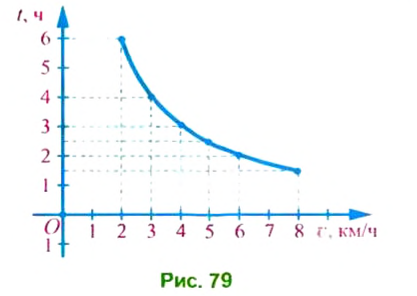
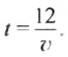
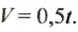

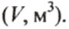
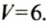
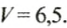
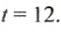
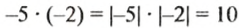 — умножили модули множителей
— умножили модули множителей 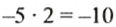 — знаки множителей разные, произведение — число отрицательное.
— знаки множителей разные, произведение — число отрицательное.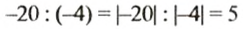 — разделили модуль делимого на модуль делителя
— разделили модуль делимого на модуль делителя 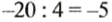 — знаки делимого и делителя разные, частное — число отрицательное.
— знаки делимого и делителя разные, частное — число отрицательное.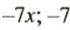 — коэффициент.
— коэффициент.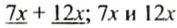 — подобные слагаемые
— подобные слагаемые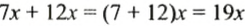 — привели подобные слагаемые, сложили коэффициенты, умножили на общую буквенную часть.
— привели подобные слагаемые, сложили коэффициенты, умножили на общую буквенную часть.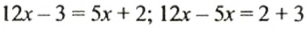 — слагаемые можно переносить из одной части уравнения в другую, меняя при этом их знаки на противоположные
— слагаемые можно переносить из одной части уравнения в другую, меняя при этом их знаки на противоположные — параллельные прямые.
— параллельные прямые.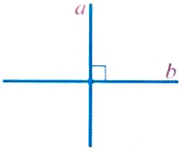 — перпендикулярные прямые.
— перпендикулярные прямые.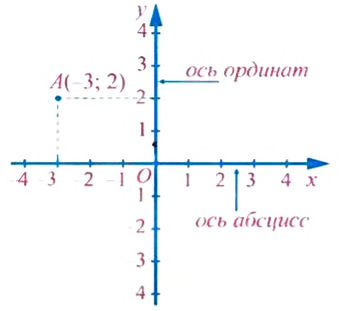


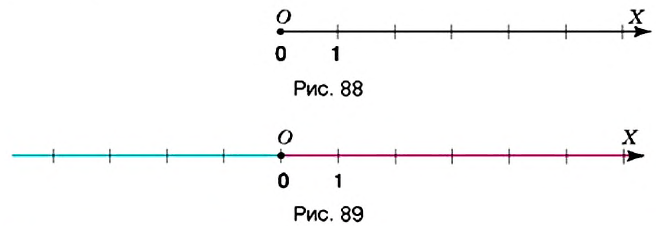


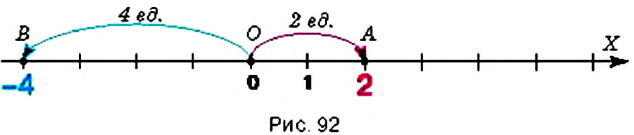

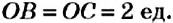

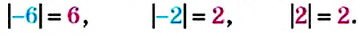
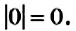
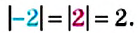



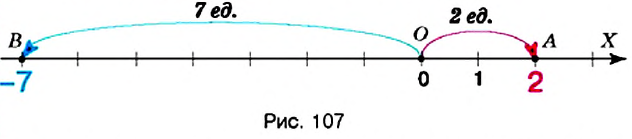
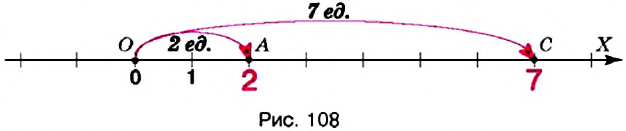
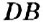
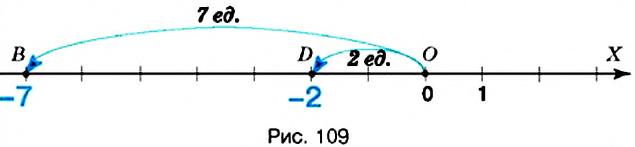
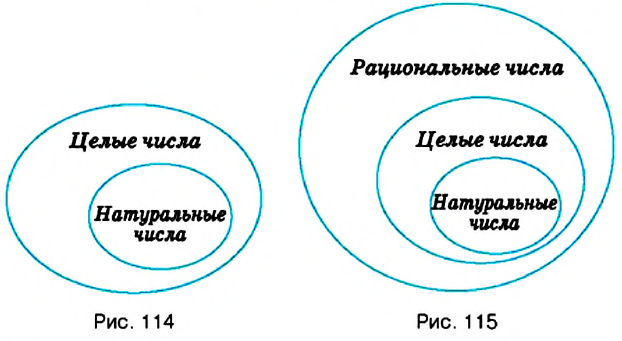

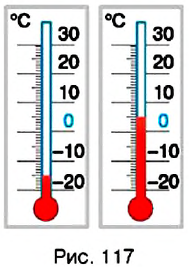

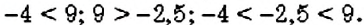
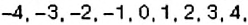
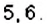

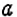 положительное, то записывают:
положительное, то записывают: 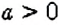 .
.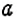 отрицательное, то записывают:
отрицательное, то записывают: 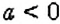 .
.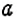 неположительное, то записывают:
неположительное, то записывают: 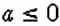 .
.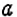 неотрицательное, то записывают:
неотрицательное, то записывают: 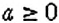 .
.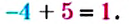
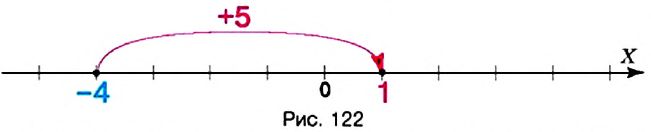
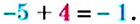

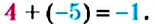
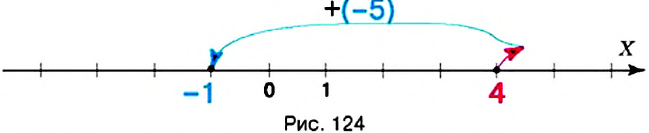
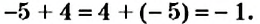
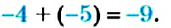

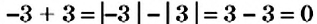
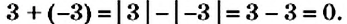
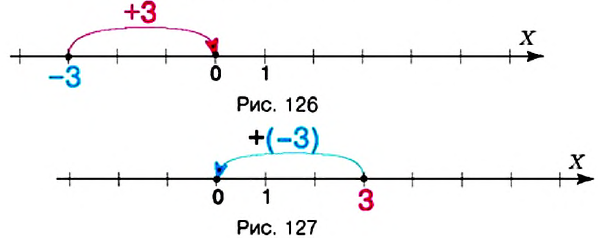
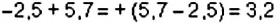
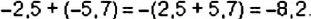
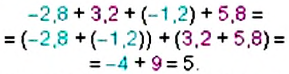
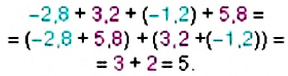
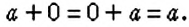

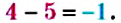


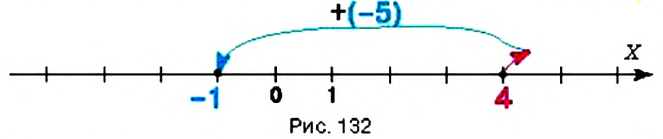
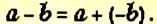
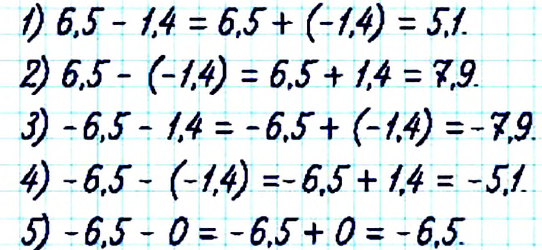
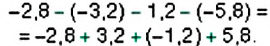
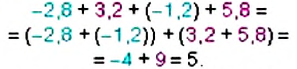
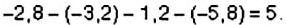
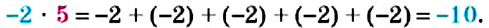
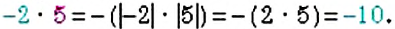
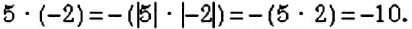
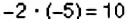
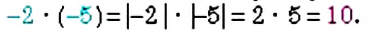
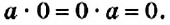
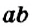 положительно, то числа
положительно, то числа 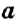 и
и 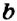 имеют одинаковые знаки, и наоборот;
имеют одинаковые знаки, и наоборот;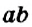 отрицательно, то числа
отрицательно, то числа 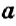 и
и 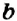 имеют разные знаки, и наоборот;
имеют разные знаки, и наоборот;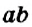 равно нулю, то хотя бы одно из чисел,
равно нулю, то хотя бы одно из чисел, 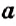 или
или 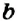 , равно нулю, и наоборот.
, равно нулю, и наоборот.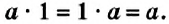
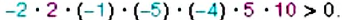
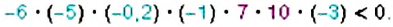
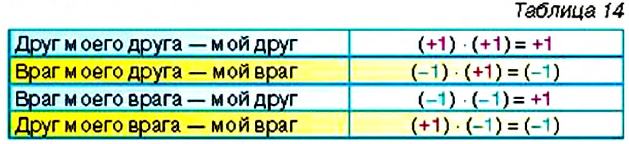
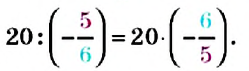
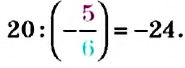
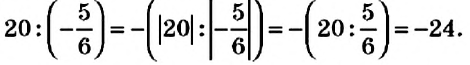
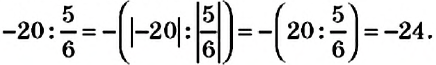
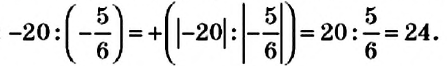
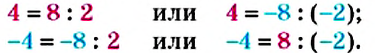
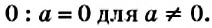
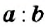 число
число 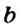 не может быть равным нулю;
не может быть равным нулю;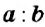 положительно, то числа
положительно, то числа 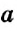 и
и 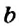 имеют одинаковые знаки, и наоборот;
имеют одинаковые знаки, и наоборот;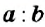 отрицательно, то числа
отрицательно, то числа 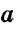 и
и 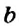 имеют разные знаки, и наоборот;
имеют разные знаки, и наоборот;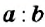 равно нулю, то
равно нулю, то 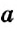 равно нулю, и наоборот.
равно нулю, и наоборот.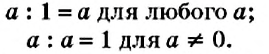
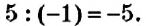
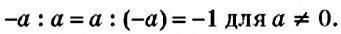
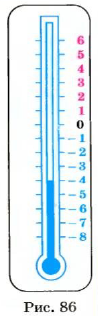
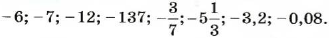
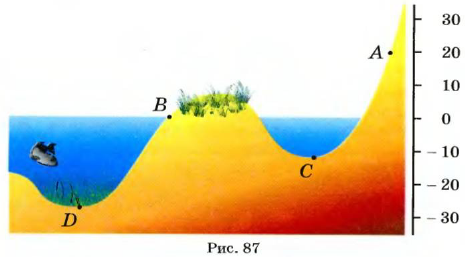
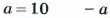 равно десяти;
равно десяти;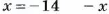 равно минус четырнадцати;
равно минус четырнадцати;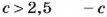 больше двух целых пяти десятых;
больше двух целых пяти десятых;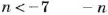 меньше минус семи.
меньше минус семи.


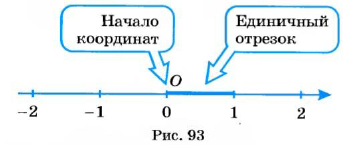

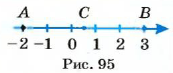
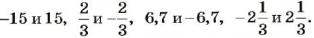
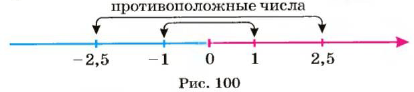
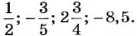
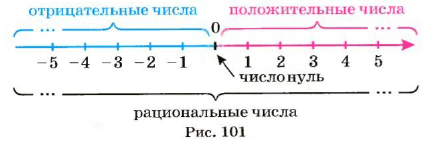

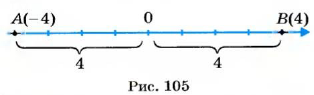

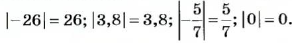
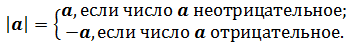



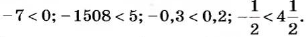
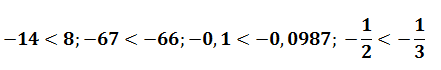
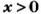 означает, что число
означает, что число 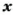 — положительное;
— положительное;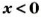 означает, что число
означает, что число  — отрицательное.
— отрицательное.