Про уравнения - легко » Статьи

Решение уравнений на деление обыкновенных дробей

Обновлено
Решение уравнений с дробями

Решение уравнений на деление обыкновенных дробей

О чем эта статья:

5 класс, 6 класс, 7 класс

Содержание
  1. Понятие дроби
  2. Основные свойства дробей
  3. Понятие уравнения
  4. Понятие дробного уравнения
  5. Как решать уравнения с дробями
  6. 1. Метод пропорции
  7. 2. Метод избавления от дробей
  8. Что еще важно учитывать при решении
  9. Универсальный алгоритм решения
  10. Примеры решения дробных уравнений
  11. Урок математики по теме «Деление дробей в уравнениях»
  12. Деление дробей. Решение уравнений
  13. Описание презентации по отдельным слайдам:
  14. Дистанционное обучение как современный формат преподавания
  15. Математика: теория и методика преподавания в образовательной организации
  16. Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
  17. Дистанционные курсы для педагогов
  18. Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
  19. Материал подходит для УМК
  20. Другие материалы
  21. Вам будут интересны эти курсы:
  22. Оставьте свой комментарий
  23. Автор материала
  24. Дистанционные курсы для педагогов
  25. Подарочные сертификаты
  26. 🔥 Видео

Видео:Решение уравнений, 6 классСкачать

Решение уравнений, 6 класс

Понятие дроби

Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.

Дробь — это рациональное число, представленное в виде a/b, где a — числитель дроби, b — знаменатель. Есть два формата записи:

  • обыкновенный вид — ½ или a/b,
  • десятичный вид — 0,5.

Дробь — это одна из форм деления, записываемая с помощью дробной черты. Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.

Дроби бывают двух видов:

  1. Числовые — состоят из чисел. Например, 2/7 или (1,8 − 0,3)/5.
  2. Алгебраические — состоят из переменных. Например, (x + y)/(x − y). Значение дроби зависит от данных значений букв.

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.

Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3/5.

Видео:Деление обычных дробей в уравненияхСкачать

Деление обычных дробей в уравнениях

Основные свойства дробей

Дробь не имеет значения, если делитель равен нулю.

Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.

Дроби a/b и c/d называют равными, если a × d = b × c.

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.

Видео:Решение уравнений с дробными числами в 6 классеСкачать

Решение уравнений с дробными числами в 6 классе

Понятие уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:

  • Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
  • Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Решить уравнение значит найти все его корни или убедиться, что корней нет.

Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.

Линейное уравнение выглядит таках + b = 0, где a и b — действительные числа.

Что поможет в решении:

  • если а не равно нулю, то у уравнения единственный корень: х = −b : а;
  • если а равно нулю, а b не равно нулю — у уравнения нет корней;
  • если а и b равны нулю, то корень уравнения — любое число.
Квадратное уравнение выглядит так:ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.

Видео:Уравнение. 5 класс.Скачать

Уравнение. 5 класс.

Понятие дробного уравнения

Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:

Решение уравнений на деление обыкновенных дробей Решение уравнений на деление обыкновенных дробей

Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.

Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:

Решение уравнений на деление обыкновенных дробей Решение уравнений на деление обыкновенных дробей

На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.

Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.

Видео:Уравнения с дробями. Как решать уравнения с дробями в 5 классе.Скачать

Уравнения с дробями. Как решать уравнения с дробями в 5 классе.

Как решать уравнения с дробями

1. Метод пропорции

Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.

Итак, у нас есть линейное уравнение с дробями:

Решение уравнений на деление обыкновенных дробей

В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.

Решение уравнений на деление обыкновенных дробей

После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.

Решение уравнений на деление обыкновенных дробей

2. Метод избавления от дробей

Возьмем то же самое уравнение, но попробуем решить его по-другому.

Решение уравнений на деление обыкновенных дробей

В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:

  • подобрать число, которое можно разделить на каждый из знаменателей без остатка;
  • умножить на это число каждый член уравнения.

Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!

Решение уравнений на деление обыкновенных дробей

Вот так просто мы получили тот же ответ, что и в прошлый раз.

Что еще важно учитывать при решении

  • если значение переменной обращает знаменатель в 0, значит это неверное значение;
  • делить и умножать уравнение на 0 нельзя.

Универсальный алгоритм решения

Определить область допустимых значений.

Найти общий знаменатель.

Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.

Раскрыть скобки, если нужно и привести подобные слагаемые.

Решить полученное уравнение.

Сравнить полученные корни с областью допустимых значений.

Записать ответ, который прошел проверку.

Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах.

Видео:Решение простых уравнений с обыкновенными дробямиСкачать

Решение простых уравнений с обыкновенными дробями

Примеры решения дробных уравнений

Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.

Пример 1. Решить дробное уравнение: 1/x + 2 = 5.

  1. Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
  2. Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
  3. Избавимся от знаменателя. Умножим каждый член уравнения на х.

Решим обычное уравнение.

Пример 2. Найти корень уравненияРешение уравнений на деление обыкновенных дробей

  1. Область допустимых значений: х ≠ −2.
  2. Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
  3. Избавимся от знаменателя. Умножим каждый член уравнения на х.

Решение уравнений на деление обыкновенных дробей

Переведем новый множитель в числитель..

Решение уравнений на деление обыкновенных дробей

Сократим левую часть на (х+2), а правую на 2.

Пример 3. Решить дробное уравнение: Решение уравнений на деление обыкновенных дробей

    Найти общий знаменатель:

Умножим обе части уравнения на общий знаменатель. Сократим. Получилось:

Выполним возможные преобразования. Получилось квадратное уравнение:

Решим полученное квадратное уравнение:

Получили два возможных корня:

Если x = −3, то знаменатель равен нулю:

Если x = 3 — знаменатель тоже равен нулю.

  • Вывод: числа −3 и 3 не являются корнями уравнения, значит у данного уравнения нет решения.

    • Видео:Обыкновенные дроби и действия над ними. Практическая часть. 5 класс.Скачать

    Обыкновенные дроби и действия над ними. Практическая часть. 5 класс.

    Урок математики по теме «Деление дробей в уравнениях»

    Разделы: Математика

    Форма урока: объяснение нового материала.

    Цели урока:

    • Обучающая: выработать навыки учащихся умножать и делить обыкновенные дроби, решать и оформлять задачи на уравнения.
    • Воспитательная: воспитывать самостоятельность, аккуратность
    • Развивающая: развивать внимание, математическую речь, вычислительные навыки учащихся, интерес к математике.

    Ожидаемые результаты: дети научаться решать задачи и уравнения на дроби.

    Этапы урокаВремя (мин)

    СлайдыОрганизационный момент.2Слайд 1Устная работа и повторение ранее изученного8Слайды 2, 3, 4, 5,6Формирование новых знаний и умений10Слайды 7, 8Физкультминутка2Слайды 9, 10Закрепление нового материала5Слайд 11Проверка знаний (с/р)10Слайд 12Постановка домашнего задания1Слайд 13Подведение итогов урока2

    I. Организационный этап

    – Здравствуйте, мы проведем сегодня урок по теме «Деление дробей в уравнених». Откройте тетради, запишите число, классная работа и тему урока.
    Целью нашего урока является закрепление и проверка умений умножать и делить обыкновенные дроби, а также повторить навыки решения задач и уравнений.

    II. Устный опрос учащихся

    Чтобы умным в жизни стать
    Надо дроби изучать

    1) Переведите смешанную дробь в неправильную (Приложение 1, слайд 3)

    Решение уравнений на деление обыкновенных дробей

    Решение уравнений на деление обыкновенных дробей

    Решение уравнений на деление обыкновенных дробей

    – Повторим правило умножения двух дробей: Чтобы умножить дробь на дробь нужно перемножить их числители и знаменатели и первое произведение записать числителем, а второе знаменателем.

    4) Выполните деление (в тетрадях с последующей взаимопроверкой, сосед у соседа) (Приложение 1, слайд 6)

    Решение уравнений на деление обыкновенных дробей

    – Повторим правило деления двух дробей: Чтобы разделить одну дробь на другую, нужно первую дробь умножить на дробь, обратную второй.

    III. Формирование новых знаний и умений

    – При изучении темы деление большое значение имеет умение решать уравнения. Рассмотрим пример и запишем его в тетрадь. (Приложение 1, слайд 7)

    Решение уравнений на деление обыкновенных дробей

    – Чтобы решить уравнение необходимо определить какой компонент в уравнении является неизвестным.
    – Какой?
    – 1 множитель
    – Правильно! Чтобы найти неизвестный множитель, что нужно сделать?
    – Чтобы найти неизвестный множитель необходимо произведение разделить на известный множитель.
    – Находим корень уравнения, выполняя деление. Выполним проверку и запишем ответ.

    Решение уравнений на деление обыкновенных дробей

    – А теперь давайте проверим ваше умение решать задачи.

    – Сколько всего прошел лыжник ? (26 км)
    – Сколько километров прошел в первый день? (неизвестно)
    – Сколько километров прошел во второй день? (неизвестно)
    – Какую величину, с какой сравнивают?
    – Что возьмем за х?
    – Как найти дробь от числа?
    – Сколько километров прошел за два дня?
    – Как найти?
    – Составим уравнение.

    Решение уравнений на деление обыкновенных дробей

    – 14 км лыжник прошел во второй день

    26 – 14 = 12 км лыжник прошел в первый день.

    – Вспомним что такое 1% (одна сотая)
    – Какой дробью запишем 75% (75/100 = 3/4)
    – Сколько грибов собрала белка? (неизвестно)
    – Сколько грибов собрал бельчонок? (неизвестно)
    – Какую величину, с какой сравнивают?
    – Что обозначим за икс?
    – Как найти дробь от числа?
    – Сколько собрали вместе белка и бельчонок?
    – Составим уравнение.

    Решение уравнений на деление обыкновенных дробей

    200 грибов собрала белка
    350 – 200 = 150 грибов собрал бельчонок

    IV. Физкультминутка

    – Встаем и выполняем несколько упражнений.

    А теперь, ребята, встали,
    Быстро руки вверх подняли,
    В стороны, вперёд, назад
    Повернулись вправо, влево,
    Тихо сели, вновь за дело.

    V. Закрепление нового материала

    – Сколько собрал Митя?
    – Сколько собрал Коля?
    – Какую величину, с какой сравнивают?
    – Что обозначим за икс?
    – Как найти дробь от числа?
    – Сколько собрали вместе мальчики?

    Решение уравнений на деление обыкновенных дробей

    28 грибов собрал Митя

    64 – 28 = 36 грибов собрал Коля

    VI. «Математический выбор»

    Уравнения, оцениваемые в 3 балла: Уравнения, оцениваемые в 5 баллов:

    1) Решение уравнений на деление обыкновенных дробей1) Решение уравнений на деление обыкновенных дробейРешение уравнений на деление обыкновенных дробей

    2) Решение уравнений на деление обыкновенных дробей2) Решение уравнений на деление обыкновенных дробей

    3) Решение уравнений на деление обыкновенных дробей3) Решение уравнений на деление обыкновенных дробей

    4) Решение уравнений на деление обыкновенных дробей4) Решение уравнений на деление обыкновенных дробей

    Уравнения, оцениваемые в 6 баллов:

    1) Решение уравнений на деление обыкновенных дробей

    2) Решение уравнений на деление обыкновенных дробей

    3) Решение уравнений на деление обыкновенных дробей

    4) Решение уравнений на деление обыкновенных дробей

    Оценки: 5 – 12 баллов; 4 – 9 баллов; 3 – 6 баллов.

    Каждый выбирает себе уравнения по «плечу».
    Учитель во время работы оценивает учеников.

    VII. Итог урока

    – С каким настроением вы сегодня работали на уроке?
    – Какая задача для вас была самой интересной?
    – Ребята чему мы научились на сегодняшнем уроке?
    – Как найти часть от числа?
    – Как найти неизвестный множитель?

    VIII. Домашнее задание

    – С листов решить любые три уравнения, из тех которые не решали в классе.

    Видео:Умножение, деление и сложение дробей #математика #алгебра #дроби #5классСкачать

    Умножение, деление и сложение дробей #математика #алгебра #дроби #5класс

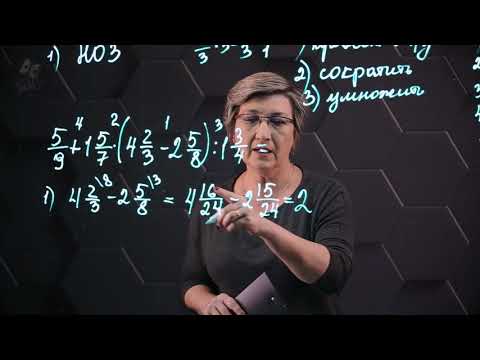
    Деление дробей. Решение уравнений

    Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

    «Актуальность создания школьных служб примирения/медиации в образовательных организациях»

    Свидетельство и скидка на обучение каждому участнику

    Решение уравнений на деление обыкновенных дробей

    Описание презентации по отдельным слайдам:

    Решение уравнений на деление обыкновенных дробей

    6 КЛАСС. Математика

    Решение уравнений на деление обыкновенных дробей

    Математика. Деление обыкновенных дробей.

    Решение уравнений на деление обыкновенных дробей

    сказка Жили-были обыкновенные дроби. Были они правильные и неправильные, а также смешанные, сократимые и несократимые, а ещё взаимно обратные.

    Решение уравнений на деление обыкновенных дробей

    Какие числа записаны? Правильные и неправильные дроби Сократимые и несократимые дроби, смешанные числа Взаимно обратные числа

    Решение уравнений на деление обыкновенных дробей

    Жили они дружно и научились выполнять различные действия. Какие? Сложение, вычитание, умножение, деление.

    Решение уравнений на деление обыкновенных дробей

    Решение уравнений на деление обыкновенных дробей

    Устный счёт Вычислите:

    Решение уравнений на деление обыкновенных дробей

    Задача Был в царстве обыкновенных дробей участок прямоугольной формы, площадью кв. км. Длина участка была равна км. А ширина была неизвестна. И думали – гадали они: « Как же найти ширину?»

    Решение уравнений на деление обыкновенных дробей

    Ответьте на вопросы: 1. Как найти неизвестное делимое. 2. Как найти неизвестный делитель. 3. Как найти неизвестное частное.

    Решение уравнений на деление обыкновенных дробей

    Ответьте на вопросы: 4. Как найти неизвестное уменьшаемое. 5. Как найти неизвестное вычитаемое. 6. Как найти неизвестное слагаемое.

    Решение уравнений на деление обыкновенных дробей

    1.Решить уравнение: Уменьшаемое Вычитаемое Разность

    Решение уравнений на деление обыкновенных дробей

    Решить уравнение: 1 3

    Решение уравнений на деление обыкновенных дробей

    Множитель Множитель Произведение 8 1 5 1

    Решение уравнений на деление обыкновенных дробей

    Решение уравнений на деление обыкновенных дробей

    2.Решить уравнение 6 4 3

    Решение уравнений на деление обыкновенных дробей

    Множитель Множитель Произведение

    Решение уравнений на деление обыкновенных дробей

    Решаем из учебника: №463, №461

    Решение уравнений на деление обыкновенных дробей

    В древности на Руси говорили: «Умножение – мучение, а деление –беда.» А мы сегодня на уроке доказывали обратное. И в этом нам помогла наша сказка. А вы помогли восстановить в царстве обыкновенных дробей мир и спокойствие.

    Решение уравнений на деление обыкновенных дробей

    Всем спасибо за урок. До свидания.

    Решение уравнений на деление обыкновенных дробей

    Курс повышения квалификации

    Дистанционное обучение как современный формат преподавания

    • Сейчас обучается 949 человек из 80 регионов

    Решение уравнений на деление обыкновенных дробей

    Курс профессиональной переподготовки

    Математика: теория и методика преподавания в образовательной организации

    • Сейчас обучается 681 человек из 75 регионов

    Решение уравнений на деление обыкновенных дробей

    Курс повышения квалификации

    Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

    • Сейчас обучается 314 человек из 70 регионов

    Ищем педагогов в команду «Инфоурок»

    Видео:Решить уравнение с дробями - Математика - 6 классСкачать

    Решить уравнение с дробями - Математика - 6 класс

    Дистанционные курсы для педагогов

    Самые массовые международные дистанционные

    Школьные Инфоконкурсы 2022

    33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

    Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

    5 569 070 материалов в базе

    Материал подходит для УМК

    Решение уравнений на деление обыкновенных дробей

    «Математика», Мерзляк А.Г., Полонский В.Б., Якир М.С.

    § 14. Деление дробей

    Другие материалы

    • 14.12.2020
    • 95
    • 0
    • 14.12.2020
    • 8889
    • 126

    Решение уравнений на деление обыкновенных дробей

    • 14.12.2020
    • 116
    • 0
    • 14.12.2020
    • 306
    • 15

    Решение уравнений на деление обыкновенных дробей

    • 14.12.2020
    • 71
    • 1
    • 14.12.2020
    • 72
    • 1
    • 14.12.2020
    • 80
    • 0
    • 14.12.2020
    • 68
    • 0

    Вам будут интересны эти курсы:

    Оставьте свой комментарий

    Авторизуйтесь, чтобы задавать вопросы.

    Добавить в избранное

    • 14.12.2020 655
    • PPTX 2 мбайт
    • 33 скачивания
    • Оцените материал:

    Настоящий материал опубликован пользователем Филимонова Татьяна Юрьевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

    Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

    Автор материала

    Решение уравнений на деление обыкновенных дробей

    • На сайте: 2 года и 11 месяцев
    • Подписчики: 0
    • Всего просмотров: 3094
    • Всего материалов: 9

    Московский институт профессиональной
    переподготовки и повышения
    квалификации педагогов

    Видео:Деление дробей. Как делить дробиСкачать

    Деление дробей. Как делить дроби

    Дистанционные курсы
    для педагогов

    663 курса от 690 рублей

    Выбрать курс со скидкой

    Выдаём документы
    установленного образца!

    Решение уравнений на деление обыкновенных дробей

    Учителя о ЕГЭ: секреты успешной подготовки

    Время чтения: 11 минут

    Решение уравнений на деление обыкновенных дробей

    Объявлен конкурс дизайн-проектов для школьных пространств

    Время чтения: 2 минуты

    Решение уравнений на деление обыкновенных дробей

    В Воронеже продлили удаленное обучение для учеников 5-11-х классов

    Время чтения: 1 минута

    Решение уравнений на деление обыкновенных дробей

    Рособрнадзор не планирует переносить досрочный период ЕГЭ

    Время чтения: 0 минут

    Решение уравнений на деление обыкновенных дробей

    ЕГЭ в 2022 году будут сдавать почти 737 тыс. человек

    Время чтения: 2 минуты

    Решение уравнений на деление обыкновенных дробей

    Тринадцатилетняя школьница из Индии разработала приложение против буллинга

    Время чтения: 1 минута

    Решение уравнений на деление обыкновенных дробей

    В России могут объявить Десятилетие науки и технологий

    Время чтения: 1 минута

    Подарочные сертификаты

    Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

    Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

    🔥 Видео

    Виленкин. 6 класс за 100 минут. Математика: теория чисел, дроби, уравненияСкачать

    Виленкин. 6 класс за 100 минут. Математика: теория чисел, дроби, уравнения

    Уравнение с дробями видео урок ( Математика 5 класс )Скачать

    Уравнение с дробями видео урок ( Математика 5 класс )

    Деление дробей и смешанных чисел. 5 класс.Скачать

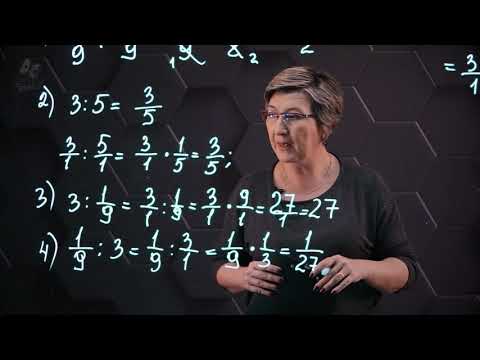
    Деление дробей и смешанных чисел. 5 класс.

    Деление смешанных чиселСкачать

    Деление смешанных чисел

    Деление обыкновенных дробей.Скачать

    Деление обыкновенных дробей.

    Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

    Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?

    Как умножать и делить дроби (Математика 5 класс)Скачать

    Как умножать и делить дроби (Математика 5 класс)

    Деление обыкновенных дробей и смешанных чисел 6 классСкачать

    Деление обыкновенных дробей и смешанных чисел 6 класс

    Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

    Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?

    МАТЕМАТИКА 6 класс: Деление дробей | Короткий видеоурокСкачать

    МАТЕМАТИКА 6 класс: Деление дробей | Короткий видеоурок
    Поделиться или сохранить к себе: