Кубическое уравнение, содержащее коэффициенты с действительным корнем, остальные два считаются комплексно-сопряженной парой. Будут рассмотрены уравнения с двучленами и возвратные, а также с поиском рациональных корней. Вся информация будет подкреплена примерами.
- Решение двучленного кубического уравнения вида A x 3 + B = 0
- Решение возвратного кубического уравнения вида A x 3 + B x 2 + B x + A = 0
- Решение кубических уравнений с рациональными корнями
- Решение кубических уравнений по формуле Кардано
- Решение уравнений ax b cx d
- Различные методы решения уравнений
- 🔍 Видео
Видео:Неполные квадратные уравнения. Алгебра, 8 классСкачать

Решение двучленного кубического уравнения вида A x 3 + B = 0
Кубическое уравнение, содержащее двучлен, имеет вид A x 3 + B = 0 . Его необходимо приводить к x 3 + B A = 0 с помощью деления на А , отличного от нуля. После чего можно применять формулу сокращенного умножения суммы кубов. Получаем, что
x 3 + B A = 0 x + B A 3 x 2 — B A 3 x + B A 2 3 = 0
Результат первой скобки примет вид x = — B A 3 , а квадратный трехчлен — x 2 — B A 3 x + B A 2 3 , причем только с комплексными корнями.
Найти корни кубического уравнения 2 x 3 — 3 = 0 .
Решение
Необходимо найти х из уравнения. Запишем:
2 x 3 — 3 = 0 x 3 — 3 2 = 0
Необходимо применить формулу сокращенного умножения. Тогда получим, что
x 3 — 3 2 = 0 x — 3 3 2 6 x 2 + 3 3 2 6 x + 9 2 3 = 0
Раскроем первую скобку и получим x = 3 3 2 6 . Вторая скобка не имеет действительных корней, потому как дискриминант меньше нуля.
Ответ: x = 3 3 2 6 .
Видео:Уравнения от вида: (ax+b)(cx+d)=0 (x=-b/a ; x=-d/c)Скачать

Решение возвратного кубического уравнения вида A x 3 + B x 2 + B x + A = 0
Вид квадратного уравнения — A x 3 + B x 2 + B x + A = 0 , где значения А и В являются коэффициентами. Необходимо произвести группировку. Получим, что
A x 3 + B x 2 + B x + A = A x 3 + 1 + B x 2 + x = = A x + 1 x 2 — x + 1 + B x x + 1 = x + 1 A x 2 + x B — A + A
Корень уравнения равен х = — 1 , тогда для получения корней квадратного трехчлена A x 2 + x B — A + A необходимо задействовать через нахождение дискриминанта.
Решить уравнение вида 5 x 3 — 8 x 2 — 8 x + 5 = 0 .
Решение
Уравнение является возвратным. Необходимо произвести группировку. Получим, что
5 x 3 — 8 x 2 — 8 x + 5 = 5 x 3 + 1 — 8 x 2 + x = = 5 x + 1 x 2 — x + 1 — 8 x x + 1 = x + 1 5 x 2 — 5 x + 5 — 8 x = = x + 1 5 x 2 — 13 x + 5 = 0
Если х = — 1 является корнем уравнения, тогда необходимо найти корни заданного трехчлена 5 x 2 — 13 x + 5 :
5 x 2 — 13 x + 5 = 0 D = ( — 13 ) 2 — 4 · 5 · 5 = 69 x 1 = 13 + 69 2 · 5 = 13 10 + 69 10 x 2 = 13 — 69 2 · 5 = 13 10 — 69 10
Ответ:
x 1 = 13 10 + 69 10 x 2 = 13 10 — 69 10 x 3 = — 1
Видео:Решение линейного уравнения ax=b. Сколько корней может быть у линейного уравнения. Алгебра 7 класс.Скачать

Решение кубических уравнений с рациональными корнями
Если х = 0 , то он является корнем уравнения вида A x 3 + B x 2 + C x + D = 0 . При свободном члене D = 0 уравнение принимает вид A x 3 + B x 2 + C x = 0 . При вынесении х за скобки получим, что уравнение изменится. При решении через дискриминант или Виета оно примет вид x A x 2 + B x + C = 0 .
Найти корни заданного уравнения 3 x 3 + 4 x 2 + 2 x = 0 .
Решение
3 x 3 + 4 x 2 + 2 x = 0 x 3 x 2 + 4 x + 2 = 0
Х = 0 – это корень уравнения. Следует найти корни квадратного трехчлена вида 3 x 2 + 4 x + 2 . Для этого необходимо приравнять к нулю и продолжить решение при помощи дискриминанта. Получим, что
D = 4 2 — 4 · 3 · 2 = — 8 . Так как его значение отрицательное, то корней трехчлена нет.
Ответ: х = 0 .
Когда коэффициенты уравнения A x 3 + B x 2 + C x + D = 0 целые, то в ответе можно получить иррациональные корни. Если A ≠ 1 , тогда при умножении на A 2 обеих частей уравнения проводится замена переменных, то есть у = А х :
A x 3 + B x 2 + C x + D = 0 A 3 · x 3 + B · A 2 · x 2 + C · A · A · x + D · A 2 = 0 y = A · x ⇒ y 3 + B · y 2 + C · A · y + D · A 2
Приходим к виду кубического уравнения. Корни могут быть целыми или рациональными. Чтобы получить тождественное равенство, необходимо произвести подстановку делителей в полученное уравнение. Тогда полученный y 1 будет являться корнем. Значит и корнем исходного уравнения вида x 1 = y 1 A . Необходимо произвести деление многочлена A x 3 + B x 2 + C x + D на x — x 1 . Тогда сможем найти корни квадратного трехчлена.
Найти корни заданного уравнения 2 x 3 — 11 x 2 + 12 x + 9 = 0 .
Решение
Необходимо произвести преобразование с помощью умножения на 2 2 обеих частей, причем с заменой переменной типа у = 2 х . Получаем, что
2 x 3 — 11 x 2 + 12 x + 9 = 0 2 3 x 3 — 11 · 2 2 x 2 + 24 · 2 x + 36 = 0 y = 2 x ⇒ y 3 — 11 y 2 + 24 y + 36 = 0
Свободный член равняется 36 , тогда необходимо зафиксировать все его делители:
± 1 , ± 2 , ± 3 , ± 4 , ± 6 , ± 9 , ± 12 , ± 36
Необходимо произвести подстановку y 3 — 11 y 2 + 24 y + 36 = 0 , чтобы получить тождество вида
1 3 — 11 · 1 2 + 24 · 1 + 36 = 50 ≠ 0 ( — 1 ) 3 — 11 · ( — 1 ) 2 + 24 · ( — 1 ) + 36 = 0
Отсюда видим, что у = — 1 – это корень. Значит, x = y 2 = — 1 2 .
Далее следует деление 2 x 3 — 11 x 2 + 12 x + 9 на x + 1 2 при помощи схемы Горнера:
| x i | Коэффициенты многочлена | |||
|---|---|---|---|---|
| 2 | — 11 | 12 | 9 | |
| — 0 . 5 | 2 | — 11 + 2 · ( — 0 . 5 ) = — 12 | 12 — 12 · ( — 0 . 5 ) = 18 | 9 + 18 · ( — 0 . 5 ) = 0 |
2 x 3 — 11 x 2 + 12 x + 9 = x + 1 2 2 x 2 — 12 x + 18 = = 2 x + 1 2 x 2 — 6 x + 9
После чего необходимо найти корни квадратного уравнения вида x 2 — 6 x + 9 . Имеем, что уравнение следует привести к виду x 2 — 6 x + 9 = x — 3 2 , где х = 3 будет его корнем.
Ответ: x 1 = — 1 2 , x 2 , 3 = 3 .
Алгоритм можно применять для возвратных уравнений. Видно, что — 1 – это его корень, значит, левая часть может быть поделена на х + 1 . Только тогда можно будет найти корни квадратного трехчлена. При отсутствии рациональных корней применяются другие способы решения для разложения многочлена на множители.
Видео:Решение биквадратных уравнений. 8 класс.Скачать

Решение кубических уравнений по формуле Кардано
Нахождение кубических корней возможно при помощи формулы Кардано. При A 0 x 3 + A 1 x 2 + A 2 x + A 3 = 0 необходимо найти B 1 = A 1 A 0 , B 2 = A 2 A 0 , B 3 = A 3 A 0 .
После чего p = — B 1 2 3 + B 2 и q = 2 B 1 3 27 — B 1 B 2 3 + B 3 .
Полученные p и q в формулу Кардано. Получим, что
y = — q 2 + q 2 4 + p 3 27 3 + — q 2 — q 2 4 + p 3 27 3
Подбор кубических корней должен удовлетворять на выходе значению — p 3 . Тогда корни исходного уравнения x = y — B 1 3 . Рассмотрим решение предыдущего примера, используя формулу Кардано.
Найти корни заданного уравнения 2 x 3 — 11 x 2 + 12 x + 9 = 0 .
Решение
Видно, что A 0 = 2 , A 1 = — 11 , A 2 = 12 , A 3 = 9 .
Необходимо найти B 1 = A 1 A 0 = — 11 2 , B 2 = A 2 A 0 = 12 2 = 6 , B 3 = A 3 A 0 = 9 2 .
Отсюда следует, что
p = — B 1 2 3 + B 2 = — — 11 2 2 3 + 6 = — 121 12 + 6 = — 49 12 q = 2 B 1 3 27 — B 1 B 2 3 + B 3 = 2 · — 11 2 3 27 — — 11 2 · 6 3 + 9 2 = 343 108
Производим подстановку в формулу Кордано и получим
y = — q 2 + q 2 4 + p 3 27 3 + — q 2 — — q 2 4 + p 3 27 3 = = — 343 216 + 343 2 4 · 108 2 — 49 3 27 · 12 3 3 + — 343 216 — 343 2 4 · 108 2 — 49 3 27 · 12 3 3 = = — 343 216 3 + — 343 216 3
— 343 216 3 имеет три значения. Рассмотрим их ниже.
— 343 216 3 = 7 6 cos π + 2 π · k 3 + i · sin π + 2 π · k 3 , k = 0 , 1 , 2
Если k = 0 , тогда — 343 216 3 = 7 6 cos π 3 + i · sin π 3 = 7 6 1 2 + i · 3 2
Если k = 1 , тогда — 343 216 3 = 7 6 cosπ + i · sinπ = — 7 6
Если k = 2 , тогда — 343 216 3 = 7 6 cos 5 π 3 + i · sin 5 π 3 = 7 6 1 2 — i · 3 2
Необходимо произвести разбиение по парам, тогда получим — p 3 = 49 36 .
Тогда получим пары: 7 6 1 2 + i · 3 2 и 7 6 1 2 — i · 3 2 , — 7 6 и — 7 6 , 7 6 1 2 — i · 3 2 и 7 6 1 2 + i · 3 2 .
Преобразуем при помощи формулы Кордано:
y 1 = — 343 216 3 + — 343 216 3 = = 7 6 1 2 + i · 3 2 + 7 6 1 2 — i · 3 2 = 7 6 1 4 + 3 4 = 7 6 y 2 = — 343 216 3 + — 343 216 3 = — 7 6 + — 7 6 = — 14 6 y 3 = — 343 216 3 + — 343 216 3 = = 7 6 1 2 — i · 3 2 + 7 6 1 2 + i · 3 2 = 7 6 1 4 + 3 4 = 7 6
x 1 = y 1 — B 1 3 = 7 6 + 11 6 = 3 x 2 = y 2 — B 1 3 = — 14 6 + 11 6 = — 1 2 x 3 = y 3 — B 1 3 = 7 6 + 11 6 = 3
Ответ: x 1 = — 1 2 , x 2 , 3 = 3
При решении кубических уравнений можно встретить сведение к решению уравнений 4 степени методом Феррари.
Видео:Решение матричных уравненийСкачать

Решение уравнений ax b cx d
Линейные уравнения и неравенства с параметром
Уравнение вида
| ax + b = 0, | (1) |
где a,b О R, x — переменная, называется уравнением первой степени (линейным уравнением).
Ниже приведены примеры линейных уравнений:
| a) 2x + 6 = 0, | где a = 2, b = 6; |
| b) x — 2 = 0 | где a = 1, b = -2; |
| c) 0·x + 0 = 0, | где a = b = 0; |
| d) 0·x + 1 /3 = 0, | где a = 0, b = 1 /3; |
| e) — 1 /2x = 0, | где a = — 1 /2; b = 0. |
Уравнение (1) равносильно уравнению ax = —b откуда следует следующее утверждение.
Утверждение 1.
- Если a ≠ 0, то уравнение (1) имеет единственное решение x = — b /a;
- Если a = 0, b ≠ 0, то множество решений уравнения (1) пусто;
- Если a = 0, b = 0, то любое действительное число является решением уравнения (1).
Таким образом, приведенные выше линейные уравнения решаются следующим образом:
a) x = — 6 /2, то есть x = -3;
b) x = 2;
c) любое действительное число является решением данного уравнения;
d) уравнение не имеет решений;
e) x = 0.
Замечание 2. Уравнение (ax + b)(cx + d) = 0 где a, b, c, d О R, сводится к совокупности линейных уравнений
 | ax + b = 0, |
| cx + d = 0. |
Пример 1. Решить уравнения
a) 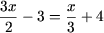 , , | c) —x + 2 = 2 — x, |
| b) 2x + 1 = 2x + 3, | d) (2x + 4)(3x — 1) = 0. |
Решение. a) 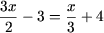
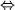
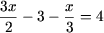
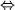
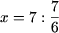
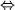
b) 2x + 1 = 2x + 3 Ы 2x — 2x = 3 — 1 Ы 0·x = 2 откуда следует, что уравнение не имеет решений.
c) —x + 2 = 2 — x Ы —x + x = 2 — 2 Ы 0·x = 0, следовательно, любое действительное число является решением уравнения.
| d) (2x + 4)(3x — 1) = 0 Ы |
| Ы |
|
В дальнейшем будут рассматриваться линейные уравнения с параметрами. Под параметром понимается (смотрите тему Уравнения с параметром) фиксированное (но неизвестное) число. Как правило, параметр обозначается первыми буквами латинского алфавита.
Пример 2. Решить уравнения
| a) ax = 1; | e)  |
| b) a 2 x — 1 = x + a; | f) 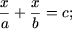 |
| c) ax + b = cx + d; | g)  |
d) 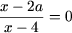 ; ; |
Решение. a) Применяя утверждение 1, получим:
при a ≠ 0 уравнение имеет единственное решение, x = 1 /a;
при a = 0 уравнение примет вид 0·x = 1 и, следовательно, оно не имеет решений.
Ответ: если a О R, то x = 1 /a; если a = 0, то уравнение не имеет решений.
b) После элементарных преобразований получим: a 2 x — 1 = x + a Ы a 2 x — x = a + 1 Ы x(a 2 — 1) = a + 1.
откуда, применяя утверждение 1, получим:
- если a 2 -1 ≠ 0, то есть a ≠ ± 1, то
или
- если a = 1, то уравнение примет вид 0·x = 2 и, следовательно, не имеет решений;
- если a = -1, то уравнение примет вид 0·x = 0, и, следовательно, любое действительное число является решением этого уравнения.
c) Перепишем уравнение следующим образом (a — c)x = d — b, откуда следует:
- если a — c ≠ 0, то есть a ≠ c, то уравнение имеет единственное решение
- если a = c и d — b ≠ 0, то уравнение примет вид 0·x = d — b ( ≠ 0) и, следовательно, оно не имеет решений;
- если a = c и d = b, то уравнение примет вид 0·x = 0, и, следовательно, множество его решений есть R
d) Область допустимых значений (ОДЗ) уравнения есть x ≠ 4. В ОДЗ уравнение решается следующим образом:
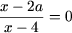 | Ы |
| Ы |
|
Таким образом, если 2a ≠ 4, то есть a ≠ 2, то уравнение имеет единственное решение x = 2a, а если a = 2, то уравнение не имеет решений.
f) Если a = 0 или b = 0, то уравнение не имеет смысла. Пусть a·b ≠ 0. Тогда уравнение равносильно следующему x(b + a) = abc откуда следует:
- если b + a ≠ 0, то есть a ≠ —b, то уравнение имеет единственное решение
- если a = —b и c ≠ 0, то уравнение не имеет решений.
- если a = —b и c = 0, то любое действительное число есть решение данного уравнения.
g) ОДЗ уравнения определяется из системы
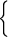 | 5x —a ≠ 0, |
| ax — 1 ≠ 0, |
откуда x ≠ a /5 и, если a ≠ 0, x ≠ 1 /a. Если a = 0, то уравнение примет вид 
откуда 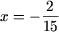

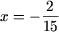
Пусть a ≠ 0. Тогда в ОДЗ уравнение примет вид 2(ax — 1) = 3(5x — a), откуда (2a — 15)x = 2 — 3a и, следовательно,
- если 2a — 15 ≠ 0, то есть
то получим
;
- если 2a-15 = 0, то есть
то уравнение не имеет решений.
Таким образом для 

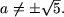
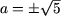
В случае второго ограничения получим 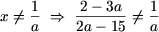
Таким образом, если 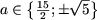
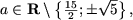
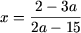
Пример 3. Решить уравнения
| a) |x — a| = 2; | c) |x — a| + |x — 2a| = a; |
| b) |x| + |x — a| = 0; | d) |x — 1| + |x — 2| = a. |
Решение. a) Используя свойство модуля, получим:
| |x — a| = 2 Ы |
| Ы |
|
Таким образом, для любого действительного a уравнение имеет два различных решения, x1 = a + 2 и x2 = a — 2.
b) Левая часть уравнения принимает неотрицательные значения (как сумма двух неотрицательных слагаемых), а правая часть равна нулю. Следовательно,
| или |
|
Таким образом, если a = 0, то система (а, следовательно, и уравнение) имеет единственное решение x = 0, а если a ≠ 0, то система (и исходное уравнение) решений не имеет.
c) Так как | f(x)| = |-f(x)| уравнение можно переписать следующим образом |x — a| + |2a — x| = a.
Очевидно, что если a 0. Тогда a = |a| = |(2a — x) + (x — a)|, и уравнение примет вид |x — a| + |2a — x| = |(2a — x) + (x — a)|. Это уравнение равносильно (см. свойства модуля) неравенству (2a — x)(x — a) ≥ 0 откуда, учитывая, что 0 О [a;2a].
если a 0, то уравнение имеет бесконечное число решений — любое число a ≤ x ≤ 2a.
d) Очевидно, что уравнение имеет решения только при a > 0. Рассмотрим три случая:
- Пусть x —x + 1 — x + 2 = a или -2x = a — 3 откуда
. Поскольку x
откуда a > 1. Таким образом, если a > 1, то
;
- Пусть x О [1;2]. Тогда |x — 1| = x — 1, |x — 2| = -(x-2) и уравнение примет вид x — 1 — x + 2 = a, 0·x = a — 1. Используя утверждение 1, получим:
если a = 1, то любое действительное число из отрезка [1;2] есть решение исходного уравнения;
если a ≠ 1, то решений нет.
Пусть x > 2. Тогда |x — 1| = x — 1, |x — 2| = x — 2 и уравнение примет вид x — 1 + x — 2 = a откуда 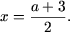
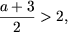
если a > 1, то уравнение имеет два различных решения 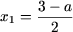
если a = 1, то любое число отрезка [1;2] есть решение уравнения;
если a Линейные неравенства
| ax + b > 0, ax + b ≥ 0, ax + b О R, x — переменная, называются неравенствами первой степени (линейными неравенствами). Поскольку все неравенства (2) решаются аналогично, приведем решение лишь первого из них: ax + b > 0. Рассмотрим следующие случаи:
Рассмотрим несколько примеров. Пример 1. Решить неравенства
|
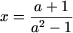 или
или 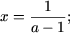
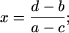
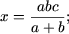
 то получим
то получим  то уравнение не имеет решений.
то уравнение не имеет решений.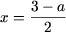 . Поскольку x
. Поскольку x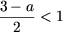 откуда a > 1. Таким образом, если a > 1, то
откуда a > 1. Таким образом, если a > 1, то 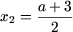

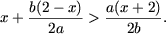
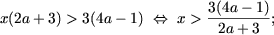
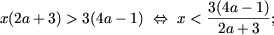
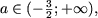 то
то 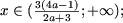
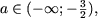 то
то 
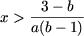
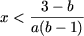

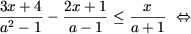
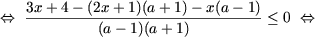
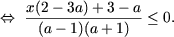
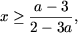
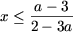 .
.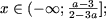
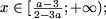
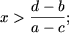
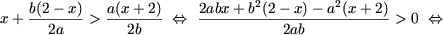
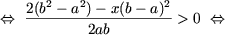
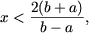
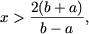
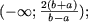 если a и b — противоположных знаков (ab
если a и b — противоположных знаков (ab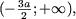 (а, следовательно, и множеством решений неравенства) явяется множество
(а, следовательно, и множеством решений неравенства) явяется множество 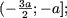
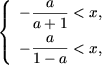 откуда (учитывая, что x > 0) получим
откуда (учитывая, что x > 0) получим 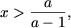 а вторая система совокупности примет вид
а вторая система совокупности примет вид 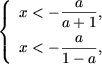 и, так как a > 1 влечет
и, так как a > 1 влечет 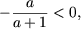 а x > 0, система не имеет решений.
а x > 0, система не имеет решений.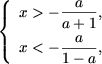 или
или 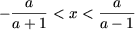 откуда, заметив, что
откуда, заметив, что 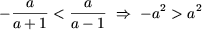 получим, что первая система совокупности несовместна. Из второй системы получим
получим, что первая система совокупности несовместна. Из второй системы получим 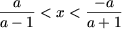 и, учитывая, что x > 0, получим
и, учитывая, что x > 0, получим 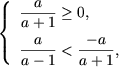 откуда a О [0;1), то неравенство не имеет решений, а если a О (-1;0), то множество решений неравенства есть
откуда a О [0;1), то неравенство не имеет решений, а если a О (-1;0), то множество решений неравенства есть 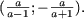
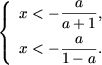 Так как a 0, то в этом случае исходное неравенство не имеет решений. Вторая система совокупности примет вид
Так как a 0, то в этом случае исходное неравенство не имеет решений. Вторая система совокупности примет вид 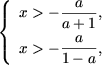 и, поскольку x > 0, получим
и, поскольку x > 0, получим 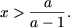
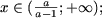






 .
. решаем квадратное уравнение a(t 2 – 2) + bt + c = 0
решаем квадратное уравнение a(t 2 – 2) + bt + c = 0 , после замены
, после замены  получаем уравнение t 2 – 2t – 3 = 0
получаем уравнение t 2 – 2t – 3 = 0 – уравнение не имеет корней.
– уравнение не имеет корней.
 имеем (t + 14)(t + 11 ) = 4.
имеем (t + 14)(t + 11 ) = 4.
















