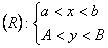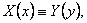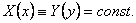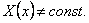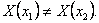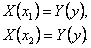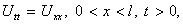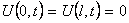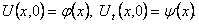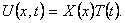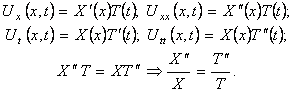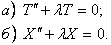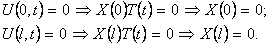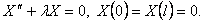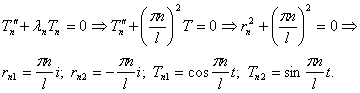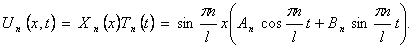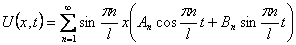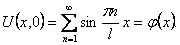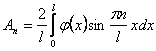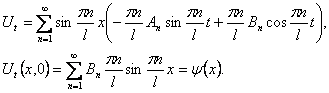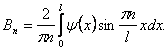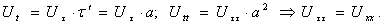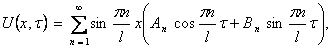Решение смешанных уравнений методом фурье

Метод Фурье — один из распространенных и эффективных методов решения уравнений с частными производными. Этот метод часто встречается и под другими названиями: метод разделения переменных или метод собственных функций.

Общая схема метода Фурье.

Основная идея этого метода состоит в том, что решение задачи для уравнения с частными производными сводится к решению вспомогательных задач для уравнений с меньшим числом независимых переменных. В частности, если заданное уравнение содержит две независимые переменные, то вспомогательные задачи будут уже зависеть только от одной переменной. Таким образом решение уравнения с частными производными сводится к решению обыкновенных дифференциальных уравнений.

При применении метода Фурье удобно использовать следующую лемму.

Основная лемма метода Фурье.

Если в прямоугольнике R плоскости XOY:

для некоторых функций выполняется тождество

то в этом случае

Доказательство. Предположим противное, т.е. что

Тогда существуют значения 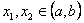такие, что

Рассмотрим точки (x₁,y) и (x₂,y), принадлежащие прямоугольнику R. На R справедливо тождество (8), а поэтому

Сравнивая эти равенства, приходим к противоречию с нашим предположением. Следовательно X(x) = const, а тогда Y(y)=const.

Решение первой начально-краевой задачи для волнового уравнения.

Рассмотрим волновое уравнение

Граничные условия первого рода

И начальные условия

Решим эту задачу методом Фурье.

Шаг 1. Представим функцию U(x,t) в виде

Найдем частные производные U_xx и U_tt и подставим в уравнение (9):

В полученном уравнении левая часть зависит только от x, а правая- только от t. Используя основную лемму, заключаем:

Из граничных условий (10) получим

Шаг 2. Решим задачу Штурма-Лиувилля

Она имеет собственные значения и собственные функции

Шаг 3. Подставим найденные значения λ_n в уравнение а) и решим его:

Шаг 4. Выпишем частные решения уравнения (9):

Для волнового уравнения эти решения называются собственными колебаниями. В лекции 6 мы изучим их подробнее. В силу линейности и однородности уравнения (9) линейная комбинация этих решений

Замечание 1. Здесь мы предполагаем, что полученный функциональный ряд равномерно сходится и его можно дважды почленно дифференцировать по x и по t в области 0 0. Об условиях, при которых это можно сделать, будет рассказано в лекции 5.

Шаг 5. Определим коэффициенты A_nи B_n в формуле (12), используя начальные условия (11). Из первого начального условия получим

Равенство (13) означает, что начальная функция φ(x) разлагается в ряд Фурье по синусам, которые в данном случае являются собственными функциями X_n(x) задачи Штурма-Лиувилля.

Коэффициенты Фурье вычисляются по формулам

Из второго начального условия находятся коэффициенты B_n.

Вычислив коэффициенты A_n и B_n для конкретных начальных функций и подставив их значения в (12), мы получим решение первой начально-краевой задачи.

Замечание 2. Используя формулу (12), можно получить решение первой начально-краевой задачи для уравнения колебания струны: Для этого проведем замену переменной τ=at и получим

При этом начальное условие не изменится, а условие преобразуется к виду Тогда решение задачи в переменных (x,τ) будет иметь вид

Возвращаясь к переменным (x,t), получим

Видео:6.1 Смешанные краевые задачи для уравнений гиперболического и параболического типов. Метод Фурье.Скачать

Метод Фурье

Содержание:

По этой ссылке вы найдёте полный курс лекций по математике:

Метод Фурье, или метод разделения переменных, является одним из наиболее распространенных методов решения уравнений с частными производными. Рассмотрим этот метод, обратившись к простейшей задаче о свободных колебаниях однородной струны длины i, закрепленной на концах. §4. Свободные колебания однородной струны, закрепленной на концах Задача о свободных колебаниях однородной струны с закрепленными концами сводится к решению уравнения при граничных условиях и начальных условиях.

Метод Фурье Задачу (1 )-(3) называют смешанной: она содержит и начальные и граничные условия. Решение задачи начнем с поиска частных решений уравнения (1) вида При этом будем предполагать, что каждое из них удовлетворяет граничным условиям (2), но не равно нулю тождественно. Подставляя функцию и<х, t) в форме (4) в уравнение (1), получаем ИЛИ Последнее равенство (его левая часть зависит только от а правая — только от х) возможнолишь втом случае, если обе его части не зависят ни от ty ни от х,т.е. равны одной и той же постоянной.

Обозначим эту постоянную (разделения) через (-А), Из равенства (5) получаем два обыкновенных дифференциальных уравнения Граничные условия (2) дают откуда (T(t) £ 0) следует, что функция Х(х) должна удовлетворять граничным условиям Чтобы получить нетривиальные решения tt(x, t) вида (4), удовлетворяющие граничным условиям (2), необходимо найти нетривиальные решения уравнения удовлетворяющие граничным условиям.

Таким образом, мы приходим к следующей задаче: найти значения параметра А, при которых существуют нетривиальные решения задачи (7)-(8), а также сами эти решения. Такие значения параметра А называются собственными значениями, а соответствующие им нетривиальные решения — собственными функциями задачи (7)-(8). Сформулированную таким образом задачу называют задачей Штурма—Лиувилля. Найдем собственные значения и собственные функции задачи (7)-(8).

Рассмотрим отдельно три случая, когда 1.

При общее решение уравнения (7) имеет вид Потребовав выполнения граничных условий (8), получим (6) (7) Так как определитель системы (9) отличен от нуля, то . Следовательно, Х(х) = 0, т. е. при нетривиальных решений задачи не существует. (9) 2. При А = 0 общее решение уравнения (7) имеет вид Граничные условия (8) дают откуда С, = С2 = 0, и следовательно, при А = 0 нетривиальных решений задачи (7)-(8) также не существует. 3.

При Л > 0 общее решение уравнения (7) имеет вид Потребовав выполнение граничных условий (8), получим Система (10) имеет нетривиальные решениятогда и толькотогда, когда определитель системы равен нулю, Метод Фурье будут собственными функциями задачи. Собственные функции определены с точностью до постоянного множителя, который мы выбрали равным единице. При А = А* общее решение у равнения (6) имеетвид ктга кчга где Аки Bk — произвольные постоянные. Таким образом, функции удовлетворяют уравнению (1) и граничным условиям (2) при любых Ак и Вку В силу линейности и однородности уравнения (1) всякая коневая сумма решений будет также решением уравнения (1).

То же справедливо и для ряда если он сходится равномерно и его можно дважды почленно дифференцировать по х и по t. Поскольку каждое слагаемое в ряде (11) удовлетворяет граничным условиям (2), то этим условиям будет удовлетворять и сумма u(s, t) этого ряда. Остается определить в формуле (11) постоянные .4* и Вк так, чтобы выполнялись и начальные условия (3). Продифференцируем формально ряд (11) по t.

Имеем Полагая в соотношениях (l 1) и (12) t = 0, в силу начальных условий (3) получим Формулы (13) представляют собой разложения заданных функций вряд Фурье по синусам в интервале Коэффициенты разложений (13) вычисляются по известным формулам / I Теорема 2. Если и удоъчетворяет условиям и удовлетворяет условию то сумма tx(x, £) ряда (11), где -А* и В* опредыяются формулами (14), имеет в области непрерывные частные производные до второго порядка включительно по каждому из аргументов, удовлетворяет уравнению (1), граничным условиям (2) и начальным условиям (3), т. е. является решением задачи (1 )-(3).

Пример. Найти закон свободных колебаний однородной струны длины I, закрепленной на концах, если в начальный момент t = 0 струна имеет форму параболы — const), а начальная скорость отсутствует. 4 Задача сводится к решению уравнения при граничных условиях и начальных условиях.

Возможно вам будут полезны данные страницы:

Метод Фурье

Применяя метод Фурье, ищем нетривиальные решения уравнения (1), удовлетворяющие граничным условиям (2), в виде Подставляя «(*,*) в форме (4) в уравнение (1) и разделяя переменные, получим откуда причем в силу (2) Как было установлю но выше, собственные значения задачи (7)-(8) а соответствующие собственные функции Для А = Ащ общее решение уравнения (6) имеет вид пяа ижа Будем иска тъ решение исходной задачи в виде ряда Для определен ия коэффициентов -4Я и Z?„ воспользуемся начальными условия ми (3).

получаем, что 2?„ = 0 для любог о п, а из (10) Метод Фурье откуда, интегрируя по частям дважды . находи м . Подставляя наеденные значения А, и в ряд (9), получим решение поставленной задачи , Замечание. Если начальные фукхдда не удовлетворяют условиям теоремы 2, то дважды непрерывно дифференцируемого решения смешанной задачи (1)-(3) может и не существовать.

Однако если , то ряд (II) сходетс* равномерно при и любом t и определяет непрерывную функюао u(xtt). В этом случае можно говорить лишь об обобщенная решении задачи. Каждая из функций определяет так называемые собств енные колебания струны, закрепленной на концах. При собственных колебаниях, отвечающих к = 1, струна издает основной, самый низкий тон.

При колебаниях, соответствующих ббльшим Л.она издает более высокие тоны, обертоны. Записав *) в виде заключаем, что собственные колебания струны — стоячие волны, при которых точки струны совершают гармонические колебания с амплитудой Нк sin частотой Метод Фурье Мы рассмотрели случай свободных колебаний однородной струны, закрепленной на концах. Рассмотрим теперьслуч ай других граничных условий.

Пусть, например, левый конец струны закреплен, u(0, t) = 0, а правый конец х — 1 упругосвязан со своим положением равновесия, что соответствует условию . Нетривиальное решение u(x, t) уравнения (1), удовлетворяющее поставленным граничным условиям, будем опять искать в виде В результате подстановки в уравнение (1) приходим к следующей задаче о собственных значениям: найти такие значения параметра Л, для которых дифференциальное уравнение при граничных условиях имеет нетривиальные решения Х(х). Общее решение уравнения (15) имеет вид (А > 0)

Первое из граничных условий

Первое из граничных условий (16) дает С = 0, так что функциями Х(х) с точностью до постоянного множителя являются sin у/Хх. Из второго граничного условия Положим А = ir. Тогда Для отыскания и получаем трансцендентное уравнение. Корни этого уравнения можно найти графически, взяв в плоскости (f, z) сечения последовательных ветвей кривой z = tg(i//) прямой линией z = (рис. 7).

Обе части уравнения (18) — нечетные функции относительно р, поэтому каждому положительному корню i/fc соответствует равный ему по абсолютной величине отрицательный корень. Поскольку изменение знака Uk не влечет за собой появления новых собственных функций (они только изменят знак, что несущественно), достаточно ограничиться положительными корнями уравнения (18).

В результате опять получается последовательность собственных значений и отвечающие им последовательности собственных функций и собственных колебаний Кстати, для n-ой собственной частоты ип получается асимптотическое соотношение в частности, для I = т имеем Если правый конец струны х = I свободен, получаем cos vl = 0. Отсюда ul = § + тиг, так что в случае свободного конца собственные значения и собственные функции соответственно равны

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Уравнение колебаний струны. Метод разделения переменных. Метод ФурьеСкачать

Классическое решение методом Фурье смешанных задач при минимальных требованиях на исходные данные Текст научной статьи по специальности « Математика»

Видео:Метод Фурье для неоднородного уравнения теплопроводностиСкачать

Аннотация научной статьи по математике, автор научной работы — Хромов А. П., Бурлуцкая М. Ш.

В статье дается новое краткое доказательство теоремы В. А. Чернятина о классическом решении методом Фурье смешанной задачи для волнового уравнения с закрепленными концами при минимальных требованиях на начальные данные. Далее, рассматривается подобная задача для простейшего функционально-дифференциального уравнения первого порядка с инволюцией в случае закрепленного конца, и также получаются результаты окончательного характера. Эти результаты получаются благодаря существенному использованию идей А. Н. Крылова по ускорению сходимости рядов, подобных рядам Фурье. Без доказательства приводятся результаты и для других схожих случаев смешанных задач .

Видео:Численные методы математической физики - Решение смешанной задачи для уравнения теплопроводностиСкачать

Похожие темы научных работ по математике , автор научной работы — Хромов А. П., Бурлуцкая М. Ш.

Видео:8.1 Решение уравнения теплопроводности на отрезкеСкачать

Classical Solution by the Fourier Method of Mixed Problems with Minimum Requirements on the Initial Data

The article gives a new short proof the V. A. Chernyatin theorem about the classical solution of the Fourier method of the mixed problem for the wave equation with fixed ends with minimum requirements on the initial data. Next, a similar problem for the simplest functional differential equation of the first order with involution in the case of the fixed end is considered, and also obtained definitive results. These results are due to a significant use of ideas A. N. Krylova to accelerate the convergence of series, like Fourier series. The results for other similar mixed problems given without proof.

Видео:Уравнение в частных производных Уравнение теплопроводностиСкачать

Текст научной работы на тему «Классическое решение методом Фурье смешанных задач при минимальных требованиях на исходные данные»

1. Smirnov V. I., Lebedev N. A. Functions of a Complex Variable: Constructive Theory. London, Iliffe Books Ltd., IX, 1968, 488 pp.

2. Privalov A. A. Divergence of nterpolation processes on sets of the second category. Math. Notes, 1975, vol. 18, no. 2, pp. 692-694.

3. Shatalina A. V. Divergence of Lagrange Processes on

the Unit Circle. Dep. v VINITI [Dep. in VINITI], Saratov State University, no. 4060-B90, 19.07.1990, 30 p. (in Russian).

4. K. Prachar. Raspredelenie prostyh chisel [The Distribution of Prime Numbers]. Moscow, Mir, 1967. 513 p. (in Russian).

УДК 517.95; 517.984

КЛАССИЧЕСКОЕ РЕШЕНИЕ МЕТОДОМ ФУРЬЕ СМЕШАННЫХ ЗАДАЧ ПРИ МИНИМАЛЬНЫХ ТРЕБОВАНИЯХ НА ИСХОДНЫЕ ДАННЫЕ

А. П. Хромов1, М. Ш. Бурлуцкая2

1 Доктор физико-математических наук, профессор кафедры дифференциальных уравнений, Саратовский государственный университет им. Н. Г. Чернышевского, KhromovAP@info.sgu.ru

2Кандидат физико-математических наук, доцент кафедры математического анализа, Воронежский государственный университет, Ь1Г^2001 @mail.ru

В статье дается новое краткое доказательство теоремы В. А. Чернятина о классическом решении методом Фурье смешанной задачи для волнового уравнения с закрепленными концами при минимальных требованиях на начальные данные. Далее, рассматривается подобная задача для простейшего функционально-дифференциального уравнения первого порядка с инволюцией в случае закрепленного конца, и также получаются результаты окончательного характера. Эти результаты получаются благодаря существенному использованию идей А. Н. Крылова по ускорению сходимости рядов, подобных рядам Фурье. Без доказательства приводятся результаты и для других схожих случаев смешанных задач.

Ключевые слова: смешанная задача, метод Фурье, инволюция, классическое решение, асимптотика собственных значений и собственных функций, система Дирака.

Настоящая публикация приурочена к 150-летию со дня рождения выдающихся отечественных ученых В. А. Стеклова (1884-1926) и А. Н. Крылова (1883-1945), внесших весомый вклад в решение смешанных задач методом Фурье.

Обоснование метода Фурье в задачах математической физики традиционно опирается на доказательство равномерной сходимости ряда, представляющего формальное решение задачи, и рядов, полученных его почленным дифференцированием нужное число раз.

Приведем мнение В. А. Стеклова, впервые давшего строгое обоснование метода Фурье: «Необходимость доказывать равномерную сходимость рассматриваемых рядов вытекает из самой сущности метода Ляме-Фурье (Эйлера — Бернулли), дающего выражение искомой функции в виде бесконечного ряда, просуммировать который или преобразовать к виду, удобному для дифференцирования, не представляется возможным» [1, с. 224].

Эта точка зрения сделала метод Фурье очень популярным, было проведено огромное количество исследований и достигнуты значительные успехи.

Информация обзорного характера содержится, в частности, в книгах И. Г. Петровского, В. И. Смирнова, О. А. Ладыженской и В. А. Ильина, В. А. Чернятина 5.

Приведем один такой результат из [2]. Рассматривается задача

Щг = ихх — д(х)п, х £ [0, п], Ь £ (-го, (0.1)

щ(х, 0) = ^(х), Щг(х, 0) = ф(х). (0.3)

Теорема 0.1 [2, с. 190]. Если д(х) £ С[0, п] и вещественна, ^(х) £ С3 [0, п], ^(х) £ С2 [0, п],

р(0) = р(п) = р»(0) = р»(п) = 0, (0.4)

то ряд, представляющий формальное решение задачи (0.1)—(0.3) по методу Фурье, и ряды, получающиеся из него дважды почленным дифференцированием по x и t, сходятся абсолютно и равномерно в области x е [0, п], t е [—T, T] при любом T и, тем самым, сумма u(x,t) данного ряда есть классическое решение.

В трудном случае числа переменных более двух наиболее глубокие результаты в данном направлении получены О. А. Ладыженской [4] и В. А. Ильиным [6].

Рассмотрим теперь частный случай задачи (0.1)-(0.3) — задачу о колебании струны с закрепленными концами:

utt = x е [0, п], t е (-го, +го), (0.6)

u(0, t) = u(n, t) = 0, (0.7)

u(x, 0) = p(x), ut(x, 0) = 0 (0.8)

(0(x) = 0 для простоты). Эта задача впервые была решена Д. Бернулли в 1753 г. и оказала огромное влияние на последующее развитие математики. Она находится в истоке теории рядов Фурье, ортогональных систем, краевых задач на собственные значения и, тем самым, она имеет определяющее значение в современной теории функций, спектральной теории, теории краевых задач в частных производных. Укажем имена крупнейших ученых, принимавших активное участие в разработке данного направления: Д. Бернулли, Эйлер, Фурье, Пуассон, Штурм, Лиувилль, Коши, Пуанкаре, Крылов, Стеклов, Петровский.

Формальное решение задачи (0.6)-(0.8) методом Фурье есть:

u(x,t) = — У sin n^)sin nx cos nt, (0.9)

где (■, ■) — скалярное произведение в L2 [0, п]. По теореме 0.1 соотношение (0.9) есть классическое решение, если ^(x) е C3[0,1], и удовлетворяет условиям (0.4) и оно получено за счет законности почленного дифференцирования дважды по x и t ряда (0.9). В то же время известно, что решение задачи (0.6)-(0.8) имеет место и при естественных минимальных условиях на функцию ^(x), когда она удовлетворяет условиям (0.4), но при этом является только дважды непрерывно дифференцируемой.

В этом случае дважды почленную дифференцируемость ряда (0.9) доказать уже невозможно. Более того, при некоторых ^(x) ряд, полученный после дважды почленного дифференцирования, может даже расходиться (при t = 0 получаем обычный ряд Фурье произвольной непрерывной функции).

Попробуем, несмотря на это, и в таком случае получить из ряда (0.9) решение задачи (это хорошо известный факт). Сам ряд (0.9) сходится абсолютно и равномерно при x е [0,п] и t е (-го, +го). Представим его в виде суммы двух рядов £+ и £_, где

£± = — У sin n^) sin n(x ± t). п

Теперь каждый из этих рядов есть уже ряд Фурье. Рассмотрим ряд

при всех x G (-ra, и пусть Ь2 дЬ V д^ дЬ V с»(1 — х) д /дм(1 — х,Ь) ,2 д /дм(х,Ь) д2 и(х,Ь) д(1 — х) дЬ у д(1 — х) дх у дх2

Уравнение (0.12) есть простейшее уравнение первого порядка с инволюцией. При решении смешанных задач для таких уравнений по методу Фурье спектральная задача сводится к системе Дирака, т.е. вместо уравнения Штурма — Лиувилля нам приходится связываться с системой Дирака. Спектральная задача для уравнения (0.12) интересна и своими приложениями к задаче на собственные значения для интегральных уравнений [21, 23, 24]. Так же, как и в параграфе 1, мы для одного самого простого (но лишь по форме) случая приводим подробные доказательства. В параграфе 4 приводятся без доказательства другие результаты по смешанным задачам с инволюцией 32.

Введение и параграфы 1, 2 написаны А. П. Хромовым, параграфы 3, 4 — М. Ш. Бурлуцкой и А. П. Хромовым.

1. ТЕОРЕМА В. А. ЧЕРНЯТИНА

Рассмотрим следующую смешанную задачу:

««(М) = «хх (х, Ь) — д(х)и(х, Ь), (1.1)

и(х, 0) = р(х), иДх, 0) = 0, (1.3)

где д(х) £ С[0, п] и вещественна.

Под классическим решением задачи (1.1)—(1.3) понимаем функцию и(х,Ь), дважды непрерывно дифференцируемую по х и Ь при х £ [0,п], Ь £ (—го, +го) и удовлетворяющую (1.1)—(1.3). Естественные минимальные требования на р(х):

р(х) £ С2[0, п], р(0) = р(п) = р»(0) = р»(п) = 0 (1.4)

(условия р»(0) = р»(п) = 0 следуют из (1.1)).

Будем искать классическое решение задачи (1.1)—(1.3) по методу Фурье при условиях (1.4). Формальное решение по методу Фурье есть:

и(х,Ь) = —-—т I (Ллр)(х)ео8 ^Л + У^ (р, Рп) Рп(х) соб д/Л^Ь, (1.5)

где Ял — резольвента оператора Ь: Ьу = — у» + д(х)у, у(0) = у(п) =0, Лп — собственные значения оператора Ь, а рп(х) — соответствующие собственные функции, для которых ||рп|| = 1 (|| ■ || — норма в Ь2 [0, п]), г > 0 фиксировано. Появление интеграла в (1.5) вызвано тем, что нумерация собственных значений Лп привязана к их асимптотике, и потому некоторое конечное число собственных значений с малыми модулями не занумеровано.

1.1. Асимптотика собственных значений и собственных функций

Оператор Ь самосопряженный, и для Лп имеет место [35, с. 71].

Теорема 1.1. Все Лп вещественные, достаточно большие по модулю простые и для них справедлива асимптотика

л/ЛП = п +—1—-, п = По,по + 1. . (1.6)

Здесь и в дальнейшем одними и теми же обозначениями, а и ап, будем обозначать произвольные числа (в том числе и комплексные), лишь бы ^ |ап|2 0. Эта лемма легко следует из (1.7).

1.2. Преобразование формального ряда (1.5)

По условиям (1.4) p(x) е DL (области определения оператора L). Тогда

где д(х) = Ьр(х) = —р»(х) + д(х)р(х). Тогда ряд в (1.5), который впредь будем обозначать £, имеет вид

£ = У^—(д, рп)рп (х)со^д/Лпь (1.14)

(для краткости |Лп| > г в знаке суммы справа опускаем). Лемма 1.4. Имеет место асимптотика

где pn (x) = у — sin nx.

Доказательство. По лемме 1.2

х) = тг-;-тл», то по лемме 1.1 получаем (1.15).

Уу(х,Мп)| Из леммы 1.4 следует

Лемма 1.5. Имеет место представление

£i = ^n) Pn(x) cos^t, £2 = ^3 Pn(x) cosv/лПt. Лемма 1.6. Имеет место представление

^ 2 (g, sin nx) _ , , , , (g, рП )r , , n, , ,

где £3 = — -2-sin nx cos nt, £4 = 2^ an (x, t), an (x, t) =-2— [Pn (x) cos v Лп t—рП (x) cos nt].

Лемма 1.7. Ряды £2, £4 и ряды, получающиеся из них почленным дифференцированием два

раза по x и t, сходятся абсолютно и равномерно по x G [0,1] и t G [T, T], где T — любое

фиксированное положительное число.

Доказательство. Заключение о ряде £2 получаем из оценок

р^ (х) = 0(па), — со^Лп Ь = 0(па), 5 = 0,1, 2,

легко следуемых из лемм 1.2 и 1.3 и абсолютной сходимости ряда ^ ап/п по неравенству Коши — Буняковского. Обратимся к ряду £4. Представим

an(x, t) = ai,n(x, t) + a2,n (x, t),

[Pn (x) — Pn (x)] cos у Лп t,

(g’ Pn) рП(x) [cosV^ t — cos nt].

В силу лемм 1.2 и 1.3 имеем оценки

J- aj)n(x, t) = O(n? n-1 + s

и утверждение леммы для £4 получаем так же, как и для ряда £2.

тт * « г. ^ N 2 ^ (g, sin nx) .

Лемма 1.8. Ряд u0(x,t) = — > -^-sin nx cos nt является классическим решением задачи

(0.6)-(0.8) когда вместо ^(x) берется (x) = L0 1g, где L0 есть L при q(x) = 0.

Доказательство. Имеем — sin nx = L01(sin nx), и тогда наш ряд есть

— у sin nx) sin nx cos nt. (1.19)

(x) = L-1 g = — I (x — t)g(t) dt + — I (n — t)g(t) dt,

то (ж) удовлетворяет условиям (1.4) и поэтому u0(x,t), равное (1.19), есть классическое решение задачи (0.6)-(0.8) для уравнения струны при ^(ж), равной (ж). □

Лемма 1.9. Для формального решения (1.5) имеет место формула

u(x, t) = u0 (ж, t) + u1 (ж, t) + u2 (ж, t), (1.20)

где u0 (x,t) из леммы 1.8,

,, 1 [ f-n, ^ тл 2 (g, sin nx)

u1 (x, t) =—(RA^)(x)cosv AtdA—> -2-sin nx cos nt

Утверждение леммы следует из (1.14), если учесть, что £2 + Е4 есть и2(х,Ь). Таким образом, (1.20) и есть реализация рекомендаций А. Н. Крылова по усилению быстроты сходимости рядов Фурье и им подобных: ряд и2(х,Ь) имеет ускоренную сходимость, и его можно почленно дифференцировать два раза, и0(х, Ь) дважды дифференцируема по х и Ь как решение уравнения струны, М1(х,Ь) дважды дифференцируемая как конечная сумма. Тем самым решен важный вопрос о гладкости формального решения при минимальных условиях на ^(х).

1.3. Классическое решение смешанной задачи

Завершаем доказательство следующего замечательного результата В. А. Чернятина. Теорема 1.3. Формальное решение (1.5) есть классическое решение смешанной задачи (1.1)-(1.3) при минимальных условиях (1.4) на ^(х).

Доказательство. В том, что м(х,Ь) удовлетворяет граничным и начальным условиям, убеждаемся тривиально, поскольку ряд (1.5) в силу (1.14) один раз по х и Ь можно законно почленно дифференцировать, не прибегая к процедуре ускорения сходимости. Далее, в силу (1.20) м(х,Ь) дважды непрерывно дифференцируема. Докажем, что м(х,Ь) удовлетворяет уравнению (1.1). Обозначим через д2 д2

М оператор М = —т — -—г. Тогда по лемме 1.8 дЬ2 дх2

Mu1 = -2- J M (ra^)cosVAt) dA. (1.22)

M ^(RAcosVAt) = q(x)^(x) cos VAt — q(x)(RA^) cos л/А t. Поэтому из (1.22) получаем:

Mu1 = У (RA^)cos VAtdt. |A|=r

Далее, в силу ускоренной сходимости ряда -u2(x,t) имеем:

где г>п — общий член ряда и2(ж, г). Имеем

Ми- = — (д, м (р-(ж) сое а/апг) = -1-(д, Р-) д(ж)р-(ж) сое а/а-^ ,

и, значит, Ми2 = —д(ж)м2. Теорема доказана. □

Замечание. Если брать и (ж, 0) = ^(ж) вместо и (ж, 0) = 0, то надо требовать, чтобы ^(ж) е е С1 [0, п] и ^(0) = ^(п) = 0.

2. ДРУГИЕ РЕЗУЛЬТАТЫ В. А. ЧЕРНЯТИНА

Приведем другие результаты В. А. Чернятина [7], полученные методом Фурье с привлечением идей А. Н. Крылова.

2.1. Неоднородная смешанная задача:

и« (ж, г) = Ихх(ж, г) — д(ж)и(ж, г) + / (ж, г), (2.1)

и(0,г) = и(п,г) = 0, г е [0,т], (2.2)

и(ж, 0) = и4(ж, 0) = 0. (2.3)

Предполагаем, что д(ж) е С2[0,п] и вещественна, /(ж,г) е С2,0(д), /(0,г) = /(п,г) = 0, г е [0,Т], д = .

Теорема 2.1. При указанных условиях классическое решение задачи (2.1)—(2.3) существует и имеет вид

u(x, t) = У —- Fn(т) sino>n(í — т) dr,

к(т) = /0П /(ж,т)уп(ж) ¿ж, где везде в этом параграфе уп(ж) нормированная собственная функция для собственного значения оператора Ь: Ьу = —у» + д(ж)у, у(0) = у(п) = 0.

В [7] приведен и более сильный результат, который не приводим из-за громоздкости.

2.2. Смешанная задача для уравнения Шредингера:

¿и (ж, г) = — (ж, г) + д(ж)и(ж, г), (2.4)

и(0,г) = и(п,г) = 0, г е [0,т], (2.5)

и(ж, 0) = р(ж), ж е [0, п]. (2.6)

Считаем, что д(ж) е С[0, п] и вещественна, р(ж) е С2[0,п], р(0) = р(п) = р»(0) = р»(п) = 0.

Теорема 2.2. Существует хотя бы одна пара д(ж) р(ж), для которой смешанная задача (2.4)—(2.6) не имеет классического решения.

Теорема 2.3. Для существования классического решения задачи (2.4)—(2.6) достаточно дополнительно потребовать сходимости ряда

где = (p(x)q(x) — p»(x), sinnx) к функции класса C(Q) в метрике L2(Q). Зто решение имеет

u(x,t) = ^Фпе»гш™ * Уп (x),

Также в [7] есть и более сильный результат.

2.3. Смешанная задача для уравнения теплопроводности:

и (ж, г) = (ж, г) — ^(ж)и(ж, г) + /(ж, г), (2.7)

и(0,г) = и(п,г) = 0, г е [0,т], (2.8)

и(ж, 0)=0, ж е [0, п]. (2.9)

Предполагаем, что д(ж) е С[0,п] и вещественна, /(ж,г) е С(д), и выполняется условие Гельдера |/(ж,г’) — /(ж,г)| Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

3. СМЕШАННАЯ ЗАДАЧА ДЛЯ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ С ИНВОЛЮЦИЕЙ

В этом параграфе рассмотрим следующую смешанную задачу: 1 ди(ж, г) дм(£, г)

^ о. +?(ж)и(ж,г), ж е [0,1], г е (—го, +го), (3.1) вг дг е=1-х

и(0,г)=0, и(ж,0) = р(ж), ж е [0,1], (3.2)

где в — вещественное число, в = 0, д(ж) е С 1[0,1] и вещественна, р(ж) удовлетворяет естественным условиям для классического решения:

р(ж) е С1 [0,1], р(0) = р'(1)=0. (3.3)

Решение ищется в классе функций, непрерывно дифференцируемых по обеим переменным в полосе [0,1] х (—го, +го).

3.1. Случай симметрического потенциала

Это случай [30], когда

и здесь можно брать д(ж) е С[0,1].

Получим явную формулу для классического решения, напоминающую формулу решения уравнения струны.

Спектральная задача по методу Фурье есть

у'(1 — ж) + 5(ж)у(ж) = Ay(ж), (3.5)

Найдем решение задачи (3.5)-(3.6). Выполняя в (3.5) замену ж на 1 — ж и полагая

¿(ж) = (г1 (ж),г2(ж))т, где г1(ж) = у(ж), г2(ж) = у(1 — ж) (Т — знак транспонирования), получим следующую систему уравнений относительно ¿(ж):

Вг ‘(ж) + Р (ж)г(ж) = Лг(ж), (3.7)

где В = ^0 0 ^ , Р(ж) = (^(ж), — ж)) = diag (#(ж), д(ж)).

Верно и обратное: если г (ж) = (г1(ж),г2 (ж))т — решение (3.7) и г1(ж) = г2 (1 — ж), то у(ж) = (ж) есть решение уравнения (3.5).

Лемма 3.1. Общее решение системы (3.7) имеет вид

где Г = ( , 1 1, V(х, Л) = diag (и1 (х)е Лгх,-и2(х)вЛгх), и1(х) = ехр (г /0 д(Ь) ¿Ь), и2(х) =

= ехр (—г /X д(Ь) ¿Ь), с = (с1, с2)т, ск — произвольные постоянные. Доказательство. Выполним в (3.7) замену г = Гг>. Получим:

г>1 (ж) — гд(х)^1(ж) = —Лг^1 (х), г>2 (х) + гд(х)^2 (х) = Лгг>2(х).

и1(х) = (ж, Л) = с1 и1(х)е-Лгх, г>2(х) = г>2(х,Л) = с2и2(х)вЛгх. □

Лемма 3.2. Общее решение уравнения (3.5) имеет вид

у(х) = у(х, Л) = с^(х,Л), (3.9)

непрерывна на (—го, го) и периодическая с периодом 1.

Лемма 3.7. Если /(ж) из леммы 3.6 есть р(ж), то при ж е [0,1] имеет место формула

/0(ж) = 2рж) [¿Р(ж) + Р(1 — ж)]. (3.12)

Доказательство. Согласно лемме 3.6 при ж е [0,1] имеем:

р(ж) = 2Е(Р,у— )у—(ж) = Е С—у— (ж) = Е С— [р(1 — ж)е2п—*(1—— ф(ж)е2™

р(ж) = р(1 — ж)/0 (1 — ж) — гр(ж)/0 (ж). (3.13)

р(1 — ж) = р(ж)/0 (ж) — гр(1 — ж)/0 (1 — ж). (3.14)

Из (3.13) и (3.14) получаем:

гр(ж) + р(1 — ж) = 2р(ж)/0(ж). (3.15)

Из (3.15) следует (3.12). □

Замечание. Функция /0(ж) в силу своей периодичности однозначно определяется на всей оси заданием ее лишь на отрезке [0,1]. Таким образом, /0(ж) определяется не рядом, а по формуле (3.12).

Лемма 3.8. Если р(ж) е С 1[0,1], р(0) = р'(1) = 0, то /0(ж) непрерывно дифференцируема на всей вещественной оси.

Доказательство. Из (3.12) следует, что /0(х) непрерывно дифференцируема на [0,1] (в концевых точках имеются в виду односторонние производные). В силу периодичности /0(х) непрерывно дифференцируема всюду на (—го, +го), кроме точек х = п (п — целое). Покажем, что /(п — 0) = /(п + 0). В силу периодичности /0(х) достаточно установить, что

/о (0 + 0) = / (0 — 0). (3.16)

Дифференцируя (3.15), получим:

V (х) — ^ (1 — х) = 2р’ (х)/о (х) + 2р(х)/ (х). (3.17)

Из (3.17), условия леммы и соотношений /0(0) = /0(1), /(1 — 0) = /(0 — 0) имеем:

2р’ (0)/0 (0) + 2р(0)/ (0 + 0) = г^(0), 2р’ (1)/(0) + 2р(1)/ (0 — 0) = —^(0),

2[р'(0) + ¿р'(1)]/0(0) + 2[р(0)/(0 + 0) + гр(1)/(0 — 0)] = 0. (3.18)

Так как р(0) = 1, р(1) = ехр г д(Ь) ¿Ь^ ега = епг/2 = г, «2(х) = —гд(х)м2(х), р'(0) = — гд(0) + га, р'(1) = д(1) — а, а также д(0) = д(1), то р'(0) + гр'(1) = 0, и из (3.18) следует (3.16). □

Замечание. Условие ^'(1) = 0 является естественным в силу дифференциального уравнения. Согласно методу Фурье решение и(х, Ь) задачи (3.1)-(3.2) представляется формальным рядом:

уП)уП(х)еЛп= £ е„уп(х)вл»вй, (3.19)

Лемма 3.9. Ряд (3.19) сходится абсолютно и равномерно по х е [0,1] и Ь е (—го, го), и для его суммы имеет место формула

^ спУп(х)еЛпвЙ = [р(1 — х)/0(1 — х + вЬ) — гр(х)/0(х + в)], (3.20)

где р(х) = и2(х)вгах.

Доказательство. Сходимость ряда (3.19) следует из леммы 3.6. Далее, имеем:

у„(х)еЛ»= ^ е„ [р(1 — х)в2пт(1—х) — гр(х)в2птх] ел»вй =

= еавй [р(1 — х)£ спе2пт(1—— гр(х) ^ спе2ппг(х+в’)],

откуда следует (3.20). □

Теорема 3.1. Если ^(х) е С1 [0,1], ^(0) = (1) = 0, д(х) е С[0,1], д(х) = д(1 — х), то классическое решение задачи (3.1)—(3.2) существует и имеет вид

и(х, Ь) = еавй [р(1 — х)/0(1 — х + вЬ) — гр(х)/0(х + вЬ)], (3.21)

где р(х) = ехр ^агх — г / д(Ь) ¿Ь^, /0(х) — периодическая с периодом 1 функция, причем на отрезке [0,1]

/0(х) = [¿^(х) + Р(1 — х)] • (3.22)

Доказательство. Как установлено выше, если функцию /0(х), заданную с помощью (3.22), продолжить периодически с периодом 1 на всю ось, то получим непрерывно дифференцируемую всюду функцию. Проверим теперь, что и(х,Ь), заданная формулой (3.21), является решением смешанной задачи (3.1)-(3.2).

Сначала покажем, что и(ж,г) удовлетворяет дифференциальному уравнению (3.1). Имеем: в^иг (ж, г) = аеавгг [р(1 — ж)/0(1 — ж + вг) — гр(ж)/(ж + вг)] + [р(1 — ж)/0(1 — ж + вг) — ¿р(ж)/0(ж + вг)],

(С, г) = еввй [—р’ (1 — с )/0(1 — С + вг) — р(1 — 0/0(1 — с + вг)—

—¿р’ (С )/0 (С + вг) — гр(С )/0 (С + вг)] =

= еавгг [—р'(ж)/0(ж + вг) — р(ж)/0(ж + вг) — —гр'(1 — ж)/0(1 — ж + вг) — гр(1 — ж)/0(1 — ж + вг) .

Подставляя данные соотношения в (3.1), получим:

Последние две квадратные скобки равны нулю. Подставляя явные выражения для р(ж) и р'(ж), получим, что первая и вторая квадратные скобки также равны нулю, т.е. и(ж,г) удовлетворяет уравнению

Далее, при ж е [0,1] имеем:

и(ж, 0) = р(1 — ж)/0(1 — ж) — гр(ж)/0(ж) = р(ж),

и(0, г) = еавй [р(1)/0(вг) — ¿р(0)/0(вг)] = 0,

т. е. начальное и краевое условия выполнены. □

3.2. Общий случай [31]

3.2.1. Асимптотические формулы для собственных значений и собственных функций задачи (3.5)-(3.6)

Приведем задачу (3.5)-(3.6) к задаче в пространстве вектор-функций размерности 2. Положим ¿(ж) = (г1 (ж),г2(ж))т, где (ж) = у(ж), ¿2(ж) = у(1 — ж). Тогда из уравнения в (3.5) получим векторно-матричное уравнение:

Вг ‘(ж) + Р (ж)г(ж) = Лг(ж), (3.23)

где В = | 0 |, Р(ж) = | ^(ж) 0 | и г1(ж) = ¿2(1 — ж). Более того, справедливо следующее 1 0 у ^ 0 д(1 — ж)у

Лемма 3.10. Число Л является собственным значением, а у(ж) — собственной функцией краевой задачи (3.5)—(3.6) тогда и только тогда, когда ¿(ж) = (г1(ж),г2(ж))т = (у(ж),у(1 — ж))т, является ненулевым решением системы (3.23) с краевыми условиями:

Нетрудно убедиться в справедливости следующего утверждения.

, Н(ж) = diag(h1 (ж),^2(ж)), где (ж) = е 0 , к = 1, 2,

р1 (ж) = —р2(ж) = — 2[д(ж) + д(1 — ж)]. Замена ¿(ж) = ГН(ж)и(ж), где и = (и1,и2)т, приводит систему (3.23) к виду

и'(ж) + д(ж)и(ж) = ЛРи(ж), (3.25)

где Б = diag (—г, г), ф(ж) = ( ( ^ ^ ), д1(ж) = 2 [ 0 и Яер 0, (ж) е С1 [0,1], то для общего решения уравнения (3.27) имеем следующую асимптотическую формулу:

и(ж, р) = и (ж,р)едВ х с, где и (ж, р) = (и^- (ж, р))г^=1)2, с = (с1 ,с2)Т — произвольный вектор и

ии(ж, р) = 1 + / Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

Полагая с1 = 1, с2 =0 и учитывая, что

е—2дт42(т) ¿т = О (д—1 е—

получим ш1(х) = 1 + О (д ^, и отсюда из (3.32) (х) = О (д 1 е2дх).

Далее, положим с2 = 1 и подставим (3.31) в (3.32). Тогда

где ^(х, д) = / е2^(Ь) ¿Ь = О (д 1 е2^х). Полагая с1 = / е 92(Ь)^2(Ь) ¿Ь, получим из (3.35), что о 0

(х) = 1 + О (д—^, а (х) = О (д—1е—. Отсюда, в частности, легко следует (3.28). Теперь дадим уточнение (х) и ш2(х). В случае с1 = 1, с2 = 0 обозначим (х) = ш11(х), и>2(х) = и>21 (х). Имеем:

е—2/,т 92 (т) ¿т = — 2де»2^т 92(т)

Тогда, поставляя найденную асимптотику для (х) = ш11 (х) в (3.33) при с1 = 1, с2 = 0, получим:

^11 (х) = 1 — е2^91 (Ь) ¿Ь / е—2дт92(т) ¿т + О (д—2)

е2^ (Ь) ¿Ь / е—2дт92 (т) ¿т =

= I е2^91 (Ь) [——92(х)е—+ —92(Ь)е—¿Ь + / е2^91 (Ь) ¿Ь — / е—2^т92(т) ¿т

= О (д—2) + У 91(Ь)92(Ь) ¿Ь + — у е—2дт92(т) ¿т у е2^91 (Ь) ¿Ь =

то из (3.36) получим:

шп(х) = 1 — У 91 (Ь)92 (Ь) ¿Ь + О ^д1

Подставим (3.37) в (3.31) при с2 = 0. Тогда

Ш2(х) = Ш21(х) = — I е2^91 (Ь) ¿Ь + О^е2^ =

51 (х)е21Х — 51(0) — е2^1 (г)

Аналогичные формулы получаются для (х) = эд12(х), эд2(х) = ш22 (х) при втором выборе с1 и с2. Образуем матрицу Ш(х, д) = («^(х))2. Тогда матрица и(х, д) = е1ВхШ(х, д)е-1Вх — искомая. □ Аналогичный результат может быть получен при Яе д 0, соответственно Яе Лг 2 (2) «21(2) — (2) ии (2)] е-2 [^2 (2) «21 (2)— (2) «11 (2)]

2 2 2 21 2 — 1 2 11 2 Для получения простейших асимптотических оценок собственных значений используем сначала

из (3.28). Обозначая [1] = 1 + О (д ^, имеем

«кк(х,д) = [1], «^(х, д)= О(д-1) , к,з = 1, 2, к = з.

Поэтому уравнение (3.39) примет вид

е* [—Л1(1) [1]+ о(¿)] е-# [Л2Й) [1] + о( 1)]

Отсюда, учитывая, что ———— = е 0 , получим е1 = —¿е 0 [1], откуда яЦ1/2)

д« = — I 2 + I ^(г) I ¿ — 2пш + о(д 1),

и О (д-1) = О (1/п). Вычисляя теперь Лп = ¿д«, придем к следующему утверждению.

Теорема 3.3. Для собственных значений Лп задачи (3.23)-(3.24) имеют место асимптотические формулы:

где Л« = 2пп + а, а = п/2 + / д(£) —Н, Яе д 0 — любое.

Для того чтобы получить более тонкие оценки для собственных значений, воспользуемся в уравнении (3.39) значениями «^(1/2) и «^(0), вычисленными по уточненным формулам из теоремы 3.2 при д = д«

Лемма 3.12. Для любого целого числа к, любой функции в(х) е С[0,1] и р = ±1 имеем:

е2р^5(Ь) ¿Ь = а„ + О (^п) , 45(Ь) ¿Ь = а„ + О (^п) .

Лемма 3.13. Для значений функций (х, дп) из теоремы 3.2 справедливы следующие асимптотические формулы:

«22(0) = 1 + О ( ДЛ , «21(0) = о(,

а ап ^ = — + — + О пп

(аргумент дп для удобства опускаем).

Теорема 3.4. Для собственных значений Ап задачи (3.23)—(3.24) имеют место уточненные асимптотические формулы:

А„ = АП + а + — + о(, п = ±п0, ±(п0 + 1). (3.45)

где АП определяется так же, как и в теореме 3.3.

Доказательство. Используя в уравнении (3.39) оценки из леммы 3.13, получим:

е»»/2 * (2 )(1 + а + От + О (£)) = ¿е^/2 *1 (1) (1 + 2 + От + О ($

— г / Л ( а ап ( 1 )) — п/2г — 2ппг—г / Л а + ОТ +°( П2 )

ем = —ге 0 1+—+ — + О ^ = е 0 е п .

Поэтому для дп имеем следующие уточненные асимптотические формулы:

_ 0. а а„ / 1 , дп = —АПг + — + — + О -з ,

откуда следует (3.45). □

Перейдем к исследованию асимптотики собственных функций задачи (3.5)-(3.6). В силу леммы 3.10 собственная функция, отвечающая значению Ап, есть уп(х) = г1(х, Ап), где (х, Ап) определена соотношением из (3.38), и, следовательно,

Уп(х) = С1 [^1 (х)е—Л»г* «11 (х,д„) — г^2 (х)е—Л»г:Е «21(х,д„ )] +

Теорема 3.5. Для собственных функций оператора Ь имеют место асимптотические формулы: ( )

Уп(х) = уП(х) + О ( 1 ) , п = ±п 0, ±(п 0 + 1).

где уП(х) = еЛТг(1—т)Л,2(1 — х) — ге^^Л,2(х), функция Л,2(х) та же, что и в лемме 3.11.

Доказательство. Воспользуемся оценками (3.40) и полученной из них асимптотикой (3.41) для собственных значений.

Из (3.46) и краевого условия у«(0) = 0 имеем:

С1 [«П(0) — ¿«21(0)] + С2[«12 (0) — ¿«22 (0)] = С1 [1] — ¿С2[1] = 0,

откуда с1 = с2¿[1]. Положим с2 = 1, тогда с1 = ¿[1]. Так как е А°гх = е А°гх[1], еА°гх = еА°гх[1], то из (3.46) и (3.40) получим:

у«(х) = ¿[1]е-А°гх [Н1(х)[1] — ¿Н2(х)^П) ] + еА»гХ [Мх)О — ¿Чх)[1]] =

= ¿ ( е»А°гхН1 (х) — еА°гхН2 (х)) + О ( П

Положим у«(х) = ¿ ^е А°гхН1 (х) — еА°гхН2(х)^. Из (3.26) следует, что

Н1 (х) = е е 0 Н2(1 — х) = —¿еагН2(1 — х) = —¿еА°г Н2(1 — х).

у« (х) = е-А°гх еА°г Н2 (1 — х) — ¿еА°гх Н2(х) = еА° г(1-х)Н2(1 — х) — ¿еА°гх Н2 (х),

откуда следует утверждение теоремы. □

Чтобы получить более тонкие оценки для собственных функций, используем уточненные оценки (3.45) для собственных значений и асимптотики из теоремы 3.2.

Теорема 3.6. Для собственных функций оператора Ь имеют место уточненные асимптотические формулы:

у«(х) = у«(х) + 01„(х) + 02„(х) + О ( -1

где у« (х) определяется так же как в теореме 3.5, и

(х) = 1 [Ь(х)е-А°гх + Ь(х)еА°гх + 6(х)а„ е-А°гх + Ь(х)а„еА°гх ],

02„(х) = п[Ь(х) / е-А°йд1 ( -^Г ) + Ь(х) / еА°й

+6(х) / еА°йд2 ‘ х + ^ . ь(х) I е-А°

(через Ь(х) обозначаем различные непрерывные функции из некоторого конечного набора).

Доказательство. Из (3.46) и краевого условия у«(0) = 0, используя оценки из леммы 3.13, имеем:

= е*Л°гх (1 + ах + —х) + О ( -1 ) ,

то по теореме 3.2 получим:

е-А°гхИ11 (х, д„) = е-А°гх (г + а х + ^ х) Л + + О (

V п п / п у п2у

л;» Л + М + ^ 6(ЖЛ+ о( 1),

ел»ix U22 (x, m) = eA™ix fl + a x + — x

(1 + ax+an x) Л + M) + о(

е-л-^х U21(x, m) = е-лП 1 + a x + ^ Л ( M + a е2Л0- i« + a f е2Л0» i(x-t) «1 ^ ¿Л +о f П =

= ^ е-л-ix + a ел-ix + a f e^;i(x-2t)«1 ^ dt + O f ,

ел-ixui2 (x, m) = ело 1 + ax + ^ xV^ + a e2^ ^^ + a i e-2^(x-t)q2(t) dt) +O f ДЛ =

M ел0ix + a е-л-ix + a Г е-л0^-2*)«2(t) dt + о( . n n n J n2y

>° i(x-2t) q1 (t) dt =2/ел0 iT «1 ( dr = 5/e-^ «К ^ ) dt + 2 / e^ «К ^ > dt,

e-^i(x-2t)q2(t) dt = е-л;ix / e^-^t) dt — е-л-i(x-2t)q2(t) dt =

е-л-ixu21 (x, m) = ^ е-л0ix + a ел0ix + a / e-^«^dt+ n n n J V 2

л / b(x) л0• a _ло . an -ло .

ел°ixu12(x, m) = елоix + — e л-ix + — e л-ix+

Полагая c2 = 1 и подставляя (3.47)-(3.51) в (3.46), получим утверждение теоремы. 3.2.2. Теорема о разложении по собственным функциям

Обозначим через Ss область, полученную из А-плоскости удалением всех чисел вида nn + а, 1

(n е Z), а = п/2 + J q(t)dt, вместе с круговыми окрестностями одного и того же достаточно малого

Так как Дл = O(1) в Ss, то стандартно получается Теорема 3.7. f (x) е C1 [0,1], f (0) = 0, wo

lim ||f(x) — Sr(f,x)|^ = 0,

где 5Г (/, х) = — ^ / ЛЛ/¿Л — частичная сумма ряда Фурье функции / по собственным и

присоединенным функциям оператора Ь.

Так как Ь — самосопряженный оператор, то по теореме 3.7 получим

Лемма 3.14. Система является ортогональной и полной в Ь2[0,1], и ||уп||2 = 2+0 (1/п), где ||— норма в Ь2[0,1].

3.2.3. Преобразование формального решения

Идеи А. Н. Крылова — В. А. Чернятина мы реализуем следующим образом. Ряд £, представляющий формальное решение рассматриваемой задачи по методу Фурье, мы берем в виде

где £0 — ряд, являющийся решением некоторой специальной эталонной задачи, а 50 — сумма этого ряда, которая явно вычисляется. В свою очередь, £ — £0 представляется в виде суммы двух составляющих, одна из которых — конечная сумма, а вторая — ряд, составленный из разностей соответствующих членов рядов £ и £0, причем этот ряд и ряды, получающиеся из него почленным дифференцированием, сходятся равномерно. Это последнее обстоятельство, а также то, что 50 есть решение эталонной задачи, позволяет весьма просто убедиться, что £ = 50 + (£ — £0) есть классическое решение исходной задачи при минимальных требованиях гладкости начальных данных.

В качестве эталонной задачи мы берем задачу (3.1)-(3.2), где д(х) заменяется на д0(х) = 2(#(х)+ + д(1 — х)). Функция д0(х) является симметричной: д0(х) = д0(1 — х). Соответствующий оператор обозначим Ь0:

Ь0 У(х) = у'(1 — х) + 50 (х)У(х), У(0) = Собственными значениями и собственными функциями этого оператора являются ЛШ и уШ(х) из п. 3.1.

3.2.4. Решение задачи (3.1 )-(3.2)

Согласно методу Фурье формальное решение задачи (3.1)-(3.2) имеет вид

«(х>*) = — 2П / (ДЛ^(х))еЛвг’¿Л + ^ (р,у„) уп(х)еЛ», (3.53)

где г таково, что при |Лп| > г все собственные значения простые. Представим ряд (3.53) в виде (3.52), где

Для суммы 50 ряда £0 справедливо утверждение.

Лемма 3.15. Если р(х) е С 1[0,1], р(0) = р'(1) = 0, то имеет место формула

50 = еавй [р(1 — х)/0 (1 — х + в) — Ф(х)/0 (х + в)], (3.54)

где /0 (х) — непрерывно дифференцируемая на всей оси функция, периодическая с периодом 1, и

гаж — г / д(£) (И 1 _ 1,1Г,о/ ^ _1_ 1 _ ^ I ^ ^ и II- ^ — , . г

/0(х) = зр^) [«р(х) + р(1 — х)] при х е [0,1]; р(х) = е 0 , а = п/2 + / д(£) Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

«1 (х,*) = — ^ I ((Лл — ЛЛ) Р(х)) еЛвг*¿Л, (3.55)

ЛЛ — резольвента оператора Ь0.

Щ2 Уп(х)еЛ™— у0 (х)еЛ»вг^

Лемма 3.16. Имеет место формула

(9, уп) уп(х)еЛ™(9, у0) уП(х)еЛ°

где у = Ьр, = у — Ь0р, у2 = Ь0у1 (здесь из области определения оператора Ь0, так как 9(х) е С 1[0,1]).

Доказательство. Из тождества Гильберта имеем:

я 9 длр , дл9 , дл92

Д Р Д 0Р (ДЛ — ДЛ)9 91 + ДЛ92 ДЛР — ДЛ Р = -Л—Д2 +

и (3.57) следует из представления слагаемых в (3.56) через интегралы от резольвенты по контурам достаточно малого радиуса с центрами в АП. □

Лемма 3.17. Если у(х) е С[0,1], то (9,) = аП/п ^ = 1,2). Доказательство. Утверждение леммы для ] = 1 очевидно. Далее,

/ Ь(х) ¿х I е»п ‘о 7 о

¿Ь I Ь(х)91 ( х + Ь | ¿х = аП,

и, аналогично рассмотрев остальные слагаемые в 02п, получим, что и (9, О2о) = аП/п. □

Лемма 3.18. Ряды в (3.57) и ряды, полученные из них почленным дифференцированием по х и Ь, равномерно сходятся по х е [0,1] и Ь е [—А, А], где А > 0 — любое.

Доказательство. Согласно неравенствам Коши — Буняковского и Бесселя ряды ^

сходятся, откуда следует равномерная сходимость рядов в (3.57). Рассмотрим ряд

(9,уп) уп(х)еЛ-(9,у^ уП(х)еЛ°

Используя асимптотические формулы для АП, уП(х), имеем: (9, уп) уП(х)еЛп(9, уп) (уП(х))’еЛ°

Поэтому ряд, полученный почленным дифференцированием по х ряда (3.58), имеет следующее пред-

(9,уп — у0) (уП(х))’еЛ»+( ) / 1

В силу леммы 3.17 (9, уп — у0) = ап/п, где ^ а0 Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

Поэтому из (3.60) и (3.61) получаем Ри + = д(х)и — до(х)£0, а значит,

Ри = д(х)и — д0 (х)£0 + д0(х)£0 = д(х)и. Теорема доказана. □

4. ДРУГИЕ РЕЗУЛЬТАТЫ

Приведем в п. 4.1-4.3 без доказательств другие результаты о смешанных задачах с инволюцией.

4.1. Смешанная задача в периодическом случае

Рассматривается смешанная задача следующего вида [33]: 1 ди(х, дм(£, £)

^ о. +д(х)и(х,г), х е [0,1],г е (—го, +го), (4.1)

и(0, £) = и(М), и(х, 0) = р(х), х е [0,1], (4.2)

где в — вещественное число, в = 0, д(х) е С 1[0,1] и вещественна. Естественные минимальные условия на р(х): р(х) е С1 [0,1], р(0) = р(1), 0 = 0,1). Введем операторы X и Х0:

¿У = У'(1 — х) + 5(х)У(х), У(0) = У(1), ¿0 У = У'(1 — х) + ?0(х)У(х), У(0) = У(1),

^0((х) = 2 [д(х) + д(1 — х)].

Лемма 4.1. Собственные значения оператора Х0 простые и равны А^ = 2пп + а, п е Ж, 1

а = / д(£) (Ь, а соответствующие собственные функции 0

УП (х) = и(1 — х)вл°г(1-х) — г-и(х)ел°гх,

где и(х) = ехр(—г / д0(т) (т).

Решение эталонной задачи (4.1)-(4.2), когда д(х) есть д0(х), полученное по методу Фурье, есть «0(х, £) = еавй [р(1 — х)У0(1 — х + в^) — гр(х)/0(х + в*)], (4.3)

где р(х) = ехр , /0(х) е С1 (—го, +го), периодична с периодом 1, причем

f0(x) = [i^(x) + ^(1 — x)] ,x G [0,1]. Математика 193

Лемма 4.2. Собственные значения АП оператора Ь, достаточно большие по модулю, простые и имеют асимптотику:

Ао = АО + — + —, п = ±п 0, ±(п 0 + 1), — пп

Теорема 4.1. Классическое решение задачи (4.1)—(4.2) существует и имеет вид

и(х, Ь) = «о (х, Ь) + Е1 + Е2,

((Дл — ЯЛ) р) (х)еЛвг4^А,

Дл, ДЛ — резольвенты операторов Ь и Ь 0,

Ряд Е2 и ряды, получающиеся из него почленным дифференцированием по х и Ь, равномерно сходятся при х е [0,1] и Ь е [—А, А] при любом А > 0. Схожий результат получен в [32] для задачи

+91 (х)«(х, Ь) + 92(х)«(1 — х, Ь),

«(0,ь) = 0, «(х, 0) = р(х), х е [0,1], ь е (—го, +го),

при условиях 9^ (х) е С1 [0,1], 91 (х) — вещественна, 92(х) = 92 (1 — х), 92(0) = 0, в = 0 — вещественное число. Естественные минимальные требования те же, что и в параграфе 3.

4.2. Смешанная задача для неоднородного уравнения

Рассматривается задача вида [33]

х е [0,1],ь е (—го, +го), «(0,ь) = 0, «(х, 0) = р(х), х е [0,1].

Считаем, что в, 9(х) те же, что и в п. 4.1. Формальное решение по методу Фурье возьмем в виде: «(х,Ь) = — ¿г / ((Дл(Р + 9)))(х)еЛвг4^А + £ (р(С) + 9о(С),уо(С)) у0^ еЛп,

где Дл = (Ь — АЕ)—1, Ьу = у'(1 — х) + 9(х)у(х), у(0) = 0, А — спектральный параметр, Е — единичный оператор, 9 = 9(х,Ь, А) = вг /о е—Лвгт/(х,т) ¿т, 9П(С) = 9(С, Ь, АП), АП и уП(х) — собственные значения и собственные функции оператора Ь соответственно.

Теорема 4.2. Пусть р(х) е С1 [0,1], р(0) = р'(1) = 0, /(х,Ь), /^(х,Ь) непрерывны по х е [0,1] и Ь е (—го, го), причем /(0, Ь) = /X(1,Ь) = 0. Классическое решение задачи (4.6)—(4.7) существует и имеет вид

«(х, Ь) = «1 (х, Ь) + и2 (х, Ь),

где и1(х,Ь) есть решение задачи (4.6)—(4.7) при /(х,Ь) = 0 (см. параграф 3), а и2(х,Ь) = = вг /о «Цх, Ь — т, т) ¿т и -Цх, Ь, т) есть классическое решение задачи

Ь,т) = 0, 0, т ) = / (х,т), т — параметр.

4.3. Смешанная задача на геометрическом графе

Рассматривается смешанная задача с инволюцией на простейшем графе из двух ребер: одно ребро образует цикл-петлю, а второе примыкает к нему. Смешанная задача в таком случае берется в виде [34]

щ (0, £) = «1 (М) = «2 (0,(4.10) «1 (х,£) = Р1 (х), «2(х,^)= Р2(х). (4.11)

Вид графа позволяет задать простейшее уравнение (без инволюции) (4.8) на петле, а вот на другом ребре надо обязательно брать уравнение с инволюцией, так как иначе соответствующая спектральная задача нерегулярна по Биркгофу [36], и потому решение смешанной задачи того же вида, что и выше, получить нельзя. Предполагаем, что д(х) £ С1 [0,1] и вещественна,

Рк(х) £ С1 [0,1], (0) = (1) = Р2(0), р2(1) + 3(0)Р2(0) + гр1(0) = 0 (4.12)

(последнее условие в силу системы (4.8)-(4.9)).

По методу Фурье соответствующая (4.8)-(4.10) спектральная задача есть

ЬУ = ЛУ, у =(У1,У2)Т (Т — знак транспонирования), где Ь — следующий оператор:

¿У = (-гу1 (х),у2(1 — х) + д(х)у2(х))т, У1(0) = У1 (1) = У2(0). 1

Лемма 4.3. Если а = п/2 + / не кратно 2п, то собственные значения оператора Ь,

достаточно большие по модулю, простые и образуют две серии: Л ‘ = 2пп, п £ Ж, Л » = +—Ь —

(п = ±п0, ±(по + 1),—.), где = 2пп + а. При этом все собственные значения оператора Ь вещественные.

Симметричным случаем задачи (4.8)-(4.11) мы будем называть задачу, когда вместо д(х) берется 30(х) = 1 [д(х) + д(1 — х)], и оператор Ь в этом случае называем Ь0. Оператор Ь* (Ь*) имеет вид Ь*г = Ьг (Ь*г = Ь0г) с краевыми условиями г2 (0) = (1) — (0) + гг2(1) = 0, одними и теми же и для Ь*, и для Ь*. Собственные значения Ь (Ь0) и Ь* (Ь*) совпадают, и для Ь0 они те же, что и в лемме 4.3, но теперь надо брать а = ап = 0.

Лемма 4.3 позволяет изучить асимптотику собственных функций операторов Ь и Ь* как и в параграфе 3 (не приводим ее из-за громоздкости).

В симметричном случае ряды формального решения по методу Фурье наподобие уравнения струны точно вычисляются, и тем самым, получаем решение м0(х,£) смешанной задачи в этом случае. Соответствующую формулу здесь не приводим из-за громоздкости. Формальное решение задачи (4.8)-(4.11) по методу Фурье есть

«(М) = — ^ / (Ялр(х))еАЙ ¿Л + £ (Р,^х’Л га)) )у(х, Л„ )вЛ»(4.13)

где м(х,£) = (и1(х,^),и2(х,£))т, ДЛ — резольвента оператора Ь, у(х, Лп) (г(х, Лп)) — собственные вектор-функции оператора Ь (Ь*) для собственного значения Лп, 7(ЛП) = (у(х, Лп),г(х,Лп)). Представим (4.13) в виде

и(х,*)= «0(х,£) — — / ((Дл — ) р) (х)вЛЙ¿Л + V (х,£), (4.14)

АП — собственное значение £0, у0(х, АП) (г0(х, АП)) — собственные функции £0 ), 7 = (у0(х, АП), г0(х,АП)) и 7 не зависит от п.

Формула (4.14) так же как и в параграфе 3, приводит к следующему результату.

Теорема 4.3. Если д(х) е С1 [0,1] и вещественна, д(0) = д(1), а = —Ь / д(Ь) ¿Ь не кратно 2п,

рк(х) удовлетворяют (4.12), то классическое решение задачи (4.9)—(4.11) существует и имеет вид (4.14). Ряды в (4.14) и ряды, получающиеся из них почленным дифференцированием по х и Ь, сходятся абсолютно и равномерно по х е [0,1] и Ь е [—А, А] при любом А > 0.

Работа выполнена при финансовой поддержке РФФИ (проект № 13-01-00238).

1. Стеклов В. А. Основные задачи математической физики. М. : Наука, 1983. 432 с.

2. Петровский И. Г. Лекции об уравнениях с частными производными. М. ; Л. : ГИТТЛ, 1953. 360 с.

3. Смирнов В. И. Курс высшей математики : в 4 т. М. : Гостехиздат, 1953. Т. 4. 804 с.

4. Ладыженская О. А. Смешанная задача для гиперболического уравнения. М. : Гостехиздат, 1953, 282 с.

5. Ильин В. А. Избранные труды : в 2 т. М. : Изд-во ООО «Макс-пресс», 2008. Т. 1. 727 с.

6. Ильин В. А. О разрешимости смешанных задач для гиперболических и параболических уравнений // УМН. 1960. Т. 15, вып. 2. С. 97-154.

7. Чернятин В. А. Обоснование метода Фурье в смешанной задаче для уравнений в частных производных. М. : Изд-во Моск. ун-та, 1991. 112 с.

8. Крылов А. Н. О некоторых дифференциальных уравнениях математической физики, имеющих приложения в технических вопросах. М. ; Л. : ГИТТЛ, 1950. 368 с.

9. Крылов А. Н. Лекции о приближенных вычислениях. М. ; Л. : ГИТТЛ, 1950. 398 с.

10. Lanczos C. Discourse of Fourier Series. Edinburgh ; London : Oliver and Boyd, Ltd., 1966. 255 p.

11. Нерсесян А. Б. Ускорение сходимости разложений по собственным функциям // Докл. НАН Армении. 2007. T. 107, № 2. C. 124-131.

12. Чернятин В. А. К уточнению теоремы существования классического решения смешанной задачи для одномерного волнового уравнения // Дифференциальные уравнения. 1985. Т. 21, № 9. С. 1569-1576.

13. Чернятин В. А. К решению одной смешанной задачи для неоднородного уравнения с частными производными четвертого порядка // Дифференциальные уравнения. 1985. Т. 21, № 2. С. 343-345.

14. Чернятин В. А. О необходимых и достаточных условиях существования классического решения смешанной задачи для одномерного волнового уравнения // Докл. АН СССР. 1986. Т. 287, № 5. С. 10801083.

15. Чернятин В. А. Классическое решение смешанной задачи для неоднородного гиперболического уравнения // Численные методы решения краевых и на-

чальных задач для дифференциальных уравнений. М. : Изд-во Моск. ун-та, 1986. С. 17-36.

16. Чернятин В. А. К уточнению теоремы существования решения смешанной задачи для неоднородного уравнения теплопроводности // Численный анализ : методы, алгоритмы, программы. М. : Изд-во Моск. ун-та,

17. Чернятин В. А. О разрешимости смешанной задачи для неоднородного гиперболического уравнения // Дифференциальные уравнения. 1988. Т. 24, № 4. С. 717-720.

18. Андреев А. А. О корректности краевых задач для некоторых уравнений в частных производных с карле-мановским сдвигом // Дифференциальные уравнения и их приложения : тр. 2-го междунар. семинара. Самара, 1998. С. 5-18.

19. Dankl Ch. G. Differential-Difference Operators Associated to Reflection Groups // Trans. Amer. Math. Soc.

1989. Vol. 311, № 1. P. 167-183.

20. Платонов С. С. Разложение по собственным функциям для некоторых функционально-дифференциальных операторов // Тр. Петрозавод. гос. ун-та. Сер. математическая. 2004. Вып. 11. С. 15-35.

21. Хромов А. П. Об обращении интегральных операторов с ядрами, разрывными на диагоналях // Мат. заметки. 1998. Т. 64, № 6. С. 932-949. DOI: 10.4213/ mzm1472.

22. Бурлуцкая М. Ш., Курдюмов В. П., Луконина А. С., Хромов А. П. Функционально-дифференциальный оператор с инволюцией // Докл. АН. 2007. Т. 414. № 4. С. 443-446.

23. Корнев В. В., Хромов А. П. О равносходимости разложений по собственным функциям интегральных операторов с ядрами, допускающими разрывы производных на диагоналях // Мат. сб. 2001. Т. 192, № 10. С. 33-50.

24. Курдюмов В. П. Хромов А. П. О базисах Рисса из собственных функций интегральных операторов с ядрами, разрывными на диагоналях // Изв. АН. Сер. математическая. 2012. Т. 76, № 6. С. 106-121.

25. Курдюмов В. П. Хромов А. П. О базисах Рисса из собственных и присоединенных функций функциональ-

но-дифференциального оператора переменной структуры // Изв. Сарат. ун-та. Нов. сер. Сер. Математика. Механика. Информатика. 2007. Т. 7, вып. 2. С. 20-25.

26. Корнев В. В., Хромов А. П. Оператор интегрирования с инволюцией, имеющей степенную особенность // Изв. Сарат. ун-та. Нов. сер. Сер. Математика. Механика. Информатика. 2008. Т. 8, вып. 4. С. 18-33.

27. Бурлуцкая М. Ш., Хромов А. П. Об одной теореме равносходимости на всем отрезке для функционально-дифференциальных операторов // Изв. Сарат. ун-та. Нов. сер. Сер. Математика. Механика. Информатика. 2009. Т. 9, вып. 4, ч. 1. С. 3-10.

28. Бурлуцкая М. Ш., Хромов А. П. Обоснование метода Фурье в смешанных задачах с инволюцией // Изв. Сарат. ун-та. Нов. сер. Сер. Математика. Механика. Информатика. 2011. Т. 11, вып. 4. С. 3-12.

29. Халова В. А., Хромов А. П. Интегральный оператор с негладкой инволюцией // Изв. Сарат. ун-та. Нов. сер. Сер. Математика. Механика. Информатика. 2013. Т. 3, вып. 1, ч. 1. С. 40-45.

30. Хромов А. П. Смешанная задача для дифференци-

ального уравнения с инволюцией и потенциалом специального вида // Изв. Сарат. ун-та. Нов. сер. Сер. Математика. Механика. Информатика. 2010. Т. 10, вып. 4. С. 17-22.

31. Бурлуцкая М. Ш., Хромов А. П. Классическое решение для смешанной задачи с инволюцией // Докл. АН. 2010. Т. 435, № 2. С. 151-154.

32. Бурлуцкая М. Ш., Хромов А. П. Метод Фурье в смешанной задаче для уравнения первого порядка с инволюцией // Журн. выч. мат. и мат. физ. 2011. Т. 51, № 12. С. 2233-2246.

33. Бурлуцкая М. Ш., Хромов А. П. Смешанные задачи для гиперболических уравнений первого порядка с инволюцией // Докл. АН. 2011. Т. 441, № 2. С. 151-154.

34. Бурлуцкая М. Ш. Смешанная задача с инволюцией на графе из двух ребер с циклом // Докл. АН. 2012. Т. 447, № 5. С. 479—482.

35. Марченко В. А. Операторы Штурма — Лиувилля и их приложения. Киев : Наук. думка, 1977. 392 с.

36. Наймарк М. А. Линейные дифференциальные операторы. М. : Наука, 1969. 528 с.

Classical Solution by the Fourier Method of Mixed Problems with Minimum Requirements on the Initial Data

A. P. Khromov1, M. Sh. Burlutskaya2

1 Saratov State University, 83, Astrakhanskaya str., 410012, Saratov, Russia, KhromovAP@info.sgu.ru 2Voronezh State University, 1, Universitetskaya pl., 394006, Voronezh, Russia, bmsh2001 @mail.ru

The article gives a new short proof the V. A. Chernyatin theorem about the classical solution of the Fourier method of the mixed problem for the wave equation with fixed ends with minimum requirements on the initial data. Next, a similar problem for the simplest functional differential equation of the first order with involution in the case of the fixed end is considered, and also obtained definitive results . These results are due to a significant use of ideas A. N. Krylova to accelerate the convergence of series, like Fourier series. The results for other similar mixed problems given without proof.

Key words: mixed problem, Fourier method, involution, classical solution, asymptotic form of eigenvalues and eigenfunctions, Dirac system.

This work was supported by the Russian Foundation for Basic Research (project no. 13-01-00238).

1. Steklov V. A. Osnovnye zadachi matematicheskoi fiziki [The main tasks of mathematical physics]. Moscow, Nauka, 1983. 432 p. (in Russian).

2. Petrovsky I. G, Lectures on partial differential equations. Dover Publ. Inc., 1992, 245 p. (Rus. ed. : Petrovskii I. G. Lektsii ob uravneniiakh s chastnymi proizvodnymi. Moscow, GITTL, 1953, 360 p.).

3. Smirnov V. I. Kurs vysshei matematiki [A Course of Higher Mathematics : in 5 vol., vol. 4]. Moscow, Gostekhizdat, 1953. 804 p. (in Russian).

4. Ladyzhenskaya O. A. Smeshannaia zadacha dlia giperbolicheskogo uravneniia [Mixed problem for a hyperbolic equation]. Moscow, Gostekhizdat, 1953, 282 p. (in Russian).

5. Il’in V. A. Izbrannye trudy [Selected works : in 2 vol.]. Moscow, OOO «Maks-press», 2008, vol. 1 727 p. (in Russian).

6. Il’in V. A. The solvability of mixed problems for hyperbolic and parabolic equations. Rus. Math. Surv., 1960, vol. 15, iss. 1, pp. 85-142.

7. Chernyatin V. A. Obosnovanie metoda Fur’e v sme-shannoi zadache dlya uravnenii v chastnykh proiz-vodnykh [Justification of the Fourier method in a mixed problem for partial differential equations]. Moscow, Moscow Univ. Press, 1991. 112 p. (in Russian).

8. Krylov A. N. O nekotorykh differentsial’nykh uravneniiakh matematicheskoi fiziki, imeiushchikh prilozheniia v tekhnicheskikh voprosakh [On some differential equations of mathematical physics with applications in technical matters]. Leningrad, GITTL, 1950. 368 p. (in Russian).

9. Krylov A. N. Lektsii o priblizhennykh vychisleniiakh [Lectures on approximate calculations]. Moscow; Leningrad, GITTL, 1950. 398 p. (in Russian).

10. Lanczos C. Discourse of Fourier Series. Edinburgh; London, Oliver and Boyd, Ltd., 1966, 255 p.

11. Nersesyan A. B. Acceleration of convergence of eigenfunction expansions. Dokl. NAN Armenii, 2007, vol. 107, no. 2, pp. 124-131 (in Russian).

12. Chernyatin V. A. To clarify the theorem of existence of the classical solution of the mixed problem for one-dimensional wave equation. Differential Equations, 1985, vol. 21, no. 9, pp. 1569-1576 (in Russian).

13. Chernyatin V. A. To the decision of one of the mixed problem for an inhomogeneous equation with partial derivatives of fourth order. Differential Equations, 1985, vol. 21, no. 2, pp. 343-345 (in Russian).

14. Chernyatin V. A. On necessary and sufficient conditions for the existence of the classical solution of the mixed problem for one-dimensional wave equation. Dokl. AN SSSR, 1986, vol. 287, no. 5. pp. 1080-1083 (in Russian).

15. Chernyatin V. A. Classical solution of the mixed problem for the inhomogeneous hyperbolic equation. Chislen-nye metody resheniia kraevykh i nachal’nykh zadach dlia differentsial [Numerical methods for solving boundary value and initial problems for differential equations]. Moscow, Moscow Univ. Press, 1986, pp. 17-36.

16. Chernyatin V. A. To clarify the existence theorem for solutions of the mixed problem for the inhomogeneous heat equation. Chislennyi analiz : metody, algoritmy, programmy [Numerical analysis : methods, algorithms, programs]. Moscow, Moscow Univ. Press, 1988, pp. 126132 (in Russian).

17. Chernyatin V. A. On the solvability of the mixed problem for the inhomogeneous hyperbolic equations. Differential Equations. 1988, vol. 24, no. 4, pp. 717-720 (in Russian).

18. Andreev A. A. About the correctness of boundary problems for some equations with calimanesti shift. Differentsial’nye uravneniia i ikh prilozheniia : trudy 2-go mezhdunarodnogo seminara [Differential equations and their applications : proceedings of the 2nd international workshop]. Samara, 1998, pp. 5-18 (in Russian).

19. Dankl Ch. G. Differential-Difference Operators Associated to Reflection Groups. Trans. Amer. Math. Soc., 1989, vol. 311, no. 1, pp. 167-183.

20. Platonov S. S. The eigenfunction expansion for some functional-differential operators. Trudy Petrozavodskogo gosudarstvennogo universiteta. Ser. matematicheskaia [Proceedings of Petrozavodsk State University. Ser. Math.], 2004. iss. 11, pp. 15-35 (in Russian).

21. Khromov A. P. Inversion of integral operators with kernels discontinuous on the diagonal. Math. Notes. 1998, vol. 64, no. 6, pp. 804-813. DOI: 10.4213/mzm1472.

22. Burlutskaya M. Sh., Kurdyumov V. P., Lukoni-na A. S., Khromov A. P. A functional-differential operator with involution. Doklady Math., 2007, vol. 75, no. 3, pp. 399-402.

23. Kornev V. V., Khromov A. P. Equiconvergence of expansions in eigenfunctions of integral operators with kernels that can have discontinuities on the diagonals. Sbornik : Mathematics, 2001, vol. 192, no. 10, pp. 14511469. DOI: 10.4213/sm601

24. Kurdyumov V. P., Khromov A. P. Riesz bases of eigenfunctions of integral operators with kernels discontinuous on the diagonals. Izvestiya : Mathematics, 2012, vol. 76, no. 6, pp. 1175-1189. DOI: 10.4213/im7797.

25. Kurdyumov V. P. , Khromov A. P. On Riesz basises of the eigen and associated functions of the functional-differential operator with a variable structurelzv. Saratov Univ. (N.S.), Ser. Math. Mech. Inform., 2007, vol. 7, iss. 2, pp. 20-25 (in Russian).

26. Kornev V. V., Khromov A. P. Operator integration with an involution having a power singularity. Izv. Saratov Univ. (N.S.), Ser. Math. Mech. Inform., 2008, vol. 8, iss. 4, pp. 18-33 (in Russian).

27. Burlutskaya M. Sh., Khromov A. P. On the same theorem on a equiconvergence at the whole segment for the functional-differential operators. Izv. Saratov Univ. (N.S.), Ser. Math. Mech. Inform., 2009, vol. 9, iss. 4, pt. 1, pp. 3-10 (in Russian).

28. Burlutskaya M. Sh., Khromov A. P. Substantiation of Fourier method in mixed problem with involution. Izv. Saratov Univ. (N.S.), Ser. Math. Mech. Inform., 2011, vol. 11, iss. 4, pp. 3-12 (in Russian).

29. Khalova V. A., Khromov A. P. Integral Operators with Non-smooth Involution. Izv. Saratov Univ. (N. S.), Ser. Math. Mech. Inform., 2013, vol. 13, iss. 1, pt. 1, pp. 40-45 (in Russian).

30. Khromov A. P. The mixed problem for the differential equation with involution and potential of the special kind. Izv. Saratov Univ. (N. S.), Ser. Math. Mech. Inform., 2010, vol. 10, iss. 4, pp. 17-22 (in Russian).

31. Burlutskaya M. Sh., Khromov A. P. Classical solution of a mixed problem with involution. Doklady Math., 2010, vol. 82. no. 3, pp. 865-868.

32. Burlutskaya M. Sh., Khromov A. P. Fourier method in an initial-boundary value problem for a first-order partial differential equation with involution. Computational Mathematics and Mathematical Physics, 2011, vol. 51, no. 12, pp. 2102-2114.

33. Burlutskaya M. Sh., Khromov A. P. Initial-boundary value problems for first-order hyperbolic equations with involution. Doklady Math., 2011, vol. 84, no. 3, pp. 783786.

34. Burlutskaya M. Sh. A mixed problem with an involution on the graph of two edges with the cycle. Doklady Math., 2012, vol. 447, no. 5, pp. 479-482.

35. Marchenko V. A. Sturm — Liouville Operators and Applications. Kiev, Naukova Dumka, 1977, 392 p. (in Russian).

36. Naymark M. A. Lineinye differentsial’nye operatory [Linear differential operators]. Moscow, Nauka, 1969, 528 p. (in Russian).

🎦 Видео

Метод Фурье для волнового уравненияСкачать

5. Решение волнового уравнения на отрезке методом ФурьеСкачать

Метод Фурье для уравнения теплопроводности (диффузии)Скачать

Решение первой начально-краевой задачи для одномерного уравнения теплопроводности.Скачать

Решение первой краевой задачи для неоднородного уравнения теплопроводности.Скачать

Неоднородное уравнение колебания струныСкачать

УМФ. Метод Фурье для параболического уравненияСкачать

4.3 Решение неоднородного волнового уравнения на бесконечной прямойСкачать

Смешанная задача на отрезке. Метод ФурьеСкачать

Классические точные аналитические методы решения уравнений гиперболического и параболического типаСкачать

Решение первой начально-краевой задачи для волнового уравнения.Скачать

Уравнения математической физики. Решение гиперболического уравнения методом Фурье.Скачать