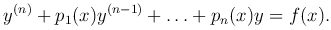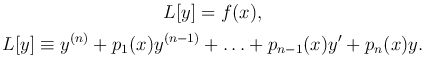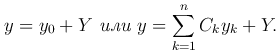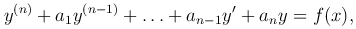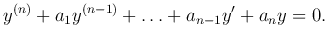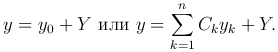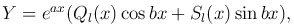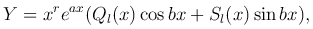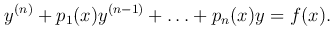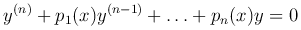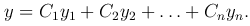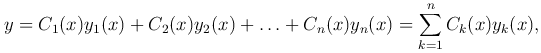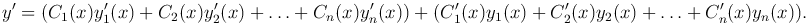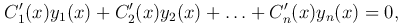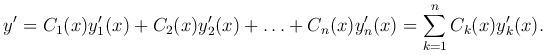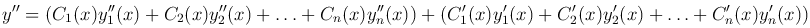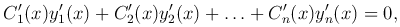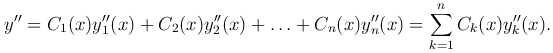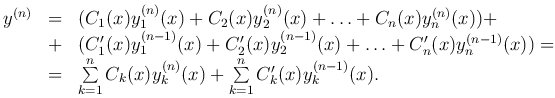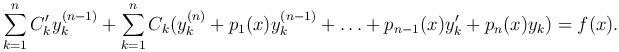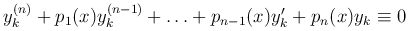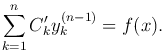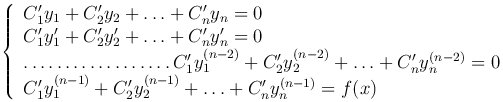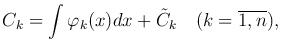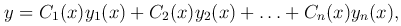Рассмотрим линейное неоднородное уравнение n-го порядка
Будем считать, что функции pk(x) (k=1, …, n) и f(x) непрерывны на отрезке [a, b]. Неоднородное уравнение кратко запишем так:
Теорема. Если y0 — решение однородного уравнения L[y]=0, y1 — решение соответствующего неоднородного уравнения L[y] = f(x), то сумма y0+y1 является решением этого неоднородного уравнения.
Структура общего решения неоднородного уравнения определяется следующей теоремой.
Теорема. Если Y — частное решение уравнения L[y] = f(x) с непрерывными коэффициентами, 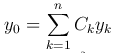
Замечание. Чтобы записать общее решение линейного неоднородного уравнения, необходимо найти какое-нибудь частное решение этого уравнения и общее решение соответствующего однородного уравнения.
- Линейные неоднородные уравнения n-го порядка с постоянными коэффициентами
- Метод вариации произвольных постоянных
- Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- Теорема общего решения ЛДНУ
- Алгоритм решения ЛДНУ
- Теорема о структуре общего решения ЛОДУ (док). Понятие ФСР
- Теорема о структуре общего решения линейного однородного диф. Уравнения n-го порядка. Характеристическое уравнение
- 🎬 Видео
Видео:16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Линейные неоднородные уравнения n-го порядка с постоянными коэффициентами
Рассмотрим линейное неоднородное уравнение n-го порядка с постоянными коэффициентами
где a1, a2, …, an — действительные числа. Запишем соответствующее однородное уравнение
Общее решение неоднородного уравнения определяется формулой
Общее решение однородного уравнения y0 находить умеем, частное решение Y может быть найдено методом неопределенных коэффициентов в следующих простейших случаях:
- 1. f(x) = e axPn(x), где Pn(x) — многочлен степени n.
Если a не является корнем соответствующего характеристического уравнения, то полагают Y= e ax Qn(x), где Qn(x) — многочлен степени n с неопределенными коэффициентами.
Если a — корень характеристического уравнения, то Y=x r e ax Qn(x), где r — кратность корня a.
2. f(x) = e ax (Pn(x) cos bx + Rm(x) sin bx).
Если a±ib не являются корнями характеристического уравнения, то полагают
где Ql(x), Sl(x) — многочлены степени l = max(n, m) с неопределенными коэффициентами.
Если a±ib — корни характеристического уравнения, то
где r — кратность корней a±ib.
В общем случае применяется метод вариации произвольных постоянных.
Видео:Теорема о структуре общего решения линейного однородного дифференциального уравненияСкачать

Метод вариации произвольных постоянных
Рассмотрим линейное неоднородное уравнение n-го порядка с переменными коэффициентами
Будем считать, что функции pk(x) (k=1, …, n) непрерывны на некотором отрезке [a, b].
Если нахождение частного решения этого уравнения оказывается затруднительным, но известно общее решение соответствующего однородного уравнения, то общее решение неоднородного уравнения можно найти методом вариации произвольных постоянных.
Пусть соответствующее однородное уравнение
имеет общее решение
Общее решение неоднородного уравнения будем искать в виде
где y1=y1(x), y2=y2(x), …, yn=yn(x) — линейно-независимые решения однородного уравнения, входящие в его общее решение, а C1(x), C2(x), …, Cn(x) — неизвестные функции. Чтобы найти эти функции, подчиним их некоторым условиям.
Потребуем, чтобы сумма во второй скобке равнялась нулю, то есть
Найдем вторую производную
и потребуем, чтобы
Продолжая аналогичный процесс, получим
В этом случае нельзя требовать, чтобы сумма во второй скобке обратилась в нуль, так как функции C1(x), C2(x), …, Cn(x) уже подчинены n-1 условиям, а нужно еще удовлетворить исходному неоднородному уравнению.
Подставим в это неоднородное уравнение выражения для функции y и ее производных, получим
Поскольку yk = yk(x) (k=1, …, n) — решения однородного уравнения, то
и последнее уравнение примет вид
Следовательно, для определения функций C′k(x) (k=1, …, n) имеем систему линейных уравнений
Определитель этой системы отличен от нуля, как определитель Вронского для линейно-независимых функций, поэтому система имеет единственное решение.
Из этой системы находим C′k=φk(x) (k=1, …, n), а потом и сами функции
где 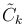
Подставляя эти выражения в формулу
получаем искомое общее решение неоднородного уравнения.
Видео:Теорема о структуре общего решения линейного неоднородного дифференциального уравненияСкачать

Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Данная статья раскрывает вопрос о решении линейных неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами. Будет рассмотрена теория вместе с примерами приведенных задач. Для расшифровки непонятных терминов необходимо обращаться к теме об основных определениях и понятиях теории дифференциальных уравнений.
Рассмотрим линейное дифференциальное уравнение (ЛНДУ) второго порядка с постоянными коэффициентами вида y » + p · y ‘ + q · y = f ( x ) , где произвольными числами являются p и q , а имеющаяся функция f ( х ) непрерывная на интервале интегрирования x .
Перейдем к формулировке теоремы общего решения ЛНДУ.
Видео:Теорема о структуре общего решения однородной системы линейных уравненийСкачать

Теорема общего решения ЛДНУ
Общим решением, находящимся на интервале х , неоднородного дифференциального уравнения вида y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 0 ( x ) · y = f ( x ) с непрерывными коэффициентами интегрирования на x интервале f 0 ( x ) , f 1 ( x ) , . . . , f n — 1 ( x ) и непрерывной функцией f ( x ) равняется сумме общего решения y 0 , которое соответствует ЛОДУ и каким-нибудь частным решением y
, где исходным неоднородным уравнением является y = y 0 + y
Отсюда видно, что решение такого уравнения второго порядка имеет вид y = y 0 + y
. Алгоритм нахождения y 0 рассмотрен в статье о линейных однородных дифференциальных уравнениях второго порядка с постоянными коэффициентами. После чего следует переходить к определению y
Выбор частного решения ЛНДУ зависит от вида имеющейся функции f ( x ) , располагающейся в правой части уравнения. Для этого необходимо рассмотреть отдельно решения линейных неоднородных дифференциальных уравнений второго порядка при постоянных коэффициентах.
Когда f ( x ) считается за многочлен n -ой степени f ( x ) = P n ( x ) , отсюда следует, что частное решение ЛНДУ находим по формуле вида y
= Q n ( x ) · x γ , где Q n ( x ) является многочленом степени n , r – это количество нулевых корней характеристического уравнения. Значение y
является частным решением y
= f ( x ) , тогда имеющиеся коэффициенты, которые определены многочленом
Q n ( x ) , отыскиваем при помощи метода неопределенных коэффициентов из равенства y
Вычислить по теореме Коши y » — 2 y ‘ = x 2 + 1 , y ( 0 ) = 2 , y ‘ ( 0 ) = 1 4 .
Решение
Иначе говоря, необходимо перейти к частному решению линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами y » — 2 y ‘ = x 2 + 1 , которое будет удовлетворять заданным условиям y ( 0 ) = 2 , y ‘ ( 0 ) = 1 4 .
Общим решением линейного неоднородного уравнения является сумма общего решения, которое соответствует уравнению y 0 или частному решению неоднородного уравнения y
, то есть y = y 0 + y
Для начала найдем общее решение для ЛНДУ, а после чего – частное.
Перейдем к нахождению y 0 . Запись характеристического уравнения поможет найти корни. Получаем, что
k 2 — 2 k = 0 k ( k — 2 ) = 0 k 1 = 0 , k 2 = 2
Получили, что корни различные и действительные. Поэтому запишем
y 0 = C 1 e 0 x + C 2 e 2 x = C 1 + C 2 e 2 x .
. Видно, что правая часть заданного уравнения является многочленом второй степени, тогда один из корней равняется нулю. Отсюда получим, что частным решением для y
= Q 2 ( x ) · x γ = ( A x 2 + B x + C ) · x = A x 3 + B x 2 + C x , где значения А , В , С принимают неопределенные коэффициенты.
Найдем их из равенства вида y
Тогда получим, что:
‘ = x 2 + 1 ( A x 3 + B x 2 + C x ) » — 2 ( A x 3 + B x 2 + C x ) ‘ = x 2 + 1 3 A x 2 + 2 B x + C ‘ — 6 A x 2 — 4 B x — 2 C = x 2 + 1 6 A x + 2 B — 6 A x 2 — 4 B x — 2 C = x 2 + 1 — 6 A x 2 + x ( 6 A — 4 B ) + 2 B — 2 C = x 2 + 1
Приравняв коэффициенты с одинаковыми показателями степеней x , получим систему линейных выражений — 6 A = 1 6 A — 4 B = 0 2 B — 2 C = 1 . При решении любым из способов найдем коэффициенты и запишем: A = — 1 6 , B = — 1 4 , C = — 3 4 и y
= A x 3 + B x 2 + C x = — 1 6 x 3 — 1 4 x 2 — 3 4 x .
Эта запись называется общим решением исходного линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами.
Для нахождения частного решения, которое удовлетворяет условиям y ( 0 ) = 2 , y ‘ ( 0 ) = 1 4 , требуется определить значения C 1 и C 2 , исходя из равенства вида y = C 1 + C 2 e 2 x — 1 6 x 3 + 1 4 x 2 + 3 4 x .
y ( 0 ) = C 1 + C 2 e 2 x — 1 6 x 3 + 1 4 x 2 + 3 4 x x = 0 = C 1 + C 2 y ‘ ( 0 ) = C 1 + C 2 e 2 x — 1 6 x 3 + 1 4 x 2 + 3 4 x ‘ x = 0 = = 2 C 2 e 2 x — 1 2 x 2 + 1 2 x + 3 4 x = 0 = 2 C 2 — 3 4
Работаем с полученной системой уравнений вида C 1 + C 2 = 2 2 C 2 — 3 4 = 1 4 , где C 1 = 3 2 , C 2 = 1 2 .
Применив теорему Коши, имеем, что
y = C 1 + C 2 e 2 x — 1 6 x 3 + 1 4 x 2 + 3 4 x = = 3 2 + 1 2 e 2 x — 1 6 x 3 + 1 4 x 2 + 3 4 x
Ответ: 3 2 + 1 2 e 2 x — 1 6 x 3 + 1 4 x 2 + 3 4 x .
Когда функция f ( x ) представляется в виде произведения многочлена со степенью n и экспоненты f ( x ) = P n ( x ) · e a x , тогда отсюда получаем, что частным решением ЛНДУ второго порядка будет уравнение вида y
= e a x · Q n ( x ) · x γ , где Q n ( x ) является многочленом n -ой степени, а r – количеством корней характеристического уравнения, равняющиеся α .
Коэффициенты, принадлежащие Q n ( x ) находятся по равенству y
Найти общее решение дифференциального уравнения вида y » — 2 y ‘ = ( x 2 + 1 ) · e x .
Решение
Уравнение общего вида y = y 0 + y
. Указанное уравнение соответствует ЛОДУ y » — 2 y ‘ = 0 . По предыдущему примеру видно, что его корни равняются k 1 = 0 и k 2 = 2 и y 0 = C 1 + C 2 e 2 x по характеристическому уравнению.
Видно, что правой частью уравнения является x 2 + 1 · e x . Отсюда ЛНДУ находится через y
= e a x · Q n ( x ) · x γ , где Q n ( x ) , являющимся многочленом второй степени, где α = 1 и r = 0 , потому как у характеристического уравнения отсутствует корень, равный 1 . Отсюда получаем, что
= e a x · Q n ( x ) · x γ = e x · A x 2 + B x + C · x 0 = e x · A x 2 + B x + C .
А , В , С являются неизвестными коэффициентами, которые можно найти по равенству y
‘ = e x · A x 2 + B x + C ‘ = e x · A x 2 + B x + C + e x · 2 A x + B = = e x · A x 2 + x 2 A + B + B + C y
‘ ‘ = e x · A x 2 + x 2 A + B + B + C ‘ = = e x · A x 2 + x 2 A + B + B + C + e x · 2 A x + 2 A + B = = e x · A x 2 + x 4 A + B + 2 A + 2 B + C
‘ = ( x 2 + 1 ) · e x ⇔ e x · A x 2 + x 4 A + B + 2 A + 2 B + C — — 2 e x · A x 2 + x 2 A + B + B + C = x 2 + 1 · e x ⇔ e x · — A x 2 — B x + 2 A — C = ( x 2 + 1 ) · e x ⇔ — A x 2 — B x + 2 A — C = x 2 + 1 ⇔ — A x 2 — B x + 2 A — C = 1 · x 2 + 0 · x + 1
Показатели при одинаковых коэффициентах приравниваем и получаем систему линейных уравнений. Отсюда и находим А , В , С :
— A = 1 — B = 0 2 A — C = 1 ⇔ A = — 1 B = 0 C = — 3
Ответ: видно, что y
= e x · ( A x 2 + B x + C ) = e x · — x 2 + 0 · x — 3 = — e x · x 2 + 3 является частным решением ЛНДУ, а y = y 0 + y = C 1 e 2 x — e x · x 2 + 3 — общим решением для неоднородного дифуравнения второго порядка.
Когда функция записывается как f ( x ) = A 1 cos ( β x ) + B 1 sin β x , а А 1 и В 1 являются числами, тогда частным решением ЛНДУ считается уравнение вида y
= A cos β x + B sin β x · x γ , где А и В считаются неопределенными коэффициентами, а r числом комплексно сопряженных корней, относящихся к характеристическому уравнению, равняющимся ± i β . В этом случае поиск коэффициентов проводится по равенству y
Найти общее решение дифференциального уравнения вида y » + 4 y = cos ( 2 x ) + 3 sin ( 2 x ) .
Решение
Перед написанием характеристического уравнения находим y 0 . Тогда
k 2 + 4 = 0 k 2 = — 4 k 1 = 2 i , k 2 = — 2 i
Имеем пару комплексно сопряженных корней. Преобразуем и получим:
y 0 = e 0 · ( C 1 cos ( 2 x ) + C 2 sin ( 2 x ) ) = C 1 cos 2 x + C 2 sin ( 2 x )
Корни из характеристического уравнения считаются сопряженной парой ± 2 i , тогда f ( x ) = cos ( 2 x ) + 3 sin ( 2 x ) . Отсюда видно, что поиск y
будет производиться из y
= ( A cos ( β x ) + B sin ( β x ) · x γ = ( A cos ( 2 x ) + B sin ( 2 x ) ) · x . Неизвестные коэффициенты А и В будем искать из равенства вида y
= cos ( 2 x ) + 3 sin ( 2 x ) .
‘ = ( ( A cos ( 2 x ) + B sin ( 2 x ) · x ) ‘ = = ( — 2 A sin ( 2 x ) + 2 B cos ( 2 x ) ) · x + A cos ( 2 x ) + B sin ( 2 x ) y
» = ( ( — 2 A sin ( 2 x ) + 2 B cos ( 2 x ) ) · x + A cos ( 2 x ) + B sin ( 2 x ) ) ‘ = = ( — 4 A cos ( 2 x ) — 4 B sin ( 2 x ) ) · x — 2 A sin ( 2 x ) + 2 B cos ( 2 x ) — — 2 A sin ( 2 x ) + 2 B cos ( 2 x ) = = ( — 4 A cos ( 2 x ) — 4 B sin ( 2 x ) ) · x — 4 A sin ( 2 x ) + 4 B cos ( 2 x )
Тогда видно, что
= cos ( 2 x ) + 3 sin ( 2 x ) ⇔ ( — 4 A cos ( 2 x ) — 4 B sin ( 2 x ) ) · x — 4 A sin ( 2 x ) + 4 B cos ( 2 x ) + + 4 ( A cos ( 2 x ) + B sin ( 2 x ) ) · x = cos ( 2 x ) + 3 sin ( 2 x ) ⇔ — 4 A sin ( 2 x ) + 4 B cos ( 2 x ) = cos ( 2 x ) + 3 sin ( 2 x )
Необходимо приравнять коэффициенты синусов и косинусов. Получаем систему вида:
— 4 A = 3 4 B = 1 ⇔ A = — 3 4 B = 1 4
= ( A cos ( 2 x ) + B sin ( 2 x ) · x = — 3 4 cos ( 2 x ) + 1 4 sin ( 2 x ) · x .
Ответ: общим решением исходного ЛНДУ второго порядка с постоянными коэффициентами считается
= = C 1 cos ( 2 x ) + C 2 sin ( 2 x ) + — 3 4 cos ( 2 x ) + 1 4 sin ( 2 x ) · x
Когда f ( x ) = e a x · P n ( x ) sin ( β x ) + Q k ( x ) cos ( β x ) , тогда y
= e a x · ( L m ( x ) sin ( β x ) + N m ( x ) cos ( β x ) · x γ . Имеем, что r – это число комплексно сопряженных пар корней, относящихся к характеристическому уравнению, равняются α ± i β , где P n ( x ) , Q k ( x ) , L m ( x ) и N m ( x ) являются многочленами степени n , k , т , m , где m = m a x ( n , k ) . Нахождение коэффициентов L m ( x ) и N m ( x ) производится, исходя из равенства y
Найти общее решение y » + 3 y ‘ + 2 y = — e 3 x · ( ( 38 x + 45 ) sin ( 5 x ) + ( 8 x — 5 ) cos ( 5 x ) ) .
Решение
По условию видно, что
α = 3 , β = 5 , P n ( x ) = — 38 x — 45 , Q k ( x ) = — 8 x + 5 , n = 1 , k = 1
Тогда m = m a x ( n , k ) = 1 . Производим нахождение y 0 , предварительно записав характеристическое уравнение вида:
k 2 — 3 k + 2 = 0 D = 3 2 — 4 · 1 · 2 = 1 k 1 = 3 — 1 2 = 1 , k 2 = 3 + 1 2 = 2
Получили, что корни являются действительными и различными. Отсюда y 0 = C 1 e x + C 2 e 2 x . Далее необходимо искать общее решение, исходя из неоднородного уравнения y
= e α x · ( L m ( x ) sin ( β x ) + N m ( x ) cos ( β x ) · x γ = = e 3 x · ( ( A x + B ) cos ( 5 x ) + ( C x + D ) sin ( 5 x ) ) · x 0 = = e 3 x · ( ( A x + B ) cos ( 5 x ) + ( C x + D ) sin ( 5 x ) )
Известно, что А , В , С являются коэффициентами, r = 0 , потому как отсутствует пара сопряженных корней, относящихся к характеристическому уравнению с α ± i β = 3 ± 5 · i . Данные коэффициенты находим из полученного равенства:
= — e 3 x ( ( 38 x + 45 ) sin ( 5 x ) + ( 8 x — 5 ) cos ( 5 x ) ) ⇔ ( e 3 x ( ( A x + B ) cos ( 5 x ) + ( C x + D ) sin ( 5 x ) ) ) » — — 3 ( e 3 x ( ( A x + B ) cos ( 5 x ) + ( C x + D ) sin ( 5 x ) ) ) = — e 3 x ( ( 38 x + 45 ) sin ( 5 x ) + ( 8 x — 5 ) cos ( 5 x ) )
Нахождение производной и подобных слагаемых дает
— e 3 x · ( ( 15 A + 23 C ) · x · sin ( 5 x ) + + ( 10 A + 15 B — 3 C + 23 D ) · sin ( 5 x ) + + ( 23 A — 15 C ) · x · cos ( 5 x ) + ( — 3 A + 23 B — 10 C — 15 D ) · cos ( 5 x ) ) = = — e 3 x · ( 38 · x · sin ( 5 x ) + 45 · sin ( 5 x ) + + 8 · x · cos ( 5 x ) — 5 · cos ( 5 x ) )
После приравнивания коэффициентов получаем систему вида
15 A + 23 C = 38 10 A + 15 B — 3 C + 23 D = 45 23 A — 15 C = 8 — 3 A + 23 B — 10 C — 15 D = — 5 ⇔ A = 1 B = 1 C = 1 D = 1
Из всего следует, что
= e 3 x · ( ( A x + B ) cos ( 5 x ) + ( C x + D ) sin ( 5 x ) ) = = e 3 x · ( ( x + 1 ) cos ( 5 x ) + ( x + 1 ) sin ( 5 x ) )
Ответ: теперь получено общее решение заданного линейного уравнения:
= = C 1 e x + C 2 e 2 x + e 3 x · ( ( x + 1 ) cos ( 5 x ) + ( x + 1 ) sin ( 5 x ) )
Видео:Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентамСкачать

Алгоритм решения ЛДНУ
Любой другой вид функции f ( x ) для решения предусматривает соблюдение алгоритма решения:
- нахождение общего решения соответствующего линейного однородного уравнения, где y 0 = C 1 ⋅ y 1 + C 2 ⋅ y 2 , где y 1 и y 2 являются линейно независимыми частными решениями ЛОДУ, С 1 и С 2 считаются произвольными постоянными;
- принятие в качестве общего решения ЛНДУ y = C 1 ( x ) ⋅ y 1 + C 2 ( x ) ⋅ y 2 ;
- определение производных функции через систему вида C 1 ‘ ( x ) + y 1 ( x ) + C 2 ‘ ( x ) · y 2 ( x ) = 0 C 1 ‘ ( x ) + y 1 ‘ ( x ) + C 2 ‘ ( x ) · y 2 ‘ ( x ) = f ( x ) , а нахождение функций C 1 ( x ) и C 2 ( x ) посредствам интегрирования.
Найти общее решение для y » + 36 y = 24 sin ( 6 x ) — 12 cos ( 6 x ) + 36 e 6 x .
Решение
Переходим к написанию характеристического уравнения, предварительно записав y 0 , y » + 36 y = 0 . Запишем и решим:
k 2 + 36 = 0 k 1 = 6 i , k 2 = — 6 i ⇒ y 0 = C 1 cos ( 6 x ) + C 2 sin ( 6 x ) ⇒ y 1 ( x ) = cos ( 6 x ) , y 2 ( x ) = sin ( 6 x )
Имеем, что запись общего решения заданного уравнения получит вид y = C 1 ( x ) · cos ( 6 x ) + C 2 ( x ) · sin ( 6 x ) . Необходимо перейти к определению производных функций C 1 ( x ) и C 2 ( x ) по системе с уравнениями:
C 1 ‘ ( x ) · cos ( 6 x ) + C 2 ‘ ( x ) · sin ( 6 x ) = 0 C 1 ‘ ( x ) · ( cos ( 6 x ) ) ‘ + C 2 ‘ ( x ) · ( sin ( 6 x ) ) ‘ = 0 ⇔ C 1 ‘ ( x ) · cos ( 6 x ) + C 2 ‘ ( x ) · sin ( 6 x ) = 0 C 1 ‘ ( x ) ( — 6 sin ( 6 x ) + C 2 ‘ ( x ) ( 6 cos ( 6 x ) ) = = 24 sin ( 6 x ) — 12 cos ( 6 x ) + 36 e 6 x
Необходимо произвести решение относительно C 1 ‘ ( x ) и C 2 ‘ ( x ) при помощи любого способа. Тогда запишем:
C 1 ‘ ( x ) = — 4 sin 2 ( 6 x ) + 2 sin ( 6 x ) cos ( 6 x ) — 6 e 6 x sin ( 6 x ) C 2 ‘ ( x ) = 4 sin ( 6 x ) cos ( 6 x ) — 2 cos 2 ( 6 x ) + 6 e 6 x cos ( 6 x )
Каждое из уравнений следует проинтегрировать . Тогда запишем получившиеся уравнения:
C 1 ( x ) = 1 3 sin ( 6 x ) cos ( 6 x ) — 2 x — 1 6 cos 2 ( 6 x ) + + 1 2 e 6 x cos ( 6 x ) — 1 2 e 6 x sin ( 6 x ) + C 3 C 2 ( x ) = — 1 6 sin ( 6 x ) cos ( 6 x ) — x — 1 3 cos 2 ( 6 x ) + + 1 2 e 6 x cos ( 6 x ) + 1 2 e 6 x sin ( 6 x ) + C 4
Отсюда следует, что общее решение будет иметь вид:
y = 1 3 sin ( 6 x ) cos ( 6 x ) — 2 x — 1 6 cos 2 ( 6 x ) + + 1 2 e 6 x cos ( 6 x ) — 1 2 e 6 x sin ( 6 x ) + C 3 · cos ( 6 x ) + + — 1 6 sin ( 6 x ) cos ( 6 x ) — x — 1 3 cos 2 ( 6 x ) + + 1 2 e 6 x cos ( 6 x ) + 1 2 e 6 x sin ( 6 x ) + C 4 · sin ( 6 x ) = = — 2 x · cos ( 6 x ) — x · sin ( 6 x ) — 1 6 cos ( 6 x ) + + 1 2 e 6 x + C 3 · cos ( 6 x ) + C 4 · sin ( 6 x )
Ответ: y = y 0 + y
= — 2 x · cos ( 6 x ) — x · sin ( 6 x ) — 1 6 cos ( 6 x ) + + 1 2 e 6 x + C 3 · cos ( 6 x ) + C 4 · sin ( 6 x )
Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Теорема о структуре общего решения ЛОДУ (док). Понятие ФСР
Опр: Система n линейно-независимого решения ЛОДУ n-го порядка называется ФСР
Теорема о структуре общего решения ЛОДУ
Если функции y1(х), y2(х), … ,yn(х) – образует ФСР ЛОДУ у ( n ) + P1y ( n -1) +…+ Pn-1 y’ + Pn y = 0 , то y(х) = C1y1(x) + C2y2(x) + … + Cnyn(x) = 
Из теоремы о неравенстве нулю вронскиана линейно-независимых решений ЛОДУ:
Если n решений y1, y2, … ,yn ЛОДУ (2) и они линейно-независимы, на интервале (а,b) то определитель Вронского не может обращаться в ноль (0) ни в одной точке х 
ð что (4) являются решением у ( n ) + P1y ( n -1) +…+ Pn-1 y’ + Pn y = 0
остается доказать, что можно подобрать const-ты то С1, С2, … Сn , таким образом что функция (4) удовлетворяет любой системе начальных условий [н.у.]
Задаем н.у. , при x0 

Определителем этой системы является определитель Вронского
W[y1, y2, … ,yn] 
Построим 
согласно свойству (если y1) α1y1 + α2y2 + …+ αnyn = 0 причем хотя бы одно hi 


1) максимальное число линейно-независимых решение ЛОДУ, коэффициенты непрерывны на (a,b) равно порядку этого уравнения.
2) независимо от н.у. все другие решения таких уравнений ЛОДУ является линейной комбинацией этих независимых решений (решений ФС)
3) Пространство решений ЛОДУ n-го порядка имеет базис из n-векторов, т.е. пространство n-мерное.
4) Для решения ЛОДУ n-го порядка необходимо найти ФСР. Общее решение получается как линейная комбинация решений ФС.
11. Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентами. Вид частных решений, характеристическое уравнение(×)
ЛОДУ с постоянными коэффициентами
у ( n ) + P1y ( n -1) +…+ Pn-1 y’ + Pn y = 0, где все Pi (i= 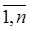
будем искать частное решение y=e kx , к – неизвестная постоянная
y ( n ) =k ( n ) e kx
k (n) e kx + P1k (n-1) e kx + … + Pne kx = e kx (k (n) + P1k (n-1) + … + Pn) = 0
e kx 
ð y=e kx — решение ДУ
(1) – характеристическое уравнение для ЛОДу с постоянными коэффициентами, выражения слева характеристический многочлен.
Решением характеристич уравнения (1) дает систему частных решений ЛОДу, структура ФСР зависит от вида корней характер уравнения.
(1) – алгебраическое уравнение n-ой степени, может иметь не более, чем n корней, обознач-м эти корни характеристического уравнения через k1 ,k2 …kn
1)все корни хар-го уранения вещественны и различны
2)все корни различны, но среди них есть комплексные
3)среди действительных корней имеются кратные
4)среди комплексных корней есть кратные
Общий алгоритм решения ЛОДу с постоянным коэффициентом
1) составим характер уравнение : y=e kx , k ( n ) + P1k ( n -1) + … + Pn = 0
2) найти корни характер уравнения k1 ,k2 …kn
3) по характеру корней находим частное линейно-независимое решение по таблице 1
4) подставляем частное решение 
| № | Вид корня | Соответственное решение |
| Действ корень кратности 1 | e kx | |
Пара корней a  bi;кратнос 1 bi;кратнос 1 | e а x cosbx , e а x sinbx | |
| Действит корень кратност α | e kx , хe kx , х 2 e kx , х 3 e kx ,…, х α-1 e kx | |
Пара сопряж корней α a  bi bi | e а x cosbx , e а x sinbx хe а x cosbx , хe а x sinbx х 2 e а x cosbx , х 2 e а x sinbx х α-1 e а x cosbx , х α-1 e а x sinbx |
13. Линейные неоднородные дифференциальные уравнения n-го порядка. Теорема о структуре общего решения (док. для n=2). Теорема о суперпозиции решений (док. для n=2).
у ( n ) + P1y ( n -1) +…+ Pn-1 y’ + Pn y = f(x) (1) Pi – непрерывна на отрезке (a,b)
Теорема о структуре общего решения ЛНДУ
Общее решение ЛНДУ есть сумма частного решения и общего решения соответственного ему однородного уравнения
Для уравнения 2-го порядка ( но теорема применима для уравнений любого порядка)
Обозначим у*(х) – частное решение ЛНДУ

(2) у= у*+ 
Дважды дифференцируем функцию (2) и подставляем у, y’,y” в (1’)
у*”(x) + 


= [у*”(x)+ P1(x) у*’(x)+ P2(x) у*(x)] + [ 



C1C2 – подбираем так, чтобы они удовлетворяли начальным условиям


Линейная неоднородная система, определитель этой системы, определитель Вронского
W[y1, y2]≠0 =>система имеет единственное решение при любых 


Теорема2 принцип суперпозиции (принцип сложения решений)
Если функция yi(x) является решением ЛНДУ
(3) y ( n ) + P1y ( n -1) + … + Pny = fi(x) то функция 
Подставим y, y’, y”, в (4) , учитываем что y1 y2 решение соответственного уравнения (3)
14. Линейные неоднородные дифференциальные уравнения n-го порядка с постоянными коэффициентами. Метод неопределенных коэффициентов для уравнений со специальной правой частью. Метод вариации произвольных постоянных (вывод рабочей формулы).
Рассмотрим ЛНДУ с постоянными коэф-ми.
Метод неопр-х коэф-в можно применять если правое ур-е имеет следующий вид: f(x)= 



| № | Вид правой части (f(x)) | Корни харак-го уравнения | Вид частного решения y* |
P  (x)=A (x)=A  x x  +A +A  x x  +… +A +… +A  x+ A x+ A  | а) число 0 не явл-ся корнем хар-го ур-я б) число 0 явл-ся корнем хар-го ур-я кратности  | а) y*=b  x x  +b +b  x x  +…+ +b +…+ +b  б) y*=x б) y*=x  (B (B  x x  +B +B  x x  +… +B +… +B  ) ) | |
P  (x)e (x)e  = e = e  ( A ( A  x x  + +A + +A  x x  +…+A +…+A  x+ A x+ A  ) p-действ-е число ) p-действ-е число | а) число p не явл-ся корнем хар-го ур-я б) число p явл-ся корнем хар-го ур-я кратности  | a) y*= e  ( b ( b  x x  +b +b  x x  +…+ +b +…+ +b  ) б) y*= e ) б) y*= e  x x  ( b ( b  x x  +b +b  x x  +…+ +b +…+ +b  ) ) | |
P  (x)cosgx+Q (x)cosgx+Q  (x)singx g-число (x)singx g-число | а) число  gi-не явл-ся корнем хар-го ур-я б) число gi-не явл-ся корнем хар-го ур-я б) число  gi-явл-ся корнем хар-го ур-я кратности gi-явл-ся корнем хар-го ур-я кратности  | а) y*=  (x)cosgx+ (x)cosgx+  (x)singx б) y*=x (x)singx б) y*=x  ( (  (x)cosgx+ (x)cosgx+  (x)singx) (x)singx) | |
P  (x)e (x)e  cosgx+ Q cosgx+ Q  (x)e (x)e  singx singx | а) число  gi-не явл-ся корнем хар-го ур-я б) число gi-не явл-ся корнем хар-го ур-я б) число  gi-явл-ся корнем хар-го ур-я кратности gi-явл-ся корнем хар-го ур-я кратности  | а) y*=  (x) e (x) e  cosgx+ cosgx+  (x)singx б) y*= x (x)singx б) y*= x  ( (  (x) e (x) e  cosgx+ + cosgx+ +  (x)singx) (x)singx) |
Замечание к таблице: 1)степени многоч-ов P и Q в случаях (3) и (4) можно считать одинаковыми, если они различны, то коэф-ты при недостающих степенях одного из многоч-ов можно считать=0.
2)правая часть ур-я может содержать несколько слагаемых; в этом случае сост-ся из неск-ких слагаемых в соотв-ии с Теоремой о неравенстве нулю вронскиана линейно-независимых решений ЛОДУ
Метод вариации производных постоянных(метод Лагранджа).
Метод позволяет найти решение ДУ независимо от вида правой части, когда известно общее решение соотв-го однородного ДУ.
Например: ДУ 2-го порядка. Пусть y”+P 



y”+P 









y*= C 











Пусть C 


















Подставим y*, y* ’, y* ” в (1): C 






















Объясним два условия и (3):
 |
C’ 



C’ 



Неопр-е ф-ии C’ 

Определитель этой системы: W[y 






C 




Для ЛНДУ n-го порядка ф-ии C 
C’ 





C’ 





C’ 








C’ 








Алгоритм решения ЛНДУ
1) найти ФСР однородного уравнения и записать его общее решение (ОУ)
2) записать частное решение неоднородного ДУ в форме общего решения ОУ считая Ci=Ci (x)
3) построить систему для определения Ci ‘(x) – решить ее
4) найти Ci (x) и подставить их в общее решение НДУ
Видео:Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

Теорема о структуре общего решения линейного однородного диф. Уравнения n-го порядка. Характеристическое уравнение
Линейным однородным уравнением n-го порядка называют уравнение вида

Частные решения y1=y1(x) , y2=y2(x), …, yn=yn(x) уравнения образуют фундаментальную систему некотором интервале , если всюду в этом интервале отличен от нуля определитель Вронского

Ø С постоянными коэффициентамит.е.
a – заданные действительные числа
Общее решение будет y=C1y1(x)+C2y2(x)+…+Cnyn(x)=0 y1(x) ,y2(x),…, yn(x) — частные решения уравнения, образующие фундаментальную систему в рассматриваемом интервале т.е. всюду отличен от нуля определитель Вронского. Частные решения будем искать в виде y=e kx
Подставив в уравнение и преобразовав получим характеристическое уравнение
Уравнение имеет n решений. Эти корни будут действительными (простыми или кратными) или комплексными (простыми или кратными). Если комплексное число α+iβ является корнем, то сопряжённое число α —iβ тоже является корнем, так как уравнение имеет действительные коэффициенты.
· Каждому простому действительному корню k характеристического уравнения соответствует одно решение e kx исходного уравнения .
· Каждому действительному корню k кратности r характеристического уравнения отвечают r решений исходного уравнения вида e kx , xe kx , x 2 e kx , …, x r -1 e kx исходного уравнения
· Каждой паре комплексно сопряжённых корней k1= α+iβ и k2= α-iβ характеристического уравнения соответствует одна пара частных решений исходного уравнения
e αx cosβx и ie αx sinβx
· Каждой паре комплексно сопряжённых корней кратности μ k1= α+iβ и k2= α-iβ характеристического уравнения отвечают μ пар решений исходного уравнения
11. Теорема о структуре общего решения линейного неоднородного диф. Уравнения второго порядка.
Общее решение данного уравнения представляется в виде суммы какого-либо частного решения y * =y * (x) этого уравнения и и общего решения 
y= y * + 
Для доказательства нужно два факта:
1) Сумма y * + 
Подставляя данную сумму в исходное уравнение получим
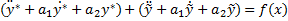

2) Для любых начальных условий можно подобрать такие значения постоянных С1 и С2 , при которых функция y= y * (x) +C1y1(x)+C2y2(x) будет удовлетворять этим начальным условиям.
Через определитель Вронского начальных условий
12. Метод вариации произвольных постоянных для нахождения частного решения линейного неоднородного уравнения второго порядка.
y * = C1(x)y1 +C2(x)y2 , где C1(x) и C2(x) – новые искомые функции. Одну из них можно выбрать произвольно или наложить на неё дополнительные требования, а вторую выбрать так чтобы функция y * = C1(x)y1 +C2(x)y2 была решением неоднородного уравнения.
Возьмём производную и получим 
Тогда 
Но поскольку y1 и y2 – решения однородного уравнения суммы в скобках обращаются нуль получаем

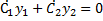

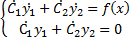








🎬 Видео
Неоднородная система линейных уравненийСкачать

✓Дифференцируемая функция. Дифференциал | матан #032 | Борис ТрушинСкачать

19. Общее решение линейного уравненияСкачать

Задача Коши ДУ I п. 1. Caushy`s ProblemСкачать

19. Метод вариации произвольных постоянных. Линейные неоднородные диф уравнения 2-го порядкаСкачать

Встреча с Путиным в общежитии МГУ на Воробьевых горах!Скачать

15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

18. Линейные неоднородные дифференциальные уравнения 2 порядка с постоянными коэффициентами. часть 3Скачать

15. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентамиСкачать

Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.Скачать