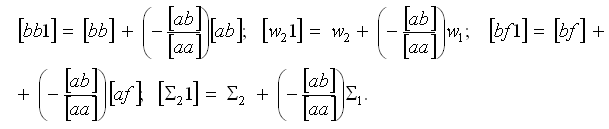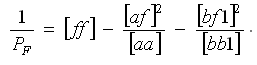Решение системы нормальных уравнений по схеме гаусса

Решение нормальных уравнений выполняют в схеме Гаусса (табл. 2).

Для вычисления преобразованных коэффициентов нужно постоянный множитель (-[ab]/[aa]), стоящий в первой элиминационной строке над квадратичным коэффициентом [bb], умножать по строке на вышестоящие числа и складывать каждый раз с элементами второго нормального уравнения

Схема решения нормальных уравнений коррелат (r = 2; π_i = 1)

Правило развертывания символа Гаусса: «Cимвол развертывается в разность. Уменьшаемое — тот же символ, но со значком на единицу меньше. Вычитаемое — дробь. Знаменатель дроби — квадратичный коэффициент, буква которого соответствует номеру развертываемого символа. Числитель — произведение двух символов, каждый из которых получен заменой буквы уменьшаемого на букву знаменателя».

Последняя коррелата равна числу, стоящему в столбце w последней элиминационной строки. Коррелата к₁ вычисляется с использованием чисел первой элиминационной строки от столбца w налево.

[vv] или [pvv] — для неравноточных измерений — получают как сумму произведений чисел элиминационных строк столбца w на вышестоящие числа того же столбца, знак «минус» отбрасывают:

(16)

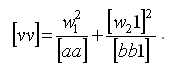
Обратный вес функции 1/P_F получают, как сумму [ff] и произведений чисел элиминационных строк столбца F на вышестоящие числа того же столбца:

Заключительный контроль решения нормальных уравнений осуществляется подстановкой коррелат в суммарное уравнение:

Видео:Решение системы уравнений методом ГауссаСкачать

Метод Гаусса онлайн

Данный онлайн калькулятор находит решение системы линейных уравнений (СЛУ) методом Гаусса. Дается подробное решение. Для вычисления выбирайте количество переменных и количество уравнений. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить.»

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Видео:Решение системы уравнений методом Гаусса 4x4Скачать

Метод Гаусса

Метод Гаусса − это метод перехода от исходной системы линейных уравнений (при помощи эквивалентных преобразований) к системе, которая решается проще, чем исходная система.

Эквивалентными преобразованиями системы линейных уравнений являются:

• перемена местами двух уравнений в системе,
• умножение какого-либо уравнения в системе на ненулевое действительное число,
• прибавление к одному уравнению другого уравнения, умноженного на произвольное число.

Рассмотрим систему линейных уравнений:

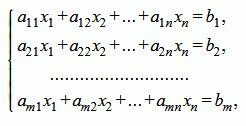(1)

Запишем систему (1) в матричном виде:

(3)

A-называется матрица коэффициентов системы, b − правая часть ограничений, x− вектор переменных, которую нужно найти. Пусть rang(A)=p.

Эквивалентные преобразования не меняют ранг матрицы коэффициентов и ранг расширеннной матрицы системы. Не меняется также множество решений системы при эквивалентных преобразованиях. Суть метода Гаусса заключается в приведении матрцы коэффициентов A к диагональному или ступенчатому.

Построим расшренную матрицу системы:

(4)

Предположим a₁₁≠0. Если это не так, то можно поменять местами эту строку со строкой с ненулевым элементом в столбце 1 (если нет таких строк, то переходим к следующему столбцу). Обнуляем все элементы столбца 1 ниже ведущего элемента a₁₁. Для этого сложим строки 2,3, . m со строкой 1, умноженной на −a₂₁/a₁₁, −a₃₁/a₁₁, . −a_m1/a₁₁, соответственно. Тогда (4) примет следующий вид:

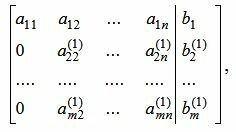(5)

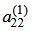
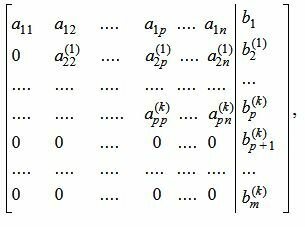На следующем этапе обнуляем все элементы столбца 2, ниже элемента . Если данный элемент нулевой, то эту строку меняем местами со строкой, лежащий ниже данной строки и имеющий ненулевой элемент во втором столбце. Далее обнуляем все элементы столбца 2 ниже ведущего элемента a₂₂. Для этого сложим строки 3, . m со строкой 2, умноженной на −a₃₂/a₂₂, . −a_m2/a₂₂, соответственно. Продолжая процедуру, получим матрицу диагонального или ступенчатого вида. Пусть полученная расширенная матрица имеет вид:

(6)

Обратим внимание на последние строки. Если 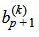. равны нулю, то система линейных уравнений имеет решение, если же хотя бы один из этих чисел отлично от нуля, то система несовместна. Иными словами, система (2) совместна тогда и только тогда, когда ранг матрицы A навен рангу расширенной матрицы (A|b).

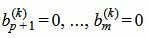
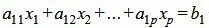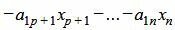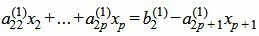Пусть . Тогда

(7)

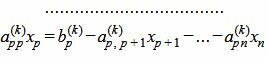Так как rangA=rang(A|b), то множество решений (7) есть (n−p)− многообразие. Следовательно n−p неизвестных можно выбрать произвольно. Остальные неизвестные из системы (7) вычисляются так. Из последнего уравнения выражаем x_p через остальные переменные и вставляем в предыдущие выражения. Далее из предпоследнего уравнения выражаем x_p−1 через остальные переменные и вставляем в предыдущие выражения и т.д. Рассмотрим метод Гаусса на конкретных примерах.

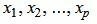
Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Примеры решения системы линейных уравнений методом Гаусса

Пример 1. Найти общее решение системы линейных уравнений методом Гаусса:

Матричный вид записи: Ax=b, где

Для решения системы, запишем расширенную матрицу:

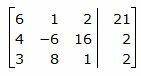Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Исключим элементы 1-го столбца матрицы ниже элемента a_{1 1}. Для этого сложим строки 2,3 со строкой 1, умноженной на -2/3,-1/2 соответственно:

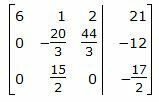Исключим элементы 2-го столбца матрицы ниже элемента a2 2. Для этого сложим строку 3 со строкой 2, умноженной на 9/8:

Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

Из вышеизложенной таблицы можно записать:

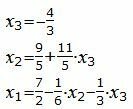Подставив верхние выражения в нижние, получим решение.

,,.

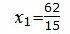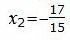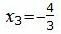Пример 2. Найти общее решение системы линейных уравнений методом Гаусса:

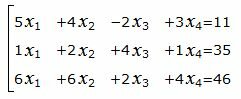Матричный вид записи: Ax=b, где

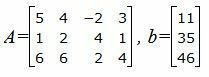Для решения системы, построим расширенную матрицу:

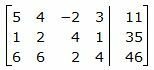Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Исключим элементы 1-го столбца матрицы ниже элемента a₁₁. Для этого сложим строки 2,3 со строкой 1, умноженной на -1/5,-6/5 соответственно:

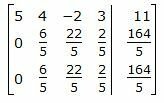Исключим элементы 2-го столбца матрицы ниже элемента a₂₂. Для этого сложим строку 3 со строкой 2, умноженной на -1:

Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

Выразим переменные x₁, x₂ относительно остальных переменных.

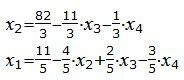где x₃, x₄− произвольные действительные числа.

Подставив верхние выражения в нижние, получим решение.

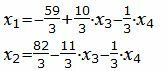где x₃, x₄− произвольные действительные числа.

Векторный вариант решения:

Запишем вышеизложенное решение, представив свободные переменные в виде тождеств:

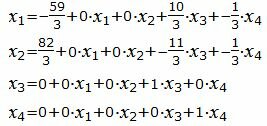Тогда векторное решение можно представить так:

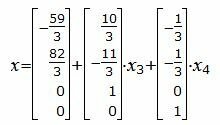где x₃, x₄− произвольные действительные числа.

Видео:Решение системы уравнений методом Гаусса. Бесконечное множество решенийСкачать

Метода Гаусса: примеры решения СЛАУ

В данной статье мы:

• дадим определение методу Гаусса,
• разберем алгоритм действий при решении линейных уравнений, где количество уравнений совпадает c количеством неизвестных переменных, а определитель не равен нулю;
• разберем алгоритм действий при решении СЛАУ с прямоугольной или вырожденной матрицей.

Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Метод Гаусса — что это такое?

Метод Гаусса — это метод, который применяется при решении систем линейных алгебраических уравнений и имеет следующие преимущества:

• отсутствует необходимость проверять систему уравнений на совместность;
• есть возможность решать системы уравнений, где:
• количество определителей совпадает с количеством неизвестных переменных;
• количество определителей не совпадает с количеством неизвестных переменных;
• определитель равен нулю.
• результат выдается при сравнительно небольшом количестве вычислительных операций.

Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Основные определения и обозначения

Есть система из р линейных уравнений с n неизвестными ( p может быть равно n ):

a 11 x 1 + a 12 x 2 + . . . + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + . . . + a 2 n x n = b 2 ⋯ a p 1 x 1 + a p 2 x 2 + . . . + a p n x n = b p ,

где x 1 , x 2 , . . . . , x n — неизвестные переменные, a i j , i = 1 , 2 . . . , p , j = 1 , 2 . . . , n — числа (действительные или комплексные), b 1 , b 2 , . . . , b n — свободные члены.

Если b 1 = b 2 = . . . = b n = 0 , то такую систему линейных уравнений называют однородной, если наоборот — неоднородной.

Решение СЛАУ — совокупность значения неизвестных переменных x 1 = a 1 , x 2 = a 2 , . . . , x n = a n , при которых все уравнения системы становятся тождественными друг другу.

Совместная СЛАУ — система, для которой существует хотя бы один вариант решения. В противном случае она называется несовместной.

Определенная СЛАУ — это такая система, которая имеет единственное решение. В случае, если решений больше одного, то такая система будет называться неопределенной.

Координатный вид записи:

a 11 x 1 + a 12 x 2 + . . . + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + . . . + a 2 n x n = b 2 ⋯ a p 1 x 1 + a p 2 x 2 + . . . + a p n x n = b p

Матричный вид записи: A X = B , где

A = a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋯ ⋯ ⋯ ⋯ a p 1 a p 2 ⋯ a p n — основная матрица СЛАУ;

X = x 1 x 2 ⋮ x n — матрица-столбец неизвестных переменных;

B = b 1 b 2 ⋮ b n — матрица свободных членов.

Расширенная матрица — матрица, которая получается при добавлении в качестве ( n + 1 ) столбца матрицу-столбец свободных членов и имеет обозначение Т .

T = a 11 a 12 ⋮ a 1 n b 1 a 21 a 22 ⋮ a 2 n b 2 ⋮ ⋮ ⋮ ⋮ ⋮ a p 1 a p 2 ⋮ a p n b n

Вырожденная квадратная матрица А — матрица, определитель которой равняется нулю. Если определитель не равен нулю, то такая матрица, а потом называется невырожденной.

Видео:Решение системы линейных уравнений методом ГауссаСкачать

Описание алгоритма использования метода Гаусса для решения СЛАУ с равным количеством уравнений и неизвестных (обратный и прямой ход метода Гаусса)

Для начала разберемся с определениями прямого и обратного ходов метода Гаусса.

Прямой ход Гаусса — процесс последовательного исключения неизвестных.

Обратный ход Гаусса — процесс последовательного нахождения неизвестных от последнего уравнения к первому.

Алгоритм метода Гаусса:

Решаем систему из n линейных уравнений с n неизвестными переменными:

a 11 x 1 + a 12 x 2 + a 13 x 3 + . . . + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + a 23 x 3 + . . . + a 2 n x n = b 2 a 31 x 1 + a 32 x 2 + a 33 x 3 + . . . + a 3 n x n = b 3 ⋯ a n 1 x 1 + a n 2 x 2 + a n 3 x 3 + . . . + a n n x n = b n

Определитель матрицы не равен нулю.

1. a 11 не равен нулю — всегда можно добиться этого перестановкой уравнений системы;
2. исключаем переменную x 1 из всех уравнений систему, начиная со второго;
3. прибавим ко второму уравнению системы первое, которое умножено на — a 21 a 11 , прибавим к третьему уравнению первое умноженное на — a 21 a 11 и т.д.

После проведенных действий матрица примет вид:

a 11 x 1 + a 12 x 2 + a 13 x 3 + . . . + a 1 n x n = b 1 a ( 1 ) 22 x 2 + a ( 1 ) 23 x 3 + . . . + a ( 1 ) 2 n x n = b ( 1 ) 2 a ( 1 ) 32 x 2 + a ( 1 ) 33 x 3 + . . . + a ( 1 ) 3 n x n = b ( 1 ) 3 ⋯ a ( 1 ) n 2 x 2 + a ( 1 ) n 3 x 3 + . . . + a ( 1 ) n n x n = b ( 1 ) n ,

где a i j ( 1 ) = a i j + a 1 j ( — a i 1 a 11 ) , i = 2 , 3 , . . . , n , j = 2 , 3 , . . . , n , b i ( 1 ) = b i + b 1 ( — a i 1 a 11 ) , i = 2 , 3 , . . . , n .

Далее производим аналогичные действия с выделенной частью системы:

a 11 x 1 + a 12 x 2 + a 13 x 3 + . . . + a 1 n x n = b 1 a ( 1 ) 22 x 2 + a ( 1 ) 23 x 3 + . . . + a ( 1 ) 2 n x n = b ( 1 ) 2 a ( 1 ) 32 x 2 + a ( 1 ) 33 x 3 + . . . + a ( 1 ) 3 n x n = b ( 1 ) 3 ⋯ a ( 1 ) n 2 x 2 + a ( 1 ) n 3 x 3 + . . . + a ( 1 ) n n x n = b ( 1 ) n

Считается, что a 22 ( 1 ) не равна нулю. Таким образом, приступаем к исключению неизвестной переменной x 2 из всех уравнений, начиная с третьего:

• к третьему уравнению систему прибавляем второе, которое умножено на — a ( 1 ) 42 a ( 1 ) 22 ;
• к четвертому прибавляем второе, которое умножено на — a ( 1 ) 42 a ( 1 ) 22 и т.д.

После таких манипуляций СЛАУ имеет следующий вид:

a 11 x 1 + a 12 x 2 + a 13 x 3 + . . . + a 1 n x n = b 1 a ( 1 ) 22 x 2 + a ( 1 ) 23 x 3 + . . . + a ( 1 ) 2 n x n = b ( 1 ) 2 a ( 2 ) 33 x 3 + . . . + a ( 2 ) 3 n x n = b ( 2 ) 3 ⋯ a ( 2 ) n 3 x 3 + . . . + a ( 2 ) n n x n = b ( 2 ) n ,

где a i j ( 2 ) = a ( 1 ) i j + a 2 j ( — a ( 1 ) i 2 a ( 1 ) 22 ) , i = 3 , 4 , . . . , n , j = 3 , 4 , . . . , n , b i ( 2 ) = b ( 1 ) i + b ( 1 ) 2 ( — a ( 1 ) i 2 a ( 1 ) 22 ) , i = 3 , 4 , . . . , n . .

Таким образом, переменная x 2 исключена из всех уравнений, начиная с третьего.

Далее приступаем к исключению неизвестной x 3 , действуя по аналоги с предыдущим образцом:

a 11 x 1 + a 12 x 2 + a 13 x 3 + . . . + a 1 n x n = b 1 a ( 1 ) 22 x 2 + a ( 1 ) 23 x 3 + . . . + a ( 1 ) 2 n x n = b ( 1 ) 2 a ( 2 ) 33 x 3 + . . . + a ( 2 ) 3 n x n = b ( 2 ) 3 ⋯ a ( n — 1 ) n n x n = b ( n — 1 ) n

После того как система приняла такой вид, можно начать обратный ход метода Гаусса:

• вычисляем x n из последнего уравнения как x n = b n ( n — 1 ) a n n ( n — 1 ) ;
• с помощью полученного x n находим x n — 1 из предпоследнего уравнения и т.д., находим x 1 из первого уравнения.

Найти решение системы уравнений методом Гаусса:

3 x 1 + 2 x 2 + x 3 + x 4 = — 2 x 1 — x 2 + 4 x 3 — x 4 = — 1 — 2 x 1 — 2 x 2 — 3 x 3 + x 4 = 9 x 1 + 5 x 2 — x 3 + 2 x 4 = 4

Коэффициент a 11 отличен от нуля, поэтому приступаем к прямому ходу решения, т.е. к исключению переменной x 11 из всех уравнений системы, кроме первого. Для того, чтобы это сделать, прибавляем к левой и правой частям 2-го, 3-го и 4-го уравнений левую и правую часть первого, которая умножена на — a 21 a 11 :

— 1 3 , — а 31 а 11 = — — 2 3 = 2 3 и — а 41 а 11 = — 1 3 .

3 x 1 + 2 x 2 + x 3 + x 4 = — 2 x 1 — x 2 + 4 x 3 — x 4 = — 1 — 2 x 1 — 2 x 2 — 3 x 3 + x 4 = 9 x 1 + 5 x 2 — x 3 + 2 x 4 = 4 ⇔

⇔ 3 x 1 + 2 x 2 + x 3 + x 4 = — 2 x 1 — x 2 + 4 x 3 — x 4 + ( — 1 3 ) ( 3 x 1 + 2 x 2 + x 3 + x 4 ) = — 1 + ( — 1 3 ) ( — 2 ) — 2 x 1 — 2 x 2 — 3 x 3 + x 4 + 2 3 ( 3 x 1 + 2 x 2 + x 3 + x 4 ) = 9 + 2 3 ( — 2 ) x 1 + 5 x 2 — x 3 + 2 x 4 + ( — 1 3 ) ( 3 x 1 + 2 x 2 + x 3 + x 4 ) = 4 + ( — 1 3 ) ( — 2 ) ⇔

⇔ 3 x 1 + 2 x 2 + x 3 + x 4 = — 2 — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 = — 1 3 — 2 3 x 2 — 7 3 x 3 + 5 3 x 4 = 23 3 13 3 x 2 — 4 3 x 3 + 5 3 x 4 = 14 3

Мы исключили неизвестную переменную x 1 , теперь приступаем к исключению переменной x 2 :

— a 32 ( 1 ) a 22 ( 1 ) = — — 2 3 — 5 3 = — 2 5 и а 42 ( 1 ) а 22 ( 1 ) = — 13 3 — 5 3 = 13 5 :

3 x 1 + 2 x 2 + x 3 + x 4 = — 2 — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 = — 1 3 — 2 3 x 2 — 7 3 x 3 + 5 3 x 4 = 23 3 13 3 x 2 — 4 3 x 3 + 5 3 x 4 = 14 3 ⇔

⇔ 3 x 1 + 2 x 2 + x 3 + x 4 = — 2 — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 = — 1 3 — 2 3 x 2 — 7 3 x 3 + 5 3 x 4 + ( — 2 5 ) ( — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 ) = 23 3 + ( — 2 5 ) ( — 1 3 ) 13 3 x 2 — 4 3 x 3 + 5 3 x 4 + 13 5 ( — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 ) = 14 3 + 13 5 ( — 1 3 ) ⇔

⇔ 3 x 1 + 2 x 2 + x 3 + x 4 = — 2 — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 = — 1 3 — 19 5 x 3 + 11 5 x 4 = 39 5 41 5 x 3 — 9 5 x 4 = 19 5

Для того чтобы завершить прямой ход метода Гаусса, необходимо исключить x 3 из последнего уравнения системы — а 43 ( 2 ) а 33 ( 2 ) = — 41 5 — 19 5 = 41 19 :

3 x 1 + 2 x 2 + x 3 + x 4 = — 2 — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 = — 1 3 — 19 5 x 3 + 11 5 x 4 = 39 5 41 5 x 3 — 9 5 x 4 = 19 5 ⇔

3 x 1 + 2 x 2 + x 3 + x 4 = — 2 — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 = — 1 3 — 19 5 x 3 + 11 5 x 4 = 39 5 41 5 x 3 — 9 5 x 4 + 41 19 ( — 19 5 x 3 + 11 5 x 4 ) = 19 5 + 41 19 39 5 ⇔

⇔ 3 x 1 + 2 x 2 + x 3 + x 4 = — 2 — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 = — 1 3 — 19 5 x 3 + 11 5 x 4 = 39 5 56 19 x 4 = 392 19

Обратный ход метода Гаусса:

• из последнего уравнения имеем: x 4 = 392 19 56 19 = 7 ;
• из 3-го уравнения получаем: x 3 = — 5 19 ( 39 5 — 11 5 x 4 ) = — 5 19 ( 39 5 — 11 5 × 7 ) = 38 19 = 2 ;
• из 2-го: x 2 = — 3 5 ( — 1 3 — 11 3 x 4 + 4 3 x 4 ) = — 3 5 ( — 1 3 — 11 3 × 2 + 4 3 × 7 ) = — 1 ;
• из 1-го: x 1 = 1 3 ( — 2 — 2 x 2 — x 3 — x 4 ) = — 2 — 2 × ( — 1 ) — 2 — 7 3 = — 9 3 = — 3 .

Ответ: x 1 = — 3 ; x 2 = — 1 ; x 3 = 2 ; x 4 = 7

Найти решение этого же примера методом Гаусса в матричной форме записи:

3 x 1 + 2 x 2 + x 3 + x 4 = — 2 x 1 — x 2 + 4 x 3 — x 4 = — 1 — 2 x 1 — 2 x 2 — 3 x 3 + x 4 = 9 x 1 + 5 x 2 — x 3 + 2 x 4 = 4

Расширенная матрица системы представлена в виде:

x 1 x 2 x 3 x 4 3 2 1 1 1 — 1 4 — 1 — 2 — 2 — 3 1 1 5 — 1 2 — 2 — 1 9 4

Прямой ход метода Гаусса в данном случае предполагает приведение расширенной матрицы к трапецеидальному виду при помощи элементарных преобразований. Этот процесс очень поход на процесс исключения неизвестных переменных в координатном виде.

Преобразование матрицы начинается с превращения всех элементов нулевые. Для этого к элементам 2-ой, 3-ей и 4-ой строк прибавляем соответствующие элементы 1-ой строки, которые умножены на — a 21 a 11 = — 1 3 , — a 31 a 11 = — — 2 3 = 2 3 и н а — а 41 а 11 = — 1 3 .

Дальнейшие преобразования происходит по такой схеме: все элементы во 2-ом столбце, начиная с 3-ей строки, становятся нулевыми. Такой процесс соответствует процессу исключения переменной . Для того, чтобы выполнить этой действие, необходимо к элементам 3-ей и 4-ой строк прибавить соответствующие элементы 1-ой строки матрицы, которая умножена на — а 32 ( 1 ) а 22 ( 1 ) = — 2 3 — 5 3 = — 2 5 и — а 42 ( 1 ) а 22 ( 1 ) = — 13 3 — 5 3 = 13 5 :

x 1 x 2 x 3 x 4 3 2 1 1 | — 2 0 — 5 3 11 3 — 4 3 | — 1 3 0 — 2 3 — 7 3 5 3 | 23 3 0 13 3 — 4 3 5 3 | 14 3

x 1 x 2 x 3 x 4

3 2 1 1 | — 2 0 — 5 3 11 3 — 4 3 | — 1 3 0 — 2 3 + ( — 2 5 ) ( — 5 3 ) — 7 3 + ( — 2 5 ) 11 3 5 3 + ( — 2 5 ) ( — 4 3 ) | 23 3 + ( — 2 5 ) ( — 1 3 ) 0 13 3 + 13 5 ( — 5 3 ) — 4 3 + 13 5 × 11 3 5 3 + 13 5 ( — 4 3 ) | 14 3 + 13 5 ( — 1 3 )

x 1 x 2 x 3 x 4

3 2 1 1 | — 2 0 — 5 3 11 3 — 4 3 | — 1 3 0 0 — 19 5 11 5 | 39 5 0 0 41 5 — 9 5 | 19 5

Теперь исключаем переменную x 3 из последнего уравнения — прибавляем к элементам последней строки матрицы соответствующие элементы последней строки, которая умножена на а 43 ( 2 ) а 33 ( 2 ) = — 41 5 — 19 5 = 41 19 .

x 1 x 2 x 3 x 4 3 2 1 1 | — 2 0 — 5 3 11 3 — 4 3 | — 1 3 0 0 — 19 5 11 5 | 39 5 0 0 41 5 — 9 5 | 19 5

x 1 x 2 x 3 x 4

3 2 1 1 | — 2 0 — 5 3 11 3 — 4 3 | — 1 3 0 0 — 19 5 11 5 | 39 5 0 0 41 5 + 41 19 ( — 19 5 ) — 9 5 + 41 19 × 11 5 | 19 5 + 41 19 × 39 5

x 1 x 2 x 3 x 4

3 2 1 1 | — 2 0 — 5 3 11 3 — 4 3 | — 1 3 0 0 — 19 5 11 5 | 39 5 0 0 0 56 19 | 392 19

Теперь применим обратных ход метода. В матричной форме записи такое преобразование матрицы, чтобы матрица, которая отмечена цветом на изображении:

x 1 x 2 x 3 x 4 3 2 1 1 | — 2 0 — 5 3 11 3 — 4 3 | — 1 3 0 0 — 19 5 11 5 | 39 5 0 0 0 56 19 | 392 19

стала диагональной, т.е. приняла следующий вид:

x 1 x 2 x 3 x 4 3 0 0 0 | а 1 0 — 5 3 0 0 | а 2 0 0 — 19 5 0 | а 3 0 0 0 56 19 | 392 19 , где а 1 , а 2 , а 3 — некоторые числа.

Такие преобразования выступают аналогом прямому ходу, только преобразования выполняются не от 1-ой строки уравнения, а от последней. Прибавляем к элементам 3-ей, 2-ой и 1-ой строк соответствующие элементы последней строки, которая умножена на

— 11 5 56 19 = — 209 280 , н а — — 4 3 56 19 = 19 42 и н а — 1 56 19 = 19 56 .

x 1 x 2 x 3 x 4 3 2 1 1 | — 2 0 — 5 3 11 3 — 4 3 | — 1 3 0 0 — 19 5 11 5 | 39 5 0 0 0 56 19 | 392 19

x 1 x 2 x 3 x 4

3 2 1 1 + ( — 19 56 ) 56 19 | — 2 + ( — 19 56 ) 392 19 0 — 5 3 11 3 — 4 3 + 19 42 × 56 19 | — 1 3 + 19 42 × 392 19 0 0 — 19 5 11 5 + ( — 209 280 ) 56 19 | 39 5 + ( — 209 280 ) 392 19 0 0 0 56 19 | 392 19

x 1 x 2 x 3 x 4

3 2 1 0 | — 9 0 — 5 3 11 3 0 | 9 0 0 — 19 5 0 | — 38 5 0 0 0 56 19 | 392 19

Далее прибавляем к элементам 2-ой и 1-ой строк соответствующие элементы 3-ей строки, которые умножены на

— 11 3 — 19 5 = 55 57 и н а — 1 — 19 5 = 5 19 .

x 1 x 2 x 3 x 4 3 2 1 0 | — 9 0 — 5 3 11 3 0 | 9 0 0 — 19 5 0 | — 38 5 0 0 0 56 19 | 392 19

x 1 x 2 x 3 x 4

3 2 1 + 5 19 ( — 19 5 ) 0 | — 9 + 5 19 ( — 38 5 ) 0 — 5 3 11 3 + 55 57 ( — 19 5 ) 0 | 9 + 55 57 ( — 38 5 ) 0 0 — 19 5 0 | — 38 5 0 0 0 56 19 | 392 19

x 1 x 2 x 3 x 4

3 2 1 0 | — 11 0 — 5 3 0 0 | 5 3 0 0 — 19 5 0 | — 38 5 0 0 0 56 19 | 392 19

На последнем этапе прибавляем элементы 2-ой строки к соответствующим элементам 1-ой строки, которые умножены на — 2 — 5 3 = 6 5 .

x 1 x 2 x 3 x 4 3 2 1 0 | — 11 0 — 5 3 0 0 | 5 3 0 0 — 19 5 0 | — 38 5 0 0 0 56 19 | 392 19

x 1 x 2 x 3 x 4

3 2 + 6 5 ( — 5 3 ) 0 0 | — 11 + 6 5 × 5 3 ) 0 — 5 3 0 0 | 5 3 0 0 — 19 5 0 | — 38 5 0 0 0 56 19 | 392 19

x 1 x 2 x 3 x 4

3 0 0 0 | — 9 0 — 5 3 0 0 | 5 3 0 0 — 19 5 0 | — 38 5 0 0 0 56 19 | 392 19

Полученная матрица соответствует системе уравнений

3 x 1 = — 9 — 5 3 x 2 = 5 3 — 19 5 x 3 = — 38 5 56 19 x 4 = 392 19 , откуда находим неизвестные переменные.

Ответ: x 1 = — 3 , x 2 = — 1 , x 3 = 2 , x 4 = 7 . ​​​

Видео:Решение системы уравнений методом Крамера.Скачать

Описание алгоритма использования метода Гаусса для решения СЛАУ с несовпадающим количеством уравнений и неизвестных, или с вырожденной системой матрицы

Если основная матрица квадратная или прямоугольная, то системы уравнений могут иметь единственное решение, могут не иметь решений, а могут иметь бесконечное множество решений.

Из данного раздела мы узнаем, как с помощью метода Гаусса определить совместность или несовместность СЛАУ, а также, в случае совместности, определить количество решений для системы.

В принципе, метод исключения неизвестных при таких СЛАУ остается таким же, однако есть несколько моментов, на которых необходимо заострить внимание.

На некоторых этапах исключения неизвестных, некоторые уравнения обращаются в тождества 0=0. В таком случае, уравнения можно смело убрать из системы и продолжить прямой ход метода Гаусса.

Если мы исключаем из 2-го и 3-го уравнения x 1 , то ситуация оказывается следующей:

x 1 + 2 x 2 — x 3 + 3 x 4 = 7 2 x 1 + 4 x 2 — 2 x 3 + 6 x 4 = 14 x — x + 3 x + x = — 1 ⇔

x 1 + 2 x 2 — x 3 + 3 x 4 = 7 2 x 1 + 4 x 2 — 2 x 3 + 6 x 4 + ( — 2 ) ( x 1 + 2 x 2 — x 3 + 3 x 4 ) = 14 + ( — 2 ) × 7 x — x + 3 x + x + ( — 1 ) ( x 1 + 2 x 2 — x 3 + 3 x 4 ) = — 1 + ( — 1 ) × 7 ⇔

⇔ x 1 + 2 x 2 — x 3 + 3 x 4 = 7 0 = 0 — 3 x 2 + 4 x 3 — 2 x 4 = — 8

Из этого следует, что 2-ое уравнение можно смело удалять из системы и продолжать решение.

Если мы проводим прямой ход метода Гаусса, то одно или несколько уравнений может принять вид — некоторое число, которое отлично от нуля.

Это свидетельствует о том, что уравнение, обратившееся в равенство 0 = λ , не может обратиться в равенство ни при каких любых значениях переменных. Проще говоря, такая система несовместна (не имеет решения).

• В случае если при проведении прямого хода метода Гаусса одно или несколько уравнений принимают вид 0 = λ , где λ — некоторое число, которое отлично от нуля, то система несовместна.
• Если же в конце прямого хода метода Гаусса получается система, число уравнений которой совпадает с количеством неизвестных, то такая система совместна и определена: имеет единственное решение, которое вычисляется обратным ходом метода Гаусса.
• Если при завершении прямого хода метода Гаусса число уравнений в системе оказывается меньше количества неизвестных, то такая система совместна и имеет бесконечно количество решений, которые вычисляются при обратном ходе метода Гаусса.

📺 Видео

12. Метод Гаусса решения систем линейных уравнений. Часть 1.Скачать

Система линейных уравнений. Общее решение. Метод ГауссаСкачать

Метод Гаусса и метод Жордана-Гаусса ➜ 2 метода за 7 минутСкачать

ФСР системы линейных уравнений. Алгоритм ГауссаСкачать

Метод Гаусса решения систем линейных уравненийСкачать

12. Решение систем линейных уравнений методом ГауссаСкачать

Метод Жордана-Гаусса (метод прямоугольников). ВидеоурокСкачать

Общее, частное, базисное решение системы линейных уравнений Метод ГауссаСкачать

6 способов в одном видеоСкачать

Матричный метод решения систем уравненийСкачать

Линейная алгебра, Матрицы: Метод Гаусса. Высшая математикаСкачать

решение системы уравнений методом ГауссаСкачать