Решение простейших тригонометрических уравнений графически

Уравнения, с которыми приходится сталкиваться при решении практических задач, как правило, значительно отличаются от тех, которые мы рассматривали. Для таких уравнений иногда вообще нельзя указать никакого способа, который позволял бы найти корни абсолютно точно. В таком случае приходится ограничиваться нахождением лишь приближенных значений корней. Современная математика располагает эффективными методами приближенного решения уравнений. Рассмотрим графический способ решения.

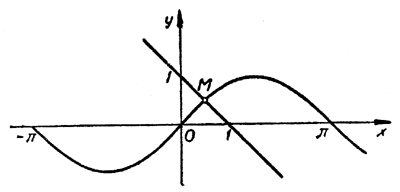
Пусть, например, нужно решить уравнение

На одном и том же рисунке начертим два графика: график функции y = sin х и график функции у = 1 — х

Эти графики пересекаются в одной точке М. Абсцисса этой точки и дает нам единственный корень нашего уравнения:

Для уточнения полученного результата полезно использовать тригонометрические таблицы или компьютерные программы. При х = 0,5

следовательно, sin х 1 — х. Но тогда, как легко понять из того же рисунка, искомый корень x₀ должен быть меньше, чем 0,6. Теперь уже мы знаем, что x₀ находится в интервале [0,5; 0,6]. Поэтому с точностью до 0,1

С помощью таблиц можно найти приближенное значение x₀ и с точностью до 0,01. Разделим интервал [0,5; 0,6] пополам. В средней точке (x = 0,55) этого интервала

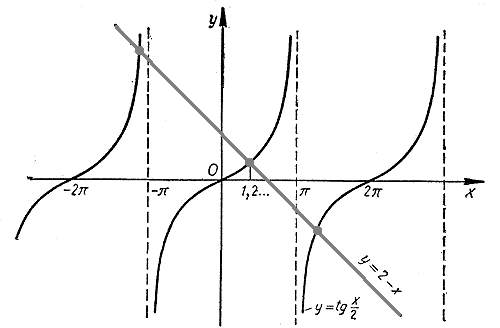
Графики функций у = tg x /₂ и у = 2 — х пересекаются в бесконечном числе точек. Значит, данное уравнение имеет бесконечное множество корней. Найдем, например, наименьший положительный корень х₀. Этот корень является абсциссой точки пересечения графиков. Примерно он равен 1,2.

Чтобы найти этот корень точнее, воспользуемся таблицами тангенсов В. М. Брадиса (или рассчитаем соответствующие значения в программе «Kалькулятор» или «Excel»). Выпишем значения функций у = tg x /₂ и у = 2 — х в окрестности точки х = 1,2.

Как видно из этой таблицы, при переходе от значения х = 1,2 к значению х = 1,3 разность tg x /₂ — (2 — х) меняет свой знак на противоположный (с — на +). Значит, в нуль эта разность обращается где-то между значениями 1,2 и 1,3. Следовательно, с точностью до 0,1 х₀ ≈ 1,2 (с недостатком) или х₀ ≈ 1,3 (с избытком). Используя таблицу тангенсов, можно найти и приближенное значение этого корня
с точностью до 0,01. Для этого рассмотрим значение х = 1,25, являющееся средним значением чисел 1,2 и 1,3. При х = 1,25

Видео:Простейшие тригонометрические уравнения. y=sinx. 1 часть. 10 класс.Скачать

РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ

Простейшими тригонометрическими уравнениями называют уравнения

Чтобы рассуждения по нахождению корней этих уравнений были более наглядными, воспользуемся графиками соответствующих функций.

19.1. Уравнение cos x = a

Объяснение и обоснование

1. Корни уравненияcosx=a.

При |a| > 1 уравнение не имеет корней, поскольку |cos x| ≤ 1 для любого x (прямая y = a на рисунке из пункта 1 таблицы 1 при a > 1 или при a 1 уравнение не имеет корней, поскольку |sin x| ≤ 1 для любого x (прямая y = a на рисунке 1 при a > 1 или при a n arcsin a + 2πn, n ∈ Z (3)

2.Частые случаи решения уравнения sin x = a.

Полезно помнить специальные записи корней уравнения при a = 0, a = -1, a = 1, которые можно легко получить, используя как ориентир единичную окружность (рис 2).

Учитывая, что синус равен ординате соответствующей точки единичной окружности, получаем, что sin x = 0 тогда и только тогда, когда соответствующей точкой единичной окружности является точка C или тока D. Тогда

Аналогично sin x = 1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка A, следовательно,

Также sin x = -1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка B, таким образом,

Примеры решения задач

Замечание. Ответ к задаче 1 часто записывают в виде:

19.3. Уравнения tg x = a и ctg x = a

Объяснение и обоснование

1.Корни уравнений tg x = a и ctg x = a

Рассмотрим уравнение tg x = a. На промежутке функция y = tg x возрастает (от -∞ до +∞). Но возрастающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение tg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арктангенса равен: x₁ = arctg a и для этого корня tg x = a.

Функция y = tg x периодическая с периодом π, поэтому все остальные корни отличаются от найденного на πn (n ∈ Z). Получаем следующую формулу корней уравнения tg x = a:

При a=0 arctg 0 = 0, таким образом, уравнение tg x = 0 имеет корни x = πn (n ∈ Z).

Рассмотрим уравнение ctg x = a. На промежутке (0; π) функция y = ctg x убывает (от +∞ до -∞). Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение ctg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арккотангенса равен: x₁=arсctg a.

Функция y = ctg x периодическая с периодом π, поэтому все остальные корни отличаются от найденного на πn (n ∈ Z). Получаем следующую формулу корней уравнения ctg x = a:

таким образом, уравнение ctg x = 0 имеет корни

Примеры решения задач

Вопросы для контроля

1. Какие уравнения называют простейшими тригонометрическими?
2. Запишите формулы решения простейших тригонометрических уравнений. В каких случаях нельзя найти корни простейшего тригонометрического уравнения по этим формулам?
3. Выведите формулы решения простейших тригонометрических уравнений.
4. Обоснуйте формулы решения простейших тригонометрических уравнений для частных случаев.

Упражнения

Решите уравнение (1-11)

Найдите корни уравнения на заданном промежутке (12-13)

Видео:10 класс, 22 урок, Простейшие тригонометрические уравнения неравенстваСкачать

«Нестандартные способы решения тригонометрических уравнений графическим методом»

Решение тригонометрического уравнения состоит из двух этапов: преобразование уравнения для получения его простейшего вида и решение полученного простейшего тригонометрического уравнения. Существует семь основных методов решения тригонометрических уравнений. И именно графический метод был один из первых. Почему?

В древности тригонометрия возникла в связи с потребностями астрономии, землемерия и строительного дела, то есть носила чисто геометрический характер и представляла главным образом «исчисление хорд».

Древние наблюдали за движением небесных светил. Ученые обрабатывали данные измерений, чтобы вести календарь и правильно определять время начала сева и сбора урожая, даты религиозных праздников.

В 10 классе мы уже немало знаем о тригонометрических уравнениях, знакомы с разнообразными способами решения. Поэтому мы теперь можем применить наши знания и оптимизировать способы графического решения подобных задач с помощью информационных технологий, таких, например, как программа GeoGebra.

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Скачать:

Видео:Простейшие тригонометрические уравнения. y=cosx. 1 часть. 10 класс.Скачать

Предварительный просмотр:

Тема: «Нестандартные способы решения тригонометрических уравнений графическим методом».

Актуальность: высокая практическая значимость работы для использования в учебном процессе и при подготовке к ЕГЭ

Основные цели работы:

• освоить способы создания динамических чертежей с помощью программы GeoGebra;
• изучить возможности использования программы GeoGebra в учебном процессе при подготовке к ЕГЭ и при подготовке докладов для научно-практических конференций;
• отработать технологию решения тригонометрических уравнений графическим способом с помощью динамической программы GeoGebra;

Объект исследования: Тригонометрические уравнения

Предмет исследования: изменение тригонометрической функции при различных значениях аргумента и других дополнительных параметров

Предположение исследования: программа GeoGebra позволяет визуально проследить изменение поведения функции при различных значениях аргумента и других дополнительных параметров.

• Использовать современные информационные технологии в ходе решения математических задач.
• Отработать алгоритм решения простейших тригонометрических уравнений графическим способом;
• Выработать прочные навыки решения простейших тригонометрических уравнений графическим способом;
• Рационально подходить к выбору прикладных программ для решения поставленных задач.
• Развивать логическое мышление, память, математическую речь.

Методы: эмпирический (практическая работа в программе); аналитический (анализ полученных результатов)

1. Знакомство с синтаксисом программы GeoGebra.

2. Освоение опций и функций программы.

3. Практическая работа: построение графиков. Сравнение графического и аналитического методов.

4. Анализ и описание полученных результатов.

Решение тригонометрического уравнения состоит из двух этапов: преобразование уравнения для получения его простейшего вида и решение полученного простейшего тригонометрического уравнения. Существует семь основных методов решения тригонометрических уравнений. И именно графический метод был один из первых. Почему?

В древности тригонометрия возникла в связи с потребностями астрономии, землемерия и строительного дела, то есть носила чисто геометрический характер и представляла главным образом «исчисление хорд».

Древние наблюдали за движением небесных светил. Ученые обрабатывали данные измерений, чтобы вести календарь и правильно определять время начала сева и сбора урожая, даты религиозных праздников.

В 10 классе мы уже немало знаем о тригонометрических уравнениях, знакомы с разнообразными способами решения. Поэтому мы теперь можем применить наши знания и оптимизировать способы графического решения подобных задач с помощью информационных технологий, таких, например, как программа GeoGebra.

Предполагается, что в результате работы будут:

1. Изучены (в первом приближении) основные возможности программы GeoGebra по созданию динамических чертежей.

2. Собрана (с использованием возможностей Интернета) библиотека файлов, содержащих графические иллюстрации к задачам типа С5 с параметрами.

3 Сформулированы основные принципы использования программы GeoGebra для иллюстрации решений тригонометрических уравнений графическим способом:

• динамическое изменение параметра позволяет демонстрировать взаимодействие графиков в режиме реального времени;
• функция «паузы» позволяет зафиксировать положение графиков при критических значениях параметра, которые потом необходимо вычислить аналитически;
• введение дополнительного параметра в условие задачи, отличного от заданного, позволяет продемонстрировать принципиальные изменения в исходной конфигурации, которые приводят к появлению новых критических значений параметра.

Видео:ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙСкачать

Предварительный просмотр:

Рабочая карта учащегося

Тема: «Нестандартные способы решения тригонометрических уравнений графическим методом».

Решите самостоятельно уравнение графическим методом в интерактивной среде Geogebra;

• Откройте Geogebra(Пуск – Все программы – Geogebra)
• Настойте координатную плоскость(по оси аргумента – единичный отрезок π/2);
• Введите через строку ввода соответствующие функции;

Для того, чтобы решить данное уравнение, нам также необходимо построить два графика функций и .

Для этого не потребуется строить таблицы, но понадобится подготовить координатную плоскость. Правой клавишей мыши щелкните по координатной плоскости. В появившемся диалоговом окне поставьте флажок «шаг» и выберите значение π/2. Закройте диалоговое окно. Внесем функции через строку ввода. Для построения первой функции вводим следующее: . Для построения второй функции вводим .

Видео:Простейшие тригонометрические уравненияСкачать

Построение графика функции y= sin x

Видео:Как решать тригонометрические неравенства?Скачать

Построение графика функции y= cos x

Видео:13 Функционально графический способ решенияСкачать

Преобразования графика функции y= sin x

Руководство: используя ползунки, выясните, как влияет на график функции

y= sin x
1) амплитуда А;
2) частота w;
3) начальная фаза φ_0;
4) свободный член b?

Видео:ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ - Решение Тригонометрических уравнений / Подготовка к ЕГЭ по МатематикеСкачать

Преобразования графика функции y= cos x

Руководство: используя ползунки, выясните, как влияет на график функции y= cos x
1) амплитуда A;
2) частота w;
3) начальная фаза φ_0;
4) свободный член b?

1. Решите следующие уравнения графическим методом и аналитическим путем.

• Упростите левую часть уравнения;
• Окройте интерактивную среду Geogebra;
• Выполните построение;

Графический метод решения в Geogebra

Аналитический метод решения

Не требуется знать формулы

Требуется знать формулы

Необходимо уметь набирать функции

Нет необходимости учиться набирать функции

1. Операция «Спасение».

«Пираты решили захватить главнокомандующий боевой крейсер, не подозревая о существовании эскадрильи из трех боевых кораблей. Вы находитесь на одном из них. Ваша задача: выяснить, в каких точках вашего маршрута вы пересечетесь с пиратским кораблем и сможете его обезвредить. Ваш маршрут движения задан графиком . Маршрут движения пиратов задан графиком функции g(x)=1 ».

«Пираты решили захватить главнокомандующий боевой крейсер, не подозревая о существовании эскадрильи из трех боевых кораблей. Вы находитесь на одном из них. Ваша задача: выяснить, в каких точках вашего маршрута вы пересечетесь с пиратским кораблем и сможете его обезвредить. Ваш маршрут движения задан графиком . Маршрут движения пиратов задан графиком функции g(x)=1 ».

«Пираты решили захватить главнокомандующий боевой крейсер, не подозревая о существовании эскадрильи из трех боевых кораблей. Вы находитесь на одном из них. Ваша задача: выяснить, в каких точках вашего маршрута вы пересечетесь с пиратским кораблем и сможете его обезвредить. Ваш маршрут движения задан графиком . Маршрут движения пиратов задан графиком функции g(x)=1 ».

Задание. Создать динамическую модель для иллюстрации поведения функции y=a cos(bx+c) в зависимости от параметров а, b и с. Рисуем график квадратичной функции в зависимости от ее коэффициентов. Изменение любого из трех коэффициентов изменяет поведение параболы. Модель можно посмотреть, перейдя по ссылке http://ggbtu.be/m221351 К онечный результат представлен на рисунке.

Предварительный просмотр:

Видео:7 класс, 35 урок, Графическое решение уравненийСкачать

Подписи к слайдам:

Тема: «Нестандартные способы решения тригонометрических уравнений графическим методом» Выполнила: Быстрова Карина Ученица 10 класса

Актуальность: высокая практическая значимость работы для использования в учебном процессе и при подготовке к ЕГЭ Основные цели работы: освоить способы создания динамических чертежей с помощью программы GeoGebra; изучить возможности использования программы GeoGebra в учебном процессе при подготовке к ЕГЭ и при подготовке докладов для научно-практических конференций; отработать технологию решения тригонометрических уравнений графическим способом с помощью динамической программы GeoGebra;

Задачи Использовать современные информационные технологии в ходе решения математических задач. Отработать алгоритм решения простейших тригонометрических уравнений графическим способом; Выработать прочные навыки решения простейших тригонометрических уравнений графическим способом; Рационально подходить к выбору прикладных программ для решения поставленных задач. Развивать логическое мышление, память, математическую речь.

Введение Решение тригонометрического уравнения состоит из двух этапов: преобразование уравнения для получения его простейшего вида и решение полученного простейшего тригонометрического уравнения. Существует семь основных методов решения тригонометрических уравнений. И именно графический метод был один из первых. Почему? В древности тригонометрия возникла в связи с потребностями астрономии, землемерия и строительного дела, то есть носила чисто геометрический характер и представляла главным образом «исчисление хорд». Древние наблюдали за движением небесных светил. Ученые обрабатывали данные измерений, чтобы вести календарь и правильно определять время начала сева и сбора урожая, даты религиозных праздников.

Ее возможности: Построение кривых: Построение графиков функций Построение сечений Окружности Параболы Гиперболы и др. Вычисления: Сложение, умножение Вычисления с комплексными числами Вычисление определителя А также работа с таблицами, создание анимации и многое другое.

При исследовании программы и работе с ресурсами интернета на официальном сайте GeoGebra я нашла простейшее построение графиков функции y= sinx и y= cosx , благодаря различным возможностям программы и анимации, мы можем увидеть как меняются графики при некотором изменении параметров , что очень облегчает работу при решении тригонометрических функций. Благодаря работам других людей я также с легкостью научилась преобразовывать графики функций, что значительно облегчило мне дальнейшее исследование программы. Построение графика функции y= sin x Построение графика функции y= cos x Преобразования графика функции y= sin x Преобразования графика функции y= cos x

Отработка практических навыков. Задание №1 Необходимо решить уравнения: 1. 2. cos x = -1 Решение: Для того, чтобы решить данное уравнение, нам также необходимо построить два графика функций и Для этого не потребуется строить таблицы, но понадобится подготовить координатную плоскость (по оси аргумента – единичный отрезок π /2). Для построения первой функции мы вводим в строку ввода следующее: На экране появляется первый график:

Далее для построения второй функции вводим: и при помощи функций программы отмечаем точки пересечения двух построенных графиков. Конечный результат: Практические1. ggb

2. Аналогично решаем и второе уравнение. В строку ввода вводим необходимые данные y = sin x и y =1/2, определяем точки пересечения графиков, это и будет являться решением данного уравнения. Конечный результат представлен на рисунке: Практические2. ggb

Задание №2. Операция «Спасение» Решим это задание графическим методом, опираясь на полученные знания.

Как и в предыдущем задании нам необходимо построить два графика: и y =1 . Отметив точки пересечения графиков мы найдём место пересечения нашего корабля и корабля пиратов. Это и будет являться решением. В нашем случае это точки А (со значением – π ), В(3 π ) и С ( π ) Практическиекорабль синих. ggb

Миноносец «Боевой» Аналогичным способом решаем и эту задачу. В строку ввода вводим заданные формулы в соответствии с синтаксисом программы и ищем точки пересечения.

Практическиекорабль красных. ggb Построив графики, мы сразу видим решение задачи. Точки А , В , С и D – точки пересечения кораблей.

Миноносец «Внушительный» Также в строку ввода вводим необходимые функции и ищем точки пересечения кораблей.

Точки пересечения кораблей – А и В . Практическиекорабль желтых. ggb

Задание № 3. Создание динамической модели. Задание. Создать динамическую модель для иллюстрации поведения функции y = a cos ( bx + c ) в зависимости от параметров а , b и с . Для выполнения этого типа задания нам потребуются ползунки, которые отвечают за динамическое изменение параметров функции при различных значениях в режиме реального времени. Для начала рисуем график квадратичной функции (вводим формулу в строку ввода в соответствии с синтаксисом программы), затем создаем ползунки для параметров a , b и c .

При изменении любого из этих коэффициентов изменяется и поведение параболы. Это в свою очередь позволяет нам наглядно представить изменение графика, а функция «паузы» позволяет зафиксировать поведения графика при критических значениях параметра. Конечный результат представлен на рисунке, а саму модель можно посмотреть, перейдя по ссылке. Практическиединамическая модель. ggb

Основные выводы работа с программой GeoGebra в динамическом режиме активизирует сильных учеников, делает их подготовку более целенаправленной и индивидуальной; работа с программой GeoGebra очень удобна для демонстрации трудностей, возникающих при использовании графического метода решения задач с параметрами; работа с программой GeoGebra требует минимального уровня информационно-компьютерной грамотности учителя и учащихся и разумных временных затрат для получения желаемого результата.

🎦 Видео

#2. Как решать тригонометрические уравнения? 3 способа!Скачать

РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ😉 #shorts #егэ #огэ #математика #профильныйегэСкачать

Простейшие тригонометрические уравнения. y=sinx. 2 часть. 10 класс.Скачать

Решение тригонометрических уравнений. Вебинар | МатематикаСкачать

КАК РЕШАТЬ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ? // УРАВНЕНИЕ COSX=AСкачать

Решение тригонометрических неравенств. 10 класс.Скачать

Простейшие тригонометрические уравнения. y=cosx. 2 часть. 10 класс.Скачать

§167 Решение тригонометрических неравенств графическиСкачать

Простейшие тригонометрические уравнения. Практическая часть. 10 класс.Скачать

Занятие 10. Простейшие тригонометрические уравненияСкачать