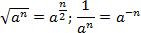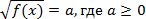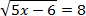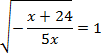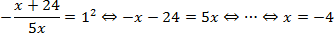Решение показательных логарифмических тригонометрических иррациональных уравнений

Все задачи B7, которые мне доводилось видеть, были сформулированы примерно одинаково: решить уравнение. При этом сами уравнения относятся к одному из трех видов:

1. Логарифмические;
2. Показательные;
3. Иррациональные.

Вообще говоря, полноценное руководство по каждому типу уравнений займет не один десяток страниц, выходя далеко за рамки ЕГЭ. Поэтому мы рассмотрим лишь самые простые случаи, требующие незатейливых рассуждений и выкладок. Этих знаний будет вполне достаточно, чтобы решить любую задачу B7.

В математике термин «решить уравнение» означает найти множество всех корней данного уравнения, либо доказать, что это множество пусто. Но в бланк ЕГЭ можно вписывать только числа — никаких множеств. Поэтому, если в задании B7 оказалось больше одного корня (или, наоборот, ни одного) — в решении была допущена ошибка.

Видео:СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать

Логарифмические уравнения

— это любое уравнение, которое сводится к виду log _a f ( x ) = k , где a > 0, a ≠ 1 — основание логарифма, f ( x ) — произвольная функция, k — некоторая постоянная.

Такое уравнение решается внесением постоянной k под знак логарифма: k = log _a a k . Основание нового логарифма равно основанию исходного. Получим уравнение log _a f ( x ) = log _a a k , которое решается отбрасыванием логарифма.

Заметим, что по условию a > 0, поэтому f ( x ) = a k > 0, т.е. исходный логарифм существует.

Решение. log₇ (8 − x ) = 2 ⇔ log₇ (8 − x ) = log₇ 7 2 ⇔ 8 − x = 49 ⇔ x = −41.

Решение. log_0,5 (6 − x ) = −2 ⇔ log_0,5 (6 − x ) = log_0,5 0,5 −2 ⇔ 6 − x = 4 ⇔ x = 2.

Но что делать, если исходное уравнение окажется сложнее, чем стандартное log _a f ( x ) = k ? Тогда сводим его к стандартному, собирая все логарифмы в одной стороне, а числа — в другой.

Если в исходном уравнении присутствует более одного логарифма, придется искать область допустимых значений (ОДЗ) каждой функции, стоящей под логарифмом. Иначе могут появиться лишние корни.

Поскольку в уравнении присутствуют два логарифма, найдем ОДЗ:

1. x + 1 > 0 ⇔ x > −1
2. x + 5 > 0 ⇔ x > −5

Получаем, что ОДЗ — это интервал (−1, +∞). Теперь решаем уравнение:

log₅ ( x + 1) + log₅ ( x + 5) = 1 ⇒ log₅ ( x + 1)( x + 5) = 1 ⇔ log₅ ( x + 1)( x + 5) = log₅ 5 1 ⇔ ( x + 1)( x + 5) = 5 ⇔ x 2 + 6 x + 5 = 5 ⇔ x ( x + 6) = 0 ⇔ x ₁ = 0, x ₂ = −6.

Но x ₂ = −6 не подходит по ОДЗ. Остается корень x ₁ = 0.

Видео:Показательные и логарифмические уравнения. Вебинар | МатематикаСкачать

Показательные уравнения

— это любое уравнение, которое сводится к виду a f ( x ) = k , где a > 0, a ≠ 1 — основание степени, f ( x ) — произвольная функция, k — некоторая постоянная.

Это определение почти дословно повторяет определение логарифмического уравнения. Решаются показательные уравнения даже проще, чем логарифмические, ведь здесь не требуется, чтобы функция f ( x ) была положительна.

Для решения сделаем замену k = a t , где t — вообще говоря, логарифм ( t = log _a k ), но в ЕГЭ числа a и k будут подобраны так, что найти t будет легко. В полученном уравнении a f ( x ) = a t основания равны, а значит, равны и показатели, т.е. f ( x ) = t . Решение последнего уравнения, как правило, не вызывает проблем.

Задача. Решить уравнение: 7 x − 2 = 49.

Решение. 7 x − 2 = 49 ⇔ 7 x − 2 = 7 2 ⇔ x − 2 = 2 ⇔ x = 4.

Задача. Решить уравнение: 6 16 − x = 1/36.

Решение. 6 16 − x = 1/36 ⇔ 6 16 − x = 6 −2 ⇔ 16 − x = −2 ⇔ x = 18.

Немного о преобразовании показательных уравнений. Если исходное уравнение отличается от a f ( x ) = k , применяем правила работы со степенями:

1. a n · a m = a n + m ,
2. a n / a m = a n − m ,
3. ( a n ) m = a n · m .

Кроме того, надо знать правила замены корней и дробей на степени с рациональным показателем:

Такие уравнения встречаются в ЕГЭ крайне редко, но без них разбор задачи B7 был бы неполным.

Задача. Решить уравнение: (5/7) x − 2 · (7/5) 2 x − 1 = 125/343

1. (7/5) 2 x − 1 = ((5/7) −1 ) 2 x − 1 = (5/7) 1 − 2 x ,
2. 125/343 = (5 3) /(7 3 ) = (5/7) 3 .

Имеем: (5/7) x − 2 · (7/5) 2 x − 1 = 125/343 ⇔ (5/7) x − 2 · (5/7) 1 − 2 x = (5/7) 3 ⇔ (5/7) x − 2 + 1 − 2 x = (5/7) 3 ⇔ (5/7) − x − 1 = (5/7) 3 ⇔ − x − 1 = 3 ⇔ x = −4.

Видео:ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать

Иррациональные уравнения

Под иррациональным понимается любое уравнение, содержащее знак корня. Из всего многообразия иррациональных уравнений мы рассмотрим лишь простейший случай, когда уравнение имеет вид:

Чтобы решить такое уравнение, возведем обе стороны в квадрат. Получим уравнение f ( x ) = a 2 . При этом автоматически выполняется требование ОДЗ: f ( x ) ≥ 0, т.к. a 2 ≥ 0. Остается решить несложное уравнение f ( x ) = a 2 .

Возводим обе стороны в квадрат и получим: 5 x − 6 = 8 2 ⇔ 5 x − 6 = 64 ⇔ 5 x = 70 ⇔ x = 14.

Сначала, как и в прошлый раз, возводим обе стороны в квадрат. А затем внесем знак «минус» в числитель. Имеем:

Заметим, что при x = −4 под корнем будет положительное число, т.е. требование ОДЗ выполнено.

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Решение рациональных, иррациональных, показательных, тригонометрических и логарифмических уравнений и систем

Опубликовано 16.09.2020Подготовка к ЕГЭ

Видео:11 класс, 17 урок, Логарифмические уравненияСкачать

Решение рациональных, иррациональных, показательных, тригонометрических и логарифмических уравнений и систем

На сегодняшний день ЕГЭ по математике проходит в форме решения заданий, содержащихся в контрольно-измерительных материалах, при этом, ответы на задания выносят на отдельный бланк.

Уравнения могут быть следующих видов:

В данной статье рассмотрена профильная математика, а именно раздел по видам и системам рациональных, иррациональных, показательных, тригонометрических и логарифмических уравнений.

При решении уравнений нужно помнить основные термины:

— Корнем уравнения называют неизвестное число, которое нужно найти;

— Решение уравнения предполагает нахождение его корня;

— Уравнения, у которых совпадают решения называют равносильными;

— ОДЗ – область допустимых значений;

— Если возможно заменить переменные, то нужно это выполнить;

— После решения уравнения необходимо провести проверку на правильность нахождения корня.

Итак, рассмотрим каждый вид уравнений по отдельности, включая примеры решения.

1. Рациональные уравнения – уравнения, у которых, как правило, слева расположено рациональное выражение, а справа – ноль.

Рациональным уравнением называют уравнение вида r(х)=0.

Если обе части уравнения являются рациональными выражениями, то рациональные уравнения называют целыми.

Дробно-рациональным называют уравнение, которое содержит дробное выражение.

Порядок действий при решении данного вида уравнения должен быть следующий:

— Все члены должны быть переведены в левую часть уравнения;

— Данную часть уравнения нужно представить в виде дроби p(x)/q(x);

— Для полученного решения нужно провести проверку, то есть.

При решение этого рационального уравнения понадобится формула (а-в)2=а2-2ав+в2.

Рассмотрим ещё один пример решения рационального уравнения:

На основе примеров показано, что рациональные уравнения могут быть с разным количеством переменных.

Иррациональными уравнениями считают уравнения с переменной под корнем. Для того, чтобы определить является ли уравнение иррациональным нужно просто посмотреть на корень переменной. Следует учитывать, что в некоторых учебниках по математике иррациональное уравнение определяют другим способом.

Способы решения таких уравнений:

— Возвести в степень обе части уравнения;

— Ввести новые переменные;

Пример решения уравнения по первому способу:

Пример решения по второму способу:

1. Показательные уравнения

Показательные уравнения – уравнение, содержащее неизвестный показатель.

В учебниках по математике разных авторов определение показательного уравнения может отличаться. Обычно такие отличия касаются незначительных деталей.

Как правило, это уравнения вида af(x)=ag(x), где а не равно одному и число а больше нуля. Из этого следует, что f(x)=g(x).

— Уравнение с одним основанием;

— Уравнение с равными основаниями.

Существует следующие способы решения таких уравнений:

— Использовать метод логарифмов;

— Привести уравнение к квадратному виду;

— Вынести за скобку общий множитель;

— Ввести новую переменную.

Итак, как решить показательное уравнение? Любое по сложности уравнение нужно привести в простую форму.

Рассмотрим наиболее простой пример решения показательного уравнения:

Для решения данного уравнения следует 2 возвести во вторую степень.

Решение даже простейших показательных уравнений имеет большую значимость. Поэтому далее вам будет легче решать уравнения более сложного уровня.

Данная тема является одной из самых сложных, поэтому следует внимательно подойти к изучению данной темы. Известны три формулы тригонометрических уравнений, запомнить которые не составляет особой сложности.

Наиболее простое тригонометрическое уравнение имеет вид sin x=a, cos x=a, tg x=а, а – число действительное.

Способы решения таких уравнений:

— Решение с помощью форму и приведение к простейшему;

— Ввод других переменных;

— Разложить уравнение по множителям.

Пример решения тригонометрического уравнения:

Здесь нужно рисовать окружность, далее выделить точки с координатой ½, соответственно, это точки 5п/6 и п/6. Если пройти по окружности, исходя из данных точек, то х=п/6+2пk, x=5п/6+2пn. При этом синус и косинус принадлежат промежутку [-1;1]. Если при решении уравнения в его правой части стоит число не принадлежащее промежутку, считается, что уравнение не имеет решения.

Также рассмотрим пример решения уравнения, разложив его по множителям.

Нужно применить формулу sin2x = 2sinxcosx.

2sinxcosx – sinx = 0.

sinx (2cosx – 1) = 0.

Таким образом, если один из множителей равен нулю, то решение уравнения также равно нулю.

Далее, sinx=0, x=пk.

1. Логарифмические уравнения

Особое значение имеет подготовка ЕГЭ по математике логарифмы, это обусловлено тем, что в КИМах чаще всего встречаются именно этого вида уравнения.

Логарифмическое уравнение – это уравнение с неизвестной величиной, находящейся внутри логарифма.

Примерами логарифмических уравнений являются уравнения следующего вида:

Способы решения уравнений данного вида:

— Применять способ уравнивания к единице;

— Применять способ умножать на единицу;

— Применять доступные правила логарифмов;

— Введение другого основания;

— Возвести в степень.

Самым простым логарифмическим уравнением принято считать уравнение вида log a x = b, при этом основание a>0,a≠1.

Пример решения уравнения:

Сначала следует найти значение области, то есть ОДЗ. При этом нужно помнить, что под логарифмом выражение всегда положительное. Воспользуемся логарифмическим определением, представим х степью основания 2 логарифма, степень будет равна 3.

Решение уравнения является ОДЗ, то есть корень уравнения найден.

Таким образом, подобное задание ЕГЭ по математике легко можно решить, зная логарифмы и способы их решения.

Оставить Комментарий Отменить ответ

Для отправки комментария вам необходимо авторизоваться.

Видео:Решение логарифмических уравнений #shortsСкачать

Выбери тему

Видео:Показательные уравнения. 11 класс.Скачать

Самые популярные записи

• Наука. Основные особенности научного мышления. Естественные и социально гуманитарные науки (3 293)
• ЕГЭ по обществознанию: мышление и деятельность; потребности и интересы (2 238)
• Строение растения. Стебель, лист и цветок. (2 196)
• Свобода и необходимость в человеческой деятельности. Свобода и ответственность. (2 189)

Видео:ЕГЭ. Промежуточный срез №3 «Показательные и логарифмические функции. Тригонометрия». ПрактикаСкачать

StudyWay

Видео:11 класс, 18 урок, Логарифмические неравенстваСкачать

Помощь

© 2021 StudyWay. Все права защищены.

Ты можешь попробовать 3 наших закрытых занятия из курса «Прорыв».

Записаться можно через Instagram

Для этого напиши в Direct (в личку) кодовое слово «Пробный«

Видео:Иррациональные уравнения и их системы. 11 класс.Скачать

Что за курс и что тебя там будет ждать?

12 мощнейших онлайн занятий по 2 часа в формате вебинаров.
Содержание вебинара: повторение предыдущей темы, теория, перерыв и практика.

Воркбук (рабочая тетрадь)абсолютно к каждому уроку со всей необходимой теорией к этой теме и практикой.

Личный куратор — это твой помощник во всех учебных вопросах.
Они занимаются проверкой твоих домашних заданий, поддерживают и мотивируют двигаться дальше, даже когда хочется сдаться.

На собственной онлайн платформе тебя ждут
Домашние задания, которые необходимо решать после каждого занятия.
Все задания построены на базе создателей ЕГЭ — Котова / Лискова.

К каждому тестовому вопросу будет подробный разбор от главного куратора.
А задания, где необходимо оценить ответ (вторая часть) — будет проверять твой личный куратор и писать подробный комментарий про ошибки

Общий чат единомышленников, поделенный на команды.
Название даете совместно (например «Воробушки»)

Ты будешь двигаться сообща с однокурсниками, поддерживая и мотивируя друг друга.
За лучшую командную успеваемость всей команде будут выделены призы в конце каждого месяца (скидка на обучение, стикерпаки и т.д).

Личный помощник — это твой верный друг и помощник, который поможет тебе со всеми техническими вопросами, ответит на вопросы про поступление, да и просто может обсудить какие-то личные вопросы, поделиться переживаниями.

Доступ к уникальной «Академии косатиков».

Там ты сможешь найти:
Банк теории, банк планов, банк аргументов, курсы по работе со всей второй частью, термины, курсы по саморазвитию, полезные лайфхаки и всю подробную информация о ЕГЭ.

Игровая система на нашей платформе StudyWay👇

За выполнение заданий получаешь баллы (XP).

При достижении нового уровня у тебя открываются новые персонажи из Marvel, DC Comics, Игра престолов и Star Wars, а также на каждом новом уровне тебя ждут призы от нашей школы.

Основная ценность курса
1. Изучение теории и практики с учетом изменений в ЕГЭ 2022
2. Заложение фундамента и основы предмета
3. Прохождение всей теории для первой части
4. Нарешивание всех возможных типов заданий
5. Повышение результата с 0 до 60 баллов

Отличия тарифа «Стандарт от «Профи».

Дополнительные домашние задания
необходимо выполнять. Это значительно повысит твою успеваемость и улучшит показатели.

Дополнительное объяснение
твой личный куратор объяснит тебе тему повторно, если останется что-то не понятным

Групповые зачеты
у тебя будут зачеты с твоим личным куратором в мини группах по 5 человек. Там спрашиваются пройденные темы, термины и так далее.

Карта памяти
будешь восполнять все пройденные в удобной интеллект карте и в конце учебы у тебя выйдет файл с полноценной теорией по всем темам и разделам.

Персональный звонок куратору
1 раз в месяц ты можешь позвонить своему куратору и обсудить все волнующие тебя вопросы в течении 20 минут.

Секретный квест
1 раз в месяц ты будешь созваниваться с другим учеником курса и проводить совместные зачеты, тем самым познакомишься с новыми ребятами из других городов, уберешь страхи знакомства, повторишь и закрепишь пройденные темы.

Видео:11 класс, 12 урок, Показательные уравненияСкачать

РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ, ПОКАЗАТЕЛЬНЫХ, ЛОГАРИФМИЧЕСКИХ, ИРРАЦИОНАЛЬНЫХ, КВАДРАТНЫХ УРАВНЕНИЙ РАЗЛИЧНЫМИ СПОСОБАМИ

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ, ПОКАЗАТЕЛЬНЫХ, ЛОГАРИФМИЧЕСКИХ, ИРРАЦИОНАЛЬНЫХ, КВАДРАТНЫХ УРАВНЕНИЙ РАЗЛИЧНЫМИ СПОСОБАМИ

Джумина Мира Шакировна

ГККП «Технологический колледж»

преподаватель математики высшей категории

Образовательные: Знать приемы устного решения квадратных уравнений.

Развивающие: Развитие логического мышления, памяти, внимания.

Воспитательные: Математической культуры речи, письма.

Форма: общеклассная, индивидуальная, групповая.

Метод: Словесный, наглядный, разноуровневая дифференциация.

Оборудование: ИД, слайды с алгоритмами решения квадратных уравнений; программированные задания, контрольный талон, рейтинговый лист.

Повторительно-обучающая работа по пройденному материалу

Обработка навыков практического применения свойств корня n -ой степени, степени с рациональным показателем, свойств логарифма при вычислении значений выражений (заполнение контрольных талонов)

Исследовательская работа с заполнением таблицы

Выполнение программированного задания

Тема: «Решение всех видов уравнения различными способами»

Под рефлексией понимается «анализ оснований собственных действий, является существенным условием в построении изменения»

Теоретическая разметка «Кросс-опрос»

Алгоритм решения уравнений

Несколько способов решения уравнений

Работа у доски в классе (решение иррациональных, показательных, логарифмических тригонометрических уравнений)

Программированное задание по уровням

Способы решения квадратных уравнений

Подведение итогов (Заполнение рейтинговых листов)

«Надо ли искать ОДЗ?»

Особое внимание в этом плане заслуживают иррациональные, показательные, логарифмические уравнения.

Определение ОДЗ дело далеко не простое и требует от вас не то глубокого значения, но и теоретического материала, но и владения рефлексивной формой деятельности. Под рефлексией понимается «анализ оснований собственных действий, является существенным условием в построении изменения».

Сегодня, вы выступаете в ране исследователей еще одного математического океана, и наш урок пойдет по 2м. направления поиска:

Надо искать ОДЗ?

Не надо искать ОДЗ?

Теоретическая разминка «Кросс – опрос»

Алгоритм решения уравнений:

Иррациональные уравнения на свойствах корня.

Показательные уравнения – на свойствах степени.

Логарифмические уравнения – на свойствах логарифмов.

Тригонометрические уравнения – на свойствах функции.

f (x) = sin x; f (x) = cos x; f (x) = tg x; f (x) = ctg x

Несколько способов решения уравнений

Разложение левой части уравнения на множители

Метод выделения полного квадрата

Решение квадратных уравнений по формуле

Решение уравнений с использованием теоремы Виета

Решение уравнений способом «переброски»

Свойства коэффициентов квадратного уравнения.

Работа в классе

Решить иррациональное уравнение

Пример:

Решить показательное уравнение

Пример:

Решить логарифмическое уравнение

Пример:

Решить тригонометрическое уравнение

Пример: 1999 sin 2 x – 1997 sinx – 2 = 0

Надо ли искать ОДЗ .

Нельзя недооценивать возможности ОДЗ, нельзя и переоценивать

Не существует общего алгоритма решения иррациональных, показательных, логарифмических, тригонометрических уравнений

В математике нет прописных истин и «царских дорог» К каждому уравнению, к каждой задаче нужно подходить творчески

ЗАДАНИЯ ПО УРОВНЯМ

1.

1.

3. log _1/7 x = — 1/ 2

х =

1.

1. х =

х =

1.

1.

х =

1.

1.

х =

х =

1.

1.

х =

Все оценки заносим в рейтинговый лист.

Краткое описание документа:

РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ, ПОКАЗАТЕЛЬНЫХ, ЛОГАРИФМИЧЕСКИХ, ИРРАЦИОНАЛЬНЫХ, КВАДРАТНЫХ УРАВНЕНИЙ РАЗЛИЧНЫМИ СПОСОБАМИ

Джумина Мира Шакировна

ГККП «Технологический колледж»

преподаватель математики высшей категории

Образовательные: Знать приемы устного решения квадратных уравнений.

Развивающие : Развитие логического мышления, памяти, внимания.

Воспитательные: Математической культуры речи, письма.

Форма : общеклассная, индивидуальная, групповая.

Метод: Словесный, наглядный, разноуровневая дифференциация.

Оборудование : ИД, слайды с алгоритмами решения квадратных уравнений; программированные задания, контрольный талон, рейтинговый лист.

1. Организационный момент

2. Повторительно-обучающая работа по пройденному материалу

3. Обработка навыков практического применения свойств корня n -ой степени, степени с рациональным показателем, свойств логарифма при вычислении значений выражений (заполнение контрольных талонов)

4. Исследовательская работа с заполнением таблицы

5. Выполнение программированного задания

6. Комментарии оценок

7. Домашнее задание.

Тема : «Решение всех видов уравнения различными способами»

Под рефлексией понимается «анализ оснований собственных действий, является существенным условием в построении изменения»

1. Организационный момент

2. Повторительно-обучающая работа

3. Теоретическая разметка «Кросс-опрос»

4. Алгоритм решения уравнений

5. Несколько способов решения уравнений

6. Работа у доски в классе (решение иррациональных, показательных, логарифмических тригонометрических уравнений)

7. Программированное задание по уровням

8. Способы решения квадратных уравнений

9. Домашнее задание

10. Подведение итогов (Заполнение рейтинговых листов)

11. Кроссворд математический

1. Организационный момент:

2. Повторительно-обучающая работа

«Надо ли искать ОДЗ?»

Особое внимание в этом плане заслуживают иррациональные, показательные, логарифмические уравнения.

Определение ОДЗ дело далеко не простое и требует от вас не то глубокого значения, но и теоретического материала, но и владения рефлексивной формой деятельности. Под рефлексией понимается «анализ оснований собственных действий, является существенным условием в построении изменения».

Сегодня, вы выступаете в ране исследователей еще одного математического океана, и наш урок пойдет по 2м. направления поиска:

1. Надо искать ОДЗ?

2. Не надо искать ОДЗ?

3. Теоретическая разминка «Кросс – опрос»

4. Алгоритм решения уравнений:

1. Иррациональные уравнения на свойствах корня.

2. Показательные уравнения – на свойствах степени.

3. Логарифмические уравнения – на свойствах логарифмов.

4. Тригонометрические уравнения – на свойствах функции.

f (x) = sin x; f (x) = cos x; f (x) = tg x; f (x) = ctg x

5. Несколько способов решения уравнений

1. Разложение левой части уравнения на множители

2. Метод выделения полного квадрата

3. Решение квадратных уравнений по формуле

4. Решение уравнений с использованием теоремы Виета

5. Решение уравнений способом «переброски»

6. Свойства коэффициентов квадратного уравнения.

6. Работа в классе

Решить иррациональное уравнение

Решить показательное уравнение

Решить логарифмическое уравнение

Решить тригонометрическое уравнение

Пример: 1999 sin 2 x – 1997 sinx – 2 = 0

Надо ли искать ОДЗ .

1. Нельзя недооценивать возможности ОДЗ, нельзя и переоценивать

2. Не существует общего алгоритма решения иррациональных, показательных, логарифмических, тригонометрических уравнений

3. В математике нет прописных истин и «царских дорог» К каждому уравнению, к каждой задаче нужно подходить творчески

7. Программированное задание

ЗАДАНИЯ ПО УРОВНЯМ

3. log 1/7 x = — 1/ 2

3. log 7 ( x – 2) = 3

3. log (1/5) x = — (1/ 2 )

Все оценки заносим в рейтинговый лист.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 949 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 681 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 314 человек из 70 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Алгебра и начала анализа. 11 класс. Показательные, логарифмические, иррациональные уравненияСкачать

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 568 309 материалов в базе

Другие материалы

• 27.11.2014
• 1364
• 1

• 27.11.2014
• 1252
• 0

• 27.11.2014
• 593
• 0

• 27.11.2014
• 796
• 0

• 27.11.2014
• 3394
• 45

• 27.11.2014
• 1032
• 0

• 27.11.2014
• 978
• 0

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 27.11.2014 3210
• DOCX 690 кбайт
• 21 скачивание
• Оцените материал:

Настоящий материал опубликован пользователем Джумина Мира Шакировна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 7 лет и 2 месяца
• Подписчики: 0
• Всего просмотров: 18276
• Всего материалов: 7

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Иррациональные, показательные, логарифмические уравнения + тригонометрия | 12 задание ЕГЭСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В России могут объявить Десятилетие науки и технологий

Время чтения: 1 минута

В Воронеже продлили удаленное обучение для учеников 5-11-х классов

Время чтения: 1 минута

Тринадцатилетняя школьница из Индии разработала приложение против буллинга

Время чтения: 1 минута

Объявлен конкурс дизайн-проектов для школьных пространств

Время чтения: 2 минуты

Рособрнадзор не планирует переносить досрочный период ЕГЭ

Время чтения: 0 минут

Онлайн-конференция о создании школьных служб примирения

Время чтения: 3 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

📺 Видео

ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ 10 класс решение показательных уравненийСкачать

Решение уравнений Показательные, логарифмические, иррациональные ОДЗ для квадратного корняСкачать

Показательные, логарифмические и тригонометрические уравненияСкачать

Решение логарифмических уравнений. Вебинар | МатематикаСкачать

Это просто! Как решать Показательные Неравенства?Скачать

Уравнения с корнем. Иррациональные уравнения #shortsСкачать

Логарифмические уравнения и их системы. Практическая часть. 11 класс.Скачать