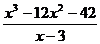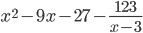Решение по схеме горнера онлайн калькулятор уравнений (8 видео)

Содержание

Метод Горнера. Деление многочлена онлайн
Схема Горнера. Примеры
РЕШЕНИЕ КУБИЧЕСКИХ УРАВНЕНИЙ ПО СХЕМЕ ГОРНЕРА
Деление многочленов столбиком
🌟 Видео

Видео:Вспоминаем схему Горнера и уравнения высших степенейСкачать

Метод Горнера. Деление многочлена онлайн

Коэффициенты многочлена разделенные пробелами

Коэффициент C в биноме вида x-C

Заданный многочлен имеет вид

если разделим его

Получим многочлен

и остаток

Рассмотрим процедуру деления многочлена вида

результат деления есть функция вида

Такой результат получается только в результате деления исходного многочлена на бином без остатка.

В общем же случае говорится, что функцию можно представить в виде

где r — это остаток от деления.

Коэффициенты функции рассчитываются по рекуррентным ф ормулам

Схема Горнера очень удобна своей простой и отсутствием функции деления. Это позволяет решать с повышенной точностью подобные уравнения, а также решать целочисленные уравнения, без каких либо машинных(компьютерных) погрешностей.

Кстати!

Есть новый калькулятор который осуществляет деление многочлена на многочлен с остатком . Работает в том числе и в комплексном поле, кроме того, делящий многочлен может быть на самом деле многочленом(!), а не биномом, как в этой статье.

Кроме этого, эта же схема позволяет решать задачу определения значения функции при каком либо значении. «Фи!» — скажете Вы. «Это же элементарно, любой калькулятор это может».

да конечно, поставивив вместо неизвестного x необходимое значение мы получим нам нужный результат, но какой ценой?

Нам придется возводить значения в степень, что несомненно внесет свою погрешность в расчеты.

Это явно проявляется при работе в поле комплексных чисел, при делении многочлена на комплексный бином.

Нам проще воспользоватся теоремой Безу, которая гласит: Остаток r от деления многочлена на на линейный двучлен равен значению многочлена при

Бот созданный на этом сайте, позволяет Вам решать поставленную задачу методом Горнера, не только для действительных чисел, но и для комплексных. Это расширяет возможности применения бота и позволяет более полно исследовать функцию.

Если делящий многочлен не является одночленом, то стоит воспользоватся калькулятором который делит произвольные многочлены друг на друга с вычислением остатка.Деление многочлена на многочлен.Division of complex polynomials Теперь рассмотрим примеры.

разделить с остатком

Пишем коэффициенты 2 0 -3 2 и через точку запятой -2. Надеюсь понятно почему пишем -2, а не+2 ?

Заданный многочлен имеет вид

если разделим его

Получим многочлен

и остаток

Следующий пример исходный полином тот же, но значение С будет комплексным например 1+i

Пишем коэффициенты 2 0 -3 2 и через точку запятой 1+i

Заданный многочлен имеет вид

если разделим его

Получим многочлен

и остаток

Таким образом мы можем писать любые значения, в том числе и комплексные, в коэффицентах как делимого полинома так и делящего бинома

Видео:Схема Горнера. 10 класс.Скачать

Схема Горнера. Примеры

РЕШЕНИЕ КУБИЧЕСКИХ УРАВНЕНИЙ ПО СХЕМЕ ГОРНЕРА

4x 3 — 19x 2 + 19x + 6 = 0

Для начала нужно методом подбора найти один корень. Обычно он является делителем свободного члена. В данном случае делителями числа 6 являются ±1, ±2, ±3, ±6.

1: 4 — 19 + 19 + 6 = 10 ⇒ число 1 не является корнем многочлена

-1: -4 — 19 — 19 + 6 = -36 ⇒ число -1 не является корнем многочлена

2: 4 ∙ 8 — 19 ∙ 4 + 19 ∙ 2 + 6 = 0 ⇒ число 2 является корнем многочлена

Мы нашли 1 из корней многочлена. Корнем многочлена является 2, а значит исходный многочлен должен делиться на x — 2. Для того, чтобы выполнить деление многочленов, воспользуемся схемой Горнера:

4	-19	19	6
2

В верхней строке выставляются коэффициенты исходного многочлена. В первой ячейке второй строки ставится найденный нами корень 2. Во второй строке пишутся коэффициенты многочлена, который получится в результате деления. Они считаются так:

4	-19	19	6
2	4

Во вторую ячейку второй строки запишем число 1, просто перенеся его из соответствующей ячейки первой строки.

4	-19	19	6
2	4	-11

2 ∙ 4 — 19 = -11

4	-19	19	6
2	4	-11	-3

2 ∙ (-11) + 19 = -3

4	-19	19	6
2	4	-11	-3	0

2 ∙ (-3) + 6 = 0

Последнее число — это остаток от деления. Если он равен 0, значит мы все верно посчитали.

Таким образом мы исходный многочлен разложили на множители:

4x 3 — 19x 2 + 19x + 6 = (x — 2)(4x 2 — 11x — 3)

И теперь, всего лишь, осталось найти корни квадратного уравнения

4x 2 — 11x — 3 = 0
D = b 2 — 4ac = (-11) 2 — 4 ∙ 4 ∙ (-3) = 169
D > 0 ⇒ уравнение имеет 2 корня

Видео:Схема ГорнераСкачать

Деление многочленов столбиком

Алгоритм деления в столбик применяется в частности при нахождении интегралов.

Решение онлайн
Видеоинструкция

Пример деления в столбик . Найти частное деления и остаток многочлена:

№1.

x 3 -12x 2 -42	x -3
x 3 -3x 2	x 2
-9x 2 -42

№2.

x 3 -12x 2 -42	x -3
x 3 -3x 2	x 2 -9x
-9x 2 -42
-9x 2 + 27x
-27x -42

№3.

x 3 -12x 2 -42	x -3
x 3 -3x 2	x 2 -9x -27
-9x 2 -42
-9x 2 + 27x
-27x -42
-27x + 81
-123

Целая часть: x 2 -9x -27
Остаток: -123

Таким образом, ответ можно записать как:
см. также и другие примеры решение столбиком.

Пример №1 . Найти частное и остаток от деления многочлена на многочлен:
P(x)=2x 5 +3x 3 -x 2 +4x+1, Q(x)=2x 2 -x+1

Пример №2 . Не производя деление найти остаток от деления многочлена на двучлен:
P(x)=-x 4 +6x 3 -2x 2 +x-2, Q(x)=x-6
Решение. Выделим общий множитель (x-6).
-x 3 (x-6)-2x(x-6)-12x+x-2 = -x 3 (x-6)-2x(x-6)-11(x-6)-66-2 = -x 3 (x-6)-2x(x-6)-11(x-6)-68
Остаток от деления: -68/(x-6)