На практике часто приходится решать уравнения с частными производными методом конечных разностей (МКР). При этом производные заменяются соответствующими разностями (рис. 4.5.)
Первая краевая задача для уравнения (4.44) формулируется так: требуется найти решение уравнения (4.44), удовлетворяющее краевым условиям:
т.е. требуется найти решение U(x, t) в прямоугольнике, ограниченном прямыми t = 0, x = 0, x = l, t = T, если заданы значения искомой функции на трех его сторонах: t = 0, x =0, x = l (рис. 4.5).
Покроем нашу область прямоугольной сеткой, образованной прямыми x = ih, t = kl (i, k = 1, 2,…), и будем определять приближенные значения решения в узлах сетки. Введем обозначения: . Напишем вместо уравнения (4.44) соответствующее ему уравнение в конечных разностях для точки , получим (для (4.64)):
Из формулы (4.66) следует, что если известны три значения в k-м ряду , то определяется значение в k+1-м ряду (слое). Нам известны все значения на прямой t = 0. Значения в крайних точках этого отрезка нам известны в силу (4.64). Так, ряд за рядом мы определим значения искомого решения во всех узлах сетки [18].
Формула (4.66) упрощается, если шаг l по оси t выбрать так, чтобы или . В этом случае уравнение (4.66) будет:
Указанным методом решение определяется в узлах сетки. Решение между узлами сетки можно получить, например, экстраполированием, проводя плоскость через каждые три точки в пространстве (x, t, u).
Замечание. По аналогии с одномерным случаем вывода уравнения теплопроводности легко можно получить уравнение теплообмена в пространстве и на плоскости.
Элемент стержня следует заменить на элемент объема .
Количество тепла, затраченное на повышение температуры за dt заменяется на , а общее количество тепла, затраченное на повышение температуры в объёме за время dt, будет , но, с другой стороны, это тепло, поступившее в объем за время dt, определяется: , где – единичный вектор нормали к поверхности S, ограничивающей объем . Баланс дает:
(здесь использовали формулу Остроградского из векторного анализа). Заменяя поверхностный интеграл тройным, получим:
Применив теорему о среднем, получим:
для некоторой точки объема . Но мы выделили произвольный объем в пространстве, где идет процесс передачи тепла, а подынтегральная функция непрерывна, поэтому последнее равенство имеет место в каждой точке пространства:
где – оператор Лапласа. Уравнение (4.68) и есть уравнение теплопроводности в пространстве. Для нахождения его единственного решения задают краевые условия.
Если искомая функция U(x,y,z,t) не зависит от z, то получаем уравнение теплопроводности тепла на плоскости:
Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00
Видео:Решение первой краевой задачи для неоднородного уравнения теплопроводности.Скачать

Первая краевая задача с подвижными границами для уравнения теплопроводности
УДК 517.958, 519.711.3, 519.6
ПЕРВАЯ КРАЕВАЯ ЗАДАЧА С ПОДВИЖНЫМИ ГРАНИЦАМИ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
1, Та Чунг Тхань2
Национальный исследовательский Иркутский государственный технический университет,
Изучена первая краевая задача с подвижными границами и найдены решения численным методом конечных разностей, а также проведена оценка точности полученных приближенных решений. Разработана и апробирована методика численного решения первой краевой задачи с подвижными границами для уравнения теплопроводности.
Ил. 6. Табл. 1. Библиогр. 12 назв.
Ключевые слова: уравнение теплопроводности; краевая задача; разностные схемы; системы линейных алгебраических уравнений.
FIRST BOUNDARY-VALUE PROBLEM WITH MOVABLE BOUNDARIES FOR HEAT CONDUCTION EQUATION
E. K. Boltvina№, T. Ta Chung І
National Research Irkutsk State Technical University,
83 Lermontov St., Irkutsk, 664074
The authors have studied the first boundary-value problem with movable boundaries and revealed the solutions by the numerical method of finite differences. In addition, the authors have evaluated the accuracy of the approximate solutions. The researchers have developed and tested a method for numerical solution of the first boundary-value problem with movable boundaries for the heat conduction equation.
Illustrations: 6 pic. Table 1. Sources: 12 refs.
Keywords: heat conduction equation, boundary-value problem, finite-difference schemes, system of linear algebraic equations
Многие задачи механики и физики приводят к исследованию дифференциальных уравнений с частными производными второго порядка. Их изучение дает возможность построить теорию широкого круга физических явлений и решить ряд физических и технических задач, которые встречаются в различных областях науки и приложениях [1–2].
Так, например, процессы распространения тепла связаны с изучением поведения температурного поля 


где константа 



Для этого уравнения рассматривается краевая задача специального вида и решения методом конечных разностей на основе явной, неявной схем и схемы Кранка-Николсона.
Данное уравнение представляет собой дифференциальную форму записи основного закона теплопроводности (закона Фурье), если предположить, что температурная функция 


Уравнение теплопроводности описывает процесс, протекающий в некоторой области с неравномерной температурой. В этой области возникают тепловые потоки, направленные из мест с более высокой температурой в места с более низкой температурой, иначе говоря, происходит теплообмен и, согласно закону Фурье, количество теплоты, проходящее через изотермическую поверхность площадью 




Результатами работы стали постановка задачи специального вида с подвижными границами и реализация её численного решения с применением модифицированной разностной схемы.
Обзор известных методов решения
Существует ряд методов для решения уравнения теплопроводности. Укажем наиболее важные методы, пригодные для практического использования.
Методы, которые позволяют свести уравнение теплопроводности к обыкновенным дифференциальным уравнениям или их системам: метод интегральных преобразований, метод разделения переменных (метод Фурье), метод преобразования координат.
К численным (приближенным) методам решения относятся: разложение в ряды Фурье (применяются к линейным задачам), методы Ритца и Галеркина (применимы и к некоторым нелинейным задачам), разностный метод (в случае нелинейных задач является итерационным; построение хорошо сходящихся итерационных процессов оказывается достаточно сложным, но во многих случаях – это единственный способ решить уравнение теплопроводности) [7, с. 262], методы, основанные на аппроксимации решения полиномиальными поверхностями, метод Монте-Карло (для задач, полностью неразрешимых другими методами из-за сложной природы физических систем, таких как нейтронная цепная реакция в системе с размножением; эксперимент моделируется на ЭВМ с использованием случайных чисел и известных вероятностных законов для элементарных процессов) [8, с. 323–326].
Метод теории возмущений (линеаризации) позволяет исходную нелинейную задачу свести к последовательности аппроксимирующих её линейных задач. Сущность метода функции Грина – начальные и граничные условия заменяются системой простейших источников, и задача решается для каждого такого источника. Метод интегральных уравнений – уравнение теплопроводности сводится к интегральному. Вариационные методы заключаются в том, что вместо уравнения с частными производными решается некоторая задача минимизации, поскольку функция, доставляющая минимум некоторому выражению, является в то же время решением исходного уравнения. При использовании метода разложения по собственным функциям решение ищется в виде ряда по собственным функциям, которые находятся как решения так называемой задачи на собственные значения, соответствующей исходной задаче для уравнения теплопроводности [9, с. 11].
Постановка первой краевой задачи
При интегрировании дифференциального уравнения в частных производных получается бесконечное множество различных решений. Чтобы получить из этого множества одно частное решение, соответствующее определенной конкретной задаче, необходимо иметь дополнительные данные, не содержащиеся в исходном дифференциальном уравнении. Этими дополнительными условиями являются начальные условия, геометрическая форма области и закон взаимодействия между окружающей средой и поверхностью области (граничные условия). Для области определенной геометрической формы с определенными (известными) физическими свойствами совокупность граничных и начальных условий называется краевыми условиями. Итак, начальное условие является временным краевым условием, а граничные условия – пространственным краевым условием [2, 4].
Дифференциальное уравнение теплопроводности (1) вместе с краевыми условиями составляет краевую задачу для уравнения теплопроводности (или тепловую задачу).
Если на границах 



где 




то задачу (1)–(3) называют первой краевой задачей для уравнения теплопроводности (1) [11].
Первая краевая задача является наиболее естественной и поэтому наиболее изучаемой краевой задачей в математической физике.
Метод конечных разностей для решения первой краевой задачи
Основным способом численного решения уравнения теплопроводности является разностный метод или метод сеток, заключающийся в аппроксимации производных конечными разностями, поскольку найти точное решение краевой задачи в элементарных функциях удается редко.
Сущность этого наиболее универсального численного метода заключается в том, что на область изменения независимых переменных 
















Поскольку уравнение теплопроводности зависит от производных неизвестных функций по двум переменным, то вариантов аппроксимации разностными уравнениями одного и того же уравнения может быть несколько. В зависимости от выбранного шаблона, получаются те или иные разностные схемы, в связи с чем, они подразделяются на несколько групп. Наиболее важная классификация разностных схем связана с отнесением их к явным или неявным — представлено на рис. 1. Указанные разностные схемы можно записать в общем виде с параметром 



при 


Видео:Решение уравнения теплопроводности методом конечных разностейСкачать

Численное решение уравнения теплопроводности методом конечных разностей
Область решения на плоскости двух переменных для уравнения теплопроводности преобразуется в дискретную сетку из узлов Здесь — целые числа. Узлы сетки ; , где — шаги сетки по координатам и соответственно, — целые числа.
Неизвестная функция , участвующая в краевой задаче, заменяется сеточной функцией на узлах сетки. Частные производные по координатам заменяются соответствующими конечными разностями. Пусть — шаг сетки вдоль рассматриваемой координаты, — значение функции в рассматриваемой точке , а и последующее и предыдущее значения функции по данной координате. Тогда первая производная по этой координате может быть заменена следующей конечной разностью
а вторая производная выглядит следующим образом:
Для первой производной по времени конечная разность имеет вид
А для второй производной по координате конечная разность выглядит следующим образом:
Чтобы написать разностную схему, приближенно описывающую решаемую задачу, нужно выполнить следующие два шага.
- 1. Необходимо заменить область непрерывного значения аргумента областью его дискретного изменения.
- 2. Необходимо заменить производные соответствующими конечными разностями, а также сформулировать разностный аналог для краевых условий и начальных данных.
После осуществления такой процедуры мы приходим к алгебраической системе уравнений. Таким образом, задача о численном решении исходной начально-краевой задачи для дифференциального уравнения теплопроводности сводится к вопросу о нахождении решения полученной алгебраической системы. Остановимся на этих вопросах подробнее.
При численном решении задачи мы не можем воспроизвести разностное решение для всех значений аргумента, изменяющегося внутри некоторой области. В выбранной области необходимо задать конечное множество точек и приближенное решение искать только в этих точках. Такое множество точек называется сеткой, а отдельные точки называют узлами сетки.
Функция, определенная в узлах сетки, называется сеточной функцией. Таким образом, мы заменили область непрерывного изменения аргумента областью дискретного значения аргумента.
Пример 1. Равномерная сетка на отрезке. Разобьем единичный отрезок [0,1] на равных частей. Расстояние между соседними узлами назовем шагом сетки. Точки деления — узлы сетки.
Пример 2. Равномерная сетка на плоскости. Рассмотрим множество функций двух аргументов . В качестве области определения выберем прямоугольник
Разобьем отрезки [0,1] оси и [0,T] оси соответственно на и частей, пусть . Через точки деления проведем прямые, параллельные соответствующим осям. В результате пересечения этих прямых получим узлы , которые и образуют сетку. Эта сетка имеет шаги h и ф соответственно по направлениям x и t.
Область изменения переменных задачи следующая . Заменяем непрерывные переменные дискретными:
— граничные условия на левом конце, — граничные условия на правом конце.
Заменяем частные производные их конечно-разностными аппроксимациями
Подставим эти выражения в уравнение и разрешим получившееся соотношение относительно ui+1,j, то есть значения функции в верхнем временном слое
Это и есть искомая формула, выражающая решение в данный момент времени через решение в предыдущий момент времени.
Граничные условия имеют следующие сеточные аналоги. Условиям теплоизолированных концов
очевидно, должны соответствовать условия вида
Условия, соответствующие заданным потокам,
заменяются, соответственно, для левого конца
Аналогично, для правого конца
При рассмотрении задачи о распределении температуры в тонком теплоизолированном кольце граничные условия в конечно-разностном виде приводят к системе двух линейных уравнений с двумя неизвестными. При этом первое уравнение выглядит так
Значение, которому равны эти величины, легко вычисляется.
Рассмотрим теперь случай , что соответствует заданию температуры среды, окружающей левый торец стержня. Конечно-разностный аналог этого условия примет вид
Для правого торца выражение определяется аналогичным образом.
Численное моделирование теплопроводности в пакете MATLAB
Рассмотрим численное решение уравнения теплопроводности для одномерного стержня, боковая поверхность которого теплоизолирована, на торцах заданы граничные условия, моделирующие фиксированные значения температуры. Уравнение теплопроводности в этом случае записывается в виде
Рассмотрим решение этого уравнения на интервале времени 0?t?4. Переменная x изменяется в пределах -5?x?5. Граничные условия представлены в виде на левом конце, на правом конце стержня. Начальные условия для распределения температуры были заданы в виде функции
Чтобы решить представленную задачу, нужно создать m-файл следующего вида
%решение одномерного уравнения теплопроводности
%векторы x и t с начальным условием u(x,t(1))=init
📸 Видео
Решение первой начально-краевой задачи для одномерного уравнения теплопроводности.Скачать

Лекция №1.1 Явная и неявная схемы для уравнения теплопроводностиСкачать

Решение уравнения теплопроводности в одномерной постановке в ExcelСкачать

Решение задачи Коши для уравнения теплопроводности (Часть 1)Скачать

6-2. Метод сетокСкачать

Решение задачи теплопроводности методом конечных разностейСкачать
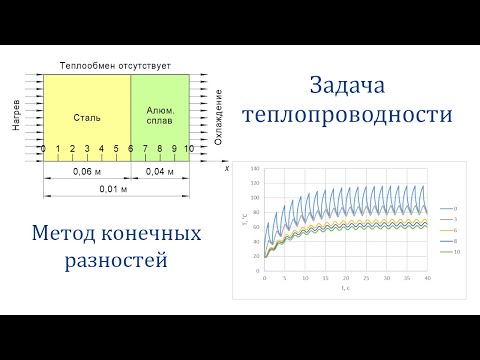
Стационарное решение одномерного уравнения теплопроводности.Скачать

8.1 Решение уравнения теплопроводности на отрезкеСкачать

Метод Фурье для неоднородного уравнения теплопроводностиСкачать

Численные методы математической физики - Решение смешанной задачи для уравнения теплопроводностиСкачать

Метод конечных элементов (Часть 1) | Пример реализации для уравнения теплопроводностиСкачать

Решение первой начально-краевой задачи для волнового уравнения.Скачать

От краевых задач к решению уравнения теплопроводностиСкачать

6-1. Уравнение теплопроводностиСкачать

Одномерное уравнение теплопроводности. Виды краевых задачСкачать

Численные методы. Лекция 14: метод конечных разностей решения краевой задачиСкачать

Уравнение в частных производных Уравнение теплопроводностиСкачать

Решение нестационарного уравнения теплопроводности в двухмерной постановке в ExcelСкачать





























