Решение неполной системы линейных уравнений (3 видео)

$ AlexLat $

Пусть задана система m линейных алгебраических уравнений с n неизвестными общего вида (СЛАУ) в матричной форме:

A – основная матрица системы (или матрица коэффициентов при неизвестных)

X – вектор-столбец решений системы (вектор неизвестных)

B – вектор свободных коэффициентов

Решением системы такого вида называется всякий n – компонентный вектор-столбец X, обращающий матричное уравнение в тождество (равенство).

Найдём решение с помощью метода последовательных исключений Жордана-Гаусса, который заключается в последовательном исключении неизвестных. Дополнительно выделим из множества решений вектор-решения минимальный по Евклидовой норме.

В MatLab стандартная функция rref(A), …/matlab/toolbox/matlab/matfun/rref.m, приводит матрицу A к треугольному виду на основе классического метода исключения Гаусса с частичным выбором ведущего элемента. В данной функции реализуется следующий код: который, не меняя местами столбцы матрицы системы, приводит матрицу к диагональному виду, работая только со строками(таким образом, использование этой функции не приведетк ошибкам).

% Loop over the entire matrix.

% Перебор каждого элемента матрицы

while (i j = j + 1;

Для этого, с помощью элементарных преобразований над строками и перестановки столбцов расширенную матрицу системы A|B (матрица, образованная добавлением столбца свободных коэффициентов B к основной матрице системы A) приведём к виду:

Необходимо отметить, что коэффициенты и полученной матрицы, отличаются от исходных коэффициентов расширенной матрицы. То есть получены новые – основная матрица системы Ấ и вектор-столбец свободных коэффициентов ß. Перемножив каждую строку матрицы Ấ на вектор X получим:

Тогда вектор-решения состоит из следующих компонент

, где k = 1 m

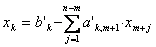
Заменим на коэффициенты j = 1 n-m. Общее решение СЛАУ имеет вид

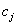
Подставляя различные числовые значения вместо можно получить бесконечное множество частных решений.

Теперь из множества полученных решений необходимо выделить минимальное по Евклидовой норме, то есть найти соответствующие значения .

Евклидова норма: 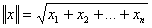. Составим функцию

. Нахождение решения минимального по норме эквивалентно нахождению значений компонентов вектора-решений в точке минимума функции F. По необходимому признаку экстремума функции нескольких переменных и в силу выпуклости функции вниз минимум функции соответствует условиям:

Т.к. функция является положительно определенной квадратичной функцией, то частные производные по всем переменным являются линейными функциями от этих переменных::

Таким образом условием минимума функции является решение системы линейных уравнений:

Построим матричную форму этой системы:

Решая эту систему получим искомое значение коэффициентов 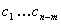при которых вектор-решений X минимален по Евклидовой норме.

В MatLab: C = E D; Откуда вектор минимального по норме решения равен

, где k = 1 m.

Содержание

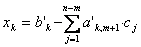
Исследование СЛАУ. Общие сведения
Общие сведения (определения, условия, методы, виды)
Ранг матрицы и его свойства
Решение задач по математике онлайн
Калькулятор онлайн. Решение систем линейных алгебраических уравнений (СЛАУ) Метод Гаусса, матричный метод, метод Крамера, исследование на совместность (теорема Кронекера-Капелли), определение количества решений, нахождение нормальной фундаментальной системы решений.
Немного теории.
Системы линейных алгебраических уравнений
Основные определения
Формы записи СЛАУ
Критерий совместности СЛАУ
Формулы Крамера
Однородные системы
Неоднородные системы
🌟 Видео

Видео:ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

Исследование СЛАУ. Общие сведения

В данной статье мы расскажем о методах, видах, условиях и определениях исследований решений систем линейных уравнений, что такое метод Кронекера-Капели, а также приведем примеры.

Видео:Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Общие сведения (определения, условия, методы, виды)

Системы линейных алгебраических уравнений с n неизвестными могут иметь:

единственное решение;
бесконечное множество решение (неопределенные СЛАУ);
ни одного решения (несовместные СЛАУ).

Пример 1

Система x + y + z = 1 2 x + 2 y + 2 z = 3 не имеет решений, поэтому она несовместна.

Система x + y = 1 2 x + 7 y = — 3 имеет единственное решение x = 2 ; y = 1 .

Система x + y = 1 2 x + 2 y = 2 3 x + 3 y = 3 имеет бесконечное множество решений x = t y = 1 — t при — ∞ t ∞ .

Перед решением системы уравнений необходимо исследовать систему, т.е. ответить на следующие вопросы:

Совместна ли система?
Если система совместна, то, какое количество решений она имеет — одно или несколько?
Как найти все решения?

Если система малоразмерна при m = n , то ответить на поставленные вопросы можно при помощи метода Крамера:

если основной определитель системы, то система совместна и имеет единственное решение, которое вычисляется методом Крамера;
если, и один из вспомогательных определителей, то система не является совместной, т.е. не имеет решений;
если и все, и один из коэффициентов СЛАУ, то система не является определенной и имеет бесконечное множество решений.

Видео:Решение систем уравнений методом подстановкиСкачать

Ранг матрицы и его свойства

Бывают случаи, которые выбиваются из представленных вариантов решения СЛАУ, например, линейные уравнения с большим количеством уравнений и неизвестных.

Для такого варианта решения существует ранг матрицы, который представляет собой алгоритм действий в случае решения системы матрицы, когда

В математике выделяют следующие подходы к определению ранга матрицы:

при помощи понятия линейной зависимости/независимости строк/столбцов матрицы. Ранг равен максимальному количеству независимых строк (столбцов) матрицы
при помощи понятия минора матрицы в качестве наивысшего порядка минора, который отличается от нуля. Минор матрицы порядка k — определитель k-го порядка, составленный из элементов, которые стоят на пересечении вычеркиваемых k-строк и k-столбцов матрицы;
при помощи метода Гаусса. По завершении прямого хода ранг матрицы равняется количеству ненулевых строк.

Обозначение ранга матрицы: r ( A ) , r g ( A ) , r A .

Свойства ранга матрицы:

квадратная невырожденная матрица обладает рангом, который отличается от нуля;
если транспонировать матрицу, то ранг матрицы не изменяется;
если поменять местами 2 параллельные строки или 2 параллельных столбца, ранг матрицы не изменяется;
при удалении нулевого столбца или строки ранг матрицы не изменяется;
ранг матрицы не изменяется, если удалить строку или столбец, которые являются линейной комбинацией других строк;
при умножении все элементов строки/столбца на число k н е р а в н о н у л ю ранг матрицы не изменяется;
ранг матрицы не больше меньшего из ее размеров: r ( А ) ≤ m i n ( m ; n ) ;
когда все элементы матрицы равны нулю, то только тогда r ( A ) = 0 .

Пример 2

А 1 = 1 1 1 2 2 2 3 3 3 , B 1 = 1 0 0 0 0 0

r ( A 1 ) = 1 , r ( B 1 ) = 1

А 2 = 1 2 3 4 0 5 6 7 0 0 0 0 ; В 2 = 1 1 3 1 2 1 4 3 1 2 5 0 5 4 13 6

Видео:Неоднородная система линейных уравненийСкачать

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Видео:Решение системы уравнений методом ГауссаСкачать

Калькулятор онлайн.
Решение систем линейных алгебраических уравнений (СЛАУ)
Метод Гаусса, матричный метод, метод Крамера, исследование на совместность (теорема Кронекера-Капелли), определение количества решений, нахождение нормальной фундаментальной системы решений.

С помощью данной математической программы вы можете решить и исследовать систему линейных алгебраических уравнений (СЛАУ).

Программа не только даёт ответ задачи, но и приводит подробное решение с пояснениями шагов решения.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Ввод дробного числа в виде десятичной дроби.
При вводе десятичной дроби, целую часть от дробной части можно отделять точкой или запятой :
Ввод: -2.34
Результат: ( -234 )

Ввод: -1,15
Результат: ( -115 )

Ввод дробного числа в виде обыкновенной дроби.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.

При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: $$ -frac $$

Целая часть отделяется от дроби знаком амперсанд: &
Ввод: 5&8/3
Результат: $$ 5frac $$
Помните, что на ноль делить нельзя!

RND CFracNum Fill RND int Fill Start MathJax
Сюда ввести строку с GET параметрами :

Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Немного теории.

Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Системы линейных алгебраических уравнений

Основные определения

Система (m) линейных алгебраических уравнений с (n) неизвестными (сокращенно СЛАУ) представляет собой систему вида
( left< begin a_x_1 + a_x_2 + cdots + a_x_n = b_1 \ a_x_1 + a_x_2 + cdots + a_x_n = b_2 \ cdots \ a_x_1 + a_x_2 + cdots + a_x_n = b_m end right. tag )

Уравнения системы называют алгебраическими потому, что левая часть каждого из них есть многочлен от (n) переменных ( x_1 , ldots x_n ), а линейными потому, что эти многочлены имеют первую степень.

Числа (a_ in mathbb ) называют коэффициентами СЛАУ. Их нумеруют двумя индексами: номером уравнения (i) и номером неизвестного (j). Действительные числа ( b_1 , ldots b_m ) называют свободными членами уравнений.

СЛАУ называют однородной, если ( b_1 = b_2 = ldots = b_m = 0 ). Иначе её называют неоднородной.

Решением СЛАУ, да и вообще всякой системы уравнений, называют такой набор значений неизвестных ( x_1^circ, ldots , x_n^circ ), при подстановке которых каждое уравнение системы превращается в тождество. Любое конкретное решение СЛАУ также называют её частным решением.

Решить СЛАУ — значит решить две задачи:
— выяснить, имеет ли СЛАУ решения;
— найти все решения, если они существуют.

СЛАУ называют совместной, если она имеет какие-либо решения. В противном случае её называют несовместной. Однородная СЛАУ всегда совместна, поскольку нулевой набор значений её неизвестных всегда является решением.

Если СЛАУ (1) имеет решение, и притом единственное, то её называют определенной, а если решение неединственное — то неопределенной. При (m=n), т.е. когда количество уравнений совпадает с количеством неизвестных, СЛАУ называют квадратной.

Формы записи СЛАУ

Кроме координатной формы (1) записи СЛАУ часто используют и другие её представления.

Рассматривая коэффициенты (a_) СЛАУ при одном неизвестном (x_j) как элементы столбца, а (x_j) как коэффициент, на который умножается столбец, из (1) получаем новую форму записи СЛАУ:
( begin a_ \ a_ \ vdots \ a_ end x_1 + begin a_ \ a_ \ vdots \ a_ end x_2 + ldots + begin a_ \ a_ \ vdots \ a_ end x_n = begin b_1 \ b_2 \ vdots \ b_m end )
или, обозначая столбцы соответственно ( a_1 , ldots , a_n , b ),
( x_1 a_1 + x_2 a_2 + ldots + x_n a_n = b tag )

Таким образом, решение СЛАУ (1) можно трактовать как представление столбца (b) в виде линейной комбинации столбцов ( a_1, ldots, a_n ). Соотношение (2) называют векторной записью СЛАУ.

Поскольку (A ;,; X) и (B) являются матрицами, то запись СЛАУ (1) в виде (AX=B) называют матричной. Если (B=0), то СЛАУ является однородной и в матричной записи имеет вид (AX=0).

Приведенные рассуждения показывают, что задачи :
а) решения СЛАУ (1)
б) представления столбца в виде линейной комбинации данных столбцов
в) решения матричных уравнений вида (AX=B)
являются просто различной формой записи одной и той же задачи.

Критерий совместности СЛАУ

«Триединство» форм записи СЛАУ позволяет легко получить критерий совместности СЛАУ. Напомним, что содержательный смысл это понятие имеет для неоднородных СЛАУ (однородные СЛАУ всегда совместны).

Матрицу
( A = begin a_ & a_ & cdots & a_ \ a_ & a_ & cdots & a_ \ vdots & vdots & ddots & vdots \ a_ & a_ & cdots & a_ end )
называют матрицей (коэффициентов) СЛАУ (1), а матрицу
( (A|B) = left( begin a_ & a_ & cdots & a_ & b_1 \ a_ & a_ & cdots & a_ & b_2 \ vdots & vdots & ddots & vdots & vdots \ a_ & a_ & cdots & a_ & b_m end right) )
расширенной матрицей СЛАУ (1). Расширенная матрица полностью характеризует СЛАУ. Это означает, что по этой матрице однозначно (если сохранить обозначения для неизвестных) восстанавливается сама СЛАУ.

Теорема Кронекера-Капелли. Для совместности СЛАУ (AX=B) необходимо и достаточно, чтобы ранг её матрицы (A) был равен рангу её расширенной матрицы ( (A|B) ).

Формулы Крамера

Теорема. СЛАУ с квадратной невырожденной матрицей имеет решение, и притом единственное, которое определяется по формулам Крамера :
$$ x_i = frac ;,quad i=overline tag $$
где (Delta_i) — определитель матрицы, получающейся из матрицы (A) заменой (i)-го столбца на столбец свободных членов.

Следствие. Однородная СЛАУ с квадратной невырожденной матрицей имеет единственное решение — нулевое.

Если матрица СЛАУ не является квадратной невырожденной, то формулы Крамера не работают и приходится использовать другие методы нахождения решений.

Однородные системы

Теорема. Если столбцы ( X^, X^, ldots , X^ ) — решения однородной СЛАУ (AX=0), то любая их линейная комбинация также является решением этой системы.

Следствие. Если однородная СЛАУ имеет ненулевое решение, то она имеет бесконечно много решений.

Естественно попытаться найти такие решения ( X^, ldots , X^ ) системы (AX=0), чтобы любое другое решение этой системы представлялось в виде их линейной комбинации и притом единственным образом. Оказывается, что это всегда возможно и приводит к следующему определению.

Определение. Любой набор из (k=n-r) линейно независимых столбцов, являющихся решениями однородной СЛАУ (AX=0), где (n) — количество неизвестных в системе, а (r) — ранг её матрицы (A), называют фундаментальной системой решений этой однородной СЛАУ.

При исследовании и решении однородных систем линейных алгебраических уравнений будем использовать следующую терминологию. Если в матрице (A) однородной СЛАУ (AX=0) фиксировать базисный минор, то ему соответствуют базисные столбцы и, следовательно, набор неизвестных, отвечающих этим столбцам. Указанные неизвестные называют базисными, или зависимыми, а остальные неизвестные — свободными, или независимыми.

Теорема. Пусть дана однородная СЛАУ (AX=0) с (n) неизвестными и ( textA = r ). Тогда существует набор из (k=n-r) решений ( X^, ldots , X^ ) этой СЛАУ, образующих фундаментальную систему решений.

Если в фундаментальной системе решений все значения независимых неизвестных равны нулю, кроме одного, которое равно единице, то такую систему решений называют фундаментальной нормальной системой решений.

Следствие. С помощью нормальной фундаментальной системы решений однородной СЛАУ множество всех решений можно описать формулой :
$$ X = c_1X^ + ldots + c_kX^ $$
где постоянные ( c_i ;, quad i=overline ), принимают произвольные значения.

Следствие. Для существования ненулевого решения у однородной квадратной СЛАУ необходимо и достаточно, чтобы её матрица была вырождена.

Неоднородные системы

Рассмотрим произвольную СЛАУ (AX=B). Заменив столбец (B) свободных членов нулевым, получим однородную СЛАУ (AX=0), соответствующую неоднородной СЛАУ (AX=B). Справедливо следующее утверждение о структуре произвольного решения неоднородной СЛАУ.

Теорема. Пусть столбец (X^circ) — некоторое решение СЛАУ (AX=B). Произвольный столбец (X) является решением этой СЛАУ тогда и только тогда, когда он имеет представление (X = X^circ + Y ), где (Y) — решение соответствующей однородной СЛАУ (AY=0).

Следствие. Пусть (X’) и (X») — решения неоднородной системы (AX=B). Тогда их разность ( Y = X’ — X» ) является решением соответствующей однородной системы (AY=0).

Эта теорема сводит проблему решения СЛАУ к случаю однородной системы: чтобы описать все решения неоднородной СЛАУ, достаточно энать одно её решение (частное решение) и все решения соответствующей однородной СЛАУ.

Чтобы решить неоднородную систему, надо, во-первых, убедиться, что она совместна (например, по теореме Кронекера-Капелли), а во-вторых, найти частное решение (X^circ) этой системы, чтобы свести её к однородной системе.

Теорема о структуре общего решения СЛАУ. Пусть (X^circ) — частное решение СЛАУ (AX=B) и известна фундаментальная система решений ( X^, ldots , X^ ) соответствующей однородной системы (AX=0). Тогда любое решение СЛАУ (AX=B) можно представить в виде $$ X = X^circ + c_1 X^ + c_2 X^ + ldots + c_k X^ $$
где ( c_i in mathbb ;, quad i=overline ).
Эту формулу называют общим решением СЛАУ.