Решение нелинейных уравнений в матлабе fzero (6 видео)

Решение нелинейных уравнений в Matlab

Доброго времени суток. В этой статье мы разберем решение простых нелинейных уравнений с помощью средств Matlab. Посмотрим в действии как стандартные функции, так и сами запрограммируем три распространенных метода для решения нелинейных уравнений.

Содержание

Общая информация
Стандартные функции Matlab
Метод перебора Matlab
Метод простых итераций Matlab
Метод половинного деления Matlab
Заключение
fzero
Syntax
Description
Examples
Root Starting From One Point
Root Starting From an Interval
Root of a Function Defined by a File
Root of Function with Extra Parameter
Nondefault Options
Solve Problem Structure
More Information from Solution
Input Arguments
fun — Function to solve function handle | function name
x0 — Initial value scalar | 2-element vector
Решение нелинейных уравнений в матлабе fzero
🎦 Видео

Общая информация

Уравнения, которые содержат переменные, находящиеся в степенях, отличающихся от единицы, или имеющие нелинейные математические выражения (корень, экспонента, логарифм, синус, косинус и т.д.), а также имеющие вид f(x) = 0 называются нелинейными. В зависимости от сложности такого уравнения применяют методы для решения нелинейных уравнений.

В этой статье, помимо стандартных функций Matlab, мы рассмотрим следующие методы:

Метод перебора
Метод простых итераций
Метод половинного деления

Рассмотрим коротко их алгоритмы и применим для решения конкретной задачи.

Стандартные функции Matlab

Для решения нелинейных уравнений в Matlab есть функция fzero. Она принимает в качестве аргументов саму функцию, которую решаем, и отрезок, на котором происходит поиск корней нелинейного уравнения.

И сразу же разберем пример:

Решить нелинейное уравнение x = exp(-x), предварительно определив интервалы, на которых существуют решения уравнения.

Итак, для начала следует привести уравнение к нужному виду: x — exp(-x) = 0 , а затем определить интервалы, в которых будем искать решение уравнения. Методов для определения интервалов множество, но так как пример достаточно прост мы воспользуемся графическим методом.

Здесь задали примерные границы по оси x, чтобы можно было построить график и посмотреть как ведет себя функция. Вот график:

Из графика видно, что на отрезке [0;1] есть корень уравнения (там, где y = 0), соответственно в дальнейшем будем использовать этот интервал. Чем точнее выбран интервал, тем быстрее метод придет к решению уравнения, а для сложных уравнений правильный выбор интервала определяет погрешность, с которой будет получен ответ.

С помощью стандартной функции Matlab находим корень нелинейного уравнения и выводим. Теперь для проверки отобразим все это графически:

Как вы видите, все достаточно точно просчиталось. Теперь мы исследуем эту же функцию с помощью других методов и сравним полученные результаты.

Метод перебора Matlab

Самый простой метод, который заключается в том, что сначала задается какое то приближение x (желательно слева от предполагаемого корня) и значение шага h. Затем, пока выполняется условие f(x) * f(x + h) > 0, значение x увеличивается на значение шага x = x + h. Как только условие перестало выполняться — это значит, что решение нелинейного уравнения находится на интервале [x; x + h].

Теперь реализуем метод перебора в Matlab:

Лучше всего создать новый m-файл, в котором и прописать код. После вызова получаем такой вывод:

Функцию объявляем с помощью очень полезной команды inline, в цикле пока выполняется условие отсутствия корней (или их четного количества), прибавляем к x значение шага. Очевидно, что чем точнее начальное приближение, тем меньше итераций необходимо затратить.

Метод простых итераций Matlab

Этот метод заключается в том, что функцию преобразуют к виду: x = g(x). Эти преобразования можно сделать разными способами, в зависимости от вида начальной функции. Помимо этого следует задать интервал, в котором и будет производиться итерационный процесс, а также начальное приближение. Сам процесс строится по схеме x_n= g(x_n-1). То есть итерационно проходим от предыдущего значения к последующему.

Процесс заканчивается как только выполнится условие: , то есть, как только будет достигнута заданная точность. И сразу же разберем реализацию метода простых итераций в Matlab для примера, который был приведен выше.

Здесь должно быть все понятно, кроме одного: зачем задавать число итераций? Это нужно для того, чтобы программа не зацикливалась и не выполняла ненужные итерации, а также потому что не всегда программа может просчитать решение с нужной точностью — поэтому следует ограничивать число итераций.

А вот и вывод программы:

Очевидно, что метод простых итераций работает гораздо быстрее и получает точное решение.

Метод половинного деления Matlab

Метод достаточно прост: существует отрезок поиска решения [a;b], сначала находят значение функции в точке середины c, где c = (a+b)/2. Затем сравнивают знаки f(a) и f(c). Если знаки разные — то решение находится на отрезке [a;c], если нет — то решение находится на отрезке [c;b]. Таким образом мы сократили область в 2 раза. Такое сокращение происходит и дальше, пока не достигнем заданной точности.

Перейдем к реализации метода в Matlab:

Все самое важное происходит в цикле: последовательно сокращаем область нахождения решения, пока не будет достигнута заданная точность.
Вот что получилось в выводе:

Этот метод хорошо работает, когда правильно определен интервал, на котором находится решение. Тем не менее, метод простых итераций считается наиболее точным и быстрым.

Заключение

Сегодня мы рассмотрели решение нелинейных уравнений в Matlab. Теперь нам известны методы перебора, половинного деления, простых итераций. А также, когда нам не важно реализация метода, то можно использовать стандартную функцию в Matlab.

На этом все — спасибо за внимание. В следующей статье мы разберем решение систем нелинейных уравнений в matlab.

Видео:MATLAB Video 17: fzero functionСкачать

fzero

Root of nonlinear function

Видео:1 - Решение систем нелинейных уравнений в MatlabСкачать

Syntax

Видео:Решение системы нелинейных уравнений. Урок 139Скачать

Description

x = fzero( fun , x0 ) tries to find a point x where fun(x) = 0 . This solution is where fun(x) changes sign— fzero cannot find a root of a function such as x^2 .

x = fzero( fun , x0 , options ) uses options to modify the solution process.

x = fzero( problem ) solves a root-finding problem specified by problem .

[ x , fval , exitflag , output ] = fzero( ___ ) returns fun(x) in the fval output, exitflag encoding the reason fzero stopped, and an output structure containing information on the solution process.

Видео:2 - Решениt систем линейных алгебраических уравнений (СЛАУ) с помощью Matlab.Скачать

Examples

Root Starting From One Point

Calculate π by finding the zero of the sine function near 3 .

Root Starting From an Interval

Find the zero of cosine between 1 and 2 .

Note that cos ( 1 ) and cos ( 2 ) differ in sign.

Root of a Function Defined by a File

Find a zero of the function f( x) = x 3 – 2 x – 5.

First, write a file called f.m .

Save f.m on your MATLAB ® path.

Find the zero of f( x) near 2 .

Since f(x) is a polynomial, you can find the same real zero, and a complex conjugate pair of zeros, using the roots command.

Root of Function with Extra Parameter

Find the root of a function that has an extra parameter.

Nondefault Options

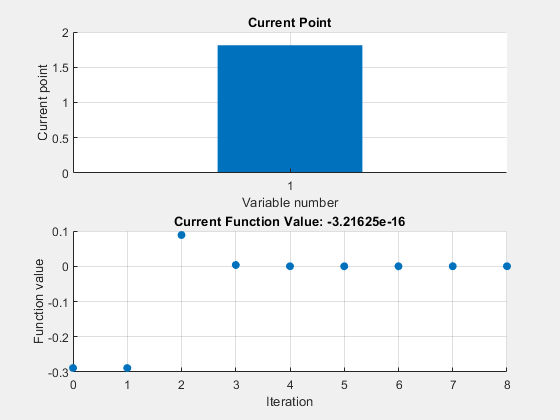
Plot the solution process by setting some plot functions.

Define the function and initial point.

Examine the solution process by setting options that include plot functions.

Run fzero including options .

Solve Problem Structure

Solve a problem that is defined by a problem structure.

Define a structure that encodes a root-finding problem.

Solve the problem.

Input Arguments

fun — Function to solve
function handle | function name

Function to solve, specified as a handle to a scalar-valued function or the name of such a function. fun accepts a scalar x and returns a scalar fun(x) .

fzero solves fun(x) = 0 . To solve an equation fun(x) = c(x) , instead solve fun2(x) = fun(x) — c(x) = 0 .

To include extra parameters in your function, see the example Root of Function with Extra Parameter and the section Parameterizing Functions.

Example: ‘sin’

Example: @myFunction

Example: @(x)(x-a)^5 — 3*x + a — 1

Data Types: char | function_handle | string

x0 — Initial value
scalar | 2-element vector

Initial value, specified as a real scalar or a 2-element real vector.

Scalar — fzero begins at x0 and tries to locate a point x1 where fun(x1) has the opposite sign of fun(x0) . Then fzero iteratively shrinks the interval where fun changes sign to reach a solution.

2-element vector — fzero checks that fun(x0(1)) and fun(x0(2)) have opposite signs, and errors if they do not. It then iteratively shrinks the interval where fun changes sign to reach a solution. An interval x0 must be finite; it cannot contain ± Inf .

Tip

Calling fzero with an interval ( x0 with two elements) is often faster than calling it with a scalar x0 .

Видео:Стрим с Борисом Надеждиным, Алексеем Ракшей и Боженой ИвановойСкачать

Решение нелинейных уравнений в матлабе fzero

Вычисление нулей функции одной переменной

Ряд функций системы MATLAB предназначен для работы с функциями. По аналогии с дескрипторами графических объектов могут использоваться объекты класса дескрипторов функций, задаваемых с помощью символа @, например: » fe=@exp.

Подфункциями понимаются как встроенные функции, например sin(x) или ехр(х),так и функции пользователя, например f(x), задаваемые как т-файлы-функции.

Численные значения таких функций, заданных дескрипторами, вычисляются с помощью функции feval:

Для совместимости с прежними версиями можно записывать функции в символьном виде в апострофах, использование функции eval для их вычисления может быть более наглядно, не нужно создавать m-файл, но в учебном курсе мы будем стараться использовать новую нотацию, с использованием дескрипторов функций и feval, так как при этом программирование становится «более объектно-ориентированным», повышается скорость, точность и надежность численных методов. Поэтому, хотя везде в нижеследующем тексте вместо @fun можно подставить и символьное значение функции в апострофах, мы будем использовать нотацию @fun в дидактических целях. Все же иногда в интерактивном режиме можно использовать старую запись, чтобы не создавать m-файл функции.

Довольно часто возникает задача решения нелинейного уравнения вида f(x) = О или/, (г) =/ ₂ (дг). Последнее, однако, можно свести к виду f(x) =f ₁ (х) — f ₂ (х) = 0. Таким образом, данная задача сводится к нахождению значений аргумента х функции f(x) одной переменной, при котором значение функции равно нулю. Соответствующая функция MATLAB, решающая данную задачу, приведена ниже:

fzero(@fun,x) — возвращает уточненное значение х, при котором достигается нуль функции fun, представленной в символьном виде, при начальном значении аргумента х. Возвращенное значение близко к точке, где функция меняет знак, или равно NaN, если такая точка не найдена;

fzero(@fun,[xl x2]) — возвращает значение х, при котором fun(x)=0 с заданием интервала поиска с помощью вектора x=[xl х2], такого, что знак fun(x(D) отличается от знака fun(x(2)). Если это не так, выдается сообщение об ошибке. Вызов функции fzero с интервалом гарантирует, что fzero возвратит значение, близкое к точке, где fun изменяет знак;

fzero(@fun,x.tol) — возвращает результат с заданной погрешностью tol;

fzero(@fun,x.tol .trace) — выдает на экран информацию о каждой итерации;

fzero(@fun,х.tol .trace,Р1.Р2. ) — предусматривает дополнительные аргументы, передаваемые в функцию fun(x.Pl,P2. ). При задании пустой матрицы для tol или trace используются значения по умолчанию. Пример:

Для функции fzero ноль рассматривается как точка, где график функции fun пересекает ось х, а не касается ее. В зависимости от формы задания функции fzero реализуются следующие хорошо известные численные методы поиска нуля функции: деления отрезка пополам, секущей и обратной квадратичной интерполяции. Приведенный ниже пример показывает приближенное вычисление р/2 из решения уравнения cos(x)=0 с представлением косинуса дескриптором:

В более сложных случаях настоятельно рекомендуется строить график функции f(x) для приближенного определения корней и интервалов, в пределах которых они находятся. Ниже дан пример такого рода (следующий листинг представляет собой содержимое m-файла fun1.m):

%Функция, корни которой ищутся

Из рисунка нетрудно заметить, что значения корней заключены в интервалах [0.5 1], [2 3] и [5 6]. Найдем их, используя функцию fzero:

Обратите внимание на то, что корень хЗ найден двумя способами и что его значения в третьем знаке после десятичной точки отличаются в пределах заданной погрешности tol =0.001. К сожалению, сразу найти все корни функция fzero не в состоянии. Решим эту же систему при помощи функции f sol ve из пакета Optimization Toolbox, которая решает систему нелинейных уравнений вида f(x)=0 методом наименьших квадратов, ищет не только точки пересечения, но и точки касания, f solve имеет почти те же параметры (дополнительный параметр — задание якобиана) и почти ту же запись, что и функция lsqnonneg, подробно рассмотренная ранее. Пример:

Columns 1 through 7

0.8905 0.8905 2.8500 2.8500 2.8500 5.8128 5.8128

Columns 8 through 11

5.8128 2.8500 2.8500 10.7429

Для решения систем нелинейных уравнений следует также использовать функцию solve из пакета Symbolic Math Toolbox. Эта функция способна выдавать результат в символьной форме, а если такого нет, то она позволяет получить решение в численном виде. Пример:

» solve(‘0.25*x + sin(x) -1) [ Пакеты расширения Symbolic Math ToolBox и Extended Symbolic Math Toolbox MATLAB 6.0 используют ядро Maple V Release 5 30 и являются поэтому исключением: они пока не поддерживают новую нотацию с использованием дескрипторов функций. — Примеч. ред. ]