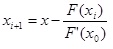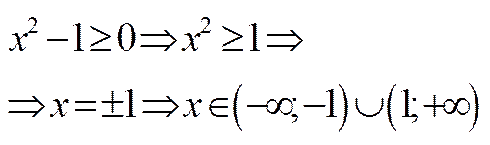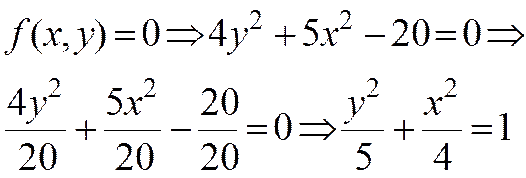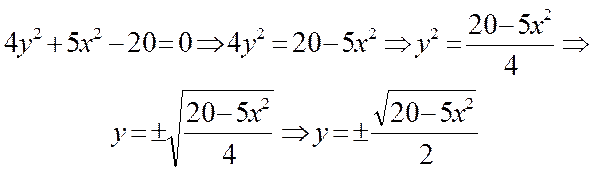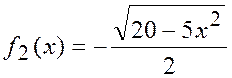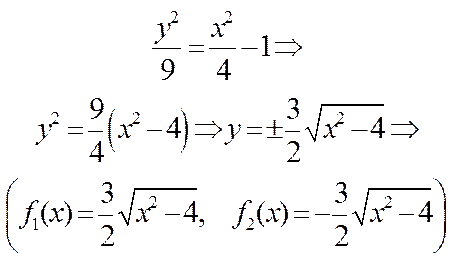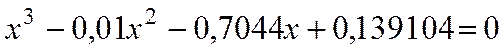Чтобы найти ее оптимальное решение, нужно выполнить следующие действия:
- Найти ОДР, определяемую ограничениями задачи. Если окажется, что эта область пуста, то это означает, что задача не имеет решения.
- Построить семейство линий уровня целевой функции f(х1, х2) = C при различных значениях числового параметра С.
- При решении задачи на минимум определить направление убывания, а для задачи на максимум — направление возрастания линий уровня ЦФ.
- Найти точку ОДР, через которую проходит линия уровня с наименьшим в задаче на минимум (соответственно, наибольшим в задачи на максимум) значением параметра С. Эта точка будет оптимальным решением. Если ЦФ не ограничена снизу в задаче на минимум (сверху — в задаче на максимум), то это означает, что задача не имеет оптимального решения.
- Найти координаты точки оптимума и определить в ней значение ЦФ.
Отметим, что в отличие от задачи ЛП точка оптимума в задаче НП не обязательно находится на границе ОДР. Ею также может быть внутренняя точка этого множества.
Пример . В задаче выпуклого программирования требуется:
- найти решение графическим методом;
- написать функцию Лагранжа и найти ее седловую точку, используя решение, полученное графически.
F(X) = x1 2 +(x2-2) 2
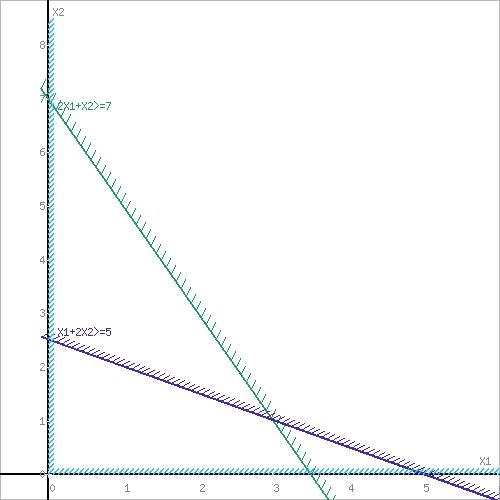
2x1+x2 ≥ 7
x1+2x2 ≥ 5
Решение. 1) Строим два ограничения, тем самым определяя ОДР. Можно использовать этот калькулятор. Также удобно строить ограничения через этот сервис.
Затем строим функцию цели. В данном случае это окружность.
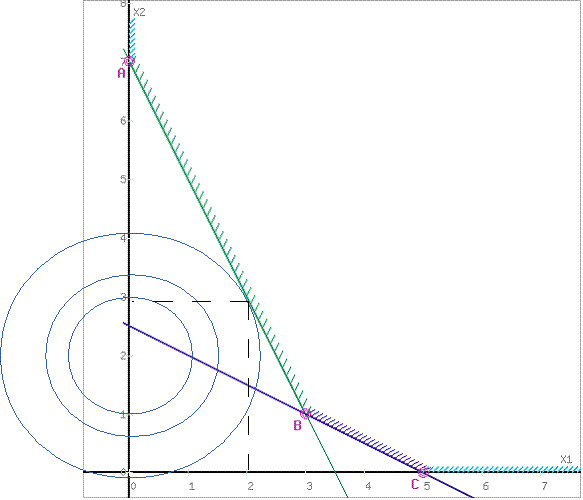
Поскольку задача минимума, то ищем первое касание линии уровня области ОДР. В данном случае это точка пересечения с прямой 2x1+x2-7=0.
Найдем точку пересечения. Для этого построим уравнение касательной, проходящей через центр окружности O(0;2) и перпендикулярно прямой 2x1+x2-7=0 (можно использовать этот калькулятор). Получаем: 2x2-x1-4=0. Решая систему уравнений:
2x1+x2-7=0
2x2-x1-4=0,
получаем: x1=2, x2=3.
2) Найдем экстремум функции F(X) = x1 2 +(x2-2) 2 , используя калькулятор Функция Лагранжа :
L( X , λ )=F( X )+∑(λi·φi)
где F( X ) — целевая функция вектора X; φi(X) — ограничения в неявном виде (i=1..n)
В качестве целевой функции, подлежащей оптимизации, в этой задаче выступает функция: F(X) = x1 2 +(x2-2) 2
Перепишем ограничение задачи в неявном виде:
φ1(X) = 7 — (2*x1+x2) = 0 (X1)
φ2(X) = 5 — (x1+2*x2) = 0 (X2)
Составим вспомогательную функцию Лагранжа: L(X, λ) = x1 2 +(x2-2) 2 — λ1*(7 — (2*x1+x2)) — λ2*(5 — (x1+2*x2))
Необходимым условием экстремума функции Лагранжа является равенство нулю ее частных производных по переменным хi и неопределенным множителям λ.
Составим систему:
∂L/∂x1 = 2*λ1+λ2+2*x1 = 0
∂L/∂x2 = λ1+2*λ2+2*x2-4 = 0
∂L/∂λ1 = 2*x1+x2-7 = 0
∂L/∂λ2 = x1+2*x2-5 = 0
Решив данную систему, получаем:
а) для случая X1: x1 = λ1/2 + λ2 + 2; x2 = 7 — 2x1
Откуда можно найти такие λ1 ≥ 0, λ2 ≥ 0. Пусть λ2 = 0. Тогда λ1 = 2; x1 = 2; x2 = 3.
Поскольку λ2 ≥ 0, то данное решение удовлетворяет условиям Куна-Таккера. Zmin(2;3)=5
б) для случая X2: x2 = λ1/2 + λ2 + 2; x1 = 5 — 2x2
Откуда можно найти такие λ1 ≥ 0, λ2 ≥ 0. Пусть λ2 = 0. Тогда λ1 = 2/5; x1 = 11/5; x2 = 3/5.
Поскольку λ1 ≥ 0, то данное решение удовлетворяет условиям Куна-Таккера. Zmin(11/5;3/5)=6.8
Минимальное значение составит Zmin(2;3)=5.
Видео:Способы решения систем нелинейных уравнений. 9 класс.Скачать

Решение нелинейных уравнений
Уравнения, в которых содержатся неизвестные функции, произведенные в степень больше единицы, называются нелинейными.
Например, y=ax+b – линейное уравнение, х^3 – 0,2x^2 + 0,5x + 1,5 = 0 – нелинейное (в общем виде записывается как F(x)=0).
Системой нелинейных уравнений считается одновременное решение нескольких нелинейных уравнений с одной или несколькими переменными.
Существует множество методов решения нелинейных уравнений и систем нелинейных уравнений, которые принято относить в 3 группы: численные, графические и аналитические. Аналитические методы позволяют определить точные значения решения уравнений. Графические методы наименее точны, но позволяют в сложных уравнениях определить наиболее приближенные значения, с которых в дальнейшем можно начинать находить более точные решения уравнений. Численное решение нелинейных уравнений предполагает прохождения двух этапов: отделение корня и его уточнение до определенно заданной точности.
Отделение корней осуществляется различными способами: графически, при помощи различных специализированных компьютерных программ и др.
Рассмотрим несколько методов уточнения корней с определенно заданной точностью.
Методы численного решения нелинейных уравнений
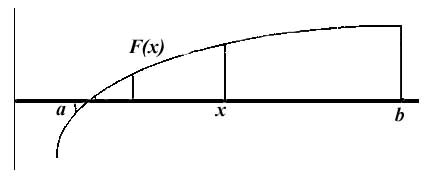
Метод половинного деления.
Суть метода половинного деления заключается в делении интервала [a,b] пополам (с=(a+b)/2) и отбрасывании той части интервала, в которой отсутствует корень, т.е. условие F(a)xF(b)
Рис.1. Использование метода половинного деления при решении нелинейных уравнений.
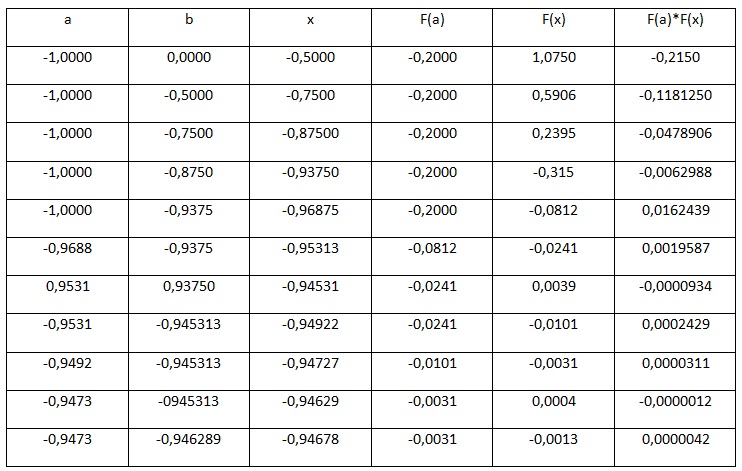
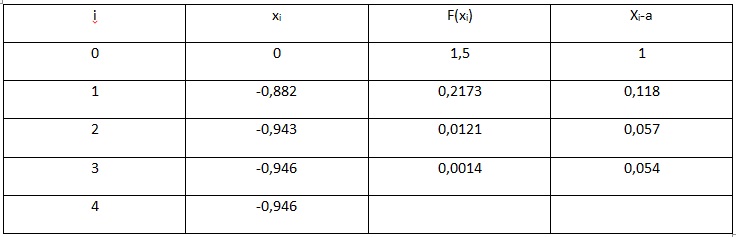
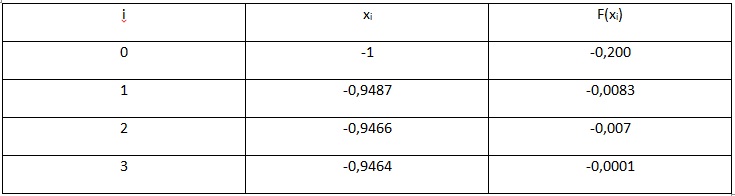
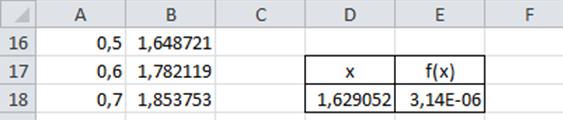
Рассмотрим пример. Необходимо решить уравнение х^3 – 0,2x^2 + 0,5x + 1,5 = 0 с точностью до e 0, то начала отрезка a переносится в x (a=x), иначе, конец отрезка b переносится в точку x (b=x). Полученный отрезок делим опять пополам и т.д. Весь произведенный расчет отражен ниже в таблице.
Рис.2. Таблица результатов вычислений
В результате вычислений получаем значение с учетом требуемой точности, равной x=-0,946
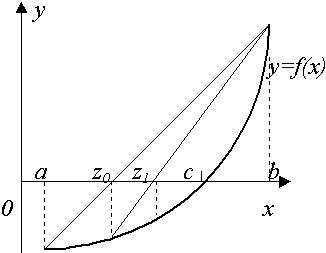
При использовании метода хорд, задается отрезок [a,b], в котором есть только один корень с установленной точностью e. Через точки в отрезке a и b, которые имеют координаты (x(F(a);y(F(b)), проводится линия (хорда). Далее определяются точки пересечения этой линии с осью абсцисс (точка z).
Если F(a)xF(z)
Рис.3. Использование метода хорд при решении нелинейных уравнений.
Рассмотрим пример. Необходимо решить уравнение х^3 – 0,2x^2 + 0,5x + 1,5 = 0 с точностью до e 0;
Определим вторую производную F’’(x) = 6x-0,4.
F’’(-1)=-6,4 0 соблюдается, поэтому для определения корня уравнения воспользуемся формулой:
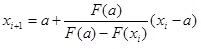
, где x0=b, F(a)=F(-1)=-0,2
Весь произведенный расчет отражен ниже в таблице.
Рис.4. Таблица результатов вычислений
В результате вычислений получаем значение с учетом требуемой точности, равной x=-0,946
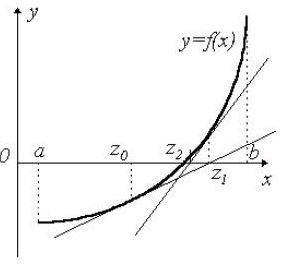
Метод касательных (Ньютона)
Данный метод основывается на построении касательных к графику, которые проводятся на одном из концов интервала [a,b]. В точке пересечения с осью X (z1) строится новая касательная. Данная процедура продолжается до тех пор, пока полученное значение не будет сравним с нужным параметром точности e (F(zi)
Рис.5. Использование метода касательных (Ньютона) при решении нелинейных уравнений.
Рассмотрим пример. Необходимо решить уравнение х^3 – 0,2x^2 + 0,5x + 1,5 = 0 с точностью до e 0 выполняется, поэтому расчеты производим по формуле:
Весь произведенный расчет отражен ниже в таблице.
Рис.6. Таблица результатов вычислений
В результате вычислений получаем значение с учетом требуемой точности, равной x=-0,946
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Видео:Как решать систему уравнений графическим методом? | Математика | TutorOnlineСкачать

Решение нелинейных уравнений.
Построение графиков в EXCEL
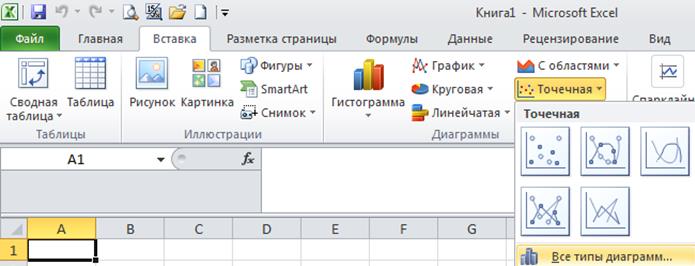
Мастер диаграмм
Вставка → Диаграмма… или кнопка
Вставка → Точечная
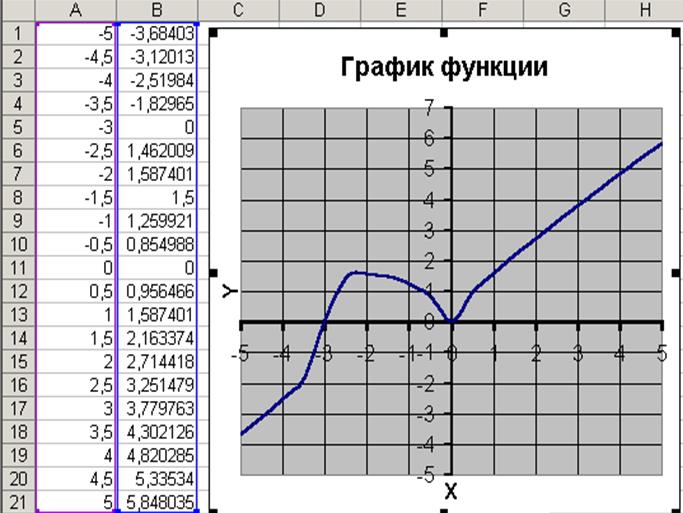
ПРИМЕР 1. Построить график функции 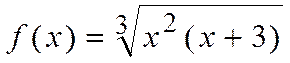
1. Определим функцию f(x).
В ячейки А1:А21 введем значение аргумента при помощи автозаполнения (например, с шагом 0,5).
В ячейку В1 введем значение функции, вычисляемое по формуле
Ячейки В2:В21 заполняются копированием формулы из ячейки В1.
2. Выделим диапазон А1:В21 и воспользуемся Мастером диаграмм. Для построения графика функции лучше выбрать точечную диаграмму, со значениями, соединенными сглаживающими линиями без маркеров.
Чтобы график получился выразительным, можно определить промежуток изменения аргумента, увеличить толщину линий, выделить оси координат, нанести на них соответствующие деления, сделать подписи на осях и вывести заголовок.
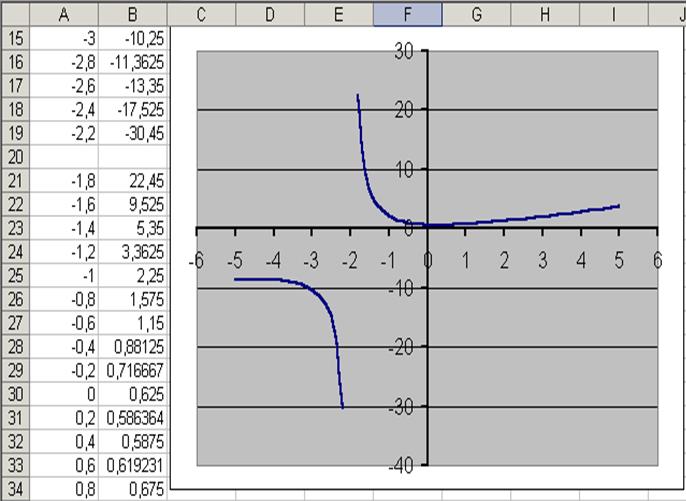
ПРИМЕР 2. Построить график функции 
При построении этого графика следует обратить внимание на область определения функции.
В данном случае функция не существует при обращении знаменателя в ноль. Решим уравнение:
Следовательно, при определении значений аргумента следует помнить, что при 
Зададим значение аргумента в два этапа, не включая (-2) с шагом 0,2.
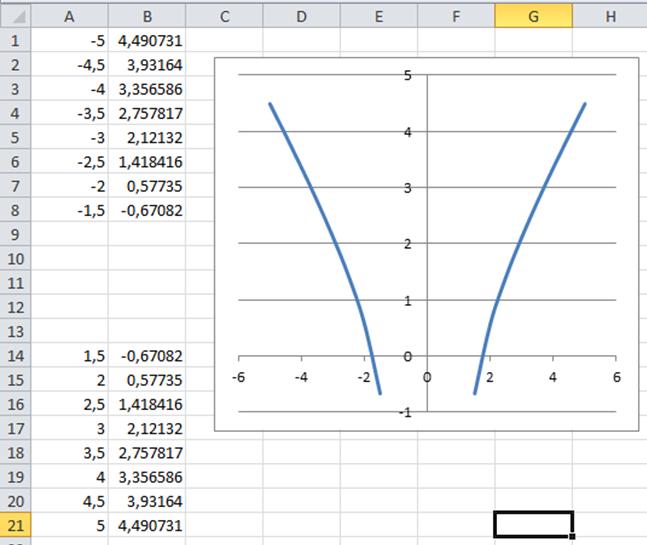
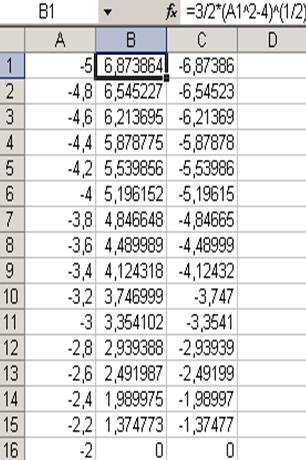
ПРИМЕР 3. Построить график функции 
Определение значения аргумента следует провести в два этапа. Например, от -5 до -1, а затем от 1 до 5.
ПРИМЕР 5. Изобразите линию заданную неявно уравнением:
Заданная уравнением f(x,y)=0функция описывает кривую линию под названием эллипс. Это можно доказать, если произвести элементарные математические операции:
Разрешим заданное уравнение относительно переменной y:
Линию f(x,y) можно изобразить, построив графики двух функций:
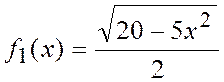
в одной графической области.
Определим ОДЗ функций 
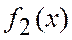
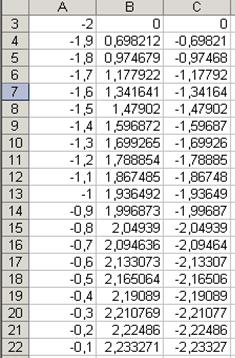
Для построения графика введем значения аргумента в диапазон А3:А43 (от -2 до 2, D=0,1).
В ячейку В3 введем формулу для вычисления значений функции 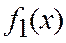
А в ячейку С3 для вычисления значений функции 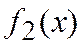
Далее скопируем эти формулы до В43 и С43соответственно.
Затем выделим диапазон А3:С43 и воспользовавшись Мастером диаграмм, построим графики функций 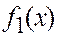
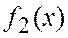
ПРИМЕР 6. Изобразите линию заданную неявно: 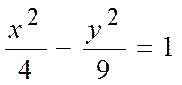
Данное уравнение описывает линию под названием гипербола. Разрешим его относительно переменной y:
Найдем ОДЗ 
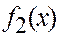
Решение нелинейных уравнений.
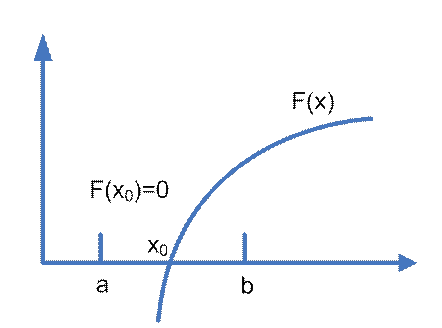
Решением уравнения вида f(x)=0 является такое значение x, при котором функция f(x) обращается в ноль.
Графическим решением уравнения f(x)=0 является точка пересечения графика функции f(x) с осью абсцисс – x0.
Интервал [a, b] на котором находится единственное графическое решение уравнения, называют интервалом изоляции корня.
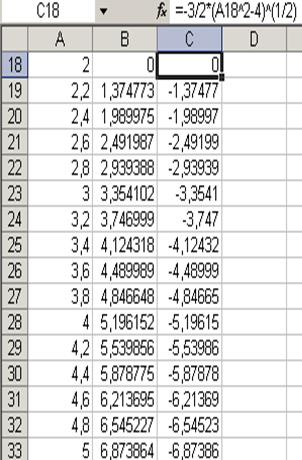
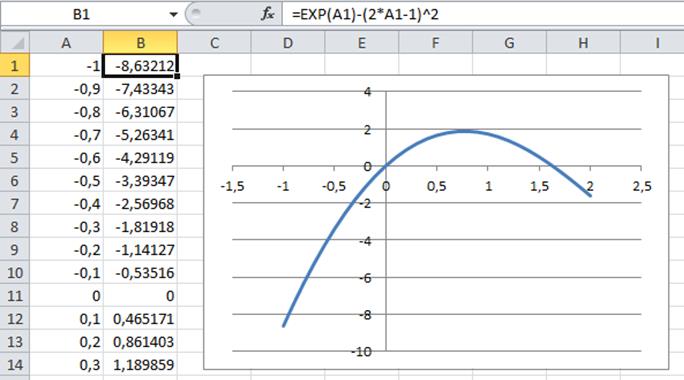
ПРИМЕР 1. Найти корни полинома
Решим уравнение графически.
Проведем табулирование полинома на интервале от -1 до 1 с шагом 0,2. В ячейку В2 введем формулу:
На графике видно, что функция три раза пересекает ось Оx.
Исходя из того, что полином третьей степени имеет не более трех вещественных корней, то графическое решение найдено.
Интервалы изоляции корней полинома:
Найдем корни полинома методом последовательных приближений с помощью команды Сервис®Подбор параметра.
В качестве начальных значений приближений к корням можно взять любые точки из интервалов изоляции. Пусть это будут -0.9, 0.3 и 0.7.
Введем эти значения в лист Excel, например так:
а в ячейку В14 введем формулу:
которую скопируем в ячейки В15 и В16.
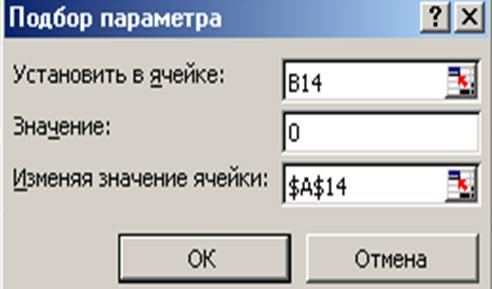
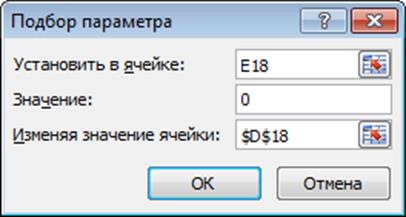
Далее обратимся к пункту меню Сервис®Подбор параметраи заполнить диалоговое окно:
В поле Установить в ячейке дается ссылка на ячейку в которую введена формула, вычисляющая значение левой части уравнения f(x)=0. В нашем случае В14.
В поле Значение вводим правую часть уравнения, т.е. ноль.
В поле Изменяя значения ячейки дается ссылка на ячейку, в которую было введено начальное приближение (А14).
Вводить ссылки на ячейки в поля диалогового окна Подбор параметров удобнее не с клавиатуры, а щелчком на соответствующей ячейке.
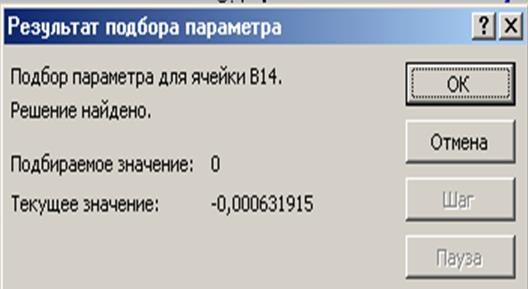
После нажатия кнопки ОКпоявится диалоговое окноРезультат подбора параметрас сообщением об успешном завершении поиска решения и приближенное значение корня будет помещено в ячейку А14.
Два оставшихся корня находим аналогично. Результаты вычислений будут помещены в ячейки А15 и А16.
ПРИМЕР 2. Решить уравнение
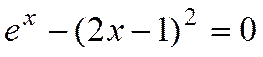
Проведем локализацию корней нелинейного уравнения. Для этого построим график функции 
Уравнение имеет два решения. Одно из них тривиальное и может быть вычислено точно:

Для второго можно определить интервал изоляции корня 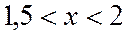
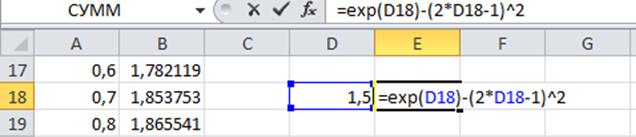
Введём начальное приближение в ячейку D18 и само уравнение, со ссылкой на начальное приближение, в ячейку E18 .
Далее воспользуемся пунктом меню Сервис®Подбор параметра(Excel 2003) или
Данные®Анализ «что если» ® Подбор параметра(Excel 2010)
Заполним диалоговое окно
Результатпоиска решения будет выведен в ячейкуD18
ПРИМЕР 3. Решить систему нелинейных уравнений:
1. Сведем систему к одному уравнению:
2. Решим уравнение графически.
3. Уточним корень X методом последовательных приближений.
📸 Видео
Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Алгебра 8 класс (Урок№6 - Решение уравнений графическим способом.)Скачать

Решение системы уравнений графическим методомСкачать

Графический метод решения систем линейных уравнений 7 классСкачать

Графический способ решения систем уравнений. Алгебра, 9 классСкачать

7 класс, 35 урок, Графическое решение уравненийСкачать

Алгебра 9 класс. Графическое решение систем уравненийСкачать

Решение системы нелинейных уравнений графическим способом средствами ExcelСкачать

Решение системы линейных уравнений графическим методом. Практическая часть. 7 класс.Скачать

Урок по теме ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ СИСТЕМ УРАВНЕНИЙ 7 КЛАСССкачать

Графический метод решения уравнений 8 классСкачать

Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать

Графический способ решения уравнений и неравенств | Алгебра 10 классСкачать

Графический способ решения систем уравнений | Алгебра 9 класс #18 | ИнфоурокСкачать

Решение системы линейных уравнений графическим способом. 7 классСкачать

Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать

Графический способ решения нелинейных уравнений/Алгебра 10Скачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать