Решение квадратных уравнений когда дискриминант меньше нуля (5 видео)

Дискриминант

Содержание

Дискриминантом квадратного трехчлена называют выражение (b^-4ac), где (a, b) и (c) – коэффициенты данного трехчлена.
Дискриминант и корни квадратного уравнения
Значение дискриминанта показывает количество корней квадратного уравнения: — если (D) положителен – уравнение будет иметь два корня; — если (D) равен нулю – только один корень; — если (D) отрицателен – корней нет.
Если дискриминант положителен
Если дискриминант равен нулю
Если дискриминант отрицателен
Квадратные неравенства
Квадратные неравенства имеют вид.
Как решать квадратные неравенства?
Дискриминант квадратного уравнения
Решение квадратных уравнений через дискриминант
📸 Видео

Дискриминантом квадратного трехчлена называют выражение (b^-4ac), где (a, b) и (c) – коэффициенты данного трехчлена.

Например, для трехчлена (3x^2+2x-7), дискриминант будет равен (2^2-4cdot3cdot(-7)=4+84=88). А для трехчлена (x^2-5x+11), он будет равен ((-5)^2-4cdot1cdot11=25-44=-19).

Дискриминант обозначается буквой (D) и часто используется при решении квадратных уравнений . Также по значению дискриминанта можно понять, как примерно выглядит график квадратичной функции (см. ниже).

Видео:Решение квадратных неравенств графическим методом, если дискриминант меньше нуля. 8 класс.Скачать

Дискриминант и корни квадратного уравнения

Значение дискриминанта показывает количество корней квадратного уравнения:
— если (D) положителен – уравнение будет иметь два корня;
— если (D) равен нулю – только один корень;
— если (D) отрицателен – корней нет.

Это не надо учить, к такому выводу несложно прийти, просто зная, что квадратный корень из дискриминанта (то есть, (sqrt) входит в формулу для вычисления корней квадратного уравнения: (x_=) (frac<-b+sqrt>) и (x_=) (frac<-b-sqrt>) . Давайте рассмотрим каждый случай подробнее.

Видео:Отрицательный дискриминантСкачать

Если дискриминант положителен

В этом случае корень из него – это некоторое положительное число, а значит (x_) и (x_) будут различны по значению, ведь в первой формуле (sqrt) прибавляется, а во второй – вычитается. И мы имеем два разных корня.

Пример: Найдите корни уравнения (x^2+2x-3=0)
Решение:

Вычисляем дискриминант по формуле (D=b^2-4ac)

Найдем корни уравнения

Получили два различных корня из-за разных знаков перед (sqrt)

На графике квадратичной функции положительный дискриминант будет означать пересечение функции с осью икс ровно в двух точках – корнях уравнения. И это логично. Вдумайтесь – если уравнение (x^2+2x-3=0) имеет корни (x_=1) и (x_=-3), значит при подстановке (1) и (-3) вместо икса, левая часть станет нулем. А значит, если те же самые единицу и минус тройку подставить в функцию (y=x^2+2x-3) получим (y=0). То есть, функция (y=x^2+2x-3) проходит через точки ((1;0)) и ((-3;0)) (подробнее смотри статью Как построить график функции ).

Видео:Дискриминант меньше нуляСкачать

Если дискриминант равен нулю

А сколько корней будет, если дискриминант равен нулю? Давайте рассуждать.

Формулы корней выглядят так: (x_=) (frac<-b+sqrt>) и (x_=) (frac<-b-sqrt>) . И если дискриминант – ноль, то и корень из него тоже ноль. Тогда получается:

То есть, значения корней уравнения будут совпадать, потому что прибавление или вычитание нуля ничего не меняет.

Пример: Найдите корни уравнения (x^2-4x+4=0)
Решение:

Вычисляем дискриминант по формуле (D=b^2-4ac)

Находим корни уравнения

Получили два одинаковых корня, поэтому нет смысла писать их по отдельности – записываем как один.

На графике квадратичной функции нулевой дискриминант означает одну точку пересечения функции с осью икс. Все аналогично изложенному выше: два корня – две точки пересечения, один корень – одна. В частности, функция (y=x^2-4x+4) будет выглядеть вот так:

Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Если дискриминант отрицателен

В этом случае корень из дискриминанта извлечь нельзя (т.к. квадратный корень из отрицательного числа – невычислим), а значит и корни квадратного уравнения мы вычислить не можем.

Пример: Найдите корни уравнения (x^2+x+3=0)
Решение

Вычисляем дискриминант по формуле (D=b^2-4ac)

Находим корни уравнения

Оба корня содержат невычислимое выражение (sqrt), значит, и сами не вычислимы

То есть, отсутствие корней у квадратного уравнения с отрицательным дискриминантом – не чья-то случайная придумка. Это не потому что «в учебнике так написано», а действительно правда: невозможно найти такое число, чтоб при подстановке его вместо икса в выражение (x^2+x+3) получился ноль.

Матхак: заметим, что если вы решаете обычное квадратное уравнение или неравенство и получаете отрицательный дискриминант, стоит проверить решение еще раз, так как это не частая ситуация в школьном курсе математики.

Ну, а на графиках все просто: нет корней – нет точек пересечения с осью икс!

Видео:Как решать квадратные уравнения ⁉ Дискриминант 🌟 ОБЪЯСНЕНИЕ 🌟 D меньше (равен, больше) нуляСкачать

Квадратные неравенства

Чтобы решить квадратные неравенства вспомним, что такое квадратичная функция?
Квадратичная функция – это функция записанная формулой : y=ax 2 +bx+c, где x – независимая переменная, a, b и c – некоторые числа, при этом a≠0.
Графиком квадратичной функции является парабола.

В зависимости от значения a ветви графика направлены вверх или вниз:

если a>0, то ветви параболы направлены вверх;
если a 2 +bx+c=0

Видео:Решение квадратных неравенств | МатематикаСкачать

Квадратные неравенства имеют вид.

ax 2 +bx+c>0
ax 2 +bx+c 2 +bx+c≥0
ax 2 +bx+c≤0

Чтобы начать решать квадратные неравенства, необходимо знать как решаются квадратные уравнения?
А также для графического метода решения неравенства, необходимо знать алгоритм построения квадратичной функции или параболы?

Видео:Решение квадратных неравенств графическим методом, если дискриминант равен нулю. 8 класс.Скачать

Как решать квадратные неравенства?

Решение квадратных неравенств рассмотрим на примерах. Для начала разберем случаи, когда у квадратного уравнения дискриминант меньше нуля (нет корней).

Пример:

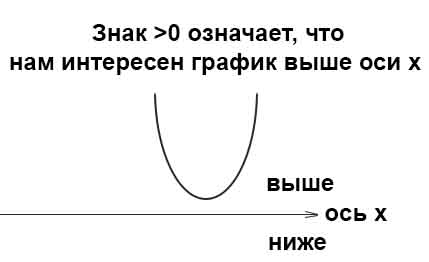
Дискриминант меньше нуля —236, следовательно у уравнения нет корней, а это значит, что весь график параболы находится выше оси х, потому что а=3>0 (ветви параболы смотрят вверх)

Можно проверить себя взяв любое число с числовой прямой, например число 1. Подставить число 1 вместо переменой х в неравенство 3x 2 +2x+20>0.

Получили верное неравенство 25>0, следовательно так как у нас нет корней уравнения нам подойдут все точки числовой прямой.

Пример:

Рассмотрим этот же пример со знаком неравенства меньше 0

3x 2 +2x+20 2 +2x+20=0

Дискриминант меньше нуля —236, следовательно у уравнения нет корней, значит парабола не пересекает ось x. Весь график параболы находится выше оси х, потому что а=3>0.

А знак уравнения меньше 2 +2x+20 2 +2•1+20 2 +x-2 2 +x-2=0

Дискриминант больше нуля, следовательно у уравнения два корня, значит парабола пересекает ось x в точка x=1 и x=-2. Ветви параболы смотрят вверх, потому что а=1>0.

Знак уравнения меньше 2 +x-2 2 +(-3)-2 2 +(0)-2 2 +(2)-2 2 +x-2>0

Знак уравнения больше >0. Нам в ответ необходимо записать часть параболы, которая находится выше оси x. Визуально графически можно оценить по картинке, нам подходят интервалы (-∞;-2) и (1;+∞).

Также можно решить методом интервалов. Ось x делится на три участка.

Первый участок (-∞;-2). На этом участке можно взять любое число меньше -2, например возьмем число -3 и подставим в неравенство x 2 +x-2 2 +(-3)-2>0

Получили верное неравенство 4>0, следовательно этот интервал (-∞; 2) подходит.

Второй участок (-2; 1). На этом участке можно взять число 0.

Получили неверное неравенство -2>0, следовательно этот интервал (-2; 1) не подходит.

Третий участок (1; +∞). На этом участке возьмем число 2.

Получили верное неравенство 4>0, следовательно этот интервал (1; +∞) подходит.

Видео:Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

Дискриминант квадратного уравнения

Дискриминант квадратного уравнения — это выражение, находящееся под корнем в формуле нахождения корней квадратного уравнения. Дискриминант обозначается латинской буквой D.

Вид уравнения	Формула корней	Формула дискриминанта
ax 2 + bx + c = 0		b 2 — 4ac
ax 2 + 2kx + c = 0		k 2 — ac
x 2 + px + q = 0
x 2 + px + q = 0		p 2 — 4q

Все формулы нахождения корней квадратных уравнений можно записать короче с помощью дискриминанта:

Вид уравнения	Формула
ax 2 + bx + c = 0	, где D = b 2 — 4ac
ax 2 + 2kx + c = 0	, где D = k 2 — ac
x 2 + px + q = 0	, где D =
x 2 + px + q = 0	, где D = p 2 — 4q

Дискриминант позволяет определить, имеет ли уравнение корни и сколько их, не решая само уравнение:

Если дискриминант больше нуля, то уравнение имеет два корня.
Если дискриминант равен нулю, то уравнение имеет один корень.
Если дискриминант меньше нуля, то уравнение не имеет корней.

Несмотря на то, что есть несколько формул дискриминанта, чаще всего используют первую:

так как она относится к формуле:

которая является универсальной формулой нахождения корней квадратного уравнения. Данная формула подходит даже для неполных квадратных уравнений.

Видео:Урок 18 как решить квадратное неравенство дискриминант меньше нуляСкачать

Решение квадратных уравнений через дискриминант

Для решения квадратного уравнения по формуле можно сначала вычислить дискриминант и сравнить его с нулём. В зависимости от результата, либо искать корни по формуле, либо сделать вывод, что корней нет.

Пример 1. Решить уравнение:

Определим, чему равны коэффициенты:

D = b 2 — 4ac = (-4) 2 — 4 · 3 · 2 = 16 — 24 = -8,

Определим, чему равны коэффициенты:

D = b 2 — 4ac = (-6) 2 — 4 · 1 · 9 = 36 — 36 = 0,

Уравнение имеет всего один корень: