Решение иррациональных уравнений домножением на сопряженное (6 видео)

Методы решения иррациональных уравнений

Методы решения иррациональных уравнений.

Цели:

Образовательная –познакомить учащихся с нестандартными методами решения иррациональных уравнений; систематизировать знания учащихся о методах решения иррациональных уравнений, способствовать формированию умений классифицировать иррациональные уравнения по методам решений, научить применять эти методы, выбирать рациональный путь решения. Развивающая –способствовать развитию математического кругозора, логического мышления. Воспитательная – содействовать воспитанию интереса к иррациональным уравнениям, воспитывать чувство коллективизма, самоконтроля, ответственности.

1. Повторить определение и основные методы решения иррациональных уравнений;

2. Продемонстрировать нестандартные методы решения иррациональных уравнений; формировать умение выбирать рациональные пути решения;

3. Освоение всеми учащимися алгоритмов решения иррациональных уравнений, закрепление теоретических знаний при решении конкретных примеров;

4. Развитие у учащихся логического мышления в процессе поиска рациональных методов и алгоритмов решения;

5. Развитие культуры научных и учебных взаимоотношений между учениками и между учениками и учителем; воспитание навыков совместного решения задач.

Тип урока:

Методы обучения:

Информационно- иллюстративный; репродуктивный; проблемный диалог; частично-поисковый; системные обобщения.

Формы организации учебной деятельности:

Фронтальная, групповая, самопроверка, взаимопроверка, коллективные способы обучения.

Оборудование урока: компьютер, проектор, карточки с заданием, лист учета знаний.

Продолжительность занятия: 2 урока по 45 минут.

План урока:

I. Организационный момент. Постановка цели, мотивация.

II. Актуализация опорных знаний, проверка домашней работы.

III. Изучение нового материала.

IV. Закрепление изученного материала на данном уроке и ранее пройденного, связанного с новым.

V. Подведение итогов и результатов урока. Рефлексия.

VI. Задание на дом.

I Организационный момент. Постановка цели, мотивация.

II Актуализация опорных знаний проводится в форме беседы по лекционному материалу по данной теме с использованием компьютерной презентации. Проверка домашнего задания.

· Определение иррационального уравнения.

Уравнение, содержащее переменные под знаком корня или дробной степени, называется иррациональным.

Назовите иррациональные уравнения:

· Что значит решить иррациональное уравнение?

Это значит найти все такие значения переменной, при которых уравнение превращается в верное равенство, либо доказать, что таких значений не существует.

· Основные методы решения иррациональных уравнений.

1. Уединение радикала. Возведение в степень.

a) При решении иррационального уравнения с радикалом четной степени возможны два пути:

1) использование равносильных преобразований

для уравнения вида

2) после возведения в степень выполнение проверки, так как возможно появление посторонних корней

b) При решении иррационального уравнения с радикалом нечетной степени возведение в нечетную степень правой и левой части уравнения всегда приводит к равносильному уравнению и потеря корней или их приобретения происходить не может.

Пример 1:

Пример 2:

Пример 3:

Проверка: x=2 x=5

— посторонний корень

Если радикалов несколько, то уравнение возводить в степень приходится возводить неоднократно.

Пример 4:

Проверка показывает, что оба корня подходят.

Ответ:

2. Метод введения вспомогательного неизвестного или “метод замены

Пример 5:

Сделаем замену причём тогда

не удовлетворяет условию

Возвращаемся к замене:

Проверка показывает, что оба корня подходят.

Иногда удобно ввести не одну, а несколько переменных.

Пример 6: .

Заметим, что знаки х под радикалом различные. Введем обозначение

, .

Тогда,

Выполним почленное сложение обеих частей уравнения .

Имеем систему уравнений

Т. к. а + в = 4, то

Значит: 9 – x = 8 , х = 1.

3. Метод разложения на множители или расщепления.

· Произведение равно нулю тогда и только тогда, когда хотя бы один из входящих в него сомножителей равен нулю, а остальные при этом имеют смысл.

Пример 7:

III Изучение нового материала.

Нестандартные методы решения иррациональных уравнений.

4. Умножение на сопряжённое выражение.

5. Переход к модулю.

6. Использование свойств функции:

§ Область определения функции (ОДЗ)

§ Область значения функции

§ Свойство ограниченности функции (метод оценок)

§ Использование суперпозиций функций

· Умножение на сопряжённое выражение.

Воспользуемся формулой

Пример 8:

Умножим обе части уравнения на сопряжённое выражение:

Проверка показывает, что число является корнем.

Ответ:

· Переход к модулю.

Для этого метода воспользуемся тождеством:

Пример 9:

§ Если , то , тогда

тогда

§ Если , тогда ,а

§ Если , тогда , а

· Использование свойств функции:

§ Область определения функции (ОДЗ)

Иногда нахождение области определения функций, входящих в уравнение, существенно облегчает его решение.

Пример 10:

ОДЗ: ОДЗ: x=0 и x=1

Проверка показывает, что только x=1 является корнем.

Ответ:

Пример 11:

, тогда

Тогда невозможно.

Ответ: корней нет.

§ Область значений функции

Пример 12:

Данное уравнение не имеет решений, так как его левая часть — функция может принимать только неотрицательные значения.

Ответ: корней нет

Пример 13:

Учитывая то, что левая часть уравнения – функция может принимать только неотрицательные значения, решим неравенство:

неравенство решений не имеет, тогда и исходное уравнение тоже.

Ответ: корней нет

§ Свойство ограниченности функции (метод оценок)

· Если и , то

Пример 14:

Заметим, что , т. е. , а

Проверка показывает, что это значение является и корнем второго уравнения.

Ответ:

· Пусть — функция, возрастающая (убывающая) на некотором промежутке I. Тогда уравнение имеет на промежутке I не более одного корня.

· Пусть — функция, возрастающая на некотором промежутке I , а функция — убывающая на этом промежутке. Тогда уравнение имеет на промежутке I. не более одного корня

Пример 15: .

Рассмотрим функции и .

монотонно возрастает, а — убывает, следовательно, уравнение имеет не более одного корня.

Значение корня легко найти подбором:

Ответ:

Пример 16:

Функция возрастает на своей области определения, как сумма двух возрастающих функций, следовательно, уравнение имеет не более одного корня. Так как , то — единственный корень .

Ответ:

§ Использование суперпозиций функций

· Если — монотонно возрастающая функция, то уравнения и равносильны.

Пример 17:

Запишем уравнение в виде

Рассмотрим функцию — монотонно возрастающую, тогда уравнение имеет вид . Оно равносильно уравнению

Сделаем замену

не удовлетворяет условию

Ответ:

IV. Закрепление изученного материала на данном уроке и ранее пройденного, связанного с новым.

Решение уравнений в группах по 6 человек.

Ребята получают карточку с заданием. Решение уравнений обсуждают вместе, записывают его.

После выполнения группами заданий проводится взаимопроверка. Группы меняются заданиями с решениями по кругу:

2 3 4

Учащиеся групп обсуждают решение, исправляют ошибки и выставляют оценки.

Потом работы с выставленными оценками возвращаются в группы для обсуждения вклада каждого в решение проблемы.

Выставляются каждому оценки с занесением в оценочную таблицу. Учитель контролирует и вносит, если нужно, свои коррективы.

V. Подведение итогов и результатов урока. Рефлексия.

8) *

Используемая литература.

1. Чулков курса «Уравнения и неравенства в школьном курсе математики»: Лекции 1-8. – М.: Педагогический университет «Первое сентября», 2006.

2. , , Морозова государственный экзамен. Математика. – Челябинск: Взгляд, 2006 –Ч.1,2

3. Шарыгин курс по математике: Решение задач. – М.: Просвещение, 1989

4. , Якушев : интенсивный курс подготовки к экзамену. – М.: Айрис-пресс, 2004.

5. , Голобородько и контрольные работы по алгебре и началам анализа для 10-11 классов. – М.: Илекса, 2006.

Задания для работы в группах:

1. Возведи обе части в квадрат:

2. Выполни замену:

4. Умножай на сопряжённое выражение:

5. Переходи к модулю:

6. Используй свойства функций:

7. Реши любым способом:

1. Возведи обе части в квадрат:

2. Выполни замену:

4. Умножай на сопряжённое выражение:

5. Переходи к модулю:

6. Используй свойства функций:

7. Реши любым способом:

Проверочная работа по теме: «Методы

Содержание

О некоторых нестандартных способах решения иррациональных уравнений
Просмотр содержимого документа «О некоторых нестандартных способах решения иррациональных уравнений»
Урок по теме: » Нестандартные методы решения иррациональных уравнений»
🔥 Видео

Видео:СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать

О некоторых нестандартных способах решения иррациональных уравнений

В данной статье рассматривается некоторые нестандартные способы решения иррациональных уравнений в школьном курсе математики. Даны примеры решения иррациональных уравнений с помощью приведения к системе рациональных уравнений, умножением на сопряженное выражение и преобразованием сумму или разности радикалов.

Просмотр содержимого документа
«О некоторых нестандартных способах решения иррациональных уравнений»

О НЕКОТОРЫХ НЕСТАНДАРТНЫХ СПОСОБАХ РЕШЕНИЯ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ

1. Приведение к системе рациональных уравнений. При решении иррациональных уравнений с помощью преобразований необходимо использовать не только одну, а несколько переменных. При этом для обеспечения однозначности значений неизвестной уравнение преобразуется в систему рациональных уравнений [1]. Например, при решении уравнения

(1)

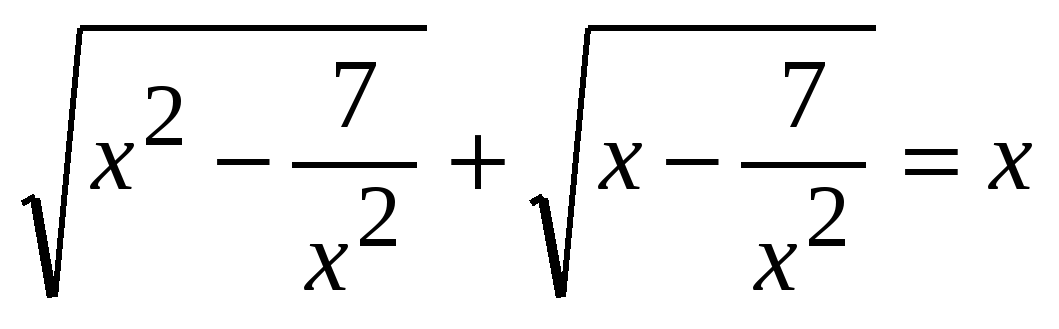
введем следующую замену переменных

(2)

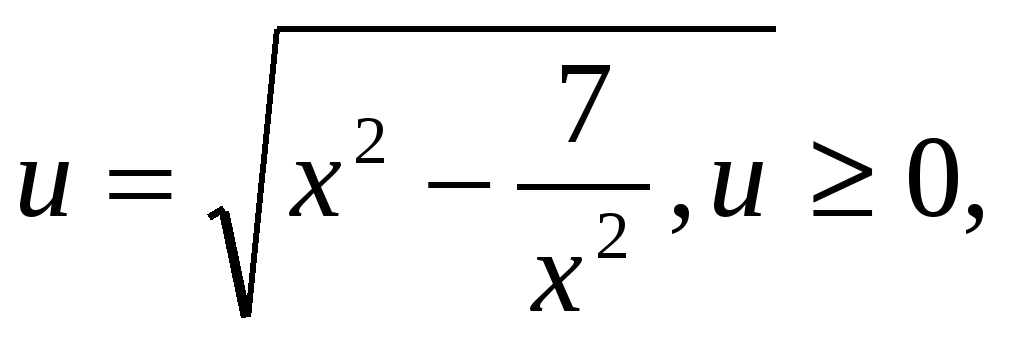
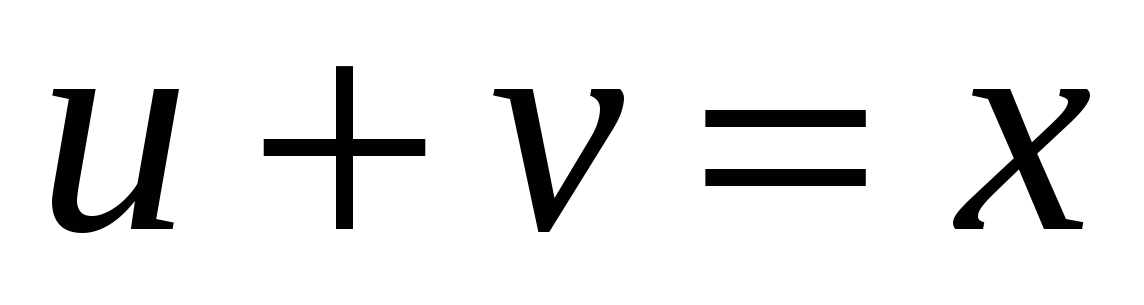
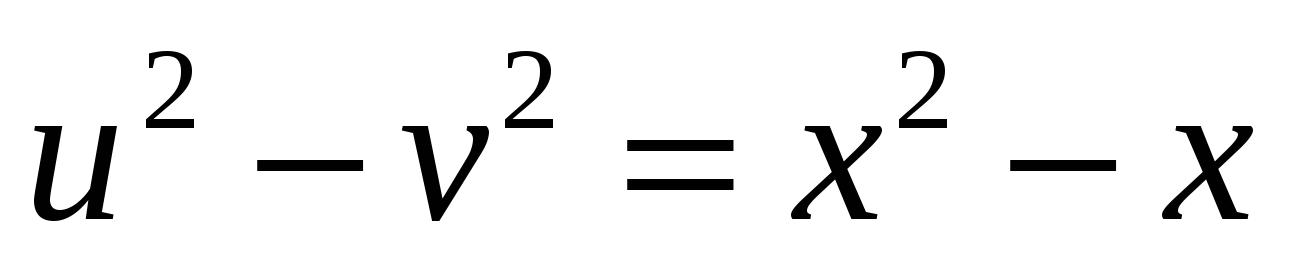
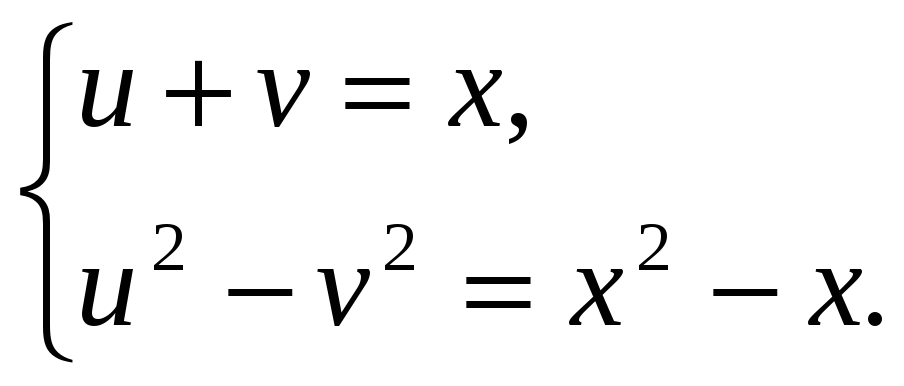
Тогда уравнение (1) будет имет вид . Связь квадратов новых переменных выражается соотношением . Значит, получим систему равнений

(3)

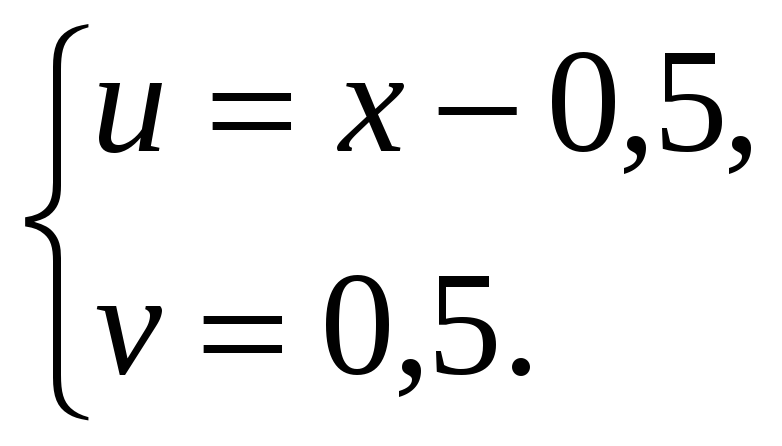
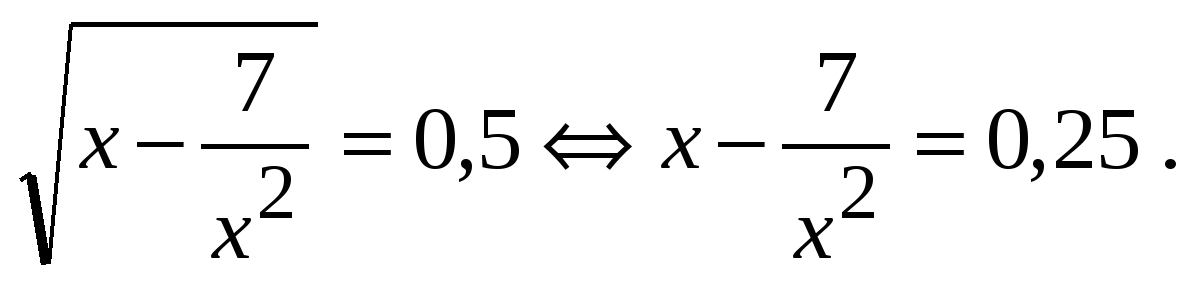
Преобразуя и решая систему (3) методом сложения придем к системе: . Тогда получаем уравнение

(4)

Уравнение (4) можно привести к кубическому уравнению. , его единственный корень . С проверкой убеждаемся, что — корень исходного уравнения (1).

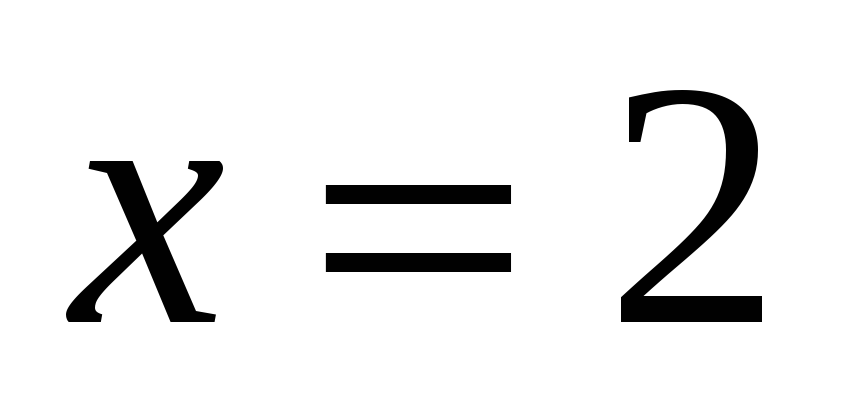
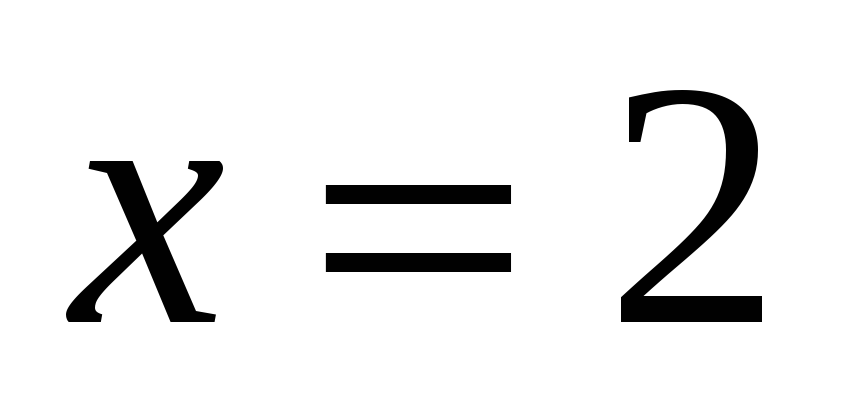
2. Умножение на сопряженное выражение.

Если в уравнение войдет сумма или разность радикалов, то можно использовать умножение на сопряженное выражение[2]. Например. при решении уравнения

(5)

так как в левой части уравнения стоит разность радикалов, то умножим обе части уравнения (5) на сумму этих радикалов. По правилу разложения множителей в произведения рассмотрим два случая:

1) если , то ; 2) если ,

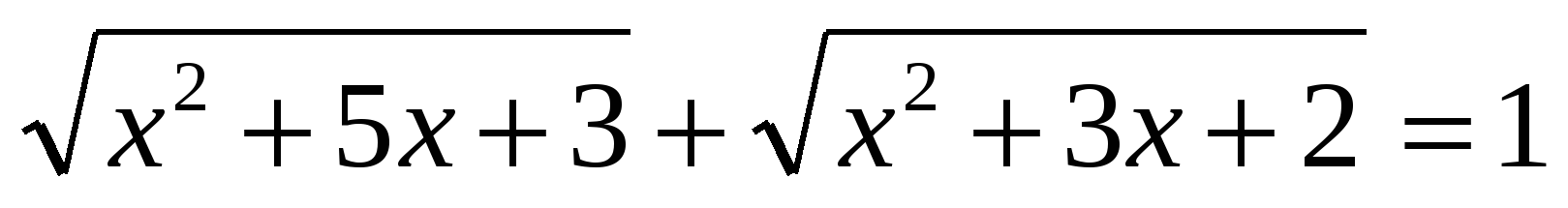
то тогда это уравнение решается возведением обеих частей в квадрат. Но в

данном случае рациональнее будет рассмотреть систему уравнений

(6)

Сумма уравнений системы (6) будет следствием уравнения (5), это уравнение имеет простой вид . Решение полученного уравнения даёт еще одно решение исходного уравнения (5) :.

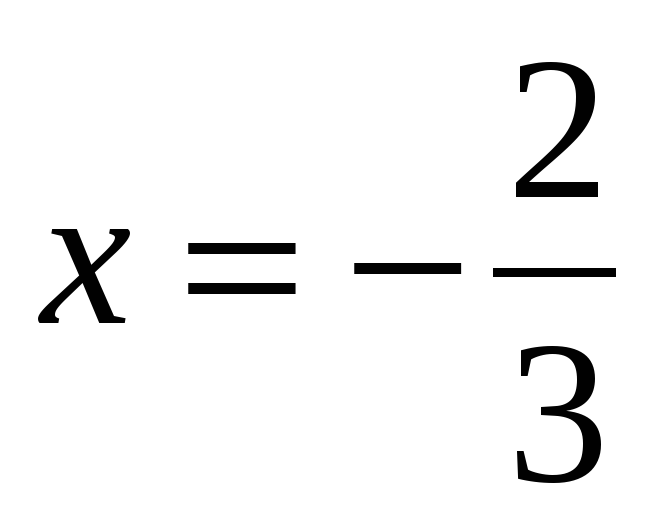
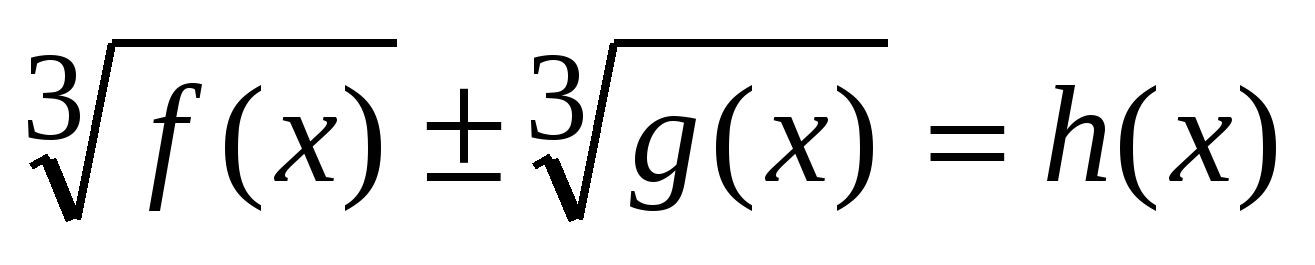
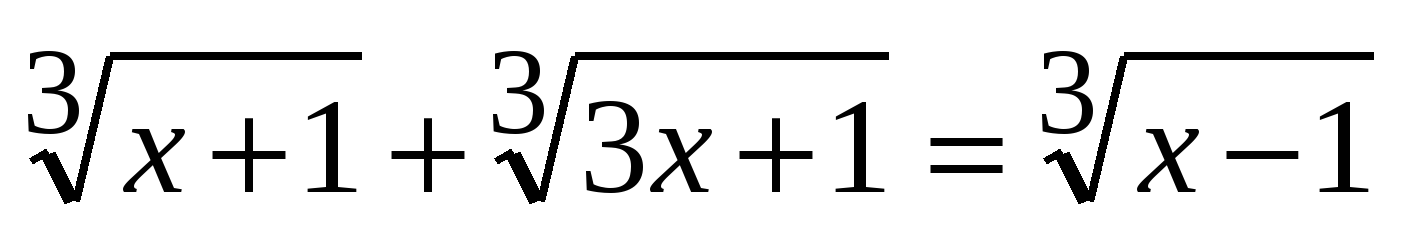
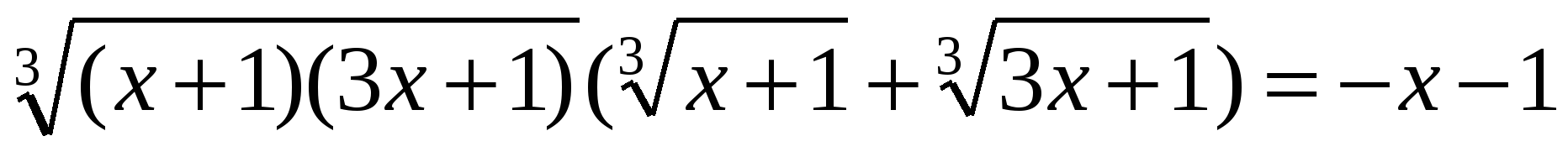
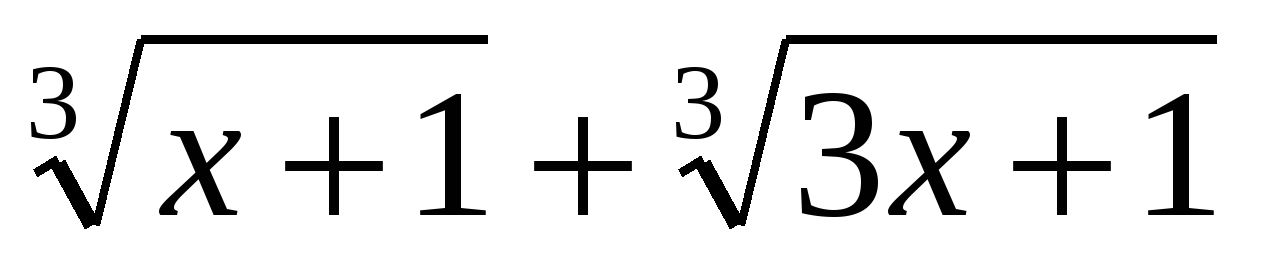
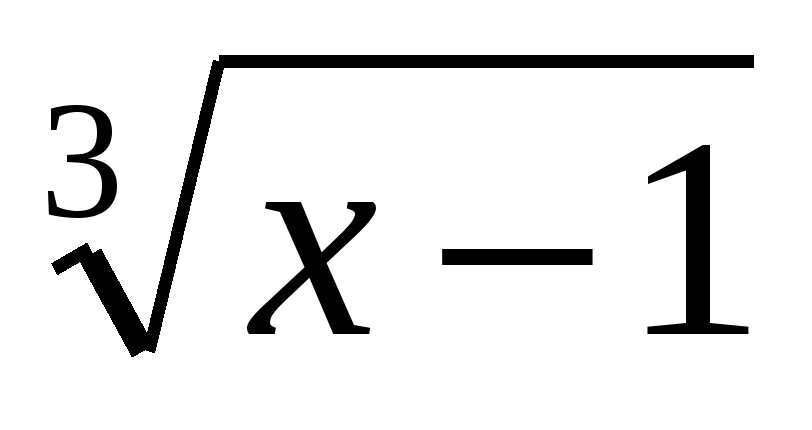
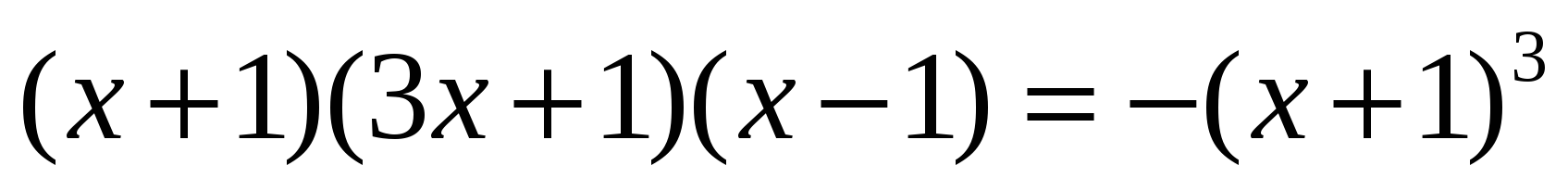
3. Преобразование сумму (разность) радикалов. Этот способ применяется при решении иррациональных уравнений вида . Его сущность заключается в том, что на определенном этапе сумма (разность) радикалов меняется на простое выражение. Такое преобразование избавялет от повторного возведения в степень и приведет к решению простого уравнения. Например, при решении уравнения сначала возведем обе части уравнения в куб, а потом выполняя серию преобразований получим уравнение . Поменяя сумму радикалов на выражение , получим уравнение . Возведя обе части ещё раз в куб будем иметь

Проверка показывает, что при в левой части уравнения:а в правой части:

значит, — корень уравнения. При левая часть уравнения равно : а правая часть: , — неправильно, значит, не является корнем данного уравнения.

1. Чулков П.В. Уравнения и неравенства в школьном курсе математики. – М.: Педагогический университет «Первое сентября», 2009

2. Литвиненко А. Мордкович А.Г. Практикум по элементарной математике. Алгебра и тригонометрия. М.: Просвещение, 1988.

Видео:Как решать уравнение с корнями Иррациональное уравнение Как решать уравнение с корнем х под корнемСкачать

Урок по теме: » Нестандартные методы решения иррациональных уравнений»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Нестандартные методы решения иррациональных уравнений

Образовательная: расширить и углубить знания учащихся по данной теме познакомив их с нестандартными методами решения иррациональных уравнений, научить применять эти методы, повысить уровень понимания и практической подготовки учащихся при решении иррациональных уравнений.

Развивающая: развитие умения самостоятельно приобретать и применять знания;

способствовать развитию математического кругозора, логического мышления.

Воспитательная – содействовать воспитанию интереса к иррациональным уравнениям, воспитывать чувство коллективизма, самоконтроля, ответственности.

1. Повторить определение и основные методы решения иррациональных уравнений.

2. Продемонстрировать нестандартные методы решения иррациональных уравнений; формировать умение выбирать рациональные пути решения.

3. Освоение всеми учащимися алгоритмов решения иррациональных уравнений, закрепление теоретических знаний при решении конкретных примеров.

4. Приобщение учащихся к исследовательской работе.

Тип урока : урок исследования

Форма урока: групповая работа

Оборудование: презентация в Pover Point, интерактивная доска, раздаточный материал.

1. Организационный момент.

Эйнштейн говорил так: “Мне приходится делить время между политикой и уравнениями. Однако, уравнения, по-моему, гораздо важнее. Политика существует для данного момента, а уравнения будут существовать вечно”.

Вот и мы займемся уравнениями.

Чтобы узнать о каких уравнениях пойдет речь, мы обратимся к домашнему заданию.

При правильном выполнении домашнего задания у вас получился знак радикала.

Как можно это связать с нашим уроком?

Какие цели мы поставим перед собой на уроке?

— Узнать новые нестандартные методы решения иррациональных уравнений.

— Рассмотреть применение новых методов при решении иррациональных уравнений.

— Расширить и углубить свои знания о иррациональных уравнениях.

На сегодняшнем уроке вы будите работать в творческих группах. У каждого из вас лежит оценочный лист, запишите свою фамилию. Максимальный балл за урок -10 баллов.

1. Основные вопросы теории открытия иррациональности.

Что вы знаете об иррациональности?

1. Иррациональное в переводе с греческого “Уму непостижимое, неизмеримое, немыслимое” .

2. Открытие иррациональности опровергало теорию Пифагора, что “всё есть число”.

3. История развития теории иррациональности знает много ученых – исследователей. Евклид, Декарт, Ньютон( Он ввёл современное изображение корня) .

2. Основные методы решения иррациональных уравнений.

Метод возведения в степень, равную показателю корня, метод «пристального взгляда», метод введения новой переменной, метод разложения на множители, функционально – графический метод.

Какой этап содержат в основном все эти методы? ( Проверка)

3. Работа в группах. Исследовательская работа.

Целью исследования является изучение нестандартных методов решения иррациональных уравнений.

Гипотеза : Если знать нестандартные методы решения иррациональных уравнений, то это позволит повысить качество выполнения некоторых олимпиадных и тестовых заданий ЕНТ.

Нестандартные методы решения иррациональных уравнений.

1. Умножение на сопряжённое выражение.

Если в левой части иррационального уравнения сумма или разность корней, а подкоренное выражение – линейная функция одинаковыми линейными коэффициентами,

а в правой части некоторое число, то левую и правую части уравнения умножают на выражение, сопряженное выражению в левой чисти ( + и — ) — сопряженные).

Рассмотрите решение иррационального уравнения методом умножения на сопряженное выражение.

Решить уравнение