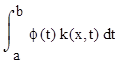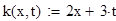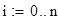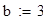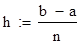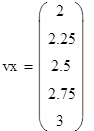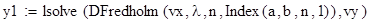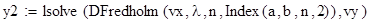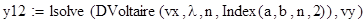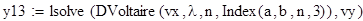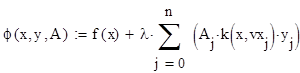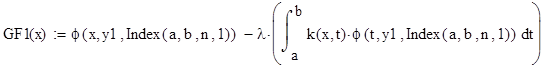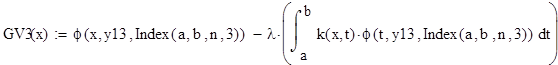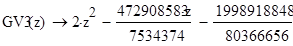Решение интегральных уравнений методом конечных сумм

Видео:Метод определителей ФредгольмаСкачать

Решение интегральных уравнений Фредгольма, Вольтера методом конечных сумм

Страницы работы

Содержание работы

Министерство образования и науки Украины

Национальный аэрокосмический университет им. Н.Е. Жуковского «Харьковский авиационный институт»

По курсу «Численные методы»

По теме: «Решение интегральных уравнений»

студент 325 группы

Цель. Решить численно интегральное уравнение Фредгольма, Вольтера методом конечных сумм.

Программная реализация в MathCad.

Исходные данные для уравнения вида ϕ(x) -λ =f(x)

1. Блок формирования весовых коэффициентов.

1. Формула Симпсона.

2. Формула трапеций.

3. Формула правых прямоугольников.

4. Формула левых прямоугольников.

2. Формирование матрицы коэффициентов для уравнения Фредгольма, Вольтера.

3. Вычисление значений f(х) (правой части уравнения) в узловых точках.

Значения источника в узловых точках:

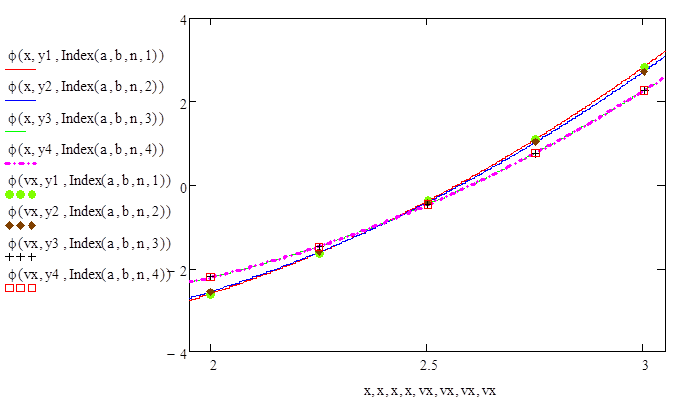
Вычисляем значения искомой функции в узловых точках: ϕ(vx(i))

Искомую функцию ɸ(х) запишем в виде :

Проверка результатов вычислений.

function res = Integral_equation(a,b,n,N,str);

lambda = 8; % параметр

%1. Табулирование значений

%2. Формируем весовые коэффициенты для формулы N

A = zeros(n,1);%матрица весовых коэффициентов

switch (N) %формула Симпсона

case 2 %формула трапеций

case %формулы правых и левых прямоугольников

otherwise error(‘This is impossible value’)

%3. Формирование матрицы коэффициентов

case ‘Fredgolm’% для уравнения Фредгольма

if (i == j) D(i,j) = 1-lambda*A(j)*k(vx(i),vx(j));

else D(i,j) = -lambda*A(j)*k(vx(i),vx(j));

case ‘Volter’% Вольтера

% 4. Вычисление значений искомой функции в узловых точках

% 5. Построение графика искомой функции fi(х) на интервале [a,b];

plot(X,VR,’-k’),hold on,plot(vx,y,’*r’),hold on;

% 6. Проверка вычислений. left side of equation

G = fi(x,lambda,y,vx,A) — lambda*int(k(x,t)*fi(t,lambda,y,vx,A),t,a,b)

function res = F(x);

% источник интегрального уравнения

function res = fi(x,lambda,y,vx,A);

Int = Int + A(i)*k(x,vx(i))*y(i);

res = F(x)+ lambda*Int;

function res = k(x,t);

% ядро интегрального уравнения

Похожие материалы

Информация о работе

• АлтГТУ 419
• АлтГУ 113
• АмПГУ 296
• АГТУ 267
• БИТТУ 794
• БГТУ «Военмех» 1191
• БГМУ 172
• БГТУ 603
• БГУ 155
• БГУИР 391
• БелГУТ 4908
• БГЭУ 963
• БНТУ 1070
• БТЭУ ПК 689
• БрГУ 179
• ВНТУ 120
• ВГУЭС 426
• ВлГУ 645
• ВМедА 611
• ВолгГТУ 235
• ВНУ им. Даля 166
• ВЗФЭИ 245
• ВятГСХА 101
• ВятГГУ 139
• ВятГУ 559
• ГГДСК 171
• ГомГМК 501
• ГГМУ 1966
• ГГТУ им. Сухого 4467
• ГГУ им. Скорины 1590
• ГМА им. Макарова 299
• ДГПУ 159
• ДальГАУ 279
• ДВГГУ 134
• ДВГМУ 408
• ДВГТУ 936
• ДВГУПС 305
• ДВФУ 949
• ДонГТУ 498
• ДИТМ МНТУ 109
• ИвГМА 488
• ИГХТУ 131
• ИжГТУ 145
• КемГППК 171
• КемГУ 508
• КГМТУ 270
• КировАТ 147
• КГКСЭП 407
• КГТА им. Дегтярева 174
• КнАГТУ 2910
• КрасГАУ 345
• КрасГМУ 629
• КГПУ им. Астафьева 133
• КГТУ (СФУ) 567
• КГТЭИ (СФУ) 112
• КПК №2 177
• КубГТУ 138
• КубГУ 109
• КузГПА 182
• КузГТУ 789
• МГТУ им. Носова 369
• МГЭУ им. Сахарова 232
• МГЭК 249
• МГПУ 165
• МАИ 144
• МАДИ 151
• МГИУ 1179
• МГОУ 121
• МГСУ 331
• МГУ 273
• МГУКИ 101
• МГУПИ 225
• МГУПС (МИИТ) 637
• МГУТУ 122
• МТУСИ 179
• ХАИ 656
• ТПУ 455
• НИУ МЭИ 640
• НМСУ «Горный» 1701
• ХПИ 1534
• НТУУ «КПИ» 213
• НУК им. Макарова 543
• НВ 1001
• НГАВТ 362
• НГАУ 411
• НГАСУ 817
• НГМУ 665
• НГПУ 214
• НГТУ 4610
• НГУ 1993
• НГУЭУ 499
• НИИ 201
• ОмГТУ 302
• ОмГУПС 230
• СПбПК №4 115
• ПГУПС 2489
• ПГПУ им. Короленко 296
• ПНТУ им. Кондратюка 120
• РАНХиГС 190
• РОАТ МИИТ 608
• РТА 245
• РГГМУ 117
• РГПУ им. Герцена 123
• РГППУ 142
• РГСУ 162
• «МАТИ» — РГТУ 121
• РГУНиГ 260
• РЭУ им. Плеханова 123
• РГАТУ им. Соловьёва 219
• РязГМУ 125
• РГРТУ 666
• СамГТУ 131
• СПбГАСУ 315
• ИНЖЭКОН 328
• СПбГИПСР 136
• СПбГЛТУ им. Кирова 227
• СПбГМТУ 143
• СПбГПМУ 146
• СПбГПУ 1599
• СПбГТИ (ТУ) 293
• СПбГТУРП 236
• СПбГУ 578
• ГУАП 524
• СПбГУНиПТ 291
• СПбГУПТД 438
• СПбГУСЭ 226
• СПбГУТ 194
• СПГУТД 151
• СПбГУЭФ 145
• СПбГЭТУ «ЛЭТИ» 379
• ПИМаш 247
• НИУ ИТМО 531
• СГТУ им. Гагарина 114
• СахГУ 278
• СЗТУ 484
• СибАГС 249
• СибГАУ 462
• СибГИУ 1654
• СибГТУ 946
• СГУПС 1473
• СибГУТИ 2083
• СибУПК 377
• СФУ 2424
• СНАУ 567
• СумГУ 768
• ТРТУ 149
• ТОГУ 551
• ТГЭУ 325
• ТГУ (Томск) 276
• ТГПУ 181
• ТулГУ 553
• УкрГАЖТ 234
• УлГТУ 536
• УИПКПРО 123
• УрГПУ 195
• УГТУ-УПИ 758
• УГНТУ 570
• УГТУ 134
• ХГАЭП 138
• ХГАФК 110
• ХНАГХ 407
• ХНУВД 512
• ХНУ им. Каразина 305
• ХНУРЭ 325
• ХНЭУ 495
• ЦПУ 157
• ЧитГУ 220
• ЮУрГУ 309

Полный список ВУЗов

Чтобы распечатать файл, скачайте его (в формате Word).

Видео:СУММА КОЭФФИЦИЕНТОВ: Как решать Квадратные Уравнения по МАТЕМАТИКЕ 8 классСкачать

ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ, УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ И ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ

Глеб Бакеев 5 лет назад Просмотров:

1 МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ имени академика С.П. КОРОЛЕВА (НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ)» А. А. Б У Х А Н Ь К О, О. П. Ч О С Т К О В С К А Я ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ, УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ И ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ Утверждено Редакционно-издательским советом университета в качестве учебно-методического пособия С А М А Р А Издательство СГАУ

2 УДК СГАУ: 59.4 (75) ББК.я7 Б 94 Рецензенты: д-р физ.-мат. наук, доц. СамГУ Л.В. Степанова; д-р физ.-мат. наук, проф. СГАУ А.И. Хромов. Б 94 Буханько А.А., Чостковская О.П. Приближенные методы решения краевых задач для обыкновенных дифференциальных уравнений, уравнений с частными производными и интегральных уравнений: учеб.-метод. пособие / А.А. Буханько, О.П. Чостковская. Самара: Изд-во Самар. гос. аэрокосм. ун-та, с.: ил. ISBN Пособие посвящено методам нахождения приближенных решений краевых задач для обыкновенных дифференциальных уравнений, уравнений с частными производными (гиперболического, параболического и эллиптического типов) и интегральных уравнений (Фредгольма, Вольтерра). Пособие содержит материалы, необходимые для выполнения курсовой работы по курсу «Уравнения математической физики». Предназначено для студентов специальностей «Механика и математическое моделирование», «Динамика и прочность машин» и других инженернотехнических специальностей, а также для аспирантов и инженернотехнических работников. Предложенный материал полезен при изучении приближенных методов решения задач некоторых разделов математики и механики. ISBN Самарский государственный аэрокосмический университет,

3 ОГЛАВЛЕНИЕ ВВЕДЕНИЕ 4 ПРИБЛИЖЕННЫЕ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 5. Метод конечных разностей Метод прогонки Базисные функции Метод Галеркина Метод коллокаций. 6 Метод Ритца для простейшей краевой задачи. МЕТОД СЕТОК ДЛЯ РЕШЕНИЯ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ 5. Метод сеток для уравнений параболического типа Метод сеток для уравнений гиперболического типа Метод сеток для задачи Дирихле Итерационный метод решения системы конечно-разностных уравнений ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ Метод последовательных приближений Метод конечных сумм Метод вырожденного ядра ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ 55 I Краевые задачи для обыкновенных дифференциальных уравнений II Уравнения в частных производных III Интегральные уравнения ПРИЛОЖЕНИЕ I. Аналитические решения уравнений в частных производных (метод Фурье) 6 I. Смешанная задача о колебаниях однородной струны. 6 I. Смешанная задача о теплопроводности в однородном стержне. 6 ПРИЛОЖЕНИЕ I I. Связь между дифференциальным уравнением и уравнением Вольтерра 64 СПИСОК ЛИТЕРАТУРЫ 66 3

4 ВВЕДЕНИЕ В самых разнообразных областях современной науки и техники часто приходится встречаться с математическими задачами, для которых невозможно получить точное решение классическими методами или же решение может быть получено в таком сложном виде, которое неприемлемо для практического использования. Цель пособия помочь студенту при изучении приближенных методов решения различных дифференциальных и интегральных уравнений. В данной работе рассмотрены основные вычислительные методы, позволяющие найти приближенные решения краевых задач для обыкновенных дифференциальных уравнений, уравнений с частными производными и интегральных уравнений. В каждом разделе для лучшего понимания алгоритмов решений приведены примеры расчетов. В первой главе пособия рассматриваются численные и аналитические методы решения краевых задач для обыкновенных дифференциальных уравнений. Вторая глава посвящена одному из самых распространенных методов численного решения уравнений с частными производными методу сеток. Рассматривается применение этого метода для уравнений параболического, гиперболического и эллиптического типов. В третьей главе рассматриваются некоторые численные методы решения интегральных уравнений: методы последовательных приближений, конечных сумм и вырожденного ядра. Четвертая глава содержит задание на курсовую работу по курсу «Уравнения математической физики». Выполнение курсовой работы требует самостоятельного составления краевых задач и интегральных уравнений, их решения приближенными методами и сравнения с точным (аналитическим) решением. Цель курсовой работы состоит в том, чтобы освоить приближенные методы решения некоторых дифференциальных и интегральных уравнений. Структура курсовой работы соответствует структуре первых трех глав данного учебно-методического пособия. 4

5 ПРИБЛИЖЕННЫЕ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ Рассматриваются методы решения линейной краевой задачи: L[ ] p( ) q( ) f ( ), (.) [ ] ( ) ( ) A, b[ ] ( b) ( b) B, (.) где p( ), q( ), f ( ) — известные непрерывные на отрезке [ bфункции,, ]. AB, — заданные постоянные, причем и. Если A B, то краевые условия (.) называются однородными. Методы приближенного решения краевой задачи (.), (.) разделяются на две группы: — разностные методы (позволяют найти приближенное решение в виде таблицы); — аналитические методы (позволяют найти приближенное решение в виде аналитического выражения).. Метод конечных разностей Одним из наиболее простых методов решения краевой задачи (.) (.) является сведение ее к системе конечно-разностных уравнений. Разобьем отрезок [ b, ] на равноотстоящих узлов с некоторым b шагом. Точки разбиения имеют абсциссы, b, Рис.. (, ). Получаемые в результате расчета приближенные значения искомой функции ( ) (рис..) и ее производных ( ), ( ) в узлах обозначим через,, соответственно. Также введем обозначения p p( ), q q( ), f f ( ). Заменим приближенно в каждом внутреннем узле производные конечноразностными отношениями 5

6 ,, (.3) а на концах отрезка положим,. (.4) Подставив (.3), (.4) в уравнение (.) и условия (.): p (, ), q f (.5) A, B, получим линейную систему алгебраических уравнений с неизвестными. Решив ее, получим таблицу приближенных значений искомой функции. Пример.. Методом конечных разностей найти приближенное решение уравнения,5,5 l 4, ( ) удовлетворяющее краевым условиям () (), ( ) (), 5 (),37, используя конечно-разностные отношения. Выберем шаг,, получим шесть узлов сетки. 4, 3,6, 4,8, 5. Используя формулы (.3), заменяем уравнение ( ) системой конечно-разностных уравнений:,5,5 l 4. 3. В результате приведения подобных членов получаем 6, 5, 5 l 4. ( 3 ) В граничных узлах краевые условия ( ) согласно (.4) принимают вид 5 4, 5,5,37. Записав предпоследнее уравнение для каждого узла. 3 и добавив последние уравнения, получим систему

7 ,8,8,8,,853,833,8, 3,877,857,86, 3 4,895,875,9, 3 4 5,8. 3,5, 3, 5 4 решая которую, получаем, 66,, 53. 3, 485, 4,89, 5, 48. Для сравнения приведем значения точного решения задачи ( ), ( ) ( ) l в соответствующих точках: ( ),, ( ),75, ( ),87, ( ),6, ( ),64, ( ), Другое приближенное решение получается, если производные заменить центрально-разностными отношениями,. Тогда получим систему p q f (, ), A, B. (.6) Замечание: Если функция ( ) достаточно гладкая, то более точные значения дают формулы ,. (.7) Оценка погрешности метода конечных разностей для задачи (.), (.) имеет вид M4 ( ) ( b ), 96 где ( ) значение точного решения при M. (4), 4 m ( ), b Пример.. Методом конечных разностей найти приближенное решение уравнения ( ), удовлетворяющее краевым условиям ( ), используя центрально-разностные отношения с шагом,. 7

8 Используя формулы (.6) и (.7), заменяем уравнение ( ) и краевые условия ( ) системой конечно-разностных уравнений:, 5, 5 l Рис.. (,,3,4), ,, 5,37. ( 4 ) Подставляя значения соответствующих коэффициентов, последняя система примет вид, 83, 98, 97,8,, 7, 98, 99,86, 3, 63, 98, 938,9, 4 3,56,98,944,, 5 4 3,6 4,4. 5, Решением этой системы будет, 37,, 99,, 99, 3, 6, 4, 55, 5, 594. На рис.. представлено графическое сравнение решений задачи ( )-( ), полученных в примерах. и., с точным решением. Из графиков видно, что значения, близкие к точным, дают в данном случае центральноразностные соотношения.. Метод прогонки При применении метода конечных разностей к краевым задачам для дифференциальных уравнений второго порядка получается «трехчленная система» линейных алгебраических уравнений, каждое из которых содержит три соседних неизвестных. Для решения такой системы разработан метод, получивший название метода прогонки. Запишем первые уравнений системы (.5) в виде m k f, (.8) m p, k p q (, ). Разрешая уравнение (.8) относительно : 8

9 f k m m m (.9) и предполагая, что с помощью полной системы (.5) из уравнения (.9) исключена неизвестная, получим c ( d ),, (.) где c, d (, ) некоторые коэффициенты. Из (.) следует, что c ( d ). (.) Подставляя (.) в уравнение (.8), получим m kc ( d ) f, откуда f kc d. m k c Сравнивая последнее выражение с (.), получим для определения c, d рекуррентные формулы: c, d f kc d (, ). (.) m k c Для определения коэффициентов c, d запишем соотношения (.), (.) при : c d, c, d f k c d m kc и выразим из первого краевого условия (.5) A Сравнивая последние два равенства, получим k A c, d f. (.3) m ( ) k Вычисления по методу прогонки проводятся следующим образом. Прямой ход. По формулам (.8) вычисляем значения m, k. Находим по формулам (.3) коэффициенты c, d, а затем, применяя последовательно рекуррентные формулы (.), получаем значения c, d при,. Обратный ход. Из уравнения (.) при и последнего уравнения (.5) получаем. 9

10 c ( d ), Разрешив полученную систему относительно B., определяем c d B ( c ), (.4). Далее, последовательно при- используя уже найденные значения c, d меняя рекуррентные формулы (.), вычисляем значения c ( d ), c ( d ), 3 3 c ( d ). (,,): (.5) Значение находим из предпоследнего уравнения системы (.5): A. (.6) Все вычисления метода прогонки рекомендуется располагать так, как показано в табл. Таблица. Порядок вычислений по методу прогонки (конечно-разностные отношения) Обратный Прямой ход m k f ход m k f c d m k c d m k f c d m k f c d Пример.3. Методом прогонки найти приближенное решение уравнения,5,5 l 4, ( ) удовлетворяющее краевым условиям c d

11 () (), (), 5 (),37, используя конечно-разностные отношения. Выберем шаг,. Согласно ( 3 ), (.8) и условий задачи имеем: m, k, 5, f, 5 l 4. 5, A, B,37. Прямой ход. Записываем в табл.. числа, и вычисляем величины m, k, f (,3 ). Далее находим по (.3). 8, c,9, d 4,5,4,385.,8,8,8,8 Записываем полученные числа в табл.. и вычисляем c, d при,,3 : : : 3: c m k c,833,853, 9 d f k c d c m, 366, 4, 538,853, 9, 385, 65; k c,857,877, 366 d f k c d c 3 m , 57, ( ) 4,644,4,877,366,65,9; k c,875,895, 57 d f k c d, 933, 4,8, 4,895, 57, 9, 49. Полученные значения c, d записываем в табл. Обратный ход. По формуле (.4) находим,5,933,49,37, 5,47.,5(,933), Далее по формулам (.5) приступаем к последовательному вычислению значений ( 4,3,,) и заполняем столбец обратного хода в табл. c ( d ),89, c ( d ),484, c ( d ),, c ( d ),5. 3 Значение находим по формуле (.6):

12 ,5,,65, и записываем в табл. в последнем столбце которой для сравнения приведены значения точного решения ( ) l. Таблица. Метод прогонки для задачи ( ), ( ), конечноразностные отношения Обратный Прямой ход m k f ход ( ), -,8,8 4,5 -,9,385,65,, -,833,853 4,538 -,366,65,5,75,4 -,857,877 4,644 -,57,9,,87 3,6 -,875,895 4,8 -,933,49,484,6 4,8,89,64 5,,47,64 Рассмотрим метод прогонки для решения системы, которая получается при замене уравнения (.) и второго краевого условия (.) центральными конечно-разностными отношениями: p (, ), q f (.7) A, B. Запишем первые уравнений системы (.7) в виде f m k, p (.8) q 4 p m, k. p p Аналогично предыдущему приводим уравнения (.8) к виду c c ( d ),, (.9) где коэффициенты c, d вычисляются по формулам: A : c, d k ; m ( ) k d, : c, d k c d. m kc (.)

13 Вычисления проводятся следующим образом. Прямой ход. По формулам (.8) вычисляем значения m, k. По форму- d, а затем по рекуррентным фор- лам (.) определяем коэффициенты c, мулам находим последовательно значения c, d при,. Обратный ход. Из уравнения (.9) при, и последнего уравнения системы (.7) получаем систему c ( d ), c ( d ), разрешая которую относительно, получим B d c d B, c c. (.) Используя уже известные значения c, d, c, d, находим. Значения (,,) получаем из рекуррентных формул (.9). Для вычисления используем предпоследнее уравнение системы (.7): A. (.) Результаты вычислений рекомендуется представлять в виде таблицы (см. табл..3). Таблица.3 Порядок вычислений по методу прогонки (центральноразностные отношения) Обратный Прямой ход m k ход m k c d m k c d m k c d m c d c k d 3

14 Пример.4. Методом прогонки найти приближенное решение задачи ( )- ( ), используя центрально-разностные отношения. Согласно ( 4 ), (.8) и условиям задачи имеем: 4 m, k,,5 l 4. 5, A, B,37. Прямой ход. Записываем в табл..4 числа, и вычисляем величины m, k, (,5 ). Далее находим по (.),, c, 99, d,68,846, 379.,88,8,846,8 Записываем полученные числа в табл..4 и вычисляем последовательно c, d при,5. Результаты приведены в табл..4. Обратный ход. По формуле (.) находим,37,,5,947,7,464 5,4.,4,5,7 9,7 Далее по формулам (.9) приступаем к последовательному вычислению значений ( 4,3,,) и заполняем столбец обратного хода в табл..4. Значение находим по формуле (.):,39,,386,8 и записываем в табл..4, в последнем столбце которой приведены значения точного решения ( ) l. Таблица.4 Метод прогонки для задачи ( ), ( ), центральноразностные отношения Обратный Прямой ход m k ход ( ),,386,, -,88,846,68 -,99,379,39,75,4 -,848,867,73 -,384,6,387,87 3,6 -,864,88,8 -,557,94,6,6 4,8 -,876,895,9 -,7,464,943,64 5, -,886,95, -9,7,947,4,64 c d 4

15 .3 Базисные функции Рассматриваемые ниже аналитические методы нахождения приближенного решения краевой задачи (.) (.) основаны на выборе системы базисных (координатных) функций. Системы базисных функций обладают тем свойством, что все остальные функции (с учѐтом некоторых ограничений) могут быть разложены на их сумму (или интеграл). Например, любая аналитическая функция одного аргумента может быть разложена в сумму степенных функций с различными коэффициентами, то есть разложена в ряд Тейлора. Если в качестве базисных выбраны синусоидальные функции, то разложение по ним есть преобразование Фурье и т.д. Система базисных функций ( ), ( ),, ( ),, (.3) заданная на отрезке[ b,, ] удовлетворяет следующим условиям: ) Система (.3) является ортогональной, т.е. b d при j, j b d ) Система (.3) является полной, т.е. не существует никакой другой отличной от нуля функции, ортогональной ко всем функциям. 3) Конечная система базисных функций, выбирается так, что функция. удовлетворяет неоднородным (заданным) краевым условиям: A, B, (.4) b а остальные функции, удовлетворяют однородным (нулевым) краевым условиям. (.5) b Отметим, что при выборе базисных функций условие ортогональности не является обязательным. Например, взяв за основу полную систему функций. ортогональных на отрезке [ b,, ] можно выбрать в качестве базисных функций линейные комбинации функций из этой системы. Достаточно лишь, чтобы выбранные функции (.3) были линейно независимы на отрезке [ b., ] Решение краевой задачи (.) (.) методами Галеркина, коллокаций и Ритца ищется в виде c. (.6) 5

16 Из условий (.4), (.5) следует, что функция (.6) удовлетворяет краевым условиям A, B. 6 b Точность приближенного решения в большой степени зависит от удачного подбора базисных функций и, вообще говоря, возрастает с увеличением их числа..4 Метод Галеркина Пусть имеем линейную краевую задачу (.) (.). Выбрав систему базисных функций (.3), удовлетворяющую краевым условиям (.), составим функцию R, c, c,, c L f c L, (.7) называемую невязкой. Коэффициенты c выбираются таким образом, чтобы значение интеграла от квадрата невязки b R, c, c,, c d было наименьшим. Доказано [], что это достигается лишь в том случае, если невязка R, c, c,, c ортогональна к базисным функциям : b R, c, c,, c d k,. k Подставляя в это условие невязку (.7), получим систему алгебраических уравнений относительно коэффициентов c : b c b k,, (.8) k k b k k k k где L d, b f L d. Подставив коэффициенты c, найденные из решения системы (.8), в выражение (.6), получим приближенное решение краевой задачи (.) (.). Пример.5. Методом Галеркина найти приближенное решение уравнения,5,5 l 4, ( ) удовлетворяющее краевым условиям (), (), 637. ( 5 ) В качестве системы базисных функций выберем следующие функции:

17 ( ),637; ( ) ; ( ) 3 ; 3 ( ) 4 8; ( ) Эти функции линейно независимы на отрезке [, ], причем функция удовлетворяет заданному краевому условию, а остальные функции однородным краевым условиям. Будем искать решение в виде (.6): 4 c. Находим L (. 3,4) : L,5,5,367,369 ; L,5,5 4 ; 3 3 L,5,5, 75 ; L 3,5 6 4 ; L 4,5 5,5 ; Коэффициенты, b равны k k f L. ( ) [ ],5 l,693,5 4,4 ; L d d 3,5,75 5,6583 ; 3 L d d L d 5, 786; L d 37, 584; L d 5,84; L d 3, 5697; L d 65,8673; L d 58, 39; L d 6, 538; L d 67, 57; L d 89, 7447; L d 458, 45; ( 6 ) 7

18 8 L d 4, 489; L d 66,4; L d 469, 3888; L d 4, 35; b d, 5 l, 693, 435; 3 b d 3, 5 l, 693 9, 68; 4 b3 d 4 8, 5 l, 693 6, 39; 5 b4 d 5, 5 l, , 376. Подставляя найденные коэффициенты в (.8), получим следующую систему алгебраических уравнений:, 4c 5, 6583c 5, 786c 37, 584c, 435, 3 4 5,84c 3, 5697c 65,8673c 58, 39c 9, 68, 3 4 6, 538c 67, 57c 89, 7447c 458, 45c 6, 39, 3 4 4, 489c 66,4c 469, 3888c 4, 35c 64, 376, 3 4 решением которой являются коэффициенты c,564, c, 766, c3, 4495, c 4, 743. Таким образом, согласно (.6) и ( 6 ) получили приближенное решение исходной задачи: ( ) 3,9946,564, 766, 4495, 743 3, 49. ( 7 ) В табл..5 приведены значения точного решения ( ) l, полученного приближенного решения и приближенного решения 3 4, 9585, 94, 5567,399, 695, полученного с помощью базисных функций,3 системы ( 6 ). Таблица.5 Точное и приближенные решения задачи ( ), ( 5 ). 4,6,8, ( ),,754,87,6,644,637 ( ),6,744,858,699,647,637 ( ),8,77,788,647,66,637

19 Из таблицы видно, что при выборе большего числа базисных функций приближенное решение дает более точный результат. Пример.6. Методом Галеркина найти приближенное решение уравнения ( ):,5,5 l 4, удовлетворяющее краевым условиям: (), (), 637. ( 8 ) В качестве системы базисных функций выберем функции вида ( ),637,637; ( ) ; ( ) ; ( 9 ) ( ) ; ( ) Аналогично примеру.5 определяем функции L, 4 и коэффициенты, b. Получим: k k, 64 3 L L 3 5 L,5,5 7 ;,87,37;,5,5 5; L L4, ;,64 f L,5,87 l 4,37 ;, 39;,44;, 83;, 54; 4 3 7,5,5,5 48,5 37 ; 3 4,66;,7;, 93;, 7; 3 4,4;, 99;, 83;, 68; , 7;, 77;, 7;, 6; b, 459; b, 36; b3 b4,44;, 97. Система алгебраических уравнений (.8) принимает вид 9

20 , 39c,44c, 836c, 54c, 459, 3 4,66c,7c, 93c, 7c, 36, 3 4,4c, 99c, 83c, 68c,44, 3 4, 7c, 77c, 7c, 6c, Откуда коэффициенты c равны: c, 63, c,37, c3, 6, c 4, 6. Приближенное решение задачи ( ), ( 8 ) имеет вид ( ), 6,578, 69 5,943 7, 8 3, 89. В табл..6 приведены значения точного решения ( ) l, полученного приближенного решения ( ) и приближенного решения 4 3,3,897 3, 953 5, 66 3, 49, полученного с помощью базисных функций (,3) из выбранной для решения системы. Таблица.6 Точное и приближенные решения задачи ( ), ( 8 ). 4,6,8. 754,87,6,644,637,,753,87,699,644,637,,754,87,63,646,637.5 Метод коллокаций Решение краевой задачи (.) (.) будем искать в виде (.6), выбрав систему функций (.3), удовлетворяющих условиям (.4), (.5). Потребуем, чтобы невязка (.7) обращалась в нуль на некоторой системе точек. отрезка [ b,, ] называемых точками коллокации, причем число таких точек должно равняться числу коэффициентов c в выражении (.6). Тогда для определения c получаем систему алгебраических уравнений: R, c, c,, c, R, c, c,, c, R, c, c,, c. (.9)

21 Разрешая систему (.9) относительно коэффициентов c, и подставляя их в (.6), получим функцию, дающую приближенное решение исходной краевой задачи. Пример.7. Методом коллокаций найти приближенное решение уравнения ( ):,5,5 l 4, удовлетворяющее краевым условиям ( 5 ): (), (), 637. В качестве базисных функций возьмем функции системы ( 6 ): 3 ( ),637; ( ) ; ( ) 3 ; ( ) 4 8; ( ) Выберем точки коллокации. 4, 3,6, 4,8. Вычисляя невязку R ( ) по (.7) в точках коллокации и приравнивая нулю, получим систему алгебраических уравнений относительно c (,4) :, 4c, 493c, 7965c, 346c, 536, 3 4, 737c,34c, 659c.739c, 668, 3 4, 5c, 453c, 548c,69c,873, 3 4, 533c, 938c,8999c, 59c, Решая эту систему, находим коэффициенты c, 6, c,367, c3,98, c 4, 568, и приближенное решение задачи ( ), ( 5 ) методом коллокаций согласно (.6) принимает вид ( ) 6,874 5, 688,49,536, 568 3,853. ( ).6 Метод Ритца для простейшей краевой задачи Путь дано линейное дифференциальное уравнение вида d p q f d с краевыми условиям (.3) ( ) A, ( b) B, (.3) где p, q, f C, b, причем p при b.

22 Краевая задача (.3) (.3) при известных условиях эквивалентна вариационной задаче для функционала вида на множестве функций b F p q f d (.3) C, b, удовлетворяющих краевым условиям (.3). Для решения вариационной задачи (.3), (.3) применяем метод Ритца. Выбираем систему линейно независимых функций (координатные функции) ( ), ( ),, ( ) таких, что A, b B, b,. Решение вариационной задачи определяется в виде линейной комбинации базисных функций (.6): c, где c, — некоторые постоянные. Очевидно, что функция (.6) удовлетворяет заданным краевым условиям (.3). Коэффициенты c, c,, c подбираются так, чтобы функция ( ) давала экстремум функционалу (.3). Подставим решение вида (.6) в выражение (.3), получим квадратичную функцию переменных c, c,, c : b F p c q c f c d c, c,, c. Для того, чтобы дифференцируемая функция ( c, c,, c ) при некоторых значениях c, c,, c имела экстремум, необходимо выполнение следующих условий. c c c (.33) Система (.33) является линейной относительно искомых коэффициентов c, c,, c, причем число уравнений равно числу неизвестных. Составив систему (.33) и решив ее относительно c, c,, c, найдем решение вариацион-

23 ной задачи, а следовательно и решение исходной краевой задачи по формуле (.6). Замечание: Определим связь функций p, q, f и p, q, f, входящих в уравнения (.) и (.3) соответственно. Запишем уравнение (.3) в виде p p q f, p q f p p p Сравнивая последнее уравнение с (.), получим p q f p, q, f, p p p откуда p d p d p d p e, q q e, f f e. (.34) Пример.8. Методом Ритца найти приближенное решение уравнения ( ):,5,5 l 4, удовлетворяющее краевым условиям ( 5 ): (), (), 637. Для того чтобы воспользоваться методом Ритца, найдем сначала функции (.34): p d d e e, p, q, f l 8. В качестве базисных функций также возьмем функции системы ( 6 ): 3 ( ),637; ( ) ; ( ) 3 ; 4 5 3( ) 4 8; 4( ) 5. Подставляя решение в виде (.6) в функционал (.3), получим: c, c, c, c c c 3 3 c 4 4 c , 637 c c 3 c3 4 8 c4 5. 3

24 l 8,637 c c 3 3 c 4 8 c 5 d Согласно (.33) получим систему алгебраических уравнений относительно коэффициентов c (, 4) : 3,967c +6,54c +47,344c +6,496c =6,5, 3 4 6,54c +69,75c +99,3c +49,677c =5,849, ,344c +99,3c +576,7c +433,7c =73,88, 3 4 6,496c +49,677c +433,7c +358,7c =8,5, 3 4 решением которой являются c 4, 378, c,, c3, 36, c4, 38. Тогда приближенное решение задачи ( ), ( 5 ) методом Ритца согласно (.6) принимает вид ( ) 5,5976 4, 378,, 36, 38 3,453. ( ) В табл..7 приведены значения точного решения ( ) l и приближенных решений задачи ( ), ( 5 ), полученных методами Галеркина ( 7 ), коллокаций ( ) и Ритца ( ). Таблица.7 Точное и приближенные решения задачи ( ), ( 5 ). 4,6,8. 754,87,6,644,637, ( 7 ),6,744,858,699,647,637, ( ),7,854,958,668,685,637, ( ),7,76,86,693,648,637 4

25 МЕТОД СЕТОК ДЛЯ РЕШЕНИЯ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ Метод сеток (метод конечных разностей) является одним из самых распространенных методов численного решения уравнений с частными производными. В его основе лежит идея замены производных конечноразностными отношениями. Для приближенного решения краевых задач для двумерных дифференциальных уравнений идея метода заключается в следующем: ) в плоской области G, в которой разыскивается решение, строится сеточная область, состоящая из одинаковых ячеек и приближающая данную область G ; ) заданное дифференциальное уравнение заменяется в узлах построенной сетки соответствующим конечно-разностным уравнением; 3) на основании граничных условий устанавливаются значения искомого решения в граничных узлах сеточной области. Решая полученную систему конечно-разностных уравнений (алгебраическая система уравнений с определенным числом неизвестных), находим значения искомой функции в узлах сетки численное решение исходной задачи. Пусть в плоскости O имеется некоторая область G, ограниченная кривой (рис..). Строим на плоскости два семейства параллельных прямых: (. ), jl ( j. ). j Точки пересечения этих прямых называются узлами. Два узла называются соседними, если они удалены друг от друга в направлении оси O или O на расстояние, равное шагу сетки или l соответственно. Те узлы, у которых все четыре соседних узла принадлежат выделенному множеству узлов, называются внутренними (узел А, рис..). Множество внутренних узлов образуют сеточную область. Те узлы, у которых Рис.. хотя бы один соседний узел не принадлежит к рассматриваемому множеству, называются граничными (узлы B, C, рис..), а их совокупность образует границу сеточной области. Обозначим значение искомой функции (, ) в узлах сетки через j (, j ). В каждом внутреннем узле (, j) заменим частные производные разностными отношениями: 5

26 , j, j, j, j, ; l j в граничных узлах используем менее точные формулы:, j j, j j,. l j Частные производные второго порядка заменяются соотношениями:, j j, j, j j, j,. l j j j j (.) (.) (.3) Все разностные схемы можно разбить на два типа: явные и неявные. Явными называются такие схемы, что при любом j в каждое из уравнений, связывающих значения искомого решения на горизонтальных рядах j, j,, j, входит лишь одна точка ряда j, так что значения решения в каждом узле j -го горизонтального ряда можно вычислить независимо от его значений в других узлах этого ряда (исключая граничные узлы), рис. а. Неявными называют такие схемы, когда для определения значений решения в узлах j -го ряда при известных значениях решения во всех предыдущих рядах нужно решать систему уравнений, связывающих значения решения в узлах j -го ряда, рис. б. (а) Рис.. Таким образом, явные схемы позволяют очень просто вычислить значения искомого решения в узлах j -го горизонтального ряда, если известны значения решения на предыдущих рядах. Но они имеют существенный недостаток: для того, чтобы они были устойчивы, необходимо налагать сильные ограничения на сетку. Кроме того, если в ходе решения необходимо уменьшить шаг по, то нельзя этого сделать, не уменьшая шага по. Неявные схемы свободны от этого недостатка, но использование их связано с другой трудностью: для отыскания значений решения в узлах j -то горизонтального ряда (б) 6

27 при известных значениях в узлах предыдущих рядов приходится решать систему алгебраических уравнений с большим числом неизвестных. При использовании конечно-разностной схемы для решения краевой задачи возникает важный вопрос об устойчивости такой схемы. Конечноразностная схема называется устойчивой, если малые погрешности, допущенные в процессе решения, затухают или, во всяком случае, остаются малыми при неограниченном увеличении номера текущего слоя, [,]. В противном случае схема называется неустойчивой. Очевидно, что неустойчивая конечно-разностная схема противопоказана для вычислений, так как неизбежные незначительные ошибки, например погрешности округлений, могут создать большие отклонения от точного решения краевой задачи и привести к результатам, не имеющим ничего общего с действительностью. Отметим, что погрешность приближенного решения, полученного разностным методом, складывается из трех погрешностей: погрешности замены дифференциального уравнения разностным; погрешности аппроксимации краевых условий; погрешности, получаемой в результате того, что система разностных уравнений решается приближенным методом.. Метод сеток для уравнений параболического типа Рассмотрим смешанную задачу для уравнения теплопроводности : найти функцию (, t ), удовлетворяющую уравнению начальному условию t, (.4) (,) f ( ) ( s ) (.5) и краевым условиям (, t) ( t), ( s, t) ( t) ( t ). (.6) Для отыскания приближенного решения задачи (.4)-(.6) методом сеток рассмотрим прямоугольную сетку узлов в полосе t, s, образуемую точками пересечения двух семейств параллельных прямых: (. ), t jl ( j. ). Введем обозначения, t j jl, j (, t j ) и приближенно заменим в каждом внутреннем узле (, t ) производную j разностным отношением Задача о распространении тепла в однородном стержне длины s, [5]. 7

28 а производную t, j j, j j одним из двух разностных отношений:, t l t l j, j j j, j j, (.7) В соответствии с предлагаемыми способами аппроксимации производных получим для уравнения (.4) два типа конечно-разностных уравнений :, j j, j j, j, l j, j, j j, j. l Первая разностная схема является явной схемой, вторая неявная. Полученные разностные уравнения содержат значения решения в четырех узлах и аппроксимируют уравнение (.4) с точностью до O( l ) []. Обозначив l, приведем эти уравнения к виду, (.8), j j, j, j, (.9) j, j, j, j При выборе числа в уравнениях (.8), (.9) следует учитывать, что: — погрешность замены дифференциального уравнения разностным должна быть наименьшей; — разностное уравнение должно быть устойчивым. В [,] доказано, что уравнение (.8) будет устойчиво при, а уравнение (.9) при любом. Наиболее простой вид уравнение (.8) принимает при :, j, j, j, (.). Использование разностного отношения неустойчивой разностной схеме []. 8 t j, j, j l приводит к

29 а при 6 :, j, j 4j, j 6. (.) Оценки погрешностей приближенных решений, получаемых из уравнений (.), (.) и (.9) в полосе s, t T соответственно имеют вид 3 [4]: 4 T M, T M, T l M, 3 35 где — точное решение задачи (.4) (.6); M m f. M m f. IV VI IV IV s s t T t T Из приведенных оценок погрешностей следует, что уравнение (.) дает более высокую точность решения по сравнению с решением (.). Но уравнение (.) имеет более простой вид, а, кроме того, шаг l по аргументу t для уравнения (.) должен быть значительно меньше, что приводит к большему объему вычислений. Уравнение (.9) дает меньшую точность, но при этом шаги l и выбираются независимо друг от друга. Уравнения (.), (.) позволяют вычислить значения функции (, t ) на каждом слое по явным формулам через значения на предыдущем слое; уравнение (.9) неявная схема этим свойством не обладает. Данным методом можно решать смешанную краевую задачу для неоднородного параболического уравнения F, t. t Тогда соответствующее разностное уравнение, использующее явную схему узлов, имеет вид Откуда при lf., j j, j, j j имеем, j, j, j lf j ; (.) 3 Оценки погрешности даны для случая. Читателю предлагается самостоятельно получить выражение оценки при. Аналогично для оценок в рассматриваемых далее методах. 9

30 при 6 :, j, j 4j, j lf. (.3) j 6 В этом случае имеют место следующие оценки погрешности [4]: T T 4 M M 4, M3 M6, где M m, M t m 3 3 3, M t m 4 4 4, M m Пример.. Используя разностное уравнение (.), найти приближенное решение уравнения t 8, удовлетворяющее условиям, 3s,, t,, t t, и сравнить его с аналитическим решением. Выберем по аргументу шаг, 5 и воспользуемся конечноразностным уравнением (.), т.е., откуда шаг по аргументу t будет l, 39. Записываем в табл.. начальные и краевые значения, т.е. заполняем строку при j и крайние столбцы (при и 8) соответственно. Значения функции (, t ) на первом слое находим, используя значения на нулевом (начальном) слое и краевые условия согласно (.) при j : Откуда получаем. 9,94 4,596, и т.д. 3,4 4,9749 8, 497 3

31 Записываем полученные значения (,,3, 4,5,6,7 ) во вторую строку табл. Переходим к вычислению значений на втором слое по формуле (.) при j . Подобным образом определяем последовательно значения j при t,39;,78;,7 и т.д. Таблица. Результаты вычислений для примера j t j,,5,5,75,,5,5,75,, 4,9749 9,94,4 3,,4 9,94 4,9749,39 4,596 8,497,96,4,96 8,497 4,596,78 4,464 7,846,56,96,56 7,846 4,464 3,7 3,93 7,49 9,47,56 9,47 7,49 3,93 4,56 3,645 6,697 8,753 9,47 8,753 6,697 3,645 5,95 3,3486 6,874 8,84 8,753 8,84 6,874 3,3486 6,34 3,937 5,764 7,4689 8,84 7,4689 5,764 3,937 7,73,858 5,83 6,93 7,4689 6,93 5,83,858 8,3,647 4,8793 6,375 6,93 6,375 4,8793,647 ( ;,3),6873 4,9655 6,4877 7,3 6,4877 4,9655,6873,466,86,6,,6,86,466 Аналитическое решение данной задачи определяется согласно приложению I формулой t, t e B s, где 3s s B d при : 3 3 B 3 s d cos d s 3. Получаем t, t 3e s — точное решение данной задачи. В последних двух строках табл.. приведены значения точного решения задачи и модуля разности при t,3. Для данной задачи 3

32 IV ( t) ( t ), f s, следовательно M и оценка 6 6 погрешности приближенного решения будет,3 3 4, Метод сеток для уравнений гиперболического типа Рассмотрим смешанную задачу для уравнения свободных колебаний однородной струны [5]: найти функцию (, t ), удовлетворяющую уравнению t, (.4) начальным условиям (,) f ( ), (,) t ( s) (.5) и краевым условиям (, t) ( t), ( s, t) ( t) ( t ). (.6) Как и для уравнения параболического типа, построив в полосе t, s прямоугольную сетку (. ), t jl ( j. ), заменяем производные в уравнении (.4) разностными отношениями (.3):, j j, j, j j, j. l l Обозначив, получим разностное уравнение, j j, j, j j, j j, (.7) которое является устойчивым при []. В частности, при уравнение (.7) принимает наиболее простой вид:. (.8), j, j, j, j Оценка погрешности приближенного решения, полученного из уравнения (.7) в полосе s, t T, имеет вид M4 M3 T T M 4, k k где — точное решение; Mk m, k 3, 4. k k t 3

33 Из уравнения (.7) видно, что для получения значений (, t ) на ( j ) слое используются значения (, t ) на слоях j и ( j ), (рис..3). Для начала вычисления необходимо знать значения (, t ) на первых двух слоях: j, j, которые можно определить одним из следующих способов, используя начальные условия (.5). П е р в ы й с п о с о б. Заменяя в начальном условии (.5) производную t (, ) разностным отношением, l для определения (, t ) на слоях j, j получим f, f l. Оценка погрешности значений имеет вид []:, m, M M В т о р о й с п о с о б. Заменяем производную t (,) разностным отношением, где,, — значение функции (, t ) на слое j. Тогда l из начальных условий (.5) получаем, f,. l Записав разностное уравнение (.8) для слоя j . и исключив из последних двух уравнений значения,, получим f, f f l. Оценка погрешности значений имеет вид []: 4 3 k k 4 3 k k k t Рис..3 M M, M m, k 3,4. 6 t. 33

34 34 Т р е т и й с п о с о б. Если функция f( ) задана аналитически и имеет конечную вторую производную, то значения можно определить с помощью формулы Тейлора: l l. t t Из уравнения (.4) и начальных условий (.5) имеем f, l, f. t t Тогда l l f. Погрешность значений, полученных по этой формуле, имеет порядок 3 Ol ( ). Аналогичным образом применяется метод сеток при решении смешанной краевой задачи для неоднородного волнового уравнения F, t. t В этом случае разностное уравнение имеет вид, j j, j, j j, j F j. Пример.. Методом сеток найти приближенное решение задачи 6, tt, s, t, s 4, 4 4, t, 4, t t с шагом,5, используя первый и второй способы для вычисления значений. Результат сравнить с аналитическим решением задачи. Для решения воспользуемся соотношением (.8) при. Тогда, учитывая, что шаг по аргументу равен,5, получим шаг по аргументу t равным l 8,5. Результаты вычислений будем заносить в таблицу следующим образом: сначала заполняем столбцы, соответствующие значениям и 8 4 (согласно краевым условиям), затем вычисляем значения (, t ) на первых двух слоях (согласно начальным условиям), и далее по формуле (.8) вычисляем значения j на последующих слоях:

35 j : ;. j : ;,3. j 3:,4,3,3, и т.д. П е р в ы й с п о с о б. Значения (, t ) на первых двух слоях находим по формулам f s, f l l s ; 4 4 заносим в табл. В т о р о й с п о с о б. Значения (, t ) на первых двух слоях находим по формулам f s, f f l s s l s, заносим в табл..3. В табл.. и.3 представлены результаты вычислений. В последних строках таблиц приведены значения точного решения задачи и модулей разности при t,875. Аналитическое решение задачи определяется по формуле (см. приложение I):, t Acos t Bs t s, где 4 s s A d и при : B l s s d, A s d cos d s, B s d cos d s Следовательно, функция, t cos t s t s является точным 4 решением рассматриваемой задачи

36 Таблица. Результаты вычислений для примера. (первый способ) j t j ,,5,,5,,5 3, 3,5 4. 7654,44,8478,8478,44,7654,5,957,699,6,397,6,699,957,5,965,7,368,4,368,7,965 3,375,7964,474,97,89,97,474,7964 4,5,5449,7,355,44,355,7,5449 5,65,6,389,585,55,585,389,6 6,75 -,559 -,879 -,3764 -,47 -,3764 -,879 -,559 7,875 -,4985 -,93 -,36 -,39 -,36 -,93 -,4985 8, -,7654 -,44 -, ,8478 -,44 -,7654 ( ;,875) -,567 -,36 -,3536 -,465 -,3536 -,36 -,567,6,47,5,6,5,47,6 Таблица.3 Результаты вычислений для примера. (второй способ) j t j ,,5,,5,,5 3, 3,5 4. 7654,44,8478,8478,44,7654,5,8574,5843,699,45,699,5843,8574,5,889,53,977,398,977,53,889 3,375,6557,6,589,735,589,6,6557 4,5,397,755,948,6,948,755,397 5,65,698,9,686,87,686,9,698 6,75 -,635 -,487 -,636 -,6888 -,636 -,487 -,635 7,875 -,5569 -,89 -,3445 -,455 -,3445 -,89 -,5569 8, -,7654 -,443 -,8478 -, -,8478 -,443 -,7654 ( ;,) -,567 -,36 -,3536 -,465 -,3536 -,36 -,567,38,7,9,,9,7,38 Сравнивая результаты вычислений, видим, что лучший результат вычислений получается при втором способе заполнения первых двух слоев таблицы. 36

37 .3 Метод сеток для задачи Дирихле Рассмотрим первую краевую задачу для уравнения Пуассона (задачу Дирихле): найти функцию (, t ), удовлетворяющую внутри некоторой области G уравнению а на границе — условию f,, (.9) (, ), где (, ) — заданная непрерывная функция. Выбрав шаги и l по и соответственно, строим сетку (. ), jl ( j. ) j и заменяем в каждом внутреннем узле, j производные, конечно разностными отношениями (.3), а уравнение (.9) конечно- разностными уравнениями:, j j, j, j j, j f j. (.) l Уравнения (.) вместе со значениями j в граничных узлах образуют систему линейных алгебраических уравнений. Наиболее простой вид эта система имеет для прямоугольной области и при l. В этом случае уравнения (.) записываются в виде f, (.), j, j, j, j 4 j j а значения в граничных узлах в точности равны значениям граничной функции. При f (, ) уравнение (.9) называется уравнением Лапласа и соответствующие конечно-разностные уравнения имеют вид j, j, j, j, j 4. (.) При этом погрешность аппроксимации имеет оценку 4 4 4, 4 m, G 4 4 Rj M M 6 При составлении уравнений (.) и (.) была использована схема узлов, представленная на рис..4. На рис..5 показана другая схема узлов, при которой конечно-разностные уравнения, соответствующие уравнению Лапласа, принимают вид. 37

38 Рис..4. Рис..5. j, j, j, j, j, 4 а для уравнения Пуассона j, j, j, j, j f j, (.3) 4 4 причем погрешность аппроксимации не превосходит M 4. 3 Другие схемы узлов, расположенных определенным образом около узла (, j ), рассмотрены в []. Пример.3. Найти решение задачи Дирихле для уравнения Пуассона в прямоугольнике A(, ), B(,), C(, ), D (, ) : AB,, 3, BC,. CD Построим сетку с шагом,5, получим три внутренних узла (рис..6). Запишем в этих узлах конечно-разностные уравнения согласно (.) и под- AD ( ) 3,5 3,5 4, 5 3 4, Рис..6.

39 ставим известные из краевых условий значения j в граничных узлах:,5,5, , ,5, После преобразования получим алгебраическую систему уравнений относительно неизвестных значений во внутренних узлах: j , , Решив эту систему методом Гаусса, получим ,54,,986, 3, Запишем теперь во внутренних узлах конечно-разностные уравнения согласно (.3) и подставим значения j в граничных узлах: 7 3, ,5,5, Выполнив несложные действия, получим, 88,,9375,, Итерационный метод решения системы конечно-разностных уравнений Непосредственное решение системы конечно-разностных уравнений методами последовательного исключения при большом числе узлов оказывается 39

40 слишком громоздким. Тогда более удобны итерационные методы решения, которые учитывают специальный вид таких систем [-3]. Рассмотрим наиболее простой метод процесс усреднения Либмана для систем вида (.), согласно которому вычисления ведутся следующим образом: выбрав начальные приближения () j, последовательные приближения узлов сеточной области определяются по формуле для внутренних ( k ) j ( k ) ( k ) ( k ) ( k ) ( k ) j, j, j, j, j k. (.4) 4 Доказано [5], что для любого шага сетки процесс Либмана сходится к точному решению независимо от выбора начальных значений, т.е. существует lm, причем погрешность приближенного решения имеет порядок k ( k ) j j O. Обычно итерации продолжаются до тех пор, пока в двух последовательных приближениях не совпадет требуемое количество десятичных знаков. Для оценки погрешности приближенного решения уравнения Лапласа можно использовать принцип Рунге [], согласно которому погрешность при- ближенного решения формулой, полученного с шагом, дается приближенной, где — приближенное решение, полученное с шагом. 3 Пример.4. Применяя метод усреднения Либмана, найти приближенное решение задачи ( ) с шагом. Итерации проводить с точностью до,. Запишем итерационную формулу для соотношения (.): ( k ) ( k) ( k) ( k) ( k) j, j, j, j, j fj k. (.5) 4 4 В предлагаемой сеточной области (рис..6) три внутренних узла,, 3, соотношение (.5) для каждого их этих узлов примет вид 4

41 ( k ) ( k ) ( k ) ( k ) ( k ) f, 4 4 ( k ) ( k ) ( k ) ( k ) ( k ) 3 f, 4 4 ( k ) ( k ) ( k ) ( k ) ( k ) f Подставляя соответствующим образом значения в граничных узлах (см. рис..6) и значения функции f (, ) в каждом внутреннем узле, получим ( k ) ( k) 7, 4 64 ( k ) ( k ) ( k ) 3 3, 4 3 ( k ) ( k) () () () В качестве начального приближения выберем 3. Результаты вычислений по полученной системе итерационных соотношений представлены в табл. 3.. Таблица 3. Результаты итерационного процесса для примера.4 k (7) (6),679,94,938,4,465,53,53,8,9688,6875,886,8984,936,948,967,9 3,3.4453,65,6553,6777,685, По результатам вычислений видно, что заданная точность вычислений, была достигнута на 7-й итерации на этом процесс останавливается. Формулы (.) (.5) используются для задачи Дирихле в случае, когда граница области G прямоугольной формы. Если граница криволинейна, то значения j для граничных узлов получаются путем переноса значений из точек границы [-3]. Погрешность, получаемую в результате такого переноса, можно значительно уменьшить, если для каждого граничного узла составлять уравнения следующего вида: 4

42 — для узла вида A (рис..7) A B — для узла вида C (рис..7) Рис..7. Получив одно из таких уравнений для каждого граничного узла и присоединив его к любой из систем конечно-разностных уравнений (.) (.5), получим систему алгебраических уравнений относительно значений j в узлах сетки. Если эту систему решать методом Либмана, то последовательные приближения граничных значений будут вычисляться по формулам. C D ( k ) ( k ) ( k ) B A ( k ) D C A, A C C A C ;. 4

43 3 ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ Интегральное уравнение уравнение, содержащее неизвестную функцию под знаком определенного интеграла. Наиболее часто встречающиеся линейные интегральные уравнения, в которых неизвестная функция входит линейно (в первой степени) интегральные уравнения Фредгольма первого и второго рода соответственно: b K, s ( s) ds f, (3.) b K, s ( s) ds f, (3.) где K, s (ядро) и f известные функции, числовой параметр 4. Интегральные уравнения вида K, s ( s) ds f, (3.3) K, s ( s) ds f (3.4) называются интегральными уравнениями Вольтерра первого и второго рода соответственно. Вводя функцию K, s при s, K, s при s, уравнения Вольтерра (3.3) и (3.4) можно свести к уравнениям Фредгольма с ядром K, s. Замечание: если ядро K, s и функция f — непрерывно дифференцируемые, причем K, при b, то уравнение Вольтерра первого рода (3.3) сводится к уравнению Вольтерра второго рода (3.4). 4 Интегральное уравнение (3.) не всегда имеет решения при данном значении параметра. Варьируя параметр, можно добиться того, чтобы решение уравнения (3.) существовало. 43

44 К линейным интегральным уравнениям может быть приведено большое количество задач математической физики. Основными проблемами здесь являются: ) нахождение приближенного или точного решения неоднородного интегрального уравнения при заданном значении параметра ; ) нахождение собственных значений и соответствующих собственных функций однородного интегрального уравнения Метод последовательных приближений Рассмотрим уравнение Фредгольма второго рода (3.) в виде где функции K, s f b f K, s ( s) ds, непрерывны. Будем искать решение этого уравнения в виде степенного ряда (по степеням ): ( ) ( ) ( ) ( ) (3.5) Подставляя выражение (3.5) в интегральное уравнение (3.) и приравнивая коэффициенты при одинаковых степенях, получим b, K, s s ds. f b K, s s ds. (3.6) Пусть K, s M и f N в области R b, s b. Из формул (3.6) по индукции получаем ряда (3.5) будет обеспечена, если Приняв M b. k ( ), M N b, и сходимость k k

45 получим приближенное решение интегрального уравнения (3.) с погрешностью k k k k N M b k N M b M b. (3.7) Формула (3.5) дает аналитическое относительно решение уравнения Фредгольма (3.) в окрестности точки. Из формул (3.6) вытекает, что решение (3.5) можно записать в виде или Здесь функция b f K, s f ( s) ds b f R, s, f ( s) ds. (3.8) R s K s. называется резольвентой уравнения (3.), определяется данным степенным рядом при малых. Пользуясь аналитическим продолжением, резольвенту R, s, можно продолжить на всю комплексную плоскость параметра, за исключением собственных значений,, (особые точки), которые являются полюсами резольвенты. Тогда формула (3.8) дает решение уравнения (3.) при любом ( k k, ). Коэффициенты K, s, так называемые итерированные ядра, могут быть найдены последовательно по формулам K, s K, s, b K, s K, t K t, s dt. b K, s K, t K t, s dt. Рассмотрим теперь соответствующее уравнение Вольтера (3.4): 45

46 где b. Полагая f K, s ( s) ds, аналогично предыдущим выкладкам получим откуда 46, (3.9) f, K, s s ds,, M N b. K, s M, f N при b, s b. (3.) Следовательно, ряд (3.9) сходится при любом и дает единственное решение уравнения (3.4). Погрешность приближенного решения k Y k k на основании оценок (3.) определяется формулой N M b M b M b Y N e k! k! k k Замечание: Неудобством метода последовательных приближений является необходимость вычисления квадратур. Если интегралы не вычисляются точно, то приходится прибегать к численным квадратурным формулам. Пример 3.. Методом последовательных приближений найти приближенное решение уравнения Фредгольма s ds. s Полагая b, имеем k f, s K, s s ds ds l. s Тогда в качестве первого приближения можно взять k.

47 ( ) ( ) ( )l. Здесь M m K, s m, N m f m. b s b s b s Следовательно, полученный ряд сходится при. В частности, при на основании (3.7) точность решения, будет, ( ) ( ). 3. Метод конечных сумм Идея метода конечных сумм заключается в замене определенного интеграла конечной суммой с помощью некоторой квадратурной формулы b F d A F R F, (3.) где, — абсциссы точек отрезка [ b;, ] A, — числовые коэффициенты, не зависящие от выбора функции F; ( ) RF — остаточный член (ошибка) формулы (3.). Обычно A и A b. В случае равноотстоящих точек,, где b, имеем: ) для формулы прямоугольников A,, A ; ) для формулы трапеций A A, A, ; b 3) для формулы Симпсона при m,, m 4 A A m, A A3 A m, A A 4 A m Погрешность приближенного решения зависит от погрешности выбранной квадратурной формулы. Рассмотрим интегральное уравнение Фредгольма второго рода (3.): 47

48 b K, s ( s) ds f b. Выбирая точки [, b ] и обозначая, K, j Kj, f f, j, на основании формулы (3.) будем иметь где A K f R,, j j j j R — соответствующие ошибки. Отбрасывая в этой системе величины для приближенных значений линейную систему алгебраических уравнений: R, решения в узлах,, получим A K f,. (3.) j j j j, j Вводя символы Кронекера j и учитывая, что j j (немой, j индекс j индекс суммирования), систему (3.) можно записать в виде Если j A K f,. (3.3) j j j j det j AK j j, (3.4) то система (3.3) имеет единственное решение, которое можно найти методами решения систем алгебраических уравнений. Найдя (, ) для решения ( ), получаем из уравнения (3.) приближенное аналитическое выражение f A K,. j j j j Замечание: метод конечных сумм дает хорошие результаты, если ядро K, s и правая часть f достаточно гладкие функции. Метод конечных сумм может быть применен также к интегральному уравнению Фредгольма первого рода (3.): b K, s ( s) ds f. 48

49 В этом случае приближенные значения определяются из системы j решения в узлах,, A K f,. j j j Особенно просто применение метода конечных сумм для решения интегрального уравнения Вольтерра второго рода (3.4): K, s ( s) ds f b, которое можно рассматривать как уравнение Фредгольма второго рода. Здесь K при j и, следовательно, соответствующая система (3.) имеет j вид Причем коэффициенты () j j j j A K f,. (3.5) A вычисляются для соответствующей квадратурной () j формулы на каждом -том шаге, поскольку интеграл, входящий в уравнение Вольтерра, имеет переменный верхний предел. Пример 3.. Применяя формулу трапеций с шагом, на отрезке [,], найти приближенное решение уравнения,5,5 l 3,5 s s ds. (3 ) Для формулы трапеций для каждого -го шага (,5 ) будем иметь ( ) ( ) ( ) A A, Aj j j,,3, 4. Полагая в уравнении (3 ) (,5), получим f,,5,5 l 4,,3,4,5. s s ds Применяя к определенным интегралам формулу трапеций с шагом,, согласно (3.5) получим систему уравнений 49

50 f, A K A K f, () () A K A K A K f () () () A K A K A K A K f, (3) (3) (3) (3) A K A K A K A K A K f (4) (4) (4) (4) (4) A K A (5) (5) K A (5) K A (5) K A (5) K A (5) K f, () () () () (3) (3) (4) (4) (5) (5) где A A A A A A3 A A4 A A4,; а остальные A, для всех j. Составляем таблицу () значений j Kj,5 j, f,5 l 4 (,5 ) (табл. 3.) и из полученной системы последовательно находим f 4,, f,k,k 3, 385, f,k, K,K 3, 8, f,k, K K,K, 779, f,k, K K K,K, 677, f ,,K, K K K K,K, 496., Таблица 3. Значения коэффициентов K K K 3 K 4 K 5 f,9333,943,95,9556, 4,,8333,843,85,8556,9 4,377,743,75,7556,8 4,435 3,65,6556,7 4,3 4,5556,6 4,53 5,5 4,869 Уравнение (3 ) соответствует краевой задаче,5,5 l 4, (), (). (3 ) 5

51 Связь между решением ( ) интегрального уравнения (3 ) и решением ( ) l краевой задачи (3 ) определена выражениями (II.3), (II.5), см. приложение II. Следовательно, точным решением уравнения (3 ) будет d d и, обратно, приближенное решение задачи (3 ) будет иметь вид: s ds,5. На рис. 3. представлено графическое сравнение точных и приближенных решений уравнений (3 ), (3 ); в табл. 3. их значения. Рис. 3. Таблица 3. Сравнение приближенных и точных решений ( ) ( ), 4, 4. 3,3889 3,385,754,676,4 3,4 3,8,87,49,6,783,779,6,4989,8,673,677,644,8345,,5,496,637, Метод вырожденного ядра Ядро K, s называется вырожденным, если оно может быть представлено в виде конечной суммы парных произведений: где функции, K, s s, (3.6) s можно считать линейно независимыми. Для таких ядер интегральное уравнение Фредгольма второго рода (3.): f K, s ( s) ds b 5

Видео:Интегральные уравнения с вырожденным ядромСкачать

Содержание

Глава I. Общие сведения об интегральных уравнениях. 7

Глава II. Вычисление определенных интегралов на Mathcad. 11

2.1. Метод Ромберга. 11

2.2. Использование пакетов MathCAD для решения дифференциальных уравнений. 14

2.3. Метод Эйлера для дифференциальных уравнений первого порядка 16

2.4. Решение дифференциальных уравнений второго порядка. 17

Глава III Численные методы решения интегральных уравнений. 20

3.1. Квадратурный метод решения интегральных уравнений Фредгольма. 24

3.2. Квадратурный метод решения интегральных уравнений Вольтерры. 27

Глава IV. Прикладные задачи, использующие решение интегральных уравнений. 29

4.1. Расчет теплоизоляции. 29

4.2. Фильтр Калмана. 33

Листинг№1 Численное интегрирование. 39

1. Функция, возвращающая значение интеграла функции помощью метода Симпсона 39

2. Функция, возвращающая значение интеграла с помощью формулы трапеции 39

3. Функция, возвращающая значение интеграла, найденного по формулам треугольников. 40

Листинг № 2 Решение обыкновенных дифференциальных уравнений. 41

1.Функция, возвращающая численное решение ДУ методом Адамса. 41

2. Задание функции возвращающей решение ДУ методом Пикара. 42

3.Метод Эйлера. 42

Листинг №3. Решение линейного интегрального уравнения Вольтерра I-го рода. 43

Листинг №4. Решение линейного интегрального уравнения Вольтера II-го рода. 44

Листинг №6. Фильтр Калмана. 45

Список литературы: 50

Видео:Интегральные уравнения ВольтерраСкачать

Введение.

Интегральные уравнения являются одними из наиболее плодотворных средств математического исследования, как в чистом, так и в прикладном анализе. Это относится, в частности, к задачам теории механических колебаний и соответствующих областей техники и теоретической физики, где интегральные уравнения не только полезны, но зачастую даже совершенно необходимы для численных расчетов.

Интегральным уравнением называется уравнение относительно неизвестно функции, содержащейся под знаком интеграла.

К интегральным уравнениям приводят многие задачи, возникающие в математике и математической физике. Исторически, первой задачей, сведенной к интегральному уравнению

cчитается задача Абеля, имеющая следующую формулировку:

Определить вид кривой , по которой в вертикальной плоскости под действием силы тяжести должна скатываться материальная точка, так чтобы, начав свое движение с нулевой начальной скоростью из точки , она диагональна оси за заданное время .

Интегральные уравнения широко используются в моделях, рассматриваемых в теории упругости, газовой динамики, электродинамике, экологии и других областях физики, в которых они являются следствием законов сохранения массы, импульса и энергии. Достоинство данных моделей состоит в том, что интегральные уравнения, в отличие от дифференциальных, не содержат производных искомой функции и, следовательно. Жесткие ограничения на гладкость решения отсутствует.

В данной работе я постаралась отобразить основные возможности применения интегральных уравнений в различных областях жизни, а так же их численное решение с помощью средств компьютерной математики.

Целью данной работы является рассмотрение решения интегральных уравнений с помощью систем компьютерной математики, решение задачи Коши, а так же их практическое применение в задачах физики и механики.

В данной теме важным оказывается выбор базового программного средства.

Пакет Mathematica является сегодня наиболее популярным среди ученых, особенно теоретиков. Пакет предоставляет широкие возможности в проведении символических (аналитических) преобразований, однако требует значительных ресурсов компьютера.

Пакет Maple также весьма популярен. Кроме аналитических преобразований, пакет в состоянии решать задачи численно. Характерной особенностью пакета является то, что он позволяет конвертировать документы в формат LaTeX — стандартный формат подавляющего большинства научных издательств мирового класса. Кроме того, ряд других программных продуктов используют интегрированный символьный процессор Maple. Например, пакет подготовки научных публикаций Scientific WorkPlace позволяет обращаться к символьному процессору Maple, производить аналитические преобразования и встраивать полученные результаты в создаваемый документ[1].

Пакет Matlab фактически представляет собой своеобразный язык программирования высокого уровня, ориентированный на решение научных задач. Характерной особенностью пакета является то, что он позволяет сохранять документы в формате языка программирования С.

Пакет Mathcad более популярен в инженерной, чем в научной, среде. Характерной особенностью является использование привычных стандартных математических обозначений, т. е. вид документа на экране максимально приближен к общепринятой математической нотации.

В отличие от упомянутых выше пакетов, Mathcad является средой визуального программирования, т. е. не требует знаний специфического набора команд. Простота освоения пакета, дружественный интерфейс, относительная непритязательность к возможностям компьютера явились главными причинами того, что именно этот пакет был выбран мной для реализации численного решения интегральных уравнений.

Видео:Простейшие интегральные уравненияСкачать

Глава I. Общие сведения об интегральных уравнениях.

Интегральными уравнениями называются функциональные уравнения, содержащие интегральные преобразования над неизвестной функцией . Интегральное уравнение называется однородным, если есть решение уравнения для произвольного . Линейное интегральное уравнение в общем виде может быть представлено:

где — ядро интегрального преобразования, правая часть и являются заданными функциями, — параметр уравнения. Область интегрирования V может быть фиксированной (интегральные уравнения типа фредгольмовых) или переменной (интегральные уравнения типа вольтерровых).

Линейное интегральное уравнение первого рода получается при , и имеет вид:

Однородное линейное интегральное уравнение второго рода получается при и имеет вид:

Неоднородное интегральное уравнение второго рода получается при g(x) = 1 и имеет вид

Уравнения вида являются неоднородными.

Линейное интегральное уравнение Вольтерра первого рода имеет вид:

Если и если функции имеют производные , непрерывные в интервале , заключенном в интервале интегрирования, внутри которого не обращается в нуль, то уравнение Вольтерра первого рода допускает в интервале непрерывное и единственное решение[2].

Представленная процедура решает уравнение методом квадратурных формул. Вычисление интеграла производится по формуле трапеций с постоянным шагом h:

,

где

Aj = 1 при j > 1 и Aj = 0.5 при j = 1

Линейное интегральное уравнение Вольтера второго рода имеет вид:

Причем независимые переменные изменяются на промежутке , ядро непрерывно внутри и на сторонах треугольника, ограниченного прямыми Функция на непрерывна.

Уравнение данного типа решается с помощью метода квадратурных формул, суть которого состоит в замене интегрального уравнения аппроксимирующей системой алгебраических уравнений относительно дискретных значений искомой функции и решении этой системы. В основе такой замены лежит приближение интеграла квадратурными формулами. Применение формулы трапеций с постоянным шагом h приводит к рекуррентной формуле:

· Aj = 1 при j > 1 и Aj = 0.5 при j = 1.

Линейное интегральное неоднородное уравнение Фредгольма второго рода имеет вид:

где ядро определено в квадрате . Кроме того, полагается, что ядро непрерывно в V. При , используя квадратурную формулу трапеций с постоянным шагом h, получим:

· Aj = 1 при j, не равном 1 или n

· Aj = 0.5 при j, равном 1 или n.

Получаем систему линейных уравнений, которую решаем методом Гаусса с частичным выбором ведущего элемента. При решении полученной системы уравнений возможны два случая — система вырождена и нам придется поделить на ноль в ходе решения, или система невырождена. Если система невырождена, то существует одно и только одно решение. Если же система вырождена, то данный алгоритм неприменим. В случае вырожденой матрицы функция возвращает False. Если матрица невырождена, то функция возвращает True, а переменная Y содержит решение системы.

Для сравнения с нолем в алгоритм передается малое число epsilon, и любое число, по модулю меньшее epsilon, считается нолем.

Видео:Решить интегральное уравнение (ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ) Свёртка функций, Умножение изображенийСкачать

Глава II. Вычисление определенных интегралов на Mathcad

Видео:Резольвента. Как легко решить интегральное уравнениеСкачать

2.1. Метод Ромберга

Пусть требуется вычислить определенный интеграл на интервале [a;b].

Далеко не всегда задача может быть решена аналитически. В частности, численное решение требуется в том случае, когда подынтегральная функция задана таблично. Для численного интегрирования подынтегральную функцию аппроксимируют какой-либо более простой функцией, интеграл от которой может быть вычислен. Обычно в качестве аппроксимирующей функции используют полином. В случае полинома нулевой степени метод численного интегрирования называют методом прямоугольников, в случае полинома первой степени – методом трапеций, в случае полинома второй степени – методом Симпсона. Все эти методы являются частными случаями квадратурных формул Ньютона-Котеса.

Итак, в методе трапеций подынтегральную функцию аппроксимируют полиномом первой степени, то есть прямой линией. Это значит, что вместо площади криволинейной трапеции мы будем искать площадь прямоугольной трапеции. Приближенное значение интеграла равно

Погрешность этой формулы равна .

Обозначим , где . Смысл введенного обозначения станет, ясен несколько позже.

Оценку значения интеграла можно сделать более точной, если разбить интервал на n частей и применить формулу трапеций для каждого такого интервала

Если разбить интервал на две части, то есть уменьшит шаг в два раза , то оценка для величины интеграла будет иметь вид

В данном случае суммирование включает только один элемент. Обратите внимание, в новую оценку вошла старая оценка. Нам потребовалось определять значение функции только в новых узлах[3].

Если имеется 2n подинтервалов, то

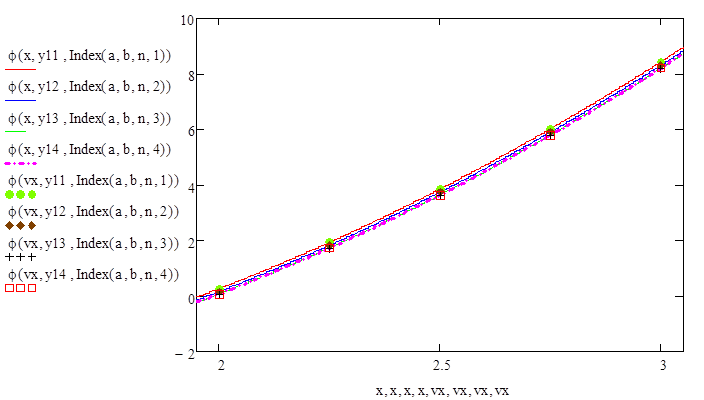
Вообще, справедливо рекуррентное соотношение

Полученное соотношение называют рекурсивной формулой трапеций и часто применяют для вычисления определенных интегралов. Преимущество этой формулы состоит в том, что при увеличении числа подинтервалов функцию нужно вычислять только во вновь добавленных точках. К сожалению, с помощью этой формулы нельзя получить сколь угодно точное значение интеграла. Во-первых, при увеличении числа разбиений объем вычислений стремительно возрастает; во-вторых, на каждом шаге накапливается ошибка округлений. Для дальнейшего уточнения значения интеграла можно сделать следующий шаг – экстраполировать полученную последовательность значений на случай бесконечного числа точек или что то же самое, на случай нулевого шага. Такой подход называется методом Ромберга.

Метод Ромберга заключается в том, что полученные оценки значения интеграла экстраполируют на случай бесконечного числа разбиений (величины шага равной нулю) по рекуррентной формуле

(1)

То есть строится следующий треугольник

R(5,1) R(5,2) R(5,3) R(5,4) R(5,5) ,

в котором первый столбец состоит из значений интеграла, полученных при последовательном удвоении числа интервалов. Второй столбец – результат уточнения значений первого столбца по рекуррентной формуле (1). Третий столбец – уточненные значения интеграла на основе второго столбца и т. д[4].

Формула (1) может быть получена различными способами. Можно, например, воспользоваться методом Невиля. Пусть имеется набор точек . Обозначим полином нулевой степени, проходящий через i-ю точку. Обозначим полином первой степени, проходящий через точки i и i+1. Совершенно аналогично будет означать полином n–1 степени, проходящий через все n точек. Легко убедиться, что

В нашем случае . В качестве выступают . Мы хотим получить значение интеграла в пределе , поэтому .

Видео:Решить интегральное уравнениеСкачать

2.2. Использование пакетов MathCAD для решения дифференциальных уравнений.

Пусть необходимо найти решение уравнения

(2)

с начальным условием . Такая задача называется задачей Коши. Разложим искомую функцию в ряд вблизи точки и ограничимся первыми двумя членами разложения Учтя уравнение (2) и обозначив , получаем Эту формулу можно применять многократно, находя значения функции во все новых и новых точках.

(3)

Такой метод решения обыкновенных дифференциальных уравнений называется методом Эйлера. Геометрически метод Эйлера означает, что на каждом шаге мы аппроксимируем решение (интегральную кривую) отрезком касательной, проведенной к графику решения в начале интервала. Точность метода невелика и имеет порядок h. Говорят, что метод Эйлера – метод первого порядка, то есть его точность растет линейно с уменьшением шага h.

Существуют различные модификации метода Эйлера, позволяющие увеличить его точность. Все они основаны на том, что производную, вычисленную в начале интервала, заменяют на среднее значение производной на данном интервале[5]. Среднее значение производной можно получить (конечно же, только приближенно) различными способами. Можно, например, оценить значение производной в середине интервала и использовать его для аппроксимации решения на всем интервале

Можно также оценить среднее значение производной на интервале

Такие модификации метода Эйлера имеет уже точность второго порядка.

Оценку значения производной можно улучшить, увеличивая число вспомогательных шагов. На практике наиболее распространенным методом решения обыкновенных дифференциальных уравнений является метод Рунге-Кутты четвертого порядка. Для оценки значения производной в этом методе используется четыре вспомогательных шага. Формулы метода Рунге-Кутты следующие

Перечисленные методы можно применять и для решения систем дифференциальных уравнений. Поскольку многие дифференциальные уравнения высших порядков могут быть сведены заменой переменных к системе дифференциальных уравнений первого порядка, рассмотренные методы могут быть использованы и для решения дифференциальных уравнений порядка выше первого.

Еще один тип задач, часто встречающихся на практике, – краевые задачи. Пусть имеется дифференциальное уравнение второго порядка . Решение уравнения требуется найти на интервале , причем известно, что . Понятно, что произвольный интервал заменой переменных может быть сведен к единичному. Для решения краевой задачи обычно применяют метод стрельб. Пусть где k – некоторый параметр. Для некоторого пробного значения k может быть решена задача Коши, например, методом Рунге-Кутты. Полученное решение будет зависеть от значения параметра . Мы хотим найти такое значение параметра, чтобы выполнялось условие . Фактически мы свели исходную задачу к задаче решения трансцендентного уравнения с таблично заданной функцией. Если найдены такие значения параметра k1 и k2, что , то дальнейшее уточнение значения параметра можно проводить методом деления отрезка пополам[6].

Видео:Решение интегральных уравнений операционным методомСкачать

2.3. Метод Эйлера для дифференциальных уравнений первого порядка

Решим задачу Коши для дифференциального уравнения первого порядка методом Эйлера.

Пусть правая часть уравнения равна

Зададим границы изменения x:

Зададим число точек и величину шага:

Зададим начальные условия:

Вычислим x и y по формулам Эйлера

Представим результат графически и сравним его с аналитическим решением

Точное аналитическое решение и решение, полученное численно, отличаются в точке x=1 на

То есть относительная ошибка составляет

Видео:6-2. Метод сетокСкачать

2.4. Решение дифференциальных уравнений второго порядка

В качестве примера решим задачу о гармоническом осцилляторе, для которого известно аналитическое решение, и легко может быть оценена точность вычислений. Дифференциальное уравнение второго порядка

преобразуем к системе из двух дифференциальных уравнений первого порядка

Пусть декремент затухания

Пусть циклическая частота

Зададим начальные условия

y0 соответствует начальной координате, а – начальной скорости. Зададим теперь матрицу D. С учетом того, что искомая величина соответствует нулевому элементу массива , ее первая производная – первому, а вторая – второму, имеем

Представим результаты расчета на графике и сравним их с аналитическим решением

Для контроля точности вычислений нарисуем фазовую траекторию (зависимость смещения от скорости). Для гармонического осциллятора фазовая траектория должна иметь вид эллипса.

Примечание: Mathcad имеет еще две функции для решения задачи Коши. Это функции Rkadapt и Bulstoer. Эти функции имеют те же самые аргументы и возвращают решения в такой же форме, что и функция rkfixed. Первая из этих функций использует метод Рунге–Кутты с переменным шагом, что позволяет повысить точность вычислений и сократить их объем, если искомое решение имеет области, где ее значения меняются быстро, и области плавного изменения. Функция Rkadapt будет варьировать величину шага в зависимости от скорости изменения решения[7].

Функция Bulstoer реализует иной численный метод – метод Булирша–Штёра. Ее следует применять, если известно, что решение является гладкой функцией.

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Глава III Численные методы решения интегральных уравнений.

Интегральное уравнение в достаточно общем виде можно записать в следующей форме:

,

где D — некоторая область n-мерного пространства;

x — неизвестная функция, зависящая от времени;

K — функция относительно x(линейная или нелинейная).

Далее мы ограничим рассмотрение одномерным линейными интегральными уравнениями, в которой функция x(t) является функцией, зависящей от одной переменной, а область D – отрезком конечной длины, в каждой точке которого подъинтегральная функция K(t, s,x(s)) представима в виде Q(t, s)x(s).

Классификация типов линейных интегральных уравнений приводится по виду верхней границы интеграла в : если верхняя граница интегрирования является постоянной, то уравнение называется уравнением Фредгольма, если переменной — уравнением Вольтерры, которые, в свою очередь, подразделяются на уравнения первого и второго рода[8]. На практике наиболее широко применяются линейные интегральные уравнения второго рода:

,

,

где f(t) – неизвестная функция;

x(t)- решение уравнения;

Q(t, s)- ядро интегрального уравнения.

Ядро интегрального уравнения Фредгольма определяется на множестве точек квадрата [a, b]x[a, b],уравнения Вольтерры – в треугольнике .

Отметим, что доопределив ядро Q(t, s) уравнения Вольтерры нулем, в треугольнике уравнение Вольтера можно считать уравнением Фредгольма и применять для его решения методы уравнения Фредгольма. Однако при этом могут быть упущены некоторые специфические особенности уравнения Вольтерры, что определяет необходимость их раздельного рассмотрения[9].

Дополнительный множитель , который может быть отнесен к интегральному ядру, введен для придания уравнениям более общего вида. Существуют теоремы устанавливающие существование решений интегральных уравнений при различных значениях , которые доказываются подобно тому, как это делается в теории линейных ДУ, через рассмотрение соответствующих однородных уравнений .

Значительно более сложной задачей оказывается задача доказательства существования, единственности и непрерывной зависимости решений от функции для интегральных уравнений первого рода:

,

,

относящиеся к классу некорректных задач.

Уравнения первого и второго рода можно записать в общем виде, используя функцию h(t), тождественно равную нулю для уравнений первого рода и единице — для уравнений второго рода:

.

Когда функция h(t) обращается в ноль в некоторых точках прямоугольника интегрирования, уравнение относится к интегральным уравнениям третьего рода. Уравнения данного типа встречаются в приложениях значительно реже, чем уравнения первых двух типов, значительно менее изучены.

Многие используемые на практике интегральные уравнения имеют ядро, зависящее только от разности t-s. Интегральные уравнения с данным типом ядра называются уравнениями с разностным ядром. Примером данного типа является уравнение, полученное в задаче Абеля[10].

Если Q(t, s) и f(t) – непрерывные функции, то при любых значениях параметра непрерывное решение уравнения Вольтерры второго рода существует, и оно единственное. Для уравнения Фредгольма второго рода при тех же требованиях единственное непрерывное решение существует, например, при условии, что

При снижении требований к гладкости возможных решений условие ослабляется. Например, для функций, интегрируемых с квадратом, в роли достаточного условия фигурирует неравенство

Известны формулы (или совокупность формул), позволяющие найти точное решение x(t). Например, решение уравнения Вольтерры, с с мультипликативным ядром

вычисляется по формуле :

Решение уравнения Фредгольма с вырожденным ядром

,

где числа — решения системы линейных алгебраических уравнений

(1)

;

.

Условие существования и единственности решения уравнения Фредгольма с вырожденным ядром, очевидно. Зависит от значения определителя D() системы линейных алгебраических уравнений (1), называемого определителем Фредгольма. Если D()≠0, то решение существует и единственно.

Наличие методов нахождения точного решения интегрального уравнения с вырожденным ядром позволяет построить приближенный метод, в основе которого лежит замена одного уравнения другим, ядро которого вырождено и в некотором смысле близко к ядру исходного уравнения. Данная замена ядра опирается на различные способы локальной аппроксимации функций, зависящих от двух переменных. Помимо упомянутого выше метода замены ядра на вырожденно, известен ряд других приближенно-аналитических методов решения интегральных уравнений, например, метод последовательных приближений, метод моментов и другие.

Далее мы рассмотрим численные методы решения интегральных уравнений, в основе которого лежит замена интеграла в интегральном уравнении конечной суммой, используя какую-либо квадратурную формулу. Это позволяет свести решение исходной задачи к решению системы линейных алгебраических уравнений, число которых определяется числом узлов временной сетки. Методы решения интегральных уравнений, основанные на данном подходе, называются квадратурными методами или методами конечных сумм.

Преимущество данных методов состоит в простоте их реализации. Отметим, что без каких-либо изменений данные методы можно применять для решения нелинейных интегральных уравнений, имея в виду, что в этом случае приходится решать систему нелинейных алгебраических уравнений.

Видео:Математика без Ху!ни. Вычисление суммы рядаСкачать

3.1. Квадратурный метод решения интегральных уравнений Фредгольма.

Заменим определенный интеграл

,

его приближенным значением, вычисляемым с помощью квадратурной формулы:

,

где j=1,2,…,n – номера узлов временной сетки; — весовые коэффициенты квадратурной формулы.

Подставив правую часть приближенного равенства с вместо интеграла в уравнение Фредгольма второго рода, получим

Данное выражение задает функцию, описывающую приближенное решение интегрального уравнения

,

Введем на отрезке [a, b] дискретную временную сетку узлы которой совпадают с узлами сетки . Для каждого момента времени выполняется равенство

,

И запишем равенство в виде системы n — линейных алгебраических уравнений с n неизвестными:

для решения, которой можно использовать любой из методов решения систем линейных алгебраических уравнений.

Таким образом, нахождение решения уравнения Фредгольма второго рода осуществляется в соответствии со следующим алгоритмом.

1. Задать временную сетку

2. Вычислить значение функции f(x) в узлах временной сетки.

3. Вычислить элементы матрицы, составленной из коэффициентов системы линейных алгебраических уравнений.

4. Решить систему линейных уравнений.

Точность численного решения интегрального уравнения зависит от нескольких факторов: применяемой квадратурной формулы, числа узлов временной сетки, свойств функции Q(t, s). В ряде книг приводятся аналитические выражения, позволяющие оценить максимальную погрешность численного решения при использовании различных вычислительных схем. Однако эти оценки оказываются малопригодными из-за их громоздкости, поэтому на практике используют менее строгий метод контроля точности численного решения — принцип Рунге.

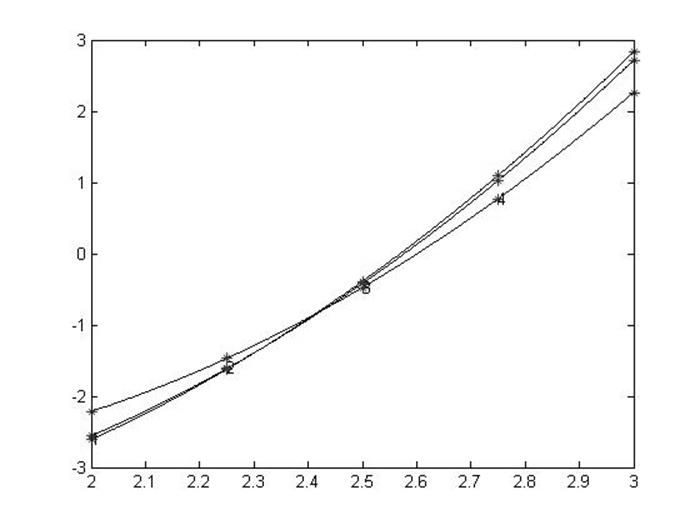
Данный принцип состоит в сравнении численных решений, полученных на временных сетках с шагом 2h и h, в одних и тех же узлах временной сетки. Абсолютное значение разности данных решений характеризует величину погрешности численного решения. Недостаток данного подхода состоит в том, что при данном способе контроля приходится ограничиваться квадратурными формулами, пригодными только для сеток с равномерным шагом[11].

Важно понимать, что необходимо согласовывать выбор конкретной квадратурной формулы (точнее порядок ее точности) со степенью гладкости ядра интегрального уравнения. Если ядро и свободный член оказываются недостаточно гладкими, то для вычисления интеграла не следует применять высокоточные квадратуры, а лучше ограничиться такими формулами, как формулы трапеций и прямоугольников.

Видео:Кобельков Г. М. - Численные методы. Часть 2 - Метод конечных элементовСкачать

3.2. Квадратурный метод решения интегральных уравнений Вольтерры.

Так как параметр λ в линейных интегральных уравнениях Вольтерры, в отличие от уравнения Фредгольма, не несет такой нагрузки, положим его равным единице и будем численно решать уравнение

,где

Учитывая что уравнение Вольтерры формально можно считать уравнением Фредгольма вида:

,

K(t, s)=

для нахождения решения рассматриваемого уравнения воспользуемся результатами предыдущей главы.

Введем в рассмотрение временную сетку из [a, b], сотоящую из n узлов, и выберем конкретную квадратурную с весами , тогда приближенное решение интегрального уравнения принимает вид

,

Составим систему линейных алгебраических уравнений, аналогичную системе (1), которая в силу свойств ядра интегрального уравнения вырождается в треугольную:

Из данной системы видно, что искомые значения находятся последовательными вычислениями по следующим формулам:

где i=2,…,n.

Видео:Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать

Глава IV. Прикладные задачи, использующие решение интегральных уравнений.

Видео:Решение интегральных уравнений AСкачать

4.1. Расчет теплоизоляции.

По стальному горизонтальному трубопроводу () внутренний и наружный диаметр которого , соответственно, движется вода со средней скоростью . Средняя температура воды . Трубопровод покрыт равномерным по толщине слоем теплоизолирующего материала (асбест, ) и охлаждается посредством естественной конвекции сухим воздухом с температурой .

Определить наружный диаметр изоляции , при котором на внешней поверхности изоляции устанавливается температура . Определить: линейный коэффициент теплопередачи от воды к воздуху ; потери теплоты с одного метра длины трубопровода ; температуру наружной поверхности стального трубопровода . Наружный диаметр изоляции должен быть рассчитан с такой точность, чтобы температура отличалась от заданной не более чем на 0.1 K.

Упрощающие предположения: течение воды в трубе является термически стабилизированным; между сталью и асбестом существует идеальный тепловой контакт; теплопроводности стали и асбеста не зависят от температуры[12].

Вывод расчетных соотношений

Расчетная модель — бесконечная цилиндрическая труба, режим стационарный, объемных источников тепла в трубе нет. Уравнение теплопроводности имеет вид:

В цилиндрической системе координат получаем:

Граничные условия (закон Ньютона — Рихмана):

(положительным считается тепловой поток, идущий от центра )

Произведем замену переменных: ( ), (), тогда

()

()

где , ,.

(т. к. ). Тогда:

,

C другой стороны:

Приравнивая выражения для , находим постоянную K:

Тепловой поток, проходящий через стенку трубы на единице длины:

где

т. е. , где — линейный коэффициент теплопередачи

Окончательные расчетные формулы для определения температур (с учетом того, что ) имеют вид:

Для определения коэффициентов теплопередачи используются эмпирические формулы для переходного режима течения ():

, где .

Поскольку , а теплофизические свойства воды меняются с температурой не очень сильно, то и можно взять при температуре и считать, что . Тогда имеем:

Аналогично для естественной конвекции:

, где ,

Теплофизические свойства воды и воздуха берутся из книги [“Задачник по технической термодинамике и теории тепломассообмена” Под. ред. и Петражицкого , “Высшая школа” , 1986].

Задача решается методом последовательных приближений, первое приближение , последующие приближения находятся из соотношения:

на каждом шаге производя уточнение и до тех пор, пока относительная температура , вычисленная по формуле не станет равна заданному значению с точностью .

4.2. Фильтр Калмана.

Представим себе некоторую систему, состояние которой в любой момент времени однозначно характеризуется определенным набором величин (например, координаты, скорости, уровни напряжения и т. д.), как правило, недоступных для непосредственного определения. Говоря терминами векторной алгебры, эти величины являются элементами вектора состояния системы, отнесенного к заданному моменту времени. Кроме того, имеется ряд переменных, некоторым образом связанных с состоянием системы, которые можно измерить с заданной точностью; такие величины составляют вектор измерений, относящихся к определенному моменту времени. Алгоритм фильтра Калмана позволяет в реальном времени построить оптимальную оценку состояния системы, основываясь на измерениях, неизбежно содержащих погрешности; при этом вектор измерений рассматривается в качестве многомерного выходного сигнала системы, отягощенного шумом, а вектор состояния — неизвестный многомерный сигнал, подлежащий определению. Условием оптимальности построенной оценки состояния является минимум ее средней квадратической ошибки[13].

Указанный критерий признан наиболее общим; доказано, что применение множество других подобных условий (например, среднее арифметическое некоторой непрерывно возрастающей, симметричной функции, такой как абсолютная величина) приводит к тому же решению (функция модуля не обладает непрерывной производной, что существенно затрудняет ее применение в алгоритмах минимизации). Фильтр Калмана явился существенным усовершенствованием своего предшественника — алгоритма, позволяющего с помощью метода наименьших квадратов выделять скалярный сигнал из шума с неизменными статистическим характеристиками, предложенного в 40-х годах XX столетия Н. Винером.

Начальными условиями на каждом новом цикле алгоритма служат оценка состояния системы и величина, характеризующая ее погрешность. В случае скалярной переменной такой характеристикой является дисперсия, которая тем больше, чем сильнее разброс индивидуальных значений относительно истинного. Распространенная оценка дисперсии — среднеквадратическое отклонение, то есть квадрат стандартного отклонения, — выражает степень разброса величины относительно среднего. Обобщением дисперсии для вектора, то есть совокупности скалярных величин, служит ковариационная матрица. Ее диагональные элементы являются дисперсиями соответствующих составляющих вектора, а недиагональные — ковариациями, характеризующими взаимосвязь между парой составляющих. Совокупность измерений, отнесенных к каждому из моментов времени, обобщает вектор измерений. Алгоритм последовательно обрабатывает вновь поступающие векторы измерений, учитывая при этом значения, вычисленные на предшествующем цикле. Эта особенность отличает алгоритм фильтра Калмана от нерекуррентных алгоритмов, которым для работы требуется хранить весь массив обрабатываемых данных[14].

На следующем шаге с помощью обрабатываемых на данном цикле измерений уточняются начальные условия. Для этого алгоритм вычисляет вес поправок к ним на основе ковариационных матриц оценки состояния и измерений. Чем меньшей погрешностью характеризуются измерения по сравнению с оценкой состояния системы, тем больший вес они получат. Относительные веса неизвестных, определяющих вектор состояния системы, зависят от степени их влияния на вектор измерений: больший вес получат те переменные, вклад которых в измерения больше.

Уточнение начальных условий на основе поступивших на данном цикле измерений, в общем случае, приводит к уменьшению неопределенности в оценке состояния системы. Исправленные таким образом начальные условия и являются выходными данными фильтра Калмана на каждом цикле. На заключительном этапе работы алгоритма происходит подготовка к поступлению нового вектора измерений. На основе заданного линейного преобразования, связывающего последующий вектор состояния с предыдущим, прогнозируется оценка состояния системы, отнесенная к моменту следующего измерения. При построении ковариационной матрицы прогнозируемого вектора состояния фильтром Калмана учитывается возможность искажения модели, описывающей поведение системы, некоторым случайным процессом с известными статистическими параметрами. Поскольку конкретные значения возмущающего эффекта не могут быть известны, данное обстоятельство способствует повышению неопределенности прогноза[15].

По мере последовательной обработки новых измерений происходит накопление фильтром полезной информации, поэтому если элементы вектора состояния уверенно выражаются через измеренные величины, то суммарная погрешность оценок, как правило, должна снижаться. Однако поскольку вместе с улучшением точности оценок на этапе их уточнения имеет место ее снижение при построении прогноза, то эти тенденции, компенсируя друг друга, в последствии приведут к стабилизации неопределенности, характеризующей оценку состояния системы. В случае отсутствия фактора, вносящего возмущения в процесс перехода системы из одного состояния в другое, погрешность оценок в итоге достигнет нуля. Изменяющаяся в процессе работы алгоритма степень неопределенности оценки состояния системы влечет за собой и изменение весов, вычисляемых на втором шаге; данное обстоятельство выделяет фильтр Калмана как алгоритм с переменными весами.

Если состояние рассматриваемой системы неизменно, то алгоритм фильтра Калмана сводится к последовательной форме классического метода наименьших квадратов, в котором матрица, обратная ковариационной, выступает в качестве весовой. Другими словами, фильтр Калмана является, по существу, рекуррентным способом решения задачи уравнивания по методу наименьших квадратов. Данная задача впервые решена в 1795 году, результаты были опубликованы в работе 1809 года под названием “Теория движения небесных тел”, в которой он применил метод наименьших квадратов к определению элементов орбит небесных тел (см. раздел “Замечания Гаусса”). Все изложенные в этой работе положения, касающиеся эффективности применения данного метода при обработке результатов измерений в равной степени относятся и к фильтру Калмана.

Применение фильтра Калмана в спутниковой навигационной аппаратуре.

Когда применение инерциальной навигационной системы становится нецелесообразным, как, например, в одиночных GPS приёмниках, ее заменяют уравнениями движения объекта, навигационные данные которого подлежат определению, с задействованием петли обратной связи. Статистические параметры погрешностей, характеризующие модели состояния системы и измерений в фильтре Калмана, определяются тщательностью составления уравнений движения. Для статичного объекта они тривиальны и строги, однако в более сложных случаях неизбежны упрощения, которые приводят к накоплению погрешностей и значительному снижению точности по сравнению с опорной траекторией, определяемой инерциальным методом. Преимущество подобной схемы применения фильтра Калмана по сравнению с обычным решением задачи определения координат по методу наименьших квадратов кроется в сглаживании выбросов случайных ошибок спутникового метода, что уменьшает их влияние на результаты навигационных определений.

Разработка навигационной системы, содержащей в своем составе фильтр Калмана, независимо от типа применяемого оборудования (инерциальная или спутниковая аппаратура, прочие устройства) заставляет учитывать ряд особенностей. Часть фильтра, занимающаяся ковариационным анализом, не требует для своей работы ни конкретных значений оценок состояния системы, ни измерений; необходимы только величины, характеризующие их погрешности. Данное свойство используется разработчиком для априорной оценки точности результатов, получаемых посредством того или иного вида аппаратуры, и тем самым позволяет осуществить выбор подходящего оборудования. В некоторых случаях приходится предварительно реализовывать алгоритм на компьютере и проверять его работу с различными начальными условиями. Далее с помощью методов статистического анализа следует убедиться в том, что реализованная в фильтре модель измерений соответствует своему реальному прототипу. Наконец, когда построенный фильтр удовлетворит всем требованиям, необходимо провести серию заключительных испытаний для оценки адекватности выбранного способа линеаризации задачи и локализации возможных ошибок вычислительного характера. В большинстве случаев расширенный вариант алгоритма с замкнутым контуром обратной связи позволяет значительно снизить нежелательные последствия линеаризации. Ошибки в вычислениях обычно вызваны ограниченной длиной машинного слова и наиболее ярко проявляются в ковариационных матрицах, которые становятся либо несимметричными, либо имеют отрицательные диагональные элементы, вследствие чего нарушается правильная работа фильтра Калмана. Влияние этого источника погрешностей можно снизить, удерживая большее число значащих цифр при вычислениях или применив численный алгоритм, менее чувствительный к ошибкам округления.

Алгоритм фильтра Калмана из-за своей кажущейся простоты и легкости реализации до сих пор является основным средством обработки измерений в навигационных системах, использующих спутниковый метод определений. Для установления весов поступающих измерительных данных требуются статистические характеристики их ошибок, а также уравнения, предоставляющие связь переменных, определяющих текущее состояние системы, с измерениями и между собой. Таким образом, фильтр Калмэна является инструментом, позволяющим на основе математической модели системы построить оптимальные оценки системных переменных по выполненным измерениям. К достоинствам алгоритма следует отнести его рекуррентную природу, эффективно проявляющуюся при работе в реальном времени, а также возможность априорной оценки точности получаемых результатов средствами самого алгоритма.

Видео:Метод конечных элементов. Основы 1.1.1 - ВведениеСкачать

Листинг№1 Численное интегрирование

Видео:Математика без ху!ни. Интегралы, часть 1. Первообразная. Дифференцирование и интегрирование.Скачать

1. Функция, возвращающая значение интеграла функции помощью метода Симпсона

2. Функция, возвращающая значение интеграла с помощью формулы трапеции.

🎬 Видео

Курс по ИДУ: Численное решение интегральных уравнений | Занятие 14Скачать

Определенный интеграл Римана. Суммы Дарбу. Предел интегральных сумм.Скачать

Метод конечного объема для решения 1D уравнений Эйлера. Finite volume method for 1D Euler equations.Скачать