Решение дифференциальных уравнений методом сплайнов

Содержание:

По этой ссылке вы найдёте полный курс лекций по математике:

Кривые и поверхности, встречающиеся в практических задачах, часто имеют довольно сложную форму, не допускающую универсального аналитического задания в целом при помощи элементарных функций. Поэтому их собирают из сравнительно простых гладких фрагментов — отрезков (кривых) или вырезков (поверхностей), каждый из которых может быть вполне удовлетворительно описан при помощи элементарных функций одной или двух переменных.

При этом вполне естественно потребовать, чтобы гладкие функции, которые используются для построения частичных кривых или поверхностей, имели схожую природу, например, были бы многочленами одинаковой степени. А чтобы получающаяся в результате кривая или поверхность оказалась достаточно гладкой, необходимо быть особенно внимательным в местах стыковки соответствующих фрагментов. Степень многочленов выбирается из простых геометрических соображений и, как правило, невелика.

Для гладкого изменения касательной вдоль всей составной кривой достаточно описывать стыкуемые кривые при помощи много-членов третьей степени, кубических многочленов. Коэффициенты таких многочленов всегда можно подобратьтак, чтобы кривизна соответствующей составной кривой была непрерывной. Кубические сплайны, возникающие при решении одномерных задач, можно приспособить к посгрое нию фрагментов составных поверхностей.

И здесь вполне естественно появляются бикубические сплайны, описываемые при помощи многочленов третьей степени по каждой из двух переменных. Работа с такими сплайнами требует уже значительно большего объема вычислений. Но правильно организованный процесс позволитучесть непрерывно нарастающие возможности вычислительной техники в максимальной степени.

Сплайн-функции Пусть на отрезке [a, 6J задана сетка и> Точки а?о и хт называются граничными у злами сетки о;, а точки внутренними узлами (рис. 1). Сетка называется равномерной, если расстояния между любыми двумя соседними узлами одинаковы. Функция S(s), заданная на отрезке (а, 6), называется сплайном порядка р 1 (степени р), если эта функция 1) на каждом из огрезков является многочленом заданной степени р ^ 2, то есть может быть записана в виде 2) p — 1 раз непрерывно дифференцируема на отрезке [a, 6], то есть Замечание.

Индекс (t) у чисел а^ указывает на то. что набор коэффициентов, которым определяется функция 5(х), на каждом частичном отрезке Д, свой. На каждом из отрезков Д1, сплайн 5(х) является многочленом степени р и определяется на этом отрезке р + 1 коэффициентом. Всего частичных отрезков — то. Значит, для того, чтобы полностью определить сплайн, необходимо найти (р + 1 )то чисел Условие ) означает непрерывность функции 5(ж) и ее производных во всех внутренних узлах сетки ш. Число таких узлов m — 1.

Тем самым, для отыскания коэффициентов всех многочленов получается р(т — 1) условий (уравнений). Для полного определения сплайна недостает ( условий (уравнений). Выбор дополнительных условий определяется характером рассматриваемой задачи, а иногда и просто — желанием пользователя. ТЕОРИЯ СПЛАЙНОВ примеры решения Наиболее часто рассматриваются задачи интерполяции и сглаживания, когда требуется построить тот или иной сплайн по заданному массиву точек на плоскости.

В задачах интерполяции требуется, чтобы график сплайна проходил через точки что накладывает на его коэффициенты m + 1 дополнительных условий (уравнений). Остальные р — 1 условий (уравнений) для однозначного построения сплайна чаще всего задают в виде значений младших производных сплайна на концах рассматриваемого отрезка [а, 6] — граничных (краевых) условий. Возможность выбора различных граничных условий позволяет строить сплайны, обладающие самыми разными свойствами.

В задачах сглаживания сплайн строят так, чтобы его график проходил вблизи точек (я»» У»), * = 0, 1. , т, а не через них. Меру этой близости можно определять по-разному, что приводит к значительному разнообразию сглаживающих сплайнов. Описанные возможности выбора при построении сплайн-функций далеко не исчерпывают всего их многообразия. И если первоначально рассматривались только кусочно полиномиальные сплайн-функции, то по мере расширения сферы их приложений стали возникать сплайны, «склеенные» и из других элементарных функций. Интерполяционные кубические сплайны Постановка задачи интерполяции.

Пусть на отрезке [а, 6) задана сетка ш Рассмотрим набор чисел Задача.

Построить гладкую на отрезке (а, 6] функцию которая принимает в узлах сетки о» заданные значения, то есть Замечание. Сформулированная задача интерполяции состоит в восстановлении гладкой функции, заданной таблично (рис. 2). Ясно, что такая задача имеет множество различных решений. Накладывая на конструируемую функцию дополнительные условия, можно добиться необходимой однозначности.

В приложениях часто возникает необходимость приблизить функцию, заданную аналитически, при помощи функции с предписанными достаточно хорошими свойствами. Например, в тех случаях, когда вычисление значений заданной функции /(х) в точках отрезка [а, 6] связано со значительными трудностями и/или заданная функция /(х) не обладает требуемой гладкостью, удобно воспользоваться другой функцией, которая достаточно хорошо приближала бы заданную функцию и была лишена отмеченных ее недостатков.

Задача интерполяции функции. Построить на отрезке [а, 6] гладкую функцию а(х), совпадающую в узлах сетки ш с заданной функцией /(х). Определение интерполяционного кубического сплайна Интерполяционным кубическим сплайном S(x) на сетке ш называется функция, которая 1) на каждом из отрезков , представляет собой многочлен третьей степени, 2) дважды непрерывно дифференцируема на отрезке [а, Ь], то есть принадлежит классу С2[а, 6], и 3) удовлетворяет условиям.

На каждом из отрезков сплайн S(x) является многочленом третьей степени и определяется на этом отрезке четырьмя коэффициентами. Всего отрезков — т. Значит, для того, чтобы полностью определить сплайн, необходимо найти 4т чисел Условие означает непрерывность функции S(x) и ее производных S'(x) и 5″(х) во всех внутренних узлах сетки ш. Число таких узлов — m — 1. Тем самым, для отыскания коэффициентов всех многочленов получается еще 3(m — 1) условий (уравнений).

Возможно вам будут полезны данные страницы:

Вместе с условиями (2) получается условия (уравнения). Граничные (краевые) условия Два недостающих условия задаются в виде ограничений на значения сплайна и/или его производных на концах промежутка [а, 6]. При построении интерполяционного кубического сплайна наиболее часто используются краевые условия следующих четырех типов. A. Краевые условия 1-го типа. — наконцах промежутка [а, Ь] задаются значения первой производной искомой функции. Б. Краевые условия 2-го типа. — наконцах промежутка (а, 6) задаются значения второй производной искомой функции. B. Краевые условия 3-го типа. называются периодическими.

Выполнения этих условий естественно требовать в тех случаях, когда интерполируемая функция является периодической с периодом Т = Ь-а. Г. Краевые условия 4-го типа. требуют особого комментария. Комментарий. Во внутренних узлах сепси третья производная функции S(x), вообще говоря, разрывна. Однако число разрывов третьей производной можно уменьшить при помоши условий 4-го типа. В этом случае построенный сплайн будет трижды непрерывно дифференцируем на промежутках Построение интерполяционного кубического сплайна.

Опишем способ вычисления коэффициентов кубического сплайна, при котором число величин, подлежащих определению, равно . На каждом из промежутков интерполяционная сплайн-функция ищется в следующем виде Здесь ТЕОРИЯ СПЛАЙНОВ примеры решения а числа являются решением системы линейных алгебраических уравнений, вид которой зависит от типа краевых условий. Для краевых условий 1-го и 2-го типов эта система имеет следующий вид где Коэффициенты зависят от выбора краевых условий.

Краевые условия 1-го типа: Краевые услоемв 2-го типа: В случае краевых условий 3-го типа система для определения чисел записывается так Число неизвестных в последней системе равно тп, так как изусловия периодичности вытекает, что по = пт. Для краевых условий 4-го типа система для определения чисел , имеет вид где По найденному решению системы числа по и пт можно определить при помощи формул Важное замечание. Матрицы всех трех линейных алгебраических систем являются матрицами с диагональным преобладавшем. Тамие матрицы не вырождены, и потому каждая из этих систем имеет единственное решение.

Теорема:

Интерполяционный кубический сплайн, удовлетворяющий условиям (2) и краевому условию одного из перечисленных четырех типов, существует и единствен. Таким образом, построить интерполяционный кубический сплайн — это значит найти его коэффициенты Когда коэффициенты сплайна найдены, значение сплайна S(x) в произвольной точке отрезка [а, Ь] можно найти г!о формуле (3). Однако для практических вычислений больше подходит следующий алгоритм нахождения величины 5(ж).

Пусть х 6 [х», Сначала вычисляются величины А и В по формулам а затем находится величина 5(ж): Применение этого алгоритма существенно сокращает вычислительные затраты на определение величины Советы пользователю Выбор граничных (краевых) условий и узлов интерполяции позволяет в известной степени управлять свойствами интерполяционных сплайнов. А. Выбор граничных (краевых) условий. Выбор граничных условий является одной из центральных проблем при интерполяции функций.

в том случае, когда необходимо обеспечить высокую точность аппроксимации функции f(x) сплайном 5(ж) вблизи концов отрезка [а, 6). Граничные значения оказывают заметное влияние на поведение сплайна 5(ж) вблизи точек а и Ь, и это влияние по мере удаления от них быстро ослабевает. Выбор граничных условий часто определяется наличием дополнительных сведений о поведении аппроксимируемой функции f(x). Если на концах отрезка (а, 6] известны значения первой производной f'(x), то естественно воспользоваться краевыми условиями 1-го типа.

Если на концах отрезка [а, 6) известны значения второй производной f»(x), то естественно воспользоваться краевыми условиями 2-го типа. Если есть возможность выбора между краевыми условиями 1-го и 2-го типов, то предпочтение следует отдать условиям 1- го типа. Если f(x) — периодическая функция, то следует остановиться накраевых условиях 3-го типа. В случае, если никакой дополнительной информации о поведении аппроксимируемой функции нет, часто используют так называемые естественные граничные условия.

Однако следует иметь ввиду, что при таком выборе граничны*условий точность аппроксимации функции f(x) сплайном S(x) вблизи концов отрезка (а, ft] резко снижается. Иногда используются краевые условия 1-го или 2-го типа, но не с точными значениями соответствующих производных, а с их разностными аппроксимациями. Точность такого подхода невысока. Практический опыт расчетов показывает, что в рассматриваемой ситуации наиболее целесообразным является выбор граничных условий 4-го типа. Б.

Выбор узлов интерполяции. Если третья производная f'»(x) функции терпитразрыв в не которыхточках отрезка [а, Ь], то для улучшения качества аппроксимации эти точки следует включить в число узлов интерполяции. Если разрывна вторая производная /»(х), то для того, чтобы избежать осцилляции сплайна вблизи точек разрыва, необходимо принять специальные меры. Обычно узлы интерполяции выбирают так, чтобы точки разрыва второй производной попадали внутрь промежутка xif ), такого, что .

ТЕОРИЯ СПЛАЙНОВ примеры решения (рис.3) интерполяционный многочлен Лагранжа определяется формулой Свойства интерполяционного многочленаЛагранжа целесообразно рассматривать с двух противоположных позиций, обсуждая основные достоинства отдельно от недостатков.

Основные достоинства 1 -го подхода: 1) график интерполяционного многочлена Лагранжа проходит через каждую точку массива, 2) конструируемая функция легко описывается (число подлежащих определению коэффициентов интерполяционного многочлена Лагранжа на сетке и> равно m + 1), 3) построенная функция имеет непрерывные производные любого порядка, 4) заданным массивом интерполяционный многочлен определен однозначно. Основные недостатки 1 -го подхода: 1) степень интерполяционного многочлена Лагранжа зависит от числа узлов сетки, и чем больше это число, тем выше степень интерполяционного многочлена и, значит, тем больше требуется вычислений,

2) изменение хотя бы одной точки в массиве требует полного пересчета коэффициентов интерполяционного многочлена Лагранжа, 3) добавление новой точки в массив увеличивает степень интерполяционного многочлена Лагранжа на единицу и таиже приводит к полному пересчету его коэффициентов, 4) при неограниченном измельчении сетки степень интерполяционного многочлена Лагранжа неограниченно возрастает.

Поведение интерполяционного многочлена Лагранжа при неограниченном измельчении сетки вообше требует особого внимания. Комментарии А. О приближении непрерывной функции многочленом. Известно (Вейерштрасс, 1885 год), что всякая непрерывная (а тем более гладкая) на отрезке функция может быть как угодно хорошо приближена на этом отрезке многочленом. Опишем этот факт на языке формул. Пусть f(x) — функция, непрерывная на отрезке [а, 6]. Тогдадл я любого е > 0 найдется такой многочлен Р„(х),чтодля любого х из промежутка [а, 6] будет выполняться неравенство (рис. 4)

Отметим, что многочленов даже одной степени, приближающих функцию f(x) с указанной точностью, существует бесконечно много. Построим наотрезке [а, 6] сетку w. Ясно, что ее узлы, вообще говоря, не совпадают с точками пересечения графиков многочлена Рп(х) и функции f(x) (рис. 5). Поэтому для взятой сетки многочлен Рп(х) не является интерполяционным. При аппроксимации непрерывной функции интерполяционным многочленом Jla-гракжа его график не только не обязан быть близким графику функции f(x) в каждой точке отрезка [а, Ь), но может уклоняться от этой функции как угодно сильно.

Приведем два примера. Пример 1 (Рунг, 1901 год). При неограниченном увеличении числа узлов для функции на отрезке [-1, 1] выполняется предельное равенство (рис.6) Пример 2 (Бериштейн, 1912год). Последовательность интерполяционных многочленов Лагранжа построенных на равномерных сетках шт для непрерывной функции /(х) = |х| на отрезке с возрастанием числе узлов т не стремится к функции /(х) (рис.7). Подход 2-й. Кусочно-лииейнм интерполяция При отказе от гладкости интерполируемой функции соотношение между числом достоинств и числом недостатков можно заметно изменить в сторону первых.

Построим кусочно-линейную функцию путем последовательного соединения точек (xit у,) прямолинейными отрезками (рис. 8). Основные достоинства 2 -го подхода: 1) график кусочно-линейной функции проходит через каждую точку массива, 2) конструируемая функция легко описывается (число подлежащих определению коэффициентов соответствующих линейных функций для сетки (1) равно 2т), 3) заданным массивом построенная функция определена однозначно, 4) степень многочленов, используемых для описания интерполяционной функции, не зависит от числа узлов сетки (равна 1),

5) изменение одной точки в массиве требует вычисления четырех чисел (коэффициентов двух прямолинейных звеньев, исходящих из новой точки), 6) добавление дополнительной точки в массив требует вычисления четырех коэффициентов. Кусочно-линейная функция достаточно хорошо ведет себя и при измельчении сетки. я Основной недостаток 2-гоподхода: аппроксимирующая кусочно-линейная функция не является гладкой: первые производи ые терпят разрыв в узлах сетки (ушах интерполяции). Подход 3-й.

Сплайн-интерполяция

Предложенные подходы можно объединить так, чтобы число перечисленных достоинств обоих подходов сохранилось при одновременном уменьшении числа недостатков. Это можно сделать путем построения гладкой интерполяционной сплайн-функции степени р. Основные достоинства 3 -го подхода: 1) график построенной функции проходит через каждую точку массива, 2) конструируемая функция сравнительно легко описывается (число подлежащих определению коэффициентов соответствующих многочленов для сетки (1) равно 3) заданным массивом построенная функция определена однозначно,

4) степень многочленов не зависит от числа узлов сетки и, следовательно, не изменяется при его увеличении, 5) построенная функция имеет непрерывные производные до порядка р — 1 включительно, 6) построенная функция обладает хорошими аппроксимационными свойствами. Краткая справка. Предложенное название — сплайн — не является случайным — введенные нами гладкие ку-сочно-полиномиальныефункции и чертежные сплайны тесно связаны.

Рассмотрим гибкую идеально тон кую линейку, проходящую через расположенные на плоскости (х, у) опорные точки массива . Согласно закону Бернулли—Эйлера линеаризованное уравнение изогнутой линейки имеет вид где S(x) — изгиб, М(х) — изменяющийся линейно от опоры к опоре изгибающий момент, Е1 — жесткость линейки. Функция S(x), описывающая формулинейки, является многочленом третьей степени между каждым и двумя соседними точками массива (опорами) и дважды непрерывно дифференцируема на всем промежутке (а, 6). Комментарий. 06 интерполировании непрерывной функции.

В отличие от интерполяционных многочленов Лагранжа, последовательность интерполяционных кубических сплайнов на равномерной сетке всегдасходится к интерполируемой непрерывной функции, причем с улучшением дифференциальных свойств этой функции скорость сходимости повышается. Пример. Для функции кубический сплайн на сетке с числом узлов m = 6 дает погрешность аппроксимации того же порядка, что и интерполяционный многочлен Ls(z), а на сетке с числом узлов m = 21 эта погрешность настолько мала, что в масштабе обычного книжного рисунка просто не может быть показана (рис.10) (интерполяционный многочлен 1>2о(г) дает в этом случае погрешность около 10 000 Ж).

Свойства имтерполяцкокного кубического сплайна А. Алпроксимационмые свойства кубического сплайна. Аппроксимационные свойства интерполяционного сплайна зависят от гладкости функции f(x) — чем выше гладкость интерполируемой функции, тем выше порядок аппроксимации и при измельчении сетки тем выше скорость сходимости. Если интерполируемая функция f(x) непрерывна на отрезке.

Экстремальное свойство кубического сплайна. Интерполяционный кубический сплайн обладает еще одним полезным свойством. Рассмотрим следующий пример. ример. Построить функцию/(х), минимизирующую функционал на классе функций из пространства С2, графики которых проходят через точки массива.

Среди всех функций, проходящих через опорные точки (х;, /(х,)) и принадлежащих указанному пространству, именно кубический сплайн 5(х), удовлетворяющий краевым условиям доставляет Экстремум (минимум) функционалу Замечание 1. Часто именно это экстремальное свойство берут в качестве определения интерполяционного кубического сплайна. Замечание 2. Интересно отметить, что интерполяционный кубический сплайн обладает описанным выше экстремальным свойством на очень широком классе функций, а именно, на классе |о, 5 ]. 1.2. Сглаживающие кубические сплайны.

О постановке задачи сглаживания Пусть заданы сетка и набор чисел Комментарий к исходным данным На практике часто приходится иметь дело со случаем, когда значения у, в массиве заданы с некоторой погрешностью. Фактически это означает, что для каждого указан интервал и любое число из этого интервала может быть взято в качестве значения у, . Величины у, удобно интерпретировать, например, как результаты измерений некоторой функции у(х) при заданных значениях переменной х, содержащие случайную погрешность.

При решении задачи восстановления функции по таким ее «экспериментальным» значениям вряд ли целесообразно использовать интерполяцию, поскольку интерполяционная функция будет послушно воспроизводить причудливые осцилляции, обусловленные случайной компонентой в массиве . Более естественным является подход, основанный на процедуре сглаживания, призванной как-то уменьшить элемент случайности в результате измерений.

Обычно в таких задачах требуется найти функцию, значения которой при х = ж,, * = 0, 1. т, попадали бы в соответствующие интервалы и которая обладала бы, кроме того, достаточно хорошими свойствами. Например, имела бы непрерывные первые и вторые производные, или же ее график был бы не слишком сильно искривлен, то есть не имел бы сильных осцилляций. Задача подобного рода возникает и тогда, когда по заданному (точно) массиву требуется построить функцию, которая проходилабы нечереззаданныеточки, а вблизи них и к тому же изменялась достаточно плавно.

Другими словами, искомая функция как бы сглаживала заданный массив, а не интерполировала его. Пусть заданы сетка ш и два набора чисел ТЕОРИЯ СПЛАЙНОВ примеры решения Задача. Построить гладкую на отрезке [а, А] функцию , значения которой в узлах сетки и» отличались от чисел у,- на заданные величины -Зшочтио. Сформулированная задача сглаживания состоит в восстановлении гладкой функции, заданной таблично. Ясно, что такая задача имеет множество различных решений. Накладывая на конструируемую функцию дополнительные условия, можно добиться необходимой однозначности.

Определение сглаживающего кубического сплайна

Сглаживающим кубическим сплайном S(x) на сетке ш называется функция, которая 1) на каждом из отрезков представляет собой многочлен третьей степени, 2) дважды непрерывно дифференцируема на отрезке [а, 6], то есть принадлежит классу С2 [а, Ь], 3) доставляет минимум функционалу где — заданные числа, 4) удовлетворяет граничным условиям одного из трех указанных ниже типов. Граничные (краевые) условия Граничные условия задаются в виде ограничений на значения сплайна и его производных в граничных узлах сетки ш. А. Граничные условия 1-го типа. — наконцах промежутка [а, Ь) задаются значения первой производной искомой функции.

Граничные условия 2-го типа. — вторые производные искомой функции на концах промежутка (а, Ь] равны нулю. В. Граничные условия 3-го типа. называются периодическими. Теорема. Кубический сплайн S(x), минимизирующий функционал (4) и удовлетворяющий краевым условиям одного из указанных трех типов, определен однозначно. Определение. Кубический сплайн, минимизирующий функционал J(f) и удовлетворяющий граничным условиям i-готипа, называется сглаживающим сплайном i-готипа.

Замечание. На каждом изотрезков(,сплайн 5(х) является миоючасном третьей степени и определяется на этом отрезке четырьмя коэффициентами. Всего отрезков — т. Значит, для того, чтобы полностью определять сплайн, необходимо найти 4т чисел Условие означает непрерывность функции 5(аг) и се производных во всех внутреннж узлах сетки о». Число таких узлов — m — 1. Тем самым, для отысивния коэффициентов всех многочленов получается 3(m — 1) условий (уравнений).

Построение сглаживающего кубического сплайна Опишем способвычисления коэффициентов кубическогосплайна, при котором число величин, подлежащих определению, равно 2т + 2. На каждом из промежутков сглаживающая сплайн-функция ищется в следующем виде Здесь а числа и , являются решением системы линейных алгебраических уравнений, вид которой зависитот типа краевых условий. Опишем сначала, как находятся величины п*. Для краевых условий 1-го и 2-го типов система линейных уравнений для определения величин Hi записывается в следующем виде где известные числа).

Коэффициенты зависят от выбора граничных условий. Граничные условия 1-го типа: Граничные условия 2-го типа: В случае граничных условий 3-го типа система для определения чисел записывается так: причем все коэффициенты вычисляются по формулам (5) (величины с индексами к и т + к считают я равными: Важно* замечание. Матрицы систем не вы рождены и потому каждая из этих систем имеет единственное решение. Если числа п,- найдены, то величины легко определяются по формулам где В случае периодических граничных условий Выбор еесоеш коэффициентов.

Выбор весовых коэффициентов р,-, входящих в функционал (4), позволяете известной степени управлять свойствами сглаживающих сплайнов. Если все и сглаживающий сплайн оказывается интерполяционным. Это, в частности, означает, что чем точнее заданы величины , тем меньше дошкн ы быть соотпетствуюшие весовые коэффициенты. Если же необходимо, чтобы сплайн прошел через точку (х^, Ук), то отвечающий ем у весовой множитель р следует поломить равным нулю. В практический вычислениях наиболее важым является выбор величин pi-Пусть Д, — погрешность измерения величины у,.

Тогда естественно потребовать, чтобы сглаживающий сплайн удовлетворял условию или, что то же, В простейшем случае весовые коэффициенты pi можно задать, например, форму- где с — некоторая достаточно малая постоянная. Однако такой выбор весов р, не позволяет использовать «коридор», обусловленный погрешностями величин у,-. Более рациональный, но и более трудоемкий алгоритм определения величин р,- может выглядеть следующим образом.

Если на fc-й итерации величины найдены,то полагают где е — малое число, которое выбирается экспериментально с учетом разрядной сетки компьютера, значений Д, и точности решения системы линейных алгебраических уравнений. Если на fc-й итерации в точке я, нарушилось условие (6), то последняя формула обеспечит уменьшение соответствующего весового коэффициента р,. Если же то на следующей итерации Увеличение р, приводит к более полному использованию «коридора» (6) и, в конечном счете, более плавно изменяющемуся сплайну. Немного теории А.

Обоснование формул для вычисления коэффициентов интерполяционного кубического сплайна. Введем обозначения где m, — неизвестные пока величины. Их число равно m + 1. Сплайн, записанный в форме , где удовлетворяет условиям интерполяции и непрерывен на всем промежутке [а, Ь: положив в формуле , получим соответственно Кроме того, он имеет на промежутке [а, 6] непрерывную первую производную: продифференцировав соотношение (7) и положив , пОлучим соответ-. ственно .

Покажем, что числа т, можно выбрать так, чтобы сплайн-функция (7) имела на отрезке [а, 6] непрерывную вторую производную. Вычислим на промежутке вторую производную сплайна : В точке х, — 0 (при t = 1) имеем Вычислим на промежутке вторую производную сплайна В точке имеем Из условия непрерывности второй производной во внутренних узлах сетки а; получаем m — 1 соотношение где Добавляя к этим т — 1 уравнениям еще два, вытекающих и з краевых условий, получаем систему из m+ 1 линейного алгебраического уравнения с т + I неизвестной miy i = 0, 1. . , m.

Система уравнений для вычисления величин гщ в случае краевых условий 1-го и 2-го типов имеет вид где (краевые условия 1 -го типа), (краевые условия 2 -го типа). Для периодических краевых условий (краевыеусловия 3-го типа) сетку о; удлиняют еще на один узел и полагают Тогда система для определения величин го* будет иметь вид Для того чтобы получить систему уравнений для определения чисел го, в случае краевых условий 4-го типа, найдем на отрезке [ третью производную сплайна (7) и потребуем ее непрерывности во втором и (го — !)-м узлах сетки.

Имеем Из последних двух соотношений получаем недостающие два уравнения, отвечающие краевым условиям 4 -го типа: Исключая из уравнений неизвестное гоо, а из уравнений неизвестное пц,, в результате получим систему уравнений Отметим, что число неизвестных в этой системе равно го — I. 6. Обоснование формул дм вычисления юэффиие кто« сглаживающего субичессого сплайна. Введем обозначения где Zi и nj — неизвестные пока величины. Их число равно 2т + 2. Сплайн-функиия, записанная в форме непрерывна на всем промежутке (а, 6]: положив в этой формуле , получим соответственно.

Покажем, что числа z, и п, можно выбратьтак, чтобы сплайн, записанный в форме (8), имел на промежутке [а, 6] непрерывную первую производную. Вычислим первую производную сплайна S(x) на промежутке [zi-i, х,]: В точке х^ — 0 (при t = 1) имеем Вычислим первую производаую сплайна 5(х) на промежутке [xj, х,»]: В точке имеем Из условия непрерывности первой производой сплайна во внутренних узлах сетки и —> получаем m — 1 соотношение Эту связь удобно записать в матричной форме.

Здесь использованы следующие обозначения Кроме того, сплайн на промежутке [а, 6> имеет непрерывную вторую производную: продифференцировав соотношение (8) и положив , получим соответственно Еше олю матричное соотношение получается из условия минимума функционала (4). Имеем Два последних матричных равенства можно рассматривать как линейную систему 2т+2 линейных алгебраических уравнений относительно 2т + 2 неизвестных . Заменяя в первом равенстве столбец г его выражением, полученным из соотношения (9), приходим к матричному уравнению.

ТЕОРИЯ СПЛАЙНОВ примеры решения для определения столбца М. Это уравнение имеет единственное решение вследствие того, что матрица A + 6HRH7 всегда невырождена. НаЙдяего, мылегко определяем г. Эамсшине. Элементы трелдмаголальн ых матриц А и Н определяющие я только параметрами сетки и (сс шагами hi) и не зависят от величин у^. Линейное пространство кубических сплайн-функций Множество кубических сплайнов, построенных на отрезке [а, 6) по сетке wcra+l узлом, является линейным пространством размерности т + 3:

1) сумма двух кубических сплайнов, построенных по сетке и>, и произведение кубического сплайна, построенного по сетке и>, на произвольное число тайнее являются кубическими сплайнами, построенными по этой сетке, 2) любой кубический сплайн, построенный по сетке и из узла, полностью определяется т + 1 значением величин у» в этих узлах и двумя граничными условиями — всего то + 3 параметрами. Выбрав в этом пространстве базис, состоящий из m + 3 линейно независимых сплайнов , мы можем записать произвольный кубический сплайн а(х) в виде их линейной комбинации причем единственным образом. Замечание.

Подобное задание сплайна широко распространено в вычислительной практике. Особенно удобным является базнс, состоящий из так называемых кубических В -сплайнов (базовых, или фундаментальных, сплайнов). Применение Д-сплайнов позволяет существенно снизить требования к объему памяти компьютера. Л-сплайны. В -сплайномнулевой степени, построенным на числовой прямой по сетке ш, называется функция вила В -сплайн степени к ^ I, построенный на числовой прямой по сетке иг, определяется посредством рекуррентной формулы Графики В -сплайнов первой В,-1′(ж) и второй в7х) степеней представлены на рис. 11 и 12 соответственно.

В-сплайн произвольной степени к может быть отличен от нуля только на некотором отрезке (определяемом к + 2 узлами). Кубические В-сплайны удобнее нумеровать так, чтобы сплайн В,-3* (я) был отличен от нуля на отрезке яг,-+2]. Приведем формулу для кубического сплайна третьей степени для случая равномерной сетки (с шагом Л). Имеем в остальных случаях. Типичный график кубического В-сплайна представлен на рис. 13.

Займами*. функция а) дважды непрерывно дифференцируема на отрезке то есть принадлежат классу С2[а, »>, к б) отлична от нуля толь ко на четырех последовательных отрезках ( Дополним сетку ш вспомогательными узлами взятыми совершенно произвольно. По расширенной сетке ш* можно построить семейство из m + 3 кубических В -сплайнов: Это семейство образует базис в пространстве кубических сплайнов на отрезке (а, Ь]. Тем самым, произвольный кубический сплайн S(z), построенный на отрезке |в, 6] посетке о; изт+1 узла, может быть представлен наэтом отрезке в виде линейной комбинации.

Условиями задачи коэффициенты ft, этого разложения определяются однозначно. . В случае, когда заданы значения у* функции в узлах сетки и значения у о и Ут первой производной функции на концах сетки'(задача интерполяций с граничными условиями первого рода), эти коэффициенты вычисляются из системы следующего вида После исключения величин б-i и &m+i получается линейная система с неизвестными 5q, . , Ьт и трех диаюнальной матрицей. Условие обеспечивает диагональное преобладание и, значит, возможность применения метода прогонки для ее разрешения. 3ММЧМЮ 1.

Линейные системы аналогичного вида возникают лрн рассмотрении и других задач интерполяции. Зммчнм* 2. В сравнении с алгоритмами, описанными в раздеде 1.1, применение Я-сплайн в * задачах интерполяции позволяет уменьшит* объем хранимой информации, то есть сушественно снизить требования к объему памяти компьютере, хотя и приводит к увеличению числа операций. Построение сплайноаых кривых при помощи сплайн-функций Выше рассматривались массивы, точки которых были занумерованы так, что их абсциссы образовывали строго возрастающую последовательность.

Например, случай, изображенный на рис. 14, когда у разных точек массива одинаковые абсциссы, не допускался. Это обстоятельств о определяло и выбор класса аппроксимирующих кривых (трафики функций), и способ их построения. Однако предложенный выше метод позволяет достаточно успешно строить интерполяционную кривую и в более общем случае, когда нумерация точек массива и их расположение на плоскости, как правило, не связаны (рис. 15). Более того, ставя задачу построения интерполяционной кривой, можно считать заданный массив неплоски м, то есть Ясно, что для решения этой общей задачи необходимо существенно расширить класс допусти мых кривых, включив в него и замкнутые кривые, и кривые, имеющие точки самопересечения, и пространственные кривые.

Такие кривые удобно описывать при помощи параметрических уравнений Потребуем. дополнительно, чтобы функции обладали достаточной гладкостью, например, принадлежали классу С1 [а, /0] или классу Для отыскания параметрических уравнений кривой, последовательно проходящей через все точки массива, поступают следующим образом. 1-й шаг. На произвольно взятом отрезке [a, /3( изменения параметра t вводится вспомогательная сетка число узлов которой совпадает с числом точек в массиве Р. 2-й шаг.

По заданному массиву Р строятся три новых вспомогательных массива (в плоском случае два) (рис. 16 (плоский случай)). 1-й шаг. Для каждого из массивов X, У и Z находятся соответствующие интерполяционные сплайн-функции x(t), y(t) и z(t). В результате мы получаем параметрические уравнения кривой, проходящей через точки (см. рис. 17 для плоского случая). Замечание 1. Предложенный подход позволяет строить замкнутые интерполяционные кривые (при Р0 = Р«); для этого при _, построении координатных функций x(t), у(

Полученная кривая будет гладкой, но не обязательно регулярной, так как возможность одновременного обращения в нуль производных для некоторого исключать нельзя. Кроме того, эта кривая может иметь точки самопересечения Замечание 3. Построение сглаживающих сплайновых кривых проводится практически так же, как я построение интерполяционных сплайновых кривых.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Линейное дифференциальное уравнение Коши-ЭйлераСкачать

Теоретические основы сплайн-интерполяции или почему IQ тесты не имеют решения

Доброго времени, Хабр!

Куча времени прошла с того момента, как я написал свою первую статью, и уже почти год с того момента, как пришла в голову идея для второй. В силу многих обстоятельств (в первую очередь – лени и забывчивости), эта идея так и не была реализована ранее, но сейчас я собрался, написал весь этот материал и готов представить его вашему вниманию.

Начну с небольшой вводной. Будучи студентом 4-го, на тот момент, курса бакалавриата, я изучал курс «Компьютерная графика». Много там было разных интересных (и не очень) заданий, но одно прямо особо запало мне в душу: интерполяция кубическими сплайнами с заданными первыми производными на концах интервала. Пользователь должен был задавать значения первых производных, а программа — считать и выводить на экран интерполяционную кривую. Особенность и основная сложность задания заключена в том, что задаются именно первые производные, а не вторые, как в классической постановке сплайн-интерполяции.
Как я ее решал, и к чему оно в итоге пришло, я как раз и изложу в этой статье. И да, если по описанию задачи вы не поняли ни в чем ее смысл, ни в чем сложность, не переживайте, все это я также постараюсь раскрыть. Итак, поехали.

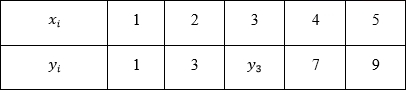
А, нет, погодите один момент. Вот вам два числовых ряда:
a) 2, 4, 6, 8, ?
b) 1, 3, ?, 7, 9

Какие числа должны стоять на месте вопросов и почему? Вы действительно уверены в своем ответе?

Видео:4.1 Интерполяция кубическими сплайнамиСкачать

Интерполяция

Интерполяция, интерполирование (от лат. inter-polis – «разглаженный, подновлённый, обновлённый; преобразованный») – в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. (с) Википедия

Поясню на примерах. Существуют задачи, когда нам требуется узнать, условно, «закон распределения» (взял в кавычки, так как это, вообще говоря, термин из другой области математики) некого параметра по нескольким известным его значениям. Чаще всего речь идет об изменении некого параметра во времени: координаты движущегося тела, температуры объекта, колебания курса валюты, etc. При этом в силу каких-либо обстоятельств у нас не было возможности наблюдать за этим параметром непрерывно, мы могли узнавать его значения лишь в какие-то отдельные моменты времени. Исходными данными в таком случае у нас является множество точек вида value(time), а целью задачи – восстановить кривую, проходящую через эти точки и непрерывно описывающую изменение этого параметра.

Следует понимать, что невозможность постоянного наблюдения за соответствующим параметром – это обычно какого-либо рода технологическое ограничение. С развитием техники таких ситуаций становится все меньше и меньше. Из современных задач такого плана – траектория движения, например, марсохода. Поддерживать непрерывный сеанс связи (пока что) все еще не представляется возможным, а контролировать его перемещение и рисовать красивые траектории хочется. Получается, что конкретные координаты можно узнать только в те моменты, когда связь все-таки налажена, а траекторию целиком приходится восстанавливать по полученным таким образом время от времени точкам.
Другой вариант применения интерполяции. Некоторые современные телевизоры показывают изображение с частотой обновления картинки до >=1000Гц (хотя это все еще запредельные значения). Большинство телевизоров так не умеет, но даже так многие отображают картинку на частоте 100Гц — такая величина уже вполне себе классика. А если верить википедии, то в кинематографе «частота 24 кадра в секунду является общемировым стандартом». Для того, чтобы превратить 24 кадра в секунду исходного видеопотока в 100 кадров в секунду результата, телевизор использует интерполяцию. А именно какие-нибудь алгоритмы в стиле «взять два соседних кадра 1 и 2, посчитать разницу между ними и сформировать из нее 3 дополнительных кадра, которые надо впихнуть между теми двумя изначальными» -> получаются кадры 1, 1_1, 1_2, 1_3, 2

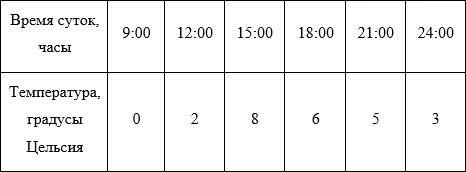
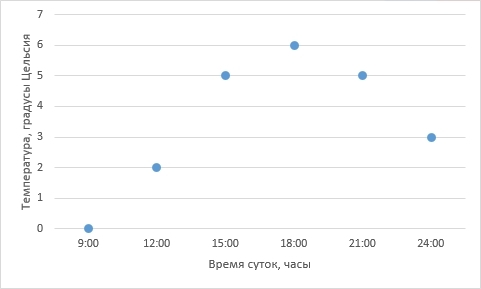
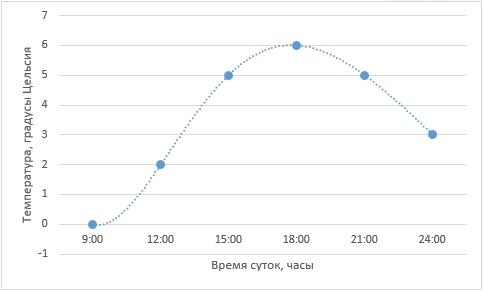
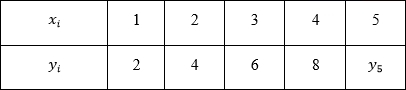
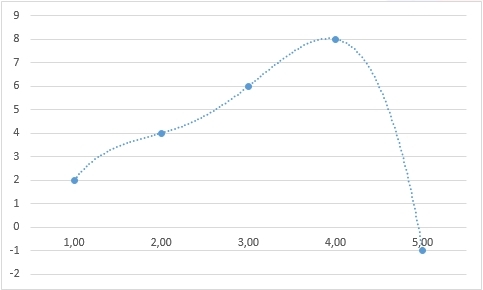
Для дальнейших рассуждений возьмем более простой пример. Представим себе, например, лабораторную работу по географии в каком-нибудь 6-ом классе (кстати, у меня когда-то и правда была такая). Необходимо каждые 3 часа измерять температуру воздуха и записывать данные, а потом сдать учителю график изменения температуры от времени суток. Допустим, по результатам измерений у нас получилась вот такая табличка (данные придуманы случайным образом и никак не претендуют на какую-либо правдоподобность):

Отобразим полученные данные на графике:

Собственно, данные записаны и отражены на графике. Мы вплотную подошли к задаче интерполяции – как по имеющимся точкам восстановить плавную кривую?

Видео:7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Количество условий и степень интерполирующего полинома

Можем ли мы вообще гарантировать, что такая функция, которая соединяет все заданные точки, вообще существует?

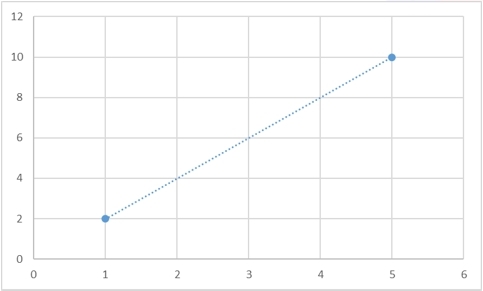
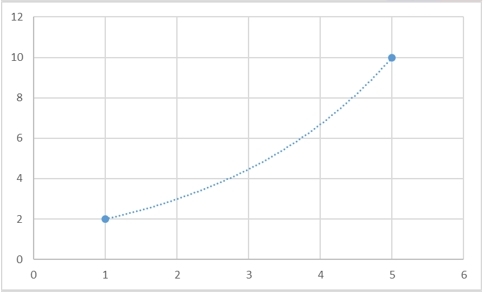
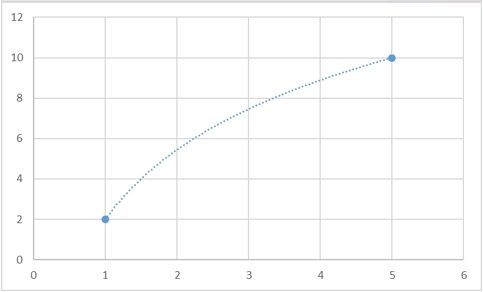
Да, такая функция гарантированно существует, и более того, таких функций будет бесконечно много. Для любого набора точек можно будет придумать сколько угодно много функций, которые через них будут проходить. И вот несколько примеров того, как две точки можно соединить разными способами:

Однако есть и способ задать интерполяционную кривую однозначно. В самом классическом случае, в качестве интерполяционной кривой берут полином:

Для того, чтобы провести через имеющиеся точки такой полином единственным образом, необходимо и достаточно, чтобы степень полинома была на 1 меньше, чем количество условий (я специально выделил это слово, потому что в конце этого раздела я вернусь к этой формулировке). Пока что, простоты ради, условием будут являться координаты точки. Говоря человеческим языком, через 2 точки однозначным образом можно провести прямую (полином 1-ой степени), через 3 точки – параболу (полином 2-ой степени) и т.д.

Возвращаясь к нашей задаче с температурой – в ней мы определили 6 точек, значит, для того, чтобы провести полином единственным образом, он должен быть 5-ой степени

Интерполирующий полином тогда будет выглядеть так:

А сейчас следует сделать важное замечание и пояснить, что я имел ввиду под «условием». Полином можно задать не только координатами точек, через которые он проходит, условиями могут быть любые параметры этого полинома. В простейшем случае это действительно координаты точек. Но в качестве условия можно взять, например, первую производную этого полинома в какой-либо из точек. Вторую производную. Третью производную. В общем, любую возможную производную в любой из точек, в которой этот полином существует. Поясню на примере:
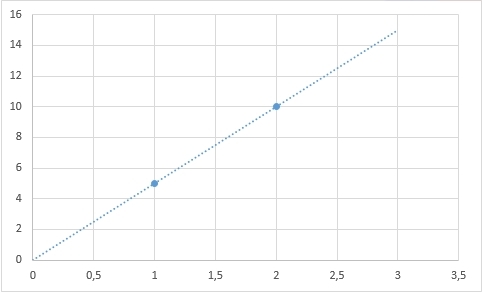
Прямую можно задать однозначно, как я уже говорил, двумя точками:

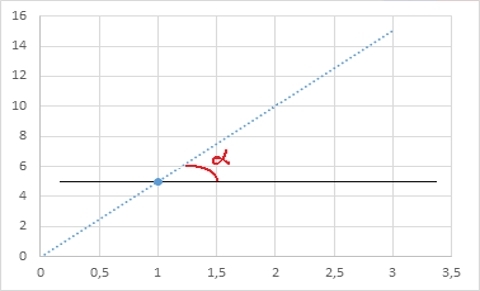
Ту же прямую, с другой стороны, можно определить координатой одной точки и углом наклона альфа к горизонтали:

С полиномами более высоких степеней можно использовать и более сложные условия (вторая производная, третья производная, etc.), и каждый такой параметр будет идти в общий счет количества условий, которые однозначным образом определят этот полином. Чтобы не быть голословным, вот еще пример:

Пусть нам заданы такие три условия:

Условий три, значит, мы хотим получить полином второй степени:

Подставляем

Считаем первую производную и считаем

Считаем вторую производную и считаем

Отсюда получаем, что наш полином выглядит так:

Видео:Дифференциальные уравнения, 5 урок, Уравнение БернуллиСкачать

Интерполяция кубическими сплайнами

Вот, по тиху, мы и подбираемся к моей задаче. Полиномиальная интерполяция – не единственно возможный способ интерполяции. Среди всех прочих методов существует метод интерполяции кубическими сплайнами.

Принципиальное отличие идеи сплайн-интерполяции от интерполяции полиномом состоит в том, что полином один, а сплайн состоит из нескольких полиномов, а именно их количество равно количеству инервалов, внутри которых мы производим интерполяцию. В примере с нашей температурой воздуха, в которой у нас определено 6 точек, у нас будет 5 интервалов – соответственно, у нас будут 5 полиномов, каждый на своем интервале.

Каждый из этих полиномов – это полином третьей степени (строго говоря, степени не выше третьей, так как на каком-то из интервалов интерполирующая кривая может становиться квадратичной параболой или даже линейной функцией, но в общем случае это все-таки полином именно третьей степени). Записывая вышесказанное формульно, получим что все наши точки будут соединены некоей кривой , где каждый – это полином третьей степени, а именно:

Возвращаясь к рассказанному в предыдущем пункте, для того, чтобы однозначно задать один полином 3-ей степени, необходимо 4 условия. В этой задаче у нас 5 полиномов, то есть, чтобы задать их все, нам нужно суммарно 5∙4=20 условий. И вот как они получаются:

1) Первый полином определен на первой и второй точках – это два условия. Второй полином определен на второй и третьей точках – еще два условия. Третий полином, четвертый, пятый – каждый из них определен на 2-х точках – суммарно это дает 10 условий.

2) Для каждой промежуточной точки из множества (а это 4 точки с временами 12:00, 15:00, 18:00, 21:00) должно выполняться условие, что первые и вторые производные для левого и правого полиномов должны совпадать. Формульно:

По два таких условия на каждую из промежуточных точек дает еще 8 условий. Следует добавить, что мы задаем только сам факт равенства, а какое конкретно значение они при этом принимают – это совершенно иная задача и считается она довольно сложно.

3) Остаются два условия, которые пока еще не определены. Это так называемые «граничные условия», от задания которых и зависит, какой именно сплайн получится. Обычно задают вторые производные на концах интервала равными 0:

Если сделать так, то мы получим так называемый «естественный сплайн». Для вычисления таких сплайнов написано уже огромное количество библиотек, бери и используй любую.

Видео:Решите уравнение ★ y'-2y=e^(2x) ★ Линейное дифференциальное уравнение 1-го порядкаСкачать

Отличие моего задания от классической постановки задачи, мои размышления над заданием и само решение

И вот мы подошли к условию моей задачи. Преподаватель придумал такое задание, что задаваться должны первые производные и на левом и правом концах интервала, а программа должна считать интерполирующую кривую. А для такого требования готовых алгоритмов я не нашел…
Я, разумеется, не стану описывать весь твой «творческий» путь от момента, когда я услышал задание, до того, как я его сдал. Расскажу лишь саму идею и покажу ее реализацию.

Сложность задания состоит в том, что, задавая первые производные на концах интервала, да, мы задаем этот сплайн. Теоретически. А вот посчитать его на практике – задача довольно сложная и совершенно неочевидная (желающие могут посмотреть код нахождения естественного сплайна на Вики – ru.wikipedia.org/wiki/Кубический_сплайн – и попробовать его понять хотя бы). Разумеется, я совершенно не хотел провести кучу времени, закопавшись в матан и пытаясь вывести нужные мне формулы. Я хотел более простое и элегантное решение. И я его нашел.
Рассмотрим наш сплайн и возьмем первый из его интервалов. На этом интервале уже заданы 3 условия:

— задается пользователем

Для того, чтобы однозначно задать кубический полином на этом интервале, нам не хватает еще лишь одного условия. Но мы можем его просто придумать! Возьмем вторую производную и положим ее равной, например, 0:

— ничем не обоснованное предположение

Таким образом, зная эти 4 условия, мы полностью определяем этот полином. Зная все параметры этого полинома, мы можем вычислить значения первой и второй производных на второй точке, и поскольку они совпадают со значениями первой и второй производной для полинома на втором интервале, это приводит к тому, что мы также определяем и второй полином:

— вычисляется из

— вычисляется из

Аналогично мы считаем третий полином, четвертый, пятый и так далее, сколько бы их ни было. То есть, по факту, воссоздаем весь сплайн. Но поскольку мы взяли совершенно случайным образом, это приведет к тому, что производная , заданная пользователем на правом конце сплайна, не будет совпадать с производной , которая получилась у нас в ходе таких вычислений. Но получается, что значение производной на правом конце сплайна – это функция, зависящая от значения второй производной на левом конце:

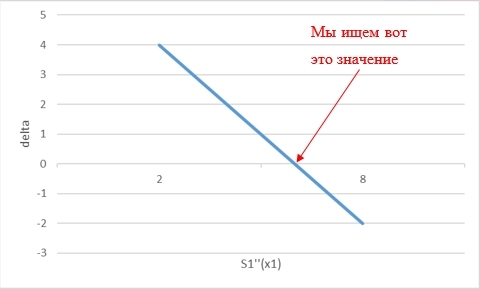
А поскольку такой сплайн, который бы удовлетворял заданным условиям, гарантированно существует, и существует в единственном экземпляре, это значит, что мы можем рассмотреть разность:

и попытаться найти такое значение , при котором обращалась бы в 0 – и это будет тем самым правильным значением , которое строит искомый пользователем сплайн:

Самое замечательное в моей идее то, что эта зависимость оказалась линейной (вне зависимости от количества точек, через которые мы проводим сплайн. Этот факт доказан теоретическими подсчетами), а значит можно случайным образом взять любые два начальные значения и , посчитать и , и сразу же посчитать то самое верное значение, которое построит нам искомый сплайн:

Итого, мы гарантированно находим искомый сплайн за 3 прогонки таких вычислений.

Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Немного кода и скриншотов программы

Синие отрезки — это первые производные сплайна в соответствующих его точках. Добавил такой вот графический элемент для большей наглядности.

Видео:13. Как решить дифференциальное уравнение первого порядка?Скачать

Достоинства и недостатки алгоритма

Признаюсь честно, я не проводил сколь-либо серьезного анализа. По-хорошему стоило бы написать тесты, проверить, как оно работает в разных условиях (мало/много точек интерполяции, равное/произвольное между точками, линейные/квадратные/кубические/тригонометрические/etc. функции и так далее), но я этого не сделал, простите 🙂

Навскидку можно сказать, что сложность алгоритма — O(N), так как, как я уже говорил, вне зависимости от количества точек, достаточно двух прогонов вычислений, чтобы получить правильное значение второй производной на левом конце интервала, и еще одного, чтобы построить сплайн.

Впрочем, если кому-то захочется покопаться в коде и провести какой-нибудь более подробный анализ этого алгоритма, я буду только рад. Напишите мне разве что о результатах, мне было бы интересно.

Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать

Так а в чем провинились тесты IQ?

В самом начале статьи я написал два числовых ряда и попросил их продолжить. Это довольно частый вопрос во всяких IQ тестах. В принципе, вопрос как вопрос, но если копнуть чуть глубже, окажется, что он довольно бредовый, потому что при некотором желании можно доказать, что «правильного» ответа на него не имеется.

Рассмотрим для начала ряд «2, 4, 6, 8, ?»
Представим себе этот числовой ряд как множество пар значений :

, где в качестве мы берем само число, а в качестве – порядковый номер этого числа. Какое значение должно быть на месте ?

Мысль, к которой я стараюсь плавно подвести – это то, что мы можем подставить абсолютно любое значение. Ведь что по факту проверяют такие задачи? Способность человека найти некое правило, которое связывает все имеющиеся числа, и по этому правилу вывести следующее число в последовательности. Говоря научным языком, здесь стоит задача экстраполяции (задача интерполяции состоит в том, чтобы найти кривую, проходящую через все точки внутри некоторого интервала, а задача экстраполяции – продолжить эту кривую за пределы интервала, «предсказав» таким образом поведение кривой в дальнейшем). Так вот, экстраполяция не имеет однозначного решения. Вообще. Никогда. Если бы было иначе, люди давным-давно бы предсказали прогноз погоды на всю историю человечества вперед, а скачки курса рубля никогда не были бы неожиданностью.

Разумеется, предполагается, что верный ответ в этой задаче все-таки есть и он равен 10, и тогда «закон», связывающий все эти числа, – это

Однако возьмем любое другое значение – и мы также сможем найти закон, который бы обосновывал именно его:

Хорошо, с экстраполяцией разобрались, она не имеет однозначного решения даже теоретически. Но, быть может, мы сможем найти пропущенное число во втором ряду?

Я считаю, верный ответ . Кто сможет оспорить? 🙂

Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Методы интерполяции и сглаживания сплайнами

Видео:Видеоурок "Нахождение частных решений по виду правой части"Скачать

Постановка задачи и основные положения

Как отмечалось ранее, в вычислительной практике при глобальном способе аппроксимации высокие степени интерполяционных многочленов использовать нецелесообразно. Поэтому часто применяется кусочно-глобальный способ на основе, например, линейной и квадратичной (параболической) интерполяции. Однако производные таких интерполяционных многочленов, получающихся на частичных отрезках, в местах их стыка терпят разрывы. На рис. 4.10,а показано поведение совокупности трех таких параболических многочленов (звеньев). Легко видеть, что производные в точках стыка частичных отрезков (шаблонов [math](x_,x_,x_),[/math] [math](x_, x_,x_),[/math] [math](x_,x_,x_)[/math] ) терпят разрывы. Это является крайне нежелательным, если вся совокупность [math]textstyle<bigcup_S_(x)>[/math] используется, например, для аппроксимации обводов конструктивных элементов сложных поверхностей. Для изготовления таких поверхностей требуется задание в узлах не только значений [math]S_(x_i)[/math] , но и первой производной [math]S’_(x_i)[/math] или даже второй производной [math]S»_(x_i)[/math] . Таким образом, вместе с функцией [math]y_i= f(x_i),

i=overline[/math] , требуется достаточно хорошо аппроксимировать и ее производные. Если восполняемая функция достаточно гладкая, то и ее производные тоже гладкие, и поэтому они должны быть непрерывными во всех внутренних узлах. В связи с этим к аппроксимирующим функциям [math]S_m(x)[/math] ( [math]m[/math] -степень многочлена) предъявляются требования непрерывности [math]S_m(x),, S’_m(x)[/math] и по возможности [math]S»_m(x)[/math] или [math]S»’_m(x)[/math] во всех точках [math]xin[a,b][/math] (рис. 4.10,б). Это и обусловливает необходимость построения сплайн-функций, обладающих указанными свойствами и имеющих интерполяционный или сглаживающий характер.

Пусть на отрезке [math][a,b][/math] задана сеточная функция [math]y_i= f(x_i)[/math] на сетке [math]Omega_n[/math] . Требуется восполнить ее функцией [math]S_m(x)[/math] , где [math]m[/math] — степень многочлена, кусочно-глобальным способом. Дадим сначала упрощенное определение сплайна, которое затем уточним.

Сплайн-функцией или сплайном называется совокупность [math]S_(x)[/math] — алгебраических многочленов степени [math]m[/math] (звеньев), определенных на частичных отрезках [math][x_,x_],

i=overline[/math] , и соединенных вместе по всем частичным отрезкам так, чтобы можно было составить многозвенную функцию [math]textstyle<S_m(x)= bigcuplimits_^ S_(x)>[/math] , определенную и непрерывную на всем отрезке [math][a,b][/math] вместе со всеми своими производными [math]S_^(x)[/math] до некоторого их порядка [math]p=1,2,ldots[/math] . Разность между [math]m[/math] и наибольшим порядком производной, непрерывной на отрезке [math][a,b][/math] , определяет дефект сплайна [math]q[/math] . Условиями согласования звеньев [math]S_(x)[/math] сплайна с исходной функцией [math]y_i= f(x_i)[/math] на соответствующем частичном отрезке [math][x_, x_][/math] называются условия, накладываемые на невязки дифференциального и интегрального типов [math]delta S_^(x_i),, delta S_(I_^)[/math] и использующиеся для вывода формулы одного звена сплайна на указанном частичном отрезке.

Сплайн, удовлетворяющий условиям (4.3) нулевых функциональных невязок, называется интерполяционным, а удовлетворяющий только интегральным условиям (4.5), — сглаживающим или интегрально-сглаживающим .

Сплайн, построение которого основано только на дифференциальных условиях согласования (4.2) при [math]p=0,!1[/math] или [math]p=0,!2[/math] , называется дифференциальным (Д-сплайном) . Если же наряду с дифференциальными условиями согласования используется интегральное условие вида (4.5), то сплайн называется интегрально-дифференциальным (ИД-сплайном) .

Количество условий согласования, необходимых для получения формулы одного звена сплайна, должно соответствовать степени сплайна (число условий на единицу больше [math]m[/math] ). После определения формулы [math]S_(x)[/math] ее правая часть выражается через известные и неизвестные величины (параметры): [math]f^(x_i)[/math] — для дифференциального сплайна или через совокупность [math]f^(x_i)[/math] и [math]textstyle<I_^= intlimits_^<x_> f(x),dx>[/math] —для интегрально-дифференциального. Эти величины будут называться параметрами сплайна. В зависимости от того, заданы те или иные параметры сплайна в постановке задачи или нет, они именуются определенными или неопределенными. Последние вычисляются на основе условий непрерывности (гладкости) сплайна [math]S_m(x)[/math] , которые здесь называются условиями стыковки. Для некоторого узла [math]x_i[/math] , общего для звена [math]i-1[/math] , относящегося к частичному отрезку [math][x_,x_i][/math] , и звена [math]i[/math] , определенного на частичном отрезке [math][x_i,x_][/math] , это условие имеет вид

При решении задачи аппроксимации с помощью сплайн-функций условия стыковки преобразуются к соотношениям, связывающим определенные и неопределенные параметры, которые называются параметрическими соотношениями (уравнениями).

Параметрические соотношения, записанные в виде уравнений, могут использоваться для нахождения неопределенных параметров применительно к сплайн-аппроксимации либо для выражения одних параметров через другие. Последний способ в данной книге применяется для вывода новых типов формул численного дифференцирования и интегрирования. Кроме того, параметрические соотношения на основе изложенного во введении принципа согласования порядков численных величин устанавливают соответствие этих порядков для различных параметров, входящих в то или иное соотношение.

При решении задачи сплайн-аппроксимации необходимо предварительно вычислить неопределенные параметры сплайна для всех его звеньев. Этот этап соответствует решению параметрической задачи. Для пояснения ее характера введем понятие порядка параметров сплайн-функции, который обозначим через [math]l[/math] . Этот порядок зависит от порядка производных исходной функции [math]y=f(x)colon[/math] для параметра [math]I_i^[/math] примем [math]l=-1[/math] , а для [math]f^(x)[/math] положим [math]l=p

Параметрическая задача называется прямой (обратной), если порядки всех неопределенных параметров больше (меньше) порядков определенных параметров. Если в задаче аппроксимации порядки одних неопределенных параметров больше, а порядки других меньше порядков определенных параметров, то параметрическая задача называется смешанной. Данная классификация используется далее при описании конкретных методов построения параболических интегрально-дифференциальных сплайн-функций.

Две совокупности параметров, относящиеся к параметрическим уравнениям и сплайнам разных степеней, называются подобными, если они могут быть получены друг из друга путем соответствующего изменения порядков параметров [math]l[/math] на одинаковую величину.

Параметрические уравнения или их системы, соответствующие двум сплайнам разных степеней, называются подобными, если они включают подобные параметры и имеют одинаковые коэффициенты, зависящие от шагов, определяющих сетку.

Два или несколько сплайнов различных степеней называются подобными, если формулы звеньев можно получить друг из друга путем дифференцирования или интегрирования и замены всех параметров одного сплайна соответствующими подобными параметрами другого сплайна.

Сплайн называется локальным, если все неопределенные параметры, относящиеся к каждому его звену [math]S_(x),

t=i[/math] , при [math]xin [x_i, x_],

i=overline[/math] , находятся локально, т.е. независимо от параметров, характеризующих все остальные (или почти все остальные) звенья [math]S_(x),

Сплайн-аппроксимация (как правило, это интерполяция) локальными сплайнами сводится, таким образом, к получению конкретных значений коэффициентов многочленов [math]S_(x)[/math] для каждого звена результирующего сплайна [math]S_(x)[/math] и неопределенных параметров путем их вычисления по аппроксимационным формулам. Недостаток локальной интерполяции состоит в том, что таким способом не удается обеспечить минимальный дефект сплайна, т.е. максимально возможную его гладкость в смысле непрерывности производных как можно большего порядка [math](p=0,1,2,ldots)[/math] .

Альтернативой локальному сплайну является глобальный сплайн, для которого неопределенные параметры, относящиеся к каждому его звену [math]S_(x),

y=i[/math] при [math]xin [x_i, x_],

i=overline[/math] , находятся совместно с параметрами, характеризующими все остальные звенья [math]S_(x),

tne i[/math] . Неопределенные параметры в глобальных сплайнах для всех звеньев вычисляются, как правило, путем решения системы линейных алгебраических уравнений трех-диагонального вида методом прогонки, причем это обеспечивает непрерывность одной из производных, а именно той, которая не включена в условия согласования. Если в условие согласования включена производная другого порядка, то ее непрерывность также гарантируется. Глобальный способ аппроксимации по сравнению с локальным способом обеспечивает минимально возможный дефект сплайна. Поэтому глобальные сплайны широко используются в вычислительной практике.

В заключение данного раздела дадим развернутое определение глобального интегрально-дифференциального сплайна.

Функция [math]textstyle<S_(x)= bigcuplimits_^ S_(x)>[/math] которая определена на отрезке [math][a,b][/math] , принадлежит классу гладкости [math]C_r[a,b][/math] и составлена из совокупности звеньев [math]S_(x),

i=overline[/math] , определенных на каждом частичном отрезке [math][x_i,x_][/math] сетки [math]Omega_n[/math] , называется алгебраическим интегрально-дифференциальным сплайном степени [math]m[/math] и дефекта [math]q

(0 leqslant r leqslant m,

q=m-r)[/math] с узлами на сетке [math]Omega_n[/math] , если каждое его звено [math]S_(x)

i=overline[/math] , представляется в виде алгебраического многочлена степени [math]mcolon[/math]

с коэффициентами [math]a_[/math] , выражаемыми из совокупности [math](m+1)[/math] интегральных и (или) дифференциальных условий согласования:

и из условий стыковки (непрерывности) звеньев [math]S_(x)[/math] по производным [math]S_^(x)colon[/math]

(0 leqslant p_1 leqslant r)[/math] принимает значения из совокупности нескольких целых чисел, соответствующих порядкам производных, а [math]p_2[/math] — целое число или в общем случае несколько целых чисел, таких, что [math]0 leqslant p_2 leqslant r[/math] , причем ни одно из этих чисел не равно ни одному значению чисел [math]p_1[/math] .

1. Данное определение является обобщенным, и оно справедливо как для интегрально-дифференциального сплайна, так и для классического дифференциального. В последнем случае условия (4.66) не используются.

2. Условия стыковки (4.67) вместе с дифференциальными условиями согласования (4.66) обеспечивают непрерывность [math]S_^(x),

p=0,1,ldots,r[/math] , во всех внутренних узлах [math]x_i[/math] определяющих точки стыковки звеньев, т.е. [math]bigl(x_i, S_(x_i)bigr),

i=overline[/math] . Это гарантирует выполнение условия [math]S_(x)in C_r[a,b][/math] .

3. Алгоритм конструирования сплайна сочетает в себе два способа аппроксимации — кусочный и глобальный и поэтому является кусочно-глобальным. На кусочном способе основан процесс отыскания звеньев сплайна [math]S_(x)[/math] , т.е. коэффициентов [math]a_[/math] многочлена (4.64), а на глобальном — соединение всех звеньев в единую (многозвенную) функцию [math]S_(x),

xin[a,b][/math] со стыковкой звеньев так, чтобы обеспечивалась непрерывность [math]S_^(x)[/math] при [math]p=0,1,2,ldots[/math] , т.е. непрерывность как самой функции [math]S_(x)[/math] , так и ее производных.

4. Порядки производных [math]p_1[/math] , выбранных для условий согласования (4.66), не должны совпадать с порядками производных, используемых в условиях стыковки (4.67), но вся совокупность порядков производных из [math]p_1[/math] и [math]p_2[/math] должна обеспечивать выполнение условия [math]S_(x)in C_r[a,b][/math] .

5. Интегральное условие согласования (4.65) может быть переписано в виде [math]textstyle<intlimits_^<x_> S_(x)dx= I_^>[/math] , и тогда [math]I_^[/math] вместе со значениями [math]f^(x_i)[/math] , входящими в дифференциальное условие согласования, причисляется к параметрам ИД-сплайна. Данные параметры могут быть заданы при формулировке задачи аппроксимации либо определены при ее решении.

Рассмотрим сначала кубические дифференциальные сплайны, являющиеся традиционными и широко используемыми при интерполяционном восполнении сеточных функций.

Видео:Дифференциальные уравнения, 4 урок, Линейные дифференциальные уравнения первого порядкаСкачать

Интерполяционные дифференциальные кубические сплайны

Рассмотрим задачу восполнения заданной сеточной функции [math]y_i=f(x_i),

x_iin[a,b][/math] на базе интерполяционных глобальных кубических дифференциальных сплайнов дефекта [math]q=1[/math] , то есть [math]S_3(x)in C_2[a,b][/math] . При этом предположим, что восполняемая функция достаточно гладкая.

Решить эту задачу можно с помощью двух алгоритмов восполнения исходной сеточной функции, различающихся выбором порядков производных, на основе которых записываются условия согласования (4.66). Первый способ, наиболее широко распространенный, соответствует выбору вторых производных [math]m_i= f»_i

(i=overline)[/math] , а второй— выбору первых производных [math]overline_i= f’_i[/math] .

Оба способа основаны на решении параметрически прямой задачи и весьма близки по характеру вычислительных процедур.

Основные этапы реализации первого способа.

Первый этап. Для алгебраического многочлена (полинома)

относящегося к одному i-му звену сплайна, для которого [math]xin[x_i,x_][/math] , выбираются два дифференциальных условия согласования (4.66) с порядком [math]p_1=[/math] , каждое из которых относится к концам отрезка [math][x_i,x_]colon[/math]

Выбор значения [math]p=0[/math] обусловлен тем, что отыскивается [math]S_3(x)[/math] — интерполяционный многочлен, а выбор производных порядка [math]p=2[/math] зависит от выбора способа. Условия (4.69), (4.70) задают параметры сплайна [math]f_i,

i=overline[/math] , первые из которых (функциональные) являются определенными, а вторые (дифференциальные) — неопределенными. Подстановка в соотношения (4.69), (4.70) полинома (4.68) приводит к системе четырех линейных алгебраических уравнений относительно неизвестных коэффициентов [math]a_

(k=0,1,2,3)[/math] . Разрешая их, подставляя полученные формулы для [math]a_[/math] в (4.68) и распространяя этот результат на все частичные отрезки, имеем:

Delta f_i= f_-f_i,

Delta m_i= m_-m_i[/math] .

Таким образом, найдена общая формула одного звена сплайна, которая выражается через определенные [math](f_i)[/math] и неопределенные [math](m_i)[/math] параметры [math](i= overline)[/math] . Эти параметры обеспечивают непрерывность сплайна: [math]Bigl.<S_(x)>Bigr|_= Bigl.<S_(x)>Bigr|_,

i=overline[/math] , для всех внутренних узлов.

Второй этап. При вычислении неопределенных параметров [math]m_i

(i=overline)[/math] , входящих в (4.71), с учетом условия стыковки (4.67) для всех внутренних узлов устанавливается связь между [math]f_i[/math] и [math]m_i[/math] ,. Эта связь получается путем записи правой части (4.71) для звена [math]S_(x)[/math] при [math]xin [x_,x_i][/math] ee дифференцирования и приравнивания производной правой части (4.71) для звена [math]S_(x)[/math] при [math]xin[x_i,x_][/math] в соответствии с условием стыковки (4.67) [math](p_2=1)[/math] . Проведя несложные выкладки и распространив найденное соотношение на все внутренние узлы, получим параметрическую систему — трехдиагональную систему линейных алгебраических уравнений, устанавливающую линейную связь комбинаций определенных [math]f_i[/math] и неопределенных параметров [math]m_i[/math] , во внутренних узлах:

Данная система относительно [math]m_i

(i=overline)[/math] является незамкнутой, так как не хватает двух уравнений. Для ее замыкания используют различные пути выбора аппроксимаций производных на концах (граничных условий):

1. В простейшем случае вторые производные на концах принимаются нулевыми, т.е. [math]m_0=0;

m_n=0[/math] . Такие условия называются условиями натурального сплайна.

Из рис. 4.11 видно, что задание условий [math]m_0=0[/math] и [math]m_n=0[/math] приводит к разрыву вторых производных [math]Bigl.Bigr|_[/math] и [math]Bigl.Bigr|_[/math] на концах отрезка [а,Ь], что может вызвать возрастание погрешности интерполирования.

2. Для первых двух и последних двух отрезков можно применить условие равенства третьей производной. Тогда получается соотношение [math]frac<Delta m_>= frac<h_>[/math] [math](k=1,n-1)[/math] . Отсюда следуют два трехточечных уравнения:

Соотношения (4.73) позволяют замкнуть систему (4.72) при [math]h= text[/math] (неравномерная сетка). При [math]h=text[/math] вторые производные на концах вычисляются по явным формулам второго порядка аппроксимации:

Отметим, что как (4.73), так и формулы (4.74) для [math]m_0[/math] и [math]m_n[/math] имеют порядки аппроксимации, соответствующие порядку сходимости [math]S_3(x)[/math] к [math]f(x)[/math] .

Третий этап. Определяются значения [math]m_i

(i=overline)[/math] путем решения систем (4.72), (4.73) (параметрически прямая задача). Для этого используется метод прогонки, причем необходимо предварительно из первых двух и последних двух уравнений исключить слагаемые с [math]m_2[/math] и [math]m_[/math] соответственно. В случае равномерной сетки, как отмечено выше, система (4.72) замыкается аппроксимацией (4.74).

Четвертый этап. Формируются массивы коэффициентов [math]a_, a_, a_, a_[/math] , для всех звеньев сплайна [math](i=overline)[/math] и определяется глобальный интерполяционный сплайн [math]textstyle<S_3(x)= bigcuplimits_^ S_(x)>[/math] путем составления многозвенной функции.

Пятый этап. При необходимости полученная сплайн-функция [math]S_3(x)[/math] используется для вычисления значений функции и производных порядка [math]pcolon[/math] [math]f^(x)= S_3^(x)+ O(h_^)[/math] [math](p=0,1,2,ldots)[/math] в произвольных точках [math]xin [x_i,x_],

Основные этапы реализации второго способа.

Первый этап. Для алгебраического многочлена (4.68), обозначаемого [math]overline_(x)[/math] , вместо вторых производных в (4.70) включаются первые производные. Тогда эти условия определяют параметры сплайна [math]f_i,

i=overline[/math] , первые из которых (функциональные) являются определенными, а вторые (дифференциальные) — неопределенными [math](p=1)[/math] . Проделав выкладки (аналогично первому этапу первого способа), получим общую формулу i-го звена искомого сплайна:

которая зависит от определенных [math](f_i)[/math] и неопределенных [math](overline_i= f’_i)[/math] параметров сплайна. Данные параметры обеспечивают непрерывность всего сплайна и его производных

Второй этап. С использованием условий стыковки (4.67) по вторым производным [math](p_2=2)[/math] во внутренних узлах получается система линейных алгебраических уравнений трехдиагонального типа, выражающая параметрическую связь между [math]overline_[/math] и [math]f_icolon[/math]

Замыкание системы (4.76) осуществляется аналогично п.2 на втором этапе реализации первого способа. При [math]h=text[/math] получаются два соотношения (граничные условия), не нарушающие трехдиагональность системы (где [math]H_^k= h_+ h_k[/math] ):

Соотношения (4.77) аппроксимируют производные на концах с третьим порядком точности, что соответствует четвертому порядку сходимости [math]overline_3(x)[/math] к [math]f(x)[/math] (см. п.2 замечаний ниже). При [math]h=text[/math] для определения значений производных на концах можно использовать соответствующие аппроксимационные формулы.

Третий этап. Трехдиагональная система линейных алгебраических уравнений (4.76), (4.77) при конструировании глобального сплайна решается методом прогонки (параметрически прямая задача).

Четвертый и пятый этапы аналогичны изложенным для первого способа.

1. Существование и единственность глобальных сплайнов [math]S_3(x)[/math] и [math]overline_3(x)[/math] следуют из рассмотренного выше построения общих формул их звеньев [math]S_(x),, overline_(x)[/math] и единственности решения трехдиагональных систем (4.72), (4.73) или (4.74) и (4.76), (4.77) в силу выполнения условия диагонального преобладания.

2. Сходимость процесса построения глобальных сплайнов [math]S_(x),, overline_(x)[/math] доказывается для непрерывных (формульных) функций, таких, что [math]f(x)in C_4[a,b][/math] . Процесс является сходящимся, если при неограниченном увеличении числа [math]n[/math] узлов сетки соответствующая последовательность сплайн-функций, построенных на этих сетках, сходится к исходной функции [math]f(x)[/math] . Доказано, что на равномерной сетке сплайн-функции [math]S_(x),, overline_(x)[/math] сходятся к [math]f(x)in C_4[a,b][/math] с четвертым порядком, причем справедливы оценки

Таким образом, при использовании сплайн-функций для вычисления производных также реализуется сходимость, но ее порядок понижается на величину [math]p[/math] .

3. В соответствии с принципом соответствия порядков аппроксимации точность вычисления интегралов на частичном отрезке [math][x_,x_][/math] , то есть [math]textstyle<I_^= intlimits_^<x_> f(x)dx approx widehat_^= intlimits_^<x_> S_3(x)dx>[/math] , на основе сплайнов [math]S_(x),, overline_(x)[/math] составляет [math]O(h_^5)[/math] , а интеграла [math]textstyle<I_a^b= intlimits_^ f(x)dx>[/math] на отрезке [math][a,b][/math] составляет [math]O(H^4),

H=max_h_[/math] (потеря порядка происходит из-за суммирования значений [math]widehat_^[/math] и остаточного слагаемого при переходе от [math]widehat_^,

4. Выражая из системы (4.72) комбинацию значений функций [math]f_,, f_,, f_[/math] через комбинацию [math]m_,, m_,, m_[/math] , получаем трехдиагональную систему линейных алгебраических уравнений относительно [math]f_icolon[/math]

Если считать, что вторые производные для некоторой функции [math]y_i=f(x_i)[/math] заданы или каким-либо способом определены, а [math]f_0[/math] и [math]f_n[/math] на концах [math][a,b][/math] известны, то из (4.79) можно восстановить значения [math]overline_i[/math] во внутренних узлах [math]x_i

(i=overline)[/math] путем решения параметрически обратной задачи. В этом случае сплайн [math]S_3(x)[/math] , построенный по [math]overline_i,

(i=overline)[/math] и (4.71), является в строгом понимании не интерполяционным, а восстанавливающим функцию [math]y_i=f(x_i)[/math] . Единственность решения задачи обеспечивается преобладанием диагональных коэффициентов в системе (4.79) относительно значений [math]f_i

5. На основе соотношения (4.76) при заданных двух значениях функций [math]f_0,,f_i[/math] или [math]f_,, f_n[/math] и всех значениях [math]overline_i

(i=overline)[/math] можно восстановить функцию [math]widetilde(x_i)[/math] во всех точках сетки [math]x_i

(i= overline)[/math] . С этой целью система (4.76) разрешается относительно приращений функций [math]Delta f_i[/math] , которые затем вычисляются рекуррентно. При задании неравномерной сетки устойчивость процесса достигается при регулярном сгущении сетки в направлении слева направо [math]left(delta_= frac<h_>leqslant 1right)[/math] или при ее регулярном разрежении 1)»>[math](delta_>1)[/math] . В первом случае восстановление осуществляется слева направо при заданных [math]f_0,, f_1colon[/math]

где [math]L_h= frac left[frac overline_+ 2! left(frac+ frac<h_>right)!overline_+ frac<h_> overline_right][/math] , а во втором — справа налево при заданных [math]f_,, f_[/math] . Такой алгоритм обеспечивает устойчивость процесса обратной прогонки.

6. Локальный способ построения интерполяционных кубических сплайнов для заданной функции [math]y_i= f(x_i)[/math] основан на многочлене (4.75) и состоит в определении [math]overline_,

i=overline[/math] , по аппроксимационным формулам третьего порядка, в дальнейшей их подстановке в (4.75) и в формировании [math]textstyle<overline_3(x)= bigcuplimits_^ overline_(x)>[/math] . Необходимость аппроксимации третьего /»о порядка следует из принципа соответствия порядков, изложенного ранее, а также из параметрической связи (4.76).

Видео:Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

Алгоритм построения интерполяционного кубического сплайна

1. Используя систему (4.72) , условия [math]m_0=0,

m_n=0[/math] или (4.73) (при [math]h= text[/math] можно использовать условия (4.74)), сформировать замкнутую систему относительно неопределенных параметров.

2. Вычислить коэффициенты системы (4.72), зависящие от шагов сетки [math]Omega_n[/math] , и решить ее методом прогонки. В результате найти неопределенные параметры [math]m_0,m_1,ldots,m_n[/math] .

3. Записать выражения для звеньев сплайна по формуле (4.71):

вычислить коэффициенты звеньев и сформировать многозвенную сплайн-функцию [math]textstyle<S_3(x)= bigcuplimits_^ S_(x)>[/math] , являющуюся сплайном дефекта [math]q=1[/math] .

Для сеточной функции [math]y_1= cos x_i,

(i=overline)[/math] найти интерполяционную кубическую сплайн-функцию [math]S_3(x)[/math] первым способом.

Решение. В поставленной задаче

1. Запишем систему (4.72) для внутренних узлов:

В силу того, что [math]h=h_1= h_2= h_3= pi!!not<phantom>,6= text[/math] , для нахождения значений [math]m_0,,m_3[/math] выбираются формулы (4.74):

2. Вычислим коэффициенты системы и значения [math]m_0,,m_3colon[/math]

Решение этой системы методом прогонки дает: [math]m_1=-0,!84642;

3. Подставляя параметры [math]m_i,

i=0,1,2,3[/math] , в формулу (4.71), получаем следующую трехзвенную сплайн-функцию:

Она является непрерывной и обеспечивает непрерывность первых и вторых производных.

Видео:Линейное дифференциальное уравнение первого порядка (1-x^2)*y'-xy=1Скачать

Интерполяционные дифференциальные параболические сплайны

Выше отмечено, что применение параболических сплайнов более оправданно при аппроксимационной обработке широкого класса сеточных функций, например, рассчитанных методами сеток второго и третьего порядка. Сплайн-методы развиваются и как самостоятельный класс методов решения задач с обыкновенными дифференциальными уравнениями. Следует отметить, что широко распространенные на практике кубические дифференциальные сплайны теоретически обеспечивают четвертый порядок сходимости. Однако для их корректного применения необходимо, чтобы исходные данные (аппроксимируемая функция [math]y_i= f(x_i)[/math] ) были заданы с порядком точности, не меньшим третьего. Это условие при обработке рассчитанных на основе методов сеток функций [math]y_i= f(x_i)[/math] , как правило, не выполняется, и поэтому применять кубические сплайны не всегда целесообразно. Это обусловливает необходимость использования параболических сплайн-функций. Однако полученные традиционным способом сплайны [math]S_2(x)[/math] неустойчивы в смысле отсутствия их сходимости к исходной функции, что связано с несимметричным характером задания условий согласования и, как следствие, с аналогичным характером граничных условий. Поэтому для регуляризации сплайнов [math]S_2(x)[/math] Шенберг в построил такой алгоритм аппроксимации с помощью Д-сплайнов, в котором узлы сплайна сдвинуты относительно узлов сеточной функции. Для нахождения параметров этого сплайна глобальным способом получается трехдиагональная система линейных алгебраических уравнений с преобладанием диагональных элементов. Однако такая модификация существенно усложняет расчетные формулы алгоритма, и в ней используется дополнительное, обычно в задачах не требующееся условие непрерывности производных в серединах отрезков между узлами интерполяции. В ряде случаев это дополнительное требование может привести к непредсказуемому снижению точности аппроксимации и к отсутствию сходимости.

Рассмотрим принцип построения параболических дифференциальных сплайнов со сдвигом узлов сплайна. Пусть исходная функция [math]y_i= f(x_i),

i=overline[/math] , задана в узлах [math]x_iin [a,b][/math] , называемых узлами интерполяции и принадлежащими некоторой сетке [math]Deltacolon, a=x_0 . Введем также в рассмотрение другую сетку [math]overlinecolon, a=overline_0 , узлы которой сдвинуты по отношению к узлам сетки [math]Delta[/math] влево, так что [math]x_ .

Функция [math]textstyle<S_2(x)= bigcuplimits_^ S_(x)>[/math] называется интерполяционной параболической сплайн-функцией, интерполирующей [math]f(x_i)[/math] на сетке [math]Delta[/math] и принадлежащей классу гладкости [math]C_1[a,b][/math] , если она составлена из совокупности звеньев [math]S_(x)

(i=overline)[/math] , определенных на каждом частичном отрезке [math][overline_i, overline_][/math] сетки [math]overline[/math] и представленных в виде алгебраических многочленов второй степени:

где [math]a_[/math] — коэффициенты, которые находятся из дифференциальных условий согласования

где [math]p_1=0[/math] или [math]p_1=1[/math] . Звенья затем стыкуются по условию непрерывности (стыковки):

с порядками [math]p_2[/math] , отличными от [math]p_1[/math] , но такими, что [math]0leqslant p_2 leqslant2[/math] .

В соответствии с этим определением приведем два сплайна [math]S_2(x)[/math] и [math]overline_2(x)[/math] и рассмотрим алгоритм построения одного из них , а именно [math]S_2(x)[/math] . Для некоторого отрезка [math][overline_i, overline_][/math] формула [math]S_(x)[/math] имеет вид (4.80)

На отрезке [math][overline_i, overline_][/math] для определения [math]a_,, a_,, a_[/math] используются условия согласования (4.81):

Для простоты предположим, что узлы сплайна расположены в серединах отрезков [math][x_i, x_],

i=overline[/math] , составленных по узлам интерполяции.

На рис. 4.12 изображена схема расположения узлов сетки [math]overline[/math] по отношению к узлам сетки [math]Delta[/math] . Между шагами сеток [math]Delta[/math] и [math]overline[/math] в этом случае существует простая связь [math]overline_= frac+ frac<h_>= fracH_^[/math] .

Из условия [math]delta S’_(overline_i)=0[/math] следует равенство [math]a_= overline_i

(overline_i= f'(overline_i))[/math] , а из условия [math]delta S’_ (overline_)=0[/math] вытекает, что [math]overline_i+ 2a_ fracH_^= overline_;

Итак, звено сплайна [math]S_(x)[/math] на произвольном отрезке [math][overline_i, overline_][/math] выражается формулой

Подставив (4.83) в (4.82), получим параметрическую систему относительно [math]overline_icolon[/math]

где [math]H_^= 2h_+h_i[/math] . Система (4.84) обладает свойством преобладания диагональных элементов, но она незамкнута, так как число неопределенных параметров равно [math]n+2[/math] . В качестве двух дополнительных уравнений (граничных условий) могут быть приняты значения производных, аппроксимированных на концах со вторым порядком аппроксимации:

где [math]overline_^= overline_n+ overline_,

overline_i= f(overline_i)[/math] . Здесь шаги [math]overline_1, overline_2, overline_, overline_n, overline_[/math] и их комбинации взяты на сетке [math]overline[/math] . После определения всех параметров [math]overline_i[/math] их подставляют во все звенья [math]S_(x),

i=overline[/math] , из которых затем формируется результирующая многозвенная сплайн-функция [math]S_2(x)[/math] , имеющая минимальный дефект [math]q=1[/math] .

При [math]h=text[/math] формулы (4.83), (4.84), (4.85) упрощаются:

Здесь вместо сетки [math]overline[/math] используется равномерная сетка [math]overline_<mathsf>= bigl(overline_<0 mathsf>, overline_1, ldots, overline_n, overline_<n+1 mathsf>bigr)[/math] , где [math]overline_<0 mathsf>=a-frac,[/math] [math]overline_<n+1 mathsf>= b+frac[/math] — дополнительные узлы; [math]overline_<0 mathsf>= f(overline_<0 mathsf>),

Другой параболический сплайн [math]overline_(x)[/math] интерполяционного типа приведен некоторыми авторами, и он построен для более общего случая, когда узлы [math]overline_i[/math] не совпадают с серединами отрезков [math][x_i, x_][/math] . При этом [math]overline_ (x)[/math] записывается для отрезка [math][x_i, x_][/math] с узлами интерполяции [math]x_i,, x_colon[/math]

где, как и раньше, [math]x_ , а

Здесь коэффициенты при [math](x-x_0)^0[/math] и [math](x-x_i)^1[/math] найдены с учетом условий согласования [math]delta overline_(x_i)=0[/math] и [math]delta overline_ (x_i)=0[/math] . Коэффициенты [math]c_i[/math] и [math]d_i[/math] определяются из аналогичных условий согласования, но заданных в точке [math]x_[/math] отрезка [math][x_i, x_]colon[/math]

Тогда для получения связи определенных и неопределенных параметров используется условие стыковки (4.82) при [math]p_2=2[/math] , т.е. условие непрерывности второй производной в точке [math]x_icolon

Подставляя в выражение [math]c_+d_=c_i[/math] соотношения (4.89), получаем систему линейных алгебраических уравнений относительно параметров [math]overline_i

В качестве двух недостающих условий могут быть взяты аппроксимационные выражения (4.85). Случаи задания других типов краевых условий здесь не рассматриваются.

Отметим, что алгоритм построения рассмотренного сплайна является достаточно сложным, так как [math]overline_(x)[/math] имеет дополнительное слагаемое [math]d_i(x-overline_)_^2[/math] , а коэффициенты сплайна и системы (4.90) зависят от шагов [math]h[/math] и [math]overline[/math] , характеризующих две сетки [math]Delta[/math] и [math]overline[/math] , которые также достаточно сложны. Кроме того, требование непрерывности второй производной, присущее сплайну второй степени, может привести не к улучшению качества аппроксимации, а к ее ухудшению, так как эта производная для [math]overline_(x)[/math] является константой.

Методика построения параболического сплайна аналогична методике, изложенной ранее для кубических сплайнов.

Замечание. Использование интегрального подхода (ИД-сплайна) позволяет строить устойчивые алгоритмы аппроксимации функций параболическими сплайнами без смещения узлов сплайна относительно узлов интерполяции. Кроме того, эти сплайны являются консервативными, в том смысле, что интегралы от [math]S_2(x)[/math] и [math]y_i= f(x_i)[/math] равны как на [math][a,b][/math] , так и на всех частичных отрезках [math][x_i, x_]

(i=overline)[/math] . С помощью интегрального подхода могут быть построены замкнутые алгоритмы аппроксимации сплайнами произвольной четной степени.

Для сеточного представления функции [math]y=x^3[/math] , то есть [math]y_i=x_i^3

(i=overline)[/math] , найти интерполяционную параболическую сплайн-функцию [math]S_2(x)[/math] со сдвигом узлов на основе формул (4.86).

Решение. Для построения равномерной сетки [math]overline_<mathsf>[/math] введем в рассмотрение фиктивные узлы [math]overline_<0 mathsf>=-5!!not<phantom>,2[/math] и [math]overline_<5 mathsf>=5!!not<phantom>,2[/math] со значениями функции [math]overline_<0 mathsf>=15,!625[/math] и [math]overline_<5 mathsf>= 15,!625[/math] . Таким образом, будем определять сплайн [math]S_2(x)[/math] на отрезке [math][-2,!5; 2,!5][/math] с сетками

1. Запишем систему (4.86):

2. Вычислим значения производных на концах отрезка [math][-2,!5; 2,!5]colon[/math]

Составим трехдиагональную систему относительно [math]overline_colon[/math]

Решим систему методом прогонки. В результате получаем значения производных [math]overline_[/math] (табл. 4.21).

3. Построим многозвенную (в данном случае пятизвенную) сплайн-функцию [math]S_2(x)[/math] . Для простоты ограничимся построением многочлена только для одного звена [math]S_(x)colon[/math]

Остальные звенья строятся аналогично.

Видео:9. Метод вариации произвольной постоянной ( метод Лагранжа ). Линейные дифференциальные уравнения.Скачать

Восстанавливающие, интерполяционные и сглаживающие интегрально-дифференциальные параболические сплайны

Ранее были приведены два интегрально-дифференциальных многочлена (4.37) (4.41), которые могут использоваться для интерполяции и сглаживания некоторых функций, заданных своими значениями и интегралами, либо интегралами и производными.

Здесь рассмотрим основанные на этих многочленах глобальные способы конструирования различных параболических ИД-сплайнов дефекта [math]q=1[/math] , позволяющие восстанавливать некоторую функцию либо ее сглаживать. Рассмотрим применение многочлена (4.37).

Построение восстанавливающих сплайнов (задача 1)

Пусть некоторая сеточная функция определена не значениями [math]f_i[/math] в узлах [math]x_i[/math] в общем случае неравномерной сетки [math]Omega_n[/math] , а значениями интегралов [math]I_^

(i=overline)[/math] .Требуется восстановить эту функцию путем построения сплайн-функции [math]widetilde_<2,mathsf>(x)[/math] дефекта [math]q=1[/math] .

Для решения этой задачи воспользуемся параболическим многочленом (4.37). Для получения [math]widetilde_<2,mathsf>(x)[/math] при известных параметрах [math]I_^

(i=overline)[/math] необходимо сначала определить функциональные параметры [math]f_i

(i=overline)[/math] . Сплайн, составленный из звеньев (4.37), при любых значениях [math]f_i[/math] обеспечивает непрерывность [math]widetilde_<2,mathsf>(x)[/math] . Поэтому для получения параметрической связи между [math]f_i[/math] и [math]I_^[/math] используются условия стыковки [math]widetilde_<2,mathsf>(x)[/math] по первым производным:

Преобразование (4.91) после подстановки многочлена (4.37) приводит к параметрической системе линейных алгебраических уравнений относительно [math]f_icolon[/math]

Из сопоставления систем (4.92) и (4.76), являющихся следствием условий стыковки параболических ИД-сплайнов и кубических Д-сплайнов, видно, что они являются подобными. Действительно, обе системы имеют одинаковые коэффициенты, а параметры в них, входящие в левую и правую части, подобны друг другу, так как различаются только порядком [math]p[/math] . Если их представить в виде [math]f_k^

(k=i-1,i,i+1)[/math] и считать [math]p=-1[/math] для [math]I_^= Delta F_i= F_-F_i[/math] ( [math]F(x)[/math] — первообразная, [math]F_i= F(x_i)[/math] ), то все порядки параметров, входящих в систему (4.76), будут на единицу больше соответствующих порядков параметров системы (4.92). Рассмотренные соотношения соответствуют также подобным звеньям (4.75) и (4.37), относящимся к кубическим и параболическим сплайнам. Действительно, звено параболического сплайна может быть получено путем дифференцирования звена кубического сплайна (4.75) и замены параметров [math]overline_i,, Delta f_i,, Delta overline_i[/math] на [math]f_i,, I_^= Delta F_i,, Delta f_i[/math] .

Вернемся к задаче построения параболического сплайна. В качестве граничных условий, замыкающих систему (4.92), используем интегрально-функциональные связи:

являющиеся подобными (4.77) и полученные разрешением системы (4.92) и соотношений [math]a_= a_,

k=0;1[/math] и [math]k=n;n-1[/math] —коэффициенты при [math](x-x_i)^2[/math] (последние равенства для коэффициентов справедливы в силу постоянства второй производной на двух соседних отрезках). Подчеркнем, что соотношения (4.93) не нарушают трехдиагональности системы (4.92) и имеют порядок аппроксимации, равный трем, что соответствует порядку сходимости выстраиваемых ИД-сплайнов.

Разрешение системы (4.92), (4.93) методом прогонки, достаточное условие устойчивости которого для данной системы выполняется безусловно, т.е. при любых разбиениях, позволяет вычислить [math]f_i

(i=overline)[/math] (параметрически прямая задача). Подстановка [math]f_i,, I_^[/math] в формулу (4.37) для звеньев [math]i=overline[/math] определяет интегрально-дифференциальную сплайн-функцию [math]S_<2,mathsf>(x)[/math] восстанавливающего типа.

Из подобия параболического ИД-сплайна [math]S_<2,mathsf>(x)[/math] Д-сплайну [math]overline_3(x)[/math] и возможности его получения путем дифференцирования кубического Д-сплайна, а также на основе соотношения (4.78), устанавливающего порядок сходимости Д-сплайна [math]overline_3(x)[/math] , можно получить оценку порядка сходимости параболического ИД-сплайна [math]S_<2,mathsf>(x)colon[/math]

свидетельствующую о сходимости [math]S_<2,mathsf>(x)[/math] с третьим порядком [math](p=0)[/math] , а производных [math]S_<2,mathsf>^(x)[/math] с порядком [math](3-p),

Методика получения восстанавливающих сплайнов аналогична изложенной выше для кубического сплайна. Приведем пример построения глобального интегрально-дифференциального сплайна для функции, заданной интегралами на частичных отрезках.

Пусть исходная функция задана значениями интегралов на частичных отрезках [math][x_i;x_],

i=overline[/math] (табл. 4.22). Требуется найти восстанавливающий сплайн [math]widetilde_<2,mathsf>(x)[/math] дефекта [math]q=1[/math] .

Решение. 1. Запишем систему (4.92) для внутренних узлов [math]x_i

(i=overline)[/math] . При этом учтем, что шаг сетки постоянный:

Данная система замыкается условиями (4.93), записанными также при [math]h=textcolon[/math]

(i=0),\ & 2f_3+ f_4= frac! left(frac I_2^3+ frac I_3^4right)

2. Подставляя [math]h=1[/math] и значения интегралов в правые части, получаем систему линейных алгебраических уравнений, которую в соответствии с методом прогонки можно записать в виде

(i=overline),quad alpha_0= gamma_4=0.[/math]

Коэффициенты системы, прогоночные коэффициенты [math]P_i,, Q_i[/math] и результат решения системы методом прогонки приведены в табл. 4.23.

4.23>>\hline i& alpha_i& beta_i& gamma_i& delta_i& P_i& Q_i& f_i\hline 0&0&-1&2&2,!000&-2&2,!000& 0,!94418\hline 1&1&-4&1&20,!000&-1!!not<phantom>,2& 9,!000&0,!52791\hline 2&1&-4&1&155,!000&-2!!not<phantom>,7&41,!714&16,!94418\hline 3&1&-4&1&611,!089&-7!!not<phantom>,26&153,!293&86,!69534\hline 4&2&-1&0&420,!574&-&246,!974& 247,!36348\hline end[/math]

3. Подставляя значения [math]f_i[/math] и [math]nabla I_^= I_^-f_ih[/math] в формулу (4.37) на каждом отрезке [math][x_i, x_],

i=overline[/math] , находим искомый параболический восстанавливающий сплайн.

Для первого и второго отрезков получаем следующие функции:

Для остальных двух отрезков выполняются аналогичные действия. Легко убедиться в том, что полученная сплайн-функция имеет дефект [math]q=1[/math] , т.е. первая производная во внутренних узлах [math]x_1,,x_2,,x_3[/math] непрерывна. Таким образом, для [math]x_1[/math] имеем

Аналогичное условие выполняется и для других оставшихся узлов.

Видео:Метод Лагранжа & Метод Бернулли ★ Решение линейных неоднородных дифференциальных уравненийСкачать

Построение интерполяционных сплайнов (задача 2)

Пусть на равномерно сгущающейся или разрежающейся сетке [math]Omega_n[/math] заданы значения сеточной функции [math]f_i=f(x_i),

i=overline[/math] . Требуется восполнить эту функцию глобальным интерполяционным интегрально-функциональным сплайном [math]S_<2,mathsf>^<(mathsf)>(x)[/math] дефекта [math]q=1[/math] .

Решение этой задачи осуществляется путем объединения многочленов-звеньев (4.37) после определения интегралов [math]I_^[/math] , выраженных из (4.92) по рекуррентным право- и левосторонним соотношениям (параметрически обратная задача):

где [math]L_i(h,f)= fracf_+ 2! left(frac+ frac<h_>right)!f_i+ frac<h_>f_[/math] — функция, равная сумме «удельных интегралов» по каждой паре смежных отрезков, [math]delta_= h_!!not<phantom>,h_i[/math] — параметр, характеризующий неравномерность сетки, который называется параметром нерегулярности. Соотношения (4.95), (4.96) записаны в виде, учитывающем характер задания сеточной функции на неравномерной сетке, которая, по предположению, либо равномерно сгущается вправо, либо равномерно разрежается. Тогда (4.95) соответствует правостороннему обратному ходу метода прогонки, а (4.96) — левостороннему обратному ходу. Необходимость такого порядка действий обусловлена достаточным условием устойчивости прогонки [math]delta_leqslant1[/math] для (4.95) и [math]delta_^leqslant1[/math] для (4.96). Заметим, что в данном случае выполняется только обратный ход метода прогонки. Соотношения (4.95), (4.96) при [math]f(x)in C_m[a,b]

(m geqslant 3)[/math] обеспечивают четвертый порядок точности вычисления интегралов.

В качестве краевых (граничных) условий для право- и левостороннего соотношений значения интегралов [math]I_0^i[/math] и [math]I_^n[/math] вычисляются по одноинтервальным, трехточечным, лево- и правосторонним квадратурным формулам:

При [math]h=text[/math] (сетка [math]Omega_n[/math] равномерная) данные формулы упрощаются:

В некоторых работах показано, что квадратурные формулы (4.97), (4.98) обеспечивают четвертый порядок аппроксимации интегралов на трехточечном шаблоне [math](x_, x_i, x_)[/math] , и поэтому порядок аппроксимации [math]I_^[/math] соотношением (4.95) или (4.96) при фиксированном [math]i[/math] за счет краевых условий не понижается. Показано также, что в данном способе построения интерполяционного сплайна достигается третий порядок сходимости. Однако способ имеет недостаток, состоящий в том, что при аппроксимации негладких функций ошибки, возникающие при расчете интегралов по формулам (4.95) или (4.96), переносятся на последующие значения. Данный недостаток устранен в задаче построения слабо сглаживающего параболического сплайна.

Построение сглаживающих сплайнов (задача 3)

Пусть в общем случае на неравномерной сетке Пп задана сеточная функция, определенная, например, в физическом эксперименте с достаточно большими погрешностями, определяющими разброс значений [math]f(x_i)[/math] , то есть [math]f(x_i)pm varepsilon_i

(i=overline)[/math] , где е, намного превышают величину [math]O(h_^3)[/math] .

Требуется восполнить эту функцию параболическим сглаживающим сплайном [math]S_<2, mathsf>(x)[/math] дефекта [math]q=1[/math] .

Поставленная задача решается глобальным способом путем сведения ее к задаче 1. Рассмотрим его особенности.

Сначала путем визуального изучения исходной функции [math]y_i= f(x_i)pm varepsilon_i[/math] исследователь-вычислитель формирует «полосу разброса» данных, офаниченную двумя функциями — «верхней» [math]y_i^<mathsf>= widehat^<(mathsf)>(x_i)[/math] и «нижней» [math]y_i^<mathsf>= widehat^<(mathsf)>(x_i)[/math] (на рис. 4.13 квадратиками условно показаны значения, полученные, например, в результате физического эксперимента). Если на некоторых участках разброс данных не заметен, функции [math]y_i^<mathsf>= widehat^<(mathsf)>(x_i),

y_i^<mathsf>= widehat^<(mathsf)>(x_i)[/math] могут быть совмещены друг с другом. В случае отсутствия значений [math]f(x_i)[/math] на концах отрезка [math][a,b][/math] они определяются приближенно путем линейной или параболической экстраполяции.

Далее на каждом отрезке [math][x_i,x_],

i=overline[/math] , по формулам (4.97) или (4.98) вычисляются интегралы [math]I_^<i+1(mathsf)>[/math] и [math]I_^<i+ 1(mathsf)>[/math] для функций [math]y_i^<mathsf>= widehat^<(mathsf)>(x_i)[/math] и [math]y_i^<mathsf>= widehat^<(mathsf)>(x_i)[/math] соответственно. Недостающие значения функций на линиях, ограничивающих «полосу разброса», определяются путем дополнительной интерполяции. Следует также учесть, что интеграл [math]I_0^1[/math] на отрезке [math][x_0,x_1][/math] вычисляется по левосторонней формуле (4.97), интеграл [math]I_^n[/math] на отрезке [math][x_,x_n][/math] — по правосторонней, а интегралы по всем внутренним отрезкам могут рассчитываться по любой из формул (4.97), (4.98).

(i=overline)[/math] по всем частичным отрезкам находятся их средние значения на каждом частичном отрезке:

Полученные значения интегралов [math]I_^[/math] используются далее в качестве исходных данных для решения задачи 1.

Таким образом, существенной особенностью сглаживающих сплайнов данного типа является формирование «полосы разброса», включающей все экспериментальные данные, которые затем двукратно усредняются. При этом в отличие от метода наименьших квадратов с помощью данного метода реализуется более полный учет локальных свойств аппроксимируемой функции.

Слабо сглаживающие интерполяционные интегрально-дифференциальные параболические сплайны

Пусть в общем случае на неравномерной сетке [math]Omega_n[/math] задана сеточная функция [math]y_i= f(x_i),

i=overline[/math] , определенная либо в численном эксперименте, либо путем измерений с небольшими погрешностями [math]varepsilon_i[/math] , не превышающими [math]O(h_^3)[/math] .

Применительно к данной задаче вводится понятие слабого сглаживания, в котором учитывается характер задания исходной функции с некоторой погрешностью, не превышающей [math]O(h_^3)[/math] . При этом допускается возможность отклонения получаемой в алгоритме сплайн-функции в узлах [math]widetilde_<2, operatornamek>^<(text)>(x_i)[/math] от [math]f(x_i)[/math] на величину не более [math]O(h_^3)[/math] , т.е. реализуется отклонение [math]max bigl|widetilde_<2, operatornamek>^<(text)>(x)-f(x)bigr|= O(H^3)[/math] по всему отрезку [math][a,b][/math] , включая и узлы интерполяции. Здесь индекс [math]k[/math] ( [math]k=1[/math] или [math]k=2[/math] ) соответствует способу построения сплайна. Подчеркнем, что для традиционных интерполяционных сплайнов данное отклонение в узлах отсутствует.

Требуется восполнить данную функцию параболическим интерполяционным слабо сглаживающим сплайном [math]widetilde_<2, operatornamek>^<(text)>(x)

(k=1;2)[/math] , компонующимся на основе ИД-многочленов (4.37) или (4.41).

Обоснованность такого расширения понятия интерполяции (дополнение его понятием слабого сглаживания) обусловлена следующими причинами.

1. Интерполяционные сплайн-функции, как и классические интерполяционные многочлены, часто применяются для восполнения и обработки сеточных функций, рассчитанных методами сеток второго и третьего порядка, и потому данные функции (исходные для задачи аппроксимации) неточные, и их погрешность обычно составляет [math]O(h_^3)[/math] . Поэтому применение условий интерполяции, обеспечивающих нулевые невязки в узлах, вообще говоря, не является оправданным.

2. Если даже значения исходной функции заданы точно (хотя класс задач, в которых значения [math]f(x_i)[/math] являются точными, указать трудно), то точность сплайн-интерполяции из-за этого не повышается. Для параболических сплайн-функций порядок сходимости оценивается как третий, а для кубических — как четвертый.

Построение слабо сглаживающего параболического ИД-сплайна может быть осуществлено так же, как и построение кубического дифференциального сплайна двумя способами, различающимися порядками производных, заданных в условиях согласования и условиях стыковки. Это соответствует отмеченному выше принципу подобия дифференциальных и интегрально-дифференциальных сплайнов, описывающихся формулами (4.75) и (4.37). Аналогично легко показать подобие Д-сплайнов (4.71) и (4.41).

Поэтому, так же как и для Д-сплайнов, здесь рассматриваются два сглаживающих интегрально-дифференциальных сплайна [math]widetilde_<2, operatorname1>^<(text)>(x)[/math] и [math]widetilde_<2, operatorname2>^<(text)>(x)[/math] .

Первый способ решения задачи слабого сглаживания (построение сплайна [math]widetilde_<2, operatorname1>^<(text)>[/math] ). Алгоритм восполнения функции [math]y_i= f(x_i)[/math] методом слабого сглаживания аналогичен алгоритму восстановления сеточной функции в задаче 1 и основан на формуле ИД-многочлена (4.37), принимаемой в качестве общей формулы звена искомого сплайна и параметрической системы (4.92), которые имеют вид

Волнистая черта указывает на отличие используемых значений [math]widetilde_i[/math] от значений [math]f_i[/math] исходной функции. В правой части равенства (4.100) обе группы параметров [math]widetilde_i

(i=overline)[/math] считаются неопределенными. При этом сначала вычисляются интегралы [math]I_^[/math] на всех частичных отрезках [math][x_i, x_]

(i=overline)[/math] по одной из явных квадратурных формул (4.97) или (4.98). После этого проводится пересчет функциональных параметров из системы (4.101), которая замыкается связями [math]widetilde_0, widetilde_1,, I_0^1,I_1^2[/math] и [math]widetilde_, widetilde_n,, I_^, I_^n[/math] (граничными условиями) соответственно на левом и правом краях отрезка [math][a,b]colon[/math]

совпадающими с граничными условиями, принятыми в задаче 1. Отметим, что оба типа неопределенных параметров находятся путем решения смешанной параметрической задачи, так как сначала определялись интегралы [math]I_^

(p=-1)[/math] , а затем значения функции [math]widetilde_i

(i=overline)[/math] из (4.101), (4.102), подстановка [math]widetilde_i

(i=overline)[/math] в (4.100) для всех звеньев и их объединение в общую формулу [math]widetilde_<2, operatorname1>^<(text)>(x)[/math] завершают решение задачи слабого сглаживания исходной приближенно заданной сеточной функции, погрешность определения которой в узлах не превышает [math]O(h_^3)[/math] . Если же погрешность задания исходной сеточной функции больше [math]O(h_^3)[/math] , to погрешность вычисления интегралов превысит величину [math]O(h_^3)[/math] и третий порядок точности аппроксимации [math]widetilde_<2, operatorname1>^<(text)>(x)[/math] не будет достигнут.

Первый способ решения задачи аппроксимации слабо сглаживающим сплайном является сходным с решением задачи 2 о восполнении сеточной функции интерполяционным интегрально-функциональным сплайном [math]widetilde_<2, operatorname1>^<(text)>(x)[/math] . Различие состоит в том, что для [math]widetilde_<2, operatorname1>^<(text)>(x)[/math] неопределенными параметрами являются только [math]I_^

(i=overline)[/math] , а определенными — значения [math]f_i

(i=overline)[/math] , и они не изменяются при решении задачи. Таким образом, задача 2 решается проще, однако изложенный способ построения сглаживающего сплайна характеризуется большей устойчивостью, так как он основан на решении трехдиагональной системы линейных алгебраических уравнений, которая удовлетворяет условию преобладания диагональных элементов.

Теорема 4.3 (о сходимости глобального параболического ИД-сплайна [math]widetilde_<2, operatorname1>^<(text)>(x)[/math] ). Пусть функцию [math]f(x),

xin[a,b][/math] , определенную в общем случае на неравномерной сетке [math]Omega_n

H=max_h_iright)[/math] с параметром неравномерности [math]D= max_<i=overline>h_i !!not<phantom>, max_<i=overline>h_i[/math] , аппроксимирует глобальный параболический слабо сглаживающий ИД-сплайн [math]widetilde_ <2, operatorname1>^<(text)>(x)[/math] . Тогда, если [math]f(x)in C_3[a,b][/math] и интегралы [math]I_^

(i=overline)[/math] находятся по квадратурным формулам (4.97) или (4.98), a [math]widetilde_i

(i=overline)[/math] — из трехдиагональной системы (4.101), (4.102), то справедливы оценки

где [math]p[/math] — порядок производной, [math]M_3= max_ bigl|f»'(x)bigr|[/math] , а константы имеют значения

Таким образом, при [math]f(x)in C_3[a,b][/math] слабо сглаживающие сплайны [math]widetilde_<2, operatorname1>^<(text)>(x)[/math] равномерно сходятся к функции [math]f(x)[/math] на последовательности сеток

с возрастающим разбиением [math]k[/math] отрезка [math][a,b]colon, k_1=1, k_2=2, ldots, k_n=n[/math] и т.д. по крайней мере с кубичной скоростью, а их производные [math]widetilde‘_<2, operatorname1>^<(text)> (x)[/math] с ростом [math]n[/math] равномерно сходятся к [math]f'(x)[/math] по крайней мере с квадратичной скоростью.

Второй способ решения задачи слабого сглаживания (построение сплайна [math]widetilde_<2, operatorname2>^<(text)>(x)[/math] ). Алгоритм восполнения функции [math]y_i= f(x_i)[/math] в данной задаче основан на формуле ИД-многочлена (4.41), принимаемой в качестве общей формулы звена искомого сплайна, и на трехдиагональной параметрической системе, вытекающей из условия непрерывности сплайна [math]widetilde_<2, operatorname2, i>^<(text)>(x)colon[/math]

где [math]overline_i= f'(x)[/math] . Подчеркнем, что формула (4.104) для [math]widetilde_<2, operatorname2, i>^<(text)>(x)[/math] и параметрическая система являются подобными соответствующим соотношениям кубического дифференциального сплайна [math]S_3(x)[/math] (4-70 и (4.72), в которых порядки всех параметров повышены на единицу.

Аналогично первому способу будем считать, что все параметры, входящие в (4.104), являются неопределенными. Их значения находятся из смешанной параметрической задачи, в которой вначале по формулам (4.97) или (4.98) определяются интегралы [math]I_^

(i=overline)[/math] , а затем с использованием системы (4.105) трехдиагонального типа методом прогонки — производные [math]overline_i

(i=overline)[/math] . Для замыкания (4.105) можно использовать два различных подхода.

В рамках первого подхода производные на концах отрезка [math][a,b][/math] определяются по аппроксимационным формулам второго порядка аппроксимации:

Во втором подходе при [math]h_= text[/math] система (4.105) замыкается двумя трехточечными соотношениями:

вытекающими из условия равенства второй производной на двух первых и последних частичных отрезках.

В случае, когда [math]h=text[/math] (сетка равномерная), производные на концах могут быть определены также и путем интегральных аппроксимаций:

Выбор конкретных типов граничных условий обусловливается особенностью постановки задачи и свойствами аппроксимируемой функции.

Построение слабо сглаживающего сплайна завершается так же, как и в первом способе. Отличительной особенностью второго способа является то, что при решении смешанной параметрической задачи (ее прямой части) вычисляются не сами функции [math]f_i[/math] , а их производные. Иногда это более удобно, например, когда в задаче восполнения требуется найти значения производных в узлах.

Выбор конкретного алгоритма сглаживания зависит от априорной информации, от аппроксимируемой функции и от требований к выходным данным.

В заключение отметим, что для сглаживающего сплайна [math]widetilde_ <2, operatorname2>^<(text)>(x)[/math] как и для сплайна [math]widetilde_ <2, operatorname1>^<(text)>(x)[/math] , имеет место третий порядок сходимости.