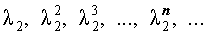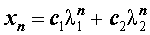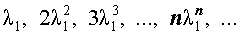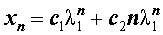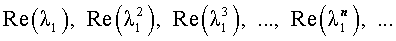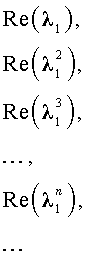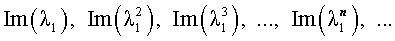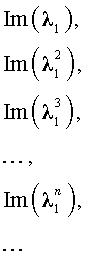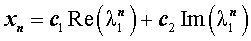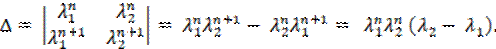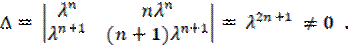рекуррентная формула, характеристическое уравнение
 Определение возвратной последовательности Определение возвратной последовательности |
 Характеристическое уравнение Характеристическое уравнение |
 Общее решение рекуррентного уравнения 2-го порядка Общее решение рекуррентного уравнения 2-го порядка |
 Схема вывода формулы общего члена возвратной последовательности второго порядка Схема вывода формулы общего члена возвратной последовательности второго порядка |
 Примеры с решениями Примеры с решениями |
- Определение возвратной последовательности
- Характеристическое уравнение
- Общее решение рекуррентного уравнения второго порядка
- Рекуррентные соотношения и уравнения
- Как решать рекуррентные соотношения?
- Метод производящих функций
- Метод характеристических функций
- Решение для последовательности чисел Фибоначчи
- Способ 1. Производящяя функция
- Способ 2. Характеристическое уравнение
- Примеры решений
- Рекуррентное уравнение 2 го порядка
- 🎬 Видео
Видео:ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

Определение возвратной последовательности
в каждой из которых символами b1 и q обозначены заданные числа – первый член и знаменатель прогрессии.
Определение . Пусть k – натуральное число. Возвратной (рекуррентной) последовательностью порядка k называют последовательность, для задания которой требуется задать первые её k членов, т.е. числа
а остальные члены последовательности определяются с помощью рекуррентной формулы (рекуррентного уравнения)
– заданные числа ( коэффициенты рекуррентной формулы ).
Замечание 1 . Числа
называют начальными условиями .
Замечание 2 . Для упрощения вычислений везде в дальнейшем будем рассматривать только случай возвратных последовательностей 2-го порядка, все члены которых являются вещественными числами.
Для задания таких последовательностей требуется задать их первые два члена, то есть вещественные числа x1 и x2 , а остальные члены последовательности
| xn = q1 xn – 1 + q2 xn – 2 , n > 2 , | (1) |
Видео:Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.Скачать

Характеристическое уравнение
Для того, чтобы получить характеристическое уравнение возвратной последовательности (1), будем искать такие числа λ , при которых последовательность вида
| xn = λ n | (2) |
удовлетворяет рекуррентной формуле (1).
| xn – 1 = λ n – 1 , xn – 2 = λ n – 2 , | (3) |
то при подстановке формул (2) и (3) в формулу (1) возникает уравнение
которое удобно переписать в виде
| λ n – q1 λ n – 1 – – q2 λ n – 2 = 0 . | (4) |
Если теперь уравнение (4) разделить на λ n–2 , то мы получим квадратное уравнение относительно λ вида:
которое и называют характеристическим уравнением .
Видео:21.04 - дискра, рекуррентные соотношенияСкачать
Общее решение рекуррентного уравнения второго порядка
В случае, когда характеристическое уравнение имеет два различных вещественных корня λ1 и λ2 , каждая из последовательностей
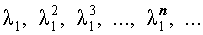
и
удовлетворяет рекуррентной формуле (1), поэтому для любых чисел c1 и c2 последовательность с общим членом
также удовлетворяет рекуррентной формуле (1).
Числа c1 и c2 называют произвольными постоянными .
В случае, когда характеристическое уравнение имеет два совпавших вещественных корня λ1 = λ2 , непосредственная проверка показывает, что каждая из последовательностей
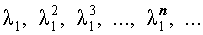
и
удовлетворяет рекуррентной формуле (1), поэтому для любых чисел c1 и c2 последовательность с общим членом
также удовлетворяет рекуррентной формуле (1).
В случае, когда характеристическое уравнение имеет два комплексно-сопряженных корня λ1, 2 = α ± i β, каждая из последовательностей
удовлетворяет рекуррентной формуле (1), поэтому для любых чисел c1 и c2 последовательность с общим членом
также удовлетворяет рекуррентной формуле (1).
Ряд примеров, в которых выводятся формулы общего члена возвратных последовательностей, разобран в разделе «Возвратные последовательности: вывод формулы общего члена» нашего справочника.
Видео:Решение неоднородного рекуррентного уравненияСкачать

Рекуррентные соотношения и уравнения
В этом разделе вы найдете бесплатные примеры решений рекуррентных соотношений методом характеристического уравнения и подбора частного решения по правой части. Также приведены краткие алгоритмы решения для двух методов и пример их использования для последовательности Фибоначчи.
Видео:Рекуррентное вычисление определителя порядка nСкачать

Как решать рекуррентные соотношения?
Для решения рекуррентных соотношений применяют один из двух основных способов:
- Метод производящих функций
- Метод характеристического уравнения
В следующем разделе мы сравним, как выглядит процесс решения для одной и той же последовательности двумя методами.
Метод производящих функций
- Записать рекуррентное соотношение и начальные данные для него в следующем виде (если порядок соотношения равен $k$) $$a_ = …, \ a_ = …, \ a_ = …, \ … \ a_ = …, ngeqslant k$$
- Домножить каждую строчку на $z$ в соответствующей степени $z^ cdot a_$ и сложить все выражения для $n ge 0$. В левой части получится сумма $displaystylesum_^ a_nz^n$ — это производящая функция, назовем ее $G(z)$. Правую часть преобразовать так, чтобы она превратилась в выражение, включающее $G(z)$.
- Решить полученное уравнение относительно $G(z)$.
- Разложить $G(z)$ в степенной ряд, тогда коэффициент при $z_n$ будет искомым выражением для $a_n$.
Метод характеристических функций
Этот метод практически полностью аналогичен методу решения линейных неоднородных дифференциальных уравнений с постоянными коэффициентами, кратко алгоритм выглядит так:
- Записать соответствующее однородное рекуррентное уравнение (РУ): $$ p_ a_ + p_a_ + . + p_n a_n =f to \ to p_ a_ + p_a_ + . + p_n a_n =0. $$
- Выписать для него характеристическое уравнение и найти его корни $lambda_i$ $$ p_ lambda^ + p_lambda^ + . + p_lambda + p_n =0. $$
- Выписать согласно полученным корням $lambda_1, . lambda_k$ общее решение однородного рекуррентного соотношения (подробнее теорию см. по ссылке [1] ниже). $$ C_1 lambda_1^n +. +C_k lambda_k^n , mbox , $$ $$ C_1 lambda_1^n + C_2 nlambda_1^n +. +C_m n^m lambda_1^n+. +C_k lambda_k^n mbox , lambda_1 , , m. $$
- Подобрать частное решение неоднородного рекуррентного соотношения по виду правой части (особенно удобно для правых частей вида $mu^n*P(n)$, $P(n)$ — многочлен от $n$).
- Представить общее решение неоднородного РУ как сумму общего решения соответствующего однородного РУ и частного решения неоднородного РУ.
- Подставить начальные условия $a_0, a_1, . a_$ и получить значения констант $C_1, . C_k$.
Видео:R-1 Рекуррентные соотношения: введениеСкачать

Решение для последовательности чисел Фибоначчи
Последовательность чисел Фибоначи — это последовательность, каждый элемент которой (кроме нулевого и первого) равен сумме двух предыдущих:
$$ 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 , . $$
Числа Фибоначчи растут быстро: $f_=55$, $f_=6765$, а $f_=354224848179261915075$.
Общая формула данной рекуррентной последовательности имеет вид6
Способ 1. Производящяя функция
Начинаем с второго шага алгоритма, домножаем на $z^n$:
$$begin 1cdot f_0 &= &0cdot 1,\ zcdot f_1 &= &1cdot z,\ zcdot f_n & = &(f_+f_)cdot z^n, quad ngeq2.\ end $$
Складываем все строчки:
На третьем шаге алгоритма приводим все суммы к замкнутому виду:
откуда выводим искомое выражение для производящей функции:
Теперь разложим ее в степенной ряд. Для этого сначала разложим знаменатель на множители. Найдем корни уравнения:
Чтобы разложить данные дроби в ряды, используем известное разложение для дроби:
Рассмотрим первую дробь и поделим в ней числитель и знаменатель на $z_1$:
Аналогично (но с делением на $z_2$) действуем со второй дробью:
Преобразуем данное выражение, используя то, что
$$1/z_1=-z_2, quad 1/z_2 = -z_1, quad z_1-z_2=sqrt $$ $$f_n=frac<sqrt>left( biggl( frac<1+sqrt> biggr)^n — biggl( frac<1-sqrt> biggr)^n right). $$
Способ 2. Характеристическое уравнение
Запишем характеристический многочлен для $f_n=f_+f_$, и найдем его корни:
Тогда общее решение однородного рекуррентного уравнения имеет вид:
Осталось найти значения произвольных постоянных $C_1, C_2$ из начальных условий $f_0=0, f_1=1$.
Решая систему, найдем
Итоговое выражение для последовательности чисел Фибоначчи:
Результаты обоих методов совпали, решение вторым методом оказалось проще и короче.
Видео:16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Примеры решений
Задача 1. Решить рекуррентное соотношение $f(n+2)=-6f(n+1)+7f(n)+n-3$ с начальными условиями $f(0)=2$ и $f(1)=4$, сделать проверку
Задача 2. Решить рекуррентное соотношение $f(n+2)=-2f(n+1)+3f(n)-3^n$ с начальными условиями $f(0)=1$, $f(1)=3$ и сделать проверку
Задача 3. 1. Решить рекуррентное соотношение $f(n+2) =-5f(n+1) -4f(n) + 3n^2$ с начальными условиями $f(0) = 2$, $f(1) = 3$.
2. Проверить, удовлетворяет ли найденное решение начальным условиям и обращает ли оно рекуррентное соотношение в справедливое тождество.
Задача 4. Найти последовательность $$, удовлетворяющую рекуррентному соотношению $a_ + 4 a_ + 3 a_ = 0$ и начальным условиям $a_1=2$, $a_2=4$.
Видео:Решение рекуррентных уравненийСкачать

Рекуррентное уравнение 2 го порядка
Индивидуальные онлайн уроки: Отправьте запрос сейчас: irina@bodrenko.org
Математика (ЕГЭ, ОГЭ), Английский язык (разговорный, грамматика, TOEFL)
Решение задач: по математике, IT, экономике, психологии
Дифференциальные и разностные уравнения
Тема лекции: «Разностные (рекуррентные) уравнения второго порядка»
1. Линейные разностные уравнения k -го порядка.
2. Линейные разностные уравнения второго порядка с постоянными коэффициентами.
3. Модели экономической динамики с дискретным временем.
1. ЛИНЕЙНЫЕ РАЗНОСТНЫЕ УРАВНЕНИЯ k -ГО ПОРЯДКА.
1.1. Определение разностного уравнения k -го порядка.
Теория разностных уравнений находит многообразные приложения во многих областях естествознания при моделировании поведения систем различной природы. Разностные уравнения обычно возникают тогда, когда рассматриваемая величина регистрируется через некоторые (как правило, равные) промежутки времени.
Например, так называемая паутинообразная модель рынка одного товара описывается разностным уравнением вида
где Pt — цена товара в период t , a и b — некоторые числа.
Уравнение (*) представляет собой линейное разностное уравнение первого порядка с постоянными коэффициентами.
В задачах описания, анализа и синтеза дискретных динамических систем управления математические модели таких систем описываются разнообразными разностными уравнениями.
В современной теории нелинейных колебаний разностные уравнения появляются либо самостоятельно, либо при переходе от дифференциальных уравнений к точечным отображениям Пуанкаре. Такой переход в трехмерном случае значительно упрощает исследование.
В математике основным источником разностных уравнений являются дифференциальные уравнения. Имеются в виду разностные схемы, используемые для приближенного решения дифференциальных уравнений.
Многие факты теории линейных дифференциальных уравнений верны и для линейных разностных уравнений, хотя есть и некоторые различия. Отличие разностных уравнений от дифференциальных уравнений проявляется в наибольшей степени, когда уравнения нелинейны. Например, поведение решений одномерных разностных уравнений может быть таким же сложным, как и поведение решений многомерных разностных уравнений. Для динамических систем, описываемых дифференциальными уравнениями, сложное поведение имеется лишь в пространствах большой размерности ( n > 3).
Приведем простейшие примеры разностных уравнений.
Разностное уравнение второго порядка
определяет признак арифметической прогрессии. Его решением является последовательность с общим членом
где a1 — первый член арифметической прогрессии, и d – разность арифметической прогрессии.
определяет признак геометрической прогрессии, и его решением является последовательность с общим членом
где b1 – первый член геометрической прогрессии, q – знаменатель геометрической прогрессии.
где k − фиксированное, а n − произвольное натуральное число, yn , yn+1 . yn+k – члены некоторой числовой последовательности, называется разностным уравнением k-го порядка.
Решить разностное уравнение означает найти его общее решение, т.е. все последовательности yn = y(n) , удовлетворяющие уравнению (1).
Разностные уравнения используются в моделях экономической динамики с дискретным временем, а также для приближенного решения дифференциальных уравнений.
Между теориями разностных и дифференциальных уравнений прослеживается определенная аналогия. Если в уравнении (1) произвести формальную замену:
то определение разностного уравнения преобразуется в общее определение обыкновенного дифференциального уравнения порядка k.
Проведя формальную замену (2), нетрудно получить нормальную форму записи разностного уравнения:
Аналогичным образом определяется и задача Коши – как задача нахождения решения уравнения (3), удовлетворяющего начальным условиям:
Ниже будет показано, что решения соответствующих классов дифференциальных и разностных уравнений (например, линейных) осуществляется схожими методами.
Теорема 1. Решение yn = y(n) задачи Коши (3), (4) при n ≥ n0 определено однозначно.
Доказательство. Подставляя значения для y(n0) , y(n0+1) , . , y (n0+ k−1) из (4) в (3), мы находим y(n0+k) . Это, в свою очередь, дает нам возможность определить y(n0+k+1) .
Продолжая этот процесс, можно рекуррентным способом по формуле (3) найти любое значение y(n) при n ≥ n0 . Теорема доказана.
Следует, однако, заметить, что нахождения общего решения разностного уравнения в отличие от задачи Коши является гораздо более сложной задачей.
1. 2. Линейные разностные уравнения k -го порядка.
Определение 2. Разностное уравнение вида
где a0 ,a1 . ak , f − некоторые функции от n (a0 ≠ 0, ak ≠ 0), называется линейным разностным уравнением k-го порядка.
Условие a0 ≠ 0 для всех n является существенным в определении линейного разностного уравнения первого порядка. Например, линейное разностное уравнение вида
не считается уравнением первого порядка, поскольку замена к+1 = m дает уравнение
которое условно можно назвать разностным уравнением нулевого порядка.
Введем следующее обозначение:
Это выражение называется линейным разностным оператором k-го порядка .
С учетом этих обозначений уравнение (6) может быть записано в виде:
называется линейным однородным разностным уравнением, соответствующим уравнению (7). Само же уравнение (7) (при f(n) ≠ 0) называется неоднородным .
Имеют место следующие утверждения.
Теорема 2 (об общем решении линейного неоднородного уравнения).
Общее решение линейного неоднородного разностного уравнения (7) есть сумма частного решения ȳ (n) этого уравнения и общего решения y 0( n ) соответствующего ему однородного уравнения (8).
Теорема 3 (об общем решении линейного однородного уравнения).
Пусть у (1) (n), . у (k) (n) – система, состоящая из k линейно независимых решений линейного однородного разностного уравнения (8), тогда общее решение этого уравнения задается формулой:
Множество решений линейного однородного разностного уравнения k-го порядка образует k- мерное линейное пространство, а любой набор у (1) (n), . у (k) (n) из k линейно независимых решений (называемый фундаментальным набором) является его базисом.
Признаком линейной независимости решений у (1) (n), . у (k) (n) однородного уравнения является неравенство нулю определителя Казорати:
∆ = det y n (1) ⋯ y n ( k ) ⋮ ⋱ ⋮ y n + k (1) ⋯ y n + k ( k ) 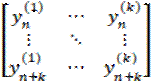
который является аналогом определителя Вронского в теории обыкновенных дифференциальных уравнений.
1.3. Линейные однородные разностные уравнения с постоянными коэффициентами k -го порядка.
В случае, когда коэффициенты a0 , a1 . ak являются постоянными, методы решения линейного однородного разностного уравнения
во многом аналогичны методам решения дифференциальных уравнений с постоянными коэффициентами.
Действительно, будем искать решения уравнения в виде:
где λ ≠ 0 – некоторая постоянная. Подставляя выражение для yn из (12) в (11), находим:
ak λ n + k + ak −1 λ n + k −1 + … + a 1 λ n +1 + a 0 λ n = 0 .
Разделим обе части этого уравнения на λ n , получим:
Уравнение (13) называется характеристическим уравнением однородного линейного разностного уравнения.
Так же, как и в случае линейных дифференциальных уравнений с постоянными коэффициентами, знание корней характеристического уравнения, позволяет построить общее решение однородного разностного уравнения.
2. ЛИНЕЙНЫЕ РАЗНОСТНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ.
Рассмотрим линейное разностное уравнение второго порядка с постоянными коэффициентами
Построим решения этого уравнения в зависимости от значения D = b 2 − 4 ac . Однако заметим, что полученные в этом случае результаты могут быть без труда перенесены на случай уравнений более высокого порядка.
В зависимости от значения дискриминанта
a λ 2 + b λ + c = 0 (15)
возможны следующие случаи.
Характеристическое уравнение (15) имеет два действительных и различных корня – λ1 и λ2 . Тогда λ1 ≠ 0 и λ2 ≠ 0 . Действительно, если хотя бы один корень равен нулю, то коэффициент приведенного квадратного уравнения (15`) c / a = λ1 λ2 также будет равен нулю, что противоречит определению линейного разностного уравнения второго порядка.
Корням λ1 и λ2 характеристического уравнения соответствуют два решения:
Покажем, что эти решения линейно независимы. Для этого вычислим определитель Казорати
∆ = det y n (1) ⋯ y n ( k ) ⋮ ⋱ ⋮ y n + k (1) ⋯ y n + k ( k )
В данном случае получим
∆ = λ 1 n λ 2 n λ 1 n +1 λ 2 n +1 = λ 1 n λ 2 n +1 — λ 2 n λ 1 n +1 = λ 1 n λ 2 n λ 2 — λ 1 .
Так как корни λ1 и λ2 различны, то λ2 − λ1 ≠ 0 , следовательно, ∆ ≠ 0 , а значит, решения линейно независимы.
В этом случае общее решение уравнения имеет вид:
где C1 , C2 – произвольные постоянные.
Решение примера 3.
Составим характеристическое уравнение, имеем:
Оно имеет два действительных различных корня: λ1 = 1 , λ2 = − 5 . Поэтому общее решение исходного уравнения в силу формулы (16) имеет вид:
Решение примера 4.
Составим характеристическое уравнение, имеем:
Оно имеет два действительных различных корня: λ1 = 3 , λ2 = 2 . Поэтому общее решение исходного уравнения в силу формулы (16) имеет вид:
Характеристическое уравнение имеет два комплексно сопряженных корня: λ1 и λ2 ,
которые, используя тригонометрическую форму записи, могут быть представлены следующим образом:
где r – модуль λ1 , а φ – его аргумент:
Соответствующие решения разностного уравнения также комплексно сопряжены и на основании формулы Муавра имеют вид:
y (1) n = r n (cos n φ + i sin n φ ) , y (2) n = r n (cos n φ − i sin n φ ) .
Чтобы получить действительные решения, заменим y n ( 1 ) и y n ( 2 ) их линейными комбинациями:
Таким образом, мы получили два линейно независимых действительных решения:
z (1) n = r n cos(n φ ) , z (2) n = r n sin(n φ ) .
Таким образом, в данном случае общее решение имеет вид:
y(n) = r n ( C1 cos (n φ )+ C2 sin (n φ ) ) . (17)
Решение примера 5.
имеет два комплексно сопряженных корня –
которые могут быть записаны как:
λ 1 = 2 (cos ( π /3) + i sin( π /3)), λ 2 = 2 (cos ( π /3) – i sin( π /3))
Следовательно, общим решением исходного уравнения в силу формулы (17) будет:
Оба корня характеристического уравнения действительны и равны ( λ1 = λ2 = λ ) .
Покажем, что в этом случае кроме решения
существует еще одно решение, линейно независимое с y n (1) .
Действительно, нетрудно убедится, что таковым является:
Сначала докажем, что yn (2) является решением уравнения (14).
В самом деле, подставляя выражение для yn (2) в уравнение (14) , получим:
a(n+2) λ n+2 + b(n+1) λ n+1 + cn λ n = λ n (a (n+2) λ 2 + b(n+1) λ + cn) =
= λ n (n (a λ 2 + b λ + c) + 2a λ 2 + b λ ) = 0
Последнее равенство получим в силу того, что aλ 2 + bλ + c = 0 и λ = − b /2 a .
Вычислим теперь определитель Казорати, мы имеем:
∆ = λ n n λ n λ n +1 ( n +1) λ n +1 = λ 2 n +1 ≠ 0 .
так как λ ≠ 0 . Следовательно, частные решения yn (1) и yn (2) линейно независимы, и общее решение уравнения (147) имеет вид:
Решение примера 6.
имеет единственный действительный корень
λ = − 3 . Следовательно, общее решение исходного уравнения таково:
Для нахождения решения неоднородного линейного разностного уравнения, так же как и в случае линейных дифференциальных уравнений, используется метод неопределенных коэффициентов, основанный на подборе частного решения неоднородного уравнения по виду правой части f(n) .
Проиллюстрируем нахождение решения неоднородного линейного разностного уравнения на примерах.
Решение примера 7.
Будем искать частное решение в виде:
Подставляя это выражение в наше уравнение (19), получим:
p (25 + 10 – 3)5 n = 64 ∙ 5 n .
Следовательно, p = 2, а значит, y*(n) = 2 ∙ 5 n .
Решая характеристическое уравнение
Общее решение однородного уравнения имеет вид:
Таким образом, общее решение неоднородного уравнения (19) имеет вид:
y( n +2) – 7y( n +1) + 10y( n ) = 4 ∙ 6 n . (20)
Решение примера 8.
Для нахождения общего решения соответствующего однородного уравнения составим характеристическое уравнение:
Для нахождения частного решения y*( n ) исходного уравнения воспользуемся методом неопределенных коэффициентов. Будем искать
Подставляя это выражение в данное уравнение (20), получим:
p6 n+2 –7 p6 n+1 + 10 p6 n = 4 ∙ 6 n .
p 6 n (36 – 42 +10) = 4 ∙ 6 n .
Следовательно, p = 1, а значит, частное решение уравнения (20) имеет вид:
Складывая общее решение соответствующего однородного уравнения и частное решение неоднородного уравнения (20), получаем общее решение уравнения:
y ( n ) = 6 n + С1 5 n + С2 2 n .
3. МОДЕЛИ ЭКОНОМИЧЕСКОЙ ДИНАМИКИ С ДИСКРЕТНЫМ ВРЕМЕНЕМ
3.1. Модель делового цикла Самуэльсона–Хикса
Рассмотрим пример, иллюстрирующий применение разностных уравнений второго порядка. Для этого мы рассмотрим модель делового цикла Самуэльсона – Хикса (динамический вариант модели Кейнса). Эта модель основывается на принципе акселерации, то есть на предположении, что объемы инвестирования прямо пропорциональны приросту национального дохода. Данное предположение характеризуется следующим уравнением:
где коэффициент V > 0 − фактор акселерации, I (t) – величина инвестиций в период t, Y (t−1) , Y (t−2) – величины национального дохода соответственно в (t−1) -м и (t−2) -м периодах.
Предполагается также, что спрос на данном этапе зависит от величины национального дохода на предыдущем этапе, то есть:
C(t) = aY(t−1) + b . (22)
Условие равенства спроса и предложения имеет вид:
Подставляя в (23) выражение для I (t) из (21) и выражение для C(t) из (22), находим:
Y(t) = (a+V)Y(t−1) − VY(t−2) + b . (24)
Уравнение (24) известно, как уравнение Хикса.
Если предположить, что на протяжении рассматриваемых периодов величины a и V постоянны, то уравнение Хикса представляет собой неоднородное линейное разностное уравнение второго порядка с постоянными коэффициентами.
Мы можем легко найти частное решение уравнения (24), если положим, что:
Y (t) = Y(t−1) = Y(t−2) = Y* , (25)
т.е. использовав в качестве частного решения равновесное решение Y* = const .
Из (24) в силу (25) имеем:
Выражение (1−a) −1 в формуле (26) носит название мультипликатора Кейнса и является одномерным аналогом матрицы полных затрат.
Рассмотреть модель Самуэльсона–Хикса при условии, что
a = 0,5 ; V = 0,5; b = 4 .
Найти общее решение уравнения Хикса.
Решение примера 9.
В этом случае уравнение (24) принимает вид:
Y(t) − Y(t−1) + 0,5 Y(t−2) = 4 .
Его частным решением (в силу формулы (26)) будет:
Y * (t) = b /(1- a ) = 4/(1 — 0,5) = 8.
Найдем корни характеристического уравнения
λ 1,2 = (1 ± i)/2 = (1/ √ 2) (cos ( π /4) ± i sin ( π /4)) .
Таким образом, общим решением соответствующего однородного уравнения является:
Следовательно, общим решением уравнения будет:
В зависимости от значений а и V возможны четыре типа динамики. Она может быть растущей или затухающей и при этом иметь или не иметь колебательный характер. Так, в рассмотренном выше примере динамика носила колебательный характер с возрастающей амплитудой.
Рассмотреть модель Самуэльсона – Хикса при условии, что
a = 0,48, V = 0,72, b = 1,3.
Найти общее решение уравнения Хикса.
Решение примера 10.
В данном случае уравнение (24) имеет вид
Y(t) – 1,2Y (t−1) + 0,72 Y(t−2) = 1,3 .
Его частным решением (в силу формулы (26)) будет:
y * (t) = b /(1- a ) = 1,3/(1 — 0,48) = 2,5.
Напишем характеристическое уравнение:
λ 2 – 1,2 λ + 0,72 = 0 .
λ1,2 = 0,6 ± 0,6 i = 0,6 √ 2 ( cos ( π /4) ± i sin ( π /4)).
Общее решение соответствующего однородного уравнения есть
Ŷ 0( t ) = (0,6 √ 2) t ( С1 cos ( t π/4) + С2 sin (t π/4) ).
Получаем общее решение данного уравнения:
В рассмотренном примере динамика носит колебательный характер с затухающей амплитудой. Очевидно, при комплексных сопряженных корнях характеристического уравнения, по модулю превышающих единицу, динамика была бы растущей. Вообще,
в зависимости от значений a и V динамика может быть растущей или затухающей и при этом иметь или не иметь колебательный характер.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
[1] Васенкова Е.К., Волкова Е.С, Шандра Е.Г. Математика для экономистов. Дифференциальные и разностные уравнения: Курс лекций. М.: Финансовая академия, 2003. 116 с.
[2] Клюшин В. Л. Высшая математика для экономистов: Учебное пособие. — М.: ИНФРА-М, 2009. — 448 с. — (Учебники РУДН).
[3] Красс М.С., Чупрынов Б.П. Основы математики и ее приложения в экономическом образовании: Учебник. — 2-е изд., испр. — М.: Дело, 2001. — 688 с.
[4] Ласунский А.В. Разностные уравнения: Конспект лекций. ФГБОУ ВПО «Новгородский государственный университет им. Ярослава Мудрого», Великий Новгород, 2011.– 62с.
[5] Романко В.К . Разностные уравнения. Учебное пособие. БИНОМ. Лаборатория знаний, 2006. — 112 с.
🎬 Видео
Райгородский А. М. - Комбинаторика - Линейные рекуррентные соотношенияСкачать

15. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентамиСкачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Семинар №13 "Определители n го порядка"Скачать

10. Линейные однородные рекуррентные соотношения. Дискретная математикаСкачать

Математика без Ху!ни. Линейные неоднородные дифференциальные уравнения 2 порядка.Скачать

Рекуррентное уравнениеСкачать

Рекуррентные уравненияСкачать

Алгебра 9 класс. Рекуррентный способ задания числовой последовательности. Примеры.Скачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

9. Решение рекуррентных соотношений. Дискретная математика.Скачать

19. Метод вариации произвольных постоянных. Линейные неоднородные диф уравнения 2-го порядкаСкачать