Регрессия виды и интерпретация уравнений

Видео:Математика #1 | Корреляция и регрессияСкачать

Регрессия: понятие, виды и уравнение

Содержание статьи:

• Уравнение регрессии
• Линейное уравнение
• Нелинейное уравнение
• Виды регрессии
• Парная регрессия
• Множественная регрессия

Регрессия. Многие из нас слышали это слово, но немногие знают, что же это такое на самом деле. Попробуем разобраться. Регрессия — это зависимость между определёнными переменными, с помощью которой можно спрогнозировать будущее поведение данных переменных. Причём, под переменными подразумеваются всевозможные периодические явления вплоть до человеческого поведения.

Видео:Уравнение линейной регрессии. Интерпретация стандартной табличкиСкачать

Уравнение регрессии

Зачастую, регрессия подаётся в виде простого уравнения, которое раскрывает зависимость и силу связи между двумя группами числовых переменных, одна из которых называется зависимой (эндогенной), а вторая — независимой (экзогенной или фактором). Если есть группа взаимосвязанных показателей, то зависимая переменная выбирается логическими размышлениями, а остальные выступают независимыми. То есть, если у нас есть расстояние между городами и затраты на путешествие, то вполне ясно, что затраты будут зависеть от расстояния. Уравнения бывают двух видов: линейные и нелинейные (это уже чистая математика). Стоит рассмотреть каждый из видов.

Видео:Эконометрика. Линейная парная регрессияСкачать

Линейное уравнение

Линейное уравнение иллюстрирует строго линейную связь между переменными, то есть в нём отсутствуют степени, дроби, тригонометрические функции. Решается стандартными математическими способами.

Видео:Что такое регрессия и какие виды регрессии имеются? Душкин объяснитСкачать

Нелинейное уравнение

Логично предположить, что в нелинейный класс уравнений входит всё то, что не вошло в линейный. Решаются такие уравнения сведением к линейному типу, а дальше – по накатанной дорожке.

Видео:Регрессия - как строить и интерпретировать. Примеры линейной и множественной регрессии.Скачать

Виды регрессии

Регрессия бывает двух видов: парная (линейная и нелинейная) и множественная (линейная и нелинейная). Разница между ними в виде уравнения и количестве независимых переменных. Логично, что парная регрессия — это когда одна зависимая переменная и одна независимая, в множественной — независимых переменных несколько. В природе имеет место исключительно множественная регрессия, так как нельзя ограничить внешнее влияние на какое-то явление строго одним фактором. Рассмотрим оба вида регрессий детальнее.

Видео:Эконометрика Линейная регрессия и корреляцияСкачать

Парная регрессия

Парная (её ещё называют двухфакторной) модель проста в использовании, так как у нас всего две переменные: эндогенная и экзогенная, а значит будет просто решить уравнение и провести анализ. А это значит, что и применять на практике такую модель очень легко.

Видео:Корреляционно-регрессионный анализ многомерных данных в ExcelСкачать

Множественная регрессия

Множественная (многофакторная) модель намного сложнее, так как мы имеем уравнение с большим количеством переменных, для решения которого существуют определённые математические способы (метод наименьших квадратов например).

Итоги

Немного разобравшись в этой теме, приходишь к выводу, что регрессия очень необходимое понятие, помогающее предугадать поведение многих явлений. Его используют в экономике, психологии, химии, биологии, метеорологии и во многих других науках, причём существует множество программ, которые проводят все необходимые расчёты автоматически и сами выводят результаты и графики для анализа. Пользователю остаётся только считать результаты и правильно расшифровать их. А уж найти им применение вообще не проблема. Поэтому, я считаю, что необходимо иметь хотя бы малейшее понятие о том, что же такое эта пресловутая регрессия и где её использовать.

Видео про линейную регрессию и корреляцию:

Видео:Что такое линейная регрессия? Душкин объяснитСкачать

Интерпретация уравнения регрессии

Видео:Занятие 6. Линейная регрессияСкачать

Интерпретация уравнения регрессии

• Интерпретация регрессионных уравнений Существует два этапа интерпретации уравнения регрессии. Первый этап Уточнить, потому что уравнения интерпретируются устно Тот, кто не является статистиком. Во вторых это Нет необходимости решать, делать это или больше. Тщательное исследование зависимости. Оба этапа очень важны.

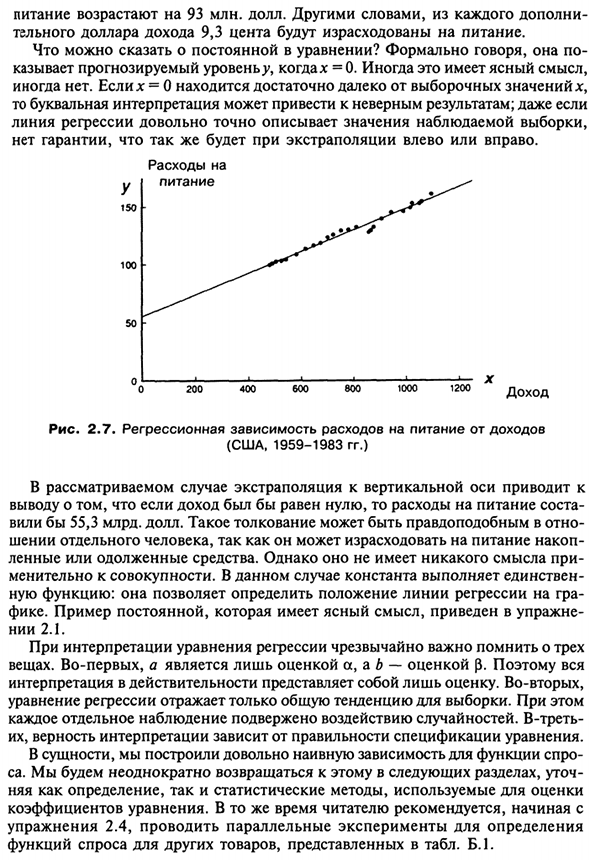
• На втором этапе мы рассмотрим несколько поз А пока давайте обратим основное внимание на первый этап. Это объясняет Определяется регрессионной моделью функции спроса, то есть регрессией между расами Потребители переходят на еду (у) и располагаемый личный доход (х) Данные Отображается в графическом формате (рисунок 2.7). Предположим, что истинная модель описывается y = a + $ x + u, (2,41) И регрессионная оценка £ = 55,3 + 0,093 *. (2,42)

Данные приведены в таблице. Б.1 в США за период с 1959 по 1983 год. Людмила Фирмаль

Полученные результаты можно интерпретировать следующим образом: коэффициент в х (коэффициент градиента) Единица у увеличивается на 0,093 единицы. х и у оба измеряются в мил Миллиарды долларов по фиксированной цене. Поэтому склон Если выручка увеличится на 1 миллиард долларов, 64 Питательные вещества увеличились на 93 миллиона долларов.

Это значит Из реальных долларовых доходов 9,3 цента тратятся на еду. Как насчет констант уравнения? Формально она Если x = 0, указывает уровень прогнозирования ^. Это ясно имеет смысл. Иногда нет. Если х = 0 достаточно далеко от значения выборки х, В этом случае буквальная интерпретация может привести к неверным результатам.

Даже если Линия регрессии является очень точным представлением наблюдаемого значения выборки. Нет гарантии, что то же самое произойдет с экстраполяцией влево или вправо. в 150 грамм 100 грамм 50 Стоимость пища 200 400 600 800 —100 • ”0 120—0 X доходов Рисунок 2.7. Зависимость расходов на питание от дохода (США, 1959-1983).

В рассматриваемом случае путем экстраполяции на вертикальную ось Если доход равен нулю, стоимость еды Сделал бы 55,3 миллиарда долларов. Такое толкование может быть правдоподобным в отношении Лица, которые могут тратить накопления пищи Кредиты или заемные средства. Тем не менее, это не имеет смысла, если По отношению ко всему.

В этом случае константа сделает единственное Функция: может определить положение линии регрессии на графике Поддельный. Примеры констант с ясным значением приведены в упражнении. Институт 2.1. При интерпретации уравнений регрессии очень важно помнить три Вещь. Во-первых, a является только оценкой a, а a b является оценкой (3. Интерпретация на самом деле просто оценка.

Во-вторых Уравнение регрессии отражает только общую тенденцию выборки. В то же время Индивидуальные наблюдения подвержены случайности. третий В этих случаях точность интерпретации зависит от точности спецификации уравнения. По сути, мы построили довольно простую зависимость от функции спроса Мы вернемся к этому в следующем разделе и уточнить.

• Определяя как определения, так и статистические методы, используемые при измерении Коэффициент уравнения. В то же время читателям рекомендуется начать с Упражнение 2.4, определить путем проведения параллельных экспериментов Функция спроса на другие товары приведена в таблице. B.1. После оценки регрессии возникают следующие вопросы:

Есть ли способ определить точность оценки? Это очень важно Рост будет обсуждаться в следующем разделе. Сначала рассмотрим дальше Подробно объясните роль остаточного члена и его влияние на оценки a и p. Интерпретация уравнений линейной регрессии.

Представьте себе простой способ интерпретации линейных коэффициентов. Людмила Фирмаль

Уравнение регрессии у = а + бх Если есть простая естественная единичная переменная Измерение. Сначала увеличим х на 1 единицу ( Единица переменной х) увеличивается у в б (единица переменной у). Второй этап Проверка того, что собой представляет хна на самом деле, Замените слово «единица измерения» на фактическое количество.

Третий этап Проверка возможности более простого выражения результата Это может быть не очень удобно. В примере В этом разделе указана единица измерения для х и у Потому что миллиарды долларов были потрачены, Замечательное упрощение. Константа а дает предсказанное значение у (единица ^). х = 0 Это может иметь или не иметь смысла в зависимости от значения Конкретная ситуация. Упражнение 1 2.1.

Регрессия стоимости продуктов питания (на основе того же Данные, для которых уже описана функция спроса, описанная в тексте) Меню определено как f = 1 в 1959 году, t = 2 в 1960 году и т. Д. Нини: у = 95,3 + 2,53 /. Интерпретация в Сравнение результатов оценки регрессии с аналогом Аналогичные результаты для модели регрессии функции спроса Пожалуйста, смотрите текст.

В этом случае постоянная Есть простая интерпретация. 2.2. Регрессивная зависимость от одноразовой зависимости стоимости жилья 1 Упражнение 2.4 особенно важно в том смысле, что оно запускает серию регрессий для развлечения. Общий спрос. Это оценивается читателем на протяжении всей книги.

Если это упражнение Если это делается группой студентов, учитель должен дать студентам задания Товарные. Более подробная информация о доступных данных доступна в Приложении B.go Личный доход в соответствии с таблицей. B.1, оба количества Можно оформить миллиарды долларов с 1959 по 1983 В следующем формате: j> = -27,6 + 0,178х.

Регрессивная зависимость и определение стоимости жилья с течением времени То же самое, что и упражнение 2.1, можно выразить как: f = 48,9 + 4,84 г. Вот экономическая интерпретация этих регрессий. У них разные предложения Описание тех же данных в переменной y. Сколько они Вы можете согласиться? 2,3.

Создайте уравнение регрессии между p и e из данных упражнения 1.3, сначала используйте все 12 наблюдений, затем исключите наблюдения 1. Дает экономическую интерпретацию для Японии. 2,4. В таблице. B.1 — потребительские расходы США располагаемый личный доход за период 1959-1983 гг. Назовите один продукт — не еду, а не домашнюю Пропустите регрессию между y и x. х — располагаемый личный доход, использующий Данные за 25 лет.

Интерпретация коэффициентов регрессии 2.5. Таким образом, регрессия между характеристиками продукта и временем Мы сделаем это в упражнении 2.1. Правильная интерпретация и сравнение У нее есть интерпретация регрессии, полученная в упражнении 2.4. 2.6. Два человека строят один и тот же набор временных тенденций 25 наблюдений за переменной y с использованием модели: у = а + р / + и

Где t — время (принимает значения непрерывно от 1 до 25), а -case Член чаепития. Получите первое уравнение: j> = 6,70 + 1,79 /. Вторая по ошибке оценивает регрессию между / и у и этим уравнением По мнению: t = -0,25 + 0,44 >>. Из этого уравнения он получает: у = 0,57 + 2,27 /. Объясните это уравнение и несоответствие между уравнениями, Получено первым исследователем. 2,7.

Как изменяется регрессионный балл в упражнении 2.1 Фактическая дата (1959-1983) используется как / вместо числа из 1 до 25? 2,8. Исследователи, 1 Не начинайте сначала вычислять коэффициент регрессии. Заполнены большинство арифметических расчетов в упражнении 1.3. 2 Учителя являются учениками, если это групповое занятие.

Удар, чтобы дать задачу оценки регрессии различных видов товаров в дополнение к еде жилья.люги, основанные на данных АМЕ (у) и общем располагаемом личном доходе (х) Риканская экономика (обе измеряются в миллиардах долларов) Фиксированная цена) с использованием данных и модели временных рядов за год: y = a + px + u. 1.

Исследователь выполняет регрессионный анализ, чтобы получить уравнение. Используйте обычный метод наименьших квадратов. Если предположить, что Обе ценности могут быть значительно недооценены внутренней системой Личные счета за желание людей не платить налоги Правительство, исследователи принимают два альтернативных улучшения Недооцененная оценка. 2.

Исследователи добавляют $ 90 млрд к показателю каждый год >> и Показатель х 200 миллиардов долларов. 3. Исследователь увеличивает x и y на 10% Каждый год. Оценить влияние корректировок (2) и (3) на результаты рег. ressii. 2.9. Исследователи имеют общие годовые данные временных рядов.

Заработная плата (W), валовой доход (P) и валовой доход (Y) Для страны сроком на n лет. По определению Y = W + T1. Получите регулярное уравнение, используя метод наименьших квадратов Рссии: fr = a0 + aiY; ft = Z> 0 + bxY. Указывает, что коэффициент регрессии автоматически удовлетворяет Следующее уравнение: но х + * я = 1; * o + K = 0. Интуитивно объясните, почему так должно быть. 2.10.

Исследователи не имеют нестохастической части истинной модели у пропорционально х. y = $ x + u. Исходя из исходного принципа, выведите формулу b, оценка МНК б. В этом случае (2.31) указывает, что это можно записать следующим образом. S = bj] + b2J, xj -2 £ Xx,. > 7 Для этого b = 2, xiyi / Zxf. 2,11. Выведите оценку наименьших квадратов модели из первого предположения. у = а + у. 68 То есть у это просто сумма констант Случайные участники с нами. Сначала переопределите 5, а затем дифференцируйте Цитирование.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Видео:Линейная регрессия. Что спросят на собеседовании? ч.1Скачать

R — значит регрессия

Статистика в последнее время получила мощную PR поддержку со стороны более новых и шумных дисциплин — Машинного Обучения и Больших Данных. Тем, кто стремится оседлать эту волну необходимо подружится с уравнениями регрессии. Желательно при этом не только усвоить 2-3 приемчика и сдать экзамен, а уметь решать проблемы из повседневной жизни: найти зависимость между переменными, а в идеале — уметь отличить сигнал от шума.

Для этой цели мы будем использовать язык программирования и среду разработки R, который как нельзя лучше приспособлен к таким задачам. Заодно, проверим от чего зависят рейтинг Хабрапоста на статистике собственных статей.

Видео:Эконометрика. Оценка значимости уравнения регрессии. Критерий ФишераСкачать

Введение в регрессионный анализ

Если имеется корреляционная зависимость между переменными y и x , возникает необходимость определить функциональную связь между двумя величинами. Зависимость среднего значения называется регрессией y по x .

Основу регрессионного анализа составляет метод наименьших квадратов (МНК), в соответствии с которым в качестве уравнения регресии берется функция такая, что сумма квадратов разностей минимальна.

Карл Гаусс открыл, или точнее воссоздал, МНК в возрасте 18 лет, однако впервые результаты были опубликованы Лежандром в 1805 г. По непроверенным данным метод был известен еще в древнем Китае, откуда он перекочевал в Японию и только затем попал в Европу. Европейцы не стали делать из этого секрета и успешно запустили в производство, обнаружив с его помощью траекторию карликовой планеты Церес в 1801 г.

Вид функции , как правило, определен заранее, а с помощью МНК подбираются оптимальные значения неизвестных параметров. Метрикой рассеяния значений вокруг регрессии является дисперсия.

• k — число коэффициентов в системе уравнений регрессии.

Чаще всего используется модель линейной регрессии, а все нелинейные зависимости приводят к линейному виду с помощью алгебраических ухищрений, различных преобразования переменных y и x .

Линейная регрессия

Уравнения линейной регрессии можно записать в виде

В матричном виде это выгладит

• y — зависимая переменная;
• x — независимая переменная;
• β — коэффициенты, которые необходимо найти с помощью МНК;
• ε — погрешность, необъяснимая ошибка и отклонение от линейной зависимости;

Случайная величина может быть интерпретирована как сумма из двух слагаемых:

• — полная дисперсия (TSS).
• — объясненная часть дисперсии (ESS).
• — остаточная часть дисперсии (RSS).

Еще одно ключевое понятие — коэффициент корреляции R 2 .

Видео:Множественная регрессия в ExcelСкачать

Ограничения линейной регрессии

Для того, чтобы использовать модель линейной регрессии необходимы некоторые допущения относительно распределения и свойств переменных.

1. Линейность, собственно. Увеличение, или уменьшение вектора независимых переменных в k раз, приводит к изменению зависимой переменной также в k раз.
2. Матрица коэффициентов обладает полным рангом, то есть векторы независимых переменных линейно независимы.
3. Экзогенность независимых переменных — . Это требование означает, что математическое ожидание погрешности никоим образом нельзя объяснить с помощью независимых переменных.
4. Однородность дисперсии и отсутствие автокорреляции. Каждая ε_i обладает одинаковой и конечной дисперсией σ 2 и не коррелирует с другой ε_i. Это ощутимо ограничивает применимость модели линейной регрессии, необходимо удостовериться в том, что условия соблюдены, иначе обнаруженная взаимосвязь переменных будет неверно интерпретирована.

Как обнаружить, что перечисленные выше условия не соблюдены? Ну, во первых довольно часто это видно невооруженным глазом на графике.

Неоднородность дисперсии

При возрастании дисперсии с ростом независимой переменной имеем график в форме воронки.

Нелинейную регрессии в некоторых случая также модно увидеть на графике довольно наглядно.

Тем не менее есть и вполне строгие формальные способы определить соблюдены ли условия линейной регрессии, или нарушены.

• Автокорреляция проверяется статистикой Дарбина-Уотсона (0 ≤ d ≤ 4). Если автокорреляции нет, то значения критерия d≈2, при позитивной автокорреляции d≈0, при отрицательной — d≈4.
• Неоднородность дисперсии — Тест Уайта, , при chi_$» data-tex=»inline»/> нулевая гипотеза отвергается и констатируется наличие неоднородной дисперсии. Используя ту же можно еще применить тест Бройша-Пагана.
• Мультиколлинеарность — нарушения условия об отсутствии взаимной линейной зависимости между независимыми переменными. Для проверки часто используют VIF-ы (Variance Inflation Factor).

В этой формуле — коэффициент взаимной детерминации между и остальными факторами. Если хотя бы один из VIF-ов > 10, вполне резонно предположить наличие мультиколлинеарности.

Почему нам так важно соблюдение всех выше перечисленных условий? Все дело в Теореме Гаусса-Маркова, согласно которой оценка МНК является точной и эффективной лишь при соблюдении этих ограничений.

Видео:Что такое полиномиальная регрессия? Душкин объяснитСкачать

Как преодолеть эти ограничения

Нарушения одной или нескольких ограничений еще не приговор.

1. Нелинейность регрессии может быть преодолена преобразованием переменных, например через функцию натурального логарифма ln .
2. Таким же способом возможно решить проблему неоднородной дисперсии, с помощью ln , или sqrt преобразований зависимой переменной, либо же используя взвешенный МНК.
3. Для устранения проблемы мультиколлинеарности применяется метод исключения переменных. Суть его в том, что высоко коррелированные объясняющие переменные устраняются из регрессии, и она заново оценивается. Критерием отбора переменных, подлежащих исключению, является коэффициент корреляции. Есть еще один способ решения данной проблемы, который заключается в замене переменных, которым присуща мультиколлинеарность, их линейной комбинацией. Этим весь список не исчерпывается, есть еще пошаговая регрессия и другие методы.

К сожалению, не все нарушения условий и дефекты линейной регрессии можно устранить с помощью натурального логарифма. Если имеет место автокорреляция возмущений к примеру, то лучше отступить на шаг назад и построить новую и лучшую модель.

Видео:Эконометрика. Множественная регрессия и корреляция.Скачать

Линейная регрессия плюсов на Хабре

Итак, довольно теоретического багажа и можно строить саму модель.
Мне давно было любопытно от чего зависит та самая зелененькая цифра, что указывает на рейтинг поста на Хабре. Собрав всю доступную статистику собственных постов, я решил прогнать ее через модель линейно регрессии.

Загружает данные из tsv файла.

• points — Рейтинг статьи
• reads — Число просмотров.
• comm — Число комментариев.
• faves — Добавлено в закладки.
• fb — Поделились в социальных сетях (fb + vk).
• bytes — Длина в байтах.

Вопреки моим ожиданиям наибольшая отдача не от количества просмотров статьи, а от комментариев и публикаций в социальных сетях. Я также полагал, что число просмотров и комментариев будет иметь более сильную корреляцию, однако зависимость вполне умеренная — нет надобности исключать ни одну из независимых переменных.

Теперь собственно сама модель, используем функцию lm .

В первой строке мы задаем параметры линейной регрессии. Строка points

. определяет зависимую переменную points и все остальные переменные в качестве регрессоров. Можно определить одну единственную независимую переменную через points

reads , набор переменных — points

Перейдем теперь к расшифровке полученных результатов.

• Intercept — Если у нас модель представлена в виде , то тогда — точка пересечения прямой с осью координат, или intercept .
• R-squared — Коэффициент детерминации указывает насколько тесной является связь между факторами регрессии и зависимой переменной, это соотношение объясненных сумм квадратов возмущений, к необъясненным. Чем ближе к 1, тем ярче выражена зависимость.
• Adjusted R-squared — Проблема с в том, что он по любому растет с числом факторов, поэтому высокое значение данного коэффициента может быть обманчивым, когда в модели присутствует множество факторов. Для того, чтобы изъять из коэффициента корреляции данное свойство был придуман скорректированный коэффициент детерминации .
• F-statistic — Используется для оценки значимости модели регрессии в целом, является соотношением объяснимой дисперсии, к необъяснимой. Если модель линейной регрессии построена удачно, то она объясняет значительную часть дисперсии, оставляя в знаменателе малую часть. Чем больше значение параметра — тем лучше.
• t value — Критерий, основанный на t распределении Стьюдента . Значение параметра в линейной регрессии указывает на значимость фактора, принято считать, что при t > 2 фактор является значимым для модели.
• p value — Это вероятность истинности нуль гипотезы, которая гласит, что независимые переменные не объясняют динамику зависимой переменной. Если значение p value ниже порогового уровня (.05 или .01 для самых взыскательных), то нуль гипотеза ложная. Чем ниже — тем лучше.

Можно попытаться несколько улучшить модель, сглаживая нелинейные факторы: комментарии и посты в социальных сетях. Заменим значения переменных fb и comm их степенями.

Проверим значения параметров линейной регрессии.

Как видим в целом отзывчивость модели возросла, параметры подтянулись и стали более шелковистыми , F-статистика выросла, так же как и скорректированный коэффициент детерминации .

Проверим, соблюдены ли условия применимости модели линейной регрессии? Тест Дарбина-Уотсона проверяет наличие автокорреляции возмущений.

И напоследок проверка неоднородности дисперсии с помощью теста Бройша-Пагана.

Видео:Парная регрессия: линейная зависимостьСкачать

В заключение

Конечно наша модель линейной регрессии рейтинга Хабра-топиков получилось не самой удачной. Нам удалось объяснить не более, чем половину вариативности данных. Факторы надо чинить, чтобы избавляться от неоднородной дисперсии, с автокорреляцией тоже непонятно. Вообще данных маловато для сколь-нибудь серьезной оценки.

Но с другой стороны, это и хорошо. Иначе любой наспех написанный тролль-пост на Хабре автоматически набирал бы высокий рейтинг, а это к счастью не так.

🎦 Видео

Лекция 8. Линейная регрессияСкачать

Линейная регрессия в Python за 13 МИН для чайников [#Машинное Обучения от 16 летнего Школьника]Скачать

РЕГРЕССИОННЫЙ АНАЛИЗ общая идея | АНАЛИЗ ДАННЫХ #16Скачать

Интерпретация коэффициента при логарифмировании в уравнениях регрессииСкачать

Линейная регрессия. Вероятностная интерпретация, связь с максимизацией правдоподобияСкачать