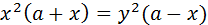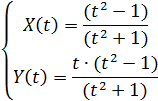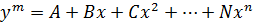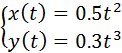Сегодня мы поговорим про то, как построить математический график при помощи языка Python за 10 минут. Мы рассмотрим построение параметрических кривых в трехмерном и двумерном пространстве с использованием различных примеров.
У многих из нас со школьной скамьи остались не самые приятные воспоминания о математике. Кто-то воспринимал её как необходимое зло: сложное и скучное, но обязательное. Кто-то же отказывался понимать математику от слова совсем.
Так или иначе, но наше школьное образование было ориентировано скорее на запоминание и заучивание, а не на размышления. По большому счету не было никакой мотивации разбираться в основах математики или в том, как она на самом деле работает. Идея заключалась в том, чтобы просто узнать, какие задачи решает определенная формула, запомнить правильный набор шагов и воспроизвести все это на экзамене.
Однако математика намного обширнее и интереснее того, что мы учили в школе. Если взять, например, кинематику, можно увидеть настоящую магию математики. Кинематика известна как «геометрия движения» – это изучение взаимодействия между движущимися телами во времени. Хотя бы раз увидите такое визуальное представление математических функций — и они оживут для вас. Возможно, в тот момент вы почувствуете, что впервые понимаете их правильно.
Итак, давайте научимся самостоятельно моделировать данные и начнем писать собственные скрипты. Сегодня мы поговорим о параметрических кривых и как их строить, используя Python и такие библиотеки, как NumPy, SymPy и Matplotlib.
- Построение параметрических кривых
- Как работает скрипт
- Подготовка
- Построение графика трехмерной параметрической кривой
- Немного поэкспериментируем
- Построение 2D параметрических кривых
- Построение математических функций
- Заключение
- Разработать программу для построения графика функции заданной параметрическим уравнением
- Примеры кривых
- Правила ввода выражений и функций
- BestProg
- Разработка программы рисования графика функции двух переменных ( 3D )
- Содержание
- Условие задачи
- ⇑
- Математическая постановка задачи
- ⇑
- Выполнение
- ⇑
- ⇑
- ⇑
- ⇑
- ⇑
- ⇑
- ⇑
- ⇑
- ⇑
- Программирование: теория и практика
- Рубрики
- Свежие записи
- Построение графиков функций, заданных в параметрической форме
- 🎬 Видео
Видео:20.12.2021 Практика 26. Построение графиков функций, заданных параметрическиСкачать

Построение параметрических кривых
Параметрические кривые поистине завораживают! Если говорить простым языком, параметрическую кривую можно понимать как след, оставляемый движением частицы в пространстве. Говоря более формально, этот след моделируется функцией, определяемой от интервала I до различных точек в пространстве E .
Для трехмерного случая, если x , y и z заданы как функции переменной t в I (это параметр), мы получаем уравнения x = f(t) , y = g(t) и z = h(t) . Оценивая каждое значение параметра t в каждом из этих уравнений, мы получаем точку p(t) = (x(t),y(t),z(t)) в пространстве. Проделав эту процедуру для значений t , меняющихся в интервале I , мы получим параметрическую кривую.
Проведя небольшое исследование, попробовав несколько моделей вручную и потратив много часов на работу над сценарием, мы нашли решение. Оно выглядит следующим образом:
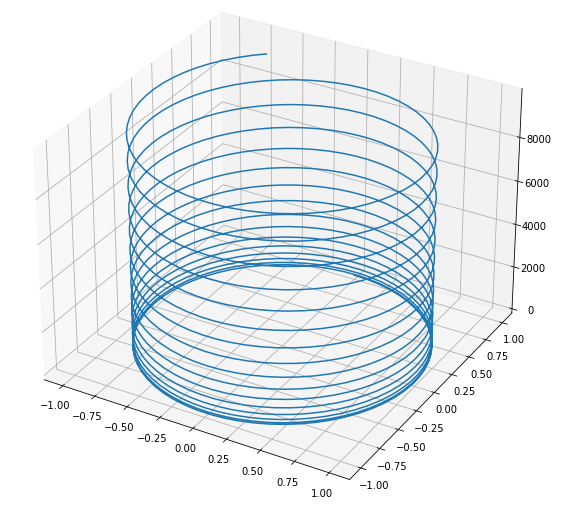
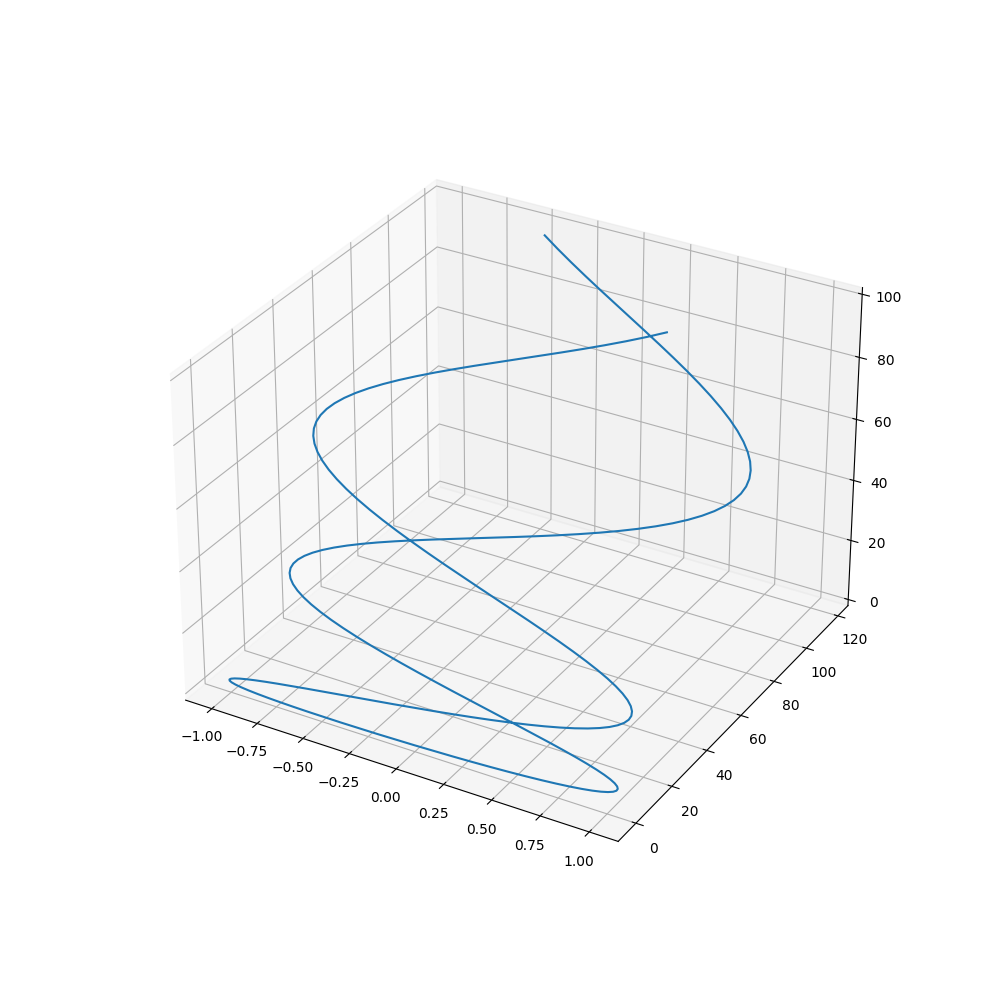
Приведенный выше скрипт позволяет нам генерировать графики для параметрических кривых. К примеру, вот так выглядит график параметрической спирали p(t) = (sin(t),cos(t),sqrt(t3)) , для интервала от 0 до 100.
Видео:Математика без Ху!ни. Нахождение асимптот, построение графика функции.Скачать

Как работает скрипт
Скрипт, который мы привели выше, использует такие библиотеки, как SymPy, NumPy и Matplotlib. Давайте разберемся со всем по порядку.
SymPy — это библиотека Python для символьной математики. Она стремится стать полнофункциональной системой компьютерной алгебры (CAS). При этом сохраняется максимально простой код (а значит, понятный и масштабируемый). Библиотека SymPy, кстати, полностью написана на Python.
NumPy — это основной пакет для научных вычислений в Python. Эта библиотека предоставляет:
- объекты многомерного массива,
- различные производные объекты (такие как маскированные массивы и матрицы)
- набор подпрограмм для быстрых операций с массивами, включая математические и логические, манипуляции с фигурами, сортировку, выборку, ввод-вывод, дискретные преобразования Фурье, основные операции линейной алгебры, основные статистические операции и случайное моделирование.
И последняя библиотека из нашего списка — Matplotlib. Это обширная библиотека для создания статических, анимированных и интерактивных визуализаций на Python.
Подготовка
Чтобы использовать перечисленные выше библиотеки в нашем скрипте, мы должны сначала установить их на свой компьютер, выполнив следующую инструкцию в терминале:
pip install numpy sympy matplotlib
Теперь, когда библиотеки установлены, мы можем импортировать их в нашу программу:
Построение графика трехмерной параметрической кривой
Символьные вычисления в SymPy выполняются с помощью символов. Переменные SymPy являются объектами класса Symbols . Выражение t = sp.Symbol(‘t’) присваивает символ t переменной t , с которой мы теперь можем работать как с математической переменной.
Выглядит это следующим образом:
В рамках этой задачи нам нужно работать с составными выражениями, хранящимися в строке. Поэтому нам нужно сделать преобразование строки в математическое выражение понятным для SymPy. Для этого мы используем функцию sympify.sp.sympify(expression) , которая преобразует параметрическое выражение в общее математическое выражение.
К примеру, наш код будет выглядеть так:
Теперь переменная function_z содержит математическое выражение t 2 +2 .
Следующим шагом является возможность оценить параметр t внутри математического выражения. Функция subs() в SymPy позволит нам оценить выражение с заданным значением. Мы можем использовать его следующим образом: expression.subs(t, value) .
Наш код будет выглядеть следующим образом:
Поскольку мы говорим о параметрических функциях, нас интересует оценка функции на последовательности вещественных значений в пределах интервала. Для этого мы используем функцию arange() в NumPy.
Функция np.arange(start, stop, step) создает массив NumPy со значениями в интервале (start,stop) с приращением шага, то есть мы идем от start до stop-1 с определенным шагом step .
Наш код будет выглядеть так:
После создания массива интервалов нам нужно перебрать значения t и оценить каждое значение внутри функции. Для этого мы будем использовать генератор списков в Python и функцию subs() библиотеки SimPy.
О генераторах списков можно почитать в статье «Генераторы списков в Python для начинающих».
Функция subs() получает символ t (который мы сохранили в переменной t ) и значение каждого из элемента в качестве параметров.
Выглядит это примерно следующим образом:
Мы повторяем эту процедуру для значений x_values и y_values и таким образом получаем массивы со значениями для построения.
Наконец, с помощью библиотеки Matplotlib мы создаем график, соответствующий нашей параметрической кривой. В трехмерном случае, чтобы указать Matplotlib, что мы хотим сделать трехмерный график, мы используем следующий оператор:
Кроме того, мы можем заменить функции и интервал на новые и получить самые разные кривые. Давайте попробуем еще раз, но с другими значениями.
Например, напишем следующий код:
Запустим наш код и получим такой график:
Немного поэкспериментируем
Давайте немного поэкспериментируем с нашим кодом: попробуем различные значения и посмотрим, что получится. С помощью параметрических кривых можно создать множество фигур. Некоторые комбинации могут генерировать кривые с уникальной симметрией и красотой.
Если вы хотите поиграть со скриптом самостоятельно, можете открыть эту ссылку и заменить значения для function_x , function_y , function_z и interval .
К примеру, можно взять следующий код:
Запустив его, мы получим такой результат:
Поиграйтесь сами и посмотрите, какие удивительные параметрические кривые можно создать!
Видео:График параметрически заданной функцииСкачать

Построение 2D параметрических кривых
С некоторыми модификациями данный скрипт также можно использовать и для построения двумерных параметрических кривых.
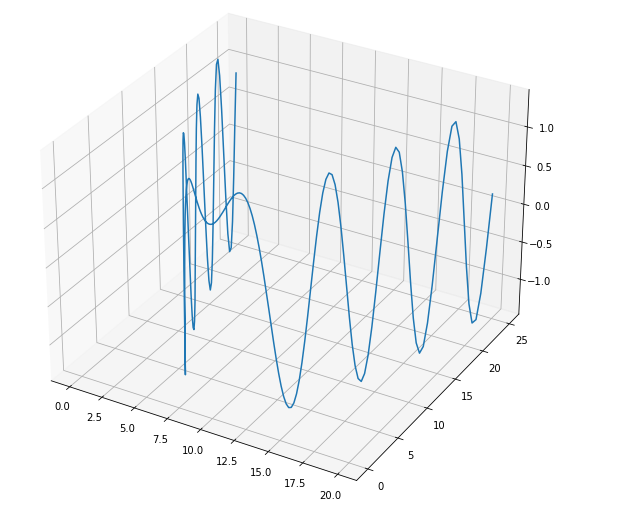
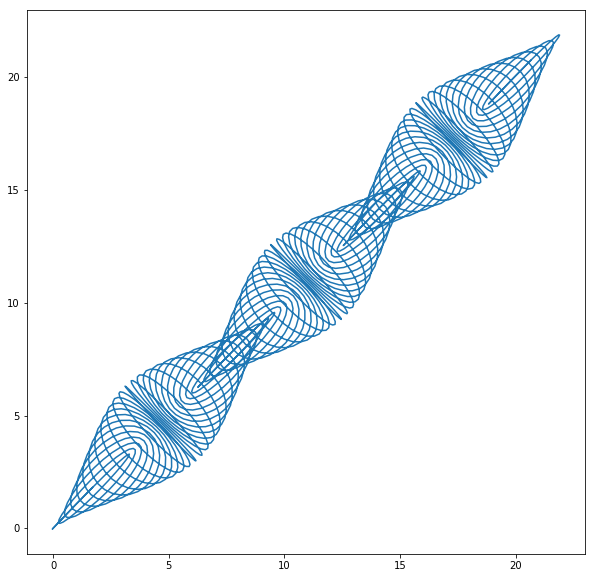
Например, давайте построим двумерный график, полученный путем оценки выражения x = t − 1,6 ∗ cos(24 ∗ t) и y = t − 1,6 ∗ sin(25 ∗ t) на интервале I=[1.5,20.5] .
Выглядеть это будет примерно следующим образом:
Для того, чтобы смоделировать параметрическую кривую, показанную выше, можно воспользоваться следующим скриптом:
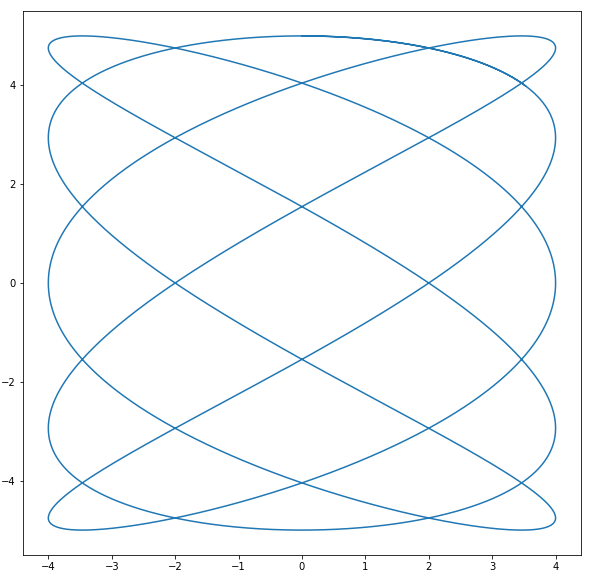
Давайте проверим наш код с другими функциями и новым интервалом. К примеру, возьмем следующие значения:
Запустим наш скрипт и получим следующий график:
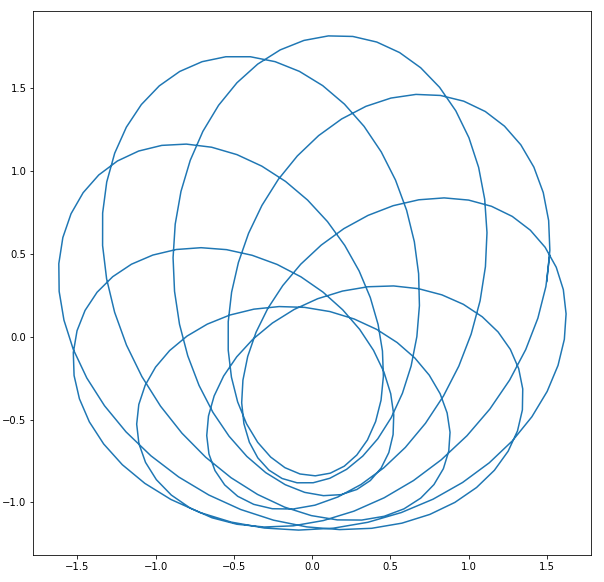
Теперь давайте проделаем это ещё раз, но уже с новыми значениями:
Тогда результат будет таким:
Удивительно! Не правда ли?
Видео:Математика без Ху!ни. Исследование функции, график. Первая, вторая производная, асимптоты.Скачать

Построение математических функций
Как только мы закончили написание скрипта для моделирования параметрических кривых, приходит осознание, что с помощью всего нескольких строк кода мы можем создать плоттер для математических функций как в двух, так и в трех измерениях! Невероятно! Это же так удобно!
К примеру, давайте рассмотрим скрипт для построения графиков математических функций в двух и трех измерениях в интервале от a до b . То есть, консоль запросит у пользователя как функцию, так и значения a и b для интервала. Вот такой код у нас получится:
Вы можете протестировать приведенный выше скрипт здесь. Запустите скрипт и введите свою конфигурацию функции и интервала.
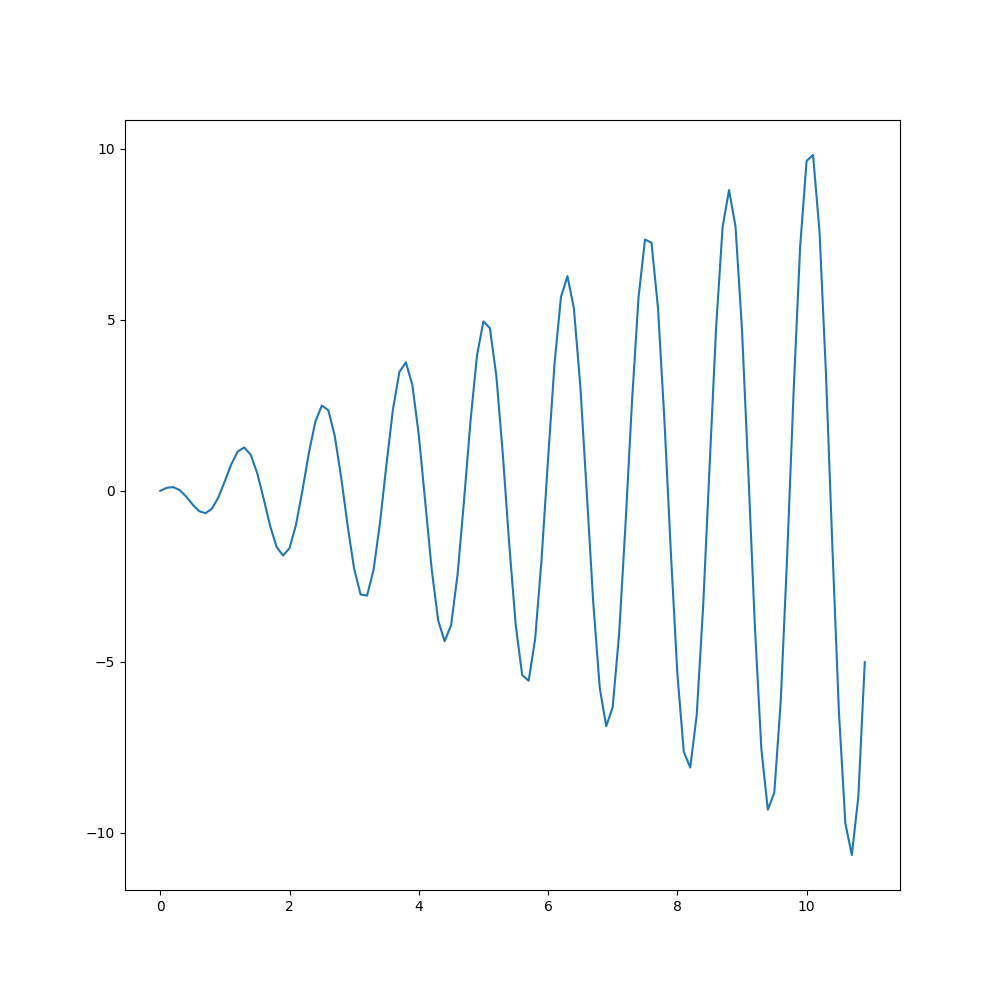
Например, возьмем следующий код:
Запустим его и получим следующий результат:
А теперь давайте поменяем значения на следующие:
Если мы это запустим, то получим такой график:
Видео:Задание 23 из ОГЭ Построение графиков функций с модулем | МатематикаСкачать

Заключение
Что ж, вот вы и дошли до конца этой статьи, поздравляем! Сегодня мы обсудили, как построить математический график на Python всего за 10 минут. Мы поговорили про построение различных параметрических кривых в двумерном и трёхмерном пространстве и разобрали процесс построения на примерах. Теперь вы видите, какой завораживающей на самом деле может быть математика! Кроме того, построение параметрических кривых, как вы понимаете, не такой уж и сложный процесс.
Надеемся, данная статья была вам полезна! Успехов в написании кода!
Видео:Построение графика параметрически заданной функцииСкачать

Разработать программу для построения графика функции заданной параметрическим уравнением
Построим график параметрической функции x=x(t) и y=y(t), которая задаёт прямую или кривую линию,
где параметр t лежит в промежутке [a, b],
и вы можете указать свои границы.
Задайте также функции x и y, зависящих от параметра.
Видео:Математический анализ. ДКР, задание 2. Построение графика функции, заданной параметрическиСкачать

Примеры кривых
| Название кривой | Уравнение |
|---|---|
| Окружность | |
| Спираль | |
| Дельтоида | |
| Астроида | |
| Гипоциклоиды | |
| Кардиоида | |
| Нефроида | |
| Эпициклоиды | |
| Бабочка | |
| Фигуры Лиссажу | |
| Сердце |
Правила ввода выражений и функций
3.14159.. e Число e — основание натурального логарифма, примерно равно
2,7183.. i Комплексная единица oo Символ бесконечности — знак для бесконечности
© Контрольная работа РУ — калькуляторы онлайн
Видео:Математический анализ, 16 урок, Исследование функции и построение графикаСкачать

BestProg
Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

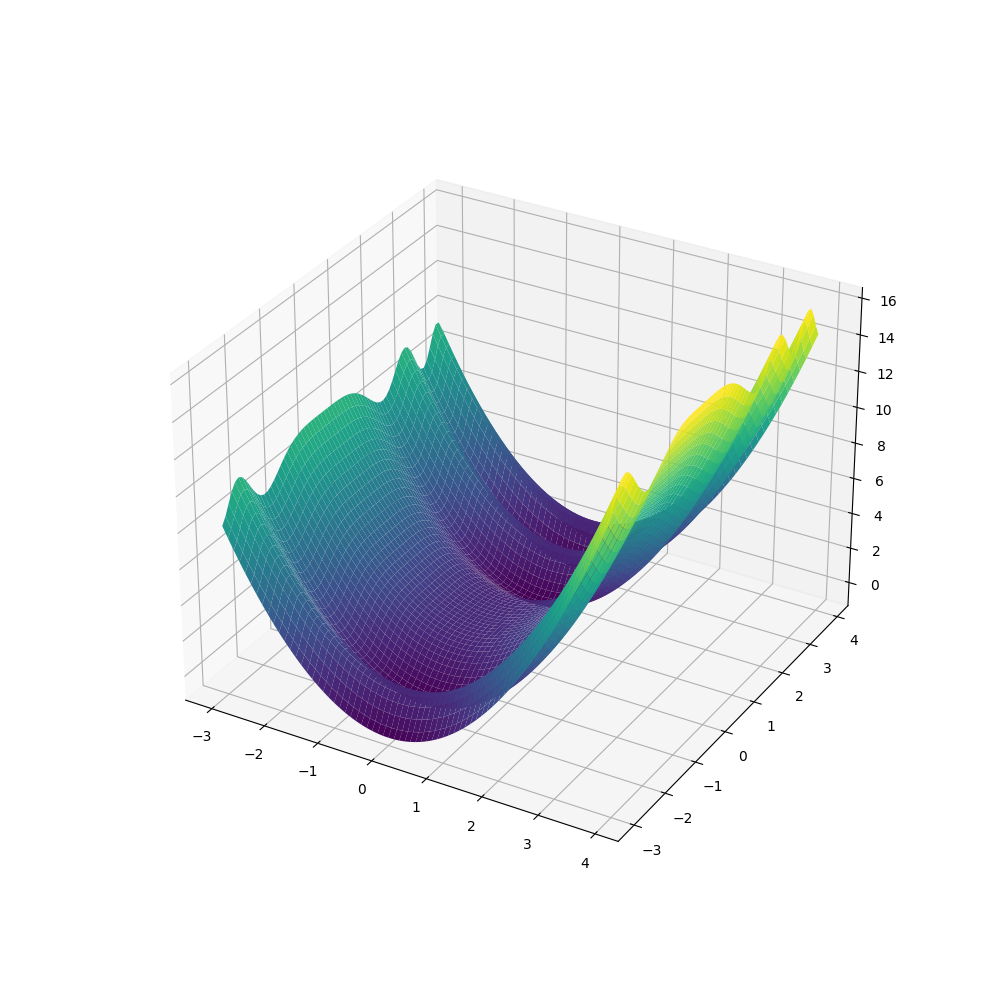
Разработка программы рисования графика функции двух переменных ( 3D )
В работе описывается разработка программы построения графика функции двух переменных
z = f(x, y)
В качестве примера, выбрана функция
z = sin(x) + cos(y)
Используя данный пример, можно создавать собственные программы для построения графиков других функций. По желанию можно модернизировать работу программы по своему усмотрению.
Видео:Как построить график функции без таблицыСкачать

Содержание
Поиск на других ресурсах:
Видео:Построить график ЛИНЕЙНОЙ функции и найти:Скачать

Условие задачи
Задана формула функции двух переменных z = sin(x) + cos(y) . Разработать приложение, которое рисует график этой функции в отдельной форме.
Дополнительно реализовать поворот графика влево, вправо, вверх, вниз. Также нужно выводить оси OX , OY , OZ .
⇑
Видео:Построение графика функцииСкачать

Математическая постановка задачи
Построение графика функции двух переменных есть математически решаемой задачей, в которой используются известные формулы вычисления.
График функции двух переменных z(x,y) строится в параллелепипеде с размерами (xx1, xx2) , (yy1, yy2) , (zz1, zz2) .
Для использования поворота системы в 3-мерном пространстве возникает понятие точки ( x0 , y0 , z0), относительно которой происходит поворот системы координат.
Также возникает понятие углов:
(альфа) – поворот системы относительно оси OZ ;
(бета) – поворот системы относительно оси OX .
Сдвиг в точку ( x0 , y0 , z0 ) с учетом поворота на углы 

После перемножения матриц получаем формулу для вычисления:
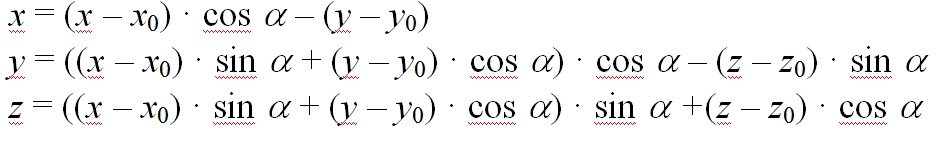
Рис. 1. Сдвиг и поворот системы координат
Необходимо определиться, в какой плоскости монитора будут лежать оси координат OX , OY , OZ . Принимаем, что в плоскости монитора лежат оси OX и OY . А ось OZ перпендикулярна экрану.
Координаты расчетной точки (x, y) прижимаются к точке (0, 0) по формулам:

⇑
Видео:Математика Без Ху!ни. Производная функции, заданной параметрически.Скачать

Выполнение
1. Создание проекта как Windows Forms Application
Создать проект. Подробный пример создания проекта по шаблону Windows Forms Application описывается здесь . Автоматически создается главная форма приложения. Имя исходного модуля главной формы « Form1.cs «.
⇑
2. Создание формы Form1 .
Создать форму по образцу, как показано на рисунке 2.

Настроить следующие свойства компонент и формы:
- в форме Form1 свойство Text = « График функции двух переменных «;
- в форме Form1 свойство MaximizeBox = False ;
- в форме Form1 свойство StartPosition = « CenterScreen «;
- в компоненте button1 свойство Text = « Показать график функции … «.
⇑
3. Создание формы Form2 .
Создать новую форму. Подробный процесс создания новой формы описывается здесь .
Имена файлов формы « Form2.cs » и « Form2.Designer.cs «.
Разместить на форме четыре компонента типа Button. Автоматически создается четыре объекта с именами button1, button2, button3, button4.
Настроить свойства компонент и формы следующим образом:
- в форме Form2 свойство StartPosition = «CenterScreen»;
- в форме Form2 свойство Text = « График функции z = f(x,y) «;
- в компоненте button1 свойство Text = « ^ «;
- в компоненте button2 свойство Text = « v «;
- в компоненте button3 свойство Text = « «;
- в компоненте button4 свойство Text = « > «.
Приблизительный вид формы Form2 изображен на рисунке 3.

4. Ввод внутренних переменных в форму Form2 .
Все внутренние переменные, использующиеся для организации вывода графика, размещаются в классе формы Form2. Поэтому, сначала надо активизировать модуль « Form2.pas ».
В модуль формы Form2 вводятся следующие внутренние переменные с классом видимости private:
- xx1, xx2, yy1, yy2 – соответствуют координатам точек, которые отображаются на экране монитора;
- массивы xx и yy предназначены для вывода плоскости из 4-х точек. Область определения функции z = f(x, y) разбивается на прямоугольники, на любом из которых функция экстраполируется ребрами четырехугольника.
В разделе public вводятся:
- переменные X_min , Y_min , X_max , Y_max вещественного типа, которые представляют реальные координаты параллелепипеда, в котором выводится график функции. Эти переменные заполняются из основной формы Form1 экспериментальным путем:
- переменные alfa, beta вещественного типа, которые отображают углы наблюдения за графиком функции. Заполняются из главной формы Form1;
- переменные x0, y0, z0 вещественного типа. Отображают величины из главной формулы вычисления (см. математическую постановку задачи);
- переменная A вещественного типа. Представляет коэффициент перспективы и подбирается экспериментально;
- переменная f_show логического типа используется для указания того, что нужно перерисовать график, в случае изменения положения углов alfa и beta.
После введения переменных в текст программы, фрагмент класса формы Form2 имеет вид:
Переменные, имеющие идентификатор доступа public, заполняются из формы Form1 .
⇑
5. Программирование внутренних методов в форме Form2 .
В текст класса Form2 вводятся три дополнительных метода:
- функция преобразования системы координат и масштабирования Zoom_XY() ;
- функция func() для которой выводится график;
- функция рисования графика Show_Graphic().
Листинг метода преобразования системы координат следующий:
Листинг метода func() следующий.
В этом методе вместо строки
можно сделать вставку собственной функции.
Непосредственный вывод графика функции реализован в методе Show_Graphic() . Листинг метода Show_Graphic() следующий.
Объясним некоторые фрагменты кода в методе Show_Graphic().
Область определения функции z = f(x,y) разбивается на прямоугольники, на любом из которых функция экстраполируется с ребрами четырехугольника. Построение четырехугольников на экране реализуется с помощью метода DrawLine().
После очистки канвы происходит рисование осей координат и методом DrawLine() выводятся фрагменты поверхности.
При рисовании поверхности, из метода Show_Graphic() вызывается метод Zoom_XY(), что осуществляет преобразование и масштабирование из реальных координат в экранные координаты.
⇑
6. Программирование события Paint формы Form2.
Чтобы получить объект Graphics, нужно запрограммировать событие Paint формы Form2. Пример программирования события в MS Visual Studio – C# описывается здесь подробно.
Обработчик события Form2_Paint() получает два параметра. Первый параметр типа System.Object , второй параметр типа PaintEventArgs .
Параметр типа PaintEventArgs содержит объект Graphics, необходимый для рисования на поверхности формы.
Событие Paint возникает, если окно становится «грязным» (dirty) – то есть, если изменяется его размер, если оно перестает закрывать (частично или полностью) другое окно или если оно было свернуто а потом развернуто. Во всех этих случаях – то есть если форму необходимо перерисовать, платформа .NET автоматически вызовет событие Paint .
Листинг обработчика события Form2_Paint() следующий.
⇑
7. Программирование обработчиков событий клика на кнопках button1, button2, button3, button4.
Поворот графика происходит в момент, когда пользователь делает клик на одной из кнопок, размещенных на форме Form2 (элементы управления button1, button2, button3, button4).
Отображение графика зависит от внутренних переменных alfa и beta. Переменная alfa содержит угол поворота относительно оси OZ . Переменная beta содержит значение угла поворота вокруг оси OX .
Поэтому, в обработчиках событий происходит изменение значений alfa и beta на некоторую величину. По желанию, можно установить собственную величину изменения alfa и beta.
Листинг обработчиков событий приведен ниже.
В вышеприведенных обработчиках событий, событие Paint генерируется явно с помощью унаследованного метода Invalidate(). Этот метод делает перерисовывание всей клиентской области программным путем.
Метод Invalidate() имеет несколько перегруженных вариантов. Например, если нужно обновить заданный прямоугольник, то нужно создать такой код:
⇑
8. Программирование обработчиков событий MouseDown, MouseMove и MouseUp.
Для осуществления поворота графика с помощью мышки нужно запрограммировать соответствующие обработчики событий.
Если нажать клавишу мыши и удерживать ее нажатой над формой Form2, а потом отпустить, то генерируются такие события (рисунок 4):
- MouseDown – генерируется, если пользователь делает клик мышкой на форме Form2;
- MouseMove – генерируется, если пользователь перемещает мышку над формой Form2 (независимо, нажата ли одна из кнопок мышки);
- MouseUp – генерируется, если пользователь отпускает кнопку мышки после нажатия.

⇑
9. Листинг модуля « Form2.cs ».
Ниже приведен полный текст файла ” Form2.cs ”, который соответствует форме Form2.
⇑
10. Программирование события клика на кнопке button1 формы Form1 (вызов формы рисования графика функции).
При клике на кнопке button1 из формы Form1 может выводиться график функции.
Обработчик события клика на кнопке Button1 имеет вид.
11. Запуск программы.
После запуска программы на выполнение, форма графика функции изображена на рисунке 5.

⇑
Видео:Построение графика функции y=2cos(x)+1Скачать

Программирование: теория и практика
Видео:Borland Delphi 7. Разработка приложения для построения графика функцииСкачать

Рубрики
- C# (160)
- Практика (42)
- MS Visual Studio 2010 (34)
- MS Visual Studio 2017 (7)
- MS Visual Studio 2019 (10)
- Теория (118)
- Практика (42)
- C++ (147)
- Практика (31)
- Borland C++ Builder 2007 (16)
- MS Visual Studio 2010 (18)
- Теория (117)
- Visual C++ (112)
- Практика (31)
- Java (103)
- Практика (6)
- Теория (97)
- JavaScript (6)
- Практика (1)
- Теория (5)
- Kotlin (19)
- Практика (1)
- Теория (18)
- Pascal/Delphi (35)
- Практика (19)
- Delphi-7 (3)
- Embarcadero RAD Studio 2010 (17)
- Теория (16)
- Практика (19)
- Python (91)
- Практика (4)
- Теория (87)
- Базы данных (42)
- Компьютерная графика (3)
- Курсовые работы (7)
- Математическое ПО (9)
- Паттерны (20)
Видео:Построение графика функции в ExcelСкачать
Свежие записи
- C++. Примеры сохранения/чтения объектов класса. Сериализация 26 апреля, 2022
- C++. Пространства имен. Ключевые слова namespace, using 17 апреля, 2022
- Java. Класс ArrayList. Методы преобразующие массив в целом 16 апреля, 2022
- Java. Класс ArrayList. Методы определяющие общие характеристики массива 13 апреля, 2022
- Java. Класс ArrayList. Методы, определяющие информацию об элементах массива 13 апреля, 2022
- C++. Умные указатели. Классы указателей unique_ptr, shared_ptr, weak_ptr 10 апреля, 2022
- C++. Умные указатели. Автоматический указатель. Класс auto_ptr 7 апреля, 2022
- Java. Класс ArrayList. Методы изменяющие данные в массиве 6 апреля, 2022
- Java. Класс ArrayList. Динамический массив. Общие сведения 5 апреля, 2022
- Java. Общие сведение о Java Collections Framework 4 апреля, 2022
При использовании материалов сайта, ссылка на сайт обязательна.
Видео:Математический анализ. ДКР, задание 1 "Построение графика функции, заданной явно"Скачать

Построение графиков функций, заданных в параметрической форме
Задание функции 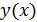
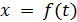
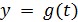
параметрическим, а вспомогательную величину 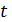
Для построения графика функции, заданной параметрически, необходимо определить массив 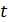
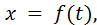
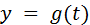
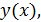
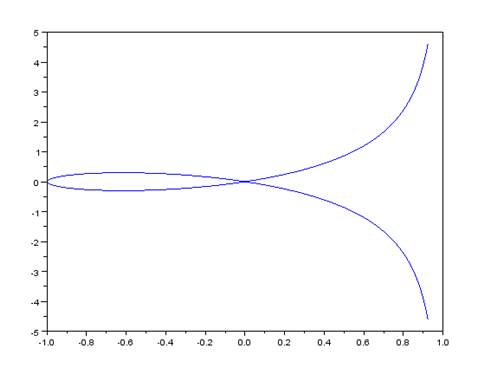
Пример. Построить график строфоиды.
Напомним, что строфоида представляет собой алгебраическую кривую третьего порядка, которая в общем виде задается уравнением:
Представим это уравнение с помощью параметра t:
Зададим массивы 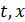
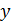
Пример. Построить график полукубической параболы.
Полукубическая парабола-это алгебраическая кривая второго порядка, которая в общем виде может быть описана следующим уравнением:
Приведем это уравнение к параметрической форме:
Как и в примере со строфоидой, 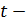
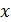
🎬 Видео
Построение графиков заданной функции в ExcelСкачать

Нахождение асимптоты параметрически заданной функции.Скачать

MathCAD Построение графика быстрым способомСкачать