При решении задач для уравнений параболического и гиперболического типов используются различные разностные схемы, среди которых важное место занимают так называемые явные и неявные разностные о-хемы.
Рассмотрим их на примере классического уравнения параболического типа — уравнения теплопроводности (нестационарного уравнения Лапласа)
со следующими начальными
условиями. Решение ищется внутри полубесконечного цилиндра (рис. 4.7). Задачу (4.16)—(4.18) называют эволюционной, имея в виду построение эволюции решения во времени. Используются также названия: ЗАДАЧА КОШИ С ГРАНИЧНЫМИ УСЛОВИЯМИ или КРАЕВАЯ ЗАДАЧА С НАЧАЛЬНЫМИ ДАННЫМИ.
Построим разностную схему. Для этого проведем линии
где hxn hy— шаги по пространственным координатам х и у соответственно ит — шаг по времени t. Плоскости k = const называют ?-слоями или слоями по времени. Сеточную функцию
обозначим через u h m п.
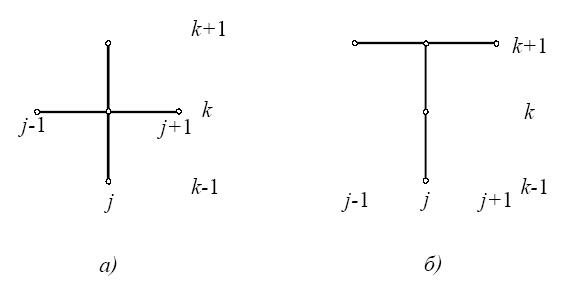
Запишем разностную аппроксимацию уравнения (4.16) с использованием шеститочечных шаблонов двух типов, показанных на рис. 4.8. Здесь пустыми кружочками обозначены узлы на k-м слое с известными значениями функции, а зачерненными — узлы на (k + 1)-м слое, на котором параметры неизвестны и должны быть определены. Шаблон на рис. 4.8, а соответствует так называемой явной схеме, а шаблон на рис. 4.8, б — неявной схеме. В явной схеме оператор Лапласа аппроксимируется с использованием известных значений функции на k-м слое, а в неявной схеме — с использованием неизвестных значений функции на (k + 1)-м слое.
Без потерь общности будем далее полагать, что шаги по пространственным координатам одинаковы, т. е. hx = Лу = А. Тогда явная разностная схема, соответствующая шаблону на рис. 4.8,о, запишется следующим образом:
Из этого соотношения следует, что искомое значение определяется явным образом через известные значения на k-м слое по соотношению
Для неявной разностной схемы, соответствующей шаблону на рис. 4.8, б, имеем
Соотношение (4.20), записанное для всех внутренних узлов (k 4- 1)-го слоя, порождает систему линейных алгебраических
уравнений, с помощью которых определяются неизвестные значения функции в узлах. Каждое уравнение этой системы содержит только пять неизвестных и* + Д ц* + 1 . ии*,* 1 ,, u m n ’ хотя общее количество неизвестных равно числу внутренних узлов на (k + 1)-м слое и может быть весьма велико (число узлов составляет порядка N 2 , при этом N может принимать значения от 50 до 100). Следовательно, матрица системы линейных уравнений является пятидиагональной и сильно разреженной. Для решения этой системы используются, как правило, итерационные методы, некоторые из которых были описаны.
Очевидно, что при одинаковых шагах разностной сетки число операций, необходимых для отыскания решения на (k + 1)-м слое, в явных схемах значительно меньше, чем в неявных. Однако в дальнейшем будет показано, что условие устойчивости разностной схемы накладывает значительные ограничения на величины шагов в явных схемах. Поскольку в конечном счете качество разностной схемы при одинаковой требуемой точности должно оцениваться количеством операций, необходимых для получения решения на всем временном интервале, в ряде случаев неявные разностные схемы оказываются более предпочтительными, чем явные.
Постановка задач для уравнений параболического типа
Классическим примером уравнения параболического типа является уравнение теплопроводности (диффузии). В одномерном по пространству случае однородное (без источников энергии) уравнение теплопроводности имеет вид
. (2.1)
Если на границах х=0 и х=l заданы значения искомой функции u(x,t) в виде
(2.2)
Видео:Разностные схемы для численного решения уравнений гиперболического типаСкачать
т.е. граничные условия первого рода, и, кроме того, заданы начальные условия
то задачу (2.1)-(2.4) называют первой начально-краевой задачей для уравнения теплопроводности (2.1).
В терминах теории теплообмена u(x,t) – распределение температуры в пространственно-временной области 
коэффициент температуропроводности, а (2.2), (2.3) с помощью функций ϕ0(t), ϕl(t) задают температуру на границах x=0 и x=l.
Если на границах х=0 и х=l заданы значения производных искомой функции по пространственной переменной
(2.5) 
(2.6)
т.е. граничные условия второго рода, то задачу (25.1), (2.5), (2.6), (2.4) называют второй начально-краевой задачей для уравнения теплопроводности (2.1). В терминах теории теплообмена на границах в этом случае заданы тепловые потоки.
Если на границах заданы линейные комбинации искомой функции и ее производной по пространственной переменной
(2.7)
(2.8)
т.е. граничные условия третьего рода, то задачу (2.1), (2.7), (2.8), (2.4) называют третьей начально-краевой задачей для уравнения теплопроводности (2.1). В терминах теории теплообмена граничные условия (2.7), (2.8) задают теплообмен между газообразной или жидкой средой и границами расчетной области с неизвестными температурами u(0,t), u(l,t).
Для пространственных задач теплопроводности в области 
первая начально-краевая задача имеет вид
Аналогично ставится вторая и третья начально-краевые задачи для пространственного уравнения задачи (2.9) – (2.11).
На практике часто ставятся начально-краевые задачи теплопроводности со смешанными краевыми условиями, когда на границах задаются граничные условия различных родов.
2.1.2. Понятие о методе конечных разностей. Применение метода конечных разностей к решению уравнений параболического типа
Основные определения, связанные с методом конечных разностей, рассмотрим на примере конечно-разностного решения первой начально-краевой задачи для уравнения теплопроводности (2.1)-(2.4). Нанесем на пространственно-временную область 0≤x≤l, 0≤t≤T конечно-разностную сетку ω hτ
(2.12)
с пространственным шагом h=l/N и шагом по времени τ=T/K (рис 2.1).
Введем два временных слоя: нижний t k =kτ , на котором распределение искомой функции u(xj,t k ), известно (при k=0 распределение определяется начальным условием (2.4) u(xj,t 0 )=ψ(xj)) и верхний временной слой t k+1 =(k+1)τ, на котором распределение искомой функции u(xjj,t k+1 ), j=0,1,…,N подлежит определению.
Рис. 2.1. Конечно-разностная сетка
Сеточной функцией задачи (2.1)-(2.4) (обозначение ) назовем однозначное отображение целых аргументов j, k в значения функции 
На введенной сетке (2.12) введем сеточные функции 
первая из которых известна, вторая – подлежит определению. Для ее определения в задаче (2.1)-(2.4) заменим (аппроксимируем) дифференциальные операторы отношением конечных разностей (см. раздел «Численное дифференцирование»), получим
(2.13)
(2.14)
Подставляя (2.13), (2.14) в задачу (2.1)-(2.4), получим явную конечно-разностную схему для этой задачи в форме
(2.15)
где для каждого j-го уравнения все значения сеточной функции известны, за исключением одного 
, которое может быть определено явно из соотношений (2.15). В соотношения (2.15) краевые условия (j=0, j=N) входят при значениях j=1 и j=N-1, а начальное условие – при k=0.
Если в (2.14) дифференциальный оператор по пространственной переменной аппроксимировать отношением конечных разностей на верхнем временном слое
(2.16)
то после подстановки (2.13), (2.16) в задачу (2.1)-(2.4), получим неявную конечно-разностную схему для этой задачи
(2.17)
Теперь сеточную функцию на верхнем временном слое можно получить из решения СЛАУ (2.17) с трехдиагональной матрицей. Эта СЛАУ в форме, пригодной для использования метода прогонки, имеет вид
Шаблоном конечно-разностной схемы называют ее геометрическую интерпретацию на конечно-разностной сетке. 
Рис. 2.2. Шаблоны явной и неявной конечно-разностных схем для уравнения теплопроводности
На рисунке 2.2 приведены шаблоны для явной (2.15) и неявной (2.17) конечно-разностных схем при аппроксимации задачи (2.1)-(2.4).
Видео:Лекция №1.1 Явная и неявная схемы для уравнения теплопроводностиСкачать
Явная конечно-разностная схема (2.15), записанная в форме
(2.18)
обладает тем достоинством, что решение на верхнем временном слое получается сразу (без решения СЛАУ) по значениям сеточных функций на нижнем временном слое 
, где решение известно (при k=0 значения сеточной функции формируются из начального условия (2.4.)). Но эта же схема обладает существенным недостатком, поскольку она является условно устойчивой с условием 
, накладываем на сеточные характеристики τ и h.
С другой стороны, неявная конечно-разностная схема (2.17), записанная форме
(2.19)
приводит к необходимости решать СЛАУ, но зато эта схема абсолютно устойчива.
Проанализируем схемы (2.18), (2.19). Пусть точное решение, которое не известно, возрастает по времени, т.е. 
. Тогда, в соответствии с явной схемой (2.18) разностное решение будет заниженным по сравнению с точным, т.к. 
определяется по меньшим значениям сеточной функции на предыдущем временном слое, поскольку решение является возрастающим по времени.
Для неявной схемы (2.19) на возрастающем решении, наоборот, решение завышено по сравнению с точным, поскольку оно определяется по значениям сеточной функции на верхнем временном слое.
На убывающем решении картина изменяется противоположным образом: явная конечно-разностная схема завышает решения, а неявная — занижает (см. рис. 2.3)
Рис. 2.3. Двусторонний метод аппроксимации
На основе этого анализа возникла идея о построении более точной неявно-явной конечно-разностной схемы с весами при пространственных конечно-разностных операторах, причем при измельчении шагов τ и h точное (неизвестное) решение может быть взято в ″вилку″ сколь угодно узкую, т.к. если явная и неявная схемы аппроксимируют дифференциальную задачу и эти схемы устойчивы, то при стремлении сеточных характеристик и h к нулю, решения по явной и неявной схемам стремятся к точному решению с разных сторон.
Рассмотрим неявно-явную схему с весами для простейшего уравнения теплопроводности
(2.20)
где θ — вес неявной части конечно-разностной схемы, 1−θ — вес для явной части, причем 0≤θ≤1. При θ=1 имеем полностью неявную схему, при θ=0 — полностью явную схему, и при θ=1/2 — схему Кранка-Николсона. Для схемы Кранка-Николсона (θ=1/2) порядок аппроксимации составляет , 
т.е. на один порядок по времени выше, чем обычные явная или неявная схемы.
Неявно-явная схема с весами (2.20) абсолютно устойчива при 1/2≤θ≤1 и условно устойчива с условием при 0≤θ 0 имеет вид:
Данное уравнение описывает, в частности, процесс малых поперечных колебаний струны. В этом случае u(x,t) — поперечные перемещения (колебания) струны, а – скорость распространения малых возмущений в материале, из которого изготовлена струна.
Если концы струны движутся по заданным законам, то есть на концах заданы перемещения (или значения искомой функции), то первая начально-краевая задача для волнового уравнения имеет вид:
(3.1)- (3.5)
причем, если концы струны жестко закреплены, то ϕ0(t)=ϕl(t)=0.
Как видно, в задачах для волнового уравнения, кроме начального распределения искомой функции, задается еще распределение начальной скорости перемещения.
Если на концах струны заданы значения силы, которая по закону Гука пропорциональна значениям производной перемещения по пространственной переменной (то есть на концах заданы значения первых производных по переменной x), то ставится вторая начально-краевая задача для волнового уравнения:
В условиях, когда концы струны свободны, функции ϕ0(t)=ϕl(t)=0.
Наконец в условиях, когда концы закреплены упруго, т.е. на концевые заделки действуют силы, пропорциональные перемещениям, ставится третья начально-краевая задача для волнового уравнения: 
Аналогично ставятся двумерные и трехмерные начально-краевые задачи для двумерного и трехмерного волнового уравнения.
3.2 Конечно-разностная аппроксимация уравнений гиперболического типа
Рассмотрим первую начально-краевую задачу для волнового уравнения (3.1)-(3.5). На пространственно-временной сетке (3.12) будем аппроксимировать дифференциальное уравнение (3.1) одной из следующих конечно-разностных схем:
(3.6) с шаблоном на рисунке 3.1а и
(3.7)
Рис. 3.1. Шаблоны конечно-разностных схем для волнового уравнения
Видео:Разностные схемы для решения уравнения переноса. Numerical Schemes for Linear Advection Equation.Скачать
с шаблоном на рисунке 3.1 б
При этом схема (3.6) является явной. С ее помощью решение 
определяется сразу, поскольку значения сеточных функции , на нижних временных слоях должны быть известны. В соответствии с шаблоном для этой схемы порядок аппроксимации равен двум, как по пространственной, так и по временной переменной. При этом явная конечно-разностная схема (3.6) для волнового уравнения условно устойчива с условием 
, накладываемым на сеточные характеристики τ , h..
Схема (3.7) является неявной схемой и обладает абсолютной устойчивостью. Ее можно свести к СЛАУ с трехдиагональной матрицей, решаемой методом прогонки.
В обеих схемах необходимо знать значения 
на нижних временных слоях. Для k=1 это делается следующим образом:
(3.8)
где 
функция из начального условия (3.5).
Для определения 
можно воспользоваться простейшей аппроксимацией второго начального условия (3.6): 
Откуда для искомых значений 
получаем следующее выражение:
Недостатком такого подхода является первый порядок аппроксимации второго начального условия. Для повышения порядка аппроксимации воспользуемся следующей процедурой.
Разложим в ряд Тейлора на точном решении по времени в окрестности t=0 :
. (3.9)
Для определения второй производной в выражении (3.9) воспользуемся исходным дифференциальным уравнением . 
В результате получаем искомую сеточную функцию со вторым порядком точности:
. После определения из начальных условий значений сеточных функций , на двух первых временных слоях вычислительный процесс продолжается согласно схемам (3.8) или (3.9). При этом аппроксимация краевых условий (3.3) и (3.4) производится аналогично тому, как это описывалось выше для уравнений параболического типа. Для иллюстрации этого этапа рассмотрим следующий пример.
Выписать явную конечно-разностную схему для третьей начально-краевой задачи.
Аппроксимация дифференциального уравнения на шаблоне (3.1б) выглядит следующим образом:
где . 
Граничные условия аппроксимируем с первым порядком:
. В результате переход на новый временной слой представляется следующим алгоритмом:
Таким образом, сначала рассчитываются значения искомой функции u во внутренних узлах на новом временном слое, после чего из аппроксимации граничных условий находятся значения функции в крайних узлах.
Для окончательного замыкания вычислительного процесса определим, исходя из начальных условий, значения искомой функции на двух первых временных слоях 
В начальный момент времени значения 
определяются точно:
. Если воспользоваться аппроксимацией первого порядка по времени, то как было показано выше, получим
. Для повышения порядка аппроксимации разложим в ряд Тейлора на точном решении по времени в окрестности t=0 :
где, согласно исходному уравнению
Окончательно получаем 
.
Тема 4. Разностные схемы для уравнений эллиптического типа Задача Дирихле для уравнения Пуассона в квадрате. Аппроксимация. Однозначная разрешимость. Принцип максимума. Устойчивость. Разностная задача Дирихле в прямоугольнике. Сложная область. Связные и несвязные области. Метод установления. Явная и неявная схемы. Схема переменных направлений. Анализ явной схемы установления и анализ схемы переменных направлений.
Классическим примером уравнения эллиптического типа является уравнение Пуассона
или уравнение Лапласа при f(x,y)≡0.
Здесь функция u(x,y) имеет различный физический смысл, а именно: стационарное, независящее от времени, распределение температуры, скорость потенциального (безвихревого) течения идеальной (без трения и теплопроводности) жидкости, распределение напряженностей электрического и магнитного полей, потенциала в силовом поле тяготения и т.п.
Если на границе Г расчетной области 
задана искомая функция, то соответствующая первая краевая задача для уравнения Лапласа или Пуассона называется задачей Дирихле
(4.1)-(4.2)
Если на границе Г задается нормальная производная искомой функции, то соответствующая вторая краевая задача называется задачей Неймана для уравнения Лапласа или Пуассона
(4.3)-(4.4)
При этом n – направление внешней к границе Г нормали.
Более приемлемой является координатная форма краевого условия (4.4)
где 
− направляющие косинусы внешнего вектора единичной нормали к границе Г, i и j орты базисных векторов.
Наконец третья краевая задача для уравнения Пуассона (Лапласа) имеет вид
4.1. Конечно-разностная аппроксимация задач для уравнений эллиптического типа
Рис. 4.1. Центрально-симметричный шаблон
Рассмотрим краевую задачу для уравнений Лапласа или Пуассона (4.1), (4.2) в прямоугольнике 
, на который наложим сетку
(4.5)
На этой сетке аппроксимируем дифференциальную задачу во внутренних узлах с помощью отношения конечных разностей по следующей схеме (вводится сеточная функция 
):
(4.6)
которая на шаблоне имеет второй порядок по переменным и , поскольку шаблон центрально симметричен.
СЛАУ имеет пяти-диагональный вид (каждое уравнение содержит пять неизвестных и при соответствующей нумерации переменных матрица имеет ленточную структуру). Решать ее можно различными методами линейной алгебры, например, итерационными методами, методом матричной прогонки и т.п.
Рис.4.2 Центрально- симметричный шаблон
Видео:Вычислительная математика 20 Уравнения параболического типаСкачать
Рассмотрим разностно-итерационный метод Либмана численного решения задачи Дирихле (4.1), (4.2). Для простоты изложения этого метода примем , тогда из схемы (4.6 ) получим (k-номер итерации)
(4.8)
На каждой координатной линии (например, 
) с помощью линейной интерполяции (см. рис.4.3) граничных значений 
определим 
на нулевой итерации, подставив которые в (4.8), получим распределение 
на первой итерации
Рис. 4.3. К разностно-итерационному методу Либмана
Это распределение снова подставляются в (4.8), получаем распределение 
и т.д. Процесс Либмана прекращается, когда 
,
где — 
наперед заданная точность.
При решении задач с граничными условиями 2-го и 3-го родов наряду с аппроксимацией дифференциального уравнения производится также аппроксимация граничных условий. Здесь в качестве примера приведем разностную схему, аппроксимирующую третью краевую задачу для уравнения Пуассона в прямоугольнике.
Как и ранее в прямоугольнике 
построим сетку 
На этой сетке аппроксимируем дифференциальную задачу во внутренних узлах по рассмотренной выше центрально-разностной схеме
. Граничные условия аппроксимируем с первым порядком с помощью направленных разностей:
. В результате получена СЛАУ, содержащая уравнений (N1+1)(N2+1)-4 относительно неизвестных 
(i=0,1,…,N1 , j=0,1,…,N2 ) при этом угловые узлы с координатами (i,j), равными 
в вычислениях не участвуют). Как и в случае граничных условий первого рода, она имеет пятидиагональный вид и может быть решена, например, итерационным методом Либмана.
Замечание. Метод простых итераций для решения СЛАУ, возникающих при аппроксимации уравнения Пуассона (Лапласа), отличается довольно медленной сходимостью. Этот недостаток может стать существенным при использовании мелких сеток, когда число уравнений в системе становится большим.
Тема 5. Вариационные и вариационно-разностные методы Метод Ритца. Описание метода Ритца. Формулировка метода и применение для решения разностной задачи Дирихле. Построение простейших разностных уравнений диффузии с помощью метода Ритца.
Глава 4, §4.1, §4.2, §4.3, §4.4 В.С. Владимиров, В.В. Жаринов Уравнения математической физики, М.: Физматлит, 2003.
Тема 6. Численные методы решения интегральных уравнений Метод конечных сумм для решения интегральных уравнений Фредгольма и Вольтерра. Метод вырожденных ядер. Резольвента. Нахождение собственных значений и собственных функций. Метод наименьших квадратов. Методы Монте-Карло.
Соболь И.М.. Численные методы Монте-Карло. М.: Наука, 1973.
Соболь И.М.. Метод Монте-Карло. М.: Наука, 1985.
Список литературы
1 .Калиткин Н.Н. Численные методы. М.: Наука, 1978.
2. Демидович Б.П., Марон И.А., Шувалова Э.Э. Численные методы анализа. М.: Наука, 1967.
3. Бахвалов Н.С. Численные методы. Том 1, изд. 2-е, стереотипное, М.,1975.
4. Ермаков СМ., Михайлов Г.А. Статистическое моделирование. Изд. 2-е. М.: Наука, 1982.
5. Соболь И.М.. Численные методы Монте-Карло. М.: Наука, 1973.
6. Соболь И.М.. Метод Монте-Карло. М.: Наука, 1985.
7. Самарский А.А. Теория разностных схем. М.: Наука, 1977.
8. Марчук Г. И. Методы вычислительной математики. М.:Наука, 1989.
Видео:Решение задачи теплопроводности (Явная разностная схема)Скачать
9. Бабенко К.И. Основы численного анализа. М.: Наука. 1986.
10. Крылов В.И., Бобков В.В., Монастырный П.И. Вычислительные методы. Т. 1. М.: Наука, 1976, Т. 2. М.: Наука, 1977.
11.Самарский А.А., Гулин А.В. Численные методы. М.: Наука, 1989.
12.Годунов С.К., Рябенький B.C. Разностные схемы, введение в теорию. М: Наука, 1977.
13. Васильев Ф.П. Численные методы решения экстремальных задач. – М., 1980 – 520 с. с илл.
14. Габассов Р. Кириллова Ф.М. Принцип максимума в теории оптимального управления. – Минск: Наука и техника, 1974.
15. Гамкрелидзе Р.В. Основы оптимального управления. – Тбилиси: Изд-во Тбилисского ун-та, 1977
1.Шакенов К.К. Методы Монте-Карло и их приложения. Алматы: КазГУ,1993.
2. Дробышевич В.И., Дымников В.П., Ривин Г.С. Задачи по вычислительной математике. М.: Наука, 1980.
3.Копченова Н.В., Марон И.А., Вычислительная математика в примерах и задачах. М.: Наука, 1972.
4.Черкасова М.П. Сборник задач по численным методам. Минск: Высшая школа, 1967.
5.ВазовВ., Дж.Форсайт. Разностные методы решения дифференциальных
уравнений в частных производных. М.: ИЛ, 1963.
6.Ортега Дж., Рейнболдт В. Итерационные методы решения нелинейных
систем уравнений со многими неизвестными. М.: Наука, 1975.
7.Митчел Э., Уэйт Р. Метод конечных элементов для уравнений с частными производными. М.: Мир, 1981.
8.Трауб Дж. Итерационные методы решения уравнений. М.: Мир, 1983.
9.Михлин С.Г. Некоторые вопросы теории погрешностей. Л.: ЛГУ, 1988.
10.Михлин С.Г. Вариационные методы в математической физике. М., 1970.
Видео:численные методы решения квазилинейных уравнений гиперболического типаСкачать
🔥 Видео
6-2. Метод сетокСкачать
Разностные схемы для решения уравнений в частных производных гиперболического типаСкачать
Численные методы для систем уравнений гиперболического типаСкачать
Сеточные методы решения дифференциальных уравнений в частных производных.Скачать
Основные понятия теории разностных схем. Fundamentals of the Numerical Schemes for the ODE.Скачать
Как решать уравнения по схеме ГорнераСкачать
Вычислительная математика 17 Теория разностных схемСкачать
Метод Фурье для неоднородного уравнения теплопроводностиСкачать
Подвеска автомобиля. Как работает стабилизатор поперечной устойчивости?Скачать
Уравнение в частных производных Уравнение теплопроводностиСкачать
Приклонский В. И. - Численные методы в физике - Дополнение к лекциямСкачать
Контрольная работа. Уравнения с МОДУЛЕМСкачать
Кобельков Г. М. - Численные методы. Часть 2 - Решение уравнений в частных производныхСкачать
Приклонский В. И. - Численные методы в физике - Лекция 16Скачать
