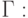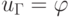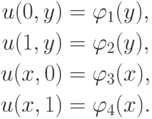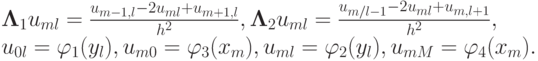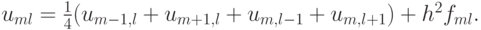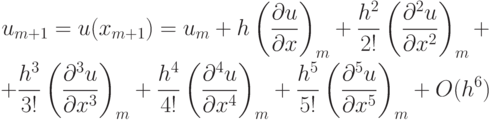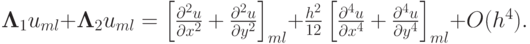Среди всех типов уравнений математической физики эллиптические уравнения с точки зрения вычислителей стоят особняком. С одной стороны, имеется хорошо развитая теория решения эллиптических уравнений и систем. Достаточно легко доказываются теоремы об устойчивости разностных схем для эллиптических уравнений. Во многих случаях получаются априорные оценки точности расчетов и числа итераций при решении возникающих систем сеточных уравнений . С другой стороны, системы сеточных уравнений , возникающие при решении уравнений методами сеток, имеют большую размерность и плохо обусловлены. Для решения таких систем разработаны специальные итерационные методы .
6.1. Постановка задачи. Простейшая разностная схема «крест». Устойчивость схемы «крест»
Будем рассматривать двухмерное уравнение Пуассона
в единичном квадрате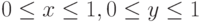 
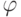
с краевыми условиями первого рода на границе расчетной области 
( 
— заданная на границе функция ).
В случае прямоугольной области граничные условия удобно записать в следующем виде:
Для простоты выкладок введем равномерную расчетную сетку с узлами <xm, yl> , m, l = 0, 1, . , M с равным количеством шагов по каждому пространственному направлению, сеточную область D — совокупность всех узлов сетки, включая граничные, и сеточную функцию < uml >. В этом случае шаги по координатам предполагаются равными. В случае неравных шагов по каждому направлению полученные результаты не изменятся, а запись уравнений станет более громоздкой.
Выбираем простейший пятиточечный шаблон разностной схемы «крест» . На этом шаблоне аппроксимирующее разностное уравнение легко выписать. Для этого производные заменим вторыми разностями:
где h — шаг по координатам, или в операторной форме
Эту же разностную схему можно записать в каноническом виде для разностных схем для эллиптических уравнений:
Такую каноническую запись не следует путать с канонической формой записи итерационного метода, которая встретится ниже.
Такая схема обладает вторым порядком аппроксимации по обеим координатам. Это легко показать, применяя разложение в ряд Тейлора функции — проекции точного решения на сетку — вплоть до членов четвертого порядка включительно. Проведем такое разложение для одного из операторов, стоящих в данном разностном уравнении:
Здесь учтено разложение проекции точного решения в ряд Тейлора
и аналогичное разложение для um — 1.
Для рассматриваемого двухмерного уравнения получим выражение для главного члена невязки
Рассмотрим устойчивость полученной схемы. Отметим, что методы исследования на устойчивость , применяемые для эволюционных (зависящих от времени) уравнений, здесь не работают. Действовать приходится на основе определения устойчивости.
Сформулируем и докажем две леммы, которые облегчат процедуру доказательства устойчивости разностной схемы.
Видео:Сеточные методы решения дифференциальных уравнений в частных производных.Скачать
Опорный конспект лекции
Ф СО ПГУ 7.18.2/06
Видео:6-2. Метод сетокСкачать
Министерство образования и науки Республики Казахстан
Павлодарский государственный университет им. С. Торайгырова
дисциплины «Численные методы решения задач математической физики»
для специальности 050601 Математика
Ф СО ПГУ 7.18.1/07
УТВЕРЖДАЮ
Проректор по УР
Видео:Лекция №1.1 Явная и неявная схемы для уравнения теплопроводностиСкачать
Составители: доцент ,
Видео:Разностные методы решения уравнений в частных производных эллиптического типаСкачать
преподаватель
Кафедра «Информатика и информационные системы»
Опорный конспект лекции
по дисциплине «Численные методы решения задач математической физики »
для студентов специальностей 050601 Математика
Рекомендована на заседании кафедры от “____”___200___г.
Видео:Разностные уравнения | Решение задачСкачать
Заведующая кафедрой ___________
Одобрена методическим советом факультета Физики, математики и информационных технологий “___”______200 _ г. Протокол №___
Видео:Математика в неожиданных местах: Разностная схема для уравнения теплопроводностиСкачать
Председатель МС__________________________
Тема 1. Основные задачи математической физики.
Разностные уравнения. Пространство сеточных функций. Разностные операторы. Разностная аппроксимация оператора Лапласа. Задачи на собственные значения для разностного оператора Лапласа. Разностные формулы Грина. Свойства разностных операторов. Априорные оценки. Аппроксимация дифференциальной начально-краевой задачи разностной схемой. Шаблон. Порядок аппроксимации. Определение устойчивости. Аппроксимация нормированного пространства. Внутренние и внешние аппроксимации. Невязка. Ошибка аппроксимации. Устойчивость. Сходимость.
Решение обыкновенных дифференциальных уравнений зависит лишь от одной переменной 
и так далее. Во многих практических задачах решения — искомые функции зависят от нескольких переменных и уравнения, описывающие данные задачи могут содержать частные производные искомых функции. Они называются уравнениями с частными производными.
Математическая постановка задачи вместе с дифференциальными уравнениями содержит и некоторые дополнительные условия. Если решение ищется в ограниченной области, то задаются условия на ее границе, называемые граничными (краевыми) условиями. Такие задачи носят названия краевых задач для уравнений с частными производными.
Задача, которая состоит в решении уравнений при заданных начальных условиях, называется задачей Коши (ЗК) для уравнений с частными производными. При этом задача решается в неограниченном пространстве , и граничные условия не задаются. Задача, у которой ставится , и начальные и граничные условия называются нестационарными (смешанными) краевыми задачами. Получающиеся при этом решения меняются с течением времени.
Задачи, решение которых существует и единственно в некотором классе начальных и граничных условий и непрерывно зависит как от этих условий, так и от коэффициентов этих уравнений, называются корректно поставленными.
Среди численных методов рассмотрим разностные методы, которые основаны на введение некоторой разностной сетки в рассматриваемой области. Все значения производных, начальные и граничные условия выражаются через значения функции в узлах сетки, в результате чего получается система линейных уравнений, называемая разностной схемой. Построение разностных схем решения уравнений с частными производными основано на введение сетки в рассматриваемой области. Узлы сетки являются расчетными точками.
 |
a £ x £ b xi = a + ih 1 ( I =0,1,…, I )
c £ y £ d yj=c+jh2 (j=0,1,…,J)
Для построения разностной схемы, частные производные в уравнений заменяются, конечно — разностными соотношениями по некоторому шаблону. При этом точные значения искомой функции U заменяются значениями сеточной функции u в узлах разностной сетки.
Разностная схема для решения уравнения теплопроводности при заданных начальных и граничных условий имеет следующий вид:
— распределение температуры на концах рассматриваемого отрезка [0,1] в любой момент, начальные и граничные условия должны быть согласованы, то есть 
. Вводим прямоугольную сетку:
— шаги. 
— значение функции в узлах сетки. Таким образом, 
 |
Получаем систему алгебраических уравнений для определения значений сеточных функции во внутренних узлах. Из граничного условия
(4)
При 
совокупность узлов называется слоем. Из (2) находим последовательно значения 
на 
слое через соответствующие значения 
на 
— том слое. Такие схемы называются явными. Для начала счета при 
необходимо решение на начальном слое, которое определяется начальным условием, имеющим следующий вид:
(5)
В отличие от явной схемы каждое разностное уравнение (3) содержит на каждом новом слое значения неизвестных в трех точках, поэтому нельзя сразу определить эти значения через известное решение на предыдущем слое. Они носят названия неявных схем. При этом разностная схема (3) состоит из линейных трехточечных уравнений, то есть каждое уравнение содержит неизвестную функцию в трех точках данного слоя. Решаются методом прогонки.
В данном примере рассматривали двухслойную схему, т. е. в каждое разностное уравнение входят значения функции их двух слоев – нижнего, на котором решение уже найдено, и верхнего, в узлах которого решение ищется.
Сходимость. Аппроксимация. Устойчивость .
Дифференциальная задача состоит в решение уравнения с частными производными при заданных начальных и граничных условии записывается в операторном виде:
(6)
Операторное уравнение включает исходное уравнение с частными производными, и дополненное, включающее начальные и граничные условия. 
описывает правые части уравнения, начальные и граничные условия, 
включает и расчетную область, и границу. Дифференциальную задачу (6) заменяем разностной задачей, где 
, где 
.
(7)
Значение сеточной функции в узлах сетки 
приближенно заменяют значения искомой функции 
в тех же узлах с погрешностями
. (8)
Вводим 
.
Разностная схема (7) называется сходящейся, если при сгущении узлов сетки, это значение погрешности стремится к нулю, т. е. если 
(9).
Если 
где 
, то разностная схема имеет k-ый порядок точности или говорят, что она сходится со скоростью 
.
Запишем уравнение (7) для погрешности решения на сетке 
. Подставляя в (7), имеем 
(10)
Величина 
называется невязкой (
погрешностью аппроксимации) разностной схемы. Вводим характеристическую величину
(11)
при 
аппроксимация имеет k — ый порядок относительно h. Разностная схема (7) аппроксимирует исходную дифференциальную задачу (6), если при измельчении сетки невязка стремится к нулю, т. е. если
(1 2 )
Абсолютной (безусловной) аппроксимацией называется аппроксимация такого типа, когда невязка стремится к нулю при 
по любому закону без каких — либо условий. При условной аппроксимации налагаются некоторые условия на размеры шагов по пространству и времени. Разностная схема (7) называется устойчивой, если ее решение непрерывно зависит от входных данных, т. е. малому изменению входных данных соответствует малое изменение решения. Устойчивость характеризует чувствительность разностной схемы к различного рода погрешностям.
Теорема: Если решение исходной дифференциональной задачи (6) существует, а разностная схема (7) устойчива и аппроксимирует (6) на данном решение, то разностное решение сходится к точному.
[1] — [5], введение, глава 5
Тема 2. Разностные схемы для уравнений параболического типа
Классы устойчивых двухслойных схем. Энергетическое тождество. Дискретизация одномерного уравнения теплопроводности. Шаблоны. Порядок разностной аппроксимации. Исследование устойчивости методом Фурье. Начально-краевые задачи. Семейство шеститочечных схем. Явная и неявная схемы. Схема Кранка-Николсона. Порядок аппроксимации, устойчивость. Трехслойные схемы для уравнения теплопроводности. Схема Дюфорта и Франкеля. Порядок аппроксимации и устойчивости. Схема «ромб». Погрешности аппроксимации, устойчивости. Схемы с весами. Погрешность аппроксимации и устойчивость.
2.1 Постановка задач для уравнений параболического типа
Классическим примером уравнения параболического типа является уравнение теплопроводности (диффузии). В одномерном по пространству случае однородное (без источников энергии) уравнение теплопроводности имеет вид
. ( 2 .1)
Если на границах х=0 и х=l заданы значения искомой функции u(x, t) в виде
( 2 .2)
т. е. граничные условия первого рода, и, кроме того, заданы начальные условия
то задачу (2.1)-(2.4) называют первой начально-краевой задачей для уравнения теплопроводности (2.1).
В терминах теории теплообмена u(x, t) – распределение температуры в пространственно-временной области 
коэффициент температуропроводности, а (2.2), (2.3) с помощью функций ϕ 0 (t), ϕ l (t) задают температуру на границах x=0 и x=l.
Если на границах х=0 и х=l заданы значения производных искомой функции по пространственной переменной
(2.5) 
(2.6)
т. е. граничные условия второго рода, то задачу (25.1), (2.5), (2.6), (2.4) называют второй начально-краевой задачей для уравнения теплопроводности (2.1). В терминах теории теплообмена на границах в этом случае заданы тепловые потоки.
Если на границах заданы линейные комбинации искомой функции и ее производной по пространственной переменной
(2.7)
(2.8)
т. е. граничные условия третьего рода, то задачу (2.1), (2.7), (2.8), (2.4) называют третьей начально-краевой задачей для уравнения теплопроводности (2.1). В терминах теории теплообмена граничные условия (2.7), (2.8) задают теплообмен между газообразной или жидкой средой и границами расчетной области с неизвестными температурами u(0,t), u(l, t).
Для пространственных задач теплопроводности в области 
первая начально-краевая задача имеет вид
Аналогично ставится вторая и третья начально-краевые задачи для пространственного уравнения задачи (2.9) – (2.11).
На практике часто ставятся начально-краевые задачи теплопроводности со смешанными краевыми условиями, когда на границах задаются граничные условия различных родов.
2 .1.2. Понятие о методе конечных разностей. Применение метода конечных разностей к решению уравнений параболического типа
Основные определения, связанные с методом конечных разностей, рассмотрим на примере конечно-разностного решения первой начально-краевой задачи для уравнения теплопроводности (2.1)-(2.4). Нанесем на пространственно-временную область 0≤x≤l, 0≤t≤T конечно-разностную сетку ω hτ
(2.12)
с пространственным шагом h=l/N и шагом по времени τ=T/K (рис 2.1).
Введем два временных слоя: нижний tk=kτ , на котором распределение искомой функции u(xj, tk), известно (при k=0 распределение определяется начальным условием (2.4) u(xj, t0)=ψ(xj)) и верхний временной слой tk+1=(k+1)τ, на котором распределение искомой функции u(x j j ,tk+1), j =0,1,…,N подлежит определению.
Рис. 2 .1. Конечно-разностная сетка
Сеточной функцией задачи (2.1)-(2.4) (обозначение ) назовем однозначное отображение целых аргументов j, k в значения функции 
На введенной сетке (2.12) введем сеточные функции 
первая из которых известна, вторая – подлежит определению. Для ее определения в задаче (2.1)-(2.4) заменим (аппроксимируем) дифференциальные операторы отношением конечных разностей (см. раздел «Численное дифференцирование»), получим
(2.13)
(2.14)
Подставляя (2.13), (2.14) в задачу (2.1)-(2.4), получим явную конечно-разностную схему для этой задачи в форме
(2.15)
где для каждого j -го уравнения все значения сеточной функции известны, за исключением одного 
, которое может быть определено явно из соотношений (2.15). В соотношения (2.15) краевые условия ( j =0, j = N ) входят при значениях j=1 и j=N-1, а начальное условие – при k=0.
Если в (2.14) дифференциальный оператор по пространственной переменной аппроксимировать отношением конечных разностей на верхнем временном слое
(2.16)
то после подстановки (2.13), (2.16) в задачу (2.1)-(2.4), получим неявную конечно-разностную схему для этой задачи
( 2 .17)
Теперь сеточную функцию на верхнем временном слое можно получить из решения СЛАУ (2.17) с трехдиагональной матрицей. Эта СЛАУ в форме, пригодной для использования метода прогонки, имеет вид
Шаблоном конечно-разностной схемы называют ее геометрическую интерпретацию на конечно-разностной сетке. 
Рис. 2 .2. Шаблоны явной и неявной конечно-разностных схем для уравнения теплопроводности
На рисунке 2.2 приведены шаблоны для явной (2.15) и неявной (2.17) конечно-разностных схем при аппроксимации задачи (2.1)-(2.4).
Явная конечно-разностная схема (2.15), записанная в форме
(2.18)
обладает тем достоинством, что решение на верхнем временном слое получается сразу (без решения СЛАУ) по значениям сеточных функций на нижнем временном слое 
, где решение известно (при k=0 значения сеточной функции формируются из начального условия (2.4.)). Но эта же схема обладает существенным недостатком, поскольку она является условно устойчивой с условием 
, накладываем на сеточные характеристики τ и h.
С другой стороны, неявная конечно-разностная схема (2.17), записанная форме
( 2 .19)
приводит к необходимости решать СЛАУ, но зато эта схема абсолютно устойчива.
Проанализируем схемы (2.18), (2.19). Пусть точное решение, которое не известно, возрастает по времени, т. е. 
. Тогда, в соответствии с явной схемой (2.18) разностное решение будет заниженным по сравнению с точным, т. к. 
определяется по меньшим значениям сеточной функции на предыдущем временном слое, поскольку решение является возрастающим по времени.
Для неявной схемы (2.19) на возрастающем решении, наоборот, решение завышено по сравнению с точным, поскольку оно определяется по значениям сеточной функции на верхнем временном слое.
На убывающем решении картина изменяется противоположным образом: явная конечно-разностная схема завышает решения, а неявная — занижает (см. рис. 2.3)
Рис. 2 .3. Двусторонний метод аппроксимации
На основе этого анализа возникла идея о построении более точной неявно-явной конечно-разностной схемы с весами при пространственных конечно-разностных операторах, причем при измельчении шагов τ и h точное (неизвестное) решение может быть взято в ″вилку″ сколь угодно узкую, т. к. если явная и неявная схемы аппроксимируют дифференциальную задачу и эти схемы устойчивы, то при стремлении сеточных характеристик и h к нулю, решения по явной и неявной схемам стремятся к точному решению с разных сторон.
Рассмотрим неявно-явную схему с весами для простейшего уравнения теплопроводности
( 2 .20)
где θ — вес неявной части конечно-разностной схемы, 1−θ — вес для явной части, причем 0≤θ≤1. При θ=1 имеем полностью неявную схему, при θ=0 — полностью явную схему, и при θ=1/2 — схему Кранка-Николсона. Для схемы Кранка-Николсона (θ=1/2) порядок аппроксимации составляет, 
т. е. на один порядок по времени выше, чем обычные явная или неявная схемы.
Неявно-явная схема с весами (2.20) абсолютно устойчива при 1/2≤θ≤1 и условно устойчива с условием при 0≤θ
Таким образом, схема Кранка-Николсона (2.20) при θ=1/2 абсолютно устойчива и имеет второй порядок аппроксимации по времени и пространственной переменной x.
2 .1.3. Аппроксимация граничных условий, содержащих производные
В задачах математической физики вообще, и в задачах теплопроводности в частности, граничные условия 1-го рода аппроксимируются точно в узлах на границе расчетной области. Граничные условия 2-го и 3-го рода отличаются тем, что в них присутствует производная первого порядка искомой функции по пространственной переменной. Поэтому для замыкания конечно-разностной схемы необходима их аппроксимация. Простейшим вариантом является аппроксимация производных направленными разностями первого порядка:
Тогда в общем случае граничных условий 3-го рода (2.7), (2.8) уравнения, связывающие значения искомой функции в двух крайних узлах разностной сетки, выглядят следующим образом:
Дополняя полученными уравнениями явную конечно-разностную аппроксимацию во внутренних узлах, получим явную разностную схему для третьей начально-краевой задачи (2.1), (2.4), (2.7), (2.8).
В результате алгоритм перехода на новый временной слой 
с использованием явной схемы можно представить в следующем виде:
Т. е. сначала рассчитываются значения искомой функции во всех внутренних узлах на новом временном слое, а затем определяются значения на границах.
При использовании неявной конечно-разностной схемы получаем следующий разностный аналог дифференциальной задачи:
В результате для получения решения на новом временном слое решается система линейных алгебраических уравнений с трехдиагональной матрицей. Аналогичная картина имеет место и при использовании неявно-явной схемы с весами.
Принципиальной особенностью рассмотренного выше подхода является первый порядок аппроксимации граничных условий. Т. е. порядок аппроксимации в граничных узлах ниже порядка аппроксимации во внутренних узлах расчетной области. При этом глобальный порядок аппроксимации (во всей расчетной области) равен наименьшему относительно всех узлов сетки порядку аппроксимации.
Одним из способов повышения порядка аппроксимации граничных условий является использование формул численного дифференцирования второго порядка:
В случае явной схемы алгоритм вычисления решения на новом временном слое при такой аппроксимации граничных условий не приобретает принципиальных изменений. Если же используется неявная схема, то получающаяся при этом СЛАУ теряет трехдиагональный вид (первое и последнее уравнение содержат три неизвестных). Этот недостаток легко устраним, т. к. путем линейной комбинации первого уравнения со вторым (последнего с предпоследним) можно добиться исключения третьего неизвестного из соответствующего уравнения. Однако при этом возможно нарушение диагонального преобладания матрицы и, следовательно, нарушение условий применимости метода прогонки.
Более эффективным является подход, позволяющий повысить порядок аппроксимации граничных условий без увеличения числа узлов в аппроксимационных соотношениях. Для иллюстрации этого подхода рассмотрим следующий пример.
Решить третью начально-краевую задачу для параболического уравнения, содержащего как конвективные члены (пропорциональные производной 
), так и источниковые члены, содержащие искомую функцию 
(2.21)-(2.24) Решение.
Во внутренних узлах конечно-разностной сетки неявная конечно-разностная схема для уравнения (2.21) имеет вид:
(2.25)
Если производные первого порядка в граничных условиях (2.22) и (2.23) аппроксимировать по следующей схеме (с помощью отношения конечных разностей справа и слева)
то граничные условия аппроксимируются с первым порядком, и глобальный порядок будет равен первому порядку несмотря на то, что во всех остальных узлах порядок аппроксимации по пространственным переменным равен двум. Для сохранения порядка аппроксимации, равного двум, в граничных узлах разложим на точном решении значение 
в окрестности точки x=0 в ряд Тейлора по переменной x до третьей производной включительно, 
— в аналогичный ряд в окрестности точки x= l , получим (в предположении что функция u(x, t) в граничных узлах имеет первые производные по времени и вторые — по x):
(2.26)
. (2.27)
Далее, подставим сюда значения второй производной в граничных узлах, полученные из дифференциального уравнения (2.21):
и найдем из полученных выражений (2.26), (2.27) значения первой производной 
в граничных узлах с порядком 
Подставляя 
в (2.22), а 
в (2.23) и аппроксимируя полученные соотношения в соответствующих граничных узлах (при этом 
получим алгебраические уравнения для граничных узлов, в каждом из которых два неизвестных:
(2.28)
(2.29)
Таким образом, (2.28) — конечно-разностная аппроксимация граничного условия 3-го рода (2.22) на левой границе x=0, а (2.29) — конечно-разностная аппроксимация граничного условия 3-го рода (2.23) на правой границе x=l, которые сохраняют тот же порядок аппроксимации, что и в конечно-разностной аппроксимации (2.25) дифференциального уравнения (2.21).
Приписывая к граничным конечно-разностным уравнениям (2.28), (2.29), каждое из которых содержит два значения сеточной функции, алгебраические уравнения (2.25), записанные в виде
(2.30)
получим СЛАУ с трехдиагональной матрицей, решаемую методом прогонки
(2.31)
Изложенный метод аппроксимации краевых условий, содержащих производные по пространственным переменным, повышает не только порядок аппроксимации, но и сохраняет консервативность конечно-разностной схемы, т. е. в конечно-разностной аппроксимации соблюдаются законы сохранения, на основе которых выведены дифференциальные соотношения задачи (2.
Аналогичный подход можно осуществить в краевых задачах для дифференциальных уравнений любых типов.
Тема 3. Разностные схемы для уравнений гиперболического типа Разностные схемы для уравнения колебания струны. Явная схема («крест»). Неявная схема (типа Кранка-Николсона). Порядок аппроксимации. Исследование устойчивости методом Фурье. Семейство схем с весами. Устойчивость. Погрешность аппроксимации. Исследование устойчивости разностных схем для уравнения колебания.
3.1. Постановка задач для уравнений гиперболического типа
Классическим примером уравнения гиперболического типа является волновое уравнение, которое в области 0 0 имеет вид:
Данное уравнение описывает, в частности, процесс малых поперечных колебаний струны. В этом случае u(x, t) — поперечные перемещения (колебания) струны, а – скорость распространения малых возмущений в материале, из которого изготовлена струна.
Если концы струны движутся по заданным законам, то есть на концах заданы перемещения (или значения искомой функции), то первая начально-краевая задача для волнового уравнения имеет вид:
(3.
причем, если концы струны жестко закреплены, то ϕ 0 (t)= ϕ l (t)=0.
Как видно, в задачах для волнового уравнения, кроме начального распределения искомой функции, задается еще распределение начальной скорости перемещения.
Если на концах струны заданы значения силы, которая по закону Гука пропорциональна значениям производной перемещения по пространственной переменной (то есть на концах заданы значения первых производных по переменной x), то ставится вторая начально-краевая задача для волнового уравнения:
В условиях, когда концы струны свободны, функции ϕ 0 (t)= ϕ l (t)=0.
Наконец в условиях, когда концы закреплены упруго, т. е. на концевые заделки действуют силы, пропорциональные перемещениям, ставится третья начально-краевая задача для волнового уравнения: 
Аналогично ставятся двумерные и трехмерные начально-краевые задачи для двумерного и трехмерного волнового уравнения.
3.2 Конечно-разностная аппроксимация уравнений гиперболического типа
Рассмотрим первую начально-краевую задачу для волнового уравнения (3.1)-(3.5). На пространственно-временной сетке (3.12) будем аппроксимировать дифференциальное уравнение (3.1) одной из следующих конечно-разностных схем:
(3.6) с шаблоном на рисунке 3.1а и
(3. 7 )
Рис. 3.1. Шаблоны конечно-разностных схем для волнового уравнения
с шаблоном на рисунке 3.1 б
При этом схема (3.6) является явной. С ее помощью решение 
определяется сразу, поскольку значения сеточных функции, на нижних временных слоях должны быть известны. В соответствии с шаблоном для этой схемы порядок аппроксимации равен двум, как по пространственной, так и по временной переменной. При этом явная конечно-разностная схема (3.6) для волнового уравнения условно устойчива с условием 
, накладываемым на сеточные характеристики τ , h ..
Схема (3.7) является неявной схемой и обладает абсолютной устойчивостью. Ее можно свести к СЛАУ с трехдиагональной матрицей, решаемой методом прогонки.
В обеих схемах необходимо знать значения 
на нижних временных слоях. Для k =1 это делается следующим образом:
(3.8)
где 
функция из начального условия (3.5).
Для определения 
можно воспользоваться простейшей аппроксимацией второго начального условия (3.6): 
Откуда для искомых значений 
получаем следующее выражение:
Недостатком такого подхода является первый порядок аппроксимации второго начального условия. Для повышения порядка аппроксимации воспользуемся следующей процедурой.
Разложим в ряд Тейлора на точном решении по времени в окрестности t=0 :
. (3.9)
Для определения второй производной в выражении (3.9) воспользуемся исходным дифференциальным уравнением. 
В результате получаем искомую сеточную функцию со вторым порядком точности:
. После определения из начальных условий значений сеточных функций, на двух первых временных слоях вычислительный процесс продолжается согласно схемам (3.8) или (3.9). При этом аппроксимация краевых условий (3.3) и (3.4) производится аналогично тому, как это описывалось выше для уравнений параболического типа. Для иллюстрации этого этапа рассмотрим следующий пример.
Выписать явную конечно-разностную схему для третьей начально-краевой задачи.
Аппроксимация дифференциального уравнения на шаблоне (3.1б) выглядит следующим образом:
где. 
Граничные условия аппроксимируем с первым порядком:
. В результате переход на новый временной слой представляется следующим алгоритмом:
Таким образом, сначала рассчитываются значения искомой функции u во внутренних узлах на новом временном слое, после чего из аппроксимации граничных условий находятся значения функции в крайних узлах.
Для окончательного замыкания вычислительного процесса определим, исходя из начальных условий, значения искомой функции на двух первых временных слоях 
В начальный момент времени значения 
определяются точно:
. Если воспользоваться аппроксимацией первого порядка по времени, то как было показано выше, получим
. Для повышения порядка аппроксимации разложим в ряд Тейлора на точном решении по времени в окрестности t=0 :
где, согласно исходному уравнению
Окончательно получаем 
.
Тема 4. Разностные схемы для уравнений эллиптического типа Задача Дирихле для уравнения Пуассона в квадрате. Аппроксимация. Однозначная разрешимость. Принцип максимума. Устойчивость. Разностная задача Дирихле в прямоугольнике. Сложная область. Связные и несвязные области. Метод установления. Явная и неявная схемы. Схема переменных направлений. Анализ явной схемы установления и анализ схемы переменных направлений.
Классическим примером уравнения эллиптического типа является уравнение Пуассона
или уравнение Лапласа при f(x, y)≡0.
Здесь функция u(x, y) имеет различный физический смысл, а именно: стационарное, независящее от времени, распределение температуры, скорость потенциального (безвихревого) течения идеальной (без трения и теплопроводности) жидкости, распределение напряженностей электрического и магнитного полей, потенциала в силовом поле тяготения и т. п.
Если на границе Г расчетной области 
задана искомая функция, то соответствующая первая краевая задача для уравнения Лапласа или Пуассона называется задачей Дирихле
(4.1)-(4.2)
Если на границе Г задается нормальная производная искомой функции, то соответствующая вторая краевая задача называется задачей Неймана для уравнения Лапласа или Пуассона
(4.3)-(4.4)
При этом n – направление внешней к границе Г нормали.
Более приемлемой является координатная форма краевого условия (4.4)
где 
− направляющие косинусы внешнего вектора единичной нормали к границе Г, i и j орты базисных векторов.
Наконец третья краевая задача для уравнения Пуассона (Лапласа) имеет вид
4.1. Конечно-разностная аппроксимация задач для уравнений эллиптического типа
Рис. 4.1. Центрально-симметричный шаблон
Рассмотрим краевую задачу для уравнений Лапласа или Пуассона (4.1), (4.2) в прямоугольнике 
, на который наложим сетку
(4.5)
На этой сетке аппроксимируем дифференциальную задачу во внутренних узлах с помощью отношения конечных разностей по следующей схеме (вводится сеточная функция 
):
(4.6)
которая на шаблоне имеет второй порядок по переменным и, поскольку шаблон центрально симметричен.
СЛАУ имеет пяти-диагональный вид (каждое уравнение содержит пять неизвестных и при соответствующей нумерации переменных матрица имеет ленточную структуру). Решать ее можно различными методами линейной алгебры, например, итерационными методами, методом матричной прогонки и т. п.
Рис.4.2 Центрально — симметричный шаблон
Рассмотрим разностно-итерационный метод Либмана численного решения задачи Дирихле (4.1), (4.2). Для простоты изложения этого метода примем, тогда из схемы (4.6 ) получим (k-номер итерации)
(4.8)
На каждой координатной линии (например, 
) с помощью линейной интерполяции (см. рис.4.3) граничных значений 
определим 
на нулевой итерации, подставив которые в (4.8), получим распределение 
на первой итерации
Рис. 4.3. К разностно-итерационному методу Либмана
Это распределение снова подставляются в (4.8), получаем распределение 
и т. д. Процесс Либмана прекращается, когда 
,
где — 
наперед заданная точность.
При решении задач с граничными условиями 2-го и 3-го родов наряду с аппроксимацией дифференциального уравнения производится также аппроксимация граничных условий. Здесь в качестве примера приведем разностную схему, аппроксимирующую третью краевую задачу для уравнения Пуассона в прямоугольнике.
Как и ранее в прямоугольнике 
построим сетку 
На этой сетке аппроксимируем дифференциальную задачу во внутренних узлах по рассмотренной выше центрально-разностной схеме
. Граничные условия аппроксимируем с первым порядком с помощью направленных разностей:
. В результате получена СЛАУ, содержащая уравнений ( N 1 +1)( N 2 +1)-4 относительно неизвестных 
( i =0,1,…, N 1 , j =0,1,…, N 2 ) при этом угловые узлы с координатами ( i , j ), равными 
в вычислениях не участвуют). Как и в случае граничных условий первого рода, она имеет пятидиагональный вид и может быть решена, например, итерационным методом Либмана.
Замечание. Метод простых итераций для решения СЛАУ, возникающих при аппроксимации уравнения Пуассона (Лапласа), отличается довольно медленной сходимостью. Этот недостаток может стать существенным при использовании мелких сеток, когда число уравнений в системе становится большим.
Тема 5. Вариационные и вариационно-разностные методы Метод Ритца. Описание метода Ритца. Формулировка метода и применение для решения разностной задачи Дирихле. Построение простейших разностных уравнений диффузии с помощью метода Ритца.
Глава 4, §4.1, §4.2, §4.3, §4.4 , Уравнения математической физики, М.: Физматлит, 2003.
Тема 6. Численные методы решения интегральных уравнений Метод конечных сумм для решения интегральных уравнений Фредгольма и Вольтерра. Метод вырожденных ядер. Резольвента. Нахождение собственных значений и собственных функций. Метод наименьших квадратов. Методы Монте-Карло.
. Численные методы Монте-Карло. М.: Наука, 1973.
. Метод Монте-Карло. М.: Наука, 1985.
5. Список литературы
1 .Калиткин методы. М.: Наука, 1978.
2. , , Шувалова методы анализа. М.: Наука, 1967.
3. Бахвалов методы. Том 1, изд. 2-е, стереотипное, М.,1975.
4. Ермаков СМ., Михайлов моделирование. Изд. 2-е. М.: Наука, 1982.
5. . Численные методы Монте-Карло. М.: Наука, 1973.
6. . Метод Монте-Карло. М.: Наука, 1985.
7. Самарский разностных схем. М.: Наука, 1977.
8. Марчук вычислительной математики. М.:Наука, 1989.
9. Бабенко численного анализа. М.: Наука. 1986.
10. , , Монастырный методы. Т. 1. М.: Наука, 1976, Т. 2. М.: Наука, 1977.
11., Гулин методы. М.: Наука, 1989.
12., Рябенький B . C . Разностные схемы, введение в теорию. М: Наука, 1977.
13. Васильев Ф .П. Численные методы решения экстремальных задач. – М., 1980 – 520 с. с илл.
14. Кириллова максимума в теории оптимального управления. – Минск: Наука и техника, 1974.
15. Гамкрелидзе оптимального управления. – Тбилиси: Изд-во Тбилисского ун-та, 1977
1.Шакенов Монте-Карло и их приложения. Алматы: КазГУ,1993.
2. , , Ривин по вычислительной математике. М.: Наука, 1980.
3., , Вычислительная математика в примерах и задачах. М.: Наука, 1972.
4.Черкасова задач по численным методам. Минск: Высшая школа, 1967.
5.ВазовВ., Дж. Форсайт. Разностные методы решения дифференциальных
уравнений в частных производных. М.: ИЛ, 1963.
6.Ортега Дж., Итерационные методы решения нелинейных
систем уравнений со многими неизвестными. М.: Наука, 1975.
7. Метод конечных элементов для уравнений с частными производными. М.: Мир, 1981.
8.Трауб Дж. Итерационные методы решения уравнений. М.: Мир, 1983.
9.Михлин вопросы теории погрешностей. Л.: ЛГУ, 1988.
10.Михлин методы в математической физике. М., 1970.
Видео:6.3 Решение разностных уравненийСкачать
Уравнение Лапласа
Многие стационарные физические задачи, т.е. такие, в которых рассматриваются явления, неизменные с течением времени (исследования потенциальных течений жидкости, определение формы нагруженной мембраны, задачи теплопроводности и диффузии в стационарных случаях и др.) сводятся к решению уравнения Пуассона вида
(2.88)
Если 
, то уравнение (2.88) называется уравнением Лапласа. Для простоты будем рассматривать двумерное уравнение Лапласа
(2.89)
Решение этого уравнения будем искать для некоторой ограниченной области Gизменения независимых переменных х, у. Границей области Gявляется замкнутая линия L. Для полной формулировки краевой задачи кроме уравнения Лапласа нужно задать граничное условие на границе L. Примем его в виде
(2.90)
Задача, состоящая в решении уравнения Лапласа (или Пуассона) при заданных значениях искомой функции на границе расчетной области, называется задачей Дирихле.
Одним из способов решения стационарных эллиптических задач, в том числе и краевой задачи (2.89), (2.90), является их сведение к решению некоторой фиктивной нестационарной задачи (гиперболической или параболической), найденное решение которой при достаточно больших значениях времени tблизко к решению исходной задачи. Такой способ решения называется методом установления.
Поскольку решение U(x,y) уравнения (2.89) не зависит от времени, то можно в это уравнение добавить равный нулю (при точном решении) член ¶U/¶t. Тогда уравнение (2.89) примет вид
(2.91)
Это известное нам уравнение теплопроводности, для которого в разд. 2.3.2, 2.3.3 уже строили разностные схемы. Остается только задать начальное условие. Его можно принять практически в произвольном виде, согласованном с граничными условиями. Примем
(2.92)
Граничное условие (2.90) при этом остается стационарным, т. е. не зависящим от времени.
Процесс численного решения уравнения (2.91) с условиями (2.92), (2.90) состоит в переходе при t→∞ от произвольного значения (2.92) к искомому стационарному решению. Счет ведется до выхода решения на стационарный режим. Естественно, решением ограничиваются при некотором достаточно большом t, если искомые значения на двух последовательных слоях совпадают с заданной степенью точности.
Метод установления фактически представляет итерационный процесс решения задачи (2.91) с условиями (2.92), (2.90), причем на каждой итерации значения искомой функции получаются путем численного решения некоторой вспомогательной задачи. В теории разностных схем показано, что этот итерационный процесс сходится к решению исходной задачи, если такое стационарное решение существует.
Другой способ решения задачи Дирихле состоит в построении разностной схемы путем аппроксимации уравнения (2.89). Введем в прямоугольной области Gсетку с помощью координатных прямых х = const и у = const. Примем для простоты значения шагов по переменным х и у равными h(предполагается, что стороны области Gсоизмеримы). Значения функции Uв узлах (xi, yj) заменим значениями сеточной функции uij. Тогда, аппроксимируя в уравнении (2.89) вторые производные с помощью отношений конечных разностей, получим разностное уравнение (шаблон изображен на рис. 2.27).
(2.93)
Рис. 2.27. Шаблон для уравнения Лапласа
С помощью данного уравнения можно записать систему линейных алгебраических уравнений относительно значений сеточной функции в узлах в виде
(2.94)
Значения сеточной функции в узлах, расположенных на границе расчетной области, могут быть найдены из граничного условия (2.90):
В теории разностных схем доказывается, что решение построенной разностной задачи существует, а сама схема устойчива.
Перейдем теперь, к практическому вычислению искомых значений, т.е. к решению системы (2.94). Каждое уравнение системы (за исключением тех, которые соответствуют узлам, расположенным вблизи границ) содержит пять неизвестных. Одним из наиболее распространенных методов решения этой системы линейных уравнений является итерационный метод. Каждое из уравнений записываем в виде, разрешенном относительно значения uij в центральном узле (см. рис. 2.27):
(2.95)
Алгоритм решения задачи Дирихле с использованием итерационного метода Гаусса-Зейделя решения системы разностных уравнений (2.95) изображен на рис. 2.28. В алгоритме предусмотрен выбор начальных значений uij. Иногда полагают, что uij=0 для всех i, j.
Рис. 2.28. Алгоритм решения задачи Дирихле
Итерационный процесс контролируется максимальным отклонением М значений сеточной функции в узлах для двух последовательных итераций. Если его значение достигнет некоторого заданного малого числа ε,итерации прекращаются и происходит вывод результатов.
Рассмотренные разностные схемы метода сеток используют конечно-разностные аппроксимации входящих в уравнения производных по всем переменным. В ряде случаев уравнение с частными производными удобно привести к системе обыкновенных дифференциальных уравнений, в которых оставлены производные искомой функции лишь по одной переменной.
Такой способ можно использовать и для решения уравнения Лапласа (2.89). Пусть требуется решить для него задачу Дирихле в прямоугольнике ABCD(рис. 2.29). Разобьем прямоугольник на полосы с помощью прямых, параллельных оси х. Для определенности проведем три отрезка l1, l2, l3, которые разделят прямоугольник на четыре полосы постоянной ширины h. Решение Uзадачи Дирихле приближенно заменим набором функций ui,каждая из которых определена на отрезке li и зависит только от одной переменной х, т.е.ui= ui(х) (i = 1,2,3). На отрезках l0 и l4 значения u0(x) и u4(x) заданы граничными условиями.
Рис. 2.29. К решению задачи Дирихле в прямоугольнике ABCD
Построим разностную схему для определения значений функций u(х). Аппроксимируя в уравнении (2.89) вторую производную по у с помощью отношения конечных разностей, получаем
(2.96)
Таким образом, решение задачи Дирихле (2.89), (2.90) сводятся к решению краевой задачи для системы обыкновенных дифференциальных уравнений (2.96) относительно значений искомой функции вдоль прямых l1, l2, l3. В этом состоит метод прямых. Граничные условия для уравнений (2.96) при х = а, х = bможно получить из уравнений
Направление дискретизации у обычно легко выбрать в тех случаях, когда заранее известен характер поведения искомой функции, это направление должно соответствовать направлению наибольшей гладкости функции.
Метод прямых широко используют для решения нестационарных задач. Например, если имеются две независимые переменные х, t, а искомый параметр является гладкой функцией переменной х, то дискретизацию вводят по этой переменной. Тогда исходную задачу заменяют задачей Коши для системы обыкновенных дифференциальных уравнений вида:
📹 Видео
Оператор ЛапласаСкачать
Лекция 124. Преобразование Лапласа. ВведениеСкачать
Метод Ньютона (метод касательных) Пример РешенияСкачать
Решение уравнения Лапласа в шареСкачать
Решение задачи теплопроводности (Явная разностная схема)Скачать
Вычислительная математика 19 Устойчивость разностных схемСкачать
Решение уравнения теплопроводности методом конечных разностейСкачать
Приклонский В. И. - Численные методы в физике - Лекция 16Скачать
Решение уравнения теплопроводности в одномерной постановке в ExcelСкачать
Лекция 125. Преобразование Лапласа. Применение.Скачать
2.1. Метод характеристик. Задача Коши для гиперболического уравнения на плоскости.Скачать
