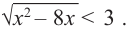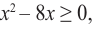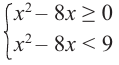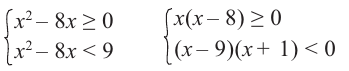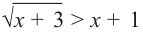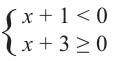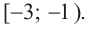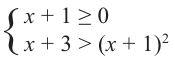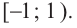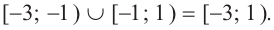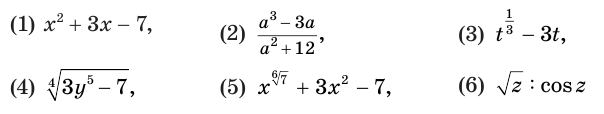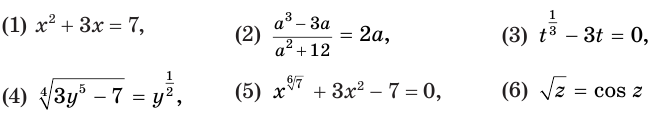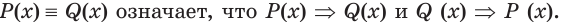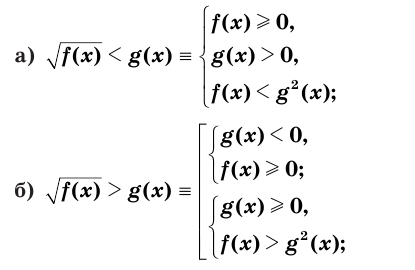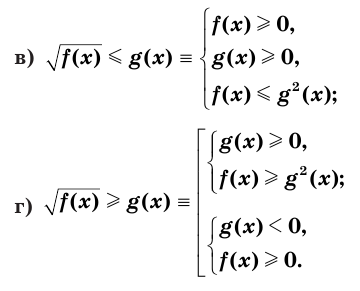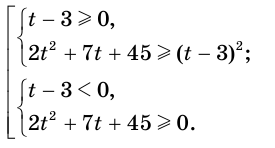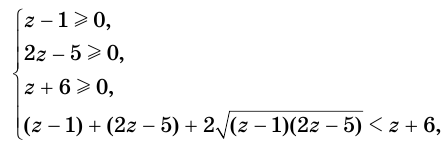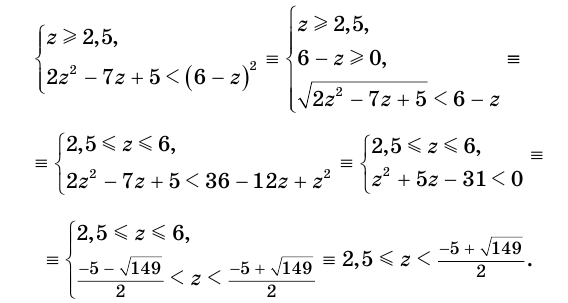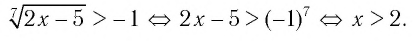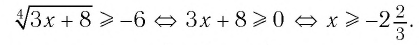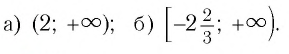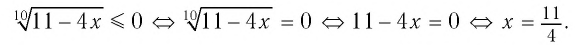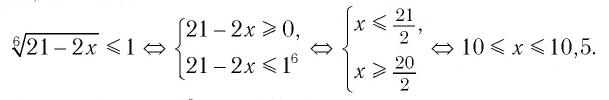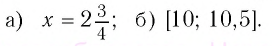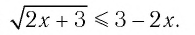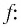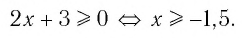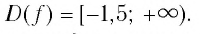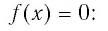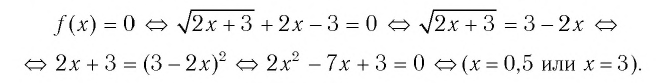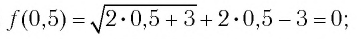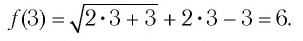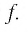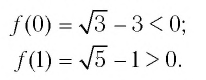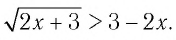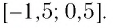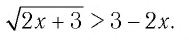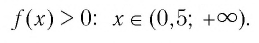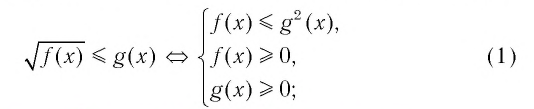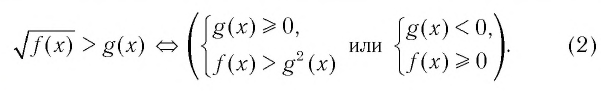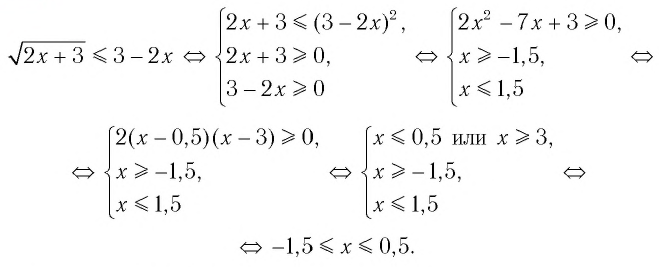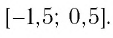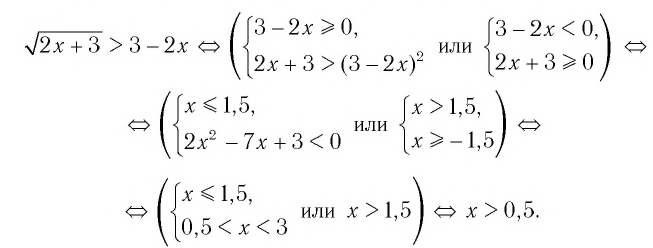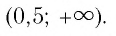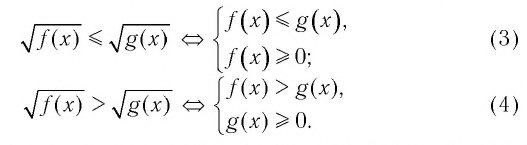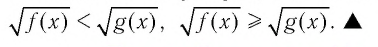Равносильные преобразования иррациональных уравнений и неравенств (8 видео)

Равносильные преобразования иррациональных уравнений и неравенств

1. Неравенство вида: $$ sqrt 0$$ — решением неравенства $$ sqrt Неравенство вида: $$ sqrt le g(x)$$

Решение:

если $$g(x) le 0 $$ — решения нет.
если $$ g(x) ge 0 $$ — решением неравенства $$ sqrt le g(x)$$ будет решение равносильной системы $$ left< beginf(x) ge 0; \ g(x) ge 0; \ f(x) le g^2 (x). \ end right.$$

3. Неравенство вида: $$ sqrt > g(x)$$

Решение: Решением неравенства $$ sqrt > g(x)$$ будет решение равносильной совокупности систем $$ left< begin g(x) ge 0; \ f(x) > g^2 (x). \ end right.$$ или $$ left< begin f(x) ge 0; \ g(x) Неравенство вида: $$ sqrt ge g(x) $$

Решение: Решением неравенства $$ sqrt ge g(x) $$ будет решение равносильной совокупности систем $$ left< begin g(x) ge 0; \ f(x) ge g^2 (x). \ end right.$$ или $$ left< begin f(x) ge 0; \ g(x) Неравенство вида: $$ sqrt cdot g(x) ge 0$$

Решение: Решением неравенства $$ sqrt cdot g(x) ge 0$$ будет решение равносильной совокупности систем $$ left< begin f(x) > 0; \ g(x) ge 0. \ end right.$$ или $$ left< begin f(x) = 0; \ g(x), — определена., \ end right.$$

6. Неравенство вида: $$ sqrt cdot g(x) > 0$$

Решение: Решением неравенства $$ sqrt cdot g(x) > 0$$ будет решение равносильной системы $$ left< begin f(x) > 0; \ g(x) > 0. \ end right.$$

7. Неравенство вида: $$ sqrt cdot g(x) le 0 $$

Решение: Решением неравенства $$ sqrt cdot g(x) le 0$$ будет решение равносильной совокупности систем $$ left< begin f(x) > 0; \ g(x) le 0. \ end right.$$ или $$ left< begin f(x) = 0; \ g(x), — ,определена. \ end right.$$

8. Неравенство вида: $$ sqrt cdot g(x) 0; \ g(x) Неравенство вида: $$ sqrt[3]<> ge sqrt[3]<> $$

Решение: Решением неравенства $$ sqrt[3]<> ge sqrt[3]<> $$ будет решение равносильного ему неравенства $$ f(x) ge g(x) $$

10. Неравенство вида: $$ sqrt[3]<> + sqrt[3]<> ge sqrt[3]<> $$

Решение: Решением неравенства $$ sqrt[3]<> + sqrt[3]<> ge sqrt[3]<>$$ будет решение равносильного ему неравенства $$f(x) cdot g(x) cdot left( right) ge 0$$

Содержание

Равносильные переходы в иррациональных уравнениях
Иррациональные неравенства с примерами решения
Способы решения иррациональных неравенств
Пример №1
Пример №2
Какие неравенства называются иррациональными
Пример №3
Пример №4
Пример №5
Пример №6
🎬 Видео

Видео:Равносильность уравнений и неравенств. Видеоурок 7. Алгебра 10 классСкачать

Равносильные переходы в иррациональных уравнениях

Здесь вы найдете алгоритмы равносильных переходов в иррациональных уравнениях.

Напомним, что два уравнения называются равносильными (эквивалентными) , если множество всех корней первого уравнения совпадает с множеством всех корней второго уравнения.

Подробный разбор примеров смотрите здесь.

или, что тоже самое + показать

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Видео:Алгебра 10 класс (Урок№20 - Иррациональные уравнения и неравенства.)Скачать

Иррациональные неравенства с примерами решения

Неравенства, содержащие переменную под знаком радикала, называются иррациональными неравенствами.

Содержание:

Решение иррациональных неравенств также ищут на множестве действительных чисел и, используя свойства корня и неравенств, сводится к решению системы рациональных неравенств.

Пример: Решите неравенство

Решение: чтобы найти множество решений данного неравенства на множестве допустимых значений, т. е. при условии

Каждое неравенство системы решим методом интервалов и найдем пересечение полученных решений:

Пример: Решите неравенство

Решение: рассмотрим два случая, в зависимости от знака правой части.

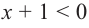
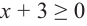
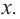
1) при для всех неравенство справедливо для всех Значит, надо решить систему

Ее решением является промежуток

2) при 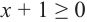обе стороны заданного неравенства можно возвести в квадрат. Тогда получим систему

Ее решением является промежуток

Решением заданного неравенства является

Видео:СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать

Способы решения иррациональных неравенств

С действием возведения в степень связаны разные виды выражений. Будем рассматривать выражения с переменными, при образовании которых используются действия сложения, вычитания, умножения, деления и возведения в степень, причем возведение в степень хотя бы один раз применено к выражению с переменной.

Если показатель степени целый, то возникает рациональное выражение, если дробный, то — иррациональное выражение, а если иррациональный, то — трансцендентное выражение.

К трансцендентным выражениям приводят и действия нахождения значений синуса, косинуса, тангенса, котангенса, арксинуса, арккосинуса, арктангенса, арккотангенса. Рациональные и иррациональные выражения вместе составляют множество алгебраических выражений.

выражения (1) и (2) являются рациональными, выражения (3) и (4) — иррациональными, выражения (5) и (6) — трансцендентными, а выражения (1)—(4) — алгебраическими.

В зависимости от того, из каких выражений составлено уравнение, говорят о рациональных, иррациональных, трансцендентных уравнениях.

уравнения (1) и (2) являются рациональными, уравнения (3) и (4) — иррациональными, а уравнения (5) и (6) — трансцендентными.

Так же говорят о рациональных, иррациональных, трансцендентных неравенствах.

В этом параграфе рассматривается решение иррациональных уравнений и неравенств. При их решении нужно следить за тем, какие преобразования выполняются при этом.

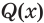
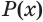
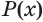
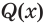
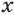
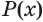
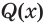
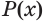
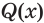
Утверждение равносильно утверждению , если утверждения и истинны при одних и тех же значениях переменной . Равносильность уравнений означает, что они имеют одни и те же корни, а равносильность неравенств — то, что они имеют одни и те же решения. Равносильность утверждений и обозначают = .

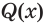
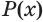
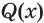
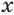
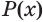
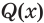
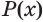
Утверждение следует из утверждения , если утверждение истинно при всех значениях переменной , при которых истинно утверждение . Следование второго уравнения из первого означает, что каждый корень первого уравнения является корнем второго уравнения, но второе уравнение может иметь и дополнительные корни. Так же понимается и следование одного неравенства из другого. Следование утверждения из утверждения обозначают .

Отношения равносильности и следования связаны:

При решении иррациональных неравенств нужно учитывать, что проверка подстановкой найденного множества чисел обычно невозможна из-за его бесконечности. Поэтому при решении неравенств нужно следить за равносильностью проводимых преобразований.

Теорема:

Верны следующие равносильности:

Доказательство проводится по схеме, использованной при доказательстве теоремы 9 с применением соответствующих свойств числовых неравенств.

Пример №1

Решим неравенство 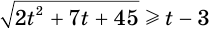. Это неравенство равносильно совокупности неравенств

Первую систему можно заменить равносильной системой 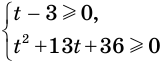, которая равносильна системе , которая, в свою очередь, равносильна неравенству .

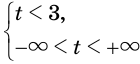
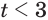
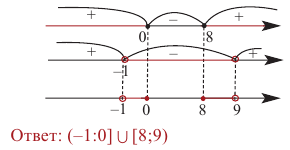
Вторая система совокупности равносильна системе , которая равносильна неравенству .

Решения данного неравенства получим, когда объединим решения и первой и второй систем совокупности, в результате получим множество всех действительных чисел.

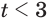
Ответ. .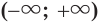

Пример №2

Решим неравенство .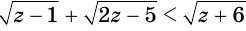

Обратим внимание на то, что на области определения левая и правая части данного неравенства обе неотрицательны, поэтому оно равносильно системе неравенств

решение которой следующее:

Ответ. .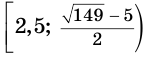

Видео:Как решать уравнение с корнями Иррациональное уравнение Как решать уравнение с корнем х под корнемСкачать

Какие неравенства называются иррациональными

В этой лекции мы будем рассматривать неравенства, содержащие переменную (неизвестное) под знаком корня. Такие неравенства называются иррациональными.

При решении иррациональных неравенств часто используют подход, который мы уже применяли, решая иррациональные уравнения. Он состоит в замене исходного неравенства равносильным ему неравенством (системой или совокупностью неравенств).

Пример №3

Решение:

а) Учитывая свойства корня нечетной степени, получаем:

б) По определению корня четной степени значения выражения

неотрицательны при всех значениях при которых это

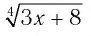
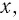
выражение имеет смысл, т. е. когда значения подкоренного выражения неотрицательны. Таким образом, имеем:

Ответ:

Пример №4

Решение:

а) По определению корня четной степени значения выражения 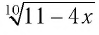отрицательными быть не могут. Поэтому имеем:

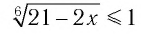
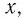
б) Поскольку обе части неравенства неотрицательны при всех значениях при которых его левая часть имеет смысл, то имеем:

Ответ:

При решении иррациональных неравенств часто используется также метод интервалов.

Пример №5

Решить неравенство

Решение:

Обозначим 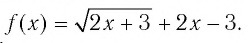Найдем область определения функции

Таким образом,

Найдем нули функции 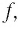т. е. корни уравнения

Проверка:

Значит, 0,5 — единственный нуль функции

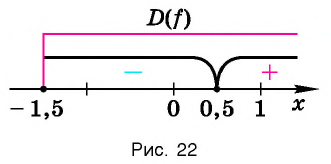
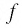
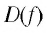
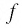
Отметим нуль функции на области определения (рис.22). Определим знаки значений функции на образовавшихся интервалах, для чего вычислим:

Используя рисунок 22, запишем решение неравенства

Ответ:

Пример №6

Решить неравенство

Решение:

Решение этого примера аналогично решению примера 3.

Используя рисунок 22, записываем решение неравенства

Ответ:

▲ При решении иррациональных неравенств часто используются следующие утверждения о равносильности неравенств и систем неравенств:

Решим пример 3, используя равносильность (1):

Ответ:

Решим пример 4, используя равносильность (2):

Ответ:

Для решения заданий такого типа, как, например, в 1.265, можно использовать следующие утверждения о равносильности:

Аналогичные утверждения можно записать и для неравенств

Рекомендую подробно изучить предметы:

Математика
Алгебра
Линейная алгебра
Векторная алгебра
Высшая математика
Дискретная математика
Математический анализ
Математическая логика

Ещё лекции с примерами решения и объяснением:

Производная в математике
Как найти производную функции
Асимптоты графика функции
Касательная к графику функции и производная
Формулы преобразования суммы и разности синусов (косинусов) в произведение
Корень n-й степени из числа и его свойства
Свойства и график функции y=ⁿ√x (n>1, n∈N)
Иррациональные уравнения

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.