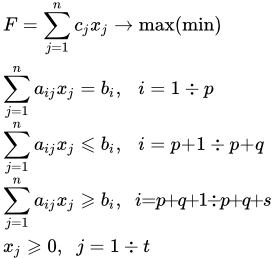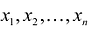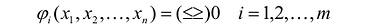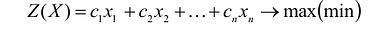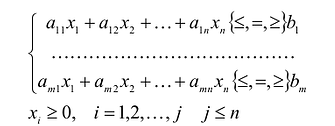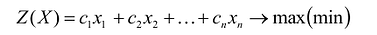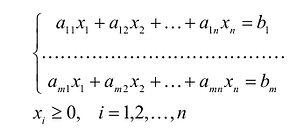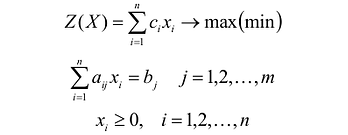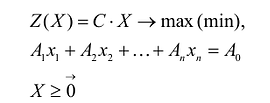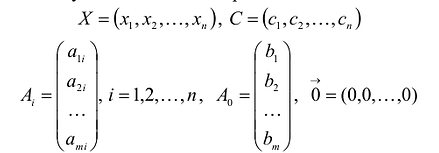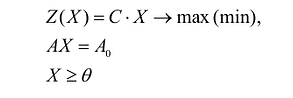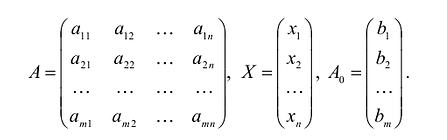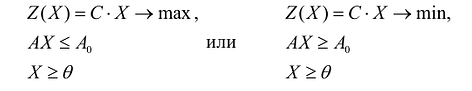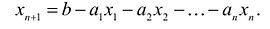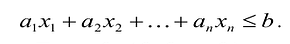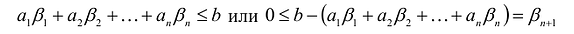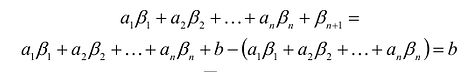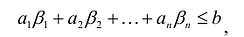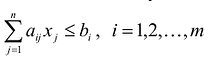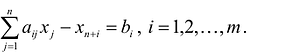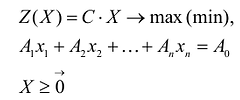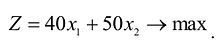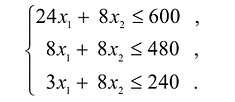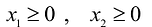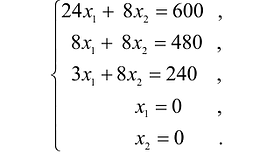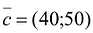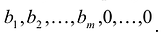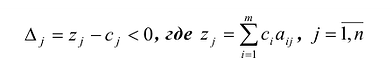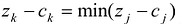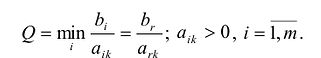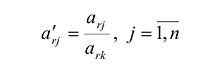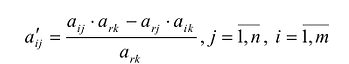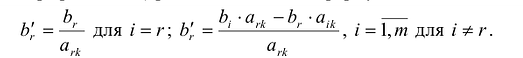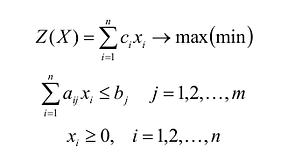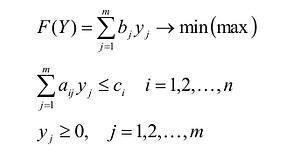В системе ограничений общей задачи линейного программирования могут присутствовать только уравнения

Видео:Cимплексный метод решения задачи линейного программирования (ЗЛП)Скачать

Линейное программирование

Видео:Решение задачи линейного программирования при помощи надстройки Поиск решенияСкачать

Введение в линейное программирование

Все или некоторые уравнения системы ограничений могут быть записаны в виде неравенств.
Чтобы составить математическую модель задачи ЛП, необходимо:

• ввести обозначения переменных;
• учитывая ограничения в использовании экономических показателей задачи и их количественные закономерности, записать систему ограничений;
• исходя из цели экономических исследований, составить целевую функцию.

Задача условной оптимизации называется задачей линейного программирования (ЛП), если целевая функция и все функции ограничений являются линейными функциями: 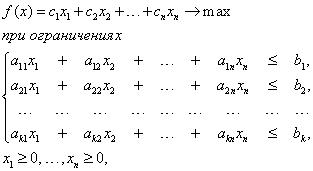(5.1)
где c_i,b_j,a_ij постоянные коэффициенты. Это есть стандартная форма задачи ЛП. В общем случае ограничения могут иметь знак „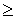» или „=». Однако, умножая неравенство на -1 и заменяя равенство двумя неравенствами „≤» и „≥», можно придти к стандартной форме. Кроме того, взяв вместо f(x) функцию — f(x), можно получить задачу на минимум.
Обозначим через c=(c₁ ,…,c_n) — вектор коэффициентов целевой функции, b =(b₁,…,b_k) — вектор свободных членов ограничений, 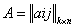— матрицу коэффициентов ограничений и запишем нашу задачу в векторной форме: (5.2)
где — скалярное произведение двух векторов c и x. Такая компактная запись удобна для теоретических исследований.
Несколько примеров задач, которые сводятся к задачам линейного программирования:

Задача оптимального раскроя материала. Фирма изготовляет изделие состоящее из р деталей. Причем в одно изделие эти детали входят в количествах k₁ . k_r . С этой целью производится раскрой m партий материала. В i-ой партии имеется b_i единиц материала. Каждую единицу материала можно раскроить на детали n способами. При раскрое единицы i-ой партии j-м способом получается а_ijr деталей r-го вида. Требуется составить такой план раскроя материала, чтобы из них получить максимальное число изделий.

Транспортная задача. Имеется n поставщиков и m потребителей одного и того же продукта. Известны выпуск продукции у каждого поставщика и потребности в ней каждого потребителя, затраты на перевозки продукции от поставщика к потребителю. Требуется построить план транспортных перевозок с минимальными транспортными расходами с учетом предложения поставщиков и спроса потребителей.

Задача о назначениях на работу. Имеется n работ и n исполнителей. Стоимость выполнения работы i исполнителем j равна c_ij. Нужно распределить исполнителей на работы так, чтобы минимизировать затраты на оплату труда.

3адача о смесях (о рационе). Из m видов исходных материалов каждый из которых состоит из n компонент, составить смесь, в которой содержание компонент должно быть не меньше b₁ . b_n. Известны цены единиц материалов с₁ . с_m и удельный вес j-го компонента в единице i-го материала. Требуется составить смесь, в которой затраты будут минимальными.

Задача о рюкзаке. Имеется n предметов. Вес предмета i равен р_i , ценность – с_i (i=1. n). Требуется при заданной ценности груза выбрать совокупность предметов минимального веса.

Видео:Прямая и двойственная задачи линейного программирования (ЗЛП)Скачать

Основные свойства задачи линейного программирования

Для любой задачи ЛП можно составить двойственную к ней задачу по следующим правилам.
1. Привести исходную задачу ЛП к стандартной форме.
2. Ввести новые переменные по числу основных ограничений исходной задачи.
3. Составить новые ограничения из новых переменных в виде линейных неравенств, знаки которых противоположны знакам неравенств исходной задачи, коэффициентами которых служат элементы транспонированной матрицы исходной задачи, а свободными членами — коэффициенты при целевой функции исходной задачи.
4. Для новых переменных написать условия неотрицательности.
В результате для исходной задачи (5.1) получим следующую двойственную задачу ЛП: (5.3)
Задача (5.1) относительно задачи (5.3) называется прямой задачей ЛП . Векторная форма задачи (5.3) имеет вид: (5.4)
Рассмотрение взаимно двойственных задач ЛП полезно как с теоретической, так и с практической точек зрения. Это видно из следующих утверждений.
1. Если одна из задач (5.1) и (5.3) имеет оптимальное решение, то и другая имеет оптимальное решение, причем
2. Если целевая функция одной из задач неограниченна, то ограничения другой задачи несовместны (т.е. множество допустимых решений пусто).
3. Для того, чтобы допустимое решение и были оптимальными решениями соответствующих задач (5.1) и (2.3) , необходимо и достаточно, чтобы

4. Для любых допустимых решений x 0 и y 0 справедливо неравенство f(x 0 ) ≤ z(y 0 ); если f(x 0 ) = z(y 0 ), то x 0 и y 0 — оптимальные решения задач (5.1) и (5.3).
5. Если прямая задача (5.1) моделирует максимизацию дохода при ограниченных ресурсах, то двойственная задача (5.3) при тех же предпосылках моделирует минимизацию затрат при фиксированном уровне дохода.

Видео:Графический метод решения задач линейного программирования | Высшая математика TutorOnlineСкачать

Основы линейного программирования

Видео:Графический метод решения задачи линейного программирования (ЗЛП)Скачать

Задача линейного программирования

Общая задача линейного программирования формулируется следующим образом.
Найти максимум (или минимум) линейной функции n переменных :
(1.1)
при ограничениях вида
(1.2)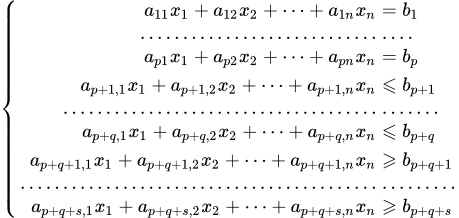
(1.3) .

Переменные задачи часто записывают в виде n-мерного вектора:
.

Линейная функция (1.1) называется целевой функцией. В задаче нужно найти такие значения переменных , которые удовлетворяют системе ограничений (1.2) – (1.3), и при которых целевая функция F имеет наибольшее (или наименьшее) значение.

Система ограничений (1.2) может состоять из равенств
,
и неравенств обоих знаков:
, или
.

В системе ограничений особо выделяют ограничения, связанные с не отрицательностью некоторых переменных (1.3), которые являются следствием физических свойств величин, описываемых этими переменными.

Допустимое решение (план) задачи линейного программирования – это такие значения переменных , которые удовлетворяют системе ограничений (1.2) и условиям не отрицательности (1.3). Допустимое решение также называют планом.
Область допустимых решений (ОДР) – это множество всех допустимых решений.
Оптимальное решение (оптимальный план) или просто решение задачи линейного программирования – это такое допустимое решение задачи, при котором целевая функция имеет экстремальное значение. Оптимальное решение также называют оптимальным планом.

Различные формы задач ЛП

Теорема
Любую общую задачу линейного программирования (1.1) – (1.3) можно привести к каноническому виду (1.4). А любую задачу в канонической форме можно привести к любой из задач в симметричной форме (1.5) или (1.6).

При таких преобразованиях переменные задач могут не совпадать. Могут вводиться новые переменные, а также переменные одной из задач могут линейно выражаться через переменные той же задачи, записанной в другой форме.

Дополнительная переменная (вспомогательная переменная) – это переменная, которая вводится для преобразования неравенства в равенство. Дополнительную переменную также называют вспомогательной переменной. Например, неравенство

переводится в равенство, введением дополнительной неотрицательной переменной :
.

Видео:СИМПЛЕКС МЕТОД: ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯСкачать

Графический метод решения

Свойства решений задач линейного программирования (ЛП) наглядно демонстрирует графический метод решения.

Решение задачи линейного программирования графическим методом.

Графическим методом можно решить задачу, если она имеет две переменные, или ее можно привести к задаче с двумя переменными.

Решим графическим способом следующую задачу.
(2.1)
(2.2)
(2.3) .

Сначала проводим оси системы координат, и построим область допустимых решений (ОДР), которая определяется системой неравенств (2.2) и условиями не отрицательности переменных (2.3). Для построения ОДР, строим прямые, проходящие через границы неравенств:
.
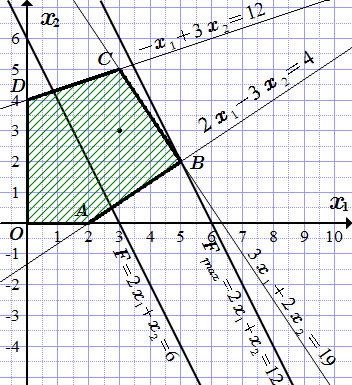
С одной стороны каждой из построенных прямых соответствующее неравенство выполняется, а с другой стороны – нет. Поэтому ОДР ограничена этими прямыми. Также ОДР может быть ограничена осями координат, в силу неравенств . Замечаем, что точка удовлетворяет всем неравенствам (2.2) и (2.3). Поэтому она принадлежит ОДР. Заштриховываем область по границам прямых и осям координат, чтобы в нее вошла точка . Получаем, что ОДР является множеством точек внутри многоугольника вместе с его границей.

Теперь рассмотрим целевую функцию (2.1). Построим ее линию уровня, приравняв F к любому значению, например :
(2.4) .
Строим прямую . С левой стороны от этой прямой . С правой стороны, . И чем больше мы удаляемся вправо и вверх, тем больше значение целевой функции F . Проводим прямую, параллельную прямой (2.4), так, чтобы она была максимально удалена в сторону увеличения значений F , то есть вправо, и при этом проходила хотя бы через одну точку ОДР. Такая прямая проходит через точку B с координатами . Это точка имеет наибольшее значение F среди всех точек ОДР. Поэтому является оптимальным планом с максимальным значением целевой функции:
.

Видео:Лекция 4 Анализ чувствительности решения задачи линейного программированияСкачать

Свойства решений задач ЛП

Графический метод иллюстрирует основные свойства решений задач ЛП. Мы увидели, что поскольку ОДР ограничена конечным числом прямых, то она является выпуклым многоугольником. Далее, целевая функция не может иметь экстремума во внутренней точке ОДР, а достигает экстремума только на границе. Причем экстремум достигается в одной из вершин многоугольника ОДР. Если взять целевую функцию , то экстремум будет на отрезке BC . То есть экстремум может достигаться в двух вершинах, и во всех точках отрезка между ними.

Эти свойства имеют место и в более общем случае, когда число переменных больше двух. Только вместо плоскостей будут гиперплоскости, а вместо многоугольников – многогранники. Так, если рассмотреть задачу ЛП в симметричной форме ⇑, то ОДР является выпуклым многогранником, ограниченным гиперплоскостями и . Целевая функция может достигать экстремум только на границе ОДР. При этом экстремум достигается обязательно на одной из вершин многогранника ОДР. Если экстремум достигается на нескольких вершинах, то оптимальными планами являются также все точки выпуклого многогранника, построенного на этих вершинах.

Далее приводим более строгую трактовку этих рассуждений.

Теорема о выпуклости ОДР
Область допустимых решений задачи линейного программирования является выпуклым множеством.

Теорема об оптимальном решении
Если задача линейного программирования имеет единственное решение, то оптимальный план является угловой точкой ОДР. Если существует несколько оптимальных планов, то в него входят две или более угловых точек, и любая выпуклая линейная комбинация этих угловых точек также является оптимальным планом. То есть задача имеет бесконечно много решений.

Выпуклое множество Возьмем две произвольные точки, принадлежащие некоторому множеству. Если все точки отрезка, соединяющего эти точки, принадлежат этому множеству, то такое множество называется выпуклым. Угловая (крайняя) точка выпуклого множества – это точка, через которую нельзя провести отрезок так, чтобы она была внутренней точкой отрезка, концы которого принадлежат множеству. Угловую точку также называют крайней точкой. Опорный план – это план (допустимое решение), который является угловой точкой (вершиной многогранника) области допустимых решений.

Поскольку в задачах линейного программирования система ограничений содержит конечное число неравенств, то ОДР является многогранником. Тогда угловые точки ОДР являются вершинами многогранника.

Лемма
Оптимальный план задачи линейного программирования является опорным планом, и может быть выбран из совокупности ее опорных планов.

Выпуклая линейная комбинация точек – это множество точек , векторы которых, относительно начала системы координат, определяются по формуле:
, где .

Для двух точек, выпуклая линейная комбинация и является отрезком с концами и . Для трех точек, если и не лежат на одной прямой, выпуклая линейная комбинация этих точек является треугольником с вершинами и . Если же эти точки лежат на одной прямой, то их выпуклая линейная комбинация является отрезком, концы которого совпадают с двумя из этих точек. При этом одна из точек будет внутренней точкой отрезка.

Теорема
Угловая точка ОДР (1.2) – (1.3) является решением системы из n уравнений, полученной из (1.2) – (1.3), вычеркиванием части неравенств, и заменой оставшихся неравенств равенствами.

Задачи линейного программирования в канонической форме

Рассмотрим задачу линейного программирования, записанную в канонической форме ⇑. В произвольном случае, не все строки матрицы коэффициентов , могут быть линейно независимыми. Пусть r – ранг матрицы коэффициентов, то есть число линейно независимых строк. Это означает, что линейными преобразованиями, систему уравнений (1.4) можно привести к эквивалентной системе, содержащей r линейно независимых строк.

Выше мы указали, что оптимальный план является угловой точкой ОДР. Но угловая точка получается из системы ограничений, заменой части неравенств равенствами, чтобы в результате получилась система из n линейно независимых уравнений. Решая эту систему, можно найти координаты угловой точки.

Для задачи в канонической форме это сводится к тому, что мы должны добавить к системе уравнений еще уравнений вида . Полученное решение такой системы уравнений является опорным планом.

Свободные переменные – это переменные задачи ЛП в канонической форме, на которые, в рассматриваемом опорном плане, наложено условие их равенства нулю: . Базисные переменные – это переменные задачи ЛП в канонической форме, которые в рассматриваемом опорном плане, не являются свободными. Они имеют неотрицательные значения, которые определяются из решения системы уравнений (1.4). Невырожденный план (невырожденное решение) – это опорный план, в котором все базисные переменные отличны от нуля. Вырожденный план (вырожденное решение) – это опорный план, в котором есть одна или несколько базисных переменных, равных нулю. Векторы условий – это n векторов, которые являются столбцами матрицы коэффициентов системы (1.4). Вектор ограничений – это вектор, который являются столбцом правой части матрицы коэффициентов системы (1.4). То есть это вектор . Базис – это r векторов, которые являются столбцами матрицы коэффициентов системы (1.4) при базисных переменных. То есть базис – это векторы условий при базисных переменных.

Если в рассматриваемой угловой точке план не вырожден, то в ней имеется только один набор базисных переменных. Если же план вырожден, то в этой точке имеется два или более набора базисных переменных.

Теорема о числе базисных переменных
При решении задачи линейного программирования в канонической форме ⇑, в любом опорном плане имеется r базисных переменных ⇑. Отсюда следует, что в опорном плане как минимум переменных равны нулю. Здесь n – число переменных; r – ранг матрицы системы ограничений (1.4), из которой определяются значения базисных переменных.

Видео:Практика 2 Способы переходов между формами задач линейного программированияСкачать

Методы решения задач

Графический метод

Решение задачи графическим методом мы рассмотрели выше ⇑. Он применим, если в задаче имеются две переменные. Также он применим, если имеется n переменных и система ограничений содержит линейно независимых уравнения. Тогда, решая систему ограничений, мы можем выразить переменных через и , или через две другие переменные. В результате получим задачу с двумя переменными, которую можно решить графическим методом.

Метод перебора вершин

В этом методе мы используем тот факт, что оптимальный план является угловой точкой ОДР. А если задача имеет множество решений, то среди них имеются угловые точки.

В методе перебора вершин мы находим все угловые точки, и вычисляем в них значения целевой функции. Далее, из этих значений, определяем наибольшее или наименьшее значение целевой функции.

Решение задачи

Решим задачу (2.1) – (2.3) методом перебора вершин. При этом мы можем использовать результаты, полученные при решении графическим методом ⇑. Там мы нашли, что ОДЗ является многоугольником OABCD . И мы нашли координаты его вершин. Для каждой вершины мы можем вычислить значение целевой функции (2.1). Сравнивая их, можно определить наибольшее значение.

Но мы применим более общий метод, который работает при любом числе переменных, а не только для двух.

Для этого приведем задачу к канонической форме, вводя три дополнительные неотрицательные переменные :
(П.1)
(П.2)
(П.3) .

В этой задаче переменных. Система ограничений (П.2) содержит 3 линейно независимых уравнения. Поэтому в произвольной угловой точке имеется свободные переменные, и 3 базисные. Перебираем все возможные сочетания свободных переменных, приравниваем их к нулю, и, решая систему (П.2), определяем значения базисных переменных.

1) В качестве свободных переменных возьмем и . Приравниваем их к нулю, и подставляем в (П.2); получаем: . Поскольку все , то мы нашли угловую точку ОДР или, что тоже самое, вершину многогранника ОДР: . На построении ⇑ ей соответствует точка O .

2) Возьмем свободные переменные и . Подставляя их нулевые значения в (П.2), получаем систему:

Решаем ее: . Поскольку все , то это угловая точка: , На построении ⇑ ей соответствует точка D .

3) Возьмем свободные переменные и . Подставляем их нулевые значения в (П.2). Решая систему, получаем: . Поскольку , то эта точка не принадлежит ОДЗ. Поэтому она не может быть планом задачи. Отбрасываем ее. На рисунке ⇑ ей соответствует точка пересечения прямой AB с осью .

4) Свободные переменные . Подставляя их нулевые значения в (П.2), находим: . Здесь также есть отрицательная переменная . Эта точка также не принадлежит ОДЗ. Отбрасываем ее. Это точка пересечения прямой BC с осью .

5) Свободные переменные . Подставляя в (П.2), находим решение системы: . Поскольку , то и эта точка не принадлежит ОДЗ. Отбрасываем ее. Это точка пересечения прямой DC с осью .

6) . Решение системы: . Поскольку все , то мы нашли угловую точку, которой на построении ⇑ соответствует точка A .

7) . Решение системы: . , точка не принадлежит ОДЗ. На рисунке ей соответствует точка пересечения прямой BC с осью .

8) . Решение системы: . , точка не принадлежит ОДЗ. Это точка пересечения прямых AB и DC.

9) . Решение системы: . Все . Это угловая точка – точка C .

10) . Решение системы: . Все . Это угловая точка. На построении ⇑ ей соответствует точка B .

Итак, мы нашли все угловые точки ОДР. Находим в них значения целевой функции.
;
;
;
;
.

Наибольшим является значение целевой функции в точке B . Решение задачи: .

Симплексный метод

Для решения задачи симплексным методом, сначала задачу приводят к канонической форме. Далее выбирают любой опорный план с некоторым набором базисных переменных. Потом определяют свободную переменную, которую нужно включить в базис, чтобы при такой замене произошло наибольшее увеличение целевой функции. Определяют переменную, выходящую из базиса и с помощью линейных преобразований, совершают переход к новым базисным переменным. В результате получают новый план, значение целевой функции которого ближе к экстремальному. Процесс повторяют до тех пор, пока целевая функция не достигнет экстремального значения.

В геометрической интерпретации это означает следующее.
1. Вначале мы выбираем любую вершину многогранника ОДР.
2. Добавляя в базис новую переменную, выбираем направление до смежной вершины вдоль ребра многогранника, двигаясь по которому целевая функция наиболее быстро возрастает.
3. Переходим на новую вершину по выбранному в пункте 2 направлению, исключая из базиса одну из переменных.
4. Повторяем пункты 2 и 3, пока не достигнем экстремума.

Решение задачи

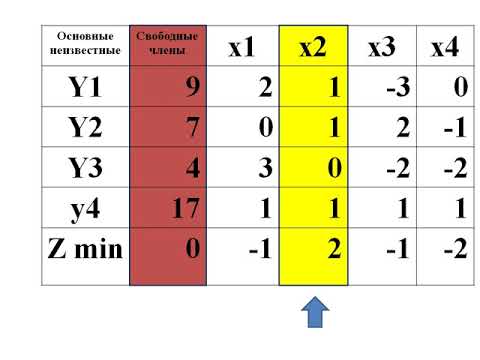
Рассмотрим задачу (2.1) – (2.3). Как и при решении методом перебора вершин, вводим три дополнительных неотрицательных переменных . Получаем задачу в канонической форме:
(С.1)
(С.2)
(С.3) .
Решаем задачу симплексным методом.

1. Вначале нам нужно найти любой опорный план, удовлетворяющий системе ограничений (С.2) – (С.3). Самый простой способ – это взять в качестве базиса дополнительные переменные . При этом из системы (С.2) мы сразу можем выразить базисные переменные через свободные:
(С.4)
Приравнивая свободные переменные и к нулю, получаем первый опорный план, который мы обозначим буквой O : , или в сокращенной форме . Значение целевой функции: .
На рисунке ⇑, этому плану соответствует точка .

2. Теперь попробуем найти смежную вершину многогранника ОДР, в которой значение целевой функции было бы больше . Для этого нужно переместиться из вершины O вдоль одного из ребра многогранника на небольшое расстояние по направлению к смежной вершине и посмотреть, увеличилась ли при этом целевая функция?

2.1. Проверим, как изменится целевая функция, если свободной переменной вместо нулевого, присвоить положительное значение . При этом считаем, что мало отличается от нуля. То есть сделаем оценку свободной переменной . Положим, . Тогда, чтобы выполнялась система ограничений (С.4), необходимо также изменить базисные переменные:
.
Свободная переменная по прежнему равняется нулю. Подставляя в (С.4), и удаляя равные слагаемые в обеих частях равенств, получаем:
(С.5)
Обозначим эту новую точку как . Найдем разность значений целевой функции в точках и :

.
Таким образом, если переменной присвоить положительное значение , то целевая функция увеличится на .

2.2. Проделаем тоже самое с переменной . То есть сделаем оценку для свободной переменной . Положим, . Чтобы выполнялась система ограничений (С.4), также изменим базисные переменные. Положим . Свободная переменная при этом равняется нулю. Подставляя в (С.4), и удаляя равные слагаемые в обеих частях равенств, получаем:
(С.6)
Обозначим эту новую точку как . Найдем разность значений целевой функции в точках и :

.
Если переменной присвоить положительное значение , то целевая функция увеличится на .

2.3. Итак, мы нашли, что если переменной или присвоить положительное значение, то целевая функция увеличится. Это означает, что первый опорный план не оптимален. Целевую функцию можно увеличить введением в базис или . При увеличении на единицу, целевая функция увеличится на . При увеличении на единицу, целевая функция увеличится на . В первом случае увеличение больше. Поэтому вводим в базис переменную . То есть считаем, что она может принимать отличные от нуля положительные значения.

3. Теперь определим следующий опорный план, то есть новую вершину многогранника ОДР с более высоким значением F . Определяем переменную, выходящую из базиса. Для этого нужно присвоить переменной максимально большое положительное значение, но чтобы при этом удовлетворялась система ограничений (С.4). При этом одна из переменных обратится в нуль. Ее мы исключим из состава базисных переменных. Переменная по прежнему имеет нулевое значение. Подставим в (С.4) :

Далее будем увеличивать до тех пор, пока одна из переменных не обратиться в нуль. Если и дальше продолжить увеличение , то эта переменная станет отрицательной, что не допустимо.

Поскольку , то переменная всегда будет положительной. Переменная обращается в нуль при . Переменная – при . Минимальное из этих величин . При этом значении, . Если положить , то переменная станет отрицательной, что не допустимо.

Выводим , и вводим в состав базисных переменных. Для этого над системой (С.4) выполняем линейные преобразования, чтобы выразить базисные переменные через свободные . В результате линейных преобразований получаем эквивалентную систему:
(С.7)
Приравнивая свободные переменные к нулю, получаем второй опорный план. Обозначим его буквой A : . Значение целевой функции:
.
На рисунке ⇑, этому плану соответствует точка . То есть в результате мы перешли из вершины в вершину многогранника ОДР.

4. Повторяем шаги 2 и 3.

4.1. Попробуем ввести в базис. Положим . Подставляем в (С.7):

Изменение целевой функции:
.

4.2. Попробуем ввести в базис . Положим . Подставляем в (С.7):

Изменение целевой функции:
.

Итак, если ввести в базис , то целевая функция увеличится. А если – уменьшится. Поэтому вводим в базис .

5. Определяем переменную, выходящую из базиса. Для этого присвоим переменной максимально большое положительное значение, но чтобы при этом удовлетворялась система ограничений (С.7). Переменная по прежнему сохраняет нулевое значение. Подставим в (С.7) :

Переменная положительна при любых значениях . Переменная обращается в нуль при ; переменная – при . Наименьшее: . При этом переменная принимает нулевое значение и выходит из базиса.

Выводим из базиса. Для этого выражаем базисные переменные через свободные , преобразовав систему (С.7):
(С.8)
Приравнивая свободные переменные и , получаем третий опорный план, который обозначим буквой B : . Значение целевой функции:
.
На рисунке ⇑, этому плану соответствует точка .

6. Повторяем шаги 4 и 5.

6.1. Попробуем ввести в базис . Положим . Подставляем в (С.8):

Изменение целевой функции:

.
. Введение в базис не приведет к увеличению значения целевой функции.

6.2. Попробуем ввести в базис . Положим . Подставляем в (С.8):

Изменение целевой функции:

.
И здесь . Введение в базис также не приведет к увеличению значения целевой функции. Поэтому последний план B оптимален.

Транспортная задача

Транспортную задачу можно решить симплексным методом. Однако имеются методы, которые позволяют получить решение другими, как правило, более легкими способами, используя специфичный вид системы ограничений (Т.2) – (Т.3). Одним из таких методов является метод потенциалов. В нем, как и в симплексном методе ⇑, используется метод последовательного улучшения плана. Мы кратко рассмотрим применение этого метода на примере решения простой транспортной задачи.

Решение транспортной задачи методом потенциалов

Пусть у нас имеется поставщика с мощностями , и потребителя с мощностями . Стоимость перевозки единицы груза от -го поставщика к -му потребителю задана в таблице:
(Т.5)
Требуется найти план перевозок, при котором суммарные затраты на перевозки минимальны.

Вначале нужно подсчитать суммы мощностей поставщиков и потребителей. Если сумма мощностей поставщиков равна сумме мощностей потребителей, то такая задача называется задачей с правильным балансом, или задачей с закрытой моделью. Задача, в которой суммы мощностей поставщиков и потребителей не совпадают, называется задачей с неправильным балансом, или задачей с открытой моделью. Если у задачи открытая модель, то ее сначала нужно привести к закрытой модели, добавлением фиктивного поставщика или потребителя с нулевыми стоимостями перевозок. В нашем случае, сумма мощностей поставщиков равна сумме мощностей потребителей:
.
Модель закрытая, задачу можно решать методом потенциалов.

Задача имеет неотрицательных переменных:
.

Задача (Т.1) – (Т.4) имеет канонический вид. Подсчитаем число базисных переменных. Система ограничений (Т.2) – (Т.3) содержит уравнений:
(Т.6)
Существует теорема, согласно которой, ранг r системы ограничений транспортной задачи равен . То есть система (Т.6) имеет линейно независимых уравнения. Тогда по теореме о числе базисных переменных ⇑, угловая точка ОДР имеет r = 4 базисных переменных, и свободных.

Поясним, почему ранг системы равен . Это означает, что эти уравнения имеют одну линейную зависимость. Найдем ее. Поскольку модель закрытая, то . Подставим (Т.2) и (Т.3):
;
.
Отсюда видно, что если сложить первые два уравнения (Т.6), и вычесть последние три, то получим тождество . Что означает, что система (Т.6) имеет линейную зависимость.

Применяем метод последовательного улучшения плана.

Метод северо-западного угла

1. Вначале нам нужно найти любой опорный план, удовлетворяющий системе ограничений (Т.6) и условию не отрицательности переменных. Существует несколько методов, позволяющих это сделать. Мы применим метод северо-западного угла.

Заносим исходные данные в таблицу и даем максимально возможную поставку в левую верхнюю клетку . В ней находится объем перевозки от 1-го поставщика к 1-му потребителю. В общем случае, максимально возможная поставка в клетку равна . В нашем случае, мощность первого поставщика равна мощности первого потребителя . Поэтому наибольшая поставка в клетку равна 5. Заносим 5 в клетку .

Теперь нам нужно вычеркнуть либо первую строку, либо первый столбец. В нашем случае, как первый поставщик, так и первый потребитель исчерпали свои мощности. Однако вычеркнуть мы можем только одну строку или один столбец. Вместе их вычеркнуть нельзя. Вычеркиваем по своему усмотрению первую строку.

Далее заполняем левую верхнюю клетку в оставшейся части таблицы, среди не зачеркнутых клеток. Это клетка . В ней находится объем перевозки от 2-го поставщика к 1-му потребителю. Нам нужно дать в нее максимально возможную поставку. Но потребности первого потребителя уже полностью удовлетворены первым поставщиком. Поэтому наибольшая поставка в клетку равна нулю. Заносим 0 в клетку . Здесь возник случай, когда переменная является базисной, но ее значение равно нулю.

Заполняем верхнюю левую ячейку предыдущей таблицы, и вычеркиваем первый столбец.

Далее нам нужно вычеркнуть либо строку, либо столбец, содержащий заполненную клетку . Поскольку потребности первого потребителя удовлетворены, то вычеркиваем первый столбец.

Снова заполняем левую верхнюю клетку в оставшейся части таблицы, среди не зачеркнутых клеток. Это клетка . Мощность второго потребителя равна 6, неизрасходованная мощность второго поставщика: 10. Минимальное из этих чисел: 6. Даем в клетку поставку 6, и вычеркиваем 2-го потребителя, поскольку его потребности удовлетворены.

Первый опорный план.

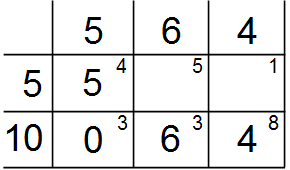
Остается клетка , которую можно заполнить единственно возможным значением 4.

В результате мы получили первый опорный план. Базисные переменные: . Свободные переменные: . Значение целевой функции:
.

Определение потенциалов

Определяем потенциалы . Для этого нужно найти любое решение системы уравнений, используя только заполненные клетки таблицы, то есть базисные переменные:
(Т.7) .

Запишем уравнения (Т.7) для заполненных клеток:
(Т.8)
Здесь 4 уравнения и 5 неизвестных. Поэтому одной переменной можно присвоить произвольное значение. Полагаем . Решаем систему (Т.8).
.

Находим оценки свободных клеток (то есть оценки свободных переменных) по формуле:
.

.

Поскольку есть отрицательная оценка , то план не оптимален. Вводим переменную с отрицательной оценкой в базис.

Переход к новому базису

Чтобы перейти к новому базису, в симплексном методе, мы выполняли линейные преобразования над системой ограничений. В транспортной задаче переход выполняется с помощью цикла.

Цикл с начальной вершиной в заданной пустой клетке – это ломаная, все вершины которой расположены в занятых клетках, кроме одной начальной вершины. И при этом две соседние вершины цикла расположены или в одной строке, или в одном столбце. 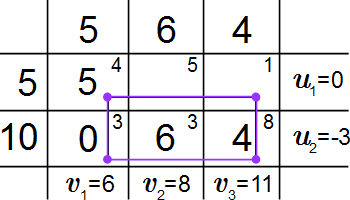Потенциалы и контур клетки (1,3).

Строим цикл для клетки . Пронумеруем его вершины, начиная со свободной клетки.

Переходим к новому базису, выполняя перераспределение поставок. Для этого находим минимальное значение поставки среди четных вершин цикла. В нашем случае это поставка 4 в клетке . В четных клетках уменьшаем поставки на 4, а в нечетных – увеличиваем на 4. Такое перераспределение поставок называют сдвигом по циклу. При этом поставка в клетке становится равной нулю. Ее мы выводим из базиса, а клетка становится заполненной, то есть входит в базис.

Второй опорный план.

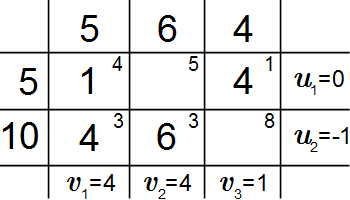
В результате получаем второй опорный план. Базисные переменные: . Свободные переменные: . Значение целевой функции:
.
Для первого опорного плана было . Мы видим, что значение целевой функции стало меньше.

Определение потенциалов нового плана

Определяем потенциалы для нового опорного плана. Запишем уравнения (Т.7) для заполненных клеток:
(Т.9)
Полагаем . Решаем систему (Т.9).
.

Находим оценки свободных клеток по формуле:
.

.

Поскольку отрицательных оценок нет, то план оптимален.

Наименьшее значение целевой функции . Оптимальный план показан в таблице 2 ⇑.

Использованная литература:
С. Гасс. Линейное программирование (методы и приложения). Москва, «Государственное издательство физико-математической литературы», 1961.
Общий курс высшей математики для экономистов. Под общей редакцией В. И. Ермакова. Москва, «ИНФРА-М», 2007.
К. Н. Лунгу. Линейное программирование. Руководство к решению задач. Москва, «ФИЗМАТЛИТ», 2005.
Д. Б. Юдин, Е. Г. Гольштейн. Задачи и методы линейного программирования. Москва, «Советское радио», 1961.

Автор: Олег Одинцов . Опубликовано: 08-04-2021

Видео:Симплексный метод (табличный оформление №1) решения задачи линейного программирования.Скачать

Линейное программирование — основные понятия с примерами решения

Содержание:

Исследование различных процессов, в том числе и экономических, обычно начинается с их моделирования, т.е. отражения реального процесса через математические соотношения. При этом составляются уравнения или неравенства, которые связывают различные показатели (переменные) исследуемого процесса, образуя систему ограничений. В этих процессах выделяются такие переменные, меняя которые можно получить оптимальное значение основного показателя данной системы (прибыль, доход, затраты и т.д.). Соответствующие методы, позволяющие решать указанные задачи, объединяются под общим названием «математическое программирование» или математические методы исследования операций.

Математическое программирование включает в себя такие разделы математики, как линейное, нелинейное и динамическое программирование. Сюда же относят и стохастическое программирование, теорию игр, теорию массового обслуживания, теорию управления запасами и некоторые другие.

Математическое программирование — это раздел высшей математики, посвященный решению задач, связанных с нахождением экстремумов функций нескольких переменных, при наличии ограничений на переменные.

Методами математического программирования решаются задачи о распределении ресурсов, планировании выпуска продукции, ценообразования, транспортные задачи и т.д.

Построение математической модели экономической задачи включает следующие этапы:

1. выбор переменных задачи;
2. составление системы ограничений;
3. выбор целевой функции.

Переменными задачи называются величины

Система ограничений включает в себя систему уравнений и неравенств, которым удовлетворяют переменные задачи и которые следуют из ограниченности ресурсов или других экономических или физических условий, например, положительности переменных и т.п.

Целевой функцией называют функцию переменных задачи, которая характеризует качество выполнения задачи, и экстремум которой требуется найти.

Общая задача математического программирования формулируется следующим образом: найти экстремум целевой функции: 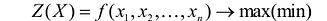и соответствующие ему переменные при условии, что эти переменные удовлетворяют системе ограничений:

Если целевая функция и система ограничений линейны, то задача математического программирования называется задачей линейного программирования и в общем виде может быть записана следующим образом:

Данная запись означает следующее: найти экстремум целевой функции задачи и соответствующие ему переменные X = (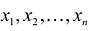). при условии, что эти переменные удовлетворяют системе ограничений и условиям неотрицательности.

Допустимым решением (планом) задачи линейного программирования называется любойX = (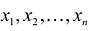). удовлетворяющий системе ограничений и условиям неотрицательности. Множество допустимых решений (планов) задачи образует область допустимых решений.

Оптимальным решением (планом) задачи линейного программирования называется такое допустимое решение задачи, при котором целевая функция достигает экстремума.

Видео:Урок 1. Решение задачи линейного программирование в Excel с помощью надстройки «Поиск решения»Скачать

Задача линейного программирования

В общем случае задача линейного программирования записывается так, что ограничениями являются как уравнения, так и неравенства, а переменные могут быть как неотрицательными, так и произвольно изменяющимися. В случае, когда все ограничения являются уравнениями и все переменные удовлетворяют условию неотрицательности, задачу линейного программирования называют канонической. Каноническая задача линейного программирования в координатной форме записи имеет вид:

Используя знак суммирования эту задачу можно записать следующим образом:

Каноническая задача линейного программирования в векторной форме имеет вид:

В данном случае введены векторы:

Здесь С — X — скалярное произведение векторов С и X.

Каноническая задача линейного программирования в матричной форме записи имеет вид:

Здесь А — матрица коэффициентов системы уравнений, X -матрица-столбец переменных задачи; — матрица-столбец правых частей системы ограничений.

Нередко используются задачи линейного программирования, называемые симметричными, которые в матричной форме записи имеют вид:

Приведение общей задачи линейного программирования к канонической форме

В большинстве методов решения задач линейного программирования предполагается, что система ограничений состоит из уравнений и естественных условий неотрицательности переменных. Однако, при составлении математических моделей экономических задач ограничения в основном формулируются системы неравенств, поэтому возникает необходимость перехода от системы неравенств к системе уравнений. Это может быть сделано следующим образом. К левой части линейного неравенства:

прибавляется величина такая, что переводит неравенство в равенство , где:

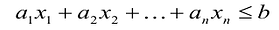
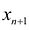
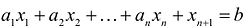
Неотрицательная переменная называется дополнительной переменной.

Основания для возможности такого преобразования дает следующая теорема.

Теорема. Каждому решению неравенства соответствует единственное решение уравнения: и неравенства и, наоборот, каждому решению уравнения: и неравенства соответствует единственное решение неравенства:

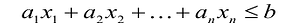
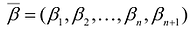
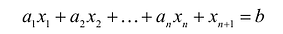
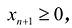
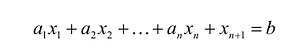
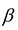
Доказательство. Пусть — решение неравенства. Тогда:

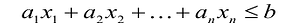
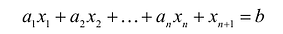
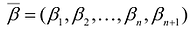
Если в уравнение вместо переменных подставить значения , получится:

Таким образом, решение удовлетворяет уравнению: и неравенству .

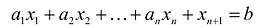
Доказана первая часть теоремы.

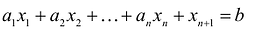
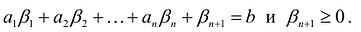
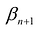
Пусть удовлетворяет уравнению и неравенству , т.е. . Отбрасывая в левой части равенства неотрицательную величину , получим:

т.е. удовлетворяет неравенству: что и требовалось доказать.

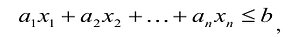
Если в левую часть неравенств системы ограничений вида

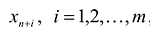
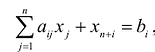
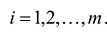
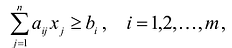
добавить переменную , то получится система ограничений — уравнений В случае, если система неравенств-ограничений имеет вид , то из левой части неравенств-ограничений нужно вычесть соответствующую неотрицательную дополнительную переменную

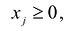
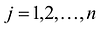
Полученная таким образом система уравнений-ограничений, вместе с условиями неотрицательности переменных, т.е. и целевой функцией является канонической формой записи задачи линейного программирования.

Дополнительные переменные вводятся в целевую функцию с нулевыми коэффициентами и поэтому не влияют на ее значения.

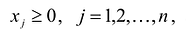
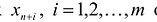
В реальных практических задачах дополнительные неизвестные имеют определенный смысл. Например, если левая часть ограничений задачи отражает расход ресурсов на производство продукции в объемах , а правые части — наличие производственных ресурсов, то числовые значения дополнительных неизвестных и означают объем неиспользованных ресурсов i-го вида.

Иногда возникает также необходимость перейти в задаче от нахождения минимума к нахождению максимума или наоборот. Для этого достаточно изменить знаки всех коэффициентов целевой функции на противоположные, а в остальном задачу оставить без изменения. Оптимальные решения полученных таким образом задач на максимум и минимум совпадают, а значения целевых функций при оптимальных решениях отличаются только знаком.

Множества допустимых решений

Множество точек называется выпуклым, если оно вместе с любыми двумя своими точками содержит их произвольную выпуклую линейную комбинацию.

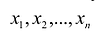
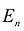
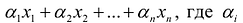
Выпуклой линейной комбинацией произвольных точек Евклидова пространства называется сумма — произвольные неотрицательные числа, сумма которых равна 1.

Геометрически это означает, что если множеству с любыми двумя его произвольными точками полностью принадлежит и отрезок, соединяющий эти точки, то оно будет выпуклым. Например, выпуклыми множествами являются прямолинейный отрезок, прямая, круг, шар, куб, полуплоскость, полупространство и др.

Точка множества называется граничной, если любая окрестность этой точки сколь угодно малого размера содержит точки, как принадлежащие множеству, так и не принадлежащие ему.

Граничные точки множества образуют его границу. Множество называется замкнутым, если оно содержит все свои граничные точки.

Ограниченным называется множество, если существует шар с радиусом конечной длины и центром в любой точке множества, содержащий полностью в себе данное множество. В противном случае множество будет неограниченным.

Пересечение двух или более выпуклых множеств будет выпуклым множеством, так как оно отвечает определению выпуклого множества.

Точка выпуклого множества называется угловой, если она не может быть представлена в виде выпуклой линейной комбинации двух других различных точек этого множества.

Так, угловые точки треугольника — его вершины, круга — точки окружности, ее ограничивающие, а прямая, полуплоскость, плоскость, полупространство, пространство не имеют угловых точек.

Выпуклое замкнутое ограниченное множество на плоскости, имеющее конечное число угловых точек, называется выпуклым многоугольником, а замкнутое выпуклое ограниченное множество в трехмерном пространстве, имеющее конечное число угловых точек, называется выпуклым многогранником.

Теорема. Любая тонка многоугольника является выпуклой линейной комбинацией его угловых точек.

Теорема. Область допустимых решений задачи линейного программирования является выпуклым множеством.

Уравнение целевой функции при фиксированных значениях самой функции является уравнением прямой линии (плоскости, гиперплоскости и т.д.). Прямая, уравнение которой получено из целевой функции при равенстве ее постоянной величине, называется линией уровня.

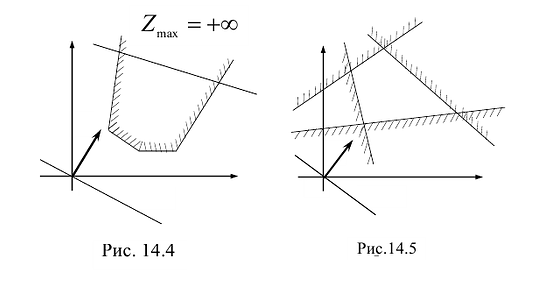
Линия уровня, имеющая общие точки с областью допустимых решений и расположенная так, что область допустимых решений находится целиком в одной из полуплоскостей, называется опорной прямой.

Теорема. Значения целевой функции в точках линии уровня увеличиваются, если линию уровня перемещать параллельно начальному положению в направлении нормали и убывают при перемещении в противоположном направлении.

Теорема. Целевая функция задачи линейного программирования достигает экстремума в угловой точке области допустимых решений; причем, если целевая функция достигает экстремума в нескольких угловых точках области допустимых решений, она также достигает экстремума в любой выпуклой комбинации этих точек.

Опорное решение задачи линейного программирования, его взаимосвязь с угловыми точками

Каноническая задача линейного программирования в векторной форме имеет вид:

Положительным координатам допустимых решений ставятся в соответствие векторы условий. Эти системы векторов зависимы, так как число входящих в них векторов больше размерности векторов.

Базисным решением системы называется частное решение, в котором неосновные переменные имеют нулевые значения. Любая система уравнений имеет конечное число базисных решений, равное 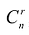, где n — число неизвестных, r- ранг системы векторов условий. Базисные решения, координаты которых удовлетворяют условию неотрицательности, являются опорными.

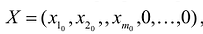
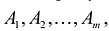
Опорным решением задачи линейного программирования называется такое допустимое решение , для которого векторы условий, соответствующие положительным координатам линейно независимы.

Число отличных от нуля координат опорного решения не может превосходить ранга r системы векторов условий (т.е. числа линейно независимых уравнений системы ограничений).

Если число отличных от нуля координат опорного решения равно m, то такое решение называется невырожденным, в противном случае, если число отличных от нуля координат опорного решения меньше т, такое решение называется вырожденным.

Базисом опорного решения называется базис системы векторов условий задачи, в состав которой входят векторы, соответствующие отличным от нуля координатам опорного решения.

Теорема. Любое опорное решение является угловой точкой области допустимых решений.

Теорема. Любая угловая точка области допустимых решений является опорным решением.

Пример:

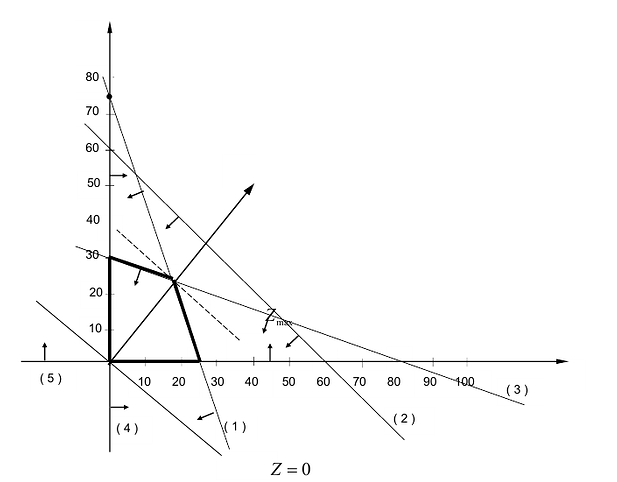
Графический метод решения задачи линейной оптимизации рассмотрим на примере задачи производственного планирования при n = 2.

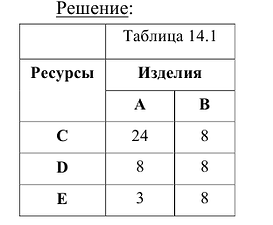
Предприятие изготавливает изделия двух видов А и В. Для производства изделий оно располагает сырьевыми ресурсами трех видов С, D и Е в объемах 600, 480 и 240 единиц соответственно. Нормы расхода ресурсов на единицу продукции каждого вида известны и представлены в табл. 14.1

Прибыль от реализации изделия А составляет 40 млн. руб., а изделия В — 50 млн.руб. Требуется найти объемы производства изделий А и В, обеспечивающие максимальную прибыль.

Построим математическую модель задачи, для чего обозначим 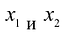— объемы производства изделий А и В соответственно.

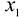
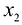
Тогда прибыль предприятия от реализации изделий А и изделий В составит:

Ограничения по ресурсам будут иметь вид:

Естественно, объемы производства должны быть неотрицательными

Решение сформулированной задами найдем, используя геометрическую интерпретацию. Определим сначала многоугольник решений, для чего систему ограничений неравенств запишем в виде уравнений и пронумеруем их:

Каждое из записанных уравнений представляет собой прямую на плоскости, причем 4-я и 5-я прямые являются координатными осями.

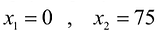
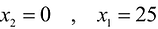
Чтобы построить первую прямую, найдем точки ее пересечения с осями координат: а при .

Далее нас интересует, по какую сторону от прямой будет находиться полуплоскость, соответствующая первому неравенству. Чтобы определить искомую полуплоскость, возьмем точку O(0,0) подставив ее координаты в неравенство, видим, что оно удовлетворяется. Так как точка O(0,0) лежит левее первой прямой, то и полуплоскость будет находиться левее прямой

. На рис 14 , расположение полуплоскости относительно первой прямой отмечено стрелками.

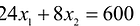
Аналогично построены 2-я и 3-я прямые и найдены полуплоскости, соответствующие 2-му и 3-му неравенству. Точки, удовлетворяющие ограничениям 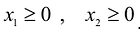, находятся в первом квадранте. Множество точек, удовлетворяющих всем ограничениям одновременно, является ОДР системы ограничений. Такой областью на графике (рис. 14.1) является многоугольник ОАВС.

Любая точка многоугольника решений удовлетворяет системе ограничений задачи и, следовательно, является ее решением. Это говорит о том, что эта задача линейной оптимизации имеет множество допустимых решений, т.е. моговариантпа. Нам же необходимо найти решение, обеспечивающее максимальную прибыль.

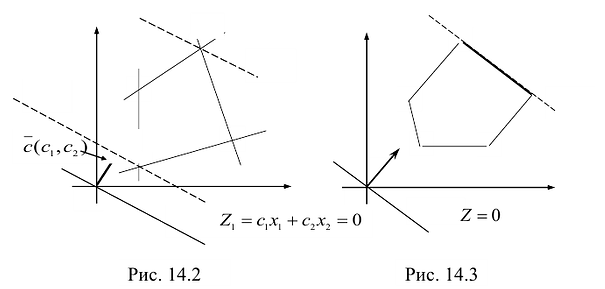
Чтобы найти эту точку, приравняем функцию к нулю и построим соответствующую ей прямую. Вектор-градиент прямой функции

имеет координаты

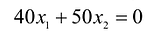
Изобразим вектор на графике и построим прямую функции перпендикулярно вектору на рис. 14.1. Перемещая прямую функции параллельно самой себе в направлении вектора, видим, что последней точкой многоугольника решений, которую пересечет прямая функции, является угловая точка В. Следовательно, в точке В функция достигает максимального значения. Координаты точки В находим, решая систему уравнений, прямые которых пересекаются в данной точке.

Решив эту систему, получаем, что

Следовательно, если предприятие изготовит изделия в найденных объемах, то получит максимальную прибыль, равную:

Алгоритм решения задачи линейного программирования графическим методом таков:

1. Строится область допустимых решений;
2. Строится вектор нормали к линии уровня с точкой приложении в начале координат;
3. Перпендикулярно вектору нормали проводится одна из линий уровня, проходящая через начало координат;
4. Линия уровня перемещается до положения опорной прямой. На этой прямой и будут находиться максимум или минимум функции.

В зависимости от вида области допустимых решений и целевой функции задача может иметь единственное решение, бесконечное множество решений или не иметь ни одного оптимального решения.

На рис. 14.3 показан случай, когда прямая функции параллельна отрезку АВ, принадлежащему ОДР. Максимум функции Z достигается в точке А и в точке В, а, следовательно, и в любой точке отрезка АВ, т.к. эти точки могут быть выражены в виде линейной комбинации угловых точек А и В.

На рисунке 14.4 изображен случай, когда система ограничений образует неограниченное сверху множество. Функция Z в данном случае стремится к бесконечности, так как прямую функции можно передвигать в направлении вектора градиента как угодно далеко, а на рисунке 14.5 представлен случай несовместной системы ограничений.

Основные понятия симплексного метода решения задачи линейного программирования.

Среди универсальных методов решения задач линейного программирования наиболее распространен симплексный метод (или симплекс-метод), разработанный американским ученым Дж.Данцигом. Суть этого метода заключается в том, что вначале получают допустимый вариант, удовлетворяющий всем ограничениям, но необязательно оптимальный (так называемое начальное опорное решение); оптимальность достигается последовательным улучшением исходного варианта за определенное число этапов (итераций). Нахождение начального опорного решения и переход к следующему опорному решению проводятся на основе применения рассмотренного выше метода Жордана-Гаусса для системы линейных уравнений в канонической форме, в которой должна быть предварительно записана исходная задача линейного программирования; направление перехода от одного опорного решения к другому выбирается при этом на основе критерия оптимальности (целевой функции) исходной задачи.

Симплекс-метод основан на следующих свойствах задачи линейного программирования:

• Не существует локального экстремума, отличного от глобального. Другими словами, если экстремум есть, то он единственный.
• Множество всех планов задачи линейного программирования выпукло.
• Целевая функция ЗЛП достигает своего максимального (минимального) значения в угловой точке многогранника решений (в его вершине). Если целевая функция принимает свое оптимальное значение более чем в одной угловой точке, то она достигает того же значения в любой точке, являющейся выпуклой линейной комбинацией этих точек.
• Каждой угловой точке многогранника решений отвечает опорный план ЗЛП.

Рассмотрим две разновидности симплексного метода: симплекс-метод с естественным базисом и симплекс-метод с искусственным базисом (или М-метод).

Симплекс-метод с естественным базисом

Для применения этого метода задача линейного программирования должна быть сформулирована в канонической форме, причем матрица системы уравнений должна содержать единичную подматрицу размерностью mхm. В этом случае очевиден начальный опорный план (неотрицательное базисное решение).

Для определенности предположим, что первые m векторов матрицы системы составляют единичную матрицу. Тогда очевиден первоначальный опорный план:

Проверка на оптимальность опорного плана проходит с помощью критерия оптимальности, переход к другому опорному плану — с помощью преобразований Жордана-Гаусса и с использованием критерия оптимальности.

Полученный опорный план снова проверяется на оптимальность и т.д. Процесс заканчивается за конечное число шагов, причем на последнем шаге либо выявляется неразрешимость задачи (конечного оптимума нет), либо получаются оптимальный опорный план и соответствующее ему оптимальное значение целевой функции.

Признак оптимальности заключается в следующих двух теоремах.

Теорема 1. Если для некоторого вектора, не входящего в базис, выполняется условие:

то можно получить новый опорный план, для которого значение целевой функции будет больше исходного; при этом могут быть два случая:

1. если все координаты вектора, подлежащего вводу в базис, неположительны, то задача линейного программирования не имеет решения;
2. если имеется хотя бы одна положительная координата у вектора, подлежащего вводу в базис, то можно получить новый опорный план.

Теорема 2. Если для всех векторов выполняется условие 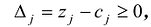то полученный план является оптимальным.

На основании признака оптимальности в базис вводится вектор Ак, давший минимальную отрицательную величину симплекс-разности:

Чтобы выполнялось условие неотрицательности значений опорного плана, выводится из базиса вектор 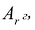, который дает минимальное положительное отношение:

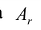
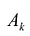
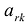
Строка называется направляющей, столбец и элемент — направляющими (последний называют также разрешающим элементом).

Элементы вводимой строки, соответствующей направляющей строке, в новой симплекс-таблице вычисляются по формулам:

а элементы любой другой i-й строки пересчитываются по формулам:

Значения базисных переменных нового опорного плана (показатели графы «план») рассчитываются по формулам:

Если наименьшее значение Q достигается для нескольких базисных векторов, то чтобы исключить возможность зацикливания (повторения базиса), можно применить следующий способ.

Вычисляются частные, полученные от деления всех элементов строк, давших одинаковое минимальное значение Q на свои направляющие элементы. Полученные частные сопоставляются по столбцам слева направо, при этом учитываются и нулевые, и отрицательные значения. В процессе просмотра отбрасываются строки, в которых имеются большие отношения, и из базиса выводится вектор, соответствующий строке, в которой раньше обнаружится меньшее частное.

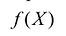
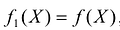
Для использования приведенной выше процедуры симплекс -метода к минимизации линейной формы следует искать максимум функции затем полученный максимум взять с противоположным знаком. Это и будет искомый минимум исходной задачи линейного программирования.

Симплексный метод с искусственным базисом (М-метод)

Симплексный метод с искусственным базисом применяется в тех случаях, когда затруднительно найти первоначальный опорный план исходной задачи линейного программирования, записанной в канонической форме.

М-метод заключается в применении правил симплекс-метода к так называемой М-задаче. Она получается из исходной добавлением к левой части системы уравнений в канонической форме исходной задачи линейного программирования таких искусственных единичных векторов с соответствующими неотрицательными искусственными переменными, чтобы вновь полученная матрица содержала систему единичных линейно-независимых векторов. В линейную форму исходной задачи добавляется в случае её максимизации слагаемое, представляющее собой произведение числа (-М) на сумму искусственных переменных, где М — достаточно большое положительное число.

В полученной задаче первоначальный опорный план очевиден. При применении к этой задаче симплекс-метода оценки А, теперь будут зависеть от числа М. Для сравнения оценок нужно помнить, что М — достаточно большое положительное число, поэтому из базиса будут выводиться в первую очередь искусственные переменные.

В процессе решения M-задачи следует вычеркивать в симплекс-таблице искусственные векторы по мере их выхода из базиса. Если все искусственные векторы вышли из базиса, то получаем исходную задачу. Если оптимальное решение М-задачи содержит искусственные векторы или М-задача неразрешима, то исходная задача также неразрешима.

Путем преобразований число вводимых переменных, составляющих искусственный базис, может быть уменьшено до одной.

Теория двойственности

Любой задаче линейного программирования можно сопоставить сопряженную или двойственную ей задачу. Причем, совместное исследование этих задач дает, как правило, значительно больше информации, чем исследование каждой из них в отдельности.

Любую задачу линейного программирования можно записать в виде:

Первоначальная задача называется исходной или прямой.

Модель двойственной задачи имеет вид:

Переменные двойственной задачи 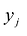называют объективно обусловленными оценками или двойственными оценками.

Связь исходной и двойственной задач заключается, в частности, в том, что решение одной из них может быть получено непосредственно из решения другой. Каждая из задач двойственной пары фактически является самостоятельной задачей линейного программирования и может быть решена независимо от другой.

Двойственная задача по отношению к исходной составляется согласно следующим правилам:

Целевая функция исходной задачи формулируется на максимум, а целевая функция двойственной задачи — на минимум, при этом в задаче на максимум все неравенства в функциональных ограничениях имеют вид

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

🔥 Видео

Линейное программирование Часть 1. Постановка задачиСкачать

РК6. Методы математического программирования. Двойственность задач линейного программированияСкачать

Виды задач линейного программированияСкачать

Транспортная задача (закрытая, с циклом). Метод потенциалов - подробно и понятноСкачать

Двойственная задача линейного программирования (ЗЛП)Скачать

Оптимизация и математические методы принятия решений. Лекция 2. Задачи линейного программирования.Скачать

Урок 1.Поиск решения, оптимизация, оптимальный план производстваСкачать

Решение задачи линейного программирования в ExcelСкачать

МОР МПУР Симплекс метод решения задач линейного программирования ЗЛП ПримерСкачать

решение общей задачи линейного программирования Симплекс методомСкачать