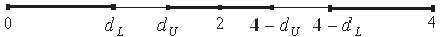Вместе с этим калькулятором также используют следующие:
Уравнение множественной регрессии
- Виды нелинейной регрессии
- Задача №1 Построение уравнения регрессии
- Требуется:
- Решение:
- Рассчитайте параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессий
- Лабораторные работы по эконометрике
- Эконометрика
- Пример выполненной лабораторной работы №1. Тема: «Парная регрессия и корреляция»
- Пример выполненной лабораторной работы № 2 Тема : «Множественная регрессия»
- Пример выполненной лабораторной работы № 3 Тема : « Аддитивная и мультипликативная модели временных рядов »
- Пример выполненной лабораторной работы №4 Тема: «Автокорреляция уровней временного ряда и выявление его структуры»
- Пример выполненной лабораторной работы № 5. Тема : «Автокорреляции в остатках. Критерий Дарбина-Уотсона»
- 🔍 Видео
Видео:Парная регрессия: линейная зависимостьСкачать

Виды нелинейной регрессии
| Вид | Класс нелинейных моделей |
| Нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам |
| Нелинейные по оцениваемым параметрам |
Здесь ε — случайная ошибка (отклонение, возмущение), отражающая влияние всех неучтенных факторов.
Уравнению регрессии первого порядка — это уравнение парной линейной регрессии.
Уравнение регрессии второго порядка это полиномальное уравнение регрессии второго порядка: y = a + bx + cx 2 .
Уравнение регрессии третьего порядка соответственно полиномальное уравнение регрессии третьего порядка: y = a + bx + cx 2 + dx 3 .
Чтобы привести нелинейные зависимости к линейной используют методы линеаризации (см. метод выравнивания):
- Замена переменных.
- Логарифмирование обеих частей уравнения.
- Комбинированный.
| y = f(x) | Преобразование | Метод линеаризации |
| y = b x a | Y = ln(y); X = ln(x) | Логарифмирование |
| y = b e ax | Y = ln(y); X = x | Комбинированный |
| y = 1/(ax+b) | Y = 1/y; X = x | Замена переменных |
| y = x/(ax+b) | Y = x/y; X = x | Замена переменных. Пример |
| y = aln(x)+b | Y = y; X = ln(x) | Комбинированный |
| y = a + bx + cx 2 | x1 = x; x2 = x 2 | Замена переменных |
| y = a + bx + cx 2 + dx 3 | x1 = x; x2 = x 2 ; x3 = x 3 | Замена переменных |
| y = a + b/x | x1 = 1/x | Замена переменных |
| y = a + sqrt(x)b | x1 = sqrt(x) | Замена переменных |
Пример . По данным, взятым из соответствующей таблицы, выполнить следующие действия:
- Построить поле корреляции и сформулировать гипотезу о форме связи.
- Рассчитать параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессии.
- Оценить тесноту связи с помощью показателей корреляции и детерминации.
- Дать с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
- Оценить с помощью средней ошибки аппроксимации качество уравнений.
- Оценить с помощью F-критерия Фишера статистическую надежность результатов регрессионного моделирования. По значениям характеристик, рассчитанных в пп. 4, 5 и данном пункте, выбрать лучшее уравнение регрессии и дать его обоснование.
- Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 15% от его среднего уровня. Определить доверительный интервал прогноза для уровня значимости α=0,05 .
- Оценить полученные результаты, выводы оформить в аналитической записке.
| Год | Фактическое конечное потребление домашних хозяйств (в текущих ценах), млрд. руб. (1995 г. — трлн. руб.), y | Среднедушевые денежные доходы населения (в месяц), руб. (1995 г. — тыс. руб.), х |
| 1995 | 872 | 515,9 |
| 2000 | 3813 | 2281,1 |
| 2001 | 5014 | 3062 |
| 2002 | 6400 | 3947,2 |
| 2003 | 7708 | 5170,4 |
| 2004 | 9848 | 6410,3 |
| 2005 | 12455 | 8111,9 |
| 2006 | 15284 | 10196 |
| 2007 | 18928 | 12602,7 |
| 2008 | 23695 | 14940,6 |
| 2009 | 25151 | 16856,9 |
Решение. В калькуляторе последовательно выбираем виды нелинейной регрессии. Получим таблицу следующего вида.
Экспоненциальное уравнение регрессии имеет вид y = a e bx
После линеаризации получим: ln(y) = ln(a) + bx
Получаем эмпирические коэффициенты регрессии: b = 0.000162, a = 7.8132
Уравнение регрессии: y = e 7.81321500 e 0.000162x = 2473.06858e 0.000162x
Степенное уравнение регрессии имеет вид y = a x b
После линеаризации получим: ln(y) = ln(a) + b ln(x)
Эмпирические коэффициенты регрессии: b = 0.9626, a = 0.7714
Уравнение регрессии: y = e 0.77143204 x 0.9626 = 2.16286x 0.9626
Гиперболическое уравнение регрессии имеет вид y = b/x + a + ε
После линеаризации получим: y=bx + a
Эмпирические коэффициенты регрессии: b = 21089190.1984, a = 4585.5706
Эмпирическое уравнение регрессии: y = 21089190.1984 / x + 4585.5706
Логарифмическое уравнение регрессии имеет вид y = b ln(x) + a + ε
Эмпирические коэффициенты регрессии: b = 7142.4505, a = -49694.9535
Уравнение регрессии: y = 7142.4505 ln(x) — 49694.9535
Видео:Эконометрика. Линейная парная регрессияСкачать

Задача №1 Построение уравнения регрессии
Имеются следующие данные разных стран об индексе розничных цен на продукты питания (х) и об индексе промышленного производства (у).
| Индекс розничных цен на продукты питания (х) | Индекс промышленного производства (у) | |
|---|---|---|
| 1 | 100 | 70 |
| 2 | 105 | 79 |
| 3 | 108 | 85 |
| 4 | 113 | 84 |
| 5 | 118 | 85 |
| 6 | 118 | 85 |
| 7 | 110 | 96 |
| 8 | 115 | 99 |
| 9 | 119 | 100 |
| 10 | 118 | 98 |
| 11 | 120 | 99 |
| 12 | 124 | 102 |
| 13 | 129 | 105 |
| 14 | 132 | 112 |
Требуется:
1. Для характеристики зависимости у от х рассчитать параметры следующих функций:
В) равносторонней гиперболы.
2. Для каждой модели рассчитать показатели: тесноты связи и среднюю ошибку аппроксимации.
3. Оценить статистическую значимость параметров регрессии и корреляции.
4. Выполнить прогноз значения индекса промышленного производства у при прогнозном значении индекса розничных цен на продукты питания х=138.
Решение:
1. Для расчёта параметров линейной регрессии
Решаем систему нормальных уравнений относительно a и b:
Построим таблицу расчётных данных, как показано в таблице 1.
Таблица 1 Расчетные данные для оценки линейной регрессии
| № п/п | х | у | ху | x 2 | y 2 |  |  |
|---|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 7000 | 10000 | 4900 | 74,26340 | 0,060906 |
| 2 | 105 | 79 | 8295 | 11025 | 6241 | 79,92527 | 0,011712 |
| 3 | 108 | 85 | 9180 | 11664 | 7225 | 83,32238 | 0,019737 |
| 4 | 113 | 84 | 9492 | 12769 | 7056 | 88,98425 | 0,059336 |
| 5 | 118 | 85 | 10030 | 13924 | 7225 | 94,64611 | 0,113484 |
| 6 | 118 | 85 | 10030 | 13924 | 7225 | 94,64611 | 0,113484 |
| 7 | 110 | 96 | 10560 | 12100 | 9216 | 85,58713 | 0,108467 |
| 8 | 115 | 99 | 11385 | 13225 | 9801 | 91,24900 | 0,078293 |
| 9 | 119 | 100 | 11900 | 14161 | 10000 | 95,77849 | 0,042215 |
| 10 | 118 | 98 | 11564 | 13924 | 9604 | 94,64611 | 0,034223 |
| 11 | 120 | 99 | 11880 | 14400 | 9801 | 96,91086 | 0,021102 |
| 12 | 124 | 102 | 12648 | 15376 | 10404 | 101,4404 | 0,005487 |
| 13 | 129 | 105 | 13545 | 16641 | 11025 | 107,1022 | 0,020021 |
| 14 | 132 | 112 | 14784 | 17424 | 12544 | 110,4993 | 0,013399 |
| Итого: | 1629 | 1299 | 152293 | 190557 | 122267 | 1299,001 | 0,701866 |
| Среднее значение: | 116,3571 | 92,78571 | 10878,07 | 13611,21 | 8733,357 | х | х |
 | 8,4988 | 11,1431 | х | х | х | х | х |
 | 72,23 | 124,17 | х | х | х | х | х |
Среднее значение определим по формуле:
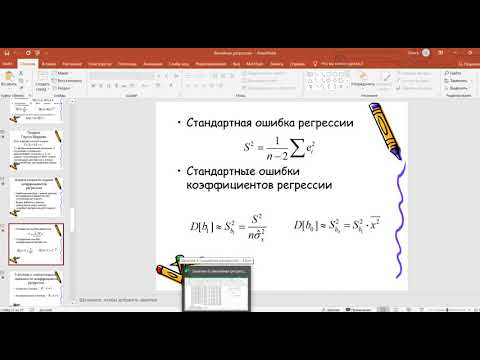
Cреднее квадратическое отклонение рассчитаем по формуле:
и занесём полученный результат в таблицу 1.
Возведя в квадрат полученное значение получим дисперсию:
Параметры уравнения можно определить также и по формулам:
Таким образом, уравнение регрессии:
Следовательно, с увеличением индекса розничных цен на продукты питания на 1, индекс промышленного производства увеличивается в среднем на 1,13.
Рассчитаем линейный коэффициент парной корреляции:
Связь прямая, достаточно тесная.
Определим коэффициент детерминации:
Вариация результата на 74,59% объясняется вариацией фактора х.
Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчётные) значения 
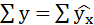
следовательно, параметры уравнения определены правильно.
Рассчитаем среднюю ошибку аппроксимации – среднее отклонение расчётных значений от фактических:
В среднем расчётные значения отклоняются от фактических на 5,01%.
Оценку качества уравнения регрессии проведём с помощью F-теста.
F-тест состоит в проверке гипотезы Н0 о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fфакт и критического (табличного) Fтабл значений F-критерия Фишера.
Fфакт определяется по формуле:
где n – число единиц совокупности;
m – число параметров при переменных х.
Таким образом, Н0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.
Полученные оценки уравнения регрессии позволяют использовать его для прогноза.
Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:
2. Степенная регрессия имеет вид:
Для определения параметров производят логарифмирование степенной функции:
Для определения параметров логарифмической функции строят систему нормальных уравнений по способу наименьших квадратов:
Построим таблицу расчётных данных, как показано в таблице 2.
Таблица 2 Расчетные данные для оценки степенной регрессии
| №п/п | х | у | lg x | lg y | lg x*lg y | (lg x) 2 | (lg y) 2 |
|---|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 2,000000 | 1,845098 | 3,690196 | 4,000000 | 3,404387 |
| 2 | 105 | 79 | 2,021189 | 1,897627 | 3,835464 | 4,085206 | 3,600989 |
| 3 | 108 | 85 | 2,033424 | 1,929419 | 3,923326 | 4,134812 | 3,722657 |
| 4 | 113 | 84 | 2,053078 | 1,924279 | 3,950696 | 4,215131 | 3,702851 |
| 5 | 118 | 85 | 2,071882 | 1,929419 | 3,997528 | 4,292695 | 3,722657 |
| 6 | 118 | 85 | 2,071882 | 1,929419 | 3,997528 | 4,292695 | 3,722657 |
| 7 | 110 | 96 | 2,041393 | 1,982271 | 4,046594 | 4,167284 | 3,929399 |
| 8 | 115 | 99 | 2,060698 | 1,995635 | 4,112401 | 4,246476 | 3,982560 |
| 9 | 119 | 100 | 2,075547 | 2,000000 | 4,151094 | 4,307895 | 4,000000 |
| 10 | 118 | 98 | 2,071882 | 1,991226 | 4,125585 | 4,292695 | 3,964981 |
| 11 | 120 | 99 | 2,079181 | 1,995635 | 4,149287 | 4,322995 | 3,982560 |
| 12 | 124 | 102 | 2,093422 | 2,008600 | 4,204847 | 4,382414 | 4,034475 |
| 13 | 129 | 105 | 2,110590 | 2,021189 | 4,265901 | 4,454589 | 4,085206 |
| 14 | 132 | 112 | 2,120574 | 2,049218 | 4,345518 | 4,496834 | 4,199295 |
| Итого | 1629 | 1299 | 28,90474 | 27,49904 | 56,79597 | 59,69172 | 54,05467 |
| Среднее значение | 116,3571 | 92,78571 | 2,064624 | 1,964217 | 4,056855 | 4,263694 | 3,861048 |
 | 8,4988 | 11,1431 | 0,031945 | 0,053853 | х | х | х |
 | 72,23 | 124,17 | 0,001021 | 0,0029 | х | х | х |
Продолжение таблицы 2 Расчетные данные для оценки степенной регрессии
| №п/п | х | у |  |  |  |  |
|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 74,16448 | 17,34292 | 0,059493 | 519,1886 |
| 2 | 105 | 79 | 79,62057 | 0,385112 | 0,007855 | 190,0458 |
| 3 | 108 | 85 | 82,95180 | 4,195133 | 0,024096 | 60,61728 |
| 4 | 113 | 84 | 88,59768 | 21,13866 | 0,054734 | 77,1887 |
| 5 | 118 | 85 | 94,35840 | 87,57961 | 0,110099 | 60,61728 |
| 6 | 118 | 85 | 94,35840 | 87,57961 | 0,110099 | 60,61728 |
| 7 | 110 | 96 | 85,19619 | 116,7223 | 0,11254 | 10,33166 |
| 8 | 115 | 99 | 90,88834 | 65,79901 | 0,081936 | 38,6174 |
| 9 | 119 | 100 | 95,52408 | 20,03384 | 0,044759 | 52,04598 |
| 10 | 118 | 98 | 94,35840 | 13,26127 | 0,037159 | 27,18882 |
| 11 | 120 | 99 | 96,69423 | 5,316563 | 0,023291 | 38,6174 |
| 12 | 124 | 102 | 101,4191 | 0,337467 | 0,005695 | 84,90314 |
| 13 | 129 | 105 | 107,4232 | 5,872099 | 0,023078 | 149,1889 |
| 14 | 132 | 112 | 111,0772 | 0,85163 | 0,00824 | 369,1889 |
| Итого | 1629 | 1299 | 1296,632 | 446,4152 | 0,703074 | 1738,357 |
| Среднее значение | 116,3571 | 92,78571 | х | х | х | х |
 | 8,4988 | 11,1431 | х | х | х | х |
 | 72,23 | 124,17 | х | х | х | х |
Решая систему нормальных уравнений, определяем параметры логарифмической функции.
Получим линейное уравнение:
Выполнив его потенцирование, получим:
Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата 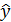
Связь достаточно тесная.
В среднем расчётные значения отклоняются от фактических на 5,02%.
Таким образом, Н0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.
Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:
3. Уравнение равносторонней гиперболы
Для определения параметров этого уравнения используется система нормальных уравнений:
Произведем замену переменных
и получим следующую систему нормальных уравнений:
Решая систему нормальных уравнений, определяем параметры гиперболы.
Составим таблицу расчётных данных, как показано в таблице 3.
Таблица 3 Расчетные данные для оценки гиперболической зависимости
| №п/п | х | у | z | yz | 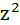 | 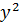 |
|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 0,010000000 | 0,700000 | 0,0001000 | 4900 |
| 2 | 105 | 79 | 0,009523810 | 0,752381 | 0,0000907 | 6241 |
| 3 | 108 | 85 | 0,009259259 | 0,787037 | 0,0000857 | 7225 |
| 4 | 113 | 84 | 0,008849558 | 0,743363 | 0,0000783 | 7056 |
| 5 | 118 | 85 | 0,008474576 | 0,720339 | 0,0000718 | 7225 |
| 6 | 118 | 85 | 0,008474576 | 0,720339 | 0,0000718 | 7225 |
| 7 | 110 | 96 | 0,009090909 | 0,872727 | 0,0000826 | 9216 |
| 8 | 115 | 99 | 0,008695652 | 0,860870 | 0,0000756 | 9801 |
| 9 | 119 | 100 | 0,008403361 | 0,840336 | 0,0000706 | 10000 |
| 10 | 118 | 98 | 0,008474576 | 0,830508 | 0,0000718 | 9604 |
| 11 | 120 | 99 | 0,008333333 | 0,825000 | 0,0000694 | 9801 |
| 12 | 124 | 102 | 0,008064516 | 0,822581 | 0,0000650 | 10404 |
| 13 | 129 | 105 | 0,007751938 | 0,813953 | 0,0000601 | 11025 |
| 14 | 132 | 112 | 0,007575758 | 0,848485 | 0,0000574 | 12544 |
| Итого: | 1629 | 1299 | 0,120971823 | 11,13792 | 0,0010510 | 122267 |
| Среднее значение: | 116,3571 | 92,78571 | 0,008640844 | 0,795566 | 0,0000751 | 8733,357 |
 | 8,4988 | 11,1431 | 0,000640820 | х | х | х |
 | 72,23 | 124,17 | 0,000000411 | х | х | х |
Продолжение таблицы 3 Расчетные данные для оценки гиперболической зависимости
| №п/п | х | у |  |  |  |  |
|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 72,3262 | 0,033231 | 5,411206 | 519,1886 |
| 2 | 105 | 79 | 79,49405 | 0,006254 | 0,244083 | 190,0458 |
| 3 | 108 | 85 | 83,47619 | 0,017927 | 2,322012 | 60,61728 |
| 4 | 113 | 84 | 89,64321 | 0,067181 | 31,84585 | 77,1887 |
| 5 | 118 | 85 | 95,28761 | 0,121031 | 105,8349 | 60,61728 |
| 6 | 118 | 85 | 95,28761 | 0,121031 | 105,8349 | 60,61728 |
| 7 | 110 | 96 | 86,01027 | 0,10406 | 99,79465 | 10,33166 |
| 8 | 115 | 99 | 91,95987 | 0,071112 | 49,56344 | 38,6174 |
| 9 | 119 | 100 | 96,35957 | 0,036404 | 13,25272 | 52,04598 |
| 10 | 118 | 98 | 95,28761 | 0,027677 | 7,357059 | 27,18882 |
| 11 | 120 | 99 | 97,41367 | 0,016024 | 2,516453 | 38,6174 |
| 12 | 124 | 102 | 101,46 | 0,005294 | 0,291565 | 84,90314 |
| 13 | 129 | 105 | 106,1651 | 0,011096 | 1,357478 | 149,1889 |
| 14 | 132 | 112 | 108,8171 | 0,028419 | 10,1311 | 369,1889 |
| Итого: | 1629 | 1299 | 1298,988 | 0,666742 | 435,7575 | 1738,357 |
| Среднее значение: | 116,3571 | 92,78571 | х | х | х | х |
 | 8,4988 | 11,1431 | х | х | х | х |
 | 72,23 | 124,17 | х | х | х | х |
Значения параметров регрессии a и b составили:
Связь достаточно тесная.
В среднем расчётные значения отклоняются от фактических на 4,76%.
Таким образом, Н0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.
Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:
По уравнению равносторонней гиперболы получена наибольшая оценка тесноты связи по сравнению с линейной и степенной регрессиями. Средняя ошибка аппроксимации остаётся на допустимом уровне.
Видео:Линейная регрессияСкачать

Рассчитайте параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессий
2. Рассчитайте параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессий.
· Рассчитаем параметры уравнений линейной парной регрессии. Для расчета параметров a и b линейной регрессии y=a+b*x решаем систему нормальных уравнений относительно a и b:
По исходным данным рассчитываем ∑y, ∑x, ∑yx, ∑x 2 , ∑y 2 (табл. 2):
| № региона | X | Y | XY | X^2 | Y^2 | Y^cp | Y-Y^cp | Ai |
| 1 | 2,800 | 28,000 | 78,400 | 7,840 | 784,000 | 25,719 | 2,281 | 0,081 |
| 2 | 2,400 | 21,300 | 51,120 | 5,760 | 453,690 | 22,870 | -1,570 | 0,074 |
| 3 | 2,100 | 21,000 | 44,100 | 4,410 | 441,000 | 20,734 | 0,266 | 0,013 |
| 4 | 2,600 | 23,300 | 60,580 | 6,760 | 542,890 | 24,295 | -0,995 | 0,043 |
| 5 | 1,700 | 15,800 | 26,860 | 2,890 | 249,640 | 17,885 | -2,085 | 0,132 |
| 6 | 2,500 | 21,900 | 54,750 | 6,250 | 479,610 | 23,582 | -1,682 | 0,077 |
| 7 | 2,400 | 20,000 | 48,000 | 5,760 | 400,000 | 22,870 | -2,870 | 0,144 |
| 8 | 2,600 | 22,000 | 57,200 | 6,760 | 484,000 | 24,295 | -2,295 | 0,104 |
| 9 | 2,800 | 23,900 | 66,920 | 7,840 | 571,210 | 25,719 | -1,819 | 0,076 |
| 10 | 2,600 | 26,000 | 67,600 | 6,760 | 676,000 | 24,295 | 1,705 | 0,066 |
| 11 | 2,600 | 24,600 | 63,960 | 6,760 | 605,160 | 24,295 | 0,305 | 0,012 |
| 12 | 2,500 | 21,000 | 52,500 | 6,250 | 441,000 | 23,582 | -2,582 | 0,123 |
| 13 | 2,900 | 27,000 | 78,300 | 8,410 | 729,000 | 26,431 | 0,569 | 0,021 |
| 14 | 2,600 | 21,000 | 54,600 | 6,760 | 441,000 | 24,295 | -3,295 | 0,157 |
| 15 | 2,200 | 24,000 | 52,800 | 4,840 | 576,000 | 21,446 | 2,554 | 0,106 |
| 16 | 2,600 | 34,000 | 88,400 | 6,760 | 1156,000 | 24,295 | 9,705 | 0,285 |
| 17 | 3,300 | 31,900 | 105,270 | 10,890 | 1017,610 | 29,280 | 2,620 | 0,082 |
| 19 | 3,900 | 33,000 | 128,700 | 15,210 | 1089,000 | 33,553 | -0,553 | 0,017 |
| 20 | 4,600 | 35,400 | 162,840 | 21,160 | 1253,160 | 38,539 | -3,139 | 0,089 |
| 21 | 3,700 | 34,000 | 125,800 | 13,690 | 1156,000 | 32,129 | 1,871 | 0,055 |
| 22 | 3,400 | 31,000 | 105,400 | 11,560 | 961,000 | 29,992 | 1,008 | 0,033 |
| Итого | 58,800 | 540,100 | 1574,100 | 173,320 | 14506,970 | 540,100 | 0,000 | |
| сред значение | 2,800 | 25,719 | 74,957 | 8,253 | 690,808 | 0,085 | ||
| станд. откл | 0,643 | 5,417 |
Система нормальных уравнений составит:
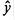
· Рассчитаем параметры уравнений степенной парной регрессии. Построению степенной модели 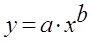
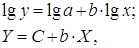
Для расчетов используем данные табл. 3:
| № рег | X | Y | XY | X^2 | Y^2 | Yp^cp | y^cp |
| 1 | 1,030 | 3,332 | 3,431 | 1,060 | 11,104 | 3,245 | 25,67072 |
| 2 | 0,875 | 3,059 | 2,678 | 0,766 | 9,356 | 3,116 | 22,56102 |
| 3 | 0,742 | 3,045 | 2,259 | 0,550 | 9,269 | 3,004 | 20,17348 |
| 4 | 0,956 | 3,148 | 3,008 | 0,913 | 9,913 | 3,183 | 24,12559 |
| 5 | 0,531 | 2,760 | 1,465 | 0,282 | 7,618 | 2,827 | 16,90081 |
| 6 | 0,916 | 3,086 | 2,828 | 0,840 | 9,526 | 3,150 | 23,34585 |
| 7 | 0,875 | 2,996 | 2,623 | 0,766 | 8,974 | 3,116 | 22,56102 |
| 8 | 0,956 | 3,091 | 2,954 | 0,913 | 9,555 | 3,183 | 24,12559 |
| 9 | 1,030 | 3,174 | 3,268 | 1,060 | 10,074 | 3,245 | 25,67072 |
| 10 | 0,956 | 3,258 | 3,113 | 0,913 | 10,615 | 3,183 | 24,12559 |
| 11 | 0,956 | 3,203 | 3,060 | 0,913 | 10,258 | 3,183 | 24,12559 |
| 12 | 0,916 | 3,045 | 2,790 | 0,840 | 9,269 | 3,150 | 23,34585 |
| 13 | 1,065 | 3,296 | 3,509 | 1,134 | 10,863 | 3,275 | 26,4365 |
| 14 | 0,956 | 3,045 | 2,909 | 0,913 | 9,269 | 3,183 | 24,12559 |
| 15 | 0,788 | 3,178 | 2,506 | 0,622 | 10,100 | 3,043 | 20,97512 |
| 16 | 0,956 | 3,526 | 3,369 | 0,913 | 12,435 | 3,183 | 24,12559 |
| 17 | 1,194 | 3,463 | 4,134 | 1,425 | 11,990 | 3,383 | 29,4585 |
| 19 | 1,361 | 3,497 | 4,759 | 1,852 | 12,226 | 3,523 | 33,88317 |
| 20 | 1,526 | 3,567 | 5,443 | 2,329 | 12,721 | 3,661 | 38,90802 |
| 21 | 1,308 | 3,526 | 4,614 | 1,712 | 12,435 | 3,479 | 32,42145 |
| 22 | 1,224 | 3,434 | 4,202 | 1,498 | 11,792 | 3,408 | 30,20445 |
| итого | 21,115 | 67,727 | 68,921 | 22,214 | 219,361 | 67,727 | 537,270 |
| сред зн | 1,005 | 3,225 | 3,282 | 1,058 | 10,446 | 3,225 | |
| стан откл | 0,216 | 0,211 |
Рассчитаем С и b:
Получим линейное уравнение: 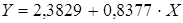
Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата y.
· Рассчитаем параметры уравнений экспоненциальной парной регрессии. Построению экспоненциальной модели 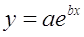
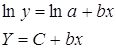
Для расчетов используем данные табл. 4:
| № региона | X | Y | XY | X^2 | Y^2 | Yp | y^cp |
| 1 | 2,800 | 3,332 | 9,330 | 7,840 | 11,104 | 3,225 | 25,156 |
| 2 | 2,400 | 3,059 | 7,341 | 5,760 | 9,356 | 3,116 | 22,552 |
| 3 | 2,100 | 3,045 | 6,393 | 4,410 | 9,269 | 3,034 | 20,777 |
| 4 | 2,600 | 3,148 | 8,186 | 6,760 | 9,913 | 3,170 | 23,818 |
| 5 | 1,700 | 2,760 | 4,692 | 2,890 | 7,618 | 2,925 | 18,625 |
| 6 | 2,500 | 3,086 | 7,716 | 6,250 | 9,526 | 3,143 | 23,176 |
| 7 | 2,400 | 2,996 | 7,190 | 5,760 | 8,974 | 3,116 | 22,552 |
| 8 | 2,600 | 3,091 | 8,037 | 6,760 | 9,555 | 3,170 | 23,818 |
| 9 | 2,800 | 3,174 | 8,887 | 7,840 | 10,074 | 3,225 | 25,156 |
| 10 | 2,600 | 3,258 | 8,471 | 6,760 | 10,615 | 3,170 | 23,818 |
| 11 | 2,600 | 3,203 | 8,327 | 6,760 | 10,258 | 3,170 | 23,818 |
| 12 | 2,500 | 3,045 | 7,611 | 6,250 | 9,269 | 3,143 | 23,176 |
| 13 | 2,900 | 3,296 | 9,558 | 8,410 | 10,863 | 3,252 | 25,853 |
| 14 | 2,600 | 3,045 | 7,916 | 6,760 | 9,269 | 3,170 | 23,818 |
| 15 | 2,200 | 3,178 | 6,992 | 4,840 | 10,100 | 3,061 | 21,352 |
| 16 | 2,600 | 3,526 | 9,169 | 6,760 | 12,435 | 3,170 | 23,818 |
| 17 | 3,300 | 3,463 | 11,427 | 10,890 | 11,990 | 3,362 | 28,839 |
| 19 | 3,900 | 3,497 | 13,636 | 15,210 | 12,226 | 3,526 | 33,978 |
| 20 | 4,600 | 3,567 | 16,407 | 21,160 | 12,721 | 3,717 | 41,140 |
| 21 | 3,700 | 3,526 | 13,048 | 13,690 | 12,435 | 3,471 | 32,170 |
| 22 | 3,400 | 3,434 | 11,676 | 11,560 | 11,792 | 3,389 | 29,638 |
| Итого | 58,800 | 67,727 | 192,008 | 173,320 | 219,361 | 67,727 | 537,053 |
| сред зн | 2,800 | 3,225 | 9,143 | 8,253 | 10,446 | ||
| стан откл | 0,643 | 0,211 |
Рассчитаем С и b:
Получим линейное уравнение: 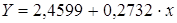
Для расчета теоретических значений y подставим в уравнение 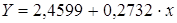
· Рассчитаем параметры уравнений полулогарифмической парной регрессии. Построению полулогарифмической модели 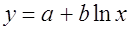
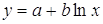
Для расчетов используем данные табл. 5:
| № региона | X | Y | XY | X^2 | Y^2 | y^cp |
| 1 | 1,030 | 28,000 | 28,829 | 1,060 | 784,000 | 26,238 |
| 2 | 0,875 | 21,300 | 18,647 | 0,766 | 453,690 | 22,928 |
| 3 | 0,742 | 21,000 | 15,581 | 0,550 | 441,000 | 20,062 |
| 4 | 0,956 | 23,300 | 22,263 | 0,913 | 542,890 | 24,647 |
| 5 | 0,531 | 15,800 | 8,384 | 0,282 | 249,640 | 15,525 |
| 6 | 0,916 | 21,900 | 20,067 | 0,840 | 479,610 | 23,805 |
| 7 | 0,875 | 20,000 | 17,509 | 0,766 | 400,000 | 22,928 |
| 8 | 0,956 | 22,000 | 21,021 | 0,913 | 484,000 | 24,647 |
| 9 | 1,030 | 23,900 | 24,608 | 1,060 | 571,210 | 26,238 |
| 10 | 0,956 | 26,000 | 24,843 | 0,913 | 676,000 | 24,647 |
| 11 | 0,956 | 24,600 | 23,506 | 0,913 | 605,160 | 24,647 |
| 12 | 0,916 | 21,000 | 19,242 | 0,840 | 441,000 | 23,805 |
| 13 | 1,065 | 27,000 | 28,747 | 1,134 | 729,000 | 26,991 |
| 14 | 0,956 | 21,000 | 20,066 | 0,913 | 441,000 | 24,647 |
| 15 | 0,788 | 24,000 | 18,923 | 0,622 | 576,000 | 21,060 |
| 16 | 0,956 | 34,000 | 32,487 | 0,913 | 1156,000 | 24,647 |
| 17 | 1,194 | 31,900 | 38,086 | 1,425 | 1017,610 | 29,765 |
| 19 | 1,361 | 33,000 | 44,912 | 1,852 | 1089,000 | 33,351 |
| 20 | 1,526 | 35,400 | 54,022 | 2,329 | 1253,160 | 36,895 |
| 21 | 1,308 | 34,000 | 44,483 | 1,712 | 1156,000 | 32,221 |
| 22 | 1,224 | 31,000 | 37,937 | 1,498 | 961,000 | 30,406 |
| Итого | 21,115 | 540,100 | 564,166 | 22,214 | 14506,970 | 540,100 |
| сред зн | 1,005 | 25,719 | 26,865 | 1,058 | 690,808 | |
| стан откл | 0,216 | 5,417 |
Рассчитаем a и b:
Получим линейное уравнение: 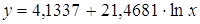
· Рассчитаем параметры уравнений обратной парной регрессии. Для оценки параметров приведем обратную модель 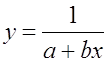
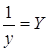
Для расчетов используем данные табл. 6:
| № региона | X | Y | XY | X^2 | Y^2 | Y^cp |
| 1 | 2,800 | 0,036 | 0,100 | 7,840 | 0,001 | 24,605 |
| 2 | 2,400 | 0,047 | 0,113 | 5,760 | 0,002 | 22,230 |
| 3 | 2,100 | 0,048 | 0,100 | 4,410 | 0,002 | 20,729 |
| 4 | 2,600 | 0,043 | 0,112 | 6,760 | 0,002 | 23,357 |
| 5 | 1,700 | 0,063 | 0,108 | 2,890 | 0,004 | 19,017 |
| 6 | 2,500 | 0,046 | 0,114 | 6,250 | 0,002 | 22,780 |
| 7 | 2,400 | 0,050 | 0,120 | 5,760 | 0,003 | 22,230 |
| 8 | 2,600 | 0,045 | 0,118 | 6,760 | 0,002 | 23,357 |
| 9 | 2,800 | 0,042 | 0,117 | 7,840 | 0,002 | 24,605 |
| 10 | 2,600 | 0,038 | 0,100 | 6,760 | 0,001 | 23,357 |
| 11 | 2,600 | 0,041 | 0,106 | 6,760 | 0,002 | 23,357 |
| 12 | 2,500 | 0,048 | 0,119 | 6,250 | 0,002 | 22,780 |
| 13 | 2,900 | 0,037 | 0,107 | 8,410 | 0,001 | 25,280 |
| 14 | 2,600 | 0,048 | 0,124 | 6,760 | 0,002 | 23,357 |
| 15 | 2,200 | 0,042 | 0,092 | 4,840 | 0,002 | 21,206 |
| 16 | 2,600 | 0,029 | 0,076 | 6,760 | 0,001 | 23,357 |
| 17 | 3,300 | 0,031 | 0,103 | 10,890 | 0,001 | 28,398 |
| 19 | 3,900 | 0,030 | 0,118 | 15,210 | 0,001 | 34,844 |
| 20 | 4,600 | 0,028 | 0,130 | 21,160 | 0,001 | 47,393 |
| 21 | 3,700 | 0,029 | 0,109 | 13,690 | 0,001 | 32,393 |
| 22 | 3,400 | 0,032 | 0,110 | 11,560 | 0,001 | 29,301 |
| Итого | 58,800 | 0,853 | 2,296 | 173,320 | 0,036 | 537,933 |
| сред знач | 2,800 | 0,041 | 0,109 | 8,253 | 0,002 | |
| стан отклон | 0,643 | 0,009 |
Рассчитаем a и b:
Получим линейное уравнение: 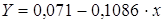
Для расчета теоретических значений y подставим в уравнение 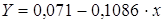
· Рассчитаем параметры уравнений равносторонней гиперболы парной регрессии. Для оценки параметров приведем модель равносторонней гиперболы 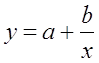
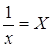
Для расчетов используем данные табл. 7:
| № региона | X=1/z | Y | XY | X^2 | Y^2 | Y^cp |
| 1 | 0,357 | 28,000 | 10,000 | 0,128 | 784,000 | 26,715 |
| 2 | 0,417 | 21,300 | 8,875 | 0,174 | 453,690 | 23,259 |
| 3 | 0,476 | 21,000 | 10,000 | 0,227 | 441,000 | 19,804 |
| 4 | 0,385 | 23,300 | 8,962 | 0,148 | 542,890 | 25,120 |
| 5 | 0,588 | 15,800 | 9,294 | 0,346 | 249,640 | 13,298 |
| 6 | 0,400 | 21,900 | 8,760 | 0,160 | 479,610 | 24,227 |
| 7 | 0,417 | 20,000 | 8,333 | 0,174 | 400,000 | 23,259 |
| 8 | 0,385 | 22,000 | 8,462 | 0,148 | 484,000 | 25,120 |
| 9 | 0,357 | 23,900 | 8,536 | 0,128 | 571,210 | 26,715 |
| 10 | 0,385 | 26,000 | 10,000 | 0,148 | 676,000 | 25,120 |
| 11 | 0,385 | 24,600 | 9,462 | 0,148 | 605,160 | 25,120 |
| 12 | 0,400 | 21,000 | 8,400 | 0,160 | 441,000 | 24,227 |
| 13 | 0,345 | 27,000 | 9,310 | 0,119 | 729,000 | 27,430 |
| 14 | 0,385 | 21,000 | 8,077 | 0,148 | 441,000 | 25,120 |
| 15 | 0,455 | 24,000 | 10,909 | 0,207 | 576,000 | 21,060 |
| 16 | 0,385 | 34,000 | 13,077 | 0,148 | 1156,000 | 25,120 |
| 17 | 0,303 | 31,900 | 9,667 | 0,092 | 1017,610 | 29,857 |
| 19 | 0,256 | 33,000 | 8,462 | 0,066 | 1089,000 | 32,564 |
| 20 | 0,217 | 35,400 | 7,696 | 0,047 | 1253,160 | 34,829 |
| 21 | 0,270 | 34,000 | 9,189 | 0,073 | 1156,000 | 31,759 |
| 22 | 0,294 | 31,000 | 9,118 | 0,087 | 961,000 | 30,374 |
| Итого | 7,860 | 540,100 | 194,587 | 3,073 | 14506,970 | 540,100 |
| сред знач | 0,374 | 25,719 | 9,266 | 0,146 | 1318,815 | |
| стан отклон | 0,079 | 25,639 |
Рассчитаем a и b:
Получим линейное уравнение: 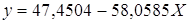
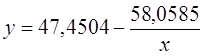
3. Оценка тесноты связи с помощью показателей корреляции и детерминации:
· Линейная модель. Тесноту линейной связи оценит коэффициент корреляции. Был получен следующий коэффициент корреляции rxy=b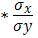
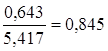
· Степенная модель. Тесноту нелинейной связи оценит индекс корреляции. Был получен следующий индекс корреляции 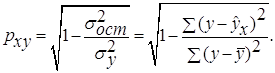
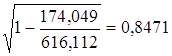
· Экспоненциальная модель. Был получен следующий индекс корреляции ρxy=0,8124, что говорит о том, что связь прямая и очень сильная, но немного слабее, чем в линейной и степенной моделях. Коэффициент детерминации r²xy=0,66. Это означает, что 66% вариации результативного признака (розничная продажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
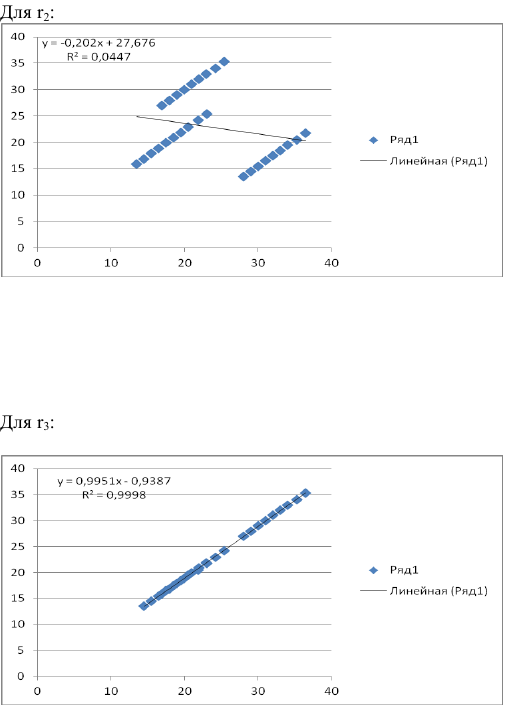
· Полулогарифмическая модель. Был получен следующий индекс корреляции ρxy=0,8578, что говорит о том, что связь прямая и очень сильная, но немного больше чем в предыдущих моделях. Коэффициент детерминации r²xy=0,7358. Это означает, что 73,58% вариации результативного признака (розничная продажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
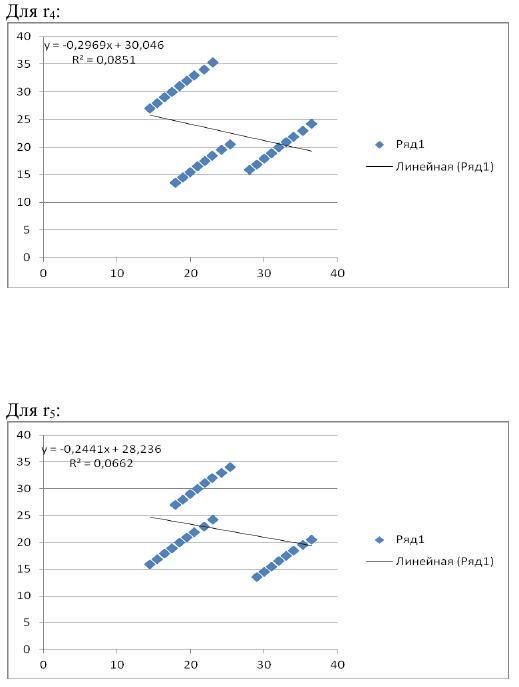
· Гиперболическая модель. Был получен следующий индекс корреляции ρxy=0,8448 и коэффициент корреляции rxy=-0,1784 что говорит о том, что связь обратная очень сильная. Коэффициент детерминации r²xy=0,7358. Это означает, что 73,5% вариации результативного признака (розничная продажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
· Обратная модель. Был получен следующий индекс корреляции ρxy=0,8114 и коэффициент корреляции rxy=-0,8120, что говорит о том, что связь обратная очень сильная. Коэффициент детерминации r²xy=0,6584. Это означает, что 65,84% вариации результативного признака (розничная продажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
Вывод: по полулогарифмическому уравнению получена наибольшая оценка тесноты связи: ρxy=0,8578 (по сравнению с линейной, степенной, экспоненциальной, гиперболической, обратной регрессиями).
Видео:Нелинейная регрессия в MS Excel. Как подобрать уравнение регрессии? Некорректное значение R^2Скачать

Лабораторные работы по эконометрике
Экономисты используют количественные данные для наблюдения за ходом развития экономики, ее анализа и прогнозов. Набор статистических методов, используемых для этих целей, называется в совокупности эконометрикой.
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
Видео:Парная регрессия: степенная зависимостьСкачать

Эконометрика
Эконометрика – это наука, связанная с эмпирическим выводом экономических законов, т.е. используются данные для того, чтобы получить количественные зависимости для экономических соотношений.
Пример выполненной лабораторной работы №1. Тема: «Парная регрессия и корреляция»
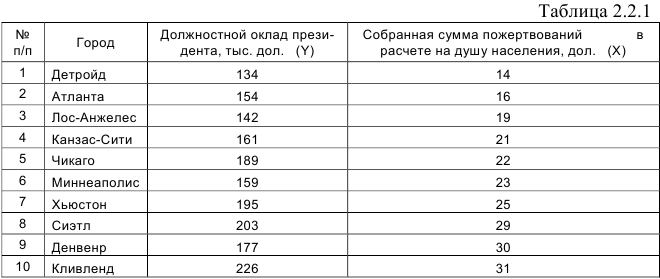
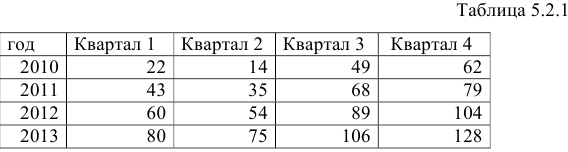
Задание: Периодически в средствах массовой информации обсуждаются высокие должностные оклады президентов благотворительных организаций. Дана информация о десяти крупнейших филиалах общества United Way в таблице 2.2.1.
- Построить поле корреляции и сформулировать гипотезу о форме связи.
- Рассчитать параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессий.
- Оценить тесноту связи с помощью показателей корреляции и детерминации.
- Дать с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
- Оценить с помощью средней ошибки аппроксимации качество уравнений.
- Оценить с помощью
-критерия Фишера статистическую надежность результатов регрессионного моделирования.
- По значениям характеристик, рассчитанных в пп. 3, 5 и 6, выберать лучшее уравнение регрессии и дайть его обоснование.
- Рассчитайть прогнозное значение результата, если прогнозное значение фактора увеличится на 6 % от его среднего уровня. Определить доверительный интервал прогноза для уровня значимости
.
- Оценить надежность и точность полученного прогноза.
Решение:
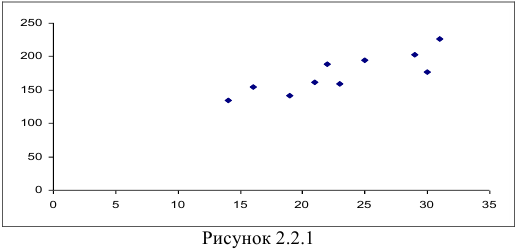
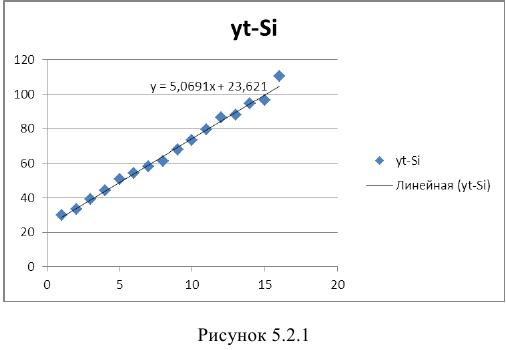
- Для условия задачи поле корреляции выглядит следующим образом (Рисунок 2.2.1):
По расположению точек можно предположить, что между должностным окладом президента 
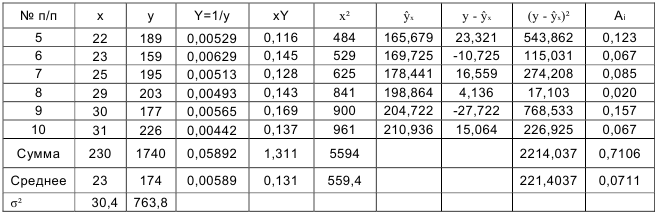
- Определим параметры уравнения парной линейной регрессии
. Вычисления организуем в таблицу 2.2.2:
Напомним, что средние значения рассчитываются по формулам
и т.д., где 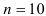
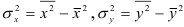
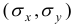
По формулам находим:
Т.о. уравнение регрессии запишется в виде:
Интерпретация коэффициента регрессии. С увеличением суммы пожертвований на душу населения на один доллар должностной оклад президента благотворительной организации увеличивается на 4,25 тыс. дол.
1) Рассчитаем линейный коэффициент корреляции по формуле:
С учетом вычислений в столбцах 2,3 и 4 таблицы получим
Т.е. связь между изучаемыми переменными прямая (так как 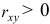
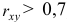
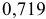
2) Рассчитаем средний коэффициент эластичности:
Это означает, что при изменении фактора (собранной суммы пожертвований на душу населения) на 1% от своего среднего значения, результат (должностной оклад президента) изменится в среднем по совокупности на 0,56% от своего среднего значения.
3) Найдем среднюю ошибку аппроксимации:
Это означает, что качество рассматриваемой модели хорошее. 4) Определим статистическую надежность результатов регрессионного моделирования, для этого находим
По таблице значений 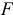
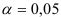
то гипотеза о статистической незначимости уравнения регрессии отвергается и принимается гипотеза о статистической значимости и надежности уравнения регрессии в целом.
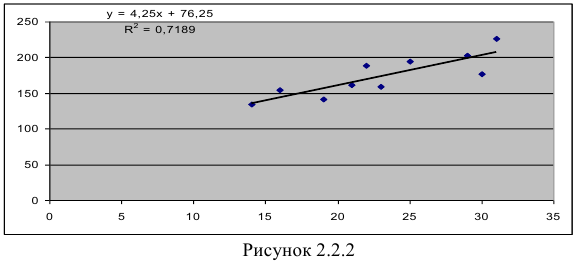
Обработка данных в табличном редакторе Excel приводит к следующему результату (Рисунок 2.2.2):
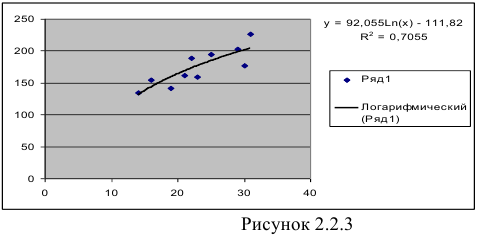
- Определим параметры уравнения полулогарифмической регрессии
. Предварительно проведем процедуру линеаризации переменных. Для этого сделаем замену
и определим параметры уравнения
. Вычисления организуем в таблицу 2.2.3:
По формулам находим:
Т.о. уравнение регрессии запишется в виде:
После замены получим
1) Рассчитаем индекс корреляции по формуле:
Определим коэффициент детерминации
Т.е. 70,6% вариации должностного оклада объясняется вариацией пожертвований.
2) Рассчитаем средний коэффициент эластичности:
Это означает, что при изменении фактора (собранной суммы пожертвований на душу населения) на 1% от своего среднего значения, результат (должностной оклад президента) изменится в среднем по совокупности на 0,53% от своего среднего значения.
3) Найдем среднюю ошибку аппроксимации:
Это означает, что качество рассматриваемой модели хорошее.
4) Определим статистическую надежность результатов регрессионного моделирования, для этого находим
По таблице значений 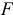
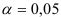
то гипотеза о статистической незначимости уравнения регрессии отвергается и принимается гипотеза о статистической значимости и надежности уравнения регрессии в целом. В Excel получим следующий результат (Рисунок 2.2.3):
- Построению степенной модели
предшествует процедура линеаризации переменных. Проведем линеаризацию путем логарифмирования обеих частей уравнения:
, где
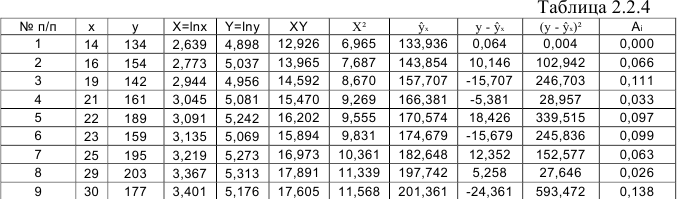
.
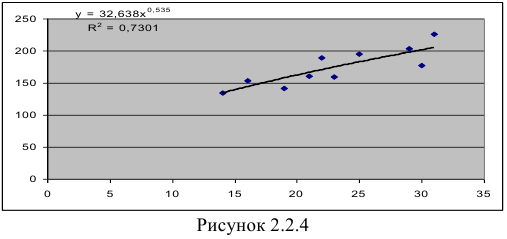
Для расчетов используем данные таблицы 2.2.4:
По формулам находим:
Т.о. уравнение регрессии запишется в виде:
После замены получим:
1) Рассчитаем индекс корреляции по формуле:
Определим коэффициент детерминации
Т. е. 71,4 % вариации должностного оклада объясняется вариацией пожертвований.
2) Рассчитаем средний коэффициент эластичности:
Это означает, что при изменении фактора (собранной суммы пожертвований на душу населения) на 1% от своего среднего значения, результат (должностной оклад президента) изменится в среднем по совокупности на 0,54% от своего среднего значения.
3) Найдем среднюю ошибку аппроксимации:
Это означает, что качество рассматриваемой модели хорошее.
4) Определим статистическую надежность результатов регрессионного моделирования, для этого находим
По таблице значений 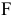
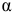
то гипотеза о статистической незначимости уравнения регрессии отвергается и принимается гипотеза о статистической значимости и надежности уравнения регрессии в целом.
В Excel получим следующий результат (Рисунок 2.2.4):
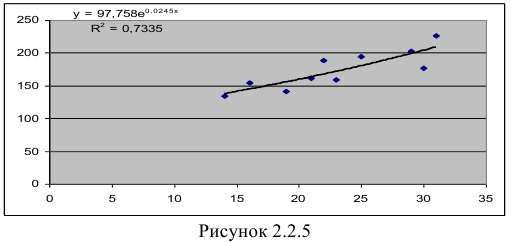
- Построению экспоненциальной модели
предшествует процедура линеаризации переменных. Проведем линеаризацию путем логарифмирования обеих частей уравнения:
, где
. Для расчетов используем данные таблицы 2.2.5:
По формулам находим:
Т.о. уравнение регрессии запишется в виде:
После замены получим:
1) Рассчитаем индекс корреляции по формуле:
Определим коэффициент детерминации
Т.е. 71,7% вариации должностного оклада объясняется вариацией пожертвований.
2) Рассчитаем средний коэффициент эластичности:
Это означает, что при изменении фактора (собранной суммы пожертвований на душу населения) на 1% от своего среднего значения, результат (должностной оклад президента) изменится в среднем по совокупности на 0,56% от своего среднего значения.
3) Найдем среднюю ошибку аппроксимации:
Это означает, что качество рассматриваемой модели хорошее. 4) Определим статистическую надежность результатов регрессионного моделирования, для этого находим
По таблице значений 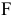
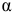
то гипотеза о статистической незначимости уравнения регрессии отвергается и принимается гипотеза о статистической значимости и надежности уравнения регрессии в целом.
В Excel получим следующий результат (Рисунок 2.2.5):
- Определим параметры уравнения обратной регрессии
.
Предварительно проведем процедуру линеаризации переменных. Для этого сделаем замену 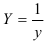
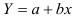
По формулам находим:
Т.о. уравнение регрессии запишется в виде:
После замены получим:
1) Рассчитаем индекс корреляции по формуле:
Определим коэффициент детерминации
Т.е. 71% вариации должностного оклада объясняется вариацией пожертвований.
2) Рассчитаем средний коэффициент эластичности:
Это означает, что при изменении фактора (собранной суммы пожертвований на душу населения) на 1% от своего среднего значения, результат (должностной оклад президента) изменится в среднем по совокупности на 0,56% от своего среднего значения.
3) Найдем среднюю ошибку аппроксимации:
Это означает, что качество рассматриваемой модели хорошее. 4) Определим статистическую надежность результатов регрессионного моделирования, для этого находим
По таблице значений 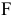
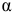
то гипотеза о статистической незначимости уравнения регрессии отвергается и принимается гипотеза о статистической значимости и надежности уравнения регрессии в целом.
- Определим параметры уравнения равносторонней гиперболы
Предварительно проведем процедуру линеаризации переменных. Для этого сделаем замену
и определим параметры уравнения
.
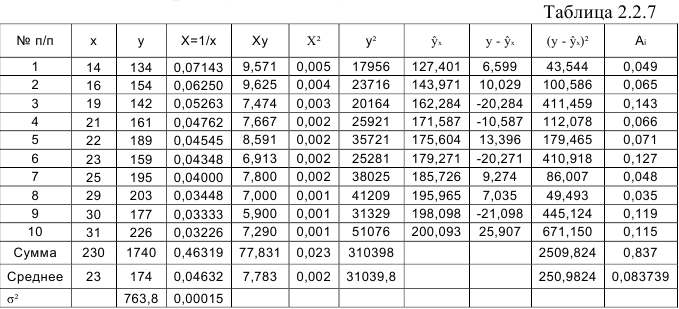
Вычисления организуем в таблицу 2.2.7:
По формулам находим:
Т. о. уравнение регрессии запишется в виде:
После замены получим
2) Рассчитаем индекс корреляции по формуле:
Определим коэффициент детерминации
Т.е. 67,1% вариации должностного оклада объясняется вариацией пожертвований.
2) Рассчитаем средний коэффициент эластичности:
Это означает, что при изменении фактора (собранной суммы пожертвований на душу населения) на 1% от своего среднего значения, результат (должностной оклад президента) изменится в среднем по совокупности на 0,53% от своего среднего значения.
3) Найдем среднюю ошибку аппроксимации:
Это означает, что качество рассматриваемой модели удовлетворительное.
4) Определим статистическую надежность результатов регрессионного моделирования, для этого находим
По таблице значений 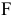
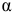
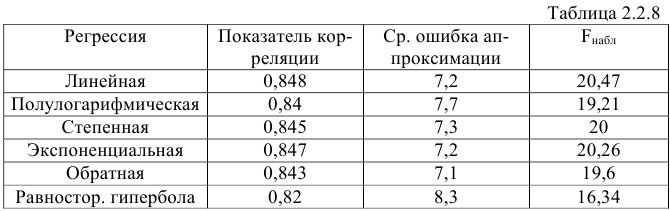
то гипотеза о статистической незначимости уравнения регрессии отвергается и принимается гипотеза о статистической значимости и надежности уравнения регрессии в целом. 8) Для анализа составим таблицу 2.2.8:
Из таблицы видим, что рассматриваемую в задаче зависимость лучше всего описывает уравнение линейной регрессии, поскольку для этой модели показатель корреляции оказался больше, при этом качество линейной модели хорошее и уравнение линейной регрессии статистически надёжно.
Рассчитаем прогнозное значение 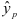
Построим точечный прогноз:
Построим 95% доверительный интервал для прогноза. Определим среднюю стандартную ошибку прогноза 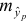
Далее строим доверительный интервал прогноза:
По таблице находим для уровня значимости по условию 
Таким образом, с вероятностью 0,95 можно утверждать, что прогнозное значение оклада президента отдельной благотворительной организации, которая соберет пожертвований в расчете на душу населения на 6% больше от среднего значения, будет находиться в интервале от 139,685 до 220,047тыс. долларов. Прогноз оказался надежным.
Оценим точность полученного прогноза
Прогноз оказался не очень точным.
Пример выполненной лабораторной работы № 2 Тема : «Множественная регрессия»
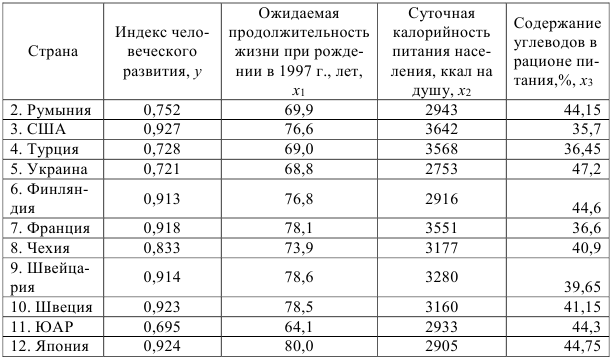
Задание: Имеются данные по странам
- Найти матрицу парных коэффициентов корреляции. Сделать выводы.
- Построить уравнение множественной регрессии в стандартизованной и естественной форме.
- Сделать выводы о силе влияния факторов на результат на основе
-коэффициентов и средних коэффициентов эластичности.
- Рассчитать линейные коэффициенты частной корреляции и коэффициент множественной корреляции. Проанализировать линейные коэффициенты парной и частной корреляции. Рассчитать значение скорректированного коэффициента множественной детерминации.
- С помощью общего
-критерия Фишера оценить статистическую надежность уравнения регрессии.
- С помощью частных
-критериев Фишера оценить, насколько целесообразно включение в уравнение регрессии фактора
, после фактора
и насколько целесообразно включение в уравнение регрессии фактора
после фактора
.
- Оценить с помощью
-критерия Стьюдента статистическую значимость коэффициентов при переменных
и
множественного уравнения регрессии.
- Сделать выводы.
Решение:
- Матрицу парных коэффициентов можно получить, рассчитав линейные коэффициенты парной корреляции аналогично тому, как это делалось в первой лабораторной работе. Однако, эффетивнее воспользоваться инструментом «Корреляция» ППП Exel. При построении матрицы парных коэффициентов корреляции исследуемых показателей, учитываем, что эта матрица должна быть симметричной относительно главной диагонали:
Очевидно, что факторы 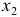
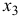
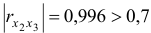
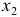
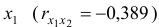
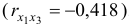
- Линейное уравнение регрессии
от
и
имеет вид:
Для расчета его параметров применим метод стандартизации переменных и построим искомое уравнение в стандартизованном масштабе:
В нашем примере число объясняющих факторов 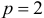
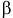
При 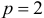
Для нахождения 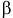
Получим уравнение в стандартизированном масштабе
Для построения уравнения в естественной форме рассчитаем 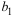
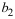
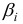
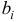
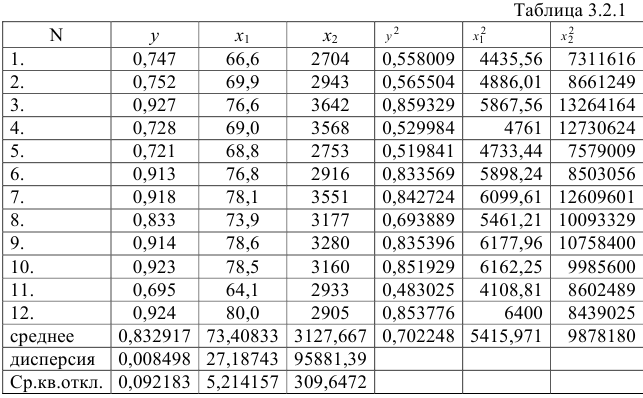
Для расчета необходимых величин составим расчетную таблицу 3.2.1.
Значение параметра 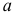
Получим уравнение в естественной форме
- При сравнении модулей значений стандартизованных коэффициентов
и
приходим к выводу, что сила влияния
на
оказалась большей, чем сила влияния
:
К аналогичным выводам можно прийти, рассчитав средние коэффициенты эластичности:
С увеличением 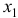
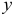
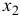
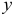
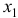
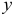
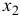
- Линейные коэффициенты частной корреляции рассчитываются по рекуррентной формуле:
При 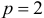
Коэффициенты частной корреляции дают более точную характеристику тесноты связи двух признаков, чем коэффициенты парной корреляции, так как очищают парную зависимость от взаимодействия данной пары признаков с другими признаками, представленным в модели. Сравним парные и частные коэффициенты корреляции:
выводы о связи между 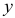
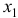
связь между 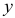
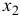
связь между 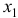
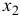
Различия в выводах на основе частных и парных коэффициентов корреляции различаются из-за довольно существенной межфакторной связи
Расчет линейного коэффициента множественной корреляции выполним с использованием коэффициентов 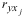
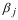
Зависимость 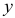
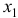
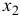
Прочие факторы, не включенные в модель, составляют соответственно 6,3 % от общей вариации
.
Скорректированный индекс множественной детерминации содержит поправку на число степеней свободы и рассчитывается следующим образом:
- Общий
-критерий проверяет гипотезу
о статистической незначимости уравнения регрессии и показателя тесноты связи:
Определяем по таблице значений 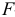
Так как 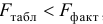
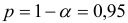
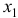
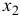
- Частные
-критерии —
и
оценивают статистическую значимость присутствия факторов
и
в уравнении множественной регрессии.
оценивает, насколько целесообразно включение в уравнение регрессии фактора
после фактора
, a
указывает целесообразность включения в уравнение регрессии фактора
после фактора
.
Фактическое значение частного 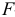
то гипотезу 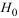
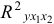
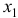
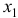
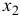
Целесообразность включения в модель фактора 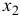
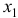
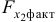
то гипотезу 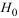
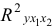
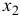
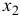
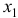
- Оценка с помощью
-критерия Стьюдента значимости коэффициентов
и
связана с сопоставлением их значений с величиной их случайных ошибок
и
. Расчет значений случайных ошибок достаточно сложен и трудоёмок. Поэтому предлагается расчёт значения
-критерия Стьюдента по следующим формулам:
Табличные (критические) значения 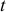
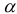
где 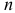
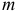
В нашем примере
Так как 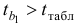
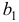
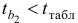
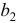
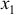
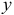
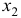
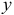
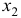
Пример выполненной лабораторной работы № 3 Тема : « Аддитивная и мультипликативная модели временных рядов »
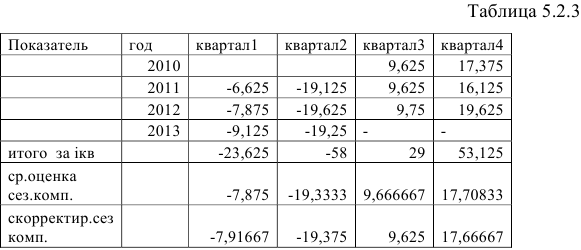
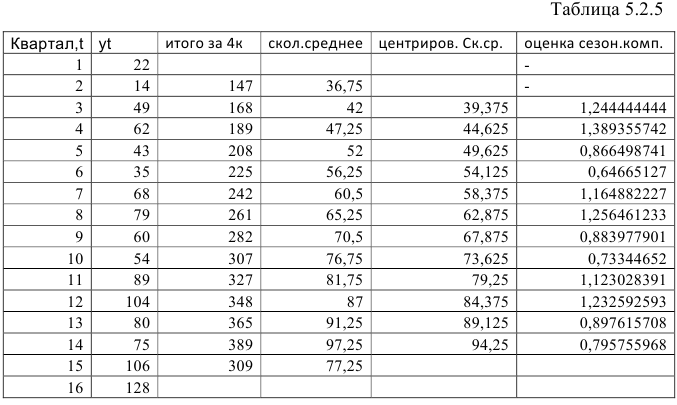
Задание: Имеются поквартальные данные об объемах потребления электроэнергии жителям региона за 4 года (Таблица 5.2.1).
1) Построить аддитивную модель;
2) Построить мультипликативную модель;
3) Выполнить прогноз потребления электроэнергии на первый квартал 2014 года.
Решение:
1) Аддитивная модель
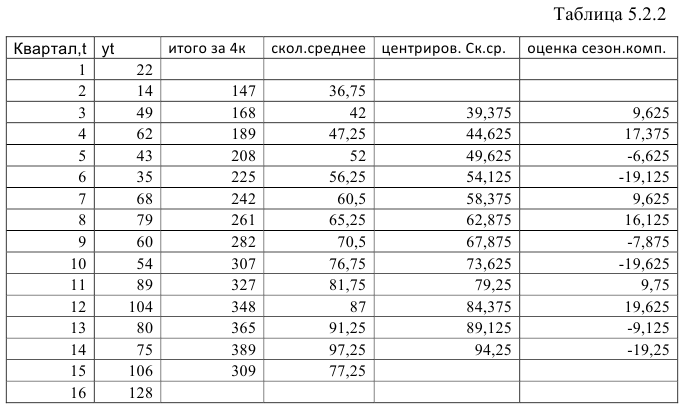
Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней, для этого:
- Просуммируем уровни ряда последовательно за каждые четыре квартала со сдвигом на один момент времени.
- Разделив полученные суммы на четыре, найдем скользящую среднюю. Полученные таким образом значения не содержат сезонной компоненты.
- Приведем эти значения в соответствии с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних — центрированные скользящие средние.
Шаг 2. Найдем оценки сезонной компоненты как разность между фактическими уровнями ряда и центрированными скользящими средними. Результат занесем в таблицу (Таблица 5.2.2).
Используем полученные оценки для расчета значений сезонной компоненты 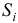
В моделях с сезонной компонентой обычно предполагается, что сезонные взаимодействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю. Этот факт мы будем использовать для корректировки сезонной компоненты (Таблица 5.2.3).
Сумма значений сезонной компоненты по всем кварталам составит:
Определим корректирующий коэффициент:
Рассчитаем скорректированные значения сезонной компоненты как разность между ее средней оценкой и корректирующим коэффициентом:
где 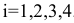
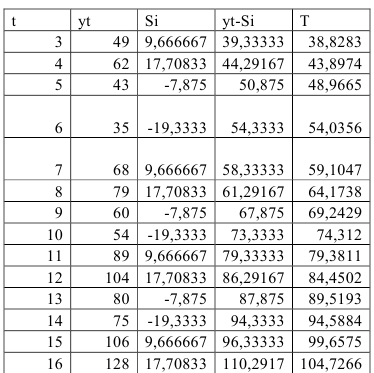
Шаг 3. Устраним сезонную компоненту, вычитая ее значение из каждого уровня исходного временного ряда. Эти значения рассчитываются для каждого момента времени и содержат только тенденцию и случайную компоненту (Таблица 5.2.4).
Шаг 4. Определим компоненту 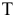
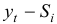
2) Мультипликативная модель.
Шаг 1. Выравнивание исходных уровней ряда методом скользящей средней были выполнены при построении аддитивной модели.
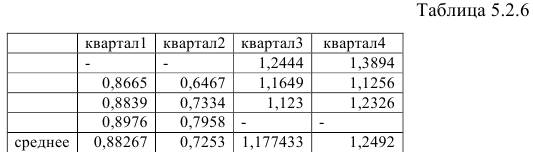
Шаг 2. Найдем оценки сезонной компоненты как отношение фактических уровней ряда к центрированным скользящим средним. Результат занесем в таблицу (Таблица 5.2.5).
Полученные значения занесем в таблицу 5.2.6:
Определим корректирующий множитель. Он равен отношению 4 к сумме вычисленных индексов:
На корректирующий множитель умножается значение каждого из четырех квартальных индексов. Сумма скорректированных индексов должна быть равна числу периодов сезонности (в данном примере числу кварталов). В данном примере скорректированные индексы следующие:
Шаг 3. Десезонализированные данные вычисляются как отношение фактических уровней временного ряда к соответствующему индексу сезонности:
Вычислим десезонализированные данные (Таблица 5.2.7):
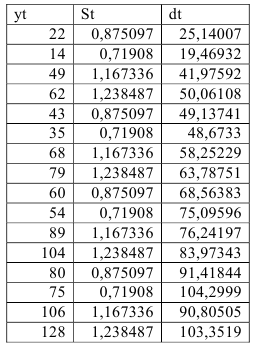
Шаг 4. По десезонализированным данным строится тренд, как уравнение парной регрессии, где 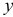
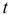
Выполним прогноз на первый квартал 2014 года по аддитивной модели:
Выполним прогноз на первый квартал 2014 года по мультипликативной модели:
Пример выполненной лабораторной работы №4 Тема: «Автокорреляция уровней временного ряда и выявление его структуры»
Задание:
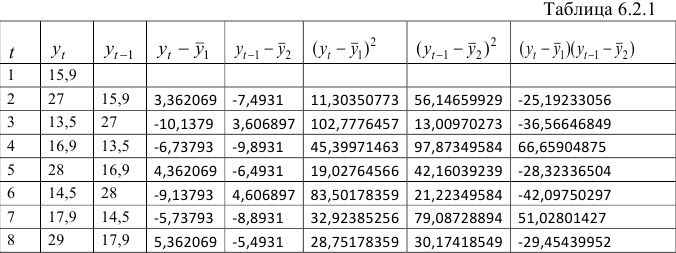
Имеются данные за 30 последовательных периодов:
Требуется: рассчитать коэффициенты автокорреляции до максимально возможного уровня; построить автокорреляционную функцию; сделать выводы о структуре ряда; предложить модель авторегрессии для описания ряда.
Решение:
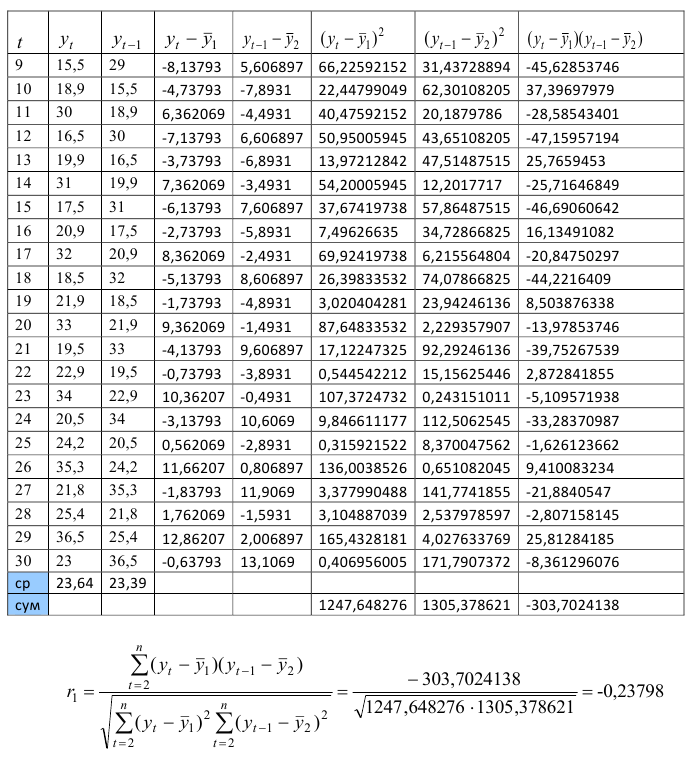
Для расчета коэффициента автокорреляции уровней ряда 1-го порядка 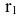
Полученное значение 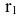
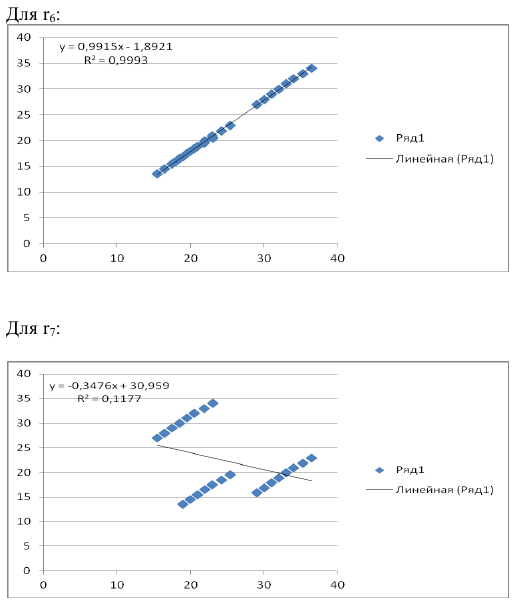
Рассчитать коэффициенты автокорреляции 2-го и последующих уровней можно путем составления аналогичной таблиц. Однако, этот процесс достаточно трудоемок. Для облегчения задачи построим линейные тренды в ППП Exel. Для этого нужно выделить соответствующий диапазон данных (например для расчета 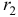
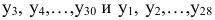
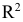
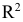
Рассчитаем коэффициенты автокорреляции нескольких уровней. Максимально возможный лаг не должен превышать
то есть можно рассчитать коэффициенты автокорреляции до 7-го порядка включительно.
Итак, автокорреляционная функция имеет вид:
Анализ значений автокорреляционной функции позволяет сделать вывод об отсутствии в изучаемом временном ряде сильной линейной тенденции и существовании сезонных колебаний с периодом три 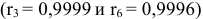
Для прогнозирования значений 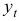
Пример выполненной лабораторной работы № 5. Тема : «Автокорреляции в остатках. Критерий Дарбина-Уотсона»
Задание: По данным за 18 месяцев построено уравнение зависимости прибыли предприятия 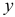
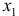
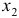
При анализе остаточных величин были использованы значения, приведенные в таблице 7.2.1.
- По трем позициям рассчитать
.
- Рассчитать критерий Дарбина — Уотсона.
- Оценить полученный результат при 5%-м уровне значимости.
- Указать, пригодно ли данное уравнение для прогноза.
Решение:
определяется путем подстановки фактических значений
и
в уравнение регрессии:
Остатки рассчитываются по формуле 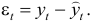
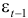
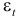
Результаты вычислений оформим в виде таблицы 7.2.2
- Критерий Дарбина — Уотеона рассчитывается по формуле:
- Выдвигаем гипотезу
об отсутствии автокорреляции в остатках. Определяем табличное значение статистики Дарбина — Уотеона. При уровне значимости
(месяцев) и
(число факторов) нижнее значение равно
, а верхнее
. Чтобы оценить значимость коэффициента автокорреляции вычислим интервалы:
В данной задаче
Это означает наличие отрицательной автокорреляции в остатках.
- Уравнение не может быть использовано для прогноза, так как в нем не устранена автокорреляция в остатках, которая может иметь различные причины: возможно, в уравнение не включен какой-либо существенный фактор, либо неточна форма связи, а, может быть, в рядах динамики имеется общая тенденция.
Возможно эти страницы вам будут полезны:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
🔍 Видео
Уравнение парной линейной регрессии с помощью Анализа ДанныхСкачать

Эконометрика Линейная регрессия и корреляцияСкачать

Эконометрика. Нелинейная регрессия. Гипербола.Скачать

Парная и множественная линейная регрессияСкачать
Парная нелинейная регрессияСкачать

Уравнение линейной регрессии. Интерпретация стандартной табличкиСкачать

Эконометрика. Нелинейная регрессия. Степенная функция.Скачать

Эконометрика. Множественная регрессия и корреляция.Скачать

Множественная линейная регрессия, часть 2Скачать

Регрессия в ExcelСкачать

Множественная регрессияСкачать

Множественная регрессия в ExcelСкачать

Степенная регрессияСкачать

Эконометрика. Оценка значимости параметров уравнения регрессии. Критерий Стьюдента.Скачать

Лекция 8. Линейная регрессияСкачать








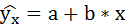
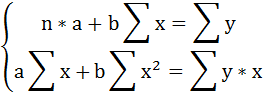
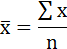
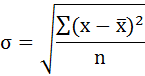
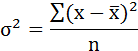
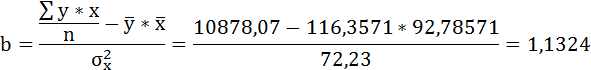
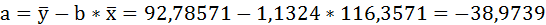
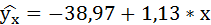
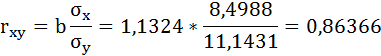
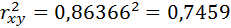
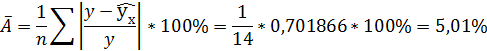
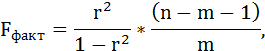
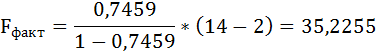
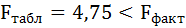
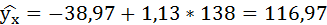
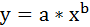
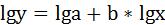
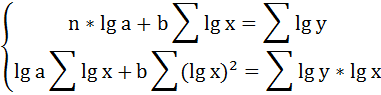
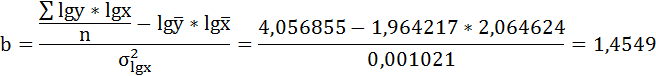
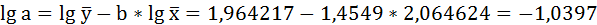
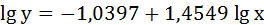
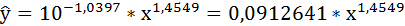
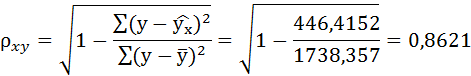
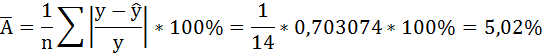
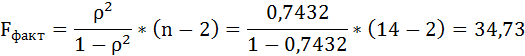
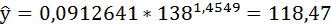
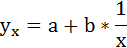
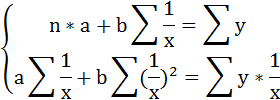
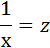
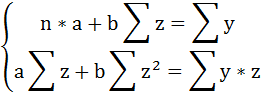
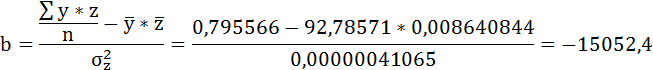
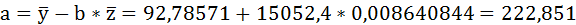
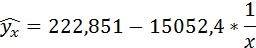
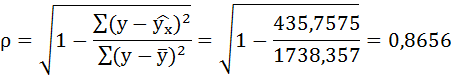
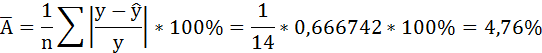
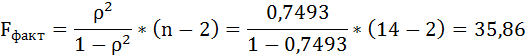
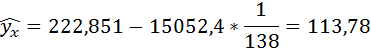
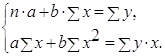
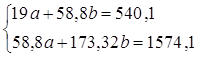
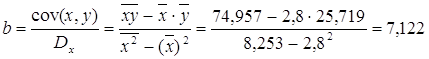
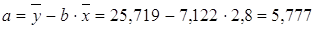
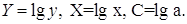
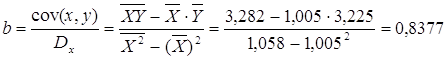
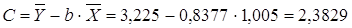
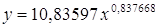
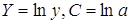
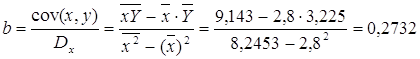
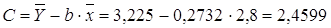
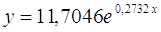
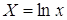
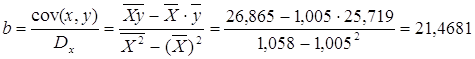
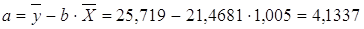
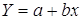
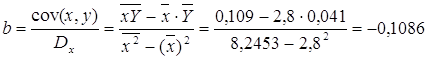
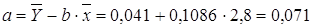
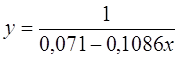
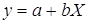
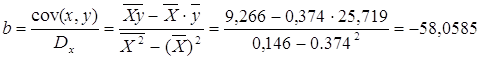
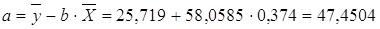

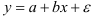 . Вычисления организуем в таблицу 2.2.2:
. Вычисления организуем в таблицу 2.2.2: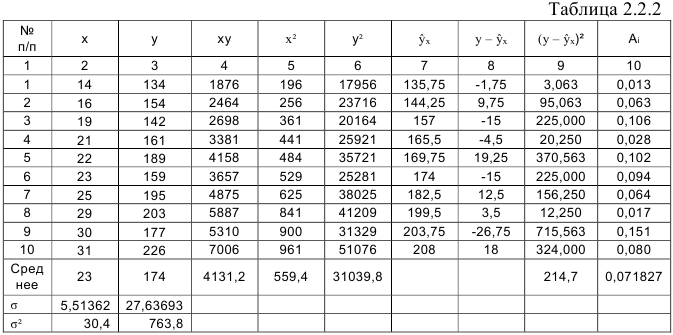
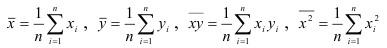
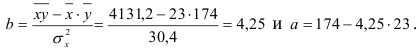
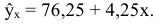
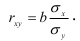
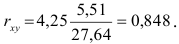
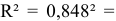
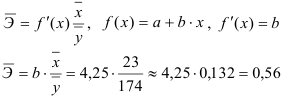
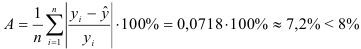
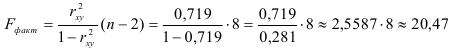

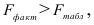
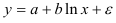 . Предварительно проведем процедуру линеаризации переменных. Для этого сделаем замену
. Предварительно проведем процедуру линеаризации переменных. Для этого сделаем замену 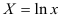 и определим параметры уравнения
и определим параметры уравнения 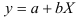 . Вычисления организуем в таблицу 2.2.3:
. Вычисления организуем в таблицу 2.2.3: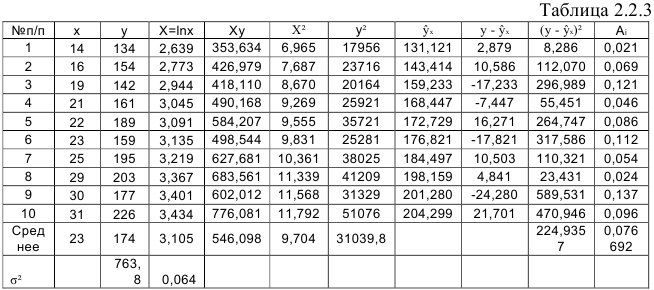
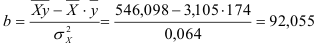
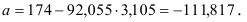
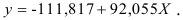
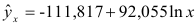
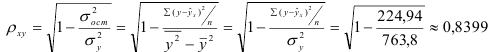
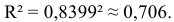
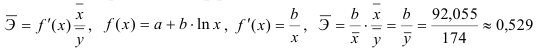
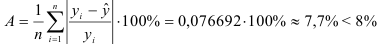
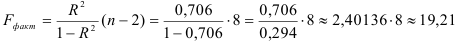
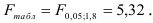
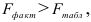
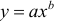 предшествует процедура линеаризации переменных. Проведем линеаризацию путем логарифмирования обеих частей уравнения:
предшествует процедура линеаризации переменных. Проведем линеаризацию путем логарифмирования обеих частей уравнения: 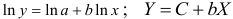 , где
, где 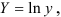
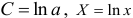 .
.

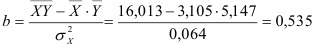
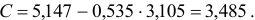
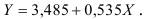
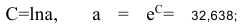
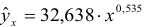
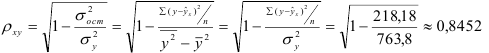
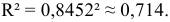
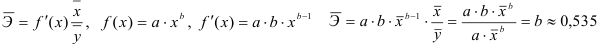
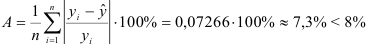
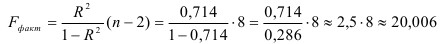
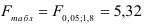
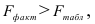
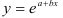 предшествует процедура линеаризации переменных. Проведем линеаризацию путем логарифмирования обеих частей уравнения:
предшествует процедура линеаризации переменных. Проведем линеаризацию путем логарифмирования обеих частей уравнения: 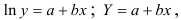 , где
, где 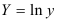 . Для расчетов используем данные таблицы 2.2.5:
. Для расчетов используем данные таблицы 2.2.5: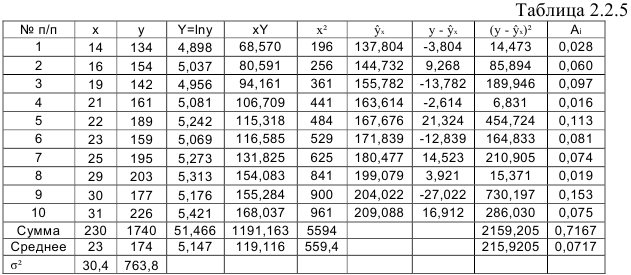
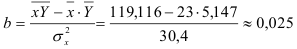
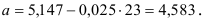
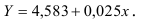
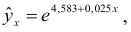
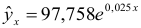
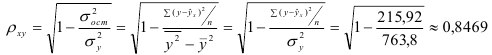
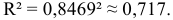
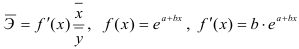
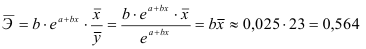
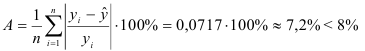
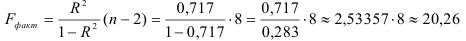
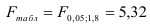
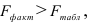
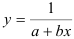 .
.
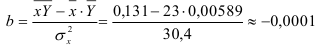
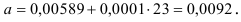
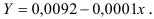
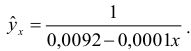
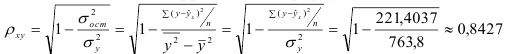
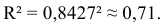
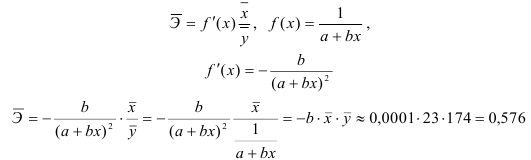
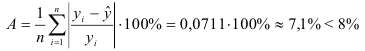
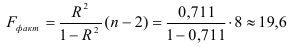
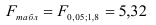
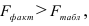
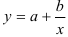 Предварительно проведем процедуру линеаризации переменных. Для этого сделаем замену
Предварительно проведем процедуру линеаризации переменных. Для этого сделаем замену 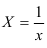 и определим параметры уравнения
и определим параметры уравнения 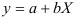 .
.
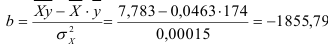
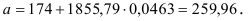
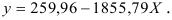
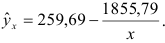
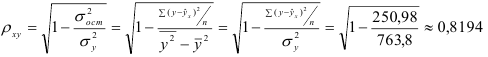
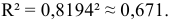
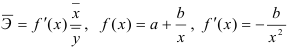
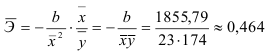
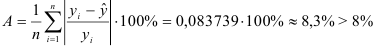
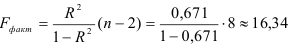
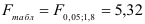
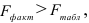
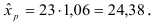
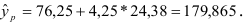
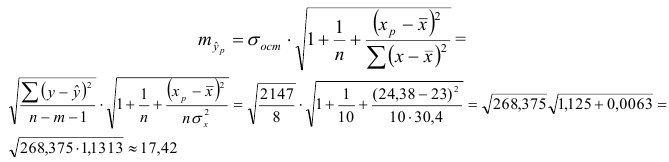
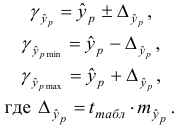
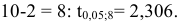
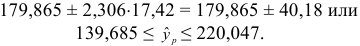
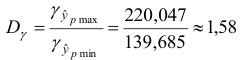

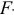 -критерия Фишера оценить статистическую надежность уравнения регрессии.
-критерия Фишера оценить статистическую надежность уравнения регрессии.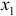 , после фактора
, после фактора 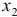 и насколько целесообразно включение в уравнение регрессии фактора
и насколько целесообразно включение в уравнение регрессии фактора 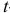 -критерия Стьюдента статистическую значимость коэффициентов при переменных
-критерия Стьюдента статистическую значимость коэффициентов при переменных 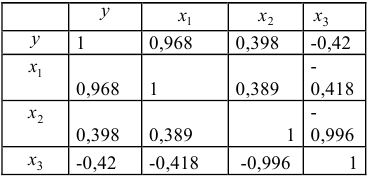
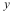 от
от 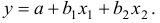
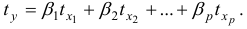
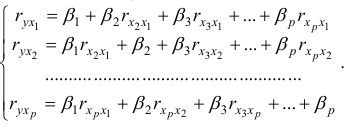
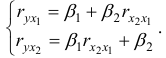
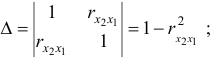

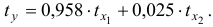
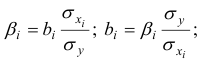
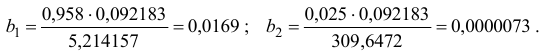
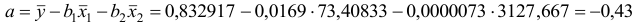
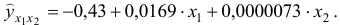
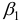 и
и 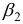 приходим к выводу, что сила влияния
приходим к выводу, что сила влияния 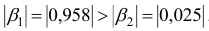
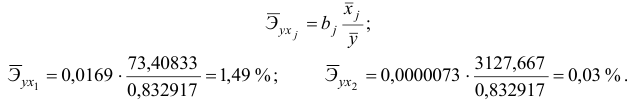
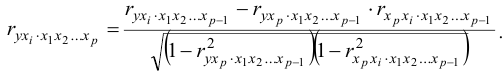
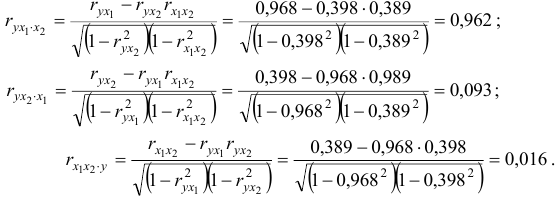
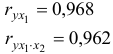
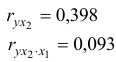
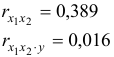
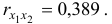
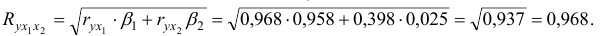
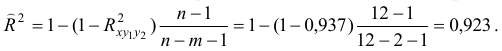
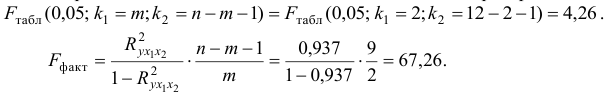
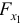 и
и 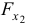 оценивают статистическую значимость присутствия факторов
оценивают статистическую значимость присутствия факторов 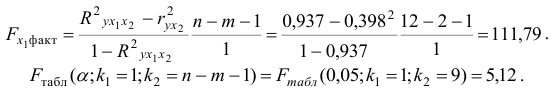
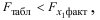
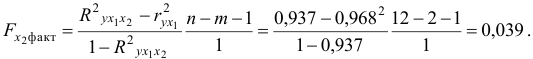
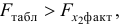
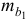 и
и 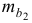 . Расчет значений случайных ошибок достаточно сложен и трудоёмок. Поэтому предлагается расчёт значения
. Расчет значений случайных ошибок достаточно сложен и трудоёмок. Поэтому предлагается расчёт значения 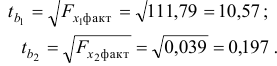
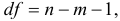
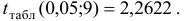
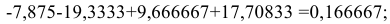
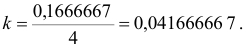
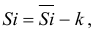
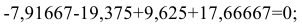

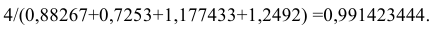
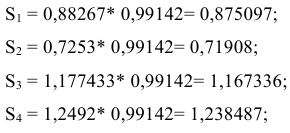
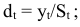
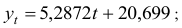
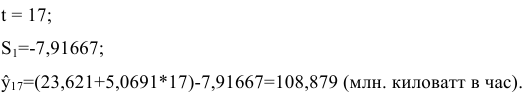
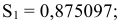
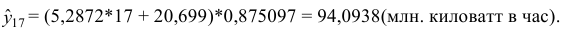

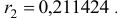
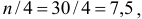

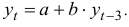
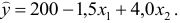

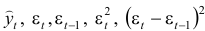 .
.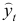 определяется путем подстановки фактических значений
определяется путем подстановки фактических значений 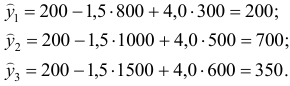
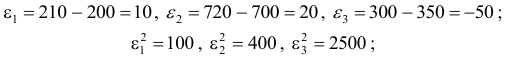
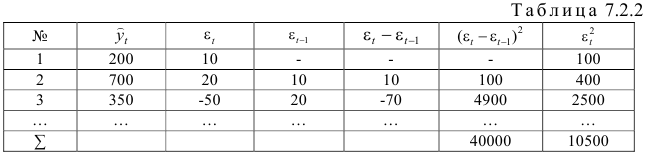
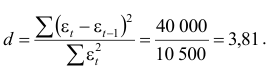
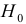 об отсутствии автокорреляции в остатках. Определяем табличное значение статистики Дарбина — Уотеона. При уровне значимости
об отсутствии автокорреляции в остатках. Определяем табличное значение статистики Дарбина — Уотеона. При уровне значимости 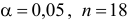 (месяцев) и
(месяцев) и 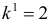 (число факторов) нижнее значение равно
(число факторов) нижнее значение равно 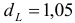 , а верхнее
, а верхнее 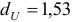 . Чтобы оценить значимость коэффициента автокорреляции вычислим интервалы:
. Чтобы оценить значимость коэффициента автокорреляции вычислим интервалы: