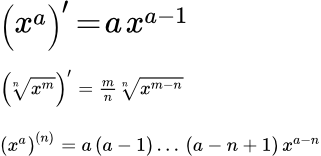Производная со степенью квадратного уравнения

Видео:ПРОИЗВОДНАЯ СТЕПЕННОЙ ФУНКЦИИ решение производных функцийСкачать

Основные формулы

Производная от x в степени a равна a , умноженному на x в степени a минус один:
(1) .

Производная от корня степени n из x в степени m равна:
(2) .

Видео:4. Вычисление производных примеры. Самое начало.Скачать

Вывод формулы производной степенной функции

Случай x > 0

Рассмотрим степенную функцию от переменной x с показателем степени a :
(3) .
Здесь a является произвольным действительным числом. Сначала рассмотрим случай .

Чтобы найти производную функции (3), воспользуемся свойствами степенной функции и преобразуем ее к следующему виду:
.

Вывод формулы производной от корня степени n из x в степени m

Теперь рассмотрим функцию, являющуюся корнем следующего вида:
(4) .

Чтобы найти производную, преобразуем корень к степенной функции:
.
Сравнивая с формулой (3) мы видим, что
.
Тогда
.

На практике нет необходимости запоминать формулу (2). Гораздо удобнее сначала преобразовать корни к степенным функциям, а затем находить их производные, применяя формулу (1) (см. примеры в конце страницы).

Случай x = 0

Если , то степенная функция определена и при значении переменной x = 0 . Найдем производную функции (3) при x = 0 . Для этого воспользуемся определением производной:
.

Подставим x = 0 :
.
При этом под производной мы понимаем правосторонний предел, для которого .

Итак, мы нашли:
.
Отсюда видно, что при , .
При , .
При , .
Этот результат получается и по формуле (1):
(1) .
Поэтому формула (1) справедлива и при x = 0 .

Случай x .
При некоторых значениях постоянной a , она определена и при отрицательных значениях переменной x . А именно, пусть a будет рациональным числом. Тогда его можно представить в виде несократимой дроби:
,
где m и n – целые числа, не имеющие общего делителя.

Если n нечетное, то степенная функция определена и при отрицательных значениях переменной x . Например, при n = 3 и m = 1 мы имеем кубический корень из x :
.
Он определен и при отрицательных значениях переменной x .

Найдем производную степенной функции (3) при и при рациональных значениях постоянной a , для которых она определена. Для этого представим x в следующем виде:
.
Тогда ,
.
Находим производную, вынося постоянную за знак производной и применяя правило дифференцирования сложной функции:

.
Здесь . Но
.
Поскольку , то
.
Тогда
.
То есть формула (1) справедлива и при :
(1) .

Видео:Производная: секретные методы решения. Готовимся к ЕГЭ | Математика TutorOnlineСкачать

Производные высших порядков

Теперь найдем производные высших порядков от степенной функции
(3) .
Производную первого порядка мы уже нашли:
.

Вынося постоянную a за знак производной, находим производную второго порядка:
.
Аналогичным образом находим производные третьего и четвертого порядков:
;

.

Отсюда видно, что производная произвольного n-го порядка имеет следующий вид:
.

Заметим, что если a является натуральным числом, , то n -я производная является постоянной:
.
Тогда все последующие производные равны нулю:
,
при .

Видео:Математика Без Ху!ни. Производная сложной функции.Скачать

Примеры вычисления производных

Пример

Найдите производную функции:
.

Преобразуем корни к степеням:
;
.
Тогда исходная функция приобретает вид:
.

Находим производные степеней:
;
.
Производная постоянной равна нулю:
.

Еще примеры

Найти производные следующих функций, зависящих от переменной x :
Решение > > > Решение > > > Решение > > > Решение > > > Решение > > >

Найти производную шестого порядка следующей функции:
.
Решение > > >

Автор: Олег Одинцов . Опубликовано: 09-04-2017

Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Нахождение производной степенной функции

В данной публикации мы рассмотрим, чему равна производная степенной функций (в т.ч. сложной), а также разберем примеры решения задач для закрепления изложенного материала.

Видео:АЛГЕБРА С НУЛЯ — Что такое Производная?Скачать

Формула производной степенной функции

Для функции f(x) = x n , где n – действительное число, справедливо следующее выражение:

Т.е. производная степенной функции равняется произведению показателя степени на основание в степени, уменьшенной на единицу.

n – может быть как положительным, так и отрицательным числом (в т.ч. дробным):

Производная сложной степенной функции

В сложной функции вместо x представлено более сложное выражение. Производная такой функции определяется по формуле:

Видео:4.2 Производная Примеры для тренировкиСкачать

Примеры задач

Задание 1:
Вычислите производную функцию f(x) = x 3 /5 .

Решение:
Согласно правилам дифференцирования константу в виде дроби можно вынести за знак производной:

Применив формулу производной, рассмотренную выше, получаем:

Задание 2:
Найдите производную функции f(x) = x 2 + √ x – 6 .

Решение:
Первоначальный вид производной функции:
f ‘ (x) = (x 2 + √ x – 6) ‘.

С учетом правила дифференцирования суммы получаем:
f ‘ (x) = (x 2 ) ‘ + (√ x ) ‘ – (6) ‘.

Остается только вычислить производные по отдельности:

(x 2 ) ‘ = 2x 2-1 = 2x

(-6) ‘ = 0 (производная константы равна нулю)

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Пошаговый калькулятор производных онлайн

Ввод распознает различные синонимы функций, как asin , arsin , arcsin

Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)

Список математических функций и констант :

• ln(x) — натуральный логарифм

• sh(x) — гиперболический синус

• ch(x) — гиперболический косинус

• th(x) — гиперболический тангенс

• cth(x) — гиперболический котангенс

• sch(x) — гиперболический секанс

• csch(x) — гиперболический косеканс

• arsh(x) — обратный гиперболический синус

• arch(x) — обратный гиперболический косинус

• arth(x) — обратный гиперболический тангенс

• arcth(x) — обратный гиперболический котангенс

• arsch(x) — обратный гиперболический секанс

• arcsch(x) — обратный гиперболический косеканс

🔍 Видео

Урок 7. Производная степенной функции. Практика. Алгебра 11 классСкачать

ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать

Матан за час. Шпаргалка для первокурсника. Высшая математикаСкачать

Производные степени и корня. Урок 4.2.Скачать

СЛОЖИТЕ ДВА КОРНЯСкачать

5. Производная сложной функции примеры №1.Скачать

Уравнение четвертой степениСкачать

Вычисление производной. Практическая часть. 1ч. 10 класс.Скачать

Вычисление производных. 10 класс.Скачать

Производная сложной функции. 10 класс.Скачать

Производная показательной функции. 11 класс.Скачать

Комплексные корни квадратного уравненияСкачать