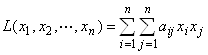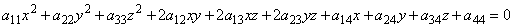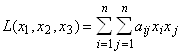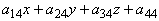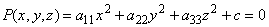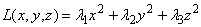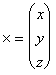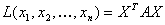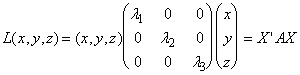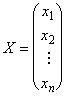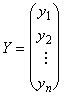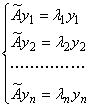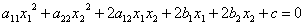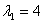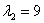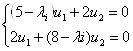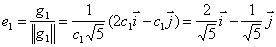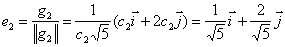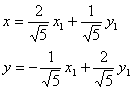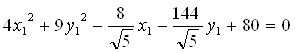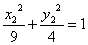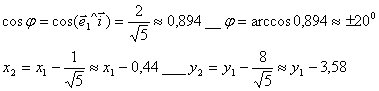Пример №1 . Привести уравнение второго порядка к каноническому виду с помощью поворота и параллельного переноса осей координат. Построить кривую.
Пример №2 . Выполнив последовательно преобразования координат: поворот, а затем параллельный перенос координатных осей, преобразовать к каноническому виду уравнение кривой второго порядка и построить ее в исходной системе координат, а также найти параметры кривой.
Видео:Приведение поверхности второго порядка к каноническому виду ортогональным преобразованием.Скачать

Алгоритм перехода кривой второго порядка к каноническому виду
Пример №1 . 4y=-6-sqrt(4x-x 2 )
sqrt(4x-x 2 ) = -(4y+6)
Возведем в квадрат
4x-x 2 = (4y+6) 2
Раскрывая скобки, получаем:
16y 2 +48y + 36 +x 2 -4x = 0
Далее решается калькулятором. Если самостоятельно решать, то получим:
4x-x 2 = (4y+6) 2
-(x 2 — 4x) = 2(y+3/2) 2
-(x 2 — 4x + 4) = (y+3/2) 2
-(x — 2) 2 = (y+3/2) 2
(y+3/2) 2 + (x — 2) 2 = 0
Пример №2 . x=1-2/3 sqrt(y 2 -4y-5)
Здесь надо сначала привести к нормальному виду.
3/2(x-1)=sqrt(y 2 -4y-5)
Возводим в квадрат
9/4(x-1) 2 =y 2 -4y-5
9/4x 2 -9/4*2x+9/4-y 2 +4y+5=0
9/4x 2 -9/2x-y 2 +4y+29/4=0
Далее можно решать как с калькулятором, так и без него:
9/4(x-1) 2 =y 2 -4y-5
9/4(x-1) 2 =y 2 -4y+4-4-5
9/4(x-1) 2 =(y 2 -2)-9
9/4(x-1) 2 -(y 2 -2) = -9
-1/4(x-1) 2 +1/9(y 2 -2) = 1
Видео:Семинар №9 "Приведение уравнения второго порядка к каноническому виду"Скачать

69. Квадратичные формы и их приведение к каноническому виду
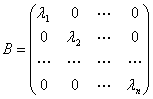
При рассмотрении евклидового пространства мы вводили определение квадратичной формы. С помощью некоторой матрицы
Строится многочлен второго порядка вида
Который называется квадратичной формой, порождаемой квадратной матрицей А.
Квадратичные формы тесно связаны с поверхностями второго порядка в n — мерном евклидовом пространстве. Общее уравнение таких поверхностей в нашем трехмерном евклидовом пространстве в декартовой системе координат имеет вид:
Верхняя строка — это не что иное, как квадратичная форма, если положить x1=x, x2=y, x3=z:

Положим для общности, что многочлен
Есть линейная форма. Тогда общее уравнение поверхности есть сумма квадратичной формы, линейной формы и некоторой постоянной.
Основной задачей теории квадратичных форм является приведение квадратичной формы к максимально простому виду с помощью невырожденного линейного преобразования переменных или, другими словами, замены базиса.
Вспомним, что при изучении поверхностей второго порядка мы приходили к выводу о том, что путем поворота осей координат можно избавиться от слагаемых, содержащих произведение xy, xz, yz или xixj (i¹j). Далее, путем параллельного переноса осей координат можно избавиться от линейных слагаемых и в конечном итоге свести общее уравнение поверхности к виду:
В случае квадратичной формы приведение ее к виду
Называется приведением квадратичной формы к каноническому виду.
Поворот осей координат есть не что иное, как замена одного базиса другим, или, другими словами, линейное преобразование.
Запишем квадратичную форму в матричном виде. Для этого представим ее следующим образом:
L(x, y,z) = x(a11x+a12y+a13z)+
Введем матрицу — столбец
Тогда 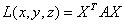
— матричная форма записи квадратичной формы. Эта формула, очевидно, справедлива и в общем случае:
Канонический вид квадратичной формы означает, очевидно, что матрица А имеет диагональный вид:
Рассмотрим некоторое линейное преобразование X = SY, где S — квадратная матрица порядка n, а матрицы — столбцы Х и У есть:
Матрица S называется матрицей линейного преобразования. Отметим попутно, что всякой матрице n-ного порядка при заданном базисе соответствует некоторый линейный оператор.
Линейное преобразование X = SY заменяет переменные x1, x2, x3 новыми переменными y1, y2, y3. Тогда:
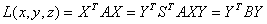
Задача приведения к каноническому виду сводится к отысканию такой матрицы перехода S, чтобы матрица В приобрела диагональный вид:
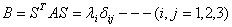
Итак, квадратичная форма с матрицей А после линейного преобразования переменных переходит в квадратичную форму от новых переменных с матрицей В.
Обратимся к линейным операторам. Каждой матрице А при заданном базисе соответствует некоторый линейный оператор А. Этот оператор имеет, очевидно, некоторую систему собственных чисел и собственных векторов. Причем, отметим, что в евклидовом пространстве система собственных векторов будет ортогональна. Мы доказывали на предыдущей лекции, что в базисе собственных векторов матрица линейного оператора имеет диагональный вид. Формула (*), как мы помним, это формула преобразования матрицы линейного оператора при смене базиса. Положим, что собственные вектора линейного оператора А с матрицей А — это вектора у1, y2, . yn.
Т. е.
А это означает, что если собственные вектора у1, y2, . yn взять за базис, то матрица линейного оператора в этом базисе будет диагональной
Или В = S-1 А S, где S – матрица перехода от первоначального базиса <E> к базису <Y>. Причем в ортонормированном базисе матрица S будет ортогональной.
Т. о. для приведения квадратичной формы к каноническому виду необходимо найти собственные числа и собственные векторы линейного оператора А, имеющего в первоначальном базисе матрицу А, которая порождает квадратичную форму, перейти к базису собственных векторов и в новой системе координат построить квадратичную форму.
Обратимся к конкретным примерам. Рассмотрим линии второго порядка.
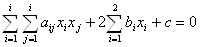
С помощью поворота осей координат и последующего параллельного переноса осей это уравнение можно привести к виду ( переменные и коэффициенты переобозначены х1 = х, х2 = у):
1) 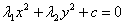
2) 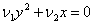
Напомним виды линий второго порядка. Центральные линии:
1) 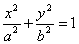
2) 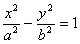
3) 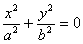
4) 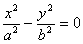
5) х2 = а2 две параллельные линии;
6) х2 = 0 две сливающиеся прямые;
7) у2 = 2рх парабола.
Для нас представляют интерес случаи 1), 2), 7).
Рассмотрим конкретный пример.
Привести к каноническому виду уравнение линии и построить ее:
5х2 + 4ху + 8у2 — 32х — 56у + 80 = 0.
Матрица квадратичной формы есть 
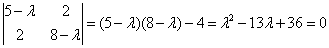
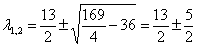
Найдем собственные векторы:
При l1 = 4: 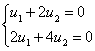
При l2 = 9: 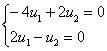
Нормируем эти векторы:
Составим матрицу линейного преобразования или матрицу перехода к базису g1, g2:
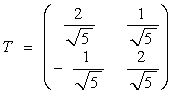
Формулы преобразования координат имеют вид:
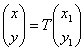
Подставим в наше уравнение линии и получим:
Сделаем параллельный перенос осей координат. Для этого выделим полные квадраты по х1 и у1:
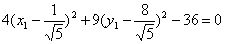
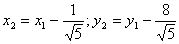
Это эллипс с полуосями 3 и 2. Определим угол поворота осей координат и их сдвиг для того, чтобы построить эллипс в старой системе.
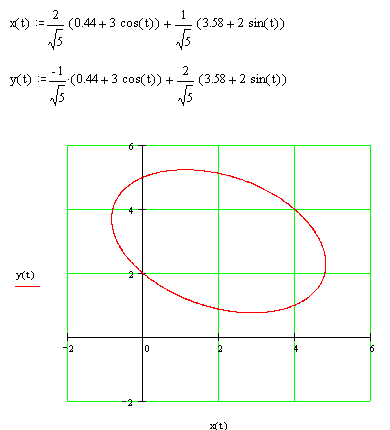
Построим:
Проверка: при х = 0: 8у2 — 56у + 80 = 0 у2 – 7у + 10 = 0. Отсюда у1,2 = 5; 2
При у =0: 5х2 – 32х + 80 = 0 Здесь нет корней, т. е. нет точек пересечения с осью Х!
Видео:§31.1 Приведение уравнения кривой к каноническому видуСкачать

Математический портал
Видео:Приведение ДУ 2 порядка в частных производных к каноническому видуСкачать

Nav view search
Navigation
Search
- Вы здесь:
- Home
- Аналитическая геометрия
- Приведение квадратичной формы к каноническому виду.
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Приведение квадратичной формы к каноническому виду.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Метод собственных векторов:
Рассмотрим квадратичную форму $A(x,x) =sumlimits_^na_x_ix_j$ в евклидовом пространстве $R^n.$ Так как ее матрица $A=(a_ij)$ симметрична, то она может быть представлена в виде $A=UDU^,$ где $D -$ диагональная матрица, на диагонали которой стоят собственные числа матрицы, а $U -$ ортогональная матрица. Столбцы матрицы $U$ являются координатами некоторого ортонормированного базиса $B’=(e_1, . e_n),$ в котором матрица $A$ имеет диагональный вид $D,$ и, следовательно, квадратичная форма — искомый канонический вид. Соответствующие преобразования координат определяются соотношением $$beginx_1\vdots\x_nend=Ubeginx_1’\vdots\x_n’end.$$
Пример.
Найти ортогональное преобразование, приводящее следующие формы к каноническому виду, и написать этот канонический вид:
4.213. $11x_1^2+5x_2^2+2x_3^2+16x_1x_2+4x_1x_3-20x_2x_3.$
Решение.
Матрица квадратичной формы имеет вид $$begin11&8&2\8&5&-10\2&-10&2end.$$
Найдем собственные числа этой матрицы. Для этого запишем характеристическое уравнение:
$$det(A-lambda E)=begin11-lambda&8&2\8&5-lambda&-10\2&-10&2-lambdaend=$$ $$=(11-lambda)(5-lambda)(2-lambda)+2cdot 8cdot (-10)+2cdot 8cdot (-10)-$$ $$-2cdot(5-lambda)cdot 2-(11-lambda)cdot(-10)cdot(-10)-8cdot 8cdot(2-lambda)=$$ $$=-lambda^3+lambda^2(2+5+11)-lambda(10+22+55)+110-160-160-20+$$ $$+4lambda-1100+100lambda-128+64lambda=$$ $$=-lambda^3+18lambda^2+81lambda-1458=-lambda(lambda^2-81)+18(lambda^2-81)=$$ $$=(lambda-9)(lambda+9)(-lambda+18)=0.$$
Отсюда находим собственные числа:
$$lambda_1=9,quad lambda_2=-9, quadlambda_3=18.$$
Далее находим собственные вектора:
Собственный вектор для собственного числа $lambda_1=9$ найдем из системы $$(A-lambda E)X=0, Xneq 0, Rightarrow (A-9E)X=0, Xneq 0$$
Решим однородную систему уравнений:
Вычислим ранг матрицы коэффициентов $A=begin2&8&2\8&-4&-10\2&-10&-7end$ методом окаймляющих миноров:
Фиксируем минор отличный от нуля второго порядка $M_2=begin2&8\8&-4end=-8-64=-72neq 0.$
Таким образом ранг матрицы $A$ равен двум.
Выберем в качестве базисного минор $M=begin2&8\8&-4end=-72neq 0.$ Тогда, полагая $x_3=c,$ получаем: $$left<begin2x_1+8x_2+2c=0\ 8x_1-4x_2-10c=0endright.Rightarrowleft<begin2x_1+8x_2=-2c\8x_1-4x_2=10cendright.$$
По правилу Крамера находим $x_1$ и $x_2:$
Таким образом, общее решение системы $X(c)=beginc\-c/2\cend.$
Из общего решения находим фундаментальную систему решений: $E=X(1)=begin1\-1/2\1end.$
Собственный вектор для собственного числа $lambda_2=-9$ найдем из системы $$(A-lambda E)X=0, Xneq 0, Rightarrow (A+9E)X=0, Xneq 0$$
Решим однородную систему уравнений:
Вычислим ранг матрицы коэффициентов $A=begin20&8&2\8&14&-10\2&-10&11end$ методом окаймляющих миноров:
Фиксируем минор отличный от нуля второго порядка $M_2=begin20&8\8&14end=280-64=216neq 0.$
Таким образом ранг матрицы $A$ равен двум.
Выберем в качестве базисного минор $M=begin20&8\8&14end=216neq 0.$ Тогда, полагая $x_3=c,$ получаем: $$left<begin20x_1+8x_2+2c=0\ 8x_1+14x_2-10c=0endright.Rightarrowleft<begin20x_1+8x_2=-2c\8x_1+14x_2=10cendright.$$
По правилу Крамера находим $x_1$ и $x_2:$
Таким образом, общее решение системы $X(c)=begin-c/2\c\cend.$
Из общего решения находим фундаментальную систему решений: $E=X(1)=begin-1/2\1\1end.$
Собственный вектор для собственного числа $lambda=18$ найдем из системы $$(A-lambda E)X=0, Xneq 0, Rightarrow (A-18E)X=0, Xneq 0$$
Решим однородную систему уравнений:
Вычислим ранг матрицы коэффициентов $A=begin-7&8&2\8&-13&-10\2&-10&-16end$ методом окаймляющих миноров:
Фиксируем минор отличный от нуля второго порядка $M_2=begin-7&8\8&-13end=91-64=27neq 0.$
Таким образом ранг матрицы $A$ равен двум.
Выберем в качестве базисного минор $M=begin-7&8\8&-13end=27neq 0.$ Тогда, полагая $x_3=c,$ получаем: $$left<begin-7x_1+8x_2+2c=0\ 8x_1-13x_2-10c=0endright.Rightarrowleft<begin-7x_1+8x_2=-2c\8x_1-13x_2=10cendright.$$
По правилу Крамера находим $x_1$ и $x_2:$
Таким образом, общее решение системы $X(c)=begin-2c\-2c\cend.$
Из общего решения находим фундаментальную систему решений: $E=X(1)=begin-2\-2\1end.$
Таким образом, мы нашли вектора
В базисе $B’=(e_1′, e_2′, e_3′)$ заданная квадратичная форма имеет вид $$A(x, x)=9x_1^2-9x_2^2+18x_3^2,$$ а соответствующее преобразование координат:
Ответ: $A(x, x)=9x_1^2-9x_2^2+18x_3^2;$
💥 Видео
Приведение кривой второго порядка к каноническому виду. ПримерСкачать

Привести квадратичную форму к каноническому видуСкачать
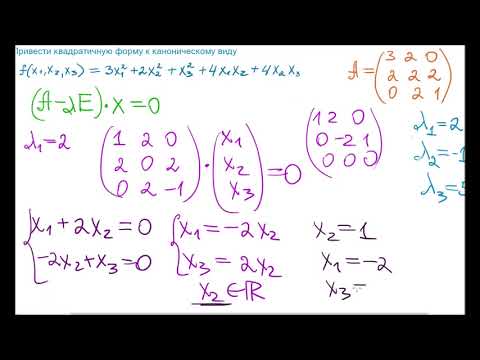
2. Приведение уравнений второго порядка к каноническому видуСкачать

Кривые второго порядка. Эллипс. Приведение к каноническому виду и чертежСкачать

13. Общие уравнения прямой в пространстве / приведение к каноническому видуСкачать

Приведение линейного уравнения в частных производных c постоянными коэфф--ми к каноническому виду.Скачать

Кривые второго порядка. Парабола. Приведение к каноническому виду и чертежСкачать

Приводим уравнение кривой 2 порядка к каноническому видуСкачать

53. Приведение общего уравнения кривой к каноническому видуСкачать

Видеоурок "Приведение к каноническому виду"Скачать

Krikovtseva_2_Привести кривую второго порядка к каноническому виду, построить.Скачать

Семинар 6. Приведение уравнения кривой II порядка к каноническому видуСкачать

Метод Лагранжа. Приведение квадратичной формы к каноническому и нормальному видамСкачать

Поворот и параллельный перенос координатных осей. ЭллипсСкачать
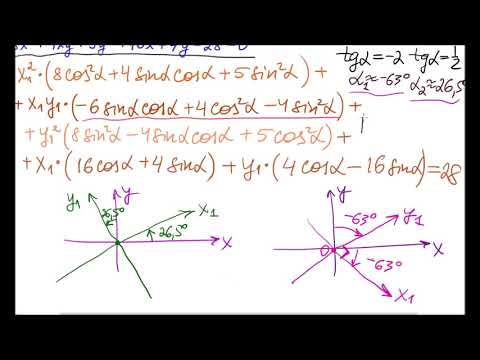
Привести к каноническому виду 2 ой порядокСкачать