Условие
Перевести к каноническому виду прямую
Решение
Найдем [b]две[/b] точки принадлежащие линии пересечения плоскостей
[m]left<begin
x+2y+4z-8=0\6x+3y+2z-18=0 endright.[/m]
Так как точек на прямой бесчисленное множество, то выберем НАПРИМЕР,
такую точку A, у которой координата z=0
и выберем такую точку В, у которой координата y=0
[m]left<beginx+4z-8=0\6x+2z-18=0 endright.[/m] умножаем второе на (-2)
Составить каноническое уравнение прямой, проходящей через точку А с направляющим вектором АВ
См формулу в скрине
Видео:§31.1 Приведение уравнения кривой к каноническому видуСкачать

Приведение кривой второго порядка к каноническому виду
Пример . Дано уравнение кривой 3x 2 +10xy+3y 2 -2x-14y-13=0 в системе координат (0,i,j), где i =(1,0) и j =(0,1).
1. Определить тип кривой.
2. Привести уравнение к каноническому виду и построить кривую в исходной системе координат.
3. Найти соответствующие преобразования координат.
Решение. Приводим квадратичную форму B=3x 2 +10xy+3y 2 к главным осям, то есть к каноническому виду. Матрица этой квадратичной формы 
Характеристическое уравнение: 

Исходное уравнение определяет гиперболу.
Заметим, что вид квадратичной формы неоднозначен. Можно записать 8x1 2 -2y1 2 , однако тип кривой остался тот же – гипербола.
Находим главные оси квадратичной формы, то есть собственные векторы матрицы B. 
Собственный вектор, отвечающий числу λ=-2 при x1=1: x 1=(1,-1).
В качестве единичного собственного вектора принимаем вектор 

Координаты второго собственного вектора, соответствующего второму собственному числу λ=8, находим из системы 
x 2=(1,1); 
Итак, имеем новый ортонормированный базис ( i 1, j 1).
По формулам (5) пункта 4.3.3. переходим к новому базису:

Задание. Привести к каноническому виду уравнение линии 17x 2 + 12xy + 8y 2 — 20 = 0.
Решение.Пример 2
Задание. Привести к каноническому виду уравнение линии второго порядка, используя теорию квадратичных форм и определить её вид. Уравнение кривой второго порядка путем выделения полного квадрата привести к каноническому виду. Решение
Задание. Привести уравнение к каноническому виду: 16x 2 — 9y 2 -64x — 8y +199 = 0.
Решение.Скачать решение
Задание. Установить, что каждое из следующих уравнений определяет гиперболу, и найти координаты ее центра С, полуоси, эксцентриситет, уравнения асимптот и уравнения директрис. Изобразить гиперболу на чертеже, указав фокусы, асимптоты и директрисы.
Решение:Скачать решение
Задание. Установить, что каждое из следующих уравнений определяет эллипс, и найти координаты его центра С, полуоси, эксцентриситет, уравнения директрис. Изобразить эллипс на чертеже, указав оси симметрии, фокусы и директрисы.
Решение:Скачать решение
Видео:Общее уравнение прямой привести к каноническому видуСкачать

Общее уравнение прямой на плоскости
В данной статье мы рассмотрим общее уравнение прямой на плоскости. Приведем примеры построения общего уравнения прямой, если известны две точки этой прямой или если известна одна точка и нормальный вектор этой прямой. Представим методы преобразования уравнения в общем виде в канонический и параметрический виды.
Пусть задана произвольная декартова прямоугольная система координат Oxy. Рассмотрим уравнение первой степени или линейное уравнение:
где A, B, C − некоторые постоянные, причем хотя бы один из элементов A и B отлично от нуля.
Мы покажем, что линейное уравнение на плоскости определяет прямую. Докажем следующую теорему.
Теорема 1. В произвольной декартовой прямоугольной системе координат на плоскости каждая прямая линия может быть задана линейным уравнением. Обратно, каждое линейное уравнение (1) в произвольной декартовой прямоугольной системе координат на плоскости определяет прямую линию.
Доказательство. Достаточно доказать, что прямая L определяется линейным уравнением при какой нибудь одной декартовой прямоугольной системе координат, поскольку тогда она будет определяться линейным уравнением и при любом выборе декартовой прямоугольной системы координат.
Пусть на плоскости задана прямая L. Выберем систему координат так, чтобы ось Ox совпадал с прямой L, а ось Oy был перпендикулярной к ней. Тогда уравнение прямой L примет следующий вид:
Все точки на прямой L будут удовлетворять линейному уравнению (2), а все точки вне этой прямой, не будут удовлетворять уравнению (2). Первая часть теоремы доказана.
Пусть задана декартова прямоугольная система координат и пусть задана линейное уравнение (1), где хотя бы один из элементов A и B отличен от нуля. Найдем геометрическое место точек, координаты которых удовлетворяют уравнению (1). Так как хотя бы один из коэффициентов A и B отличен от нуля, то уравнение (1) имеет хотя бы одно решение M(x0,y0). (Например, при A≠0, точка M0(−C/A, 0) принадлежит данному геометрическому месту точек). Подставляя эти координаты в (1) получим тождество
| Ax0+By0+C=0. | (3) |
Вычтем из (1) тождество (3):
| A(x−x0)+B(y−y0)=0. | (4) |
Очевидно, что уравнение (4) эквивалентно уравнению (1). Поэтому достаточно доказать, что (4) определяет некоторую прямую .
Поскольку мы рассматриваем декартову прямоугольную систему координат, то из равенства (4) следует, что вектор с компонентами <x−x0, y−y0> ортогонален вектору n с координатами <A,B>.
Рассмотрим некоторую прямую L, проходящую через точку M0(x0, y0) и перпендикулярной вектору n (Рис.1). Пусть точка M(x,y) принадлежит прямой L. Тогда вектор 


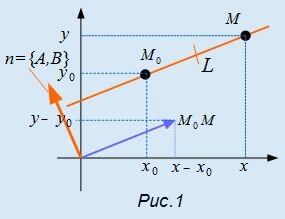 |
Вектор n=<A,B> называется нормальным вектором прямой L.
Замечание 1. Если два общих уравнения прямой
| A1x+B1y+C1=0 | (5) |
| A2x+B2y+C2=0 | (6) |
определяют одну и ту же прямую, то найдется такое число λ, что выпонены равенства
| A2=A1λ, B2=B1λ, C2=C1λ. | (7) |
| (A1λ−A2)x0+(B1λ−B2)x0+(C1λ−C2)=0. | (8) |
Так как выполнены первые два равенства из выражений (7), то C1λ−C2=0. Т.е. C2=C1λ. Замечание доказано.
Заметим, что уравнение (4) определяет уравнение прямой, проходящей через точку M0(x0, y0) и имеющий нормальный вектор n=<A,B>. Поэтому, если известен нормальный вектор прямой и точка, принадлежащая этой прямой, то можно построить общее уравнение прямой с помощью уравнения (4).
Пример 1. Прямая проходит через точку M=(4,−1) и имеет нормальный вектор n=. Построить общее уравнение прямой.
Решение. Имеем: x0=4, y0=−1, A=3, B=5. Для построения общего уравнения прямой, подставим эти значения в уравнение (4):
Упростив получим общее уравнение прямой:
Пример 2. Прямая проходит через точки M1=(−5, 2) и M2=(−2, 3). Построить общее уравнение прямой.
Решение. Вычислим вектор 
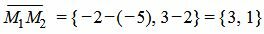 |
Вектор 

Для построения общего уравнения прямой воспользуемся формулой (4). Подставим в (4) координаты точки M1 (можем взять также координаты точки M2) и нормального вектора n:
Упростим полученное уравнение:
Подставляя координаты точек M1 и M2 в (9) можем убедится, что прямая заданная уравнением (9) проходит через эти точки.
Видео:13. Общие уравнения прямой в пространстве / приведение к каноническому видуСкачать

Приведение общего уравнения прямой на плоскости к каноническому виду
Нам нужно привести уравнение (1) к каноническому виду. Для этого найдем некоторую точку M0(x0,y0) на этой прямой. Тогда имеем:
| Ax0+By0+C=0 | (10) |
| A(x−x0)+B(y−y0)=0 | (11) |
Вторую слагаемую уравнения (11) переместим на право и разделим обе части уравнения на −AB:
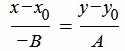 | (12) |
Мы получили каноническое уравнение прямой. Вектор q=<−B, A> является направляющим вектором прямой (12).
Обратное преобразование смотрите здесь.
Пример 3. Прямая на плоскости представлена следующим общим уравнением:
Привести данное уравнение прямой к каноническому виду.
Решение: Найдем некоторую точку на прямой (13). Для этого подставим в (13) y=1 и найдем x. Получим x=2. Запишем уравнение прямой пользуясь формулой (11):
Переместим на право вторую слагаемую и разделим обе части уравнения на 2·5:
 |
 |
Видео:Приводим уравнение кривой 2 порядка к каноническому видуСкачать

Приведение общего уравнения прямой на плоскости к параметрическому виду
В предыдущем параграфе мы привели общее уравнение прямой (1) к каноническому виду (12). Из канонического уравнения легко получить параметрическое уравнение прямой. для этого левый и правый части уравнения (12) обозначим через параметр t. Тогда получим:
 |
Выразив x и y через параметр t, получим параметрическое уравнение прямой:
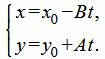 |
Обратное преобразование смотрите здесь.
Пример 4. Прямая на плоскости представлена следующим общим уравнением:
Привести данное уравнение прямой к параметрическому виду.
Решение: Найдем некоторую точку на прямой (13). Для этого подставим в (14) x=3 и найдем y. Получим y=11. Запишем уравнение прямой пользуясь формулой (11):
Переместим на право вторую слагаемую и разделим обе части уравнения на 5·2:
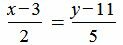 |
Обозначим обе части уравнения через параметр t:
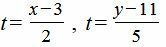 |
Выразим x и y через параметр t:
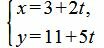 |
Ответ. Параметрическое уравнение прямой имеет следующий вид:
📸 Видео
Видеоурок "Приведение к каноническому виду"Скачать

Семинар №9 "Приведение уравнения второго порядка к каноническому виду"Скачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Каноническое уравнение прямой в пространстве Преход от общего уравненияСкачать

Видеоурок "Общие уравнения прямой"Скачать

2. Приведение уравнений второго порядка к каноническому видуСкачать

Написать канонические и параметрические уравнения прямой в пространствеСкачать

53. Приведение общего уравнения кривой к каноническому видуСкачать

Кривые второго порядка. Эллипс. Приведение к каноническому виду и чертежСкачать

Семинар 6. Приведение уравнения кривой II порядка к каноническому видуСкачать

Приведение ДУ 2 порядка в частных производных к каноническому видуСкачать

Кривые второго порядка. Парабола. Приведение к каноническому виду и чертежСкачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Приведение кривой второго порядка к каноническому виду. ПримерСкачать

Видеоурок "Канонические уравнения прямой"Скачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать


