(по А. И. Чеботареву)
Уравнение водного баланса в общем виде. Метод водного баланса основан на следующем очевидном равенстве: для любого объема пространства, ограниченного некоторой произвольной поверхностью, количество воды, вошедшее внутрь этого объема, за вычетом количества воды, вышедшего наружу, должно равняться увеличению (или соответственно уменьшению) количества ее внутри данного объема. Это равенство справедливо для любого промежутка времени и для любого произвольно взятого пространства, ограниченного замкнутой поверхностью.
Водный баланс речного водосбора отражает важные с точки зрения гидрологии звенья процесса круговорота воды в природе. При анализе воднобалансовых соотношений многие гидрологические явления рассматриваются в их совокупности и взаимодействии.
Пользуясь методом водного баланса, представляется возможным производить сопоставление отдельных источников поступления влаги в различные периоды времени в пределы изучаемой территории и устанавливать степень их влияния на общий ход формирования водного режима изучаемого объекта. На основе взаимной увязки отдельных компоненгов водного баланса можно установить и путем анализа устранить возможные ошибки измерений и оценить точность полученных выводов.
Наконец, метод водного баланса позволяет косвенным путем определить по разности между изученными величинами тот из компонентов баланса влаги (сток, осадки, испарение, фильтрация и т. д.), который в данных условиях трудно измерить, но знание которого бывает необходимо или для решения чисто инженерных задач, или для выяснения общих закономерностей влагооборота к пределах рассматриваемого пространства.
Все это определило весьма широкое распространение этого метода в гидрологии. Исходя из изложенных основных принципиальных положений, составим уравнение водного баланса для произвольно взятой части земной поверхности. Контур, ограничивающий рассматриваемую часть земной поверхности, в общем случае пересекает входящие и выходящие водотоки. Через этот контур мысленно проведем вертикальную поверхность, которая будет являться боковой поверхностью выделяемого объема.
Эту боковую поверхность продолжим до горизонта, ниже которого воды не проникают (например, до водонепроницаемого слоя). Учтем все возможные пути поступления и расходования влаги в рассматриваемом объеме.
Приходную часть баланса влаги в рассматриваемом объеме будут составлять:
1) осадки х, выпавшие за рассматриваемый период времени на поверхность выделенного объема;
2) количество влаги z1, конденсирующейся в почве и на ее поверхности;
3) количество воды w1, поступившей путем подземного притока;
4) количество воды у1, поступившей на данную площадь через поверхностные водотоки (русловой и склоновый сток).
Расходование влаги из рассматриваемого объема может осуществляться следующими путями:
1) испарение z2 с поверхности воды, снега, почвы, растительного покрова и транспирация;
2) отток воды w2 путем подземного стока;
3) стекание воды у2 поверхностными водотоками (русловой и склоновый сток).
Превышение приходной части баланса над расходной будет вызывать увеличение запасов влаги в рассматриваемом объеме.
Наоборот, превышение расходной части баланса над приходной может произойти только за счет уменьшения запасов влаги.
Таким образом, чтобы получить равенство приходной и расходной частей уравнения баланса, нужно в левую (приходную) часть уравнения добавить член u1, характеризующий убыль запасов влаги за рассматриваемый период, а в правую (расходную) часть — член u2, характеризующий прибыль запасов влаги.
Все величины, входящие в уравнение баланса, выразим не в виде объема воды, поступившей в пределы, ограниченные заданным контуром, или, наоборот, вышедшей за пределы контура, а в виде слоя воды, т. е. объема, деленного на площадь рассматриваемой территории.
В соответствии с принятыми обозначениями общее уравнение баланса влаги для произвольного контура и произвольного промежутка времени напишется в виде
Частные случаи уравнения водного баланса. Если рассматривать не произвольный контур, а речной бассейн, для которого можно точно провести линию водораздела, то в этом случае замкнутую линию водосбора будет пересекать только один вытекающий водоток.
В этом случае у1 и y2 следует заменить значением стока через один водоток у, а уравнение (1) после некоторых преобразований можно написать так:
Далее в целях большей компактности вывода будем рассматривать не каждый в отдельности из всех случаев прихода — расхода влаги, а результат совместного действия прямо противоположных факторов (испарение — конденсация, подземный приток — сток через контур, прибыль-убыль запасов воды).
Обозначим в этом случае через z испарение за вычетом конденсации, т. е. z = (z2 — z1), через u — положительное (прибыль) или отрицательное (убыль) изменение запасов влаги в бассейне, например возрастание или убывание снежного покрова, поднятие или опускание уровня грунтовых вод, подъем или падение уровня воды в реках, озерах и т. д. Наконец, через w обозначим положительное (в случае отекания за пределы бассейна) или отрицательное (в обратном случае) значение подземного водообмена данного бассейна с соседним.
Так как х и у всегда положительны, разность z = z2 — z1 почти всегда положительна, ибо конденсация в подавляющем большинстве случаев меньше испарения, а и и w могут иметь и положительные и отрицательные значения, то окончательно самое общее выражение баланса влаги для речного бассейна можно записать в виде:
Относительно члена w необходимо заметить, что эта величина, полученная от деления на площадь водосбора подземного притока (оттока), совершающегося по периметру контура, убывает для подобных фигур с возрастанием их размеров, т. е. при прочих равных условиях член w будет тем меньше, чем больше площадь бассейна. Поэтому, применяя уравнение (3) к бассейну, достаточно большому, можно пренебречь членом w, убывающим с возрастанием площади.
Применительно к этому случаю уравнение (3) напишется в виде:
Теперь рассмотрим не произвольный период времени, а гидрологический год, под которым будем понимать такой годичный период, в течение которого завершается цикл накопления и расходования влаги на поверхности бассейна. В этот цикл необходимо включить весь период накопления снега и весь период снеготаяния и половодья, весь период интенсивных дождей и по возможности весь период стока этих дождевых вод. Очень часто за начало гидрологического года для равнинной части Европейской территории принимают обычно 1 октября. Теоретически начало гидрологического года различное для каждой климатической зоны и даже для каждого года в зависимости от гидрологической и метеорологической обстановки, однако практически это ведет к значительному усложнению расчетов, в большинстве случаев не оправдываемому требованиями практики. Поэтому обработка данных гидрологических и метеорологических наблюдений не в пределах календарного, а в пределах гидрологического года производится главным образом при исследовании специальных вопросов и при научных разработках.
Итак, если применить уравнение баланса (4) к периоду гидрологического года, то член ± u будет означать накопление или расходование подземных вод
Знак у uподз будет меняться с чередованием лет, причем в засушливые годы часть подземных вод будет расходоваться на сток и испарение, а во влажные, наоборот, часть осадков пойдет на пополнение запасов подземных вод. Поэтому применительно к многолетнему периоду, включающему в себя и засушливые и влажные годы, можно написать
Применительно к бессточному бассейну, например к бассейну озера, не имеющего стока (у=0), уравнение баланса для многолетнего периода примет следующий простой вид:
х = z, т. е. для бессточного бассейна осадки за многолетний период равны испарению.
Непосредственное измерение составляющих уравнения водного баланса. Рассмотрим каждый из составляющих членов уравнение баланса влаги речного бассейна в отдельности.
Измерение осадков менее сложное, чем других элементов водного баланса, поэтому распределение их по земной поверхности изучено наиболее подробно. Некоторые важные особенности, относящиеся к измерению осадков, изложены в п. 3.2.
Роль конденсации как дополнительного фактора, способствующего увеличению запасов влаги, обычно невелика по сравнению с общим объемом влаги, учитываемым уравнением водного баланса. Систематические измерения этого элемента не производятся. Поэтому в расчетах при пользовании метеорологическими данными неизбежно допускают некоторую погрешность.
Только в отдельных частных случаях при исследовании баланса сравнительно неболь-ших количеств влаги (например, формирования подземных вод в пустынях) организуют специальные исследования для учета конденсации.
Непосредственное измерение расхода воды на испарение, происходящее с поверхности воды, снега и льда, почвы и растений, а также на транспирацию для достаточно больших водосборов представляет значительные трудности. Обычно оценка этой составляющей водного баланса производится путем расчета, основываясь на зависимостях, рассмотренных в п. 3.3.
Сток у при надлежащей организации работ может быть измерен приемами гидрометрии сравнительно точно. Подземный водообмен через контур w (за счет несовпадения подземного и поверхностного водосборов) обычно не учитывается, во-первых, ввиду его незначительной величины (особенно для больших территорий) по сравнению с остальными составляющими водного баланса, во-вторых, ввиду чрезвычайной сложности его определения.
В отдельных случаях при наличии мощных подземных водотоков (карстовые области), направление которых не совпадает с направлением поверхности стока, ошибка из-за неучета этого члена равенства может оказаться весьма существенной, особенно по отношению к подземному питанию данной реки.
Наконец, рассмотрим последний член уравнения и — изменение запасов влаги в пределах рассматриваемого объема.
Эти запасы слагаются из поверхностных и подземных вод. Увеличение их ведет к повышению уровня водоемов и грунтовых вод, увеличению влажности почво-грунтов, возрастанию мощности снежного покрова и т. д. Уменьшение запасов влаги характеризуется обратными явлениями.
Изменение запасов поверхностных вод может быть учтено с некоторым приближением по данным наблюдений за уровнем озер, рек, прудов, снегомерных съемок и пр.
Вопрос о колебаниях запасов подземных вод и влажности почво-грунтов, будучи связан с характеристиками горных пород, слагающих изучаемую территорию, с колебанием уровня грунтовых вод, скорости и направления их движения и т. д., является сложным и точной количественной оценке для достаточно крупных водосборов не поддается.
Таким образом, из пяти членов, входящих в уравнение водного баланса, только два могут быть измерены непосредственно — осадки х и сток у, а остальные, как правило, определяются приближенно.
Рассмотренные уравнения описывают основные наиболее типичные воднобалансовые соотношения, которые применительно к отдельным, частным ситуациям могут быть записаны в более детальной форме.
Например, можно считать, что общий сток включает поверхностную и подземную составляющие. Изменение запасов влаги в пределах речного водосбора иногда целесообразно представить раздельно в форме изменения запасов, накапливающихся в понижениях рельефа на поверхности водосбора, изменения запасов подземных вод, возникающих в результате их сработки или пополнения за счет фильтрации поверхностных вод, и т. д. Уравнение водного баланса, записываемое с той или иной степенью детализации, иногда называют дифференцированным уравнением водного баланса.
Количество возможных для использования ресурсов поверхностных и подземных вод (приходная часть) и потребности в воде населения и всех отраслей народного хозяйства в пределах какой-либо территории, экономического района или населенного пункта (расходная часть) при неблагоприятном соотношении ресурсов и потребления обычно выражают в форме водохозяйственного баланса.
Таким образом, водный баланс характеризует соотношения, устанавливающиеся между приходом и расходом влаги под влиянием природных процессов (иногда с учетом воздействия хозяйственной деятельности), а водохозяйственный баланс — сложившуюся или проектируемую ситуацию между возобновляемыми в процессе круговорота воды запасами природных (обычно пресных) вод и потребностями в воде народного хозяйства. При этом общий речной сток, являющийся расходным элементом водного баланса, в водохозяйственном балансе выступает как основная его приходная часть.
Видео:Фролова Н. Л. - Гидрология - Лекция 9Скачать

Тепловой баланс водных объектов
Общий вид уравнения теплового баланса. При решении весьма многих гидрологических вопросов широкое применение находят законы сохранения энергии и материн, записанные в форме уравнения теплового баланса, применительно к условиям водных объектов.
Использование уравнения теплового баланса позволяет решать задачи, относящиеся к области расчета нагревания и охлаждения воды в реках и озерах, таяния снега, испарения воды, нарастания льда, и выяснять закономерность развития ряда других важных гидрологических процессов, совершающихся под влиянием теплообмена между водными объектами и окружающей средой, количественным выражением которого и является уравнение теплового баланса.
При составлении уравнения теплового баланса необходимо осуществить учет всех потоков тепла, поглощаемых рассматриваемым водным объектом или расходуемых им через плоскости раздела, ограничивающие его от окружающего пространства. Элементами теплообмена между водным объектом и окружающей средой являются:
Sср — поглощаемая водой (снежным, ледяным покровом) суммарная (прямая и рассеянная) коротковолновая солнечная радиация;
Sиа — поглощаемое водой (снежным, ледяным покровом) встречное длинноволновое излучение атмосферы;
Sив — потери тепла водой (снежным, ледяным покровом) путем длинноволнового излучения;
Sтa — турбулентный обмен тепла с атмосферой путем конвекции, молекулярной и турбулентной теплопроводности (за счет разности температуры воды и воздуха);
Sик — тепло, затрачиваемое на испарение или выделяемое при конденсации;
Sтд — теплообмен с дном;
Sпр — тепло, приносимое водой притоков и источников; на бесприточном участке реки — тепло, поступающее через входной створ участка;
Sст — тепло, выносимое поверхностным и подземным стоком; на бесприточном участке реки — тепло, приносимое через выходной створ участка;
Soc — тепло, поступающее от дождевых осадков или затрачиваемое на таяние снега, выпадающего в водоем;
Sик — тепло, теряемое вместе с испарившейся водой или приходящее вместе с конденсирующимся паром воды;
Sл — тепло, выделяемое при образовании льда или затрачиваемое при его таянии на месте (в пределах данного водоема или в пределах рассматриваемого участка);
Sлп — тепло, затрачиваемое на таяние льда, внесенного на рассматриваемый участок реки или водоем притоками;
Sкэ — тепло, выделяемое при рассеянии кинетической энергии.
Помимо указанных элементов теплообмена, на температуру воды оказывает влияние тепло, выделяющееся при биохимических процессах, тепло, поступающее из недр земли; отраженная от берега и суммарная солнечная радиация и т. п. Существенного влияния эти источники тепла обычно не оказывают и поэтому в тепловом балансе не учитываются. Тепло Sкэ, выделяющееся при движении жидкости за счет сил трения, начинает играть заметную роль лишь при скоростях течения, превышающих 0,4-0,5 м/с, наблюдающихся в реках и сильно проточных озерах и водохранилищах.
Составляющие теплового баланса Scp, Sиа, Sпр и Sкэ всегда положительны; Sив, Sст и Sлп всегда отрицательны; остальные составляющие могут обусловливать как увеличение, так и уменьшение запаса тепла в водной массе. Тепловой поток Sик положителен при конденсации и отрицателен при испарении. Если тепловые потоки Sта и Sтд направлены от водной массы в атмосферу или литосферу, то они будут иметь отрицательный знак, при обратном потоке тепла эти составляющие войдут в уравнение теплового баланса со знаком плюс. При образовании льда тепловой поток Sд положителен, при таянии — отрицателен; значение Soc положительно при дождевых осадках и отрицательно при снеге.
Сопоставляя положительные и отрицательные тепловые потоки, можно найти величину результирующего теплового потока S, характеризующую изменение теплосодержания в рассматриваемом объеме воды за промежуток времени T. При увеличении содержания тепла в озере S положительно, а при уменьшении — отрицательно.
Учитывая изложенное, уравнение теплового баланса для некоторого периода времени T может быть записано в виде
Во многих случаях нет необходимости учитывать все перечисленные составляющие теплового баланса. Так, в теплый период года, а на незамерзающих водных объектах и в течение любого периода нет необходимости учитывать теплоту образования и таяния льда Sл, Sлп. Применительно к условиям бессточных озер отпадает тепловой поток Sст.
Часто можно пренебречь теплом, приносимым притоками (Sпр), дождевыми осадками (Soc) и затрачиваемым на таяние льда (Sлп), приносимого притоками. На глубоких озерах (глубиной более 20 м) можно пренебречь и членом Sтд, так как годовой ход температуры у дна таких озер сильно сглажен и потому теплообмен между водной массой и ложем очень мал. На мелководных озерах, особенно в период ледостава, роль теплообмена с дном возрастает и пренебрегать членом Sтд уже нельзя.
Для периода, когда на водоеме отсутствуют ледовые образования, основную роль в тепловом балансе играет суммарная солнечная радиация Scp, излучение атмосферы Sиа, излучение воды Sив, расход тепла на испарение Sис и турбулентный теплообмен с атмосферой Sта, характеризующие теплообмен водной массы с атмосферой.
При наличии снежно-ледяного покрова и установившегося в его толще теплового режима тепловые потоки, характеризующие теплообмен с атмосферой (Scp, Sиа, Sис, Sта), можно заменить одним потоком Sтлс, выражающим тепловой поток от воды в атмосферу сквозь снежно-ледяную толщу. Допускаемая при такой замене неточность, являющаяся следствием неучета части солнечной радиации, проникающей в воду, становится существенной лишь для условий весны, когда после схода снежного покрова некоторая часть солнечной радиации начинает проникать сквозь лед в воду.
Если уравнение теплового баланса составляется для годового периода, то составляющие Sтд (теплообмен с дном) и Sл (тепло, выделяемое при образовании льда или затрачиваемое при его таянии) в него не войдут, так как в течение года теплоотдача дну компенсируется приходом тепла от него, а тепло, выделяемое при образовании льда, компенсируется затратами тепла при его таянии.
Для периода весеннего снеготаяния уравнение теплового баланса снежного покрова сокращается до вида
В этом случае теплоприход от почвы обычно невелик и им можно пренебречь. Приток тепла за счет жидких осадков также достаточно мал и может не приниматься во внимание. Обычно не учитывается и тепло, расходуемое на изменение температуры снега.
При составлении уравнения теплового баланса все его составляющие должны быть выражены в одинаковых тепловых единицах в виде количества тепла (кал, ккал) или в форме теплового потока, отнесенного к единице поверхности [кал/(см 2 *сут), кал/(см 2 *год)].
Видео:Гриневский С.О. - Гидрогеология. Часть 1 - 2. Круговорот воды на ЗемлеСкачать

Тепловой баланс
Общие положения. Колебания температуры воды в реках и водоемах, нагревание и охлаждение почвы, таяние снега, нарастание и разрушение ледяного покрова — все эти явления связаны с тепловым балансом участков земной поверхности или воды в реках и водоемах. Решая соответствующее уравнение, можно определить интенсивность этих процессов в конкретных условиях.
Уравнение теплового баланса составляется или для некоторого замкнутого объема, например для объема воды на участке реки, как это делается и при расчетах водного баланса, или для поверхности воды, снега, льда. Так, при расчете нарастания льда на водоемах используют уравнение теплового баланса для поверхности воды подо льдом, а при расчете снеготаяния — для самого верхнего слоя снега.
При составлении уравнения теплового баланса включаются все слагаемые, вносящие существенный вклад в баланс данной среды. Некоторые второстепенные элементы не учитываются, если величина их того же порядка, что и погрешность главных слагаемых. Решая уравнение, можно определить неизвестное слагаемое, если известны все остальные. С помощью метода теплового баланса можно вывести также расчетные уравнения, например уравнение для расчета толщины льда на водоемах, как это будет показано в главе о ледовом режиме рек.
Уравнение теплового баланса для участков суши. Используется для определения испарения, таяния снега и ледников.
Для поверхности суши с любым покровом уравнение теплового баланса запишется:
В теплый период, когда на поверхности нет ни снега, ни льда, слагаемое Qc выпадает, но зато F приобретает большое значение, так как происходит нагревание или остывание почвы до значительной глубины. Нагревание наблюдается весной после схода снега и в первой половине лета, а остывание — осенью. Сезонные колебания температуры распространяются до глубины 1 — 1,5 м, а в скальных грунтах — до 3 м.
Зимой, когда поверхность земли покрыта слоем снега, слагаемое Qc ничтожно мало, так как тепло, выделяющееся при замерзании воды в почве, не достигает поверхности снега. Тепловой поток из почвы вообще незначителен и даже при непромерзшей почве не распространяется через толщу снега. Слагаемое F в этом: случае характеризует главным образом изменение количества тепла в самом верхнем слое снега.
Весной, когда снег тает, роль слагаемого Qc резко возрастает. При стаивании 25-30 мм снега в сутки (в пересчете на воду) расходуется 840-1050 Дж (200-250 кал), что составляет около половины суточной суммы прямой солнечной радиации, поступающей к поверхности снега в средних широтах. Слагаемое F по-прежнему мало, так как снег накапливает мало тепла, а теплообмен с почвой при сплошном снежном покрове, как показали исследования П. П. Кузьмина, не превышает ±42 Дж/см 2 (±10 кал/см 2 ) в сутки, что составляет не более 2-3% прихода тепла от радиации.
Уравнение теплового баланса для участка реки. В данном случае рассматривается объем воды на участке реки, ограниченном двумя створами. На участке могут впадать притоки и иметь место поступление грунтовых вод или фильтрация в грунт. Уравнение теплового баланса записывается:
Все слагаемые левой части уравнения выражаются в Дж/см 2 поверхности воды на участке реки и могут быть как положительными, так и отрицательными, за исключением qэ — перехода кинетической энергии в тепловую, которая всегда положительна. Результирующая величина S может иметь как тот, так и другой знак, причем знак плюс означает, что вода приобретает некоторое количество тепла и нагревается, а знак минус — потерю тепла и охлаждение или нарастание льда.
Иногда в уравнении учитывают также поступление тепла с жидкими осадками или его расходование на таяние снега, выпадающего на водную поверхность.
В период открытого русла, когда солнечная радиация и теплообмен с воздухом абсолютно преобладают, qэ и qд иногда пренебрегают за их малостью. Слагаемое qл также выпадает, так как льда на реке нет и таяние его или образование не происходит. В некоторых случаях можно пренебречь и слагаемым mr, когда поступление грунтовых вод или фильтрация речной воды в грунт на участке малы.
При ледоставе картина совершенно меняется. Радиационный баланс воды подо льдом становится очень малым, при этом теплообмен с воздухом также почти прекращается. Зато возрастает роль теплообмена с ложем и поступление тепла с грунтовыми водами, особенно там, где выходы их в русло значительны. Поступление тепла от грунта в зимние месяцы может доходить до 85-125 Дж/см 2 (20-30 кал/см 2 ) в сутки, тогда как в летние месяцы наблюдается расходование тепла приблизительно в тех же размерах. Таким образом, при составлении уравнения баланса применительно к конкретному участку реки и определенному сезону его можно упростить путем исключения малозначащих элементов на основе учета гидрогеологических особенностей местности, фазы водного режима реки и условий погоды.
Видео:Определение водного балансаСкачать

Уравнения водного баланса
Читайте также:
|
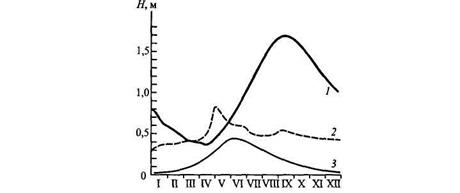
| Рис. 3.23. Типичные графики сезонных колебаний уровня озер Телецкого (1), Плещеева (2), Ладожского (3) (I–XII – месяцы). |
Дата добавления: 2016-02-10 ; просмотров: 2642 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
🎥 Видео
Урок 113 (осн). Задачи на уравнение теплового балансаСкачать

Как посчитать баланс водопотребления и водоотведенияСкачать

Фролова Н. Л. - Гидрология - Лекция 3Скачать

Решение задач на уравнение теплового баланса. Физика 8 классСкачать

Фролова Н. Л. - Гидрология - Лекция 17Скачать

Урок 132. Основные понятия гидродинамики. Уравнение непрерывностиСкачать

Фролова Н. Л. - Гидрология - Лекция 16Скачать

Курс "Основы динамики и гидрогеохимии подземных вод". Часть 1. АннотацияСкачать

Фролова Н. Л. - Гидрология - Лекция 5Скачать

Баланс в УНФ / Самоучитель по 1С:Управление нашей фирмой / АйтонСкачать

Фролова Н. Л. - Гидрология - Лекция 4Скачать

Воды и человек. Водные ресурсы. Видеоурок по географии 8 классСкачать

Вывод уравнения неразрывности - Лекция 1Скачать

Как научиться читать баланс за 12 минут. Что такое баланс из чего он состоит. Актив и пассив балансаСкачать

Происходжение болот, их морфология и типыСкачать

Гидролиз солей и среда водных растворов веществ, Задание 21 | ЕГЭ по химии 2024Скачать





 Эту боковую поверхность продолжим до горизонта, ниже которого воды не проникают (например, до водонепроницаемого слоя). Учтем все возможные пути поступления и расходования влаги в рассматриваемом объеме.
Эту боковую поверхность продолжим до горизонта, ниже которого воды не проникают (например, до водонепроницаемого слоя). Учтем все возможные пути поступления и расходования влаги в рассматриваемом объеме. (2)
(2) , (8)
, (8) — теплота, поступающая к данному объекту извне и выделяющаяся в пределах объекта при переходе части механической энергии в тепловую, а также при ледообразовании, конденсации водяного пара, разложении некоторых веществ;
— теплота, поступающая к данному объекту извне и выделяющаяся в пределах объекта при переходе части механической энергии в тепловую, а также при ледообразовании, конденсации водяного пара, разложении некоторых веществ;  — теплота, удаляемая за пределы объекта, затрачиваемая в пределах объекта на испарение воды, плавление льда, химические и биохимические процессы;
— теплота, удаляемая за пределы объекта, затрачиваемая в пределах объекта на испарение воды, плавление льда, химические и биохимические процессы; 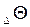 — изменение за время ∆t содержания теплоты в объекте, равное
— изменение за время ∆t содержания теплоты в объекте, равное 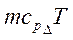 , где т – масса объекта, ср – его удельная теплоемкость при постоянном давлении, ∆Т – изменение температуры Ткон-Тнач.
, где т – масса объекта, ср – его удельная теплоемкость при постоянном давлении, ∆Т – изменение температуры Ткон-Тнач. , (9)
, (9) , где т – масса системы,
, где т – масса системы,  — ее ускорение.
— ее ускорение. , где т – масса выделенного объема,
, где т – масса выделенного объема, 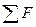 — сумма действующих на этот объем внешних объемных (массовых) и поверхностных сил.
— сумма действующих на этот объем внешних объемных (массовых) и поверхностных сил.
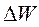 за расчетный период равно
за расчетный период равно 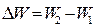 , где
, где 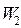 и
и 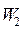 запасы воды в конце и в начале периода (м 3 ).
запасы воды в конце и в начале периода (м 3 ).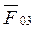 + упр + wnp ) – (уот + wст + 1000 Z
+ упр + wnp ) – (уот + wст + 1000 Z 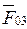 ) =
) = 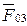 – площадь поверхности озера (км 2 ), средняя за расчетный период. Напомним, что осадки и испарение в уравнении водного баланса выражены в мм слоя воды.
– площадь поверхности озера (км 2 ), средняя за расчетный период. Напомним, что осадки и испарение в уравнении водного баланса выражены в мм слоя воды.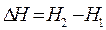 (Н1 и Н2 – уровни воды в конце и в начале периода) по формуле
(Н1 и Н2 – уровни воды в конце и в начале периода) по формуле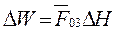 .
.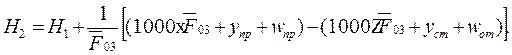 . (3.33)
. (3.33)