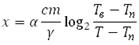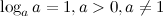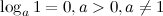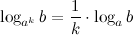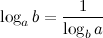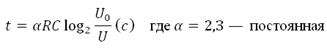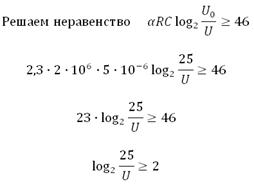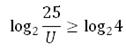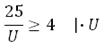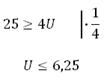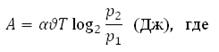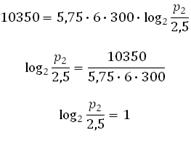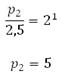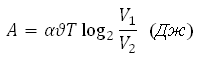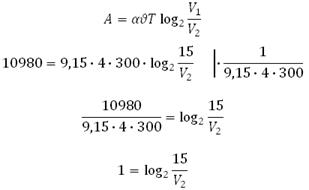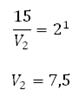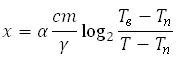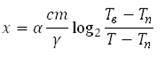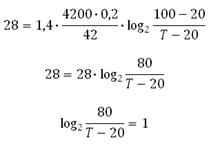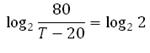Про уравнения - легко » Статьи

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Обновлено
Логарифмы в решении практических задач
Содержание
  1. Презентация к уроку
  2. МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ — Тема: Приближенные вычисления и решения прикладных задач.
  3. Приближенные значения логарифма и решение прикладных задач
  4. Описание презентации по отдельным слайдам:
  5. Краткое описание документа:
  6. Математика: теория и методика преподавания в образовательной организации
  7. Дистанционное обучение как современный формат преподавания
  8. Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
  9. Дистанционные курсы для педагогов
  10. Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
  11. Другие материалы
  12. Вам будут интересны эти курсы:
  13. Оставьте свой комментарий
  14. Автор материала
  15. Дистанционные курсы для педагогов
  16. Подарочные сертификаты
  17. 💡 Видео

Презентация к уроку

Загрузить презентацию (278 кБ)

“Изобретение логарифмов, сократив работу астронома, продлило ему жизнь”.
П.С.Лаплас

Образовательные:

  • Обобщить знания учащихся по теме “Применение логарифмов при решении практических задач”; расширить кругозор, знания о возможном применении логарифма к решению практических задач; показать межпредметные связи; прививать познавательный интерес к математике; повысить мотивацию студентов к обучению.

Развивающие:

  • Развивать математическое мышление, умение применять обобщенные знания, умения и навыки в новых условиях.

Воспитательные:

  • Воспитывать у студентов устойчивый интерес к изучению математики, познавательную активность, математическую культуру речи.

Тип урока: комбинированный урок.

Оборудование: ноутбук, мультимедиа, экран, доска, раздаточный материал, тетрадь, презентация на электронном носителе.

1. Организационный момент.

Организация готовности студентов к работе.

2. Формулирование темы, постановка цели и мотивации к учебной деятельности.

Введение темы урока используя эпиграф; формирование цели урока.

(Презентация, Слайд № 1)

3. Актуализация знаний.

Устная работа: вспомнить определение и свойства логарифма.

(Презентация, Слайд № 2)

4. Всесторонняя проверка знаний.

Выполните задания, записанные на доске.

(Трое студентов работают в качестве консультантов с учениками своего варианта, остальные в тетрадях. Затем, консультанты записывают образцы решения на доске, комментируя их, и, обращая внимание студентов на недочеты в работе).

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений+Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

5. Изучение нового материала.

Преподаватель:

Мы с вами уже знаем, что более 300 лет логарифмы использовались для облегчения вычислений. Но вычисления не исчерпывают роль логарифмов. Использование логарифмов необходимо для описания самых разнообразных процессов роста, происходящих в природе и обществе.

Рассмотрим и решим две задачи, которые связывают понятия разных дисциплин.

К доске вызывается сильный ученик, получивший опережающее домашнее задание — подготовить тему “Измерение количества информации”.

Задача дисциплины “Информатика”

Ученик:

— Информация является важнейшим понятием и основным объектом изучения в информатике. Неудивительно поэтому, что проблема измерения информации имеет фундаментальное значение.

Пусть алфавит, с помощью которого записываются все сообщения, состоит из M символов. Для простоты предположим, что все они появляются в тексте с одинаковой вероятностью.

Тогда в рассматриваемой постановке применима формула Хартли для вычисления количества информации:

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Решить задачу:

Определить информацию, которую несет в себе один символ в кодировках ASCII и Unicode.

1) В алфавите ASCII предусмотрено 256 различных символов, т.е.

M = 256, а I = log2 256 = 8 бит = 1 байт

2) В современной кодировке Unicode заложено гораздо большее количество символов. В ней определено 256 алфавитных страниц по 256 символов в каждой.

I = log2 (256 * 256) = 8 + 8 = 16 бит = 2 байта

(Презентация, Слайды № 3-5)

Задача из дисциплины “Биология”. Решает весь класс под руководством учителя.

В начальный момент времени было 8 бактерий. Через 2 часа после помещения бактерий в питательную среду, их число возросло до 100. Через сколько времени с момента размещения в питательную среду следует ожидать появления 500 бактерий?

Для решения данной задачи, необходимо вспомнить понятия скорости и ускорения.

Было -8

Стало- 100

 Приближенные вычисления и решения прикладных задач решение логарифмических уравнений
1 изменение:

=> Приближенные вычисления и решения прикладных задач решение логарифмических уравненийконечное значение скорости распространения бактерий при первом изменении — Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Было -8

Стало- 500

 Приближенные вычисления и решения прикладных задач решение логарифмических уравнений
2 изменение:

=> Приближенные вычисления и решения прикладных задач решение логарифмических уравненийконечное значение скорости распространения бактерий при втором изменении — Приближенные вычисления и решения прикладных задач решение логарифмических уравнений.

Составим формулу для ускорения, учитывая, что начальная скорость Приближенные вычисления и решения прикладных задач решение логарифмических уравнений(т.е. было -8, стало -8):

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений= Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений= Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Т.к. ускорение постоянно => Приближенные вычисления и решения прикладных задач решение логарифмических уравнений =>

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Перейдем к натуральному основанию логарифмов, для того, чтобы можно было воспользоваться табличными значениями:

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Ответ: приблизительно 3часа 15 минут.

(Презентация, Слайды № 6-9)

6. Рефлексия.

Учащиеся получают карточки для проведения опроса.

Отметьте букву выбранного Вами ответа:

1. Знаете ли вы определение логарифма?

А) да Б) нет В) Приблизительно

2. Знаете ли вы свойства логарифмов?

А) да Б) нет В) Больше половины

3. Умеете ли ВЫ применять определение и свойства логарифмов при вычислениях?

А) да Б) нет В) Не всегда

4. Научились ли вы применять определение и свойства логарифмов при решении практических задач?

А) да Б) нет В) Не всегда

№ вопроса1234
Буква ответа

7. Домашнее задание.

Задача из дисциплины “Физика”.

Для обогрева помещения, температура в котором равна Тп = 20 0 С, через радиатор отопления, пропускают горячую воду температурой Тв = 100 0 С. Расход проходящей через трубу воды m = 0,2 кг/с. Проходя по трубе расстояние x (м), вода охлаждается до температуры Т 0 С, при чём

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

где с = 4200Дж/кг*С — теплоемкость воды

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений= 42 Вт/м * 0 С— коэффициент теплообмена

a = 1,4 — постоянная.

До какой температуры (в градусах Цельсия) охладится вода, если длина трубы 28 м?

8. Итог урока:

Мы с вами завершили тему “Логарифмы”, научились вычислять логарифмы и применять полученные знания в новых условиях, рассмотрели применение логарифмов на практике при решении задач различных дисциплин, узнали какое широкое применение имеют логарифмы в различных областях человеческой деятельности.

А теперь пусть каждый из вас задаст себе вопрос: (Презентация, Слайды № 11). и попробует ответить на него.

Видео:Решение логарифмических уравнений #shortsСкачать

Решение логарифмических уравнений #shorts

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ — Тема: Приближенные вычисления и решения прикладных задач.

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ В СПО

Разработал преподаватель: Игнатьева Елена Сергеевна

Приближенные вычисления и решения прикладных задач.

— применить умения по владению методами доказательств и алгоритмов решения, умение их применять, проводить доказательные рассуждения в ходе решения задач.

1. Рабочая тетрадь в клетку

2. Раздаточные материалы: карточки-задания, инструкционные карты – 20 штук.

3. Калькулятор простой.

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

В начальный момент времени было 8 бактерий. Через 2 часа после помещения бактерий в питательную среду, их число возросло до 100. Через сколько времени с момента размещения в питательную среду следует ожидать появления 500 бактерий?

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Для обогрева помещения, температура в котором равна Тп = 20 0 С, через радиатор отопления, пропускают горячую воду температурой Тв = 100 0 С. Расход проходящей через трубу воды m = 0,2 кг/с. Проходя по трубе расстояние x (м), вода охлаждается до температуры Т 0 С, при чём

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

где с = 4200Дж/кг*С — теплоемкость воды

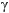
Приближенные вычисления и решения прикладных задач решение логарифмических уравнений= 42 Вт/м * 0 С— коэффициент теплообмена

a = 1,4 — постоянная.

До какой температуры (в градусах Цельсия) охладится вода, если длина трубы 28 м?

1. Внимательно прочитать тему и цель практической работы .

2. Изучить учебный материал по теме.

3. Ответить на вопросы.

4. Выполнить задания.

5. Подготовить отчет.

Пояснения к работе (учебный материал):

1° 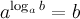Приближенные вычисления и решения прикладных задач решение логарифмических уравнений— основное логарифмическое тождество .

2° Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

3° Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Логарифм единицы по любому положительному, отличному от 1, основанию равен нулю. Это возможно потому, что из любого действительного числа можно получить 1 только возведя его в нулевую степень.

4° 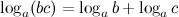Приближенные вычисления и решения прикладных задач решение логарифмических уравнений— логарифм произведения .

Логарифм произведения равен сумме логарифмов сомножителей.

5° 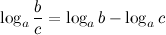Приближенные вычисления и решения прикладных задач решение логарифмических уравнений— логарифм частного .

Логарифм частного (дроби) равен разности логарифмов сомножителей.

6° 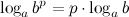Приближенные вычисления и решения прикладных задач решение логарифмических уравнений— логарифм степени .

Логарифм степени равен произведению показателя степени на логарифм ее основания.

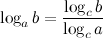
7° Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

8° Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

9° Приближенные вычисления и решения прикладных задач решение логарифмических уравнений— переход к новому основанию.

При выполнении практической работы рассмотрите следующие примеры:

Ёмкость высоковольтного конденсатора в телевизоре C = 5∙10 -6 Ф. Параллельно с конденсатором подключен резистор с сопротивлением R = 2∙10 Ом. Во время работы телевизора напряжение на конденсаторе U0 = 25 кВ. После выключения телевизора напряжение на конденсаторе убывает до значения U (кВ) за время, определяемое выражением:

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Определите (в киловольтах), наибольшее возможное напряжение на конденсаторе, если после выключения телевизора прошло не менее 46 с.

Нам необходимо найти наибольшее возможное U на конденсаторе, при условии, что прошло не менее 46 секунд, то есть t ≥ 46.

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Двойку представим в виде логарифма с основанием 2:

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Знаки логарифмов мы можем снять, так как основания логарифмов в обеих частях равны. Знак неравенства не изменяется, так как основание логарифма больше единицы. Таким образом, далее будем неравенство:

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Напряжение величина положительная, знак неравенства не меняется (при умножении частей неравенства на отрицательное число знак изменяется на противоположный):

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Наибольшее возможное напряжение на конденсаторе 6,25 кВ.

Находящийся в воде водолазный колокол, содержащий υ = 6 моля воздуха при давлении p1 = 2,5 атмосферы, медленно опускают на дно водоема. При этом происходит изотермическое сжатие воздуха. Работа, совершаемая водой при сжатии воздуха, определяется выражением:

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

α = 5,75— постоянная — постоянная

Т = 300К — температура воздуха

p1 (атм) — начальное давление

p2 (атм) — конечное давление воздуха в колоколе.

До какого наибольшего давления p2 можно сжать воздух в колоколе, если при сжатии воздуха совершается работа не более чем 10350 Дж? Ответ приведите в атмосферах.

Сказано, что «совершается работа не более, чем 10350 Дж», то есть максимальная работа, которая совершается при сжатии воздуха это 10350 Дж. Наибольшее давление будет достигнуто именно при максимальной работе, поэтому подставив все известные величины в выражение, решим уравнение и найдём p2:

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Используем понятие основного логарифмического тождества:

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

При заданных условиях воздух можно сжать до 5 атмосфер.

Водолазный колокол, содержащий в начальный момент времени υ = 4 моля воздуха объемом V1 = 15л, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного объёма V2. Работа, совершаемая водой при сжатии воздуха, определяется выражением:

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

где α = 9,15— постоянная

Т = 300К— температура воздуха.

Какой объём V2 (в литрах) станет занимать воздух, если при сжатии газа была совершена работа в 10980 Дж.

В данной задаче необходимо найти V2, подставив все известные значения в формулу:

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

В отличие от уже решённых задач, так можно использовать определение основного логарифмического тождества:

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Воздух станет занимать 7,5 литра.

Для обогрева помещения, температура в котором равна Тп = 20 0 С, через радиатор отопления, пропускают горячую воду температурой Тв = 100 0 С. Расход проходящей через трубу воды m = 0,2 кг/с. Проходя по трубе расстояние x (м), вода охлаждается до температуры Т 0 С, при чём

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

где с = 4200Дж/кг∙С — теплоемкость воды

γ = 42 Вт/м∙ 0 С— коэффициент теплообмена

α = 1,4 — постоянная.

До какой температуры (в градусах Цельсия) охладится вода, если длина трубы 28 м?

В данном случае необходимо решить уравнение:

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Найдём Т, подставив все известные значения:

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Единицу представим в виде логарифма с основанием 1:

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Так как основания логарифмов равны, то равны их подлогарифмические выражения:

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Вода охладится до температуры 60 градусов Цельсия.

Вопросы для закрепления теоретического материала к практическому занятию:

1. Перечислите свойства логарифма?

Название практической работы.

Решение заданий практической работы.

Ответы на вопросы для закрепления теоретического материала.

1. Алимов Ш.А. и др. Алгебра и начала математического анализа: Учебник 10—11 классы. — М.И., 2016.

2. Атанасян Л.С., Бутузов В. Ф., Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа. Геометрия. Геометрия (базовый и углубленный уровни). 10—11 классы. — М., 2016.

3. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: учебник для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

4. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Сборник задач профильной направленности: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

5. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Задачник: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

6. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Электронный учеб.- метод. комплекс для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

7. Башмаков М.И. Математика: Учебник. — М., 2016.

Видео:Решение логарифмических уравнений. Вебинар | МатематикаСкачать

Решение логарифмических уравнений. Вебинар | Математика

Приближенные значения логарифма и решение прикладных задач

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 300 дидактических материалов для школьного и домашнего обучения

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Описание презентации по отдельным слайдам:

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Приближенные вычисления и решение прикладных задач

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Краткое описание документа:

Приближенные вычисления и решение прикладных задач

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

  • Сейчас обучается 692 человека из 75 регионов

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

  • Сейчас обучается 862 человека из 78 регионов

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Курс повышения квалификации

Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС

  • Сейчас обучается 48 человек из 20 регионов

«Мотивация здорового образа жизни. Организация секций»

Свидетельство и скидка на обучение каждому участнику

  • Для всех учеников 1-11 классов
    и дошкольников
  • Интересные задания
    по 16 предметам

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

«Как закрыть гештальт: практики и упражнения»

Свидетельство и скидка на обучение каждому участнику

Видео:ЕГЭ база #7 / Логарифмические уравнения / Свойства, определение логарифма / решу егэСкачать

ЕГЭ база #7 / Логарифмические уравнения / Свойства, определение логарифма / решу егэ

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 843 021 материал в базе

Ищем педагогов в команду «Инфоурок»

Другие материалы

  • 23.11.2017
  • 580
  • 0

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

  • 23.11.2017
  • 402
  • 0

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

  • 23.11.2017
  • 367
  • 3
  • 23.11.2017
  • 612
  • 5
  • 23.11.2017
  • 360
  • 1

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

  • 23.11.2017
  • 4365
  • 69
  • 23.11.2017
  • 405
  • 3

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

  • 23.11.2017
  • 639
  • 3

«Учись, играя: эффективное обучение иностранным языкам дошкольников»

Свидетельство и скидка на обучение
каждому участнику

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

  • 23.11.2017 984
  • PPTX 1.1 мбайт
  • 10 скачиваний
  • Оцените материал:

Настоящий материал опубликован пользователем Усенко Ольга Александровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

  • На сайте: 9 лет
  • Подписчики: 0
  • Всего просмотров: 80639
  • Всего материалов: 46

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:✓ Как решать логарифмические уравнения и неравенства, не помня свойства логарифмов | Борис ТрушинСкачать

✓ Как решать логарифмические уравнения и неравенства, не помня свойства логарифмов | Борис Трушин

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Госдума рассматривает проект о регулировании «продленок» в школах

Время чтения: 1 минута

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Минпросвещения рекомендует школьникам сдавать телефоны перед входом в школу

Время чтения: 1 минута

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Российские школьники начнут изучать историю с первого класса

Время чтения: 1 минута

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Вузы РФ не будут повышать стоимость обучения на первом курсе

Время чтения: 1 минута

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

С 1 сентября в российских школах будут исполнять гимн России

Время чтения: 1 минута

Приближенные вычисления и решения прикладных задач решение логарифмических уравнений

Онлайн-конференция о профессиональном имидже педагога

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

💡 Видео

Логарифмы с нуля за 20 МИНУТ! Introduction to logarithms.Скачать

Логарифмы с нуля за 20 МИНУТ! Introduction to logarithms.

Проще простого! Как решить Логарифмическое Уравнение?Скачать

Проще простого! Как решить Логарифмическое Уравнение?

Круговорот воды в природе ➜ Решение логарифмических уравнений из ЕГЭ #ShortsСкачать

Круговорот воды в природе ➜ Решение логарифмических уравнений из ЕГЭ #Shorts

ЕГЭ 2022: Логарифмическое уравнение с разным основанием | Задание №1Скачать

ЕГЭ 2022: Логарифмическое уравнение с разным основанием | Задание №1

Логарифмическое уравнение / Как решить?Скачать

Логарифмическое уравнение / Как решить?

11 класс, 17 урок, Логарифмические уравненияСкачать

11 класс, 17 урок, Логарифмические уравнения

Логарифмические уравнения. Видеоурок 18. Алгебра 10 классСкачать

Логарифмические уравнения. Видеоурок 18. Алгебра 10 класс

Интересная задача на логарифмы в ЕГЭСкачать

Интересная задача на логарифмы в ЕГЭ

ЛОГАРИФМЫ | решение логарифмов | ЕГЭ по математикеСкачать

ЛОГАРИФМЫ | решение логарифмов | ЕГЭ по математике

Логарифмические уравнения. 11 класс.Скачать

Логарифмические уравнения. 11 класс.

Логарифм с нуля до уровня про. Уравнения, неравенства и параметр. Профильный ЕГЭСкачать

Логарифм с нуля до уровня про. Уравнения, неравенства и параметр. Профильный ЕГЭ

Все типы логарифмических уравнений №13 | Математика ЕГЭ для 10 класса | УмскулСкачать

Все типы логарифмических уравнений №13 | Математика ЕГЭ для 10 класса | Умскул

84 людей этого не знают! Секретный способ решения Логарифмических УравненийСкачать

84 людей этого не знают! Секретный способ решения Логарифмических Уравнений

Алгебра. 11 класс. Решение логарифмических уравнений .Скачать

Алгебра. 11 класс. Решение логарифмических уравнений .

Логарифмические уравнения 🥷🏿Скачать

Логарифмические уравнения 🥷🏿
Поделиться или сохранить к себе: